深海结构物比如载人潜水器其工作环境是深海,需要承受巨大的海水压力,其耐压壳所受的主应力为压应力,这与常规船舶和海洋平台所受的拉应力和弯曲应力有着很大的不同。就传统观点而言,压缩载荷下裂纹不会发生扩展的,只有拉伸应力范围下的有效应力强度因子
疲劳裂纹扩展速率曲线和裂纹尖端应力强度因子是疲劳裂纹扩展寿命预报的2个关键因素。若两者确定下来,则可以采用cycle by cycle循环积分的方法计算得到结构从初始裂纹尺寸到临界裂纹尺寸的的疲劳裂纹扩展寿命。
1.1 改进的McEvily疲劳裂纹扩展模型崔维成[7]通过将固定斜率改为变斜率、引入虚拟强度代替屈服强度、将疲劳扩展的3个区域统一等多处改进发展了McEvily模型,提出一种统一疲劳裂纹扩展速率模型,称为改进的McEvily模型,其表达式如下:
| $\frac{{{\rm{d}}a}}{{{\rm{d}}N}} = \frac{{A{{\left[ {{K_{\max }} \cdot \left( {1 - {f_{{\rm{op}}}}} \right) - \Delta {K_{{\rm{effth}}}}} \right]}^m}}}{{1 - {{\left( {{K_{\max }}/{K_C}} \right)}^n}}}{\text{。}}$ | (1) |
其中:
| $\left\{ \begin{array}{l}{K_{\max }} = \sqrt {{\text{π}} {r_e}\left( {{\rm Sec}\displaystyle\frac{{{\text{π}} \left| {{\sigma _{\max }}} \right|}}{{2{\sigma _{\rm{V}}}}} + 1} \right)} \left[ {1 + Y\left( a \right)\sqrt {\displaystyle\frac{a}{{2{r_e}}}} } \right]{\sigma _{\max }},\\{K_{\min }} = \sqrt {{\text{π}} {r_e}\left( {{\rm Sec}\displaystyle\frac{{{\text{π}} \left| {{\sigma _{\min }}} \right|}}{{2{\sigma _{\rm{V}}}}} + 1} \right)} \left[ {1 + Y\left( a \right)\sqrt {\displaystyle\frac{a}{{2{r_e}}}} } \right]{\sigma _{\min }},\\\Delta K = {K_{\max }} - {K_{\min{\text{。}} }}\end{array} \right.$ |
| ${f_{{\rm{op}}}} = \left\{ \begin{array}{l}\max \left\{ {R,{A_0} + {A_1}R + {A_2}{R^2} + {A_2}{R^3}} \right\},\;\;\;\;0 \leqslant R < 1,\\{A_0} + {A_1}R,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - 2 \leqslant R < 0{\text{。}}\end{array} \right.$ |
| $\left\{ \begin{array}{l}{A_0} = \left( {0.825 - 0.34\alpha ' + 0.05{{\alpha '}^2}} \right) \cdot {\left[ {\cos \left( {{\text{π}} {\sigma _{\max }}/2{\sigma _{{\rm{fl}}}}} \right)} \right]^{1/\alpha '}},\\{A_1} = \left( {0.415 - 0.071\alpha '} \right) \cdot {\sigma _{\max }}/{\sigma _{{\rm{fl}}}},\\{A_2} = 1 - {A_0} - {A_1} - {A_3},\\{A_3} = 2{A_0} + {A_1} - 1,\\{\sigma _{{\rm{fl}}}} = \left( {{\sigma _Y} + {\sigma _u}} \right)/2,\\\alpha ' = \displaystyle\frac{1}{{1 - 2v}} + \displaystyle\frac{{1 - \frac{1}{{1 - 2v}}}}{{{{\left[ {1 + 0.886\ 1 \cdot {{\left( {t/{{\left( {{K_{\max }}/{\sigma _{\rm{Y}}}} \right)}^2}} \right)}^{3.2251}}} \right]}^{0.75952}}}}{\text{。}}\end{array} \right.$ |
| $\left\{\!\!\! \begin{array}{l}{K_C} = \left[ {\displaystyle\frac{{{{\left( {1 - 2v} \right)}^2} - \sqrt {1 - {v^2}} }}{{{{\left( {1 - 2v} \right)}^2} - 1}} \cdot \frac{{{\text{π}} \cdot \lambda }}{{{{\left( {1 - 2v} \right)}^2}}} + \frac{{\sqrt {1 - {v^2}} - 1}}{{{{\left( {1 - 2v} \right)}^2} - 1}}} \right] \cdot {K_{{\rm{IC}}}},\\\lambda = \displaystyle\frac{{{{\left( {1 - 1.65v} \right)}^2}}}{5} - \frac{1}{{20n'}}{\left[ {{{\left( {1 - 1.65v} \right)}^2}} \right]^{\frac{1}{{n'}}}} +\\ \displaystyle\frac{{\frac{1}{{\text{π}} } - \frac{1}{{2.2n'}}{{\left( {\frac{1}{{\text{π}} }} \right)}^{\frac{1}{{n'}}}} - \left[ {\frac{{{{\left( {1 - 1.65v} \right)}^2}}}{5} - \frac{1}{{20n'}}{{\left( {{{\left( {1 - 1.65v} \right)}^2}} \right)}^{\frac{1}{{n'}}}}} \right]}}{{{{\left[ {1 + \frac{{t/{{\left( {{K_{\max }}/{\sigma _Y}} \right)}^2}}}{{1 + 1/n'}}} \right]}^{1.6 + 1/n'}}}}{\text{。}}\end{array} \right.$ |
| $\frac{{{\sigma _v}}}{{{\sigma _u}}} = \frac{{\text{π}} }{2} \cdot \frac{1}{{{{\cos }^{ - 1}}\left( {\frac{1}{{{\beta ^2} - 1}}} \right)}},\beta = \frac{{{K_{_C}}}}{{{\sigma _u}\sqrt {{\text{π}} {r_e}\left( {1 + \frac{{Y\left( {{r_e}} \right)}}{{\sqrt 2 }}} \right)} }} > \sqrt 2 {\text{。}}$ |
式中:
基于上述模型已经开展了很多研究工作,比如考虑载荷次序的影响、循环压缩载荷的影响等。但在纯粹的压缩循环载荷作用下,应力比
裂纹尖端附近的残余应力可以采用弹塑性有限元分析获得,本文通过多载荷步结合节点释放分析技术,在循环压缩应力达到最小值时得到对应的残余应力,再通过下式计算其线性应力强度因子[11]。
| ${K_{res}}\left( {linear} \right) = 2\sqrt {a/{\text{π}}} \int_0^a {\frac{{{\sigma _{res}}\left( x \right)}}{{\sqrt {{a^2} - {x^2}} }}} {\text{。}}$ | (2) |
式(2)计算的应力强度因子是线性的,按照式(3)和式(4)将其转换成改进McEvily模型中的非线性应力强度因子。
| ${\bar \sigma _{res}} = {K_{res}}\left( {linear} \right)/\left[ {Y\left( a \right)\sqrt {{\text{π}}a} } \right],$ | (3) |
| ${K_{res}} = \sqrt {{\text{π}} {r_e}\left( {{\rm Sec}\frac{{\text{π}} }{2}\frac{{{{\bar \sigma }_{res}}}}{{{\sigma _v}}} + 1} \right)} \left( {1 + Y\left( a \right)\sqrt {\frac{a}{{2{r_e}}}} } \right){\bar \sigma _{res}}{\text{。}}$ | (4) |
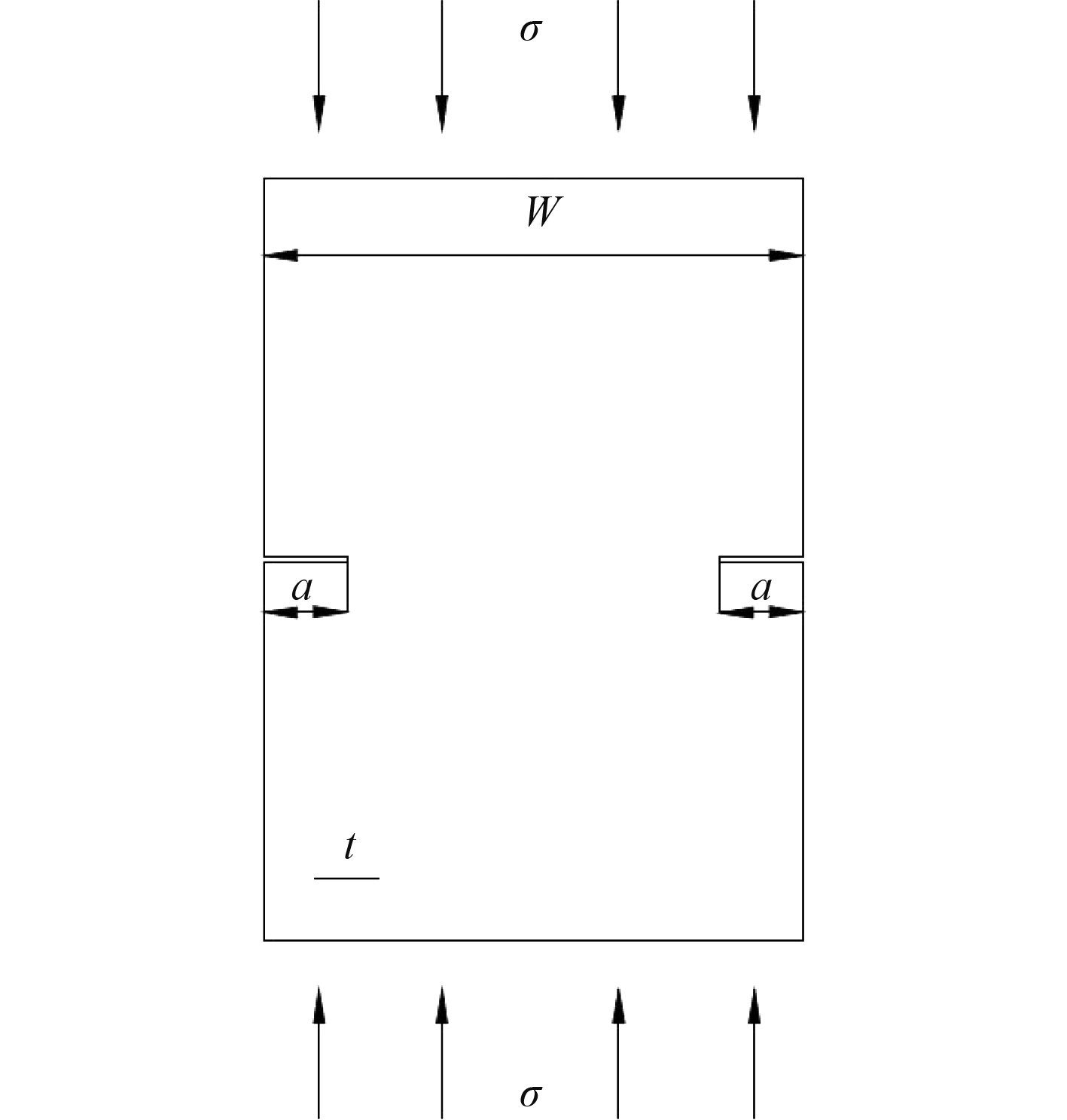
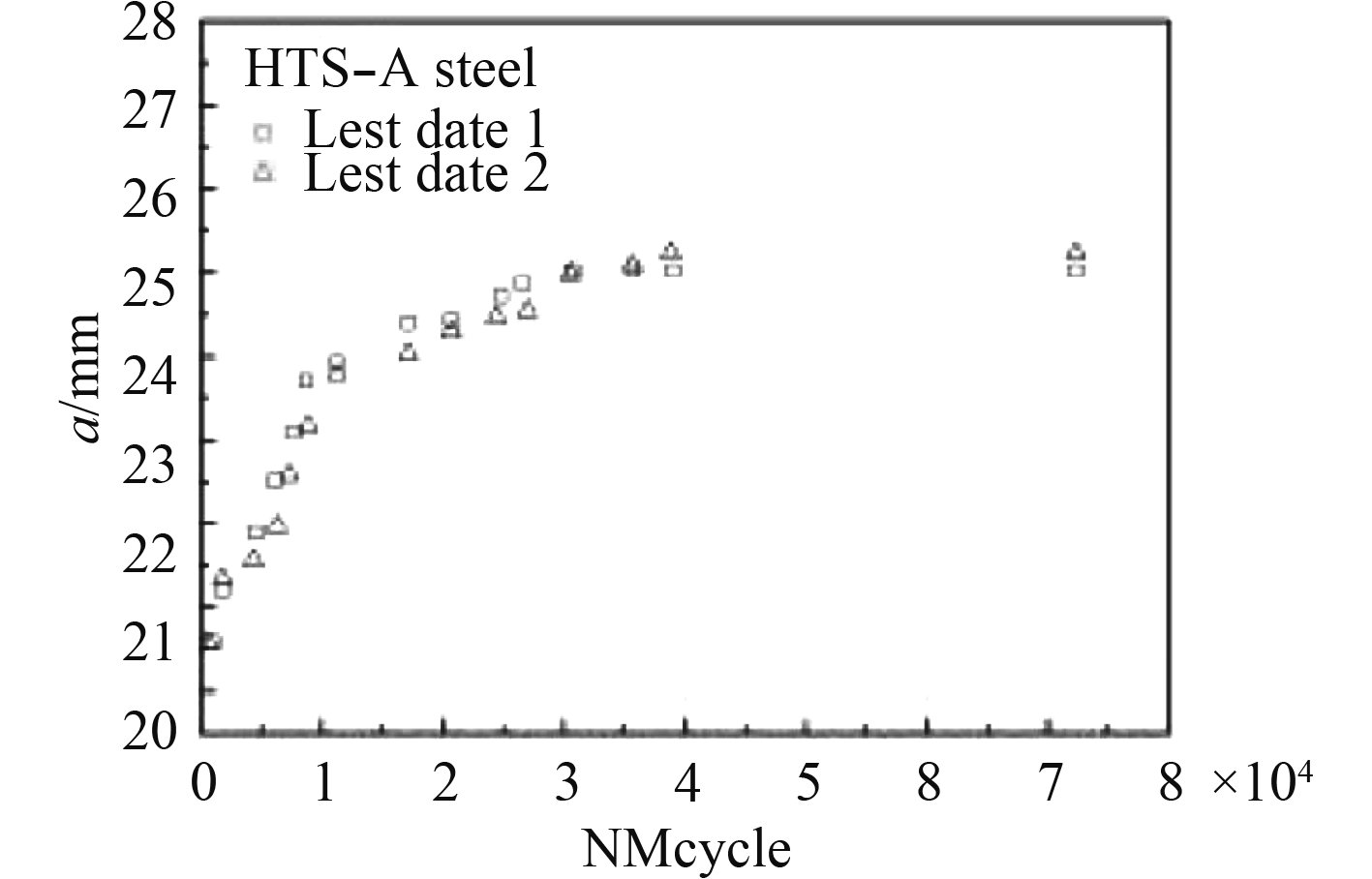
黄小平[6]通过MTS 810材料试验系统开展了循环压缩载荷下的疲劳裂纹扩展试验,所选用的材料为深潜器上广泛使用的HTS-A高拉伸应力钢材,试件采用双边初始裂纹形式,加载环境和试件外形如图1所示,具体几何尺寸和加载工况如表1所示,试验所得裂纹扩展速率曲线如图2所示。
|
图 1 加载环境和试件外形 Fig. 1 Loading environment and specimen shape |
|
|
表 1 试件几何尺寸和加载工况 Tab.1 Specimen geometry and loading conditions |
|
图 2 裂纹扩展速率曲线 Fig. 2 Crack growth rate curve |
罗广恩与崔维成[12]提出了在不同应力比下的ANN方法来预报裂纹扩展速率。分别用
现采用此方法计算应力比
| $\frac{{{\rm{d}}a}}{{{\rm{d}}N}} = \frac{{1.513 \times {{10}^{ - 11}} \cdot {{\left[ {{K_{\max }} \cdot (1 - {f_{{\rm{op}}}}) - 2.83} \right]}^{2.791}}}}{{1 - {{({K_{\max }}/150)}^6}}}{\text{。}}$ | (5) |
根据之前的论述,改进的McEvily公式扩展速率公式在循环压缩载荷作用下又可改进为下式:
| $\frac{{{\rm{d}}a}}{{{\rm{d}}N}} = \frac{{1.513 \times {{10}^{ - 11}} \cdot {{\left[ {{K_{\max }} \cdot (1 - 0) - 0} \right]}^{2.791}}}}{{1 - {{({K_{\max }}/150)}^6}}}{\text{。}}$ | (6) |
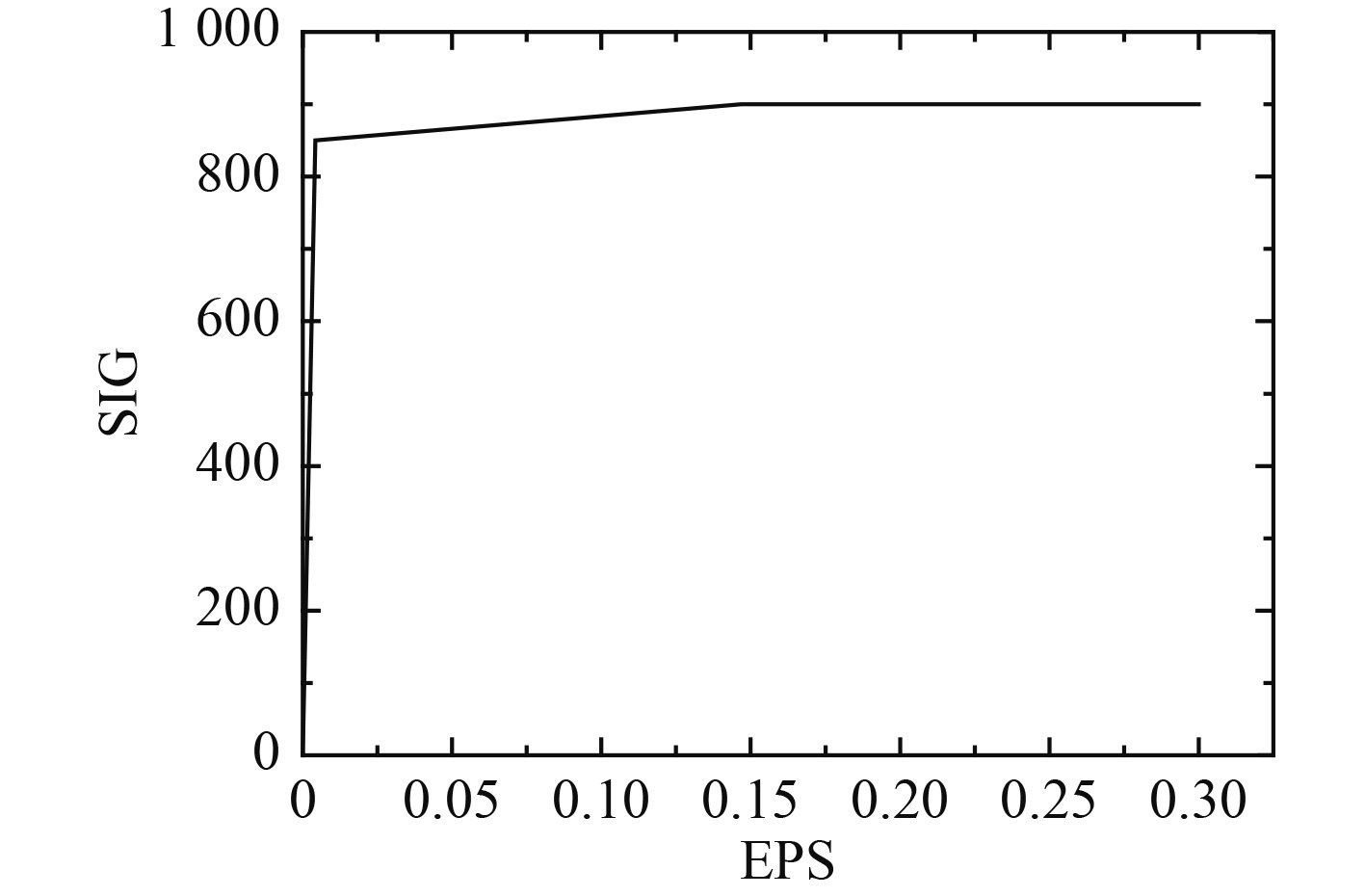
裂纹尖端的残余应力主要通过Ansys弹塑性有限元分析来得到,通过设置其双线性随动硬化材料模型来定义其材料参数,具体材料应力应变曲线如图3所示。
|
图 3 材料应力应变曲线 Fig. 3 Stress-strain curves of materials |
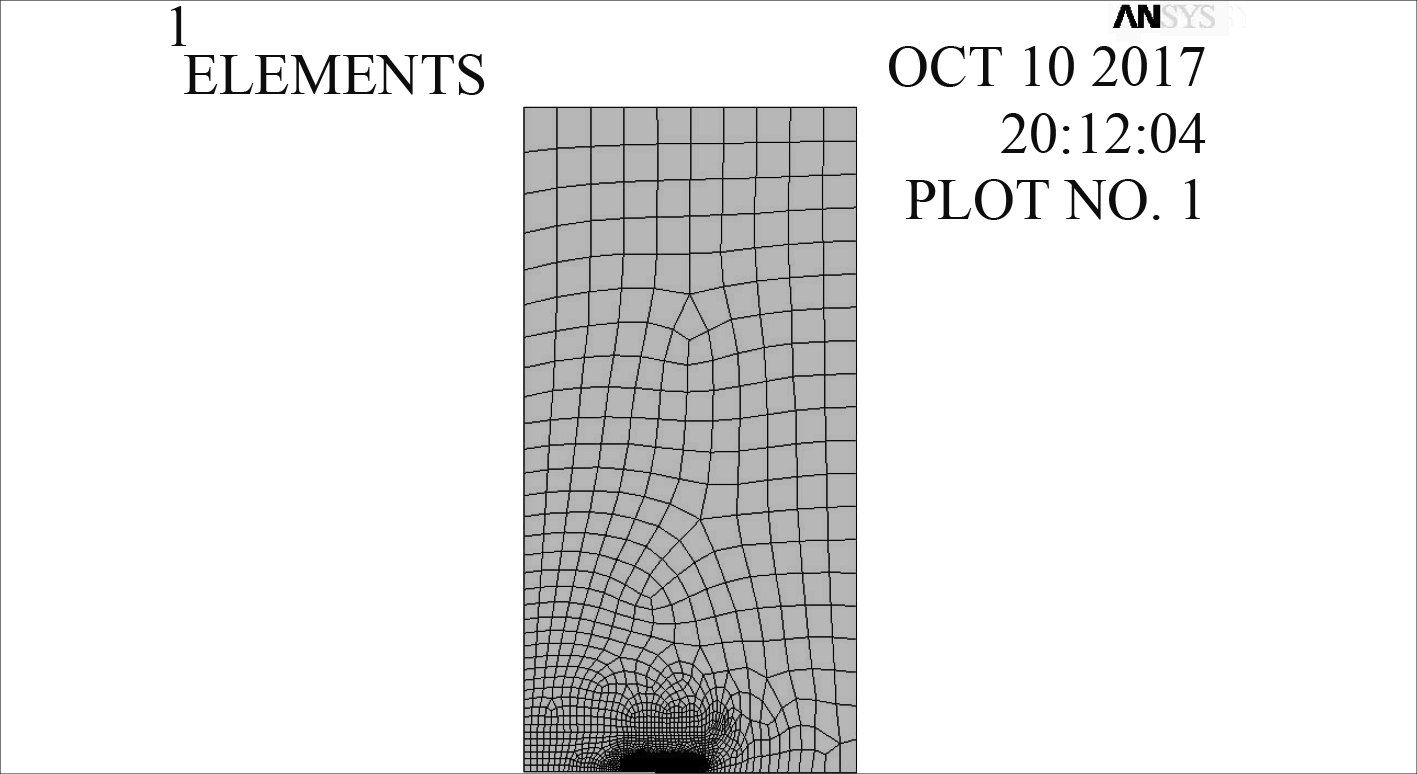
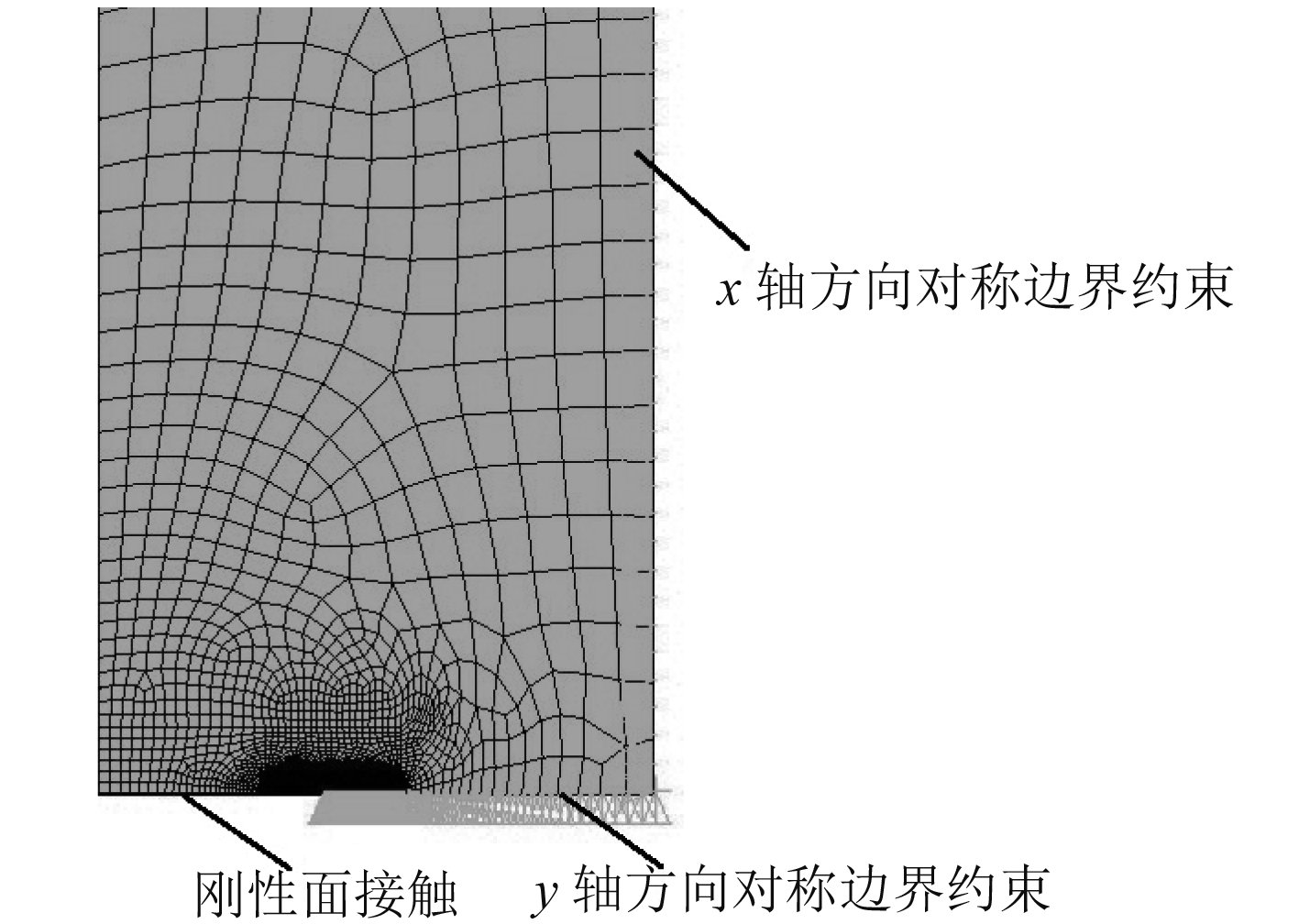
由于试件几何对称,建立1/4模型,如图4所示。裂纹面处设置刚性面来模拟由循环压缩载荷所带来裂纹的闭合效应,并定义对称约束条件,如图5所示。
|
图 4 试件有限元网格划分 Fig. 4 Finite element mesh generation of specime |
|
图 5 接触面定义及边界条件 Fig. 5 Contact surface and boundary condition |
有限元分析是现如今计算裂纹尖端附近残余应力最为常用的一种分析方法,其网格细化程度对于计算结果的精度以及计算时间有着很强的影响作用。细化过度的网格尺寸会让计算难以进行且耗时过多,而过于粗糙的网格尺寸会使计算结果不够准确影响整个计算的正确性。本文着重研究了裂纹尖端区域有限元单元尺寸对于计算结果的影响。
Solanki[13]研究了平面应力和平面应变状态下CT、MT模型,指出裂纹尖端反复塑性区范围内至少包含3~4个单元,Newman[14]将塑性区单元数从10改进为20,以获取更为准确的计算结果。
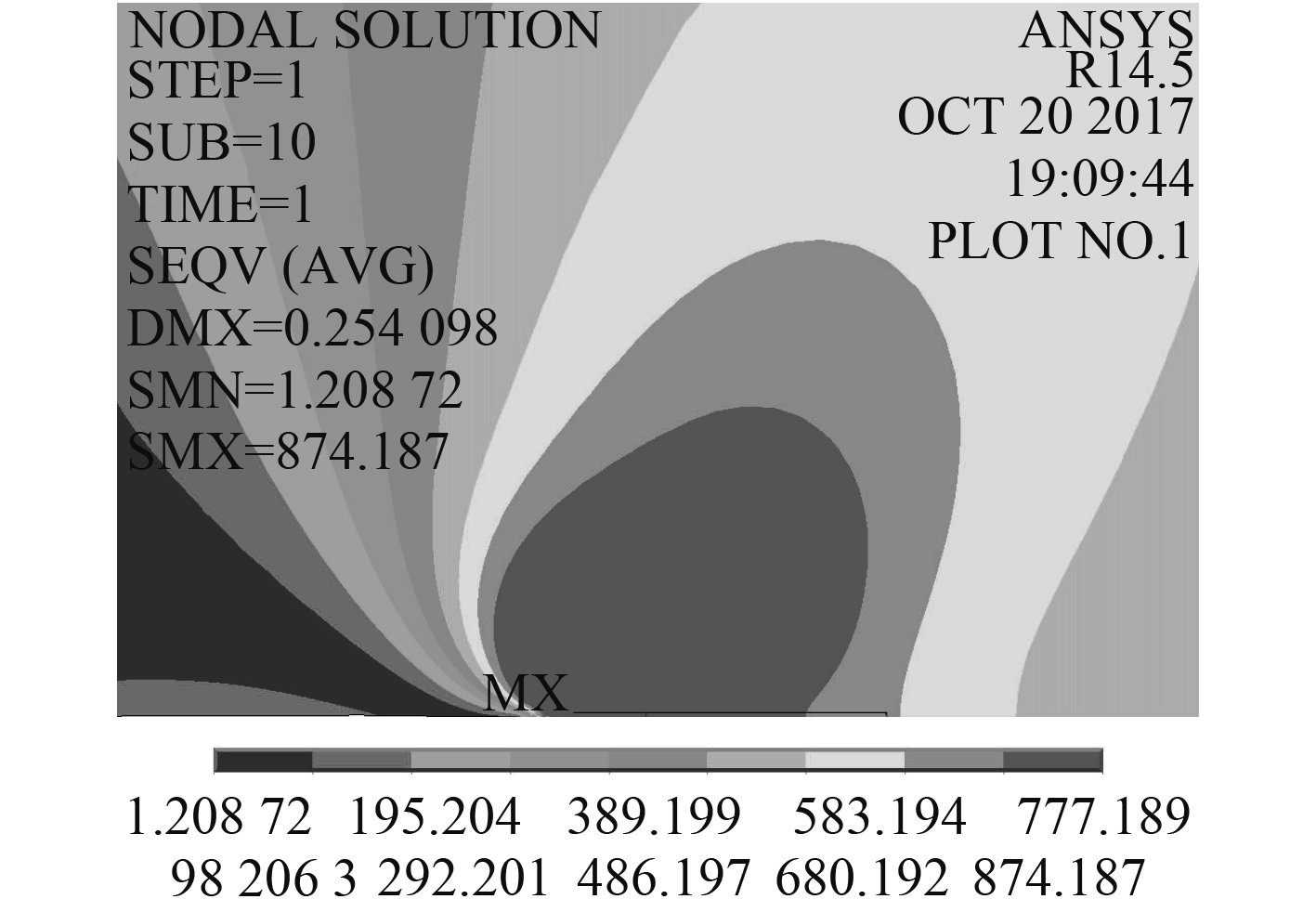
图6和图7分别为压压疲劳试验时试件在最大载荷和卸载时候的尖端应力场分布,红色区域为塑性区。裂纹面前沿轴线上的塑性区尺寸分别为4.12 mm和0.38 mm。前者塑性区大小约为后者的10倍。
|
图 6 最大载荷时裂纹尖端塑性区 Fig. 6 Crack tip plastic zone under maximum load |

|
图 7 卸载时裂纹尖端塑性区 Fig. 7 Crack tip plastic zone at unloading |
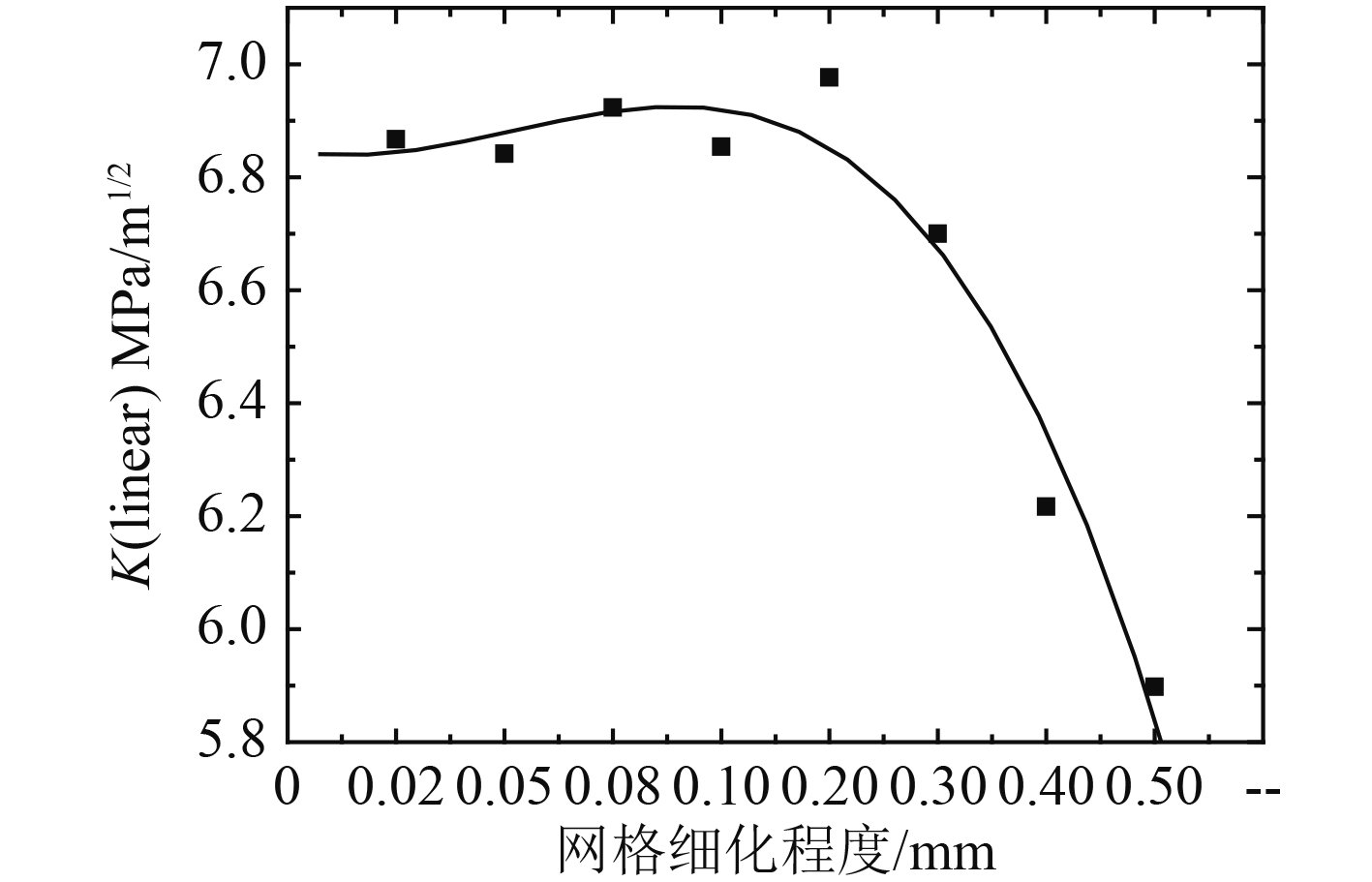
本文在Solanki[13]和Newman[14]的研究基础上,研究单元尺寸对计算结果的影响,在塑性区内划分的有限元单元数从8个变化到200,选取相对应的单元尺寸0.5 mm,0.4 mm,0.3 mm,0.2 mm,0.1 mm,0.08 mm,0.05 mm,0.02 mm进行计算研究。计算得到残余应力分布并结合式(2)得到裂纹尖端线性应力强度因子,具体计算结果如图8所示。
|
图 8 网格细化尺寸-线性应力强度因子关系 Fig. 8 Relationship between mesh size and linear stress intensity factor |
从图8可知,随着网格尺寸的不断细化,应力强度因子的数值呈现出先上升后趋于稳定波动的趋势。当单元尺寸在0.2~0.5 mm范围内时,计算结果随着单元尺寸的减小而增大,说明此单元尺寸下的计算结果还不够准确,当单元尺寸小于0.2 mm后,随着单元尺寸的减小计算结果有小幅波动,当单元尺寸小于0.1 mm后结果趋于稳定。此时,单元尺寸为0.2 mm时,裂纹轴线方向最大载荷塑性区内为20个单元,网格尺寸为0.1 mm时裂纹轴线方向最大载荷塑性区内为40个单元。因此,本文裂纹尖端区域单元尺寸选取为0.1 mm,即裂尖最大塑性区尺寸
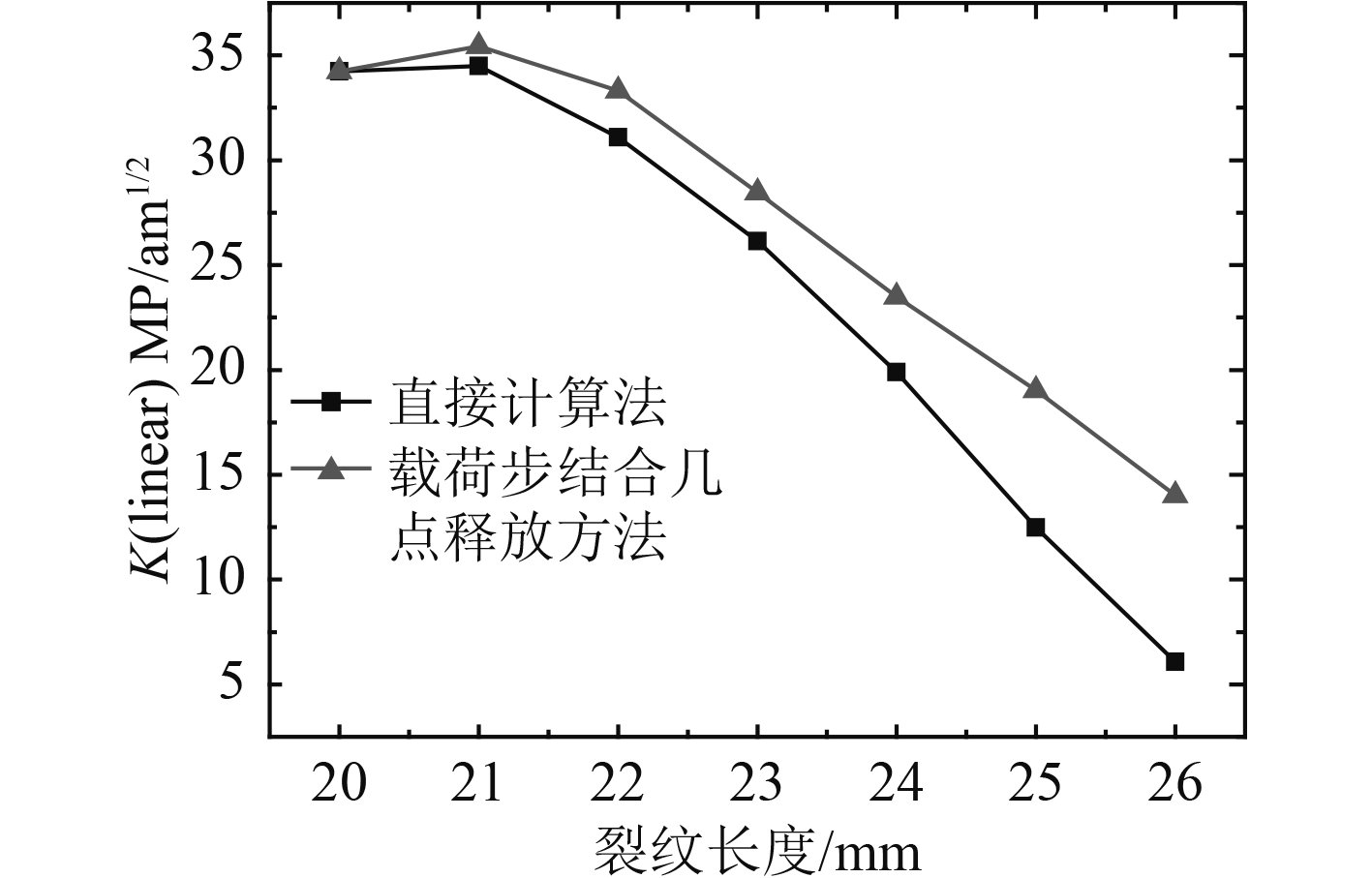
循环压缩载荷下,板材所受应力发生周期性变化,在每个周期的卸载过程中,由于材料塑性产生了裂纹尖端的拉伸应力,促使裂纹向前扩展,材料塑性在此过程中起了关键性的作用。本文模拟真实板材受载情况,采用多载荷步结合节点释放技术,在每个周期卸载完成后释放裂纹尖端的第1个节点来模拟裂纹扩展,并且从初始裂纹处开始计算,使材料塑性在每一个循环中发挥作用,模拟真实裂纹扩展场景。此方法主要通过Ansys APDL语言来实现,首先完成载荷步的编写,并施加所对应的加载,最后通过删除对应节点上的约束释放相应的节点,每一个循环都有对应的载荷步也有对应释放的节点。具体计算结果如图9所示。图9对比了多载荷步结合节点释放分析方法与单独计算各裂纹长度处应力强度因子的计算结果,可以看出随着裂纹尺寸的增大2种方法的计算结果K值差别越来越大,因此,本文采用多载荷步分析方法来更好地模拟疲劳裂纹扩展和塑性引起的残余应力。
|
图 9 直接计算法对比载荷步结合节点释放方法 Fig. 9 Comparison of node release method and direct calculation method |
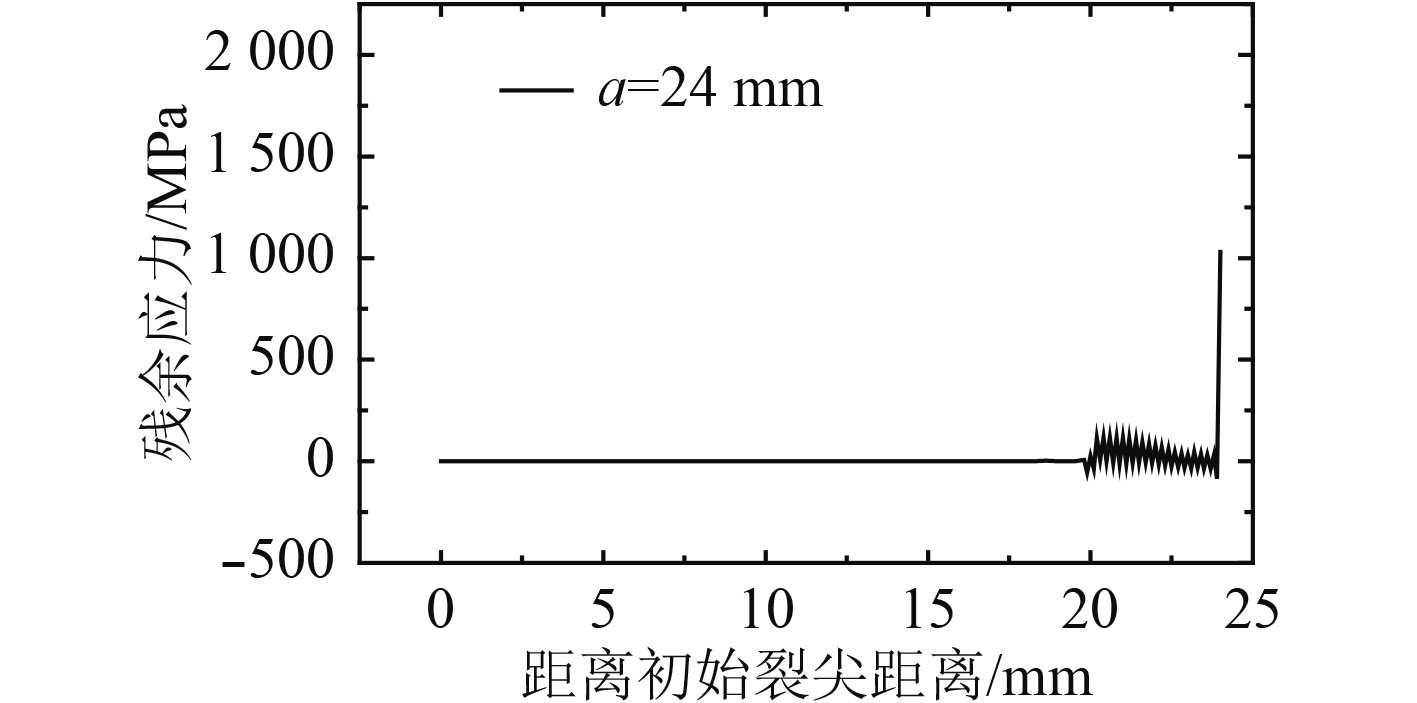
不同裂纹尺寸时:对应的裂纹面上的残余应力分布计算结果如图10~图16所示。
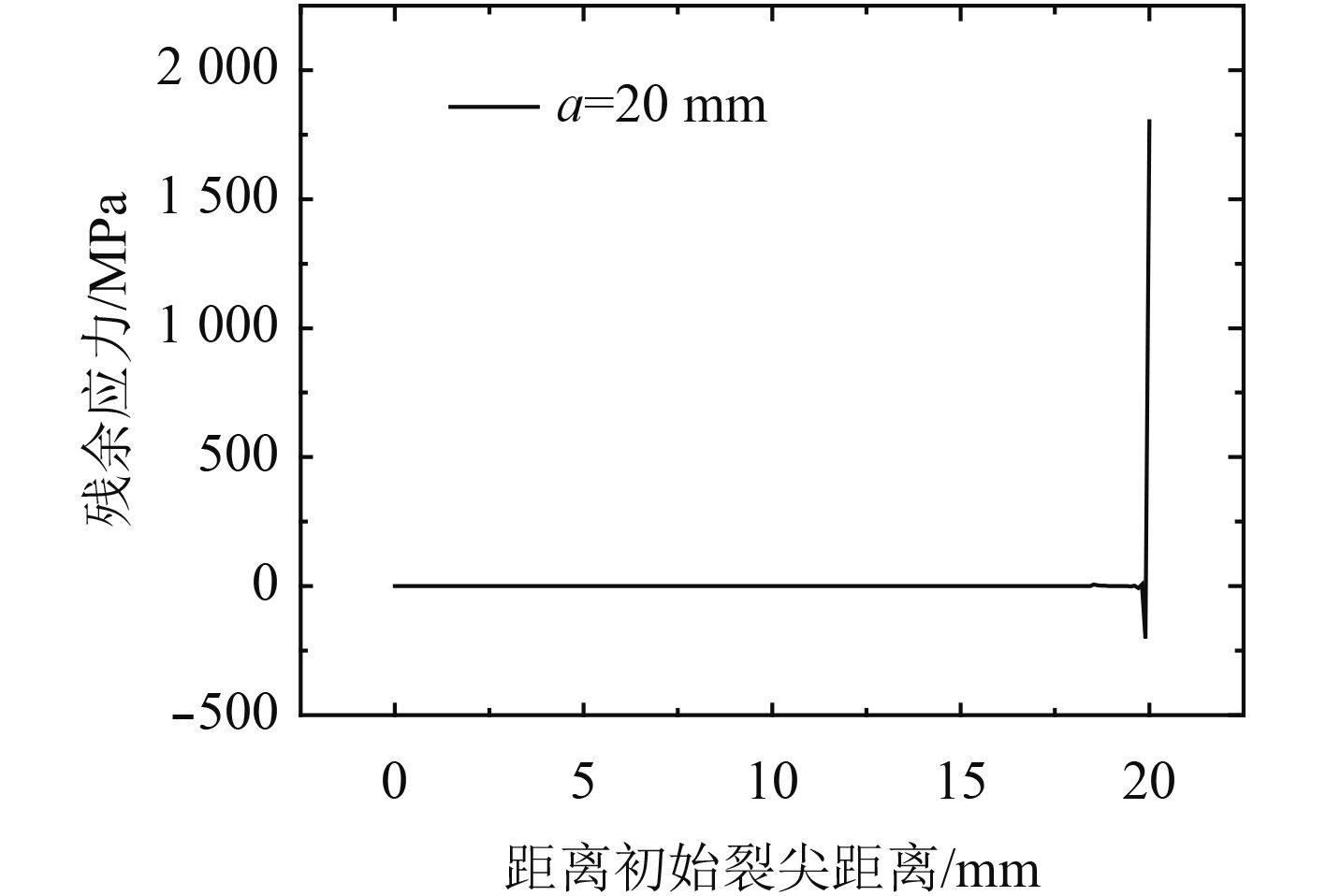
|
图 10 a=20 mm时的残余应力分布 Fig. 10 Residual stress distribution at a=20 mm |
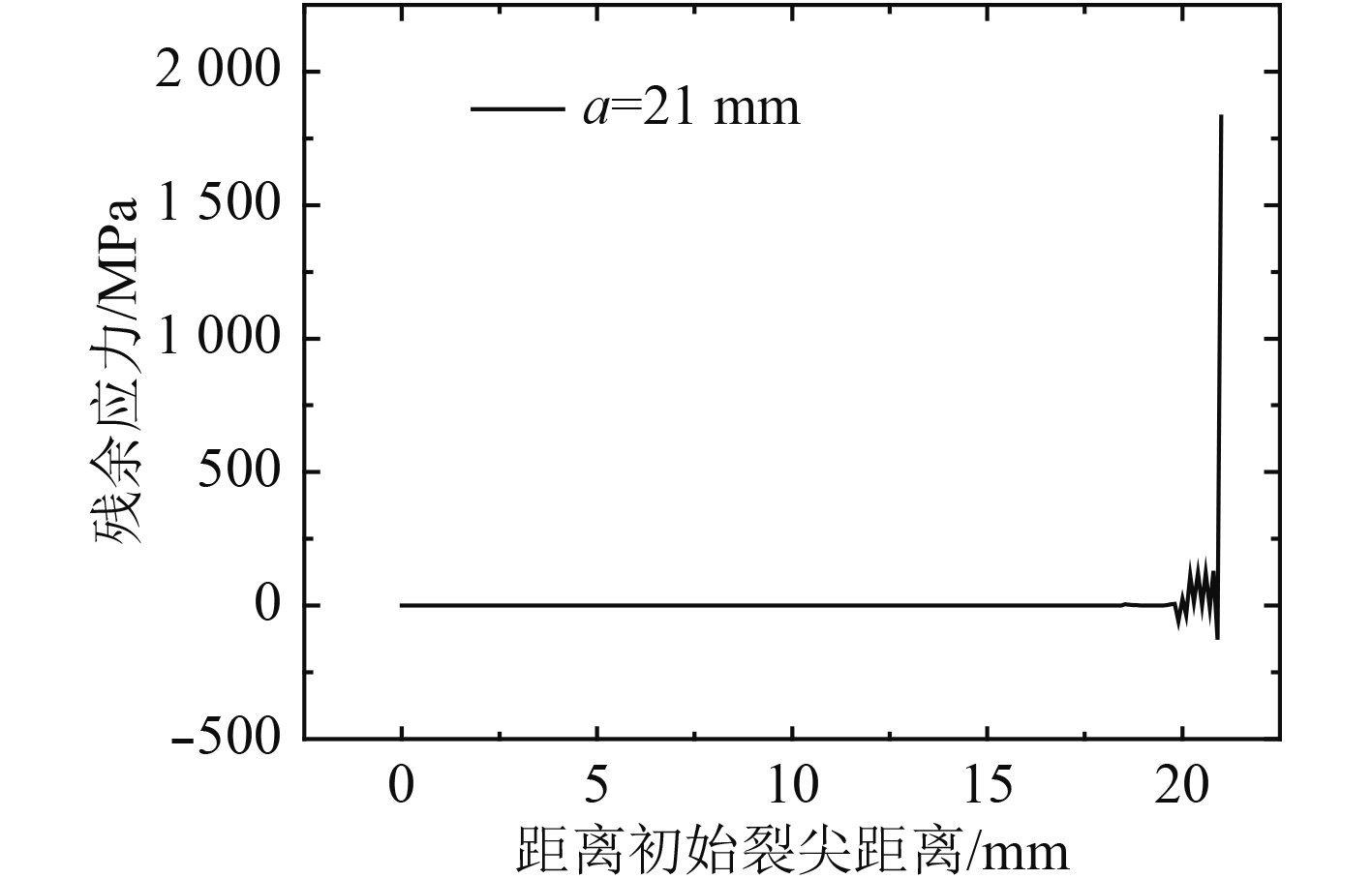
|
图 11 a=21 mm时的残余应力分布 Fig. 11 Residual stress distribution at a=21 mm |
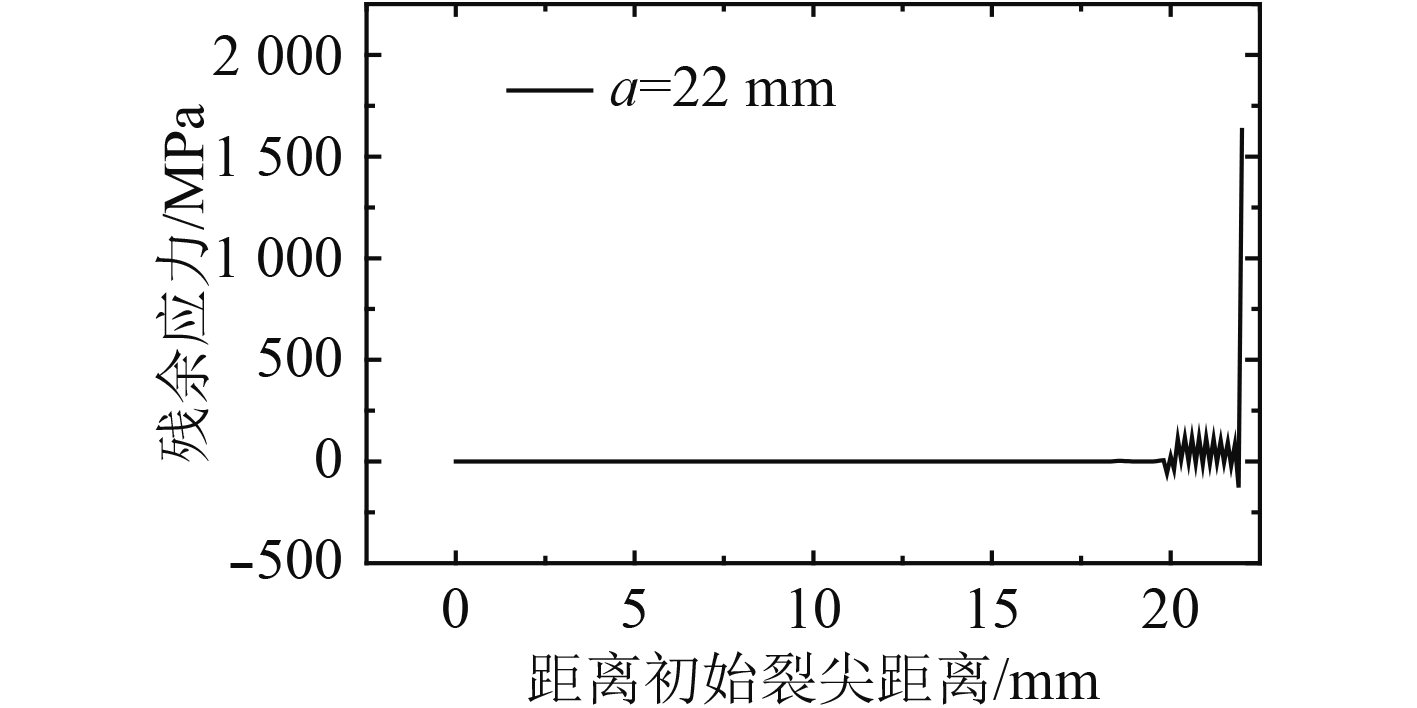
|
图 12 a=22 mm时的残余应力分布 Fig. 12 Residual stress distribution at a=22 mm |
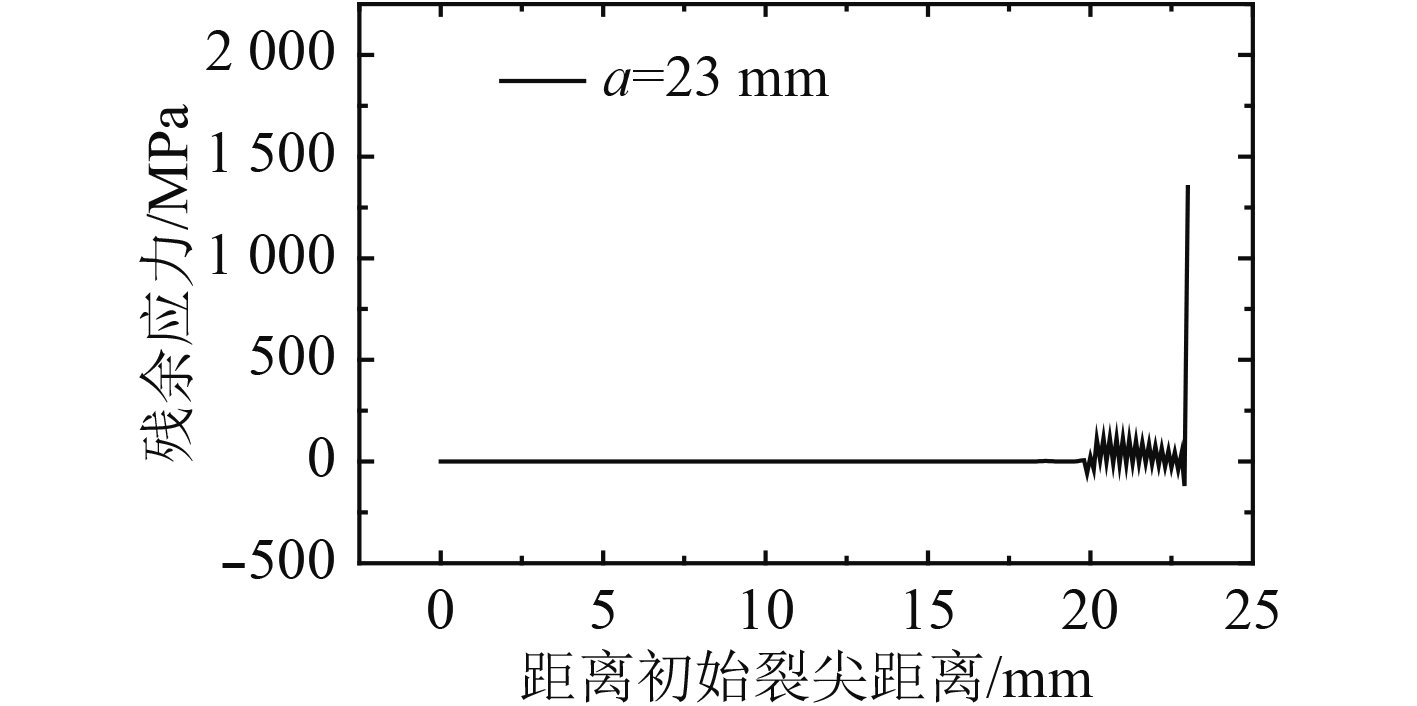
|
图 13 a=23 mm时的残余应力分布 Fig. 13 Residual stress distribution at a=23 mm |
|
图 14 a=24 mm时的残余应力分布 Fig. 14 Residual stress distribution at a=24 mm |
|
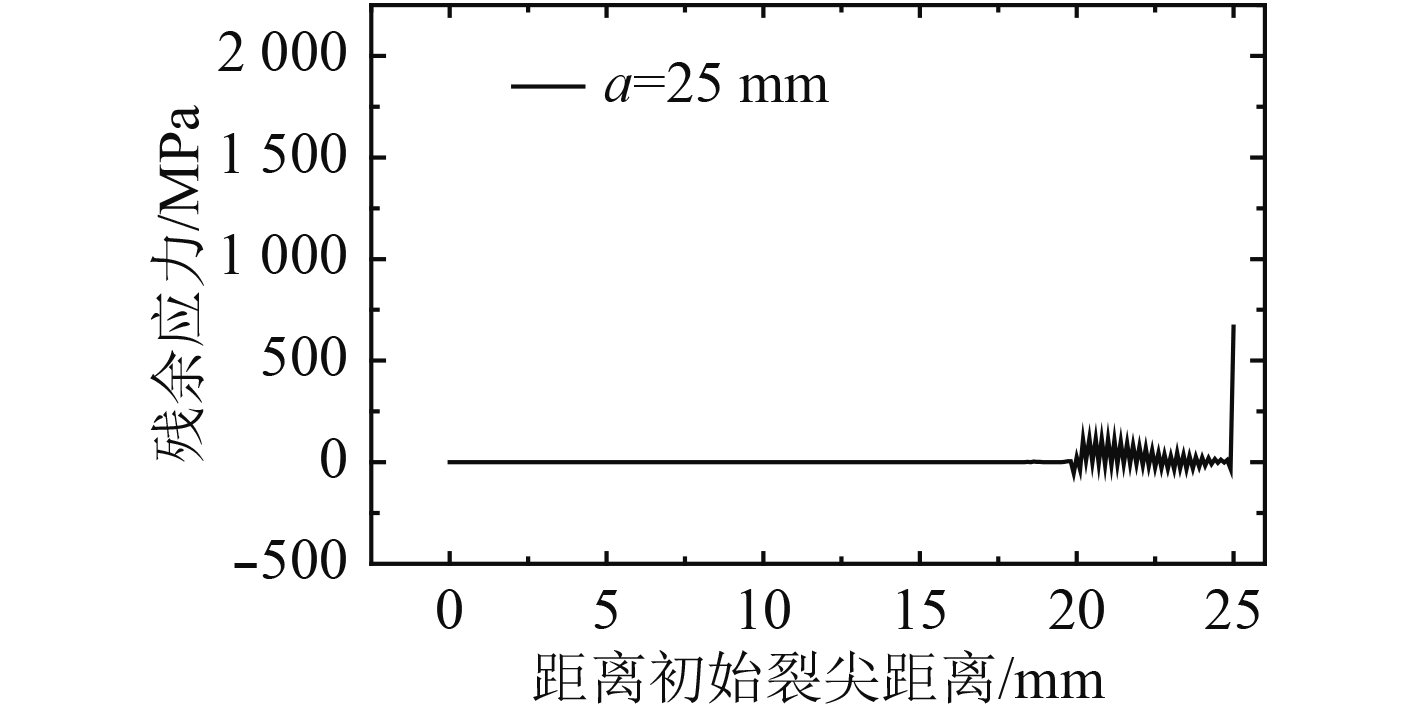
图 15 a=25 mm时的残余应力分布 Fig. 15 Residual stress distribution at a=25 mm |
|
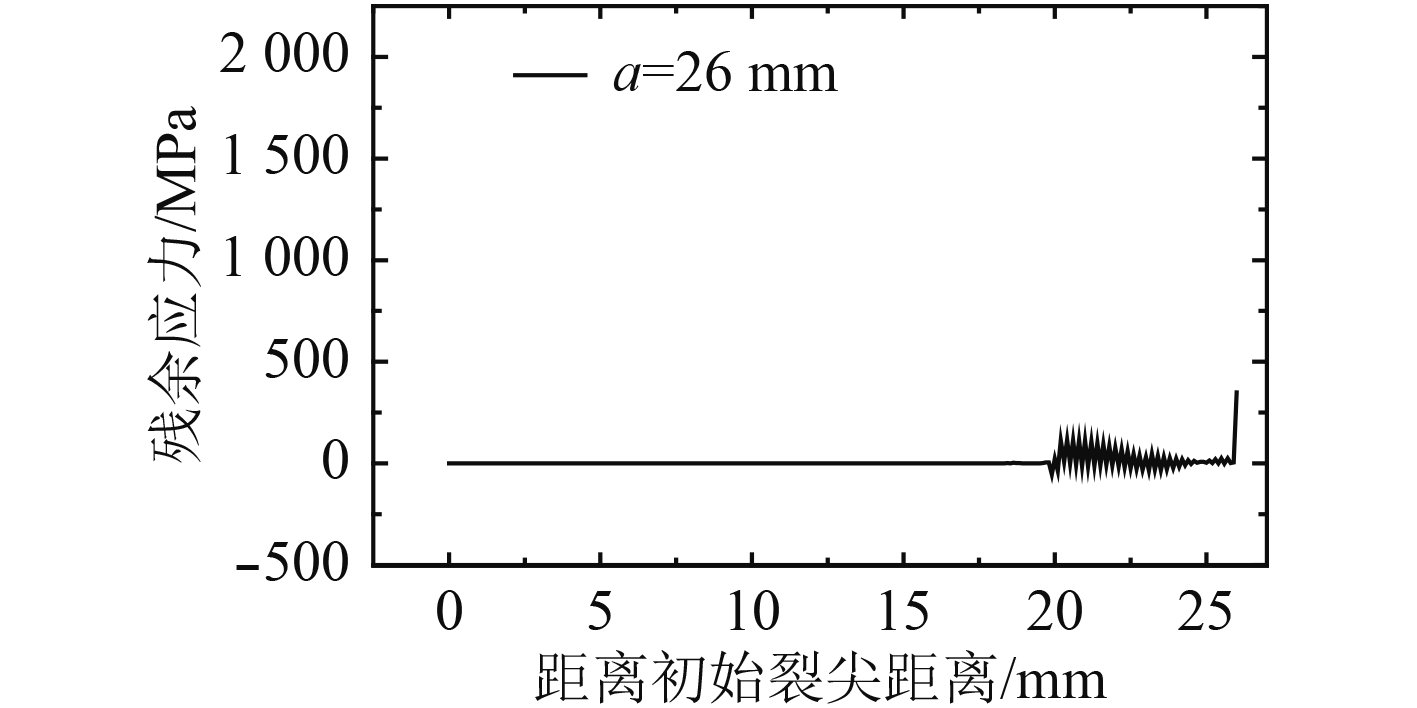
图 16 a=26 mm时的残余应力分布 Fig. 16 Residual stress distribution at a=26 mm |
将有限元分析得到的裂纹面残余应力分布按照式(2)计算可得对应的线性应力强度因子,计算结果见表2。
|
|
表 2 各裂纹长度处的线性应力强度因子 Tab.2 Linear stress intensity factors at the crack length |
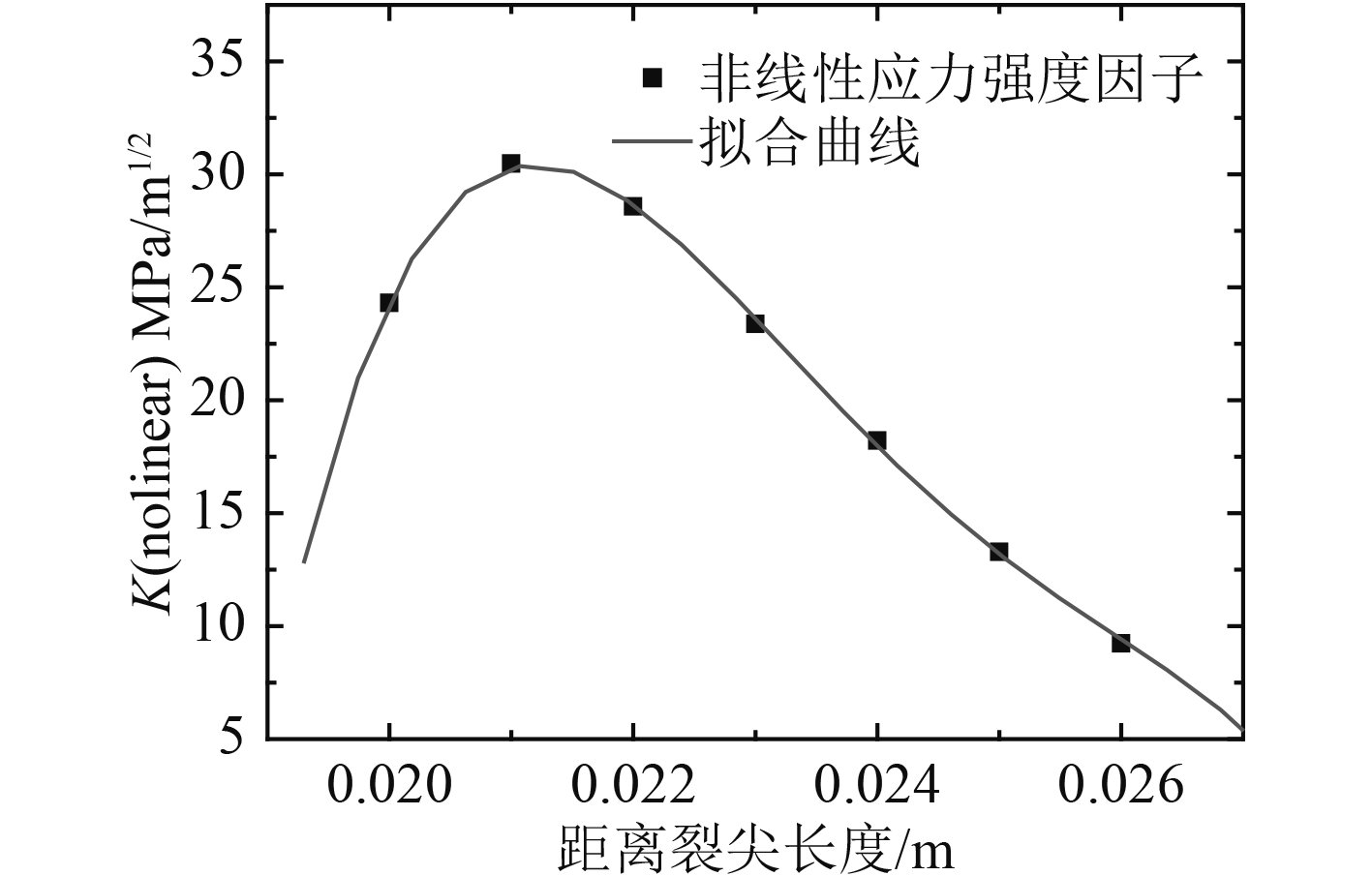
通过式(3)及式(4)将线性应力强度因子转换成改进McEvily模型中的非线性应力强度因子,具体计算结果见表3,拟合曲线如图17所示。
|
|
表 3 等效残余应力与非线性应力强度因子 Tab.3 Equivalent residual stress and nonlinear stress intensity factor |
|
图 17 非线性应力强度因子拟合曲线-裂纹长度关系 Fig. 17 Relationship between nonlinear stress intensity factor fitting curve and crack length |
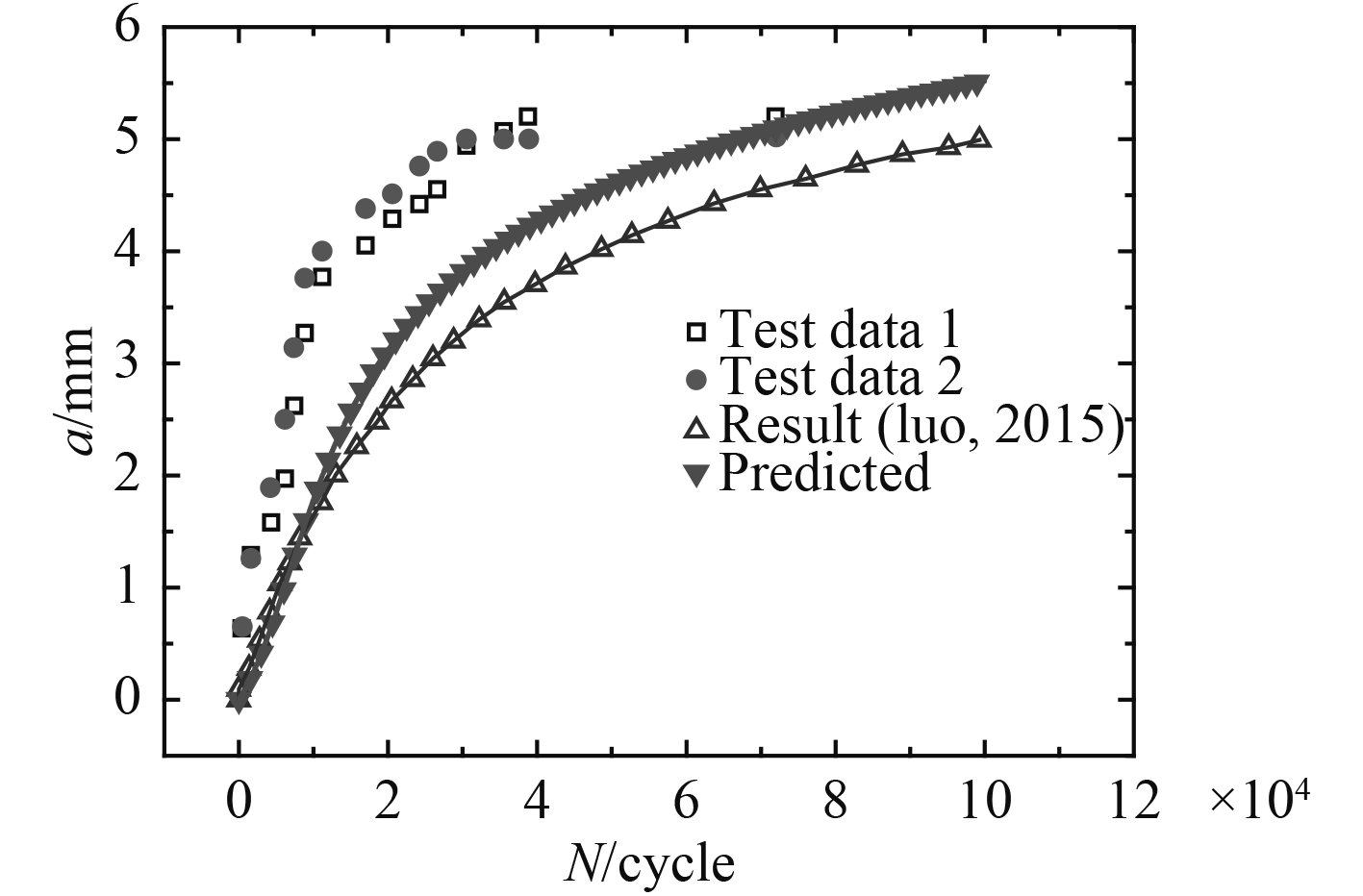
将计算得到的非线性应力强度因子结合改进的McEvily模型,通过Matlab编程计算循环压缩载荷下的疲劳裂纹扩展曲线。计算结果与试验对比如图18所示。
|
图 18 预测的a-N曲线与试验结果对比 Fig. 18 Comparison of predicted a-N curves and experiment results |
由图18可知,最终裂纹尺寸计算结果为5.52 mm,与试验结果5.20 mm的误差为6.15%。图18中a-N曲线的斜率是裂纹扩展速率方面,可知计算结果比试验扩展速率结果偏小,但优于文献[15]的计算结果。导致此差距的原因可能有:输入的材料属性与真实材料属性有所不同,导致计算裂纹面残余应力时有误差;本文考虑了塑性引起的残余应力但没有考虑到裂纹表面粗糙度的影响,致使结果有所偏差。因此,本文的计算结果与文献[15]中的计算结果相比更接近实验结果,同时说明本文基于压-压疲劳寿命预测方法是有效的、可行的。
3 结 语本文通过弹塑性有限元分析得到了沿着裂纹面的残余应力分布,计算其残余拉应力和应力强度因子,采用改进的McEvily模型计算其裂纹扩展寿命,与试验结果对比验证了该方法的有效性,主要结论如下:
1)由于材料塑性,压缩循环载荷会在裂纹尖端区域产生残余拉伸应力,它是压-压载荷下疲劳裂纹扩展的主要驱动力。
2)裂纹尖端区域有限元单元尺寸对塑性引起的残余应力和应力强度因子的计算结果有较大影响,本文研究了一系列不同单元尺寸对计算结果的影响,综合考虑计算精度和计算时间,建议裂尖区域单元尺寸值取为
3)多载荷步结合节点释放技术能较好模拟材料塑性对于每个载荷循环的影响,能够较为准确地计算沿着裂纹的残余应力分布。
| [1] |
PIPPAN R, BERGER M, STÜWE H P. The influence of crack length on fatigue crack growth in deep sharp notches[J]. Metallurgical Transactions A, 1987, 18(3): 429-435. |
| [2] |
KASABA K, SANO T, KUDO S, et al. Fatigue crack growth under compressive loading[J]. Journal of Nuclear Materials, 1998, s258-263(S1): 2059-2063. |
| [3] |
SURESH S. Fatigue of materials[M]. Cambridge: Cambridge University Press, 1999.
|
| [4] |
耿小亮, 张克实, 郭运强. 循环压缩应力作用下的疲劳裂纹扩展机制研究[J]. 机械强度, 2004, 26(2): 227-230. DOI:10.3321/j.issn:1001-9669.2004.02.022 |
| [5] |
卞如冈, 崔维成, 万正权. 基于双参数统一方法研究压一压疲劳下的裂纹扩展[J]. 船舶力学, 2009(5): 734-738. DOI:10.3969/j.issn.1007-7294.2009.05.009 |
| [6] |
HUANG X, WANG A, CUI W, et al. The Fatigue Crack Growth Under Compressive to Compressive Fluctuating Loading[C]// ASME 2010, International Conference on Ocean, Offshore and Arctic Engineering. 2010: 59–64.
|
| [7] |
CUI W, WANG F, HUANG X. A unified fatigue life prediction method for marine structures[J]. Marine Structures, 2011, 24(2): 153-181. DOI:10.1016/j.marstruc.2011.02.007 |
| [8] |
GARDIN C, FIORDALISI S, SARRAZIN-BAUDOUX C, et al. Numerical simulation of fatigue plasticity-induced crack closure for through cracks with curved fronts[J]. Engineering Fracture Mechanics, 2016, 160: 213-225. DOI:10.1016/j.engfracmech.2015.11.023 |
| [9] |
GARDIN C, FIORDALISI S, SARRAZIN-BAUDOUX C, et al. Numerical prediction of crack front shape during fatigue propagation considering plasticity-induced crack closure[J]. International Journal of Fatigue, 2016, 88: 68-77. DOI:10.1016/j.ijfatigue.2016.03.018 |
| [10] |
YANG J, LI H, LI Z. A plasticity-corrected stress intensity factor for fatigue crack growth in ductile materials under cyclic compression[J]. International Journal of Fatigue, 2014, 59(2): 208-214. |
| [11] |
TAN M L, FITZPATRICK M E, EDWARDS L. Stress intensity factors for through-thickness cracks in a wide plate: Derivation and application to arbitrary weld residual stress fields[J]. Engineering Fracture Mechanics, 2007, 74(13): 2030-2054. DOI:10.1016/j.engfracmech.2006.10.017 |
| [12] |
LUO G E, CUI W C. Prediction of fatigue crack growth rate of metal based on Bayesian regularized BP neural network[J]. Journal of Ship Mechanics, 2012, 16(4): 433-441. |
| [13] |
SOLANKI K, DANIEWICZ S R, JR J C N. Finite element modeling of plasticity-induced crack closure with emphasis on geometry and mesh refinement effects[J]. Engineering Fracture Mechanics, 2003, 70(12): 1475-1489. DOI:10.1016/S0013-7944(02)00168-6 |
| [14] |
WALKER K F, WANG C H, JR J C N. Closure measurement and analysis for small cracks from natural discontinuities in an aluminium alloy[J]. International Journal of Fatigue, 2016, 82: 256-262. DOI:10.1016/j.ijfatigue.2015.03.016 |
| [15] |
LUO G E, DONG J H. Fatigue Crack Propagation of Deepwater Structures Under Cyclic Compression Based on Extended McEvily Model[C]// ASME 2015, International Conference on Ocean, Offshore and Arctic Engineering. 2015: V003T02A034.
|
 2018, Vol. 40
2018, Vol. 40
