传统的波浪载荷计算方法[1 – 2]将船体看成刚性体,在求得6个自由度的刚体运动和受力后,通过静平衡方法得到船体各截面上由波浪引起的弯矩和剪力。然而,实际的船体结构是一个弹性体,在波浪上运动时,除具有6个自由度的刚体运动外,还将产生弹性振动和变形,有必要将流体动力学与船体结构动力学理论相结合,统一地处理船体弹性变形与流体运动的相互作用问题,这时水弹性力学应运而生。70年代末,Bishop和Price[3]最早建立了二维水弹性理论与分析方法。1984年Wu[4]将三维势流理论与结构动力学结合起来,给出了广义的流固耦合界面条件,开创了三维线性水弹性理论。进入21世纪,Hidars与Price等[5]研究了1艘散货船在规则波中的二维及三维水弹性响应。田超[6]采用上述三维水弹性理论,对小水线面双体船的水弹性响应进行研究,并探讨了二阶波浪力的影响。杨鹏等[7]采用水弹性方法对一单模块超大型浮体的水弹性响应和结构强度进行分析。Ren Hui-long等[8]基于三维水弹性理论研究了8 500箱集装箱船与10 000箱集装箱船由于波激振动与颤振引起的疲劳损伤。Benneett等[9]研究了船舶在遭遇极端海况下的波浪载荷与颤振响应。Heo等[10]基于二维切片理论发展了一种数值方法,可以用来预报船舶的波激振动响应。Ding等[11]对近岛礁超大型浮体的单模块水弹性响应进行计算,并与试验结果进行对比。Lin等[12]采用频域二维切片理论与三维有限元方法分析了1艘350 000 DWT超大型油船的波激振动响应。Kara[13]和Sengupta[14]基于边界元方法以及三维瞬态自由面格林函数发展了三维时域水弹性方法并将其用来预报浮体的水弹性响应。
从上述国内外的研究结果可以看出,三维水弹性理论在大型船舶和超大型海上浮体中得到了日益广泛的应用。但是,迄今为止主流的商业计算软件尚不能考虑水弹性的影响。THAFTS(Three-dimensional Hydroelastic Analysis of Floating and Translating Structure)是中国船舶科学研究中心自主研制开发的三维水弹性力学计算软件,可用于预报和评估船舶及海洋工程结构的运动特性、波浪载荷、结构安全性与可靠性。目前该软件已经形成了专用的前、后处理程序,操作界面简洁,数据处理方便,这为其在船舶与海洋工程领域的推广使用奠定了基础。本文应用该软件对大型散货船的运动、波浪载荷及水弹性响应进行计算,探讨了波激振动对船体结构疲劳损伤的影响,所得结论为大型船舶的结构设计提供了参考。
1 计算理论模型 1.1 三维水弹性理论基于模态叠加原理,船体结构任一点的位移、应力、剪力和弯矩可以表示为:
| $\left\{ \begin{array}{l}\overrightarrow u (t) = \sum\limits_{r = 1}^m {\overrightarrow {u_r^0} {p_r}(t)} {\text{,}}\\{\sigma _{ij}}(t) = \sum\limits_{r = 7}^m {{\sigma _{ijr}}{p_r}(t)} {\text{,}}\\V(t) = \sum\limits_{r = 7}^m {{V_r}{p_r}(t)} {\text{,}}\\M(t) = \sum\limits_{r = 7}^m {{M_r}{p_r}(t)} {\text{。}}\end{array} \right.$ | (1) |
其中:
| $[ - {\omega _e}^2([ a] \!+\! [ A]) + i{\omega _e}([ b] \!+\! [ B]) \!+\! ([ c] \!+\! [ C])]\{ p\} \!=\! \{ F\} {\text{,}}$ | (2) |
式中,
| $\left\{ \begin{array}{l}{A_{rk}} = \displaystyle\frac{\rho }{{\omega _e^2}}{\mathop{\rm Re}\nolimits} \iint\limits_{{S_0}} {\overrightarrow n \cdot \overrightarrow {u_r^0} (i{\omega _e} + \overrightarrow W \cdot \nabla ){\phi _k}{\rm d}S}{\text{,}} \\{B_{rk}} = - \displaystyle\frac{\rho }{{{\omega _e}}}{\mathop{\rm Im}\nolimits} \iint\limits_{{S_0}} {\overrightarrow n \cdot \overrightarrow {u_r^0} (i{\omega _e} + \overrightarrow W \cdot \nabla ){\phi _k}{\rm d}S}{\text{,}} \\{C_{rk}} = - \displaystyle\rho g\iint\limits_{{S_0}} {\overrightarrow n \cdot \overrightarrow {u_r^0} [g{\omega _k} + \frac{1}{2}(\overrightarrow {u_r^0} \cdot \nabla ){W^2}]{\rm d}S}{\text{,}} \\{F_r} = \rho \iint\limits_{{S_0}} {\overrightarrow n \cdot \overrightarrow {u_r^0} (i{\omega _e} + \overrightarrow W \cdot \nabla )({\phi _0} + {\phi _D}){\rm d}S}{\text{。}} \end{array} \right.$ | (3) |
其中:下标rk为第k个模态的结果对第r个模态的影响,
| $\overrightarrow W = U\nabla (\overline \phi - x){\text{。}}$ | (4) |
三维水弹性分析方法将总的速度势在平衡坐标系下分解为两部分[6]:
| ${\varPhi _{{T}}}(x,y,z,t) = U\overline \varPhi (x,y,z) + \phi (x,y,z,t){\text{,}}$ | (5) |
其中:
| $\phi (x,y,z,t) = [{\phi _I}(x,y,z) + \sum\limits_{r = 1}^{m{\rm{ + }}1} {{\phi _r}(x,y,z)]{e^{i{\omega _e}t}}} {\text{,}}$ | (6) |
其中:
根据广义流固耦合界面条件[4],非定常扰动势的定解条件为:
| $\left\{ {\begin{aligned}&{{\nabla ^2}{\phi _r} = 0{\text{,}}\quad\quad\quad\quad\quad\quad\quad\;\,{\text{在流域中}}}{\text{;}}\\&\begin{aligned}&- {\omega _e}^2{\phi _r} + g\displaystyle\frac{{\partial {\phi _r}}}{{\partial z}} = 0{\text{,}}\quad\quad\quad\quad\;\;\;\;\,{\text{自由面条件}}{\text{;}}\\&\begin{aligned}{\displaystyle\frac{{\partial {\phi _r}}}{{\partial n}} \!=\! \left\{\begin{aligned}&[i{\omega _e}\overrightarrow {{u_r}} \!+\! \overrightarrow {{\theta _r}} \!\times\! \overrightarrow W \!-\! (\overrightarrow {{u_r}} \cdot \nabla )\overrightarrow W ] \cdot \overrightarrow n{\text{,}} \;\;\;r \!\!=\!\! 1,2,...m{\text{,}}\\& - \displaystyle\frac{{\partial {\phi _I}}}{{\partial n}}{\text{,}}\quad\quad\quad\quad\quad\quad\;\,\,\, r = m + 1{\text{;}}\end{aligned} \right.}(7)\\\begin{aligned}&\displaystyle\frac{{\partial {\phi _r}}}{{\partial z}} = 0{\text{,}}\quad\quad\quad\quad\quad\quad\quad\quad z = - \infty{\text{;}} \\&\mathop {\lim }\limits_{R \to \infty } \sqrt R \left(\displaystyle\frac{{\partial {\phi _r}}}{{\partial R}} - i{k_0}{\phi _r}\right) = 0{\text{,}}\qquad\quad\quad {\text{远场辐射条件}}{\text{。}}\end{aligned}\end{aligned}\end{aligned}\end{aligned}} \right.$ | (7) |
式中,
使用谱分析法对散货船的疲劳损伤进行研究,首先,通过三维水弹性模态叠加法获取结构的应力传递函数
| ${S_0}\left( \omega \right) = {\left| {{H_0}\left( \omega \right)} \right|^2} \cdot {S_W}\left( \omega \right){\text{,}}$ | (8) |
其中
由于考虑波激振动对疲劳损伤的影响,获得的应力谱将出现2个峰值,文章采取在频率为1.90 rad/s处截断,分别考虑波频应力谱与高频应力谱对疲劳分析的影响,加权后获得新的应力谱
| ${\sigma _3} = \sqrt {{m_{1,0}} + {m_{2,0}}} ,{f_3} = \sqrt {f_1^2{m_{1,0}} + f_2^2{m_{2,0}}} {\text{,}}$ | (9) |
| $\begin{split}{\lambda _3} =& \frac{{{v_p}}}{{{v_c}}}\left[ {\lambda _H^{\frac{m}{2} + 2}\left( {1 - \sqrt {\frac{{{\lambda _W}}}{{{\lambda _H}}}} } \right) + \frac{{m\Gamma \left( {\frac{m}{2} + \frac{1}{2}} \right)}}{{\Gamma \left( {\frac{m}{2} + 1} \right)}}\sqrt {{\text{π}} {\lambda _W}{\lambda _H}} } \right] +\\& \frac{{{v_w}}}{{{v_c}}}\lambda _W^{\frac{m}{2}}{\text{,}}\end{split}$ | (10) |
式中:m1, 0为波频应力谱谱距;m2, 0为波激部分应力谱距,其中:
| $\begin{array}{l}{v_p} = {\lambda _H}{v_H}\sqrt {1 + \displaystyle\frac{{{\lambda _W}}}{{{\lambda _H}}}{{\left( {\displaystyle\frac{{{v_W}}}{{{v_H}}}\varepsilon } \right)}^2}}{\text{,}} \\{v_c} = \sqrt {{\lambda _H}v_H^2 + {\lambda _W}v_W^2}{\text{,}} \\{\lambda _H} = \displaystyle\frac{{{m_{2,0}}}}{{\sigma _3^2}},{\lambda _W} = \displaystyle\frac{{{m_{1,0}}}}{{\sigma _3^2}},{v_H} = {f_2},{v_W} = {f_1}{\text{,}}\\\varepsilon = \sqrt {1 - \displaystyle\frac{{m_{3,2}^2}}{{{m_{3,0}}{m_{3,4}}}}} {\text{。}}\end{array}$ |
完成了应力响应谱的计算后,结合海区的长期波浪散布图便可以进行结构疲劳损伤的计算,计算的具体公式如下:
| $\begin{split}&D = \frac{T}{C}{\left( {2\sqrt 2 } \right)^m}\Gamma \left( {1 + \frac{m}{2}} \right)\times\\&\mathop \sum \limits_{n = 1}^{{n_l}} \mathop \sum \limits_{j = 1}^{{n_s}} \mathop \sum \limits_{i = 1}^{{n_h}} \left[ {{\lambda _{nji}}{p_n}{p_j}{p_i}{f_{nji}}{{\left( {{\sigma _{nji}}} \right)}^m}{\mu _{nji}}} \right]{\text{。}}\end{split}$ | (11) |
式中:T为计算疲劳寿命;C为S-N曲线常数;m为S-N曲线的反斜率,本文采用规范中d曲线的对应值为3.0;Γx为完全GAMMA函数值;nl,ns,nh分别为装载工况数,海况总数,浪向总数;λnji为第n装载工况,第j海况,第i浪向应力响应的谱宽修正系数;pn,pj,pi分别为第n装载工况、第j海况、第i浪向发生的概率;fnji为第n装载工况,第j海况,第i浪向应力响应的跨零上穿频率;σnji为第n装载工况,第j海况,第i浪向应力响应的标准差;μnji为:
| ${\mu _{{{nji}}}} \!=\! 1 \!-\! \frac{{\Gamma \left[1 + \displaystyle\frac{m}{2},\upsilon _{nji}^2\right] - \upsilon _{nji}^{ - \Delta m}\Gamma \left[1 + \displaystyle\frac{{m + \Delta m}}{2},\upsilon _{nji}^2\right]}}{{\Gamma \left[1 + \displaystyle\frac{m}{2}\right]}}{\text{,}}$ | (12) |
其中:
| ${\nu _{nji}} = \frac{{{S_Q}}}{{2\sqrt 2 {\sigma _{nji}}}}{\text{。}}$ |
式中:
以1艘大型散货船为对象,采用THAFTS软件对其进行水弹性响应计算,散货船主尺度参数见表1。图1给出了整船有限元模型,包括货舱区域、首尾结构、机舱、上层建筑等在内的所有构件,共包含31 839个单元,其中梁单元16 187个。另外,建立水动力网格模型,共包含1 242个面元,见图2。
|
|
表 1 散货船主尺度参数 Tab.1 Main particulars of the bulk carrier |

|
图 1 大型散货船有限元模型 Fig. 1 FEM model of the bulk carrier |

|
图 2 船体湿表面网格 Fig. 2 Hydrodynamic panel model |
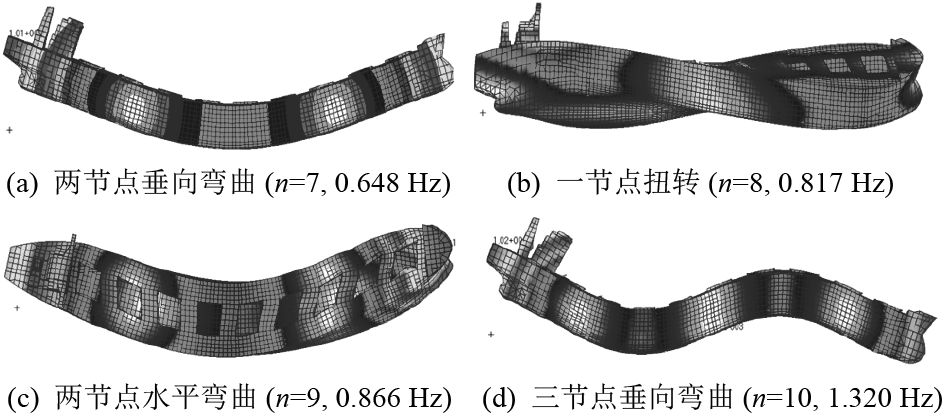
首先,在真空中对散货船有限元模型进行了模态分析,获得了固有频率和振型。图3给出了散货船前4阶弹性模态,按照固有频率从低到高分别为:2节点垂向弯曲、1节点扭转、2节点水平弯曲和3节点垂向弯曲。在后续的水弹性响应计算中,除考虑6个刚体运动外,还将考虑此4个弹性模态。
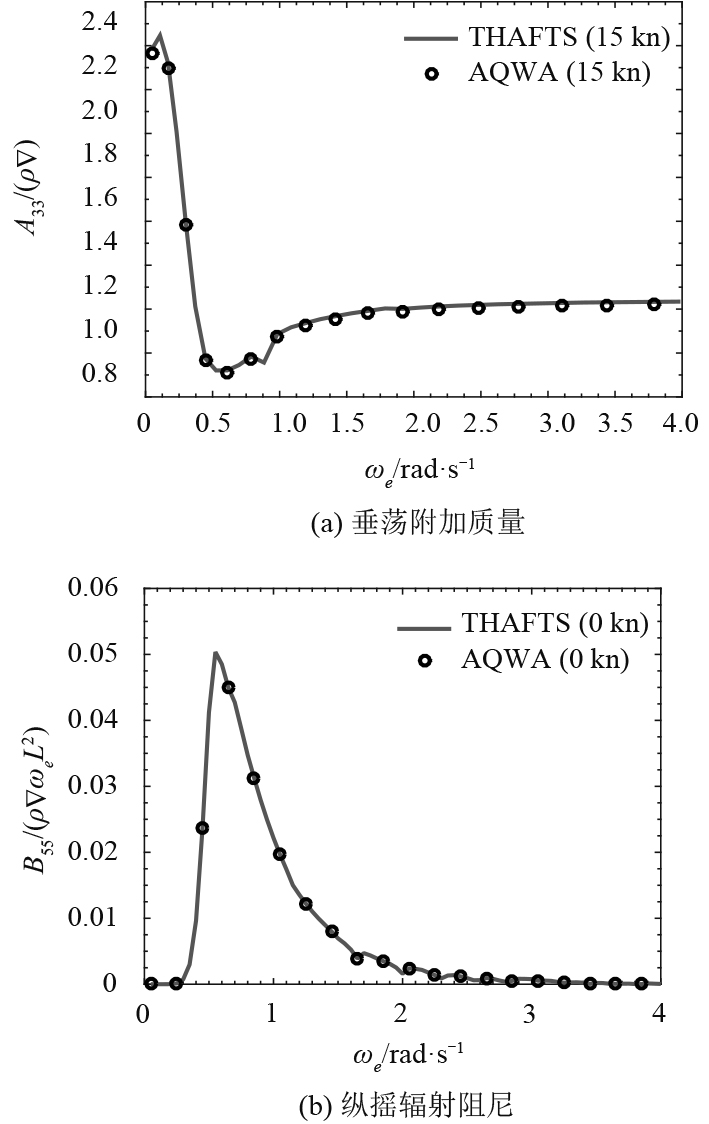
2.2 水动力系数与波浪激励力图4给出了顶浪下船体水动力系数的计算结果,其中图3(a)为垂荡附加质量系数,图3(b)为纵摇附加质量系数。
|
图 3 真空中大型散货船的干模态 Fig. 3 Dry mode of the bulk carrier in vacuum |
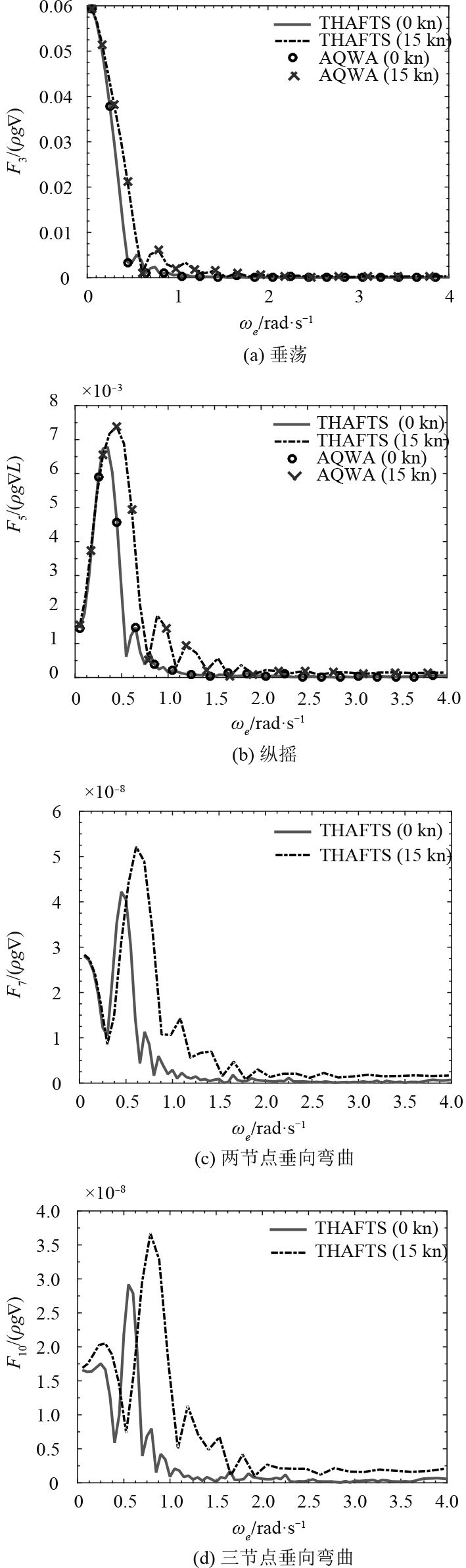
图5给出了波浪激励力的计算结果,另外也给出了基于AQWA软件得到的结果。从图4以及图5可以看出,AQWA结果与水弹性软件THAFTS的计算结果非常吻合。从图5可以发现,15 kn航速时散货船波浪激励力峰值点对应的遭遇频率较之零航速有所增加;从图5还可以看出,当遭遇频率低于0.5 rad/s时,15 kn航速散货船波浪激励力结果与零航速结果非常接近;当遭遇频率大于0.5 rad/s时,15 kn航速散货船波浪激励力结果要高于零航速结果。
|
图 4 水动力系数计算结果(顶浪) Fig. 4 Results of the hydrodynamic coefficent (head sea) |
|
图 5 波浪激励力计算结果(顶浪) Fig. 5 Results of the excitation force (head sea) |
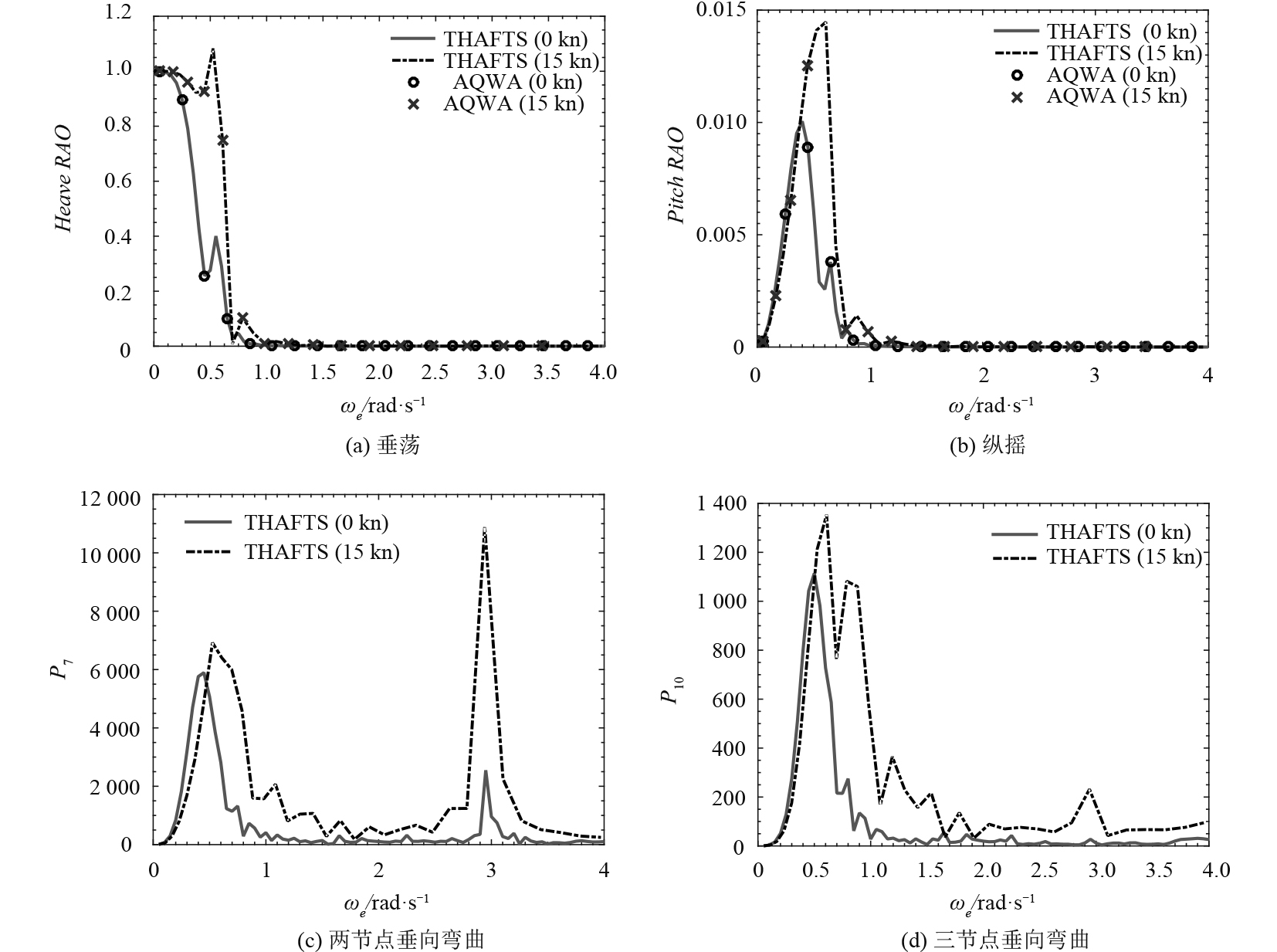
图6为散货船顶浪下零航速与15 kn航速的主坐标频率响应曲线计算结果,其中图6(a)、图6(b)分别为垂荡与纵摇运动,同时给出了AQWA软件得到的垂荡与纵摇计算结果,图6(c)、图6(d)给出了船体结构的两节点垂向弯曲(P7)与3节点垂向弯曲(P10)主坐标频率响应曲线结果。从图6(a)、图6(b)可以发现,当波浪频率在0.3~0.6 rad/s范围时,散货船在15 kn航速时的垂荡响应与纵摇响应较之零航速结果明显增大,其中从图6(b)还可知航速使纵摇固有频率增大。从图6(c)、图6(d)可以发现,当遭遇频率低于0.5 rad/s时,15 kn航速两节点垂向弯曲响应与3节点垂向弯曲响应均略低于零航速结果;在波浪能量集中的低频区(0.5 rad/s附近)时,15 kn航速的两节点垂向弯曲响应与3节点垂向弯曲响应均大于零航速计算结果;当遭遇频率高于0.5 rad/s时,15 kn航速计算结果大于零航速计算结果;还可以看出,零航速与15 kn航速2节点垂向弯曲响应与3节点垂向弯曲响应在低频区(0.5 rad/s附近)与高频区(3 rad/s附近)均出现了2个峰值,其中第1个峰值为低频区共振峰值,第2个峰值表示船体结构波激振动响应,其中从图6(c)可知,航速使波激振动响应峰值明显增加,且波激振动响应的峰值大于低频区共振峰值,这必然会加大船体结构的疲劳损伤。因此,由航速增大而引起的波激振动现象在大型船舶的结构设计中不容忽视。
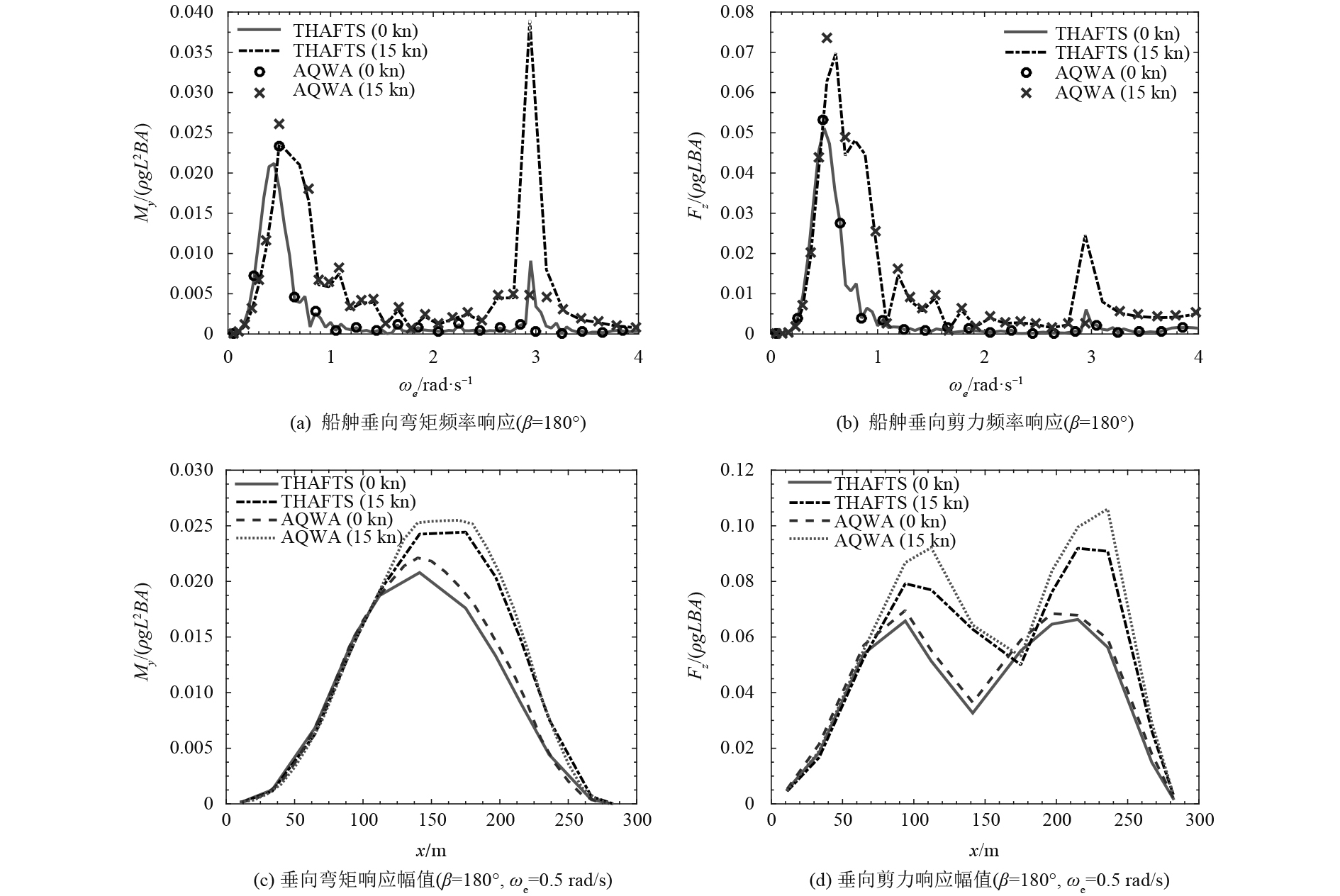
2.4 船体剖面载荷图7给出了零航速与15 kn航速大型散货船在顶浪下的剖面载荷计算结果,并与AQWA刚体计算结果进行比较,其中My,Fz分别表示船体剖面垂向弯矩和垂向剪力。
图7(a)、图7(b)分别为零航速与15 kn航速下垂向弯矩与垂向剪力随遭遇频率变化曲线的对比结果。可以看出,当遭遇频率高于0.5 rad/s时,15 kn航速下的垂向弯矩与垂向剪力明显大于零航速结果;还可以看到,零航速与15 kn航速的垂向弯矩与剪力均出现了2个峰值,其中第1个峰值为低频区共振峰值,第2个峰值表示船体结构波激振动响应,这与前述主坐标响应曲线一致;波激振动频率(3 rad/s)附近的垂向弯矩远大于低频共振频率(0.5 rad/s)时的垂向弯矩,进一步说明波激振动引起的高频载荷在大型船舶的设计中不容忽视。在低频区,AQWA结果与THAFTS结果基本吻合,但是,由于AQWA不考虑水弹性效应,因而无法模拟波激振动响应现象。
图7(c)、图7(d)分别为零航速与15 kn航速下垂向弯矩与垂向剪力沿船长分布的结果。由图7(c)可以看出,无论是零航速还是15 kn航速垂向弯矩均在船中处达到最大,其中15 kn航速下计算得到的船首至船中的垂向弯矩明显大于零航速的结果;由图7(d)可以看出,15 kn航速下计算得到的船首至3/4船长处的垂向剪力大于零航速的结果。另外可以发现,THAFTS结果要略小于AQWA刚体计算结果,这可能是由于在AQWA计算中采用了简化的质量分布模型。
|
图 6 水弹性主坐标响应(顶浪) Fig. 6 Principal coordinate responses of the bulk carrier (head sea) |
|
图 7 剖面载荷计算结果(顶浪) Fig. 7 Results of the section load (head sea) |
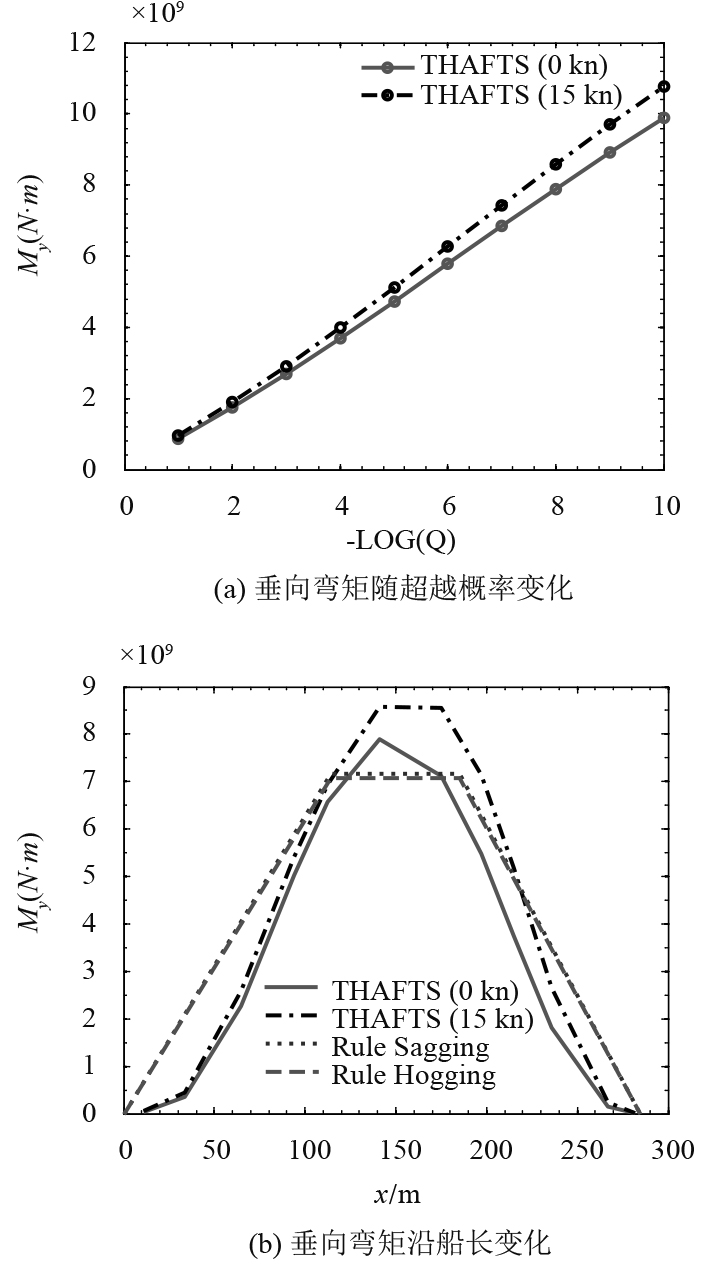
采用北大西洋的海况资料,选用双参数PM谱,计算了不同超越概率下波浪弯矩的长期预报结果。图8(a)给出了船中剖面垂向弯矩随超越概率的变化曲线,可以看到,各个超越概率水平下对应的15 kn航速的垂向弯矩计算结果明显大于零航速计算结果。图8(b)给出了超越概率水平为10–8时,此散货船在零航速与15 kn航速垂向弯矩随船长的变化曲线,并与CCS共同规范给出的中垂与中拱波浪弯矩结果进行比较,可以发现,针对满载工况,通过直接计算得到的船中处的垂向波浪弯矩最大值比规范结果大21.4%左右,下一步还需考虑压载等其他工况对载荷预报结果的影响。
|
图 8 长期预报结果 Fig. 8 The long-term prediction for vertical bending moment |
本文使用考虑波激振动影响的谱分析法对全船模型疲劳损伤进行校核,得到了主船体的疲劳危险区域,另外还与传统的疲劳分析方法得到的结果进行对比。使用IACS推荐的北大西洋波浪散布图,海浪谱选用双参数PM谱,浪向从0°~180°变化,间隔为30°,假定每个浪向发生的概率相同。
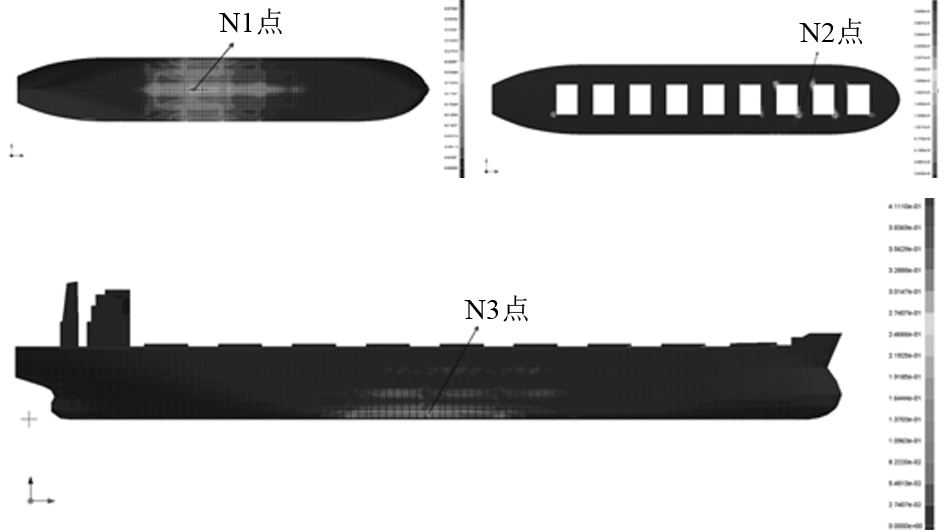
图9给出了大型散货船的不同区域的疲劳损伤云图,从图中可以看出主船体底部(N1点),甲板第3个舱口角隅处(N2点)以及船中处有开孔的舱壁肋板(N3点)处疲劳损伤最大,容易发生疲劳失效。3点处的疲劳损伤与疲劳寿命对比如表2所示,可以看到,在给出的7个浪向中,60°浪向所引起的疲劳损伤最大。同时可以看到,N2点疲劳损伤最大,说明舱口角隅是该模型最危险疲劳失效区域。还可以看到,当未考虑波激振动时,N1,N2,N3点的疲劳寿命分别为96.0年,24.2年,31.0年;当考虑波激振动时,N1,N2,N3点的疲劳寿命分别为53.7年、14.5年、17.4年,说明波激振动引起的船体结构疲劳损伤不可忽略,这对大型船体结构设计具有重要的参考价值。
|
图 9 疲劳损伤云图 Fig. 9 Fatigue damage cloudimage |
|
|
表 2 大型散货船疲劳损伤 Tab.2 The fatigue damage of the bulk carrier |
本文基于三维频域水弹性软件THAFTS研究了零航速与15kn航速下大型散货船的运动及水弹性响应,并计算了船体的剖面载荷,给出了长期预报以及疲劳损伤的结果,得出以下结论:
1)三维水弹性分析软件THAFTS可以计算大型散货船的运动与波浪载荷,计算结果表明:无论是零航速还是15 kn航速,2节点垂向弯曲主坐标响应和3节点垂向弯曲主坐标响应以及垂向弯矩与垂向剪力在高频处均出现了波激振动现象。
2)航速增大将会引起波激振动峰值增大,且波激振动峰值甚至大于低频共振时的峰值,这必然会增大船体结构的疲劳损伤,在大型船舶的设计中应该考虑波激振动的影响。
3)对此散货船的疲劳分析发现疲劳失效的热点区域主要分布于甲板舱口角隅处以及有开孔的舱壁肋板处,且散货船在60°浪向时的疲劳损伤最大;另外,当考虑波激振动的影响时,船体的疲劳寿命明显减少。
本文后续还将进一步考虑航速的非线性、不同装载工况对波浪载荷长期预报结果的影响,同时还将进一步研究颤振响应对大型船舶结构水弹性响应及疲劳性能的影响。
| [1] |
刘应中, 缪国平. 船舶在波浪上的运动理论[M]. 上海: 上海交通大学出版社, 1987.
|
| [2] |
戴仰山, 沈进威, 宋竞正. 船舶波浪载荷[M]. 北京: 国防工业出版社, 2007
|
| [3] |
BISHOP R E D, PRICE W G. Hydroelasticity of ships[M], Cambridge University Press, 1979.
|
| [4] |
WU Y S. Hydroelasticity of floating bodies[D]. Brunel University, UK, 1984.
|
| [5] |
HIRDARS S E, PRICE W G, TEMAREL P. Two and three dimensial hydroelastic modelingof a bulker in regular waves[J]. Marine Structures, 2003(16): 627-658. |
| [6] |
田超. 航行船舶的非线性水弹性理论与应用研究[D]. 上海: 上海交通大学, 2007.
|
| [7] |
杨鹏, 顾学康. 超大型浮体模块水弹性响应和结构强度分析[J]. 船舶力学, 2015. DOI:10.3969/j.issn.1007-7294.2015.03.011 |
| [8] |
REN Hui-long, ZHANG Kai-hong, LI hui, et al. Large containership’s fatigue analysis due to spring and whipping[C]// 2016, Proceeding of the ASME 2016 35th interinational Conference on Ocean, Offshore and Arctic Engineering.
|
| [9] |
BENNETT S S. HUDSON D A, TEMAREL P. The effect of abnormal wave sequences on 2D hydroelastic predictions of global loads[C]// Proceedings of 7th International Conference on Hydroelasticity in Marine Technology, September 16–19, 2015, Split, Croatia, 363–374.
|
| [10] |
HEO K. Quadratic strip theory for high order dynamic behaviour of a large container ship with 3D flow effects[J]. International Journal of Naval Architecture and Ocean Engineering, 2016, 8: 127-136. DOI:10.1016/j.ijnaoe.2015.11.001 |
| [11] |
DING J, TIAN C, WU Y. Hydroelastic analysis and model tests of a single module VLFS deployed near islands and reefs[J]. Ocean Engineering, 2017, 144: 224-234. DOI:10.1016/j.oceaneng.2017.08.043 |
| [12] |
LIN Y, MA N, WANG D Y, et al. Hydroelastic analysis and experimental validation of a 350, 000 DWT very large crude carrier [C]// Proceedings of the ASME 2017 36th International Conference on Ocean. Offshoreand Arctic Engineering, June 25–30, 2017, Trondheim, Norway.
|
| [13] |
KARA, F. Time domain prediction of hydroelasticity of floating bodies[J]. Applied Ocean Research, 2015, 51: 1-13. DOI:10.1016/j.apor.2015.02.001 |
| [14] |
SENGUPTA, D. A simplified approach for computation of nonlinear ship loads and motions using a 3D time-domain panel method[J]. Ocean Engineering, 2016, 17: 99-113. |
 2018, Vol. 40
2018, Vol. 40
