0 引　言

圆柱壳结构是船舶领域被广泛应用的一种工程结构形式，许多研究者对其水下振动已做了大量研究。线性范围内，圆柱壳在外力作用下的振动响应可看作是其振动模态的叠加^[1]，大多数值方法均是基于这一思想，比如瑞利-里兹法^[2]、传递矩阵法^[3]、基于模态叠加的有限元法等。数值计算追求最小的计算成本达到较高的计算精度。在运用模态叠加法研究结构振动响应时，模态阶数的选取决定计算的经济性和准确性。选取的模态阶数越高，计算结果越准确，但消耗的计算时长却越高。当模态数量大于一定值时计算结果变化不大，趋于稳定，把该值定义为截断模态数。对截断模态数的研究通常是在理论方法基础上对数值计算的相关参数的研究。比如王宇等^[4]采用Love壳体理论分析了薄壁短圆柱壳在3种边界条件下的振动位移响应，指出截取前八阶模态就可达到相当精度。王献忠等^[5]结合精细积分法和传递矩阵法，提出精细传递矩阵法法，在对方法有效性验证的同时开展了模态收敛性分析。李榆银等^[6]基于NASTRAN软件对薄壁圆柱壳进行强迫振动分析时对截断模态数进行了灵敏度研究，得到了有效的截断波数。

也有学者专门研究了结构的模态截断对结果的影响。李兴泉等^[7]基于有限元法对频率截断和有效模态质量截断这2种截断方法进行对比研究。张淼等^[8]针对重频阻尼系统提出了高精度截模态算法，并对该算法进行了模态灵敏度和误差分析。金国光等^[9]对高速凸轮结构进行动力学分析的同时进行了模态截断研究，基于有限元法研究了不同截取阶数对计算精度和计算速度的影响。也有学者未采用截断模态数确定结构湿表面有限元网格尺度，而是以主模态分量波长作为参考尺度确定的网格尺度划分原则^[10]。但对于宽频的振动响应计算，主模态变化较大，仍要以最高频率确定网格尺度。以上对截断模态的研究评判标准大多为单个节点的位移响应或声压响应，不具有代表性，且研究对象为单一圆柱壳，不具有普适性。

本文基于瑞利-里兹法求解圆柱壳振动方程，研究了35个不同尺度的圆柱壳在环频率以下的水下振动响应，研究分析了截断模态数随长径比和环频率的变化关系，并且对其规律性进行总结，通过有限元仿真验证了其正确性，结论对于圆柱壳水下振动问题的研究具有重要的参考意义。

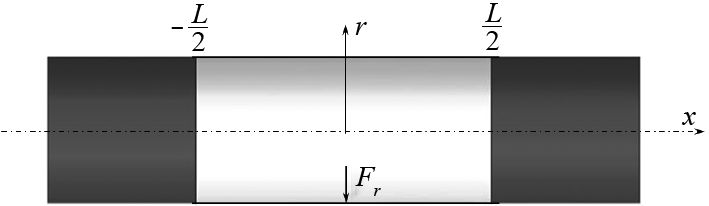
1 圆柱壳水下振动方程推导

研究对象为水下有限长薄壁圆柱壳，长度为L，半径R，厚度为h，h/R≤0.01，材料密度为 ${\rho _{{s}}}$ ，泊松比为μ，模量为 $E\left( {1 + \eta } \right)$ ， $\eta $ 为损耗因子，本文取0.01。壳体完全浸没于水中，两端简支在无限长刚性圆柱障板上，如图1所示。本文基于Donnell壳体理论研究圆柱壳径向激励下的振动问题，其运动方程为：

$\left( {\begin{array}{*{20}{c}}{{l_{11}}} & {{l_{12}}} & {{l_{13}}}\\{{l_{21}}} & {{l_{22}}} & {{l_{23}}}\\{{l_{31}}} & {{l_{32}}} & {{l_{33}}}\end{array}} \right)\left( {\begin{array}{*{20}{c}}u\\v\\w\end{array}} \right) = \left( {\begin{array}{*{20}{c}}0\\0\\{\displaystyle\frac{{{R^2}\left( {1 - {\mu ^2}} \right)}}{{Eh}}({F_r} - {p_r})}\end{array}} \right)\text{，}$

(1)

其中：位移系数矩阵各项表达式具体形式可查询文献[12]；u，v，w分别为轴向，环向和径向位移；F_r为径向载荷力，作用点位于壳体中部； ${p_r}$ 为流体载荷。

为了分离圆柱壳的轴向和环向振型，采用分离变量法对轴向和环向位移进行分解，且基于里兹法的思想，位移可假定为一系列模态振型的线性叠加，其公式如下（忽略时间项e^iωt）：

$\begin{array}{l}u(x,\theta ) = \displaystyle\sum\limits_{mn} {{U_{mn}}} \cos n\theta \sin {k_m}x\text{，}\\v(x,\theta ) = \displaystyle\sum\limits_{mn} {{V_{mn}}} \sin n\theta \cos {k_m}x\text{，}\\w(x,\theta ) = \displaystyle\sum\limits_{mn} {{W_{mn}}} \cos n\theta \cos {k_m}x\text{。}\end{array}$

(2)

其中：m，n分别为轴向模态半波数和环向模态波数， ${k_m}$ 与边界条件有关，对于本文的对称激励情况，圆柱壳的振动响应仅仅是对称模态的叠加，即轴向半波数m为奇数的情况，因此将 ${k_m}$ 取为 $\left( {2m + 1} \right)\displaystyle\frac{\text{π} }{L}$ ，m=0，1，2……。

由模态展开法可对激励力和圆柱壳周围的流体载荷进行分解：

$\begin{array}{l}{F_{{r}}}(x,\theta ) = \displaystyle\sum\limits_{mn} {{F_{mn}}} \cos n\theta \cos {k_m}x\text{，}\\{p_{{r}}}(x,\theta ) = \displaystyle\sum\limits_{mn} {{{\rm{p}}_{mn}}} \cos n\theta \cos {k_m}x\text{。}\end{array}$

(3)

其中： ${F_{mn}} = \displaystyle\frac{{{\varepsilon _n}}}{{2{\text{π}} LR}}{F_0},{\varepsilon _n} = \left\{ {\begin{array}{*{20}{c}} {1,n = 0} \\ {2,n \geqslant 1} \end{array}} \right.$ ，F₀为激振力幅值，本文为单位力1 N。 ${{{p}}_{mn}}$ 为模态声压，表达式为 ${{{p}}_{mn}} = {\left|\displaystyle\sum {\dot w} _{mn}\right. }{Z^s}_{qmn}$ ， ${\dot w_{mn}}$ 为径向模态振速， ${Z^s}_{qmn}$ 为声辐射阻抗，q≠m时，为互辐射阻抗，q=m时，为自辐射阻抗。一般情况下，圆柱壳的互辐射阻抗对声辐射的影响可以忽略，因此模态声压变为 ${{{p}}_{mn}} = {\dot w_{mn}}{Z^s}_{mn}$ 。

将式（2）和式（3）代入式（1）中，可得

${\dot w_{mn}} = \frac{{{F_{mn}}}}{{{Z^M}_{mn} + {Z^s}_{mn}}}\text{，}$

(4)

式中， ${Z^M}_{mn}$ 为机械阻抗，表达式为

${Z^M}_{mn} = \frac{{ - iEh\left| A \right|}}{{\omega {R^2}(1 - {\mu ^2})\left| B \right|}}\text{，}$

(5)

其中， $\left| A \right| = \left| {\begin{array}{*{20}{c}} {{l_{11}}}&{{l_{12}}}&{{l_{13}}} \\ {{l_{21}}}&{{l_{22}}}&{{l_{23}}} \\ {{l_{31}}}&{{l_{32}}}&{{l_{33}}} \end{array}} \right|$ ， $\left| B \right| = \left| {\begin{array}{*{20}{c}} {{l_{11}}}&{{l_{12}}} \\ {{l_{21}}}&{{l_{22}}} \end{array}} \right|$ 。

求解表面振速，还需要事先求得声辐射阻抗，求解声辐射阻抗的方法主要有流固耦合方法和声固耦合法^[13]2种。本文基于声固耦合法计算Helmholtz方程^[14]求解圆柱壳表面声压载荷，表达式为：

$\frac{{{\partial ^2}p}}{{\partial {r^{\rm{2}}}}} + \frac{1}{r}\frac{{\partial p}}{{\partial r}} + \frac{1}{{{r^2}}}\frac{{{\partial ^2}p}}{{\partial {\theta ^2}}} + \frac{{{\partial ^2}p}}{{\partial {x^{\rm{2}}}}} + {k^2}p = 0\text{。}$

(6)

将式（3）代入上述方程，依据贝塞尔方程形式求解得声辐射阻抗为：

${Z^s}_{mn} = \left\{ {\begin{array}{*{20}{c}} {\displaystyle\frac{{ - i\rho \omega {H_n}^{(2)}\left(\sqrt {{k^2} - {k_m}^2} R\right)}}{{\sqrt {{k^2} - {k_m}^2} {H_n}{{^{(2)}}^\prime }\left(\sqrt {{k^2} - {k_m}^2} R\right)}},{k_m} \leqslant k}\text{，} \\ {\displaystyle\frac{{ - i\rho \omega {H_n}^{(2)}\left(\sqrt {{k_m}^2 - {k^2}} R\right)}}{{\sqrt {{k_m}^2 - {k^2}} {H_n}{{^{(2)}}^\prime }\left(\sqrt {{k_m}^2 - {k^2}} R\right)}},{k_m} > k} \text{。}\end{array}} \right.$

(7)

此时将式（5）和式（7）代入式（4）便可求得圆柱壳表面振速表达式。

圆柱壳表面均方振速公式为：

$\left\langle {\dot w(x,\theta ) \times {{\dot w}^*}(x,\theta )} \right\rangle = \frac{1}{{2S}}\int\limits_S {\dot w(x,\theta ) \times {{\dot w}^*}(x,\theta ){\rm{d}}s} \text{，}$

(8)

其中：

$\dot w(x,\theta ) = \sum\limits_{mn} {{{\dot w}_{mn}}} \cos n\theta \cos {k_m}x\text{。}$

(9)

将式（9）代入式（8），依据余弦函数的正交性推导可得均方振速为：

$\left\langle {\dot w(x,\theta ) \times {{\dot w}^*}(x,\theta )} \right\rangle = \frac{1}{4}\sum\limits_{mn} {\frac{1}{{{\varepsilon _n}}}} {\dot w_{mn}}{\dot w^*}_{mn}\text{，}$

(10)

表面均方振速级公式：

${L_W} = 10\lg \frac{{\left\langle {\dot w(x,\theta ) \times {{\dot w}^*}(x,\theta )} \right\rangle }}{{{v_0}^2}}\text{。}$

(11)

其中，基准速度 ${v_0} = 5 \times {10^{ - 8}}$ m/s。

2 圆柱壳的模态截断

在基于模态叠加法对圆柱壳进行水下振动特性问题研究时发现，不同尺度的圆柱壳，其截断模态数量不同。因此针对不同尺寸的圆柱壳，根据上述圆柱壳振动理论方程，基于Mathematica软件进行编程计算，得到圆柱壳表面均方振速。以表面均方振速级为评判标准，进行轴向半波数m和环向波数n的无关性研究。

2.1 圆柱壳模型

本文以35个不同尺度的圆柱壳为对象，计算它们在环频率以下的水下振动响应，研究轴向截断模态数m、环向截断模态数n随长径比L/R和环频率f_r的变化关系。圆柱壳模型参数见表1。其中，环频率公式为：

${{{f}}_{{r}}} = \frac{1}{{2{\text{π}} R}}\sqrt {\frac{E}{{{\rho _{\rm{s}}}}}} \text{。}$

(12)

2.2 截断模态研究

在结构的动态力学特性计算中，为提高计算效率，在不影响计算精度的情况下，往往选取有限个模态数目作为主模态截断，进而通过模态叠加得到结构表面的振动响应。本文目标是研究不同尺度的圆柱壳截断模态数的选取规律，由于计算样本较多，为提高计算效率，将环频率以下的1/3倍频程中心频率作为计算频率点，1/3倍频程中心频率计算式为：

${{{f}}_{{r}}} = 1000 \times {10^{\frac{{3{{j}}}}{{30}}}}{\rm{Hz}},\;\;\left( {{{j}} = \cdots - 2, - 1,0,1,2 \cdots } \right)\text{。}$

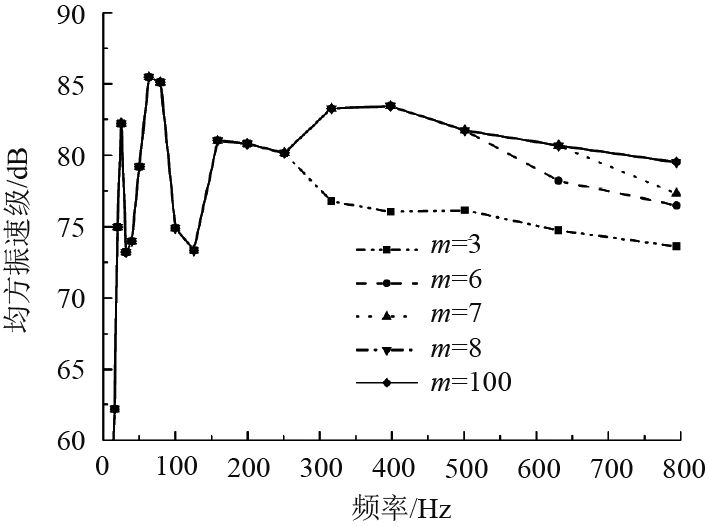
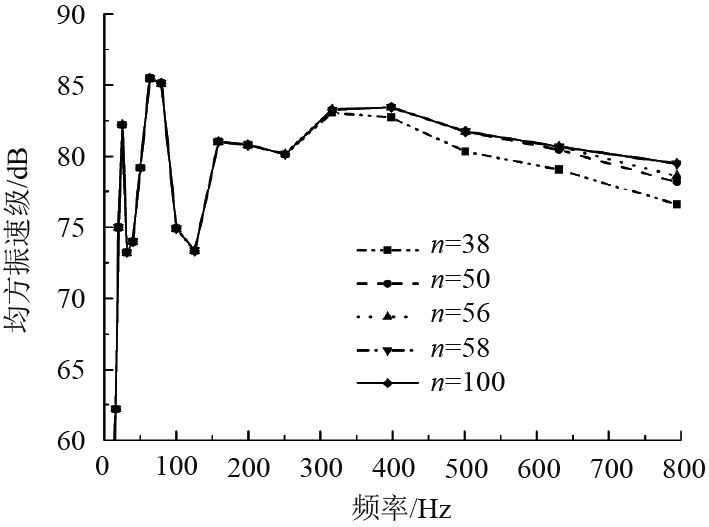
以均方振速级为精度判断指标，具体要求是在环频率以下，模态截断时的计算结果与准确解误差小于1%。理论上，m和n取无穷大时可得到准确解，但在实际计算中难以实现，因此可取一个相对较大的值进行计算作为准确解。以L=1 m，R=1 m圆柱壳为例，经计算分析，当轴向和环向截断模态数达到100时，就能得到准确解。图2和图3分别反映了该圆柱壳轴向和环向截断模态数取不同值时均方振速曲线对比。图中可看出，随着截断模态数的增加，均方振速级曲线与准确解的吻合频率区间不断扩大，当轴向截断模态数m达到8时，当环向截断模态数n达到56时，就与m=n=100时的均方振速级曲线完全吻合，最大误差低于1%，因此可将m=8，n=56作为该圆柱壳的截断模态数。

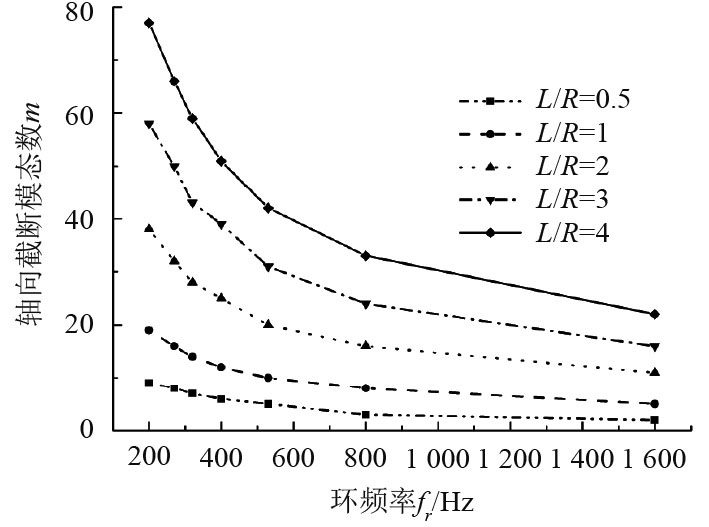
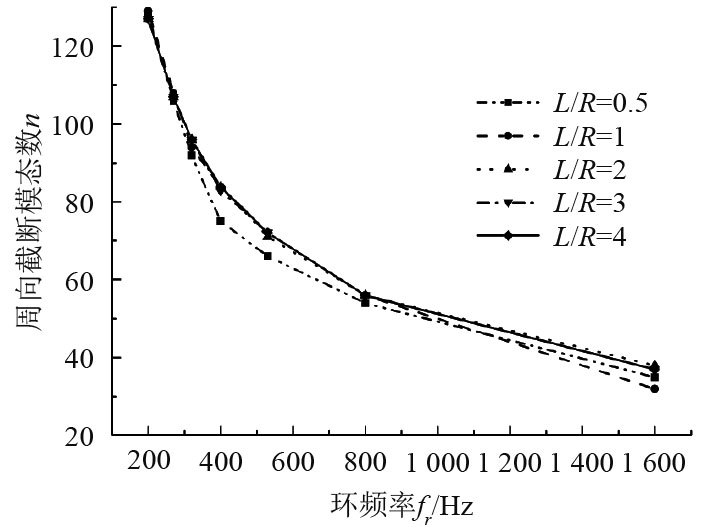
对于表1中每个尺寸的圆柱壳都采用上述方法选取截断模态，进行大量计算后将结果进行整理分析，其中专门研究了截断模态数随环频率的变化关系，如图4和图5所示。图中可看出，长径比相同的情况下，随着环频率的增大，轴向和环向截断模态数均呈下降趋势，且下降趋势逐渐平缓。对于轴向截断模态m，长径比越大，截断模态数越高；但对于环向截断模态n，不同长径比圆柱壳其截断模态数随环频率变化曲线趋于重合，说明环向截断模态数对长径比变化不敏感，它仅与环频率有关，也就是与圆柱壳的半径相关。

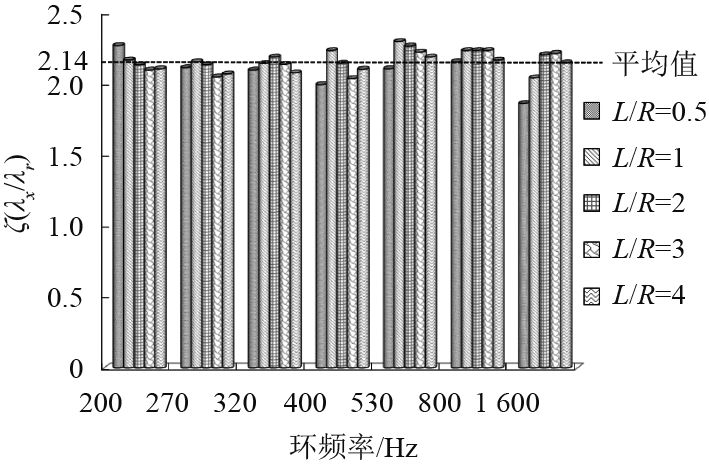
为研究圆柱壳振动截断模态在轴向和环向的相对关系，建立关系式 $\zeta = \displaystyle\frac{1}{{\text{π}} } \times \frac{L}{R} \times \frac{n}{m}$ ，研究 $\zeta $ 与环频率的关系。简单推导可得： $\zeta = \displaystyle\frac{{{\lambda _x}}}{{{\lambda _r}}}$ ，即 $\zeta $ 代表了轴向波长和环向波长的比值。图6反映了不同尺度的圆柱壳轴向和环向截断模态波长之比。由图可知，每个圆柱壳截断模态对应的轴向波长与环向波长之比大体相同，均在2～2.5之间，平均值为2.14，即在保证圆柱壳环频率以下的表面均方振速级最大误差不超过1%的情况下，截断模态满足轴向波长大约为环向的2倍。

3 有限元仿真对比分析

上述对截断模态的研究是基于瑞利-里兹法求解圆柱壳振动方程，为验证理论模型的可靠性和截断模态选取规律的正确性，基于有限元方法进行圆柱壳水下振动特性计算，与理论算法进行对比。

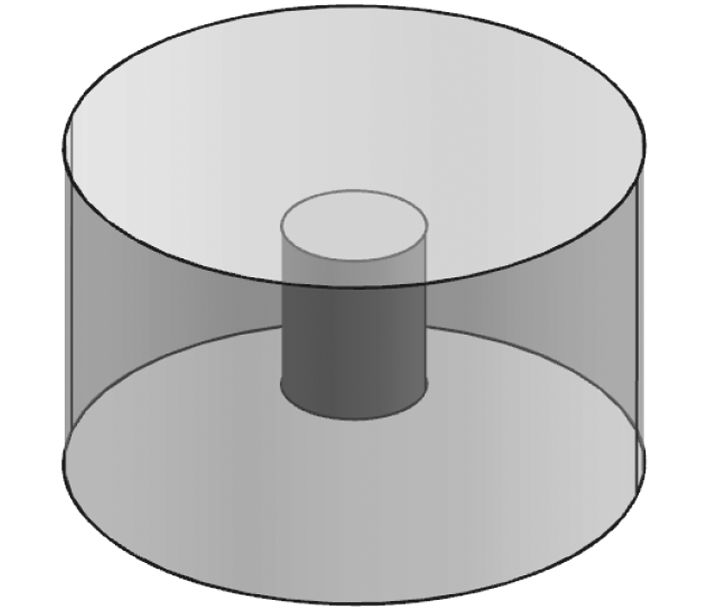
算例对象：圆柱壳材料为铝，长L为2 m，半径R为0.8 m，厚度为2 mm，则长径比L/R为2.5，环频率为1 000 Hz。有限元计算采用结构有限元和流体有限元相结合的方法，基于直接稳态动力学法，对模型的原始方程直接积分计算。其中，圆柱壳周围流场域截断方案已在文献[15]进行了探讨，此处直接取柱形流场域半径为5R，如图7所示。

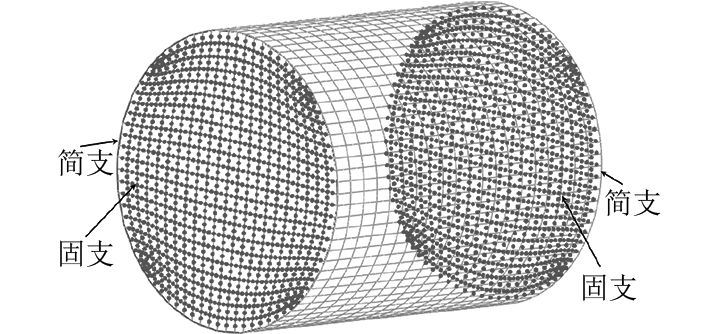
与理论模型不同的是，采用流体有限元法计算圆柱壳水下振动，壳体两端必须进行封闭处理，为了消除两端面对壳体振动的影响，端面除了边缘一圈节点简支，其余所有节点进行固支约束，如图8所示。

首先基于Mathematica软件编程计算圆柱壳水下振动固有频率，并与有限元仿真结果进行对比。结果如表2所示。表中可看出，低阶模态计算误差相比高阶模态低，但最大误差在6%左右，一致性较好。验证了理论算法和有限元仿真的准确性。

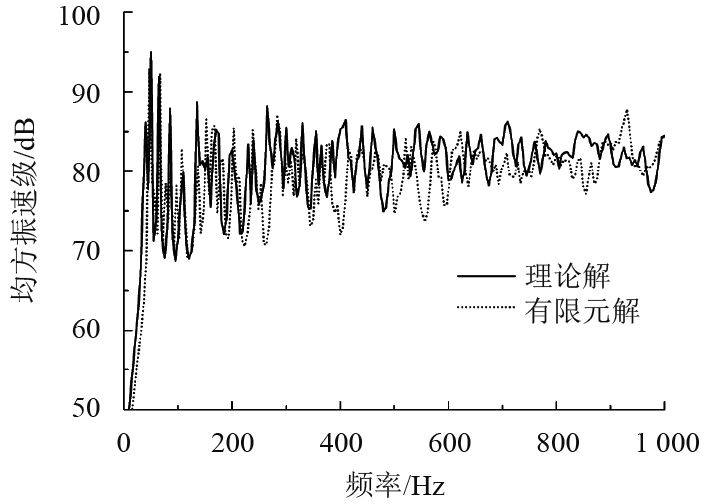
其次基于Mathematica软件编程计算圆柱壳水下振动响应，依据图4和图5插值可得截断模态数m取20，n取50。求取环频率以下的表面均方振速级，与有限元仿真结果进行对比，结果如图9所示。由图可知，在环频率以下，理论方法和有限元仿真计算求得的均方振速曲线吻合较好，验证了截断模态选取的正确性。

4 结　语

本文基于瑞利-里兹法求解圆柱壳振动方程，研究了35个不同尺度的圆柱壳在环频率以下的水下振动响应，以表面均方振速为评判标准，研究分析了轴向截断模态数m、环向截断模态数n随长径比和环频率的变化关系，得到了同等精度下的截断模态数，并且对其规律性进行总结，得出以下结论：

1）对于轴向截断模态m，其大小与长径比和环频率均相关。长径比相同，随着环频率的增大，截断模态m逐渐降低，且下降趋势逐渐平缓；环频率相同，长径比越大，截断模态m值越高。

2）对于环向截断模态n，其大小仅与环频率相关。随着环频率的增大，n值逐渐减小。

3）在保证圆柱壳环频率以下的表面均方振速级最大误差不超过1%的情况下，截断模态对应的轴向波长与环向波长之比大概满足2倍的关系。

4）采用理论方法和有限元法计算了圆柱壳的固有频率和均方振速，通过对比，验证了理论计算的正确性和截断模态选取的合理性。