2. 海军工程大学 兵器工程学院,湖北 武汉 430033;
3. 海军大连舰艇学院 航海系,辽宁 大连 116018
2. College of Naval Weapons, Naval University of Engineering, Wuhan 430033, China;
3. Departmeng of Navigation, Dalian Naval Academy, Dalian 116018, China
随着声呐系统以及各种先进水下探测技术的发展,水下潜器的隐蔽性在现代战争中显得极为重要。加肋圆柱壳结构是水下潜器的主要组成部分和结构形式,因此,研究它的振动及声辐射特性非常重要,也一直得到众多学者的关注。
在以往的圆柱壳研究中,研究的对象主要是环肋等间距布置的圆柱壳,也就是通常所说的周期性结构或等间距结构,对这类结构的振动特性的研究表明[1 – 3],振动在频域上有交替存在通带与止带的特征,其中,通带代表结构波能自由传播时的频带,止带代表随传播距离的增大结构波幅值成指数衰减的频带。目前,对不等间距结构振动的研究多集中于一维简单结构[4 – 10],虽然得出了一些重要结论,如不等间距结构振动特性存在安德森定域效应现象,但针对不等间距加肋圆柱壳的振动特性的研究并不多,而且主要是针对无限长非周期加肋圆柱壳[11],文献[11]的研究表明,对于无限长非周期加肋圆柱壳,除低阶周向振动模式外,不等间距加肋圆柱壳在轴向上的振动传播均具有明显的安德森定域效应,且安德森定域效应作用随周向振动模式阶数的升高而加强,主要原因是:随着周向振动模式阶数的升高,肋骨的阻抗作用变大,相邻子结构间的耦合作用受肋骨阻抗影响而减弱。
在实际工程中,加肋圆柱壳有限长,本文研究肋骨不等间距布置对有限长加肋圆柱壳在一定频率范围内振动的抑制作用。
1 基本理论 1.1 一维不等间距结构振动理论上世纪末至本世纪初,国外学者[5, 7]对一维不规则耦合振子系统、一维不等间距支撑梁等简单结构的振动特性进行研究,发现不等间距结构振动特性的主要特征是存在安德森定域效应(Aderson localization)。相比等间距结构上结构波在通带内能无衰减地自由传播,安德森定域效应描述了不等间距结构上的结构波幅值因为非阻尼的原因随传播距离增大成指数衰减的现象。
对一维无限长无阻尼单支座简支支撑梁结构,若令支座处入射波为
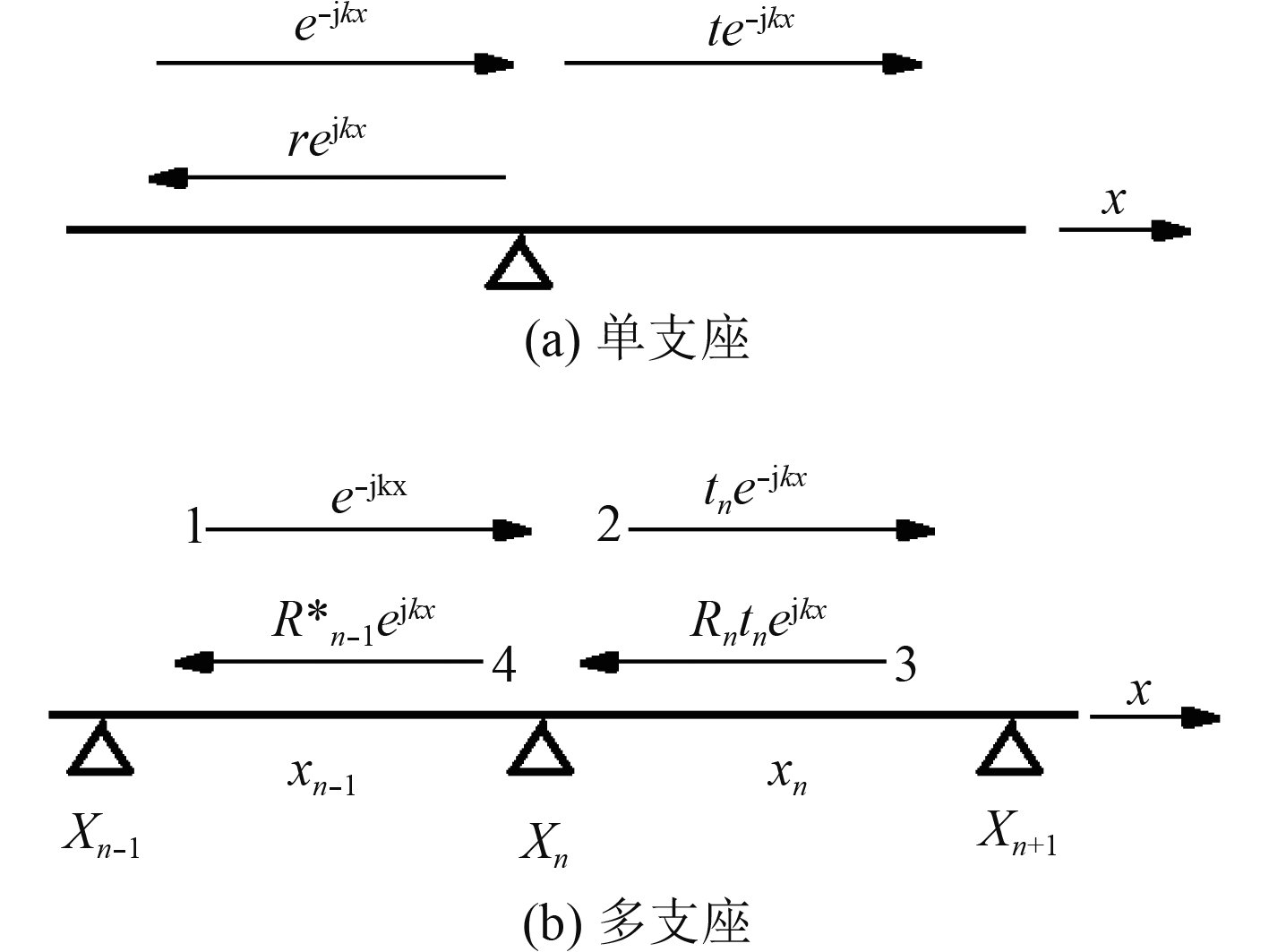
|
图 1 无限长单支座与多支座简支支撑梁 Fig. 1 Infinite beam supported by single or multi simple supports |
对一维无阻尼多跨度简支支撑梁结构,由于结构波在各支座间存在来回的反射与透射,使得结构波的传播较为复杂。假设仅考虑结构波的两重反射,则在任意支座处,结构波的入射、透射、反射关系如图1(b)所示。图中,
从图1(b)可知,1标示为1的结构波为初始入射波。2标示为3的结构波为经支座
| $\left\{\!\!\!\! \begin{array}{l}{t_n} = r{R_n}{t_n} + t\text{,}\\R_{n - 1}^* = r + t{R_n}{t_n}\text{,}\\{R_{n - 1}} = {{\rm{e}}^{ - {\rm{j}}k(2{x_{n - 1}})}}R_{n - 1}^*\text{。}\end{array} \right.$ | (1) |
根据式(1)可得结构波在第n个支座处的透射系数:
| ${t_n} = \frac{t}{{(1 - r{R_n})}}\text{,}$ | (2) |
若结构波传递经过N个支座,则总传递系数
| ${T_N} = \prod\limits_N {{t_n}} = {t^N}\prod\limits_N {\left\{ {{{(1 - r{R_n})}^{ - 1}}} \right\}} \text{,}$ | (3) |
对总传递系数取对数可得:
| $\begin{array}{l}\ln {T_N} = N\ln t - \displaystyle\sum\nolimits_1^N {\ln (1 - r{R_n})}= \\\;\;\;\;\;\;\;\; N\ln t + \displaystyle\sum\nolimits_1^N {\sum\nolimits_{p = 1}^\infty {\frac{{{{(r{R_n})}^p}}}{p}} } \text{,}\end{array}$ | (4) |
式中,由于
若不等间距支撑梁的支座间距为随机分布,则重整后反射系数间的相位因子也为随机分布,因此式(4)可化为[5]:
| $\ln {T_N} = N\ln t \pm O({N^{1/2}})\text{。}$ | (5) |
由上式可知,随着结构波传播经过支座数N的增加,总传递系数减小,结构波幅值随传播距离的增加成指数衰减,显现了结构振动的安德森定域效应现象。
安德森定域效应的物理机理在于:结构的不等间距布置,破坏了结构传播波在各支座位置处的相位匹配关系,使得支座对结构波的反射作用增强,传播衰减增大。
1.2 肋骨间距设计方法安德森定域效应以及文献[11]结论,是从无限长结构、支座或者肋骨间距为随机分布且数量较大得出的,而实际工程当中,加肋圆柱壳是有限长的,从工艺等角度看,肋骨间距随机分布较难实现,所以,要寻找既能抑制圆柱壳振动,又能较容易实现的肋骨不等间距布置的方法。下面,把安德森定域效应的结论进行推广,应用到有限长不等间距加肋圆柱壳,并通过数值计算进行检验,但问题的关键是肋骨间距的确定。
无论是无限长还是有限长的结构,肋骨间距的分布,应该满足安德森定域效应产生的物理机理:结构的不等间距布置,要能破坏结构传播波在各支座或肋骨处的相位匹配关系,使得支座或肋骨对结构波的反射作用增强,传播衰减增大。根据文献[11],可以看出,安德森定域效应作用随周向振动模式阶数的升高而加强,也就是随着固有频率的提高,肋骨的阻抗作用变大,相邻子结构间的耦合作用受肋骨阻抗影响而减弱,因此,本文从工程实用的角度出发,采取如下研究思路:
1)研究肋骨不等间距布置对有限长圆柱壳在中高频段的振动特性的影响。
2)取2种肋距,交替排列,为了最大程度满足安德森定域效应产生的条件,尽量增加相邻子结构固有频率差来减弱相邻子结构的耦合作用,这一点,也可以将文献[12]的研究结果进行推广得到:文献[12]通过不等间距分舱增加相邻舱段的固有频率差,从而控制圆柱壳结构振动响应的谱峰频率和幅值,取得了一定效果,把不等间距分舱推广到不等间距肋距,并且研究的频率范围由不等间距分舱的低频段推广到中高频段,能够达到减弱振动的目的。
2 肋骨间距设计在2种情况下,一是只改变肋骨间距,二是只改变壳板厚度,研究两端带肋骨的圆环振动固有频率的变化规律,为后面的加肋圆柱壳肋骨排列形式、壳板厚度分布设计奠定基础。
2.1 肋骨间距对肋骨间圆环振动固有频率的影响 2.1.1 计算模型肋距均匀分布的加肋圆柱壳的结构形式如图2所示,圆柱壳两端用舱壁封堵,改变肋骨间距,外壳板厚度和肋骨尺寸不变,

|
图 2 加肋圆柱壳的结构形式简图 Fig. 2 Diagram of structure form of ring-stiffened cylindrical shell |
计算模型的主要尺度如表1所示,各个模型肋骨间距不同。
|
|
表 1 各计算模型的主要尺度 Tab.1 Main dimensions of models |
对于表1中的5个模型,以每个加肋圆柱壳中间相邻2根肋骨间的圆环为对象,提取周向2个波形的圆环的固有频率,振型如图3所示。
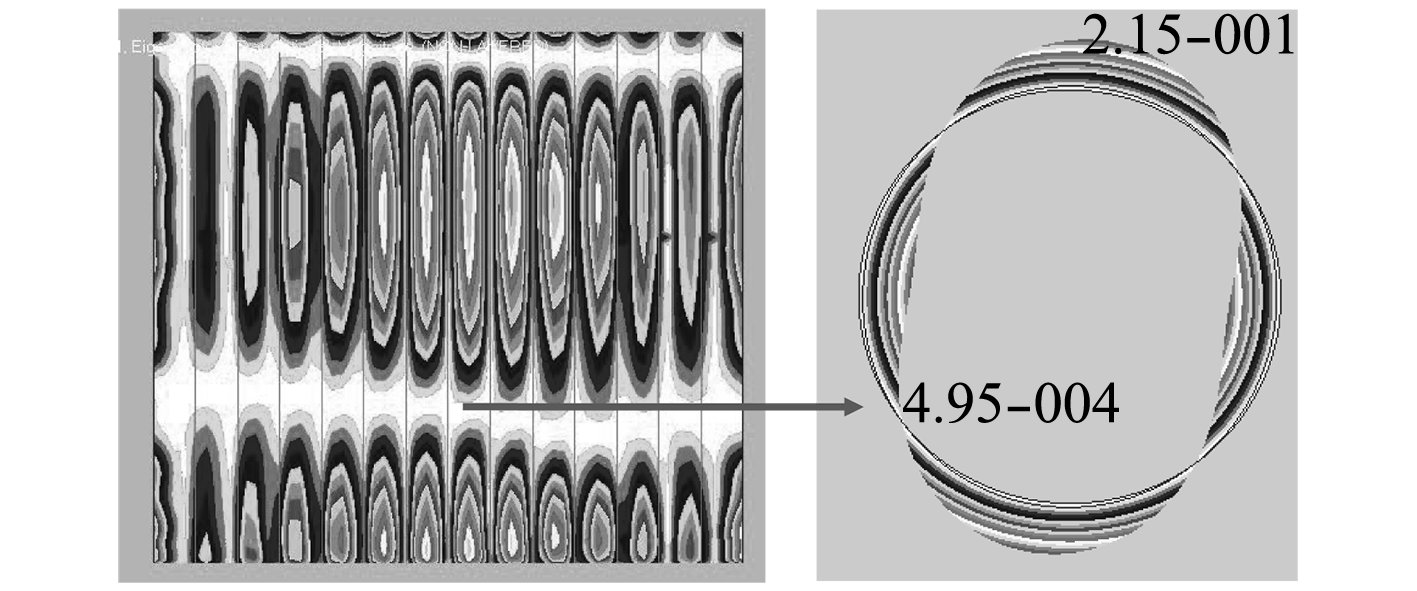
|
图 3 振型图 Fig. 3 Vibration mode |
固有频率随肋骨间距的变化曲线以及该曲线的拟合曲线如图4所示,拟合曲线斜率的绝对值随肋骨间距的变化曲线如图5所示。
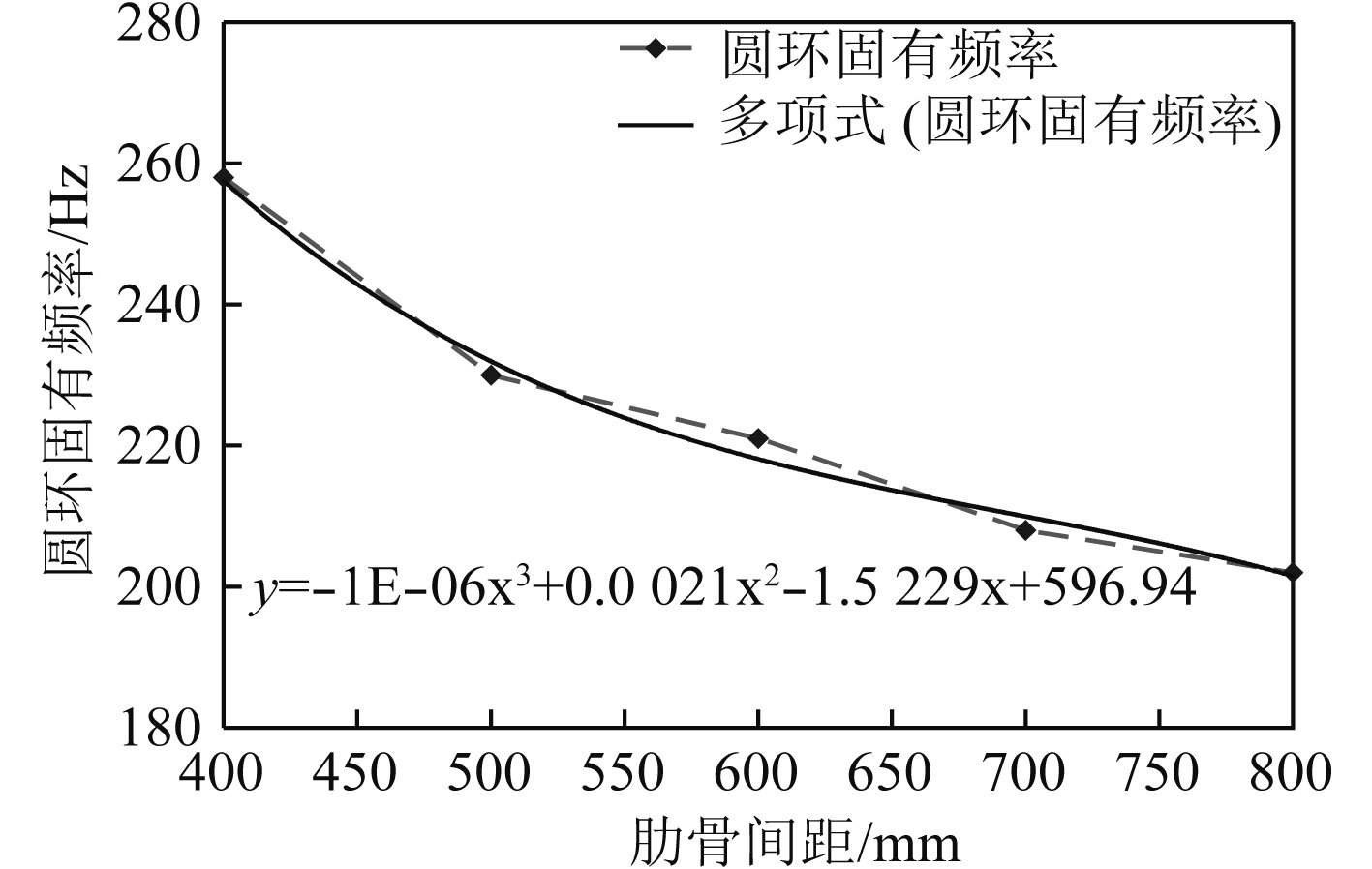
|
图 4 圆环固有频率随肋距的变化 Fig. 4 Variation of natural frequency of ring shell with frame spacing |
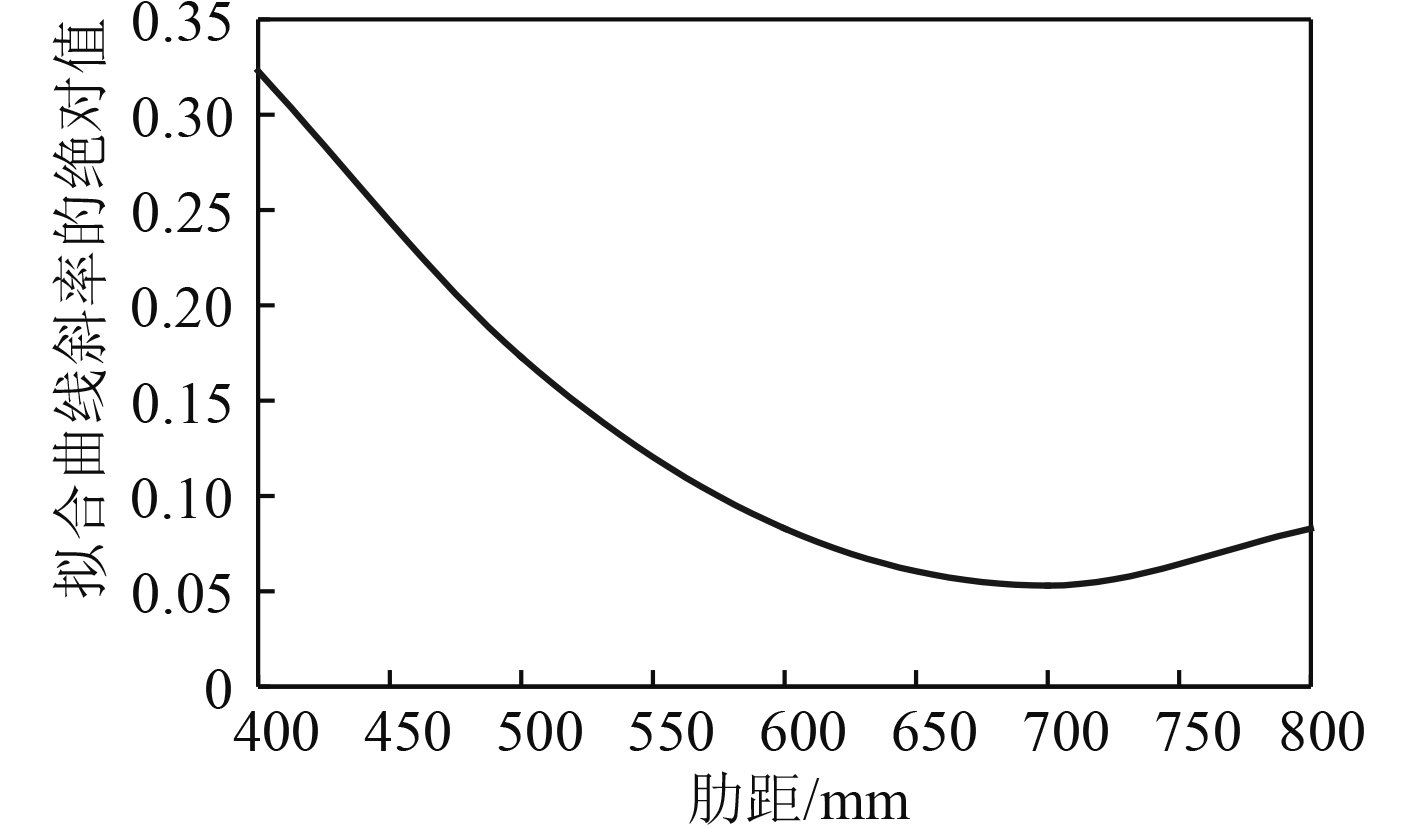
|
图 5 拟合曲线斜率的绝对值 Fig. 5 Absolute value of fitting curve slope |
根据拟合曲线斜率变化的情况,可以看出,肋距在600 mm之前,固有频率变化较快,在600~800 mm之间,固有频率变化较慢,因此,在选择肋骨间距时,在满足布置和工艺等要求的情况下,小间距的应尽量小,大间距的选择700 mm左右就可以,因为再增大肋骨间距,对固有频率变化的改变效果不大。
2.2 板厚对肋骨间圆环振动固有频率的影响 2.2.1 计算模型肋距均匀分布的加肋圆柱壳的结构形式如图2所示,肋骨间距取3个值,分别是400 mm,600 mm,800 mm,对每个肋骨间距,圆柱壳板厚分别取28 mm,32 mm,36 mm,40 mm,44 mm,因此,构造了3组圆柱壳,每组5个,各圆柱壳肋骨尺寸不变,同2.1.1节模型,圆柱壳两端用舱壁封堵。
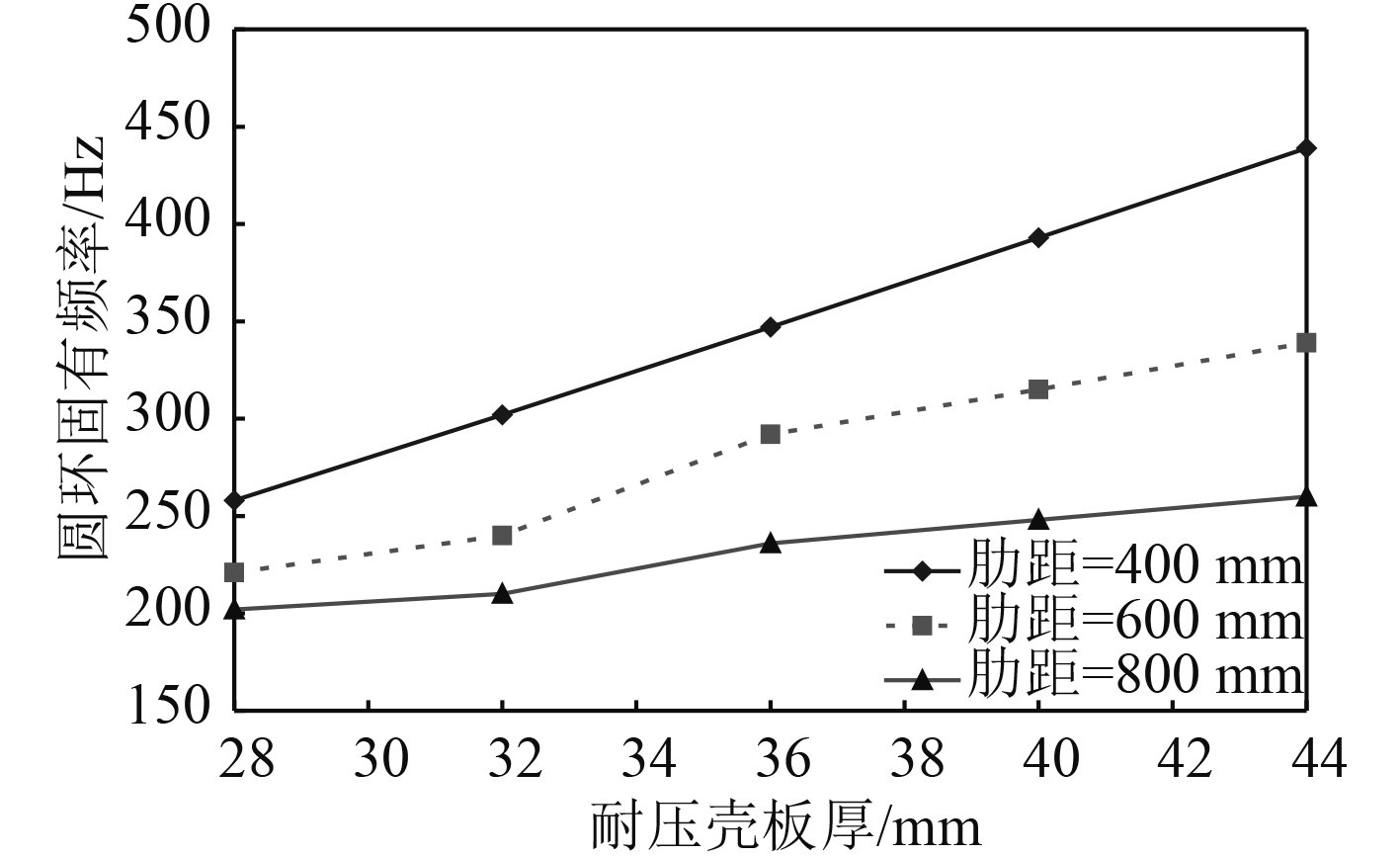
2.2.2 计算结果以每个加肋圆柱壳中间相邻2根肋骨间的圆环为对象,提取周向2个波形圆环的固有频率,结果如图6所示。
|
图 6 圆环固有频率随壳板板厚的变化 Fig. 6 Variation of natural frequency of ring shell with shell plate thickness |
根据图6的结果,可以看出:
1)圆环固有频率随着圆柱壳板厚的增加而增大;
2)肋骨间距小,固有频率增大的速度快,肋骨间距大,固有频率增大的速度慢;
3)随着圆柱壳板厚的增加,肋距600 mm与肋距400 mm,800 mm相比,固有频率差别都较大,因此,当肋距选择800 mm时,为了与肋距600 mm时的固有频率差尽量大,板厚应大于36 mm。
3 加肋圆柱壳振动响应对比研究 3.1 加肋圆柱壳结构设计1)等间距加肋圆柱壳结构设计
肋骨间距600 mm,圆柱壳板厚28 mm,圆柱壳长度8 400 mm,两端的舱壁不变,圆柱壳的结构形式如图7(a)所示。
2)不等间距加肋圆柱壳结构设计
根据2.1.2节和2.2.2节的结论,选择2种肋骨间距,分别是400 mm,800 mm,肋距400 mm之间圆柱壳板厚28 mm,肋距800 mm之间圆柱壳板厚分别选28 mm,32 mm,36 mm,40 mm,44 mm,因此,一共构造了5个不等间距加肋圆柱壳,即5个计算模型,圆柱壳长度都是8 400 mm,两端的舱壁不变,圆柱壳的结构形式如图7(b)所示。

|
图 7 加肋圆柱壳结构设计 Fig. 7 Structure design of ring-stiffened cylindrical shell |
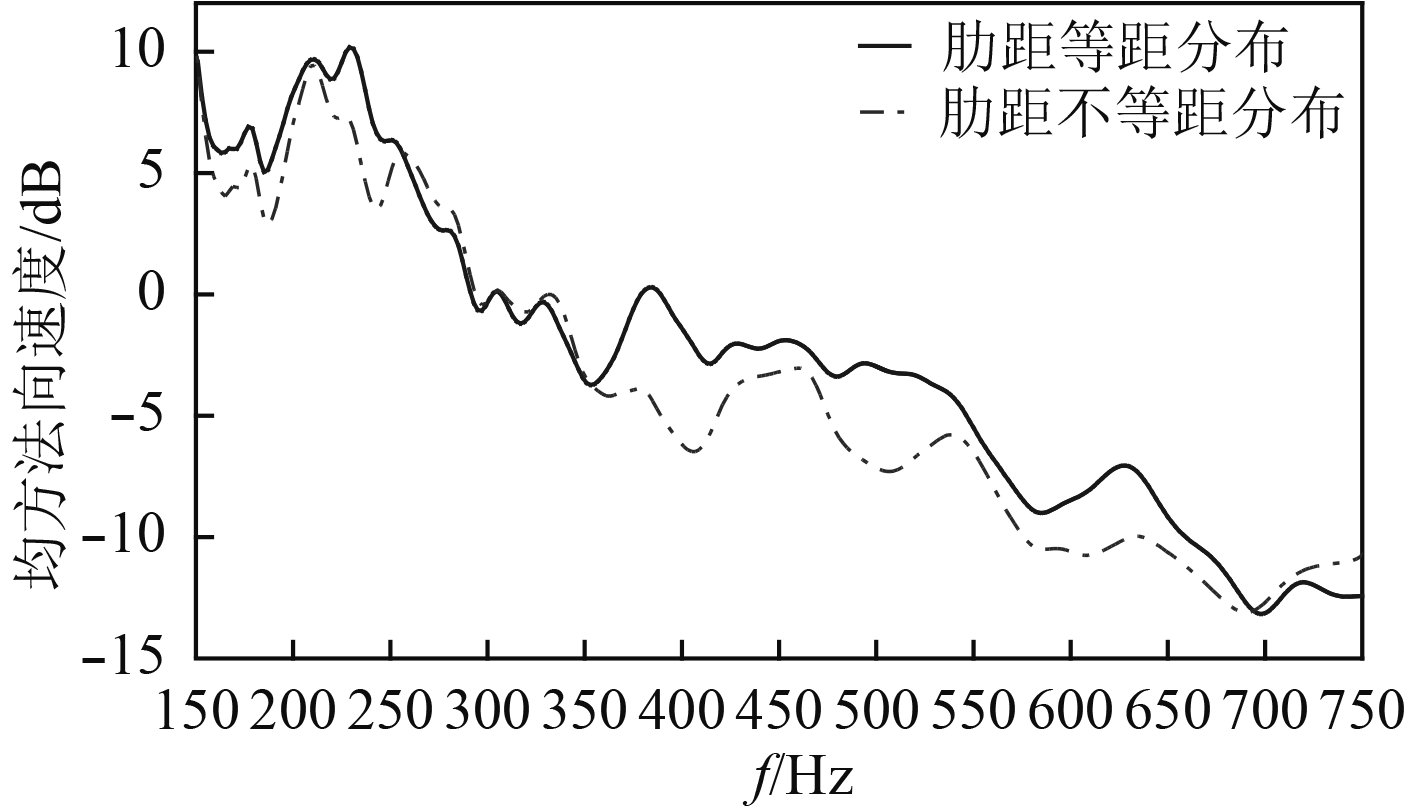
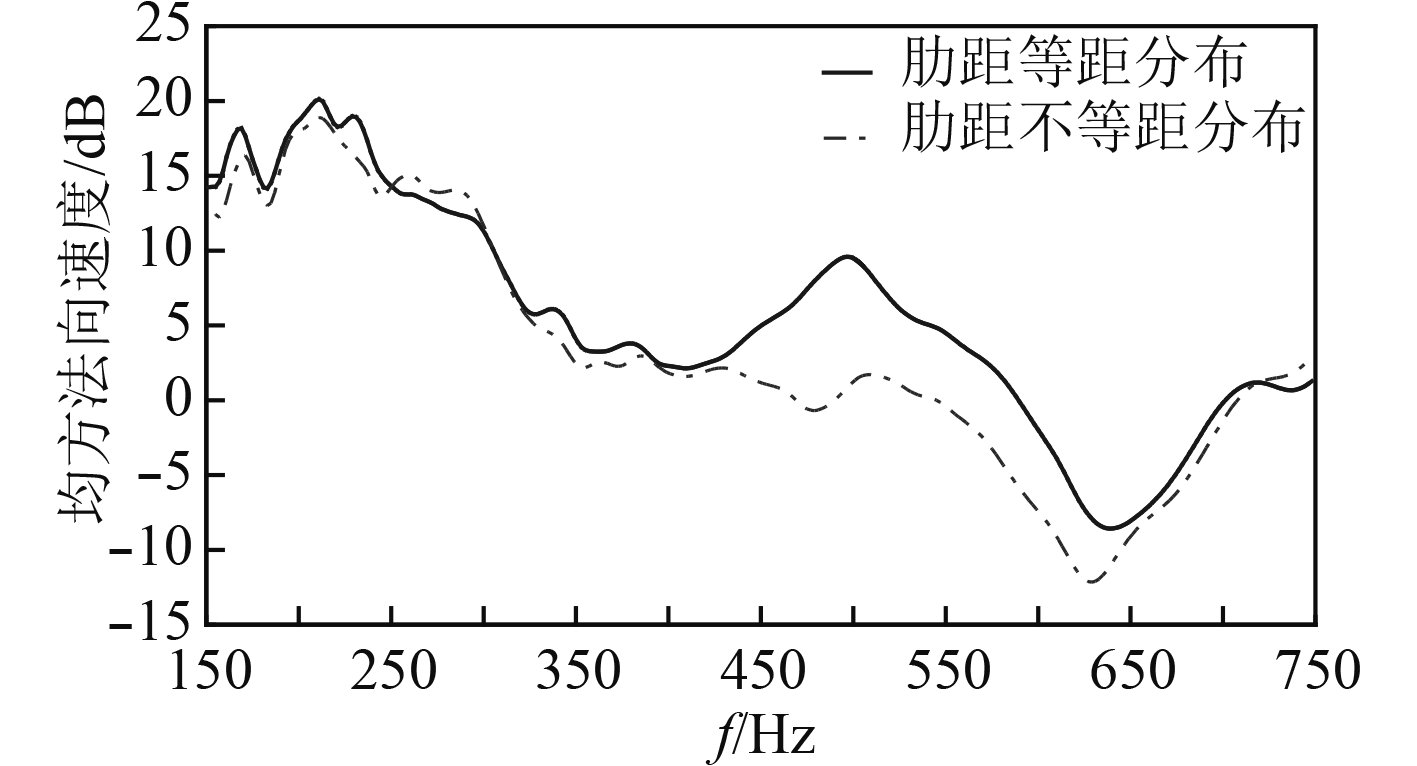
分别计算等间距和不等间距加肋圆柱壳在空气中的振动响应,计算工况有2个,分别是舱壁浮筏基座处轴向激振、垂向激振,激振力的频率范围20~1 000 Hz,对比分析各模型的均方振速,均方振速的计算公式参见文献[12]。可以看出,等间距加肋圆柱壳和不等间距加肋圆柱壳中的肋距800 mm之间圆柱壳板厚44 mm的模型的振动响应差别最为明显,如图8和图9所示。图8表示轴向激振的结果,图9表示垂向激振的结果。
|
图 8 轴向激振力作用下圆柱壳均方振速级比较 Fig. 8 Comparison of level of mean square speed of cylindrical shell under axial loads |
|
图 9 垂向激振力作用下圆柱壳均方振速级比较 Fig. 9 Comparison of level of mean square speed of cylindrical shell under vertical loads |
1)对于有限长加肋圆柱壳,当激振力的激振频率小于350 Hz时,肋骨采用等间距排列形式和不等间距排列形式,振动响应相差不大其原因是:低频时结构波长较长,肋骨排列形式对壳体总振动影响较小,随着频率增高,结构波长变短,肋骨排列形式对壳体振动的影响才体现出来;当激振力的激振频率大于350 Hz而小于700 Hz时,肋骨采用不等间距排列形式,相对于肋骨采用等间距排列形式,可以减弱结构振动。
2)对于有限长圆柱壳,肋距不等间距分布,可以达到降低圆柱壳振动的目的,但是,只是在较窄的一定的频率(一般是中高频率)范围内。
4 结 语本文对不等间距加肋圆柱壳的振动特性进行研究。将安德森定域效应的原理进行推广,按照尽量增加相邻子结构固有频率差来减弱相邻子结构的耦合作用的思路,设计了不等间距加肋圆柱壳肋骨间距的分布形式,计算并比较了加肋圆柱壳的振动响应,可以看出:
1)肋骨排列形式对圆柱壳振动的影响主要体现在结构波波长小于肋间距的中高频,低频时影响不大;
2)在一定频率(一般是中高频率)范围内,采取不等间距肋距分布形式可以减弱加肋圆柱壳的振动响应;
3)采用尽量增加相邻子结构固有频率差的思路确定有限长圆柱壳肋骨间距可行;
4)在以后的研究中,可以基于此基础上进行进一步的研究。
| [1] |
SEN GUPTA G. Natural flexural waves and the normal modes of periodically-supported beams and plates[J]. Journal of Sound and Vibration, 1970, 13(1): 89-101. DOI:10.1016/S0022-460X(70)80082-7 |
| [2] |
ICHCHOU M N, BERTHAUT J, COLLET M. Multi-mode wave propagation in ribbed plates: part II, predictions and comparisons[J]. International Journal of Solids and Structures, 2008, 45: 1179-1195. DOI:10.1016/j.ijsolstr.2007.09.032 |
| [3] |
MEAD D J. Wave propagation in continuous periodic structures: research contributions from Southampton, 1964-1995[J]. Journal of Sound and Vibration, 1996, 190(3): 495-524. DOI:10.1006/jsvi.1996.0076 |
| [4] |
BANSAL A S. Collective and localized modes of mono-coupled multi-span beams with large deterministic disorders[J]. The Journal of Acoustical Society of America, 1997, 102(6): 3806-3809. DOI:10.1121/1.420406 |
| [5] |
HODGES C H. Confinement of vibration by structural irregularity[J]. Journal of Sound and Vibration, 1982, 82(3): 411-424. DOI:10.1016/S0022-460X(82)80022-9 |
| [6] |
BANSAL A S. Flexural waves and deflection mode shapes of periodic and disordered beams[J]. The Journal of Acoustical Society of America, 1982, 72(2): 476-481. DOI:10.1121/1.388103 |
| [7] |
BANSAL A S. Free waves in periodically disordered systems: natural and bounding frequencies of unsymmetric systems and normal mode localization[J]. Journal of Sound and Vibration, 1997, 207(3): 365-382. DOI:10.1006/jsvi.1997.1094 |
| [8] |
BOUZIT D, PIERRE C. An experimental investigation of vibration localization in disordered multi-span beams[J]. Journal of Sound and Vibration, 1995, 187(4): 649-669. DOI:10.1006/jsvi.1995.0550 |
| [9] |
HODGES C H, WOODHOUSE J. Confinement of vibration by one-dimensional disorder I: theory of ensemble averaging[J]. Journal of Sound and Vibration, 1989, 130(2): 237-251. DOI:10.1016/0022-460X(89)90552-X |
| [10] |
HODGES C H, WOODHOUSE J. Confinement of vibration by one-dimensional disorder II: a numerical experiment on different ensemble averages[J]. Journal of Sound and Vibration, 1989, 130(2): 253-268. DOI:10.1016/0022-460X(89)90553-1 |
| [11] |
PHOTIADIS D M. Localization of helical flexural waves by irregularity[J]. The Journal of Acoustical Society of America, 1994, 96(4): 2291-2301. DOI:10.1121/1.410101 |
| [12] |
刘文玺, 周其斗. 不等间距分舱结构声辐射特性研究[J]. 船舶力学, 2016, 20(8): 1045-1058. LIU Wenxi, ZHOU Qidou. Study on characteristics of acoustic radiation from the cabin structure with nonuniform subdivision[J]. Journal of Ship Mechanics, 2016, 20(8): 1045-1058. DOI:10.3969/j.issn.1007-7294.2016.08.014 |
 2018, Vol. 40
2018, Vol. 40
