环肋加强圆柱壳结构是潜艇耐压结构的典型结构型式。真实结构形状与理论圆柱之间的偏差称为初挠度,这种初挠度对结构的强度和承载能力都有一定影响[1]。国内学者和科研工作者针对耐压圆柱壳初挠度的影响做了大量分析工作:徐秉汉等[2]推导了计及初始挠度的潜艇耐压圆柱壳大挠度弹塑性失稳临界压力的理论计算方法;王林等[3]研究壳板初挠度在一定范围内对耐压结构极限承载能力的影响;朱邦俊等[4]从理论上分析了壳板和肋骨初挠度允许标准的合理性并提出了建议;邱昌贤等[5]研究了内、外肋骨局部内凹、外凸和整体椭圆度对圆柱壳结构强度和稳定性的具体影响特征,算例表明,肋骨径向初挠度在一定范围内,环肋圆柱壳结构的局部、总体弹性稳定性基本不变,对初挠度不敏感,考虑材料非线性的破坏压力也基本不变;李明[6]根据工程实际,研究了潜艇肋骨初挠度的换算方法。
耐压圆柱壳的肋骨是保证耐压船体结构强度和稳定性的关键部件。我国现行的潜艇设计规范[7](以下简称《规范》)中,规定肋骨径向初挠度的允许值
针对耐压圆柱壳肋骨的超差加强方案,文献[8]提出从强度和稳定性2个方面考虑,既保证肋骨的强度又保证壳体的稳定。文献[8]从强度的观点出发,得出肋骨超差加强所需面积的计算公式与《规范》中的式(16.7)相同;在限制超差肋骨附加挠度基础上、从舱段稳定性的角度,推导了肋骨超差加强所需面积的计算公式。杨正忠[9]通过分析认为仅仅控制超差肋骨附加挠度不合理,并建议限制肋骨初挠度和附加挠度之和,虽然比文献[8]合理,但附加挠度允许值如何确定,在工程上还无法量化,导致公式缺乏实用性。
通过上述分析,结合工程实际情况,针对耐压圆柱壳肋骨超差加强计算中的2个问题进行研究:1)《规范》中从肋骨强度观点出发的公式(16.4)和(16.7)略有不同,2个公式不同会引起一定的误差;2)肋骨超差加强是否有必要从稳定性的角度考虑。本文通过理论分析、仿真计算和对比分析,为肋骨超差加强方案提供参考依据和合理化建议。
1 规范中肋骨径向初挠度的超差加强公式分析从强度的观点来看,肋骨初挠度的存在将使肋骨应力增加[8]。环肋加强的耐压圆柱壳在均布外压下,外肋骨内凹(或内肋骨外凸)时,肋骨最大应力
| ${\sigma _{{\rm{max}}}} = {\sigma _{{f}}} + {M_{\max }}/{W_{\min }}{\text{。}}$ | (1) |
其中:
| ${M_{\max 1}} = {P_c}Rl\left( {{\omega _f} + {\omega _c}} \right){\text{,}}$ | (2) |
| ${M_{\max 2}} = \frac{{EI}}{{{R^2}}}({n^2} - 1){\omega _f}{\text{。}}$ | (3) |
其中:
| ${\omega _f} = \frac{{{\omega _c}}}{{\displaystyle\frac{{{P_E}}}{{{P_c}}} - 1}}{\text{。}}$ | (4) |
在计算肋骨应力时,《规范》根据最大超差值,通过公式(16.4)、式(1)、式(2)推导得到最大应力,并判断是否超过
| ${\omega _{f1}} = \frac{{{\omega _c}}}{{\displaystyle\frac{{{P_E}}}{{{P_e}}} - 1}}{\text{。}}$ | (5) |
其中:
《规范》中第1步计算得到的肋骨最大应力如果超过
《规范》中公式(16.4)与公式(16.7)均从强度的观点计算肋骨应力,但最大附加弯矩
|
|
表 1 舱段典型部位计算结果 Tab.1 The result of typical parts on cabin |
|
|
表 2 肋骨附加弯矩计算公式不同时的肋骨应力计算结果 Tab.2 The stress result of rib with different formulas for additional bending moment |
从表2可知,计算得到的肋骨应力值大,且当初挠度引起肋骨应力超过时,2个公式计算得到的加强扁钢规格也不同。
为了验证2个公式的准确性,采用仿真软件Ansys来计算肋骨应力值。有限元模型利用APDL参数化编写程序[11],参照《规范》中肋骨径向偏差16点测量法,首先根据肋骨的半径和偏差值确定肋骨上16个点的坐标,再用拟合曲线模拟带初挠度的肋骨形状,最后以肋骨为边界建立壳板有限元模型。本文按文献[10]中假设的肋骨周向波数为3的正弦波形作为肋骨初挠度形状,有限元模型中,壳板单元采用SHELL181单元,肋骨采用BEAM188单元,带初挠度的肋骨有限元示意图见图1所示。
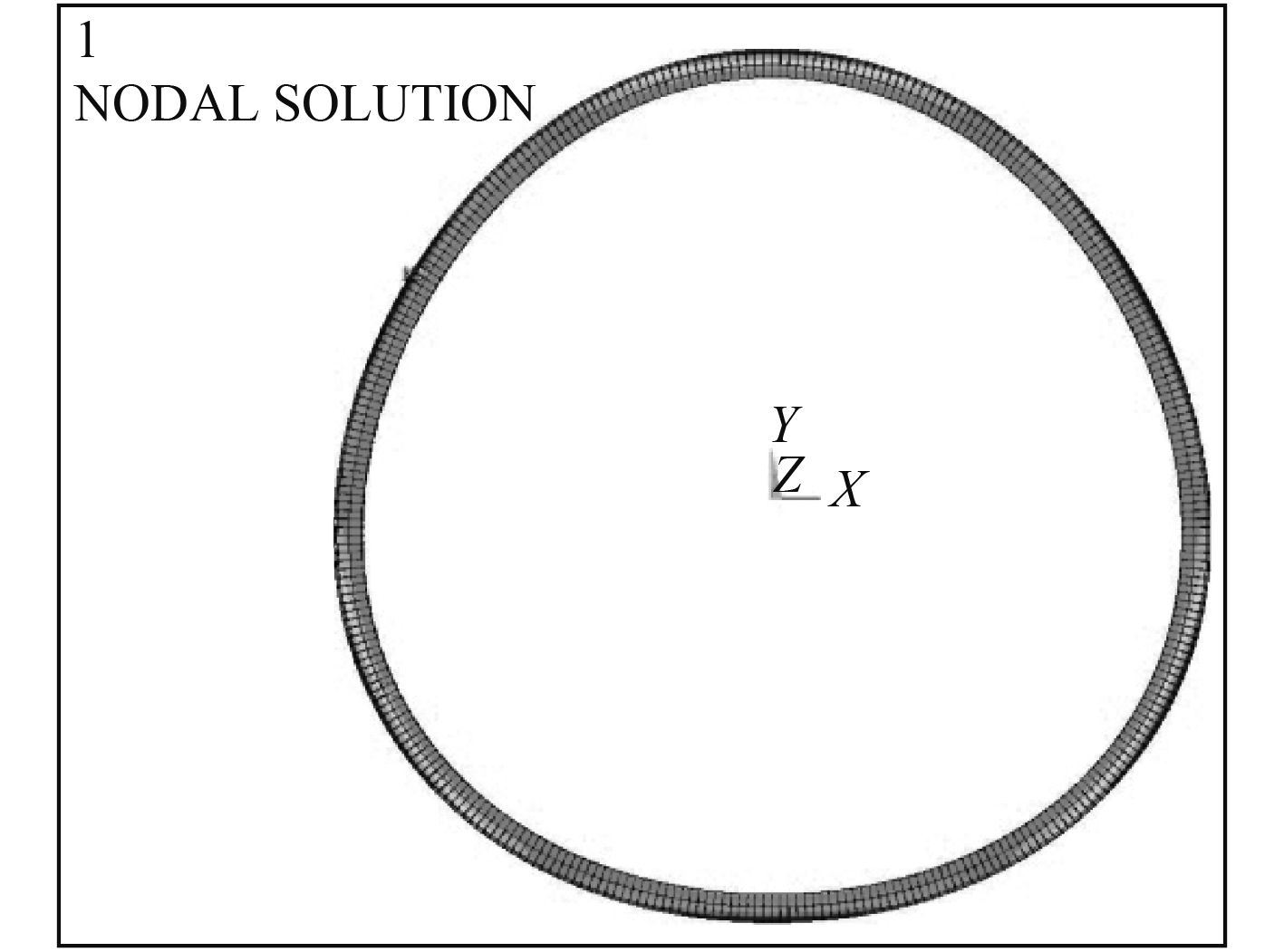
|
图 1 带初挠度的肋骨有限元模型示意图 Fig. 1 The finite element model of rib with initial radial deformation |
分别计算所有肋骨初挠度为0.002 5R,0.003 1R,0.005R时的肋骨应力,计算结果表明:1)外肋骨外凸时肋骨应力减小、内凹时肋骨应力增大;2)有限元计算得到上述3种初挠度的肋骨最大应力值分别为–455 MPa,–493 MPa,–626 MPa,与公式I的理论计算值接近,最大误差1.1%,初挠度为0.005R时的计算结果见图2所示。
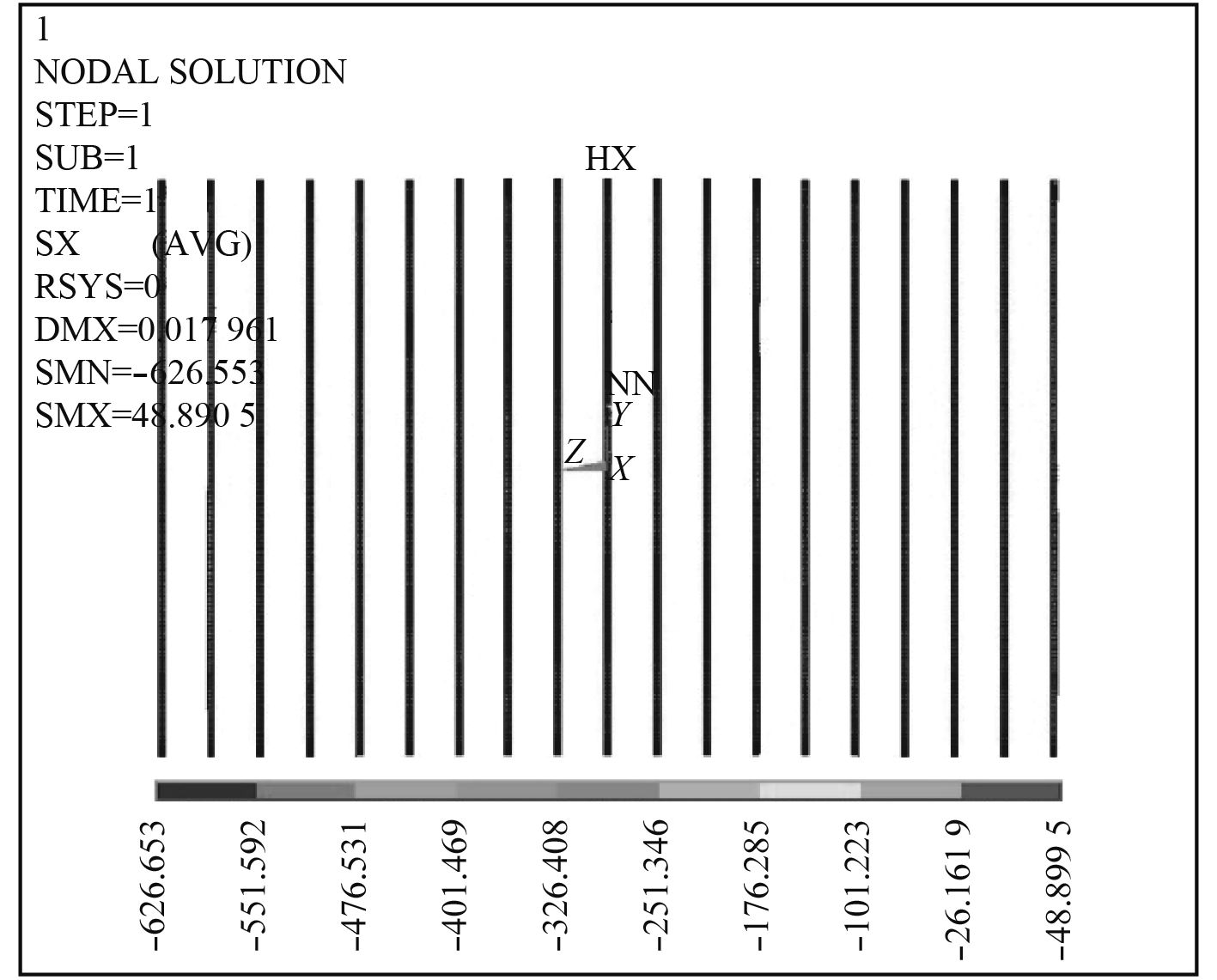
|
图 2 初挠度为0.005R时肋骨的有限元仿真计算结果 Fig. 2 Finite element simulation result of ribs with 0.002 5R initial radial deformation |
《规范》中规定对外肋骨内凹超差点向外侧各延伸
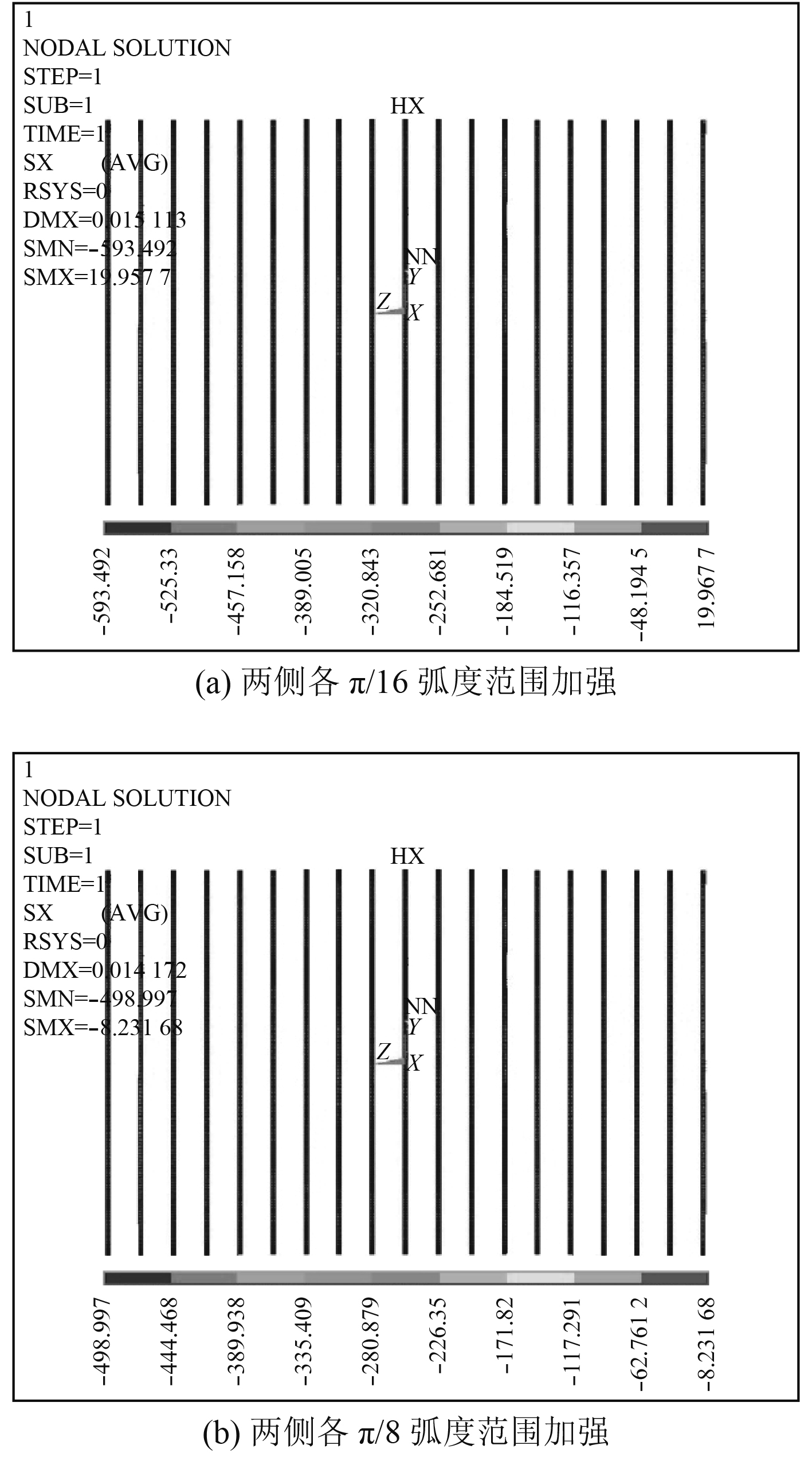
|
图 3 超差肋骨加强后的的仿真计算结果 Fig. 3 Finite element simulation results of strengthened ribs with initial radial deformation |
结合理论与仿真计算结果的对比,建议采用计算公式I校核肋骨的应力及计算超差肋骨加强扁钢的面积,经推导,加强扁钢面积A应满足下式:
| $A \geqslant \left(\frac{{{P_c}Rl{\omega _c}}}{{{\sigma _s} - {\sigma _f}}} \times \frac{{{P_E}}}{{{P_E} - {P_e}}} - {W_{\min }}\right)/h{\text{。}}$ | (6) |
其中,h为肋骨型材的高度,其余各参数同本文前述定义。
3 肋骨径向初挠度对舱段结构稳定性的影响《规范》中计算舱段的实际失稳临界压力,首先基于弹性稳定性理论导出理论临界压力,然后引入2个修正系数,分别计及几何和材料非线性的影响,最终得到耐压圆柱壳实际失稳临界压力,其中,几何非线性考虑了肋骨0.002 5R初挠度的影响。在通过非线性仿真计算前述舱段的失稳临界压力值时,材料非线性采用简化的材料应力—应变曲线,几何非线性通过拟合肋骨初挠度实现、计算求解控制中考虑大变形对非线性计算的影响。图4为舱段仿真计算结果,舱段理想弹性失稳临界压力7.98 MPa,失稳临界压力为4.22 MPa、与理论值吻合。
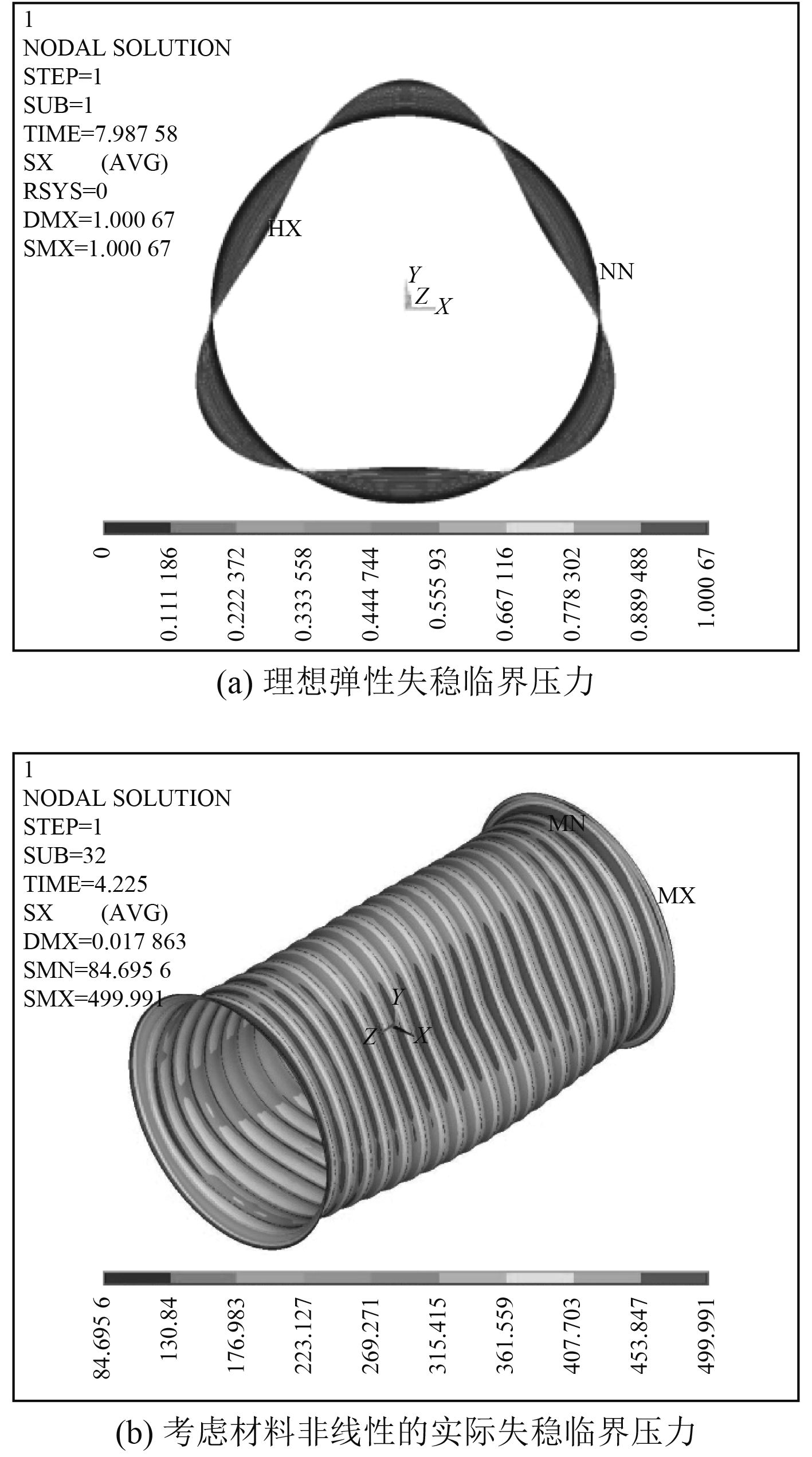
|
图 4 考虑肋骨0.002 5R初挠度时舱段失稳临界压力仿真计算结果 Fig. 4 Finite element simulation result of cabin's critical pressure when ribs have 0.002 5R initial radial deformation |
随着船厂建造工艺水平的提高,在潜艇的实际建造中,肋骨初挠度超差的肋骨数量很少,即使舱段有1~2根肋骨初挠度超过允许值,超过的幅度也不会很大。本文假设一种实艇超差的极限情况,即舱段中间最多有连续3根肋骨同时超差,且超差相位角相同,通过仿真来计算舱段的失稳临界压力。
从强度的观点出发,本文前述舱段方案中肋骨初挠度0.003 1R时,肋骨仍不需要加强;肋骨初挠度为0.005R时,肋骨取70 mm×16 mm的扁钢进行加强。各方案计算结果如表3所示,仿真结果如图5所示。计算结果表明:不考虑材料非线性影响时,初挠度对舱段的理想弹性失稳临界压力基本没有影响;部分肋骨超差、采取必要的加强措施后,舱段失稳临界压力值均比典型舱段的临界压力值大。因此,部分肋骨具有径向初挠度时按强度要求加强后,对舱段结构稳定性没有影响,可不从稳定性的角度考虑肋骨超差加强方案。
|
|
表 3 肋骨不同初挠度时舱段临界压力 Tab.3 The cabin's critical pressure when ribs have different initial radial deformation |

|
图 5 舱段临界压力仿真计算结果 Fig. 5 Finite element simulation result of cabin's critical pressure |
针对环肋圆柱结构的肋骨径向初挠度超差加强方案,基于理论分析、仿真计算和对比分析,提出可供实际工程借鉴的结论和合理化建议。主要结论如下:
1)《规范》中采用的肋骨最大应力计算公式(16.4)是基于本文所示计算公式I推导得到,系列仿真计算结果与理论计算结果吻合,可验证计算公式的准确性。
2)肋骨超差加强的扁钢面积建议按本文式(6)计算,且《规范》中要求的加强范围自超差点向外侧各延伸
3)部分肋骨具有径向初挠度时按强度要求加强后,可满足舱段稳定性要求,不需从稳定性的角度考虑肋骨超差加强方案。
| [1] |
谢祚水, 王自力, 吴剑国. 潜艇结构分析[M]. 武汉: 华中科技大学出版社, 2004.
|
| [2] |
徐秉汉, 朱邦俊, 欧阳吕伟, 等. 现代潜艇结构强度的理论与试验[M]. 北京: 国防工业出版社, 2007.
|
| [3] |
王林, 李峰, 田冀锋. 初始缺陷对耐压圆柱壳结构极限承载能力的影响[J]. 江苏科技大学学报(自然科学版), 2009, 23(1): 1-4. WANG Lin, LI Feng, TIAN Ji-feng. Effects of initial defects to the limit load of pressure cylinder shell[J]. Journal of Jiangsu University of Technology (Natural Science), 2009, 23(1): 1-4. DOI:10.3969/j.issn.1673-4807.2009.01.001 |
| [4] |
朱邦俊, 葛沈瑜, 王丹. 潜艇耐压船体初挠度的应力分析及允许偏差的讨论[J]. 纪念徐秉汉院士船舶与海洋结构力学学术会议论文集, 2011, 33-41. ZHU Bang-jun, GE Shen-yu, WANG Dan. Stress analysis of submarine pressure hull structures with initial deflection and discussion of allowable deflection[J]. Proceedings of the Academic Conference on Ship and Marine Structural Mechanics in Memory of Academician Xu Binghan, 2011, 33-41. |
| [5] |
邱昌贤, 黄进浩, 秦天. 内外肋骨径向初挠度对环肋圆柱壳结构强度的影响分析[J]. 舰船科学技术, 2016, 38(1): 24-31. QIU Chang-xian, HUANG Jin-hao, QIN Tian. Strength analysis for cylindrical shell circumferentially stiffened by internal or external ribs with initial radial deformation[J]. Ship Science and Technology, 2016, 38(1): 24-31. DOI:10.3404/j.issn.1672-7649.2016.1.005 |
| [6] |
李明. 潜艇肋骨初挠度计算研究[J]. 船海工程, 2012, 41(2): 40-42. LI Ming. Study on calculation of initial deflection of submarine ribs[J]. Ship and Ocean Engineering, 2012, 41(2): 40-42. |
| [7] |
国防科学技术工业委员会. 潜艇结构设计计算方法: GJB/Z21A-2001[S]. 北京: 国防科学技术工业委员会, 2001. National defense science & Technology Industry Committee. Methods for design and calculation of submarine structure: GJB/Z 21A-2001[S]. Beijing: National defense science & Technology Industry Committee, 2001. |
| [8] |
许辑平. 潜艇强度[M]. 北京: 国防工业出版社, 1980.
|
| [9] |
杨正忠. 潜艇肋骨圆度超差加强计算存在的问题及改进建议[J]. 舰船科学技术, 1985, 10: 61-66. YANG Zheng-zhong. Problems existing in strengthening calculation of skeleton roundness exceeding difference of submarine and suggestions for improvement[J]. Ship Science and Technology, 1985, 10: 61-66. |
| [10] |
第六机械工业部. 潜艇结构设计计算规则说明书. CB/Z 148.2-20[S]. 北京: 第六机械工业部, 1980. Sixth Ministry of Machinery Industry. Specification for calculation rules of submarine structure design. CB/Z148.2-20[S]. Beijing: Sixth Ministry of Machinery Industry, 1980. |
| [11] |
阚前华. ANSYS高级工程应用示例分析与二次开发[M]. 北京: 电子工业出版社, 2006.
|
 2018, Vol. 40
2018, Vol. 40
