随着深海资源的开采探测越来越频繁,船舶动力定位(DP)系统越来越受到重视。DP主要通过推进装置抵御外界风、浪、流的干扰,实现海上勘探、钻井、布管等作业。海浪干扰可分为一阶波浪引起的高频分量和二阶波浪引起的低频分量。其中高频分量使船舶推进器产生不必要的机械磨损和燃料消耗,需要进行滤除,因此动力定位系统滤波器的研究一直是一个热点[1]。
20世纪60年代第1代动力定位系统采用了陷波滤波器,其结构简单,易于实现,但是会产生相位滞后,使系统稳定性变差。80年代后,第2代动力定位系统采用卡尔曼滤波器 [2],其设计基于船舶模型,实时更新滤波参数,不会产生相位滞后,滤波效果比陷波滤波器更好。但卡尔曼滤波算法是一种线性算法,针对复杂海况下非线性的船舶系统滤波效果并不理想。为解决线性化问题,采用扩展卡尔曼滤波器,按首摇角度均分为36个工作点,进行分段线性化,但是需要调节的参数很多,过程噪声、测量噪声的协方差矩阵只能根据设计者的经验来确定,系统的稳定性无法得到保证。近些年,非线性滤波器算法的研究成为了重点[3-7]。
无源性理论最早由Popov提出[8],有效解决了非线性问题,1974年Desoer从理论上给出了无源系统的稳定性证明[9]。将无源性理论引入动力定位系统滤波器设计中,可以直接解决非线性问题,不需要进行模型线性化,滤波更精确;其滤波器参数可以根据海浪参数进行确定,调节简单,易于实现;其稳定性可以由李亚普诺夫稳定性判据进行证明,能实现滤波算法收敛稳定[10]。
1 无源性理论m输入l输出非线性系统如下式所示:
| $S:\left\{ {\begin{aligned}& {\dot x = f(x,u)}{\text{,}}\\& {y = h(x,u)}{\text{。}}\end{aligned}} \right.$ | (1) |
其中:
无源性定义:如果存在半正定函数
| $\int_0^\tau {{u^{\rm T}}} y{\rm d}t \geqslant S(x(\tau )) - S(x(0)) + \int_0^\tau {W(x){\rm d}t}{\text{,}}$ | (2) |
无源性证明:
KYP引理:设
| ${{PA}} + {{A}^{\rm T}}{{P}}= - {{{L}}^{\rm T}}L - \varepsilon {{P}}{\text{,}}$ |
| ${{PB}}= {{{C}}^{\rm T}} - {{{L}}^{\rm T}}{{W}}{\text{,}}$ |
| ${{{W}}^{\rm T}}{{W}} ={{D}} + {{{D}}^{\rm T}}$ |
时,
无约束的船舶模型是六自由度的,如图1所示。
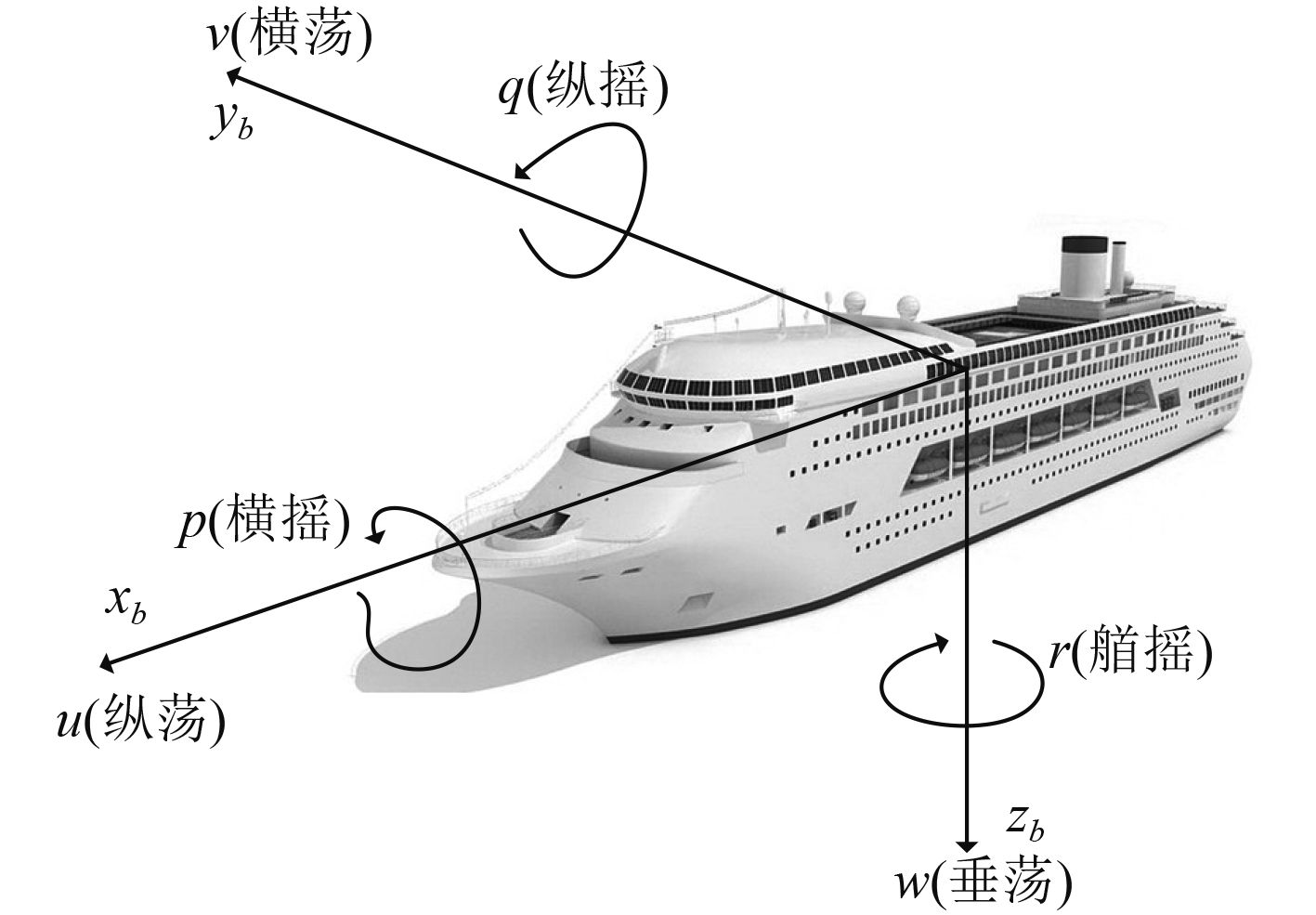
|
图 1 六自由度船舶示意图 Fig. 1 Schematic diagram of 6-DOF ships |
水面船舶可以只考虑纵荡、横荡、首摇等3个自由度运动。为描述船舶运动,建立地球固定坐标系

|
图 2 固定坐标系和随船坐标系 Fig. 2 Earth fixed and body fixed coordinates |
定义向量
| $\dot{\eta} = {{J}}(\varphi ){\upsilon}{\text{,}} $ | (3) |
其中
| ${{J}}(\varphi ) = \left[ {\begin{array}{*{20}{c}}{\cos \varphi }&{ - \sin \varphi }&0\\{\sin \varphi }&{\cos \varphi }&0\\0&0&1\end{array}} \right]{\text{。}}$ | (4) |
船舶动力学模型如式(5)–式(8)所示:
| $\dot{\xi} = {\varOmega}{\xi}+ {\varSigma} { w}{\text{,}}$ | (5) |
| $\dot b = - {{{T}}^{ - 1}}b + {{ w}_b}{\text{,}}$ | (6) |
| ${{M}}\dot{\upsilon} + {{D}}{\upsilon} = {\tau}+ {{J}}(\varphi )b + {{ w}_l}{\text{,}}$ | (7) |
| $y ={\eta}+ {\varGamma}{\xi}+ {{ w}_y}{\text{。}}$ | (8) |
其中:
| $\mathop {\hat {\xi}}\limits^ \cdot = {\varOmega}\hat {\xi}+ {{ K}_1}\tilde y{\text{,}}$ | (9) |
| $\mathop {\hat{\eta}}\limits^. ={ J}(\varphi )\dot {\upsilon}+ {{ K}_2}\tilde y{\text{,}}$ | (10) |
| $\mathop {\hat b}\limits^. = - {{ T}^{ - 1}}\hat b + {{ K}_3}\tilde y{\text{,}}$ | (11) |
| ${ M}\mathop {\hat {\upsilon}}\limits^. = -{ D}\hat {\upsilon} + {{ J}^{\rm T}}(\varphi )\hat b + \tau + {{ K}_4}\tilde y{\text{,}}$ | (12) |
| $\tilde y = \hat{\eta}+ {\hat{\eta}_w}{\text{。}}$ | (13) |
其中:K1,K2,K3,K4为调节参数;
定义变量
| $\mathop {{{\hat \eta }_o}}\limits^ \cdot = {A_o}{\hat \eta _o} + {B_o}{ J}(\varphi )\hat{\upsilon}+ {K_o}\tilde y{\text{,}}$ | (14) |
| $\hat y = {C_o}{\hat \eta _o}{\text{。}}$ | (15) |
其中:
定义滤波器估计误差
| $\mathop {\tilde x}\limits^. ={ A}\tilde x +{{BJ}}(\varphi )\tilde{\upsilon}{\text{,}}$ | (16) |
| $\tilde z = { C}\tilde x{\text{。}}$ | (17) |
其中
滤波器误差动态特性如图3所示。

|
图 3 滤波器动态误差示意图 Fig. 3 Schematic diagram of filter dynamic errors |
选取正定函数V满足
| $V = \frac{1}{2}{\tilde {\upsilon}^{\rm T}}{ M}\tilde{\upsilon}{\text{,}}$ | (18) |
对时间求导得:
| $\dot V = - \frac{1}{2}{\tilde {\upsilon}^{\rm T}}({ D} + {{ D}^{\rm T}})\tilde{\upsilon} - {\tilde z^{\rm T}}{ J}(\varphi )\tilde{\upsilon} {\text{,}}$ | (19) |
代入
| $\dot V = - \frac{1}{2}{\tilde {\upsilon}^{\rm T}}({ D} + {{ D}^{\rm T}})\tilde {\upsilon}+ {\tilde{\upsilon} ^{\rm T}}{\varepsilon _z}{\text{,}}$ | (20) |
进行积分得到:
| $\int_{{t_0}}^t {\varepsilon _z^{\rm T}} \tilde{\upsilon} (\tau ){\rm d}\tau \geqslant \alpha {\tilde {\upsilon}^{\rm T}}\tilde{\upsilon}+ \beta {\text{。}}$ | (21) |
其中:
由无源性定义式(2)可知子系统H1是严格无源的。
4.3 子系统H2无源性分析选取合适的增益矩阵
设
由于
| $\tilde z(s) = {H_o}(s){H_B}(s){\varepsilon _\upsilon }(s){\text{,}}$ | (22) |
其中
| $h_{od}^i = \frac{{{s^2} + 2{\xi _i}{\omega _{oi}}s + \omega _{oi}^2}}{{({s^2} + 2{\xi _{ni}}{\omega _{oi}}s + \omega _{oi}^2)(s + {\omega _{ci}})}}{\text{,}}$ |
令
| ${k_{1i}} = - 2{\omega _{ci}}({\xi _{ni}} - {\xi _i})/{\omega _{oi}}{\text{,}}$ |
| ${k_{2i}} = 2{\omega _{oi}}({\xi _{ni}} - {\xi _i}),{k_{3i}} = {\omega _{ci}}{\text{,}}$ |
| $1/T \ll {k_{5i}}/{k_{4i}} < {\omega _{oi}} < {\omega _{ci}}{\text{。}}$ |
其中:
由复合系统无源性理论可知,子系统H1H2具有无源性,总系统无源。
4.4 稳定性证明选取Lyaponov函数V满足:
| $V = {\tilde{\upsilon}^{\rm T}}{ M}\tilde{\upsilon}+ {\tilde{ x}^{\rm T}}{ P}\tilde { x}{\text{,}}$ | (23) |
两边求导并代入KYP引理公式得:
| $\dot V = - {\tilde {\upsilon}^{\rm T}}({ D} + {{ D}^{\rm T}})\tilde{\upsilon} - {\tilde { x}^{\rm T}}{ Q}\tilde{ x}{\text{。}}$ | (24) |
根据Lyaponov稳定性判据可知,系统稳定。
5 实验仿真本文以动力定位船舶Northern Clipper为模型进行仿真验证[12],船长L=76.2 m,重量
| ${ M} = \left[ {\begin{array}{*{20}{c}}{5.3122 \times {{10}^6}}&0&0\\0&{8.2831 \times {{10}^6}}&0\\0&0&{3.7454 \times {{10}^9}}\end{array}} \right]{\text{,}}$ |
| ${ D}= \left[ {\begin{array}{*{20}{c}}{5.0242 \times {{10}^4}}&0&0\\0&{2.7229 \times {{10}^5}}&{ - 4.3933 \times {{10}^6}}\\0&{ - 4.3933 \times {{10}^6}}&{4.1894 \times {{10}^8}}\end{array}} \right]{\text{。}}$ |
时间常数
根据国际海事组织(IMO)定义4种典型海况参数如表1所示。4种海况能量频谱函数如图4所示。由仿真结果可知,当海况由平静变为恶劣时,高频波浪峰值频率逐渐减小,幅值逐渐增大,符合实际海况情况。

|
图 4 四种海况高频波浪能量频谱图 Fig. 4 Frequency spectrums of high-frequency waves in four different sea conditions |
|
|
表 1 四种典型海况下模型参数 Tab.1 Model parameters of four typical sea conditions |
卡尔曼仿真原理可以参见文献[11]。仿真时间500 s。在4种海况下仿真结果如图5所示。黑色曲线为实测值,浅色曲线为滤波值。分析可得,当海况相对平稳时(海况1和海况2)卡尔曼滤波器能够有效滤除高频波浪噪声,滤波曲线平缓;但当海况复杂时(海况3和海况4),卡尔曼滤波器滤波效果变差,仍然有高频分量未被滤除。
5.3 非线性无源滤波器仿真仿真时间500 s,4种海况下仿真结果如图6所示。黑色曲线为实测值,浅色曲线为滤波值。4种海况下滤波器的陷波作用如图7所示,结果显示4种海况下滤波器的陷波频率和高频波浪噪声的峰值频率均相近,能够有效的滤除波浪高频成分。分析可得,无源非线性滤波器在4种海况下均能够有效滤除高频分量,对比图5可得,当海况平稳时,2种滤波器滤波效果近似,但当高海况和恶劣海况时,无源非线性滤波器效果明显更好。

|
图 6 四种海况下无源非线性滤波器滤波结果 Fig. 6 Results of nonlinear passive filter in four different sea conditions |

|
图 7 四种海况下非线性无源滤波器波特图 Fig. 7 Bode diagrams of nonlinear passive filter in four different sea conditions |
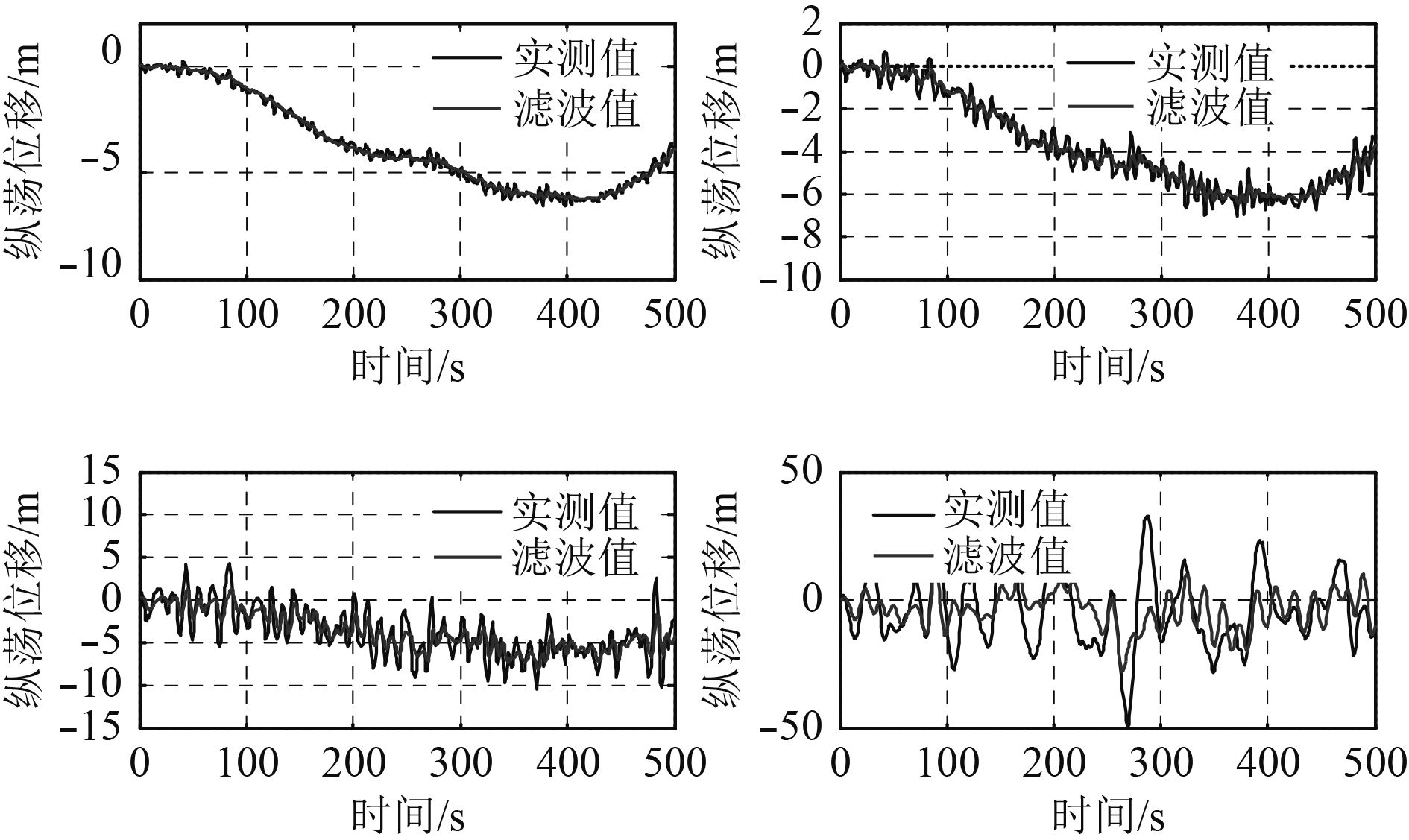
|
图 5 四种海况下卡尔曼滤波器滤波结果 Fig. 5 Results of Kalman filter in four different sea conditions |
针对动力定位系统中高频环境干扰的问题,设计了无源非线性滤波器,并与卡尔曼滤波器分别在不同海况下进行了滤波性能对比分析,结果显示,无源非线性滤波器滤波效果更强。
| [1] |
边信黔, 付明玉, 王元慧. 船舶动力定位[M]. 北京: 科学出版社, 2011.
|
| [2] |
SAELID S, JENSSEN N, BALCHEN J. Design and analysis of a dynamic positioning system based on Kalman filtering and optimal control[J]. Automatic Control IEEE Transactions on, 1983, 28(3): 331-339. DOI:10.1109/TAC.1983.1103225 |
| [3] |
BUI VP, JI SW. Nonlinear observer and sliding mode control design for dynamic positioning of a surface vessel[J]. International Conference on Control, 2012, 1900-1904. |
| [4] |
XIE Y, LIN X. Multiple model adaptive nonlinear observer for dynamic posi-tioning ship[J]. Mathematical Prob-lems in Engineering, 2013, 3: 532-548. |
| [5] |
DU J, HU X LIU H. Adaptive robust output feedback control for a marine dynamic positioning system based on high-gain observer[J]. IEEE Transactions on Neu-ral Network and learning systems, 2015, 26(11): 2775-2786. DOI:10.1109/TNNLS.2015.2396044 |
| [6] |
TOMERA, Miroslaw. Nonlinear observers design for multivariable ship motion control[J]. Polish Maritime Research, 2012, 19(S1): 55-56. |
| [7] |
DU JL, WANG SY, ZHANG XK. Nonlinear observer design for ship dynamic posi-tioning system[J]. Ship Engineering, 2012, 307-312. |
| [8] |
POPOV VM. Hyper stability of control sys-tems[M]. Springer-Verlag, 1973.
|
| [9] |
MOYLAN PJ. Implication of passivity in a class of nonlinear systems[J]. IEEE Transactions on Automatic control, 1974, 19(4): 373-381. DOI:10.1109/TAC.1974.1100603 |
| [10] |
XIA G, SHAO X. Passive nonlinear ob-server design for special structure ves-sels[J]. Oceans, 2013, 1-8. |
| [11] |
It Fossen, T Perez. Kalman filtering for positioning and heading control of ships and offshore rigs[J]. IEEE Control Systems, 2009, 29(6): 32-46. DOI:10.1109/MCS.2009.934408 |
| [12] |
TI Fossen, JP Strand. Passive nonlinear observer design for ships using Lya-punov methods: full-scale experiments with a supply vessel[J]. Automatica, 1999, 35(1): 3-16. DOI:10.1016/S0005-1098(98)00121-6 |
 2018, Vol. 40
2018, Vol. 40
