0 引　言

密集度是火炮主要的战技性能指标之一，密集度越好，击毁目标所消耗的弹药量越少。影响密集度的因素很多，主要与火炮自身的弹道与结构性振动情况有关。以转管火炮为例，火炮结构刚度、射击振动、控制系统、弹药生产加工一致性、发射平台以及作战环境等都对密集度会产生影响。转管火炮由于射击时身管组有圆周旋转运动, 产生的不平衡惯性力和支撑身管组的炮箱与卡箍的刚性等对转管武器的振动特性也会产生影响, 特别是振动对炮口扰动的影响, 会引起射击密集度变大.因此, 转管火炮的炮口扰动研究对提高转管火炮射击密集度有重要意义。

1 立靶密集度

经过长期的理论和实践证明，转管火炮的旋转与振动会严重影响到转管火炮系统的射击精度。炮弹在身管膛内运动的过程中，受到膛压的变化和火炮身管振动的影响，引起炮口扰动，这样就会导致每一发弹丸在出炮口的瞬间位置都不一样，从而引起转管火炮的弹丸散布变大，影响射击密集度。

立靶密集度是指在一定距离上通过某种测量方法求得火炮射击时弹丸在立靶面上的密集程度，常用立靶密集度来反映火炮的射击精度，所以它是衡量火炮射击精度性能的主要战技术指标。密集度受偶然误差的影响，偶然误差是以火炮的设计制造有关的，所以仿真分析只能判断射击密集度的好坏，在此只对射击密集度进行分析研究。

工程上，常用方位中间偏差E_x和高低中间偏差E_y来表示立靶射击密集度。具体计算方法如下：

方位中间偏差E_x公式为：

${E_x} = 0.6745 \times \sqrt {\frac{{\sum\limits_{i = 1}^n {{{\left( {{x_i} - \overline x } \right)}^2}} }}{{n - 1}}}{\text{，}}\left( {{{i}} = 1,2, \cdots ,{{n}}} \right){\text{。}}$

(1)

式中：E_x为方位中间偏差，m；x_i为方位散布坐标，m； $\overline {{x}} $ 为方位散布坐标平均值， $\overline {{x}} = \displaystyle\frac{1}{{n}}\sum\limits_{i = 1}^n {{{x}_{{i}}}} $ ；n为射弹总数。

高低中间偏差E_y公式为：

${{{E}}_{{y}}} = 0.6745 \times \sqrt {\frac{{\sum\limits_{i = 1}^{{n}} {{{\left( {{{{y}}_{{i}}} - \overline {{y}} } \right)}^2}} }}{{{{n}} - 1}}}{\text{，}}\left( {{{i}} = 1,2, \cdots ,{{n}}} \right){\text{。}}$

(2)

式中：E_y为高低中间偏差，m；y_i为高低散布坐标，m； $\overline {{y}} $ 为高低散布坐标平均值， $\overline {{y}} = \displaystyle\frac{1}{{{n}}}\sum\limits_{i = 1}^{{n}} {{{{y}}_{{i}}}} $ ；n为射弹总数。

在实际应用中，通常用中间误差除以靶距L，立靶密集度利用角度的形式来表达，即方位立靶密集度： $\displaystyle\frac{{{{{E}}_{{X}}}}}{{{L}}}$ ，rad；高低立靶密集度： $\displaystyle\frac{{{{E}_{{Y}}}}}{{L}}$ ，rad。

2 炮口振动响应分析

转管火炮在不同结构形式、不同发射率下，对射击激励响应也不同，且发射率对火炮振动的固有频率影响较大。对于某一转管火炮而言，在一定发射率下振动固有频率是一个定值，所以激励的输出响应也是相同的。本文转管火炮以发射率4 000发/min，对转管火炮连续射击100发进行仿真分析，得出弹丸出炮口瞬间的线位移、线速度以及角位移变化曲线。

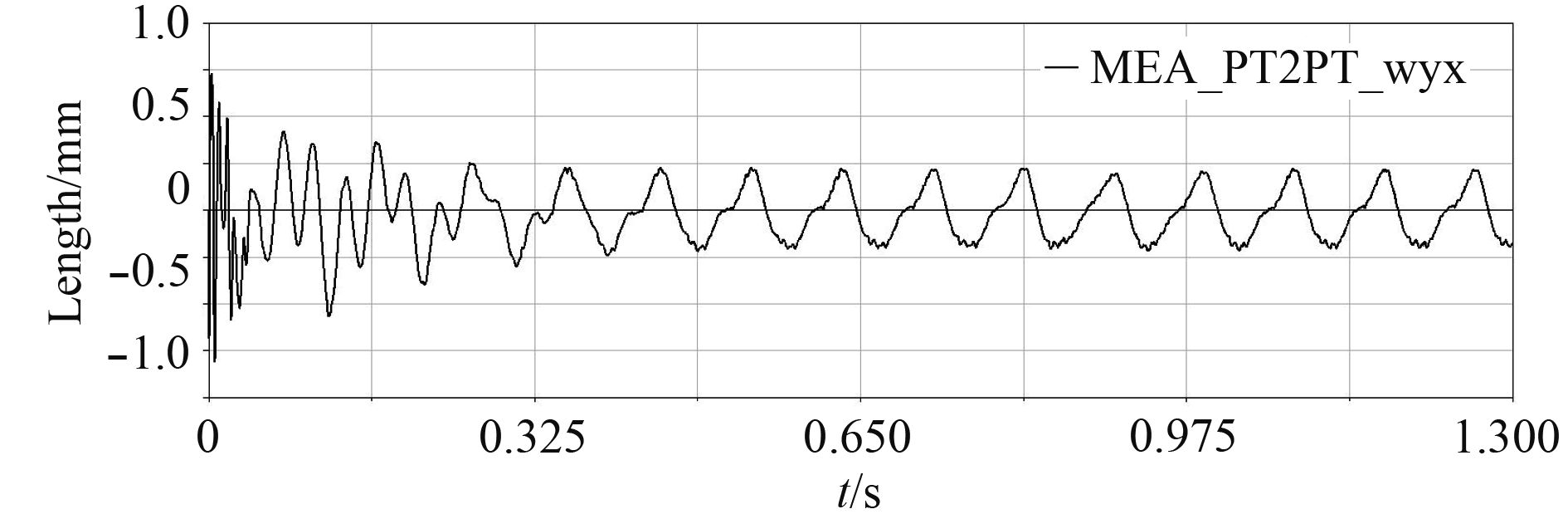
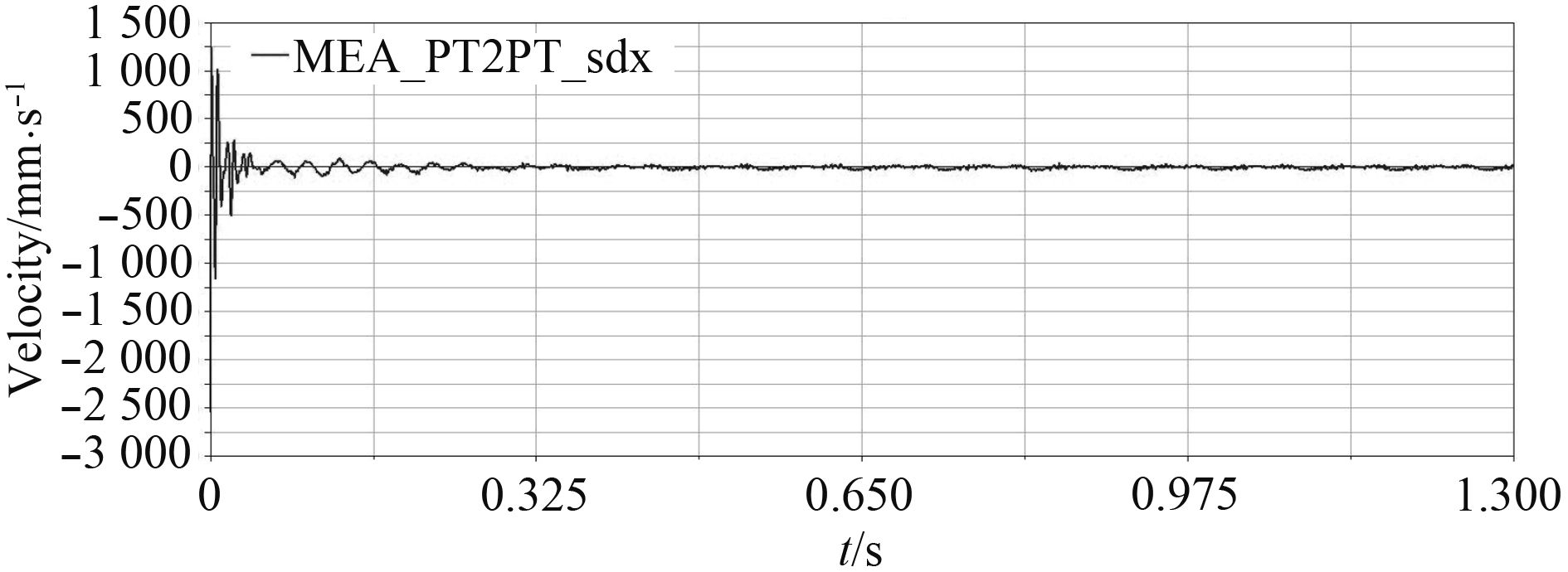
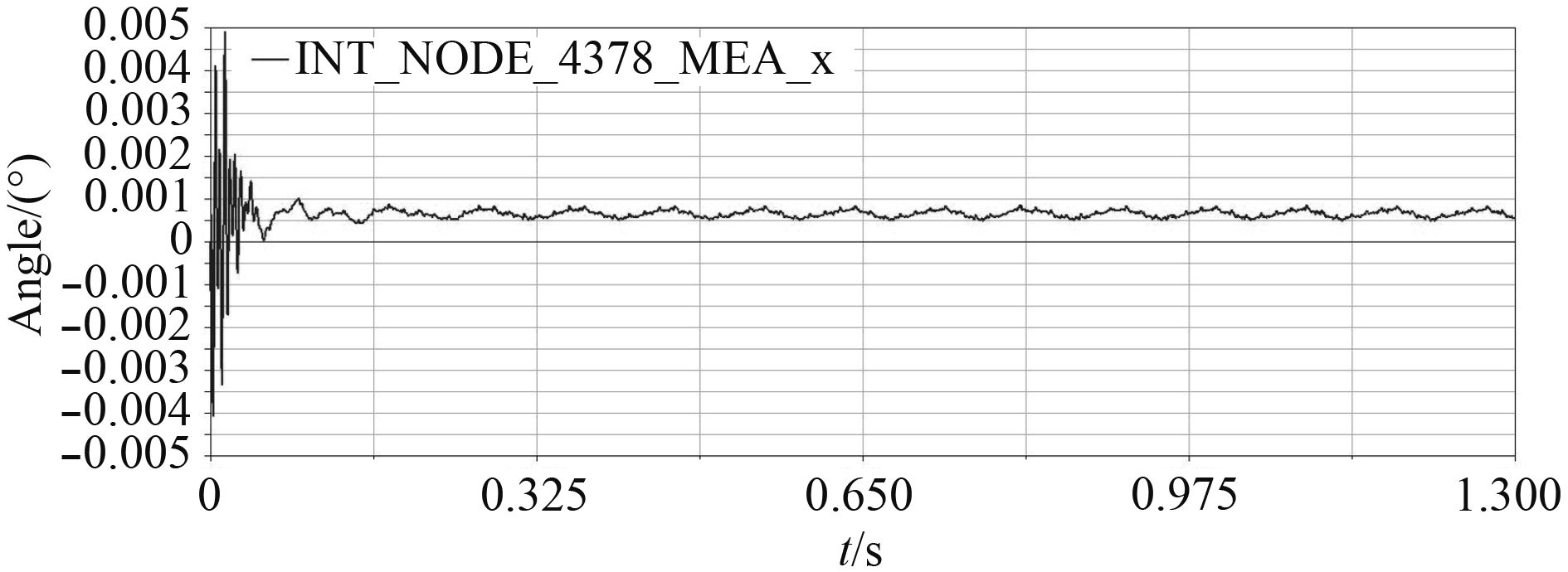
2.1 炮口点水平方向振动分析

由图1可以得出，炮口点水平方向的振动在初始启动发射率上升阶段振动位移波动较大，振幅变化量最大达1.53 mm，发射率稳定后移位一致性好且变小；由图2可以得出，炮口点水平方向的振动线速度振幅变化量最大值为2.15 m/s；由图3可以得出，炮口点水平方向的振动角位移振幅变化量最大值为0.008 8 deg。

2.2 炮口点垂直方向振动分析

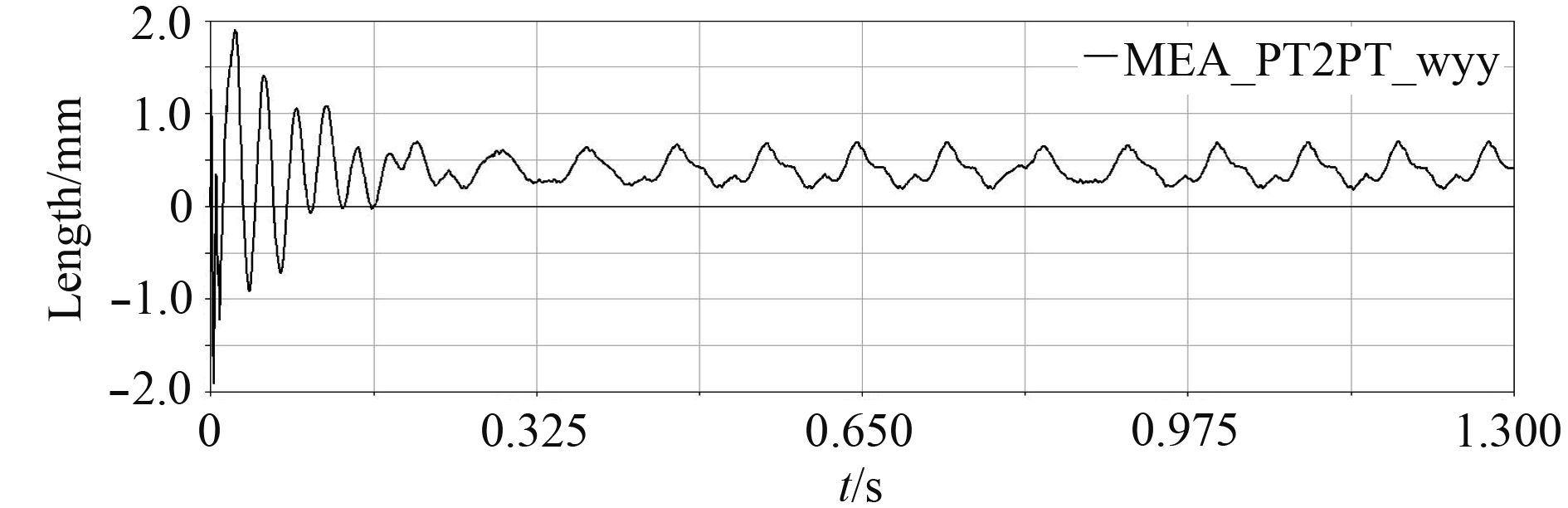
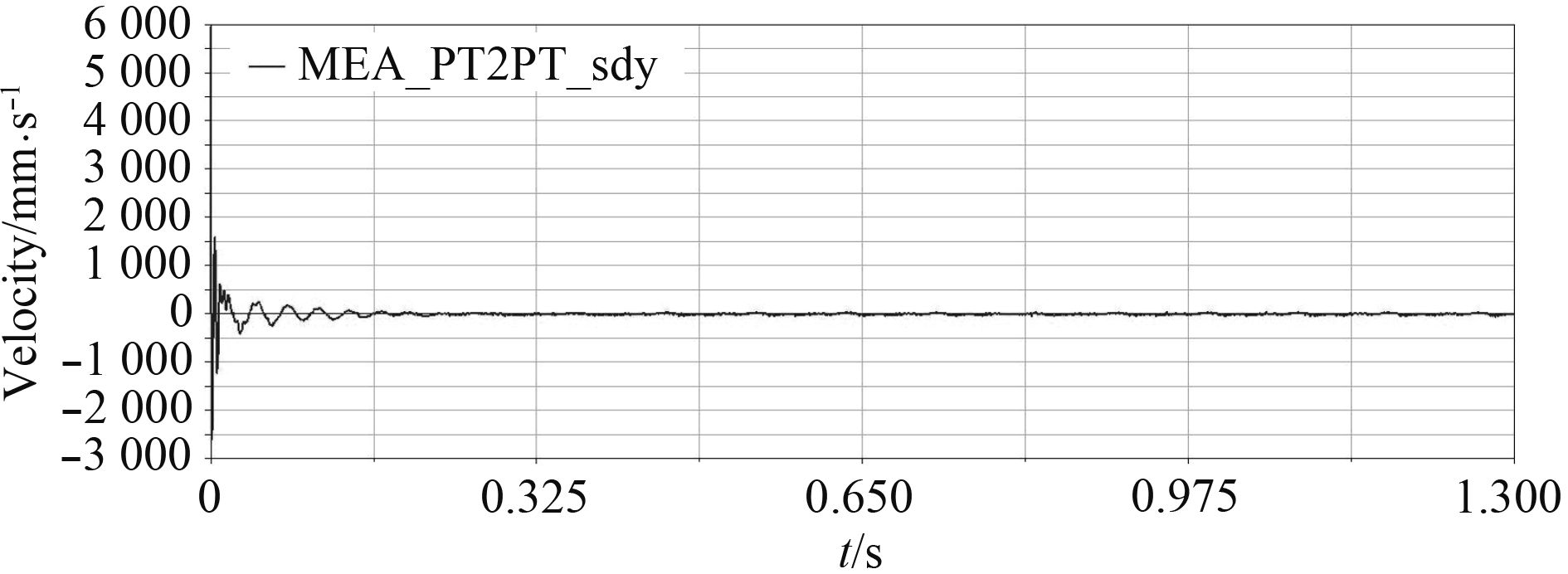
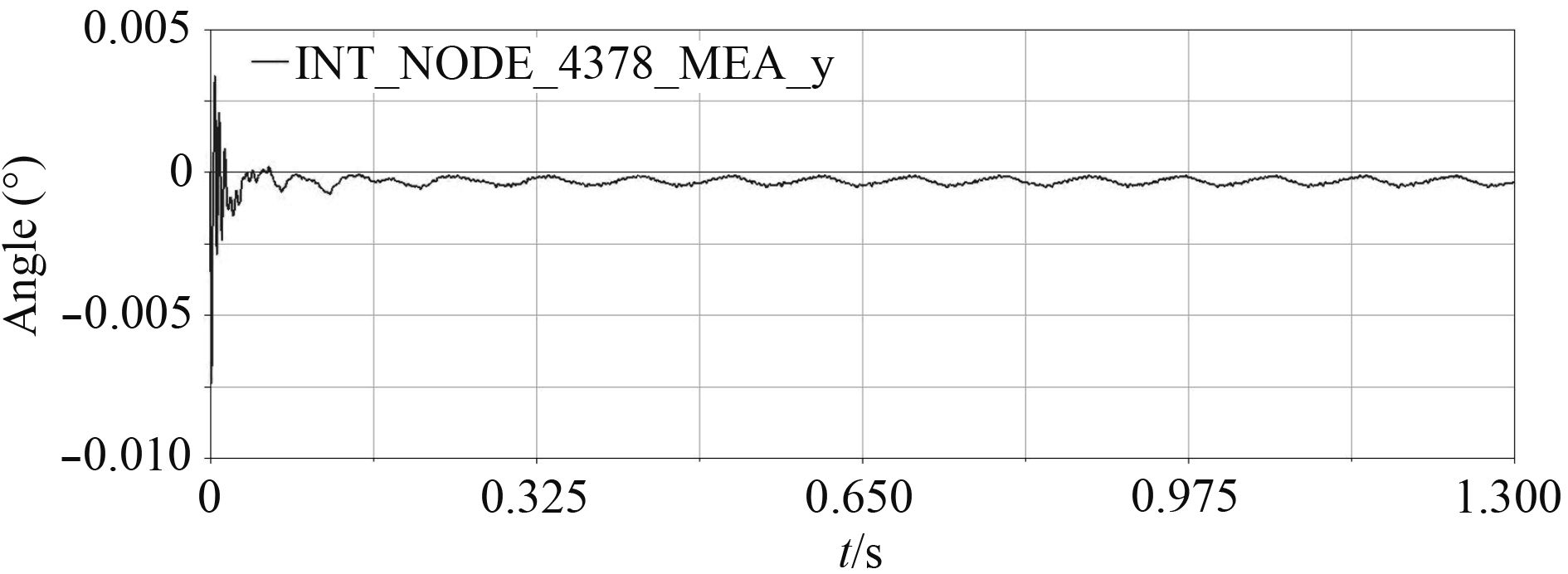
由图4可以得出，炮口点垂直方向的振动在初始启动发射率上升阶段振动位移波动较大，振幅变化量最大达3.86 mm，发射率稳定后移位一致性好且变小；由图5可以得出，炮口点垂直方向的振动线速度振幅变化量最大值为4.15 m/s；由图6可以得出，炮口点垂直方向的振动角位移振幅变化量最大值为0.011 4 deg。

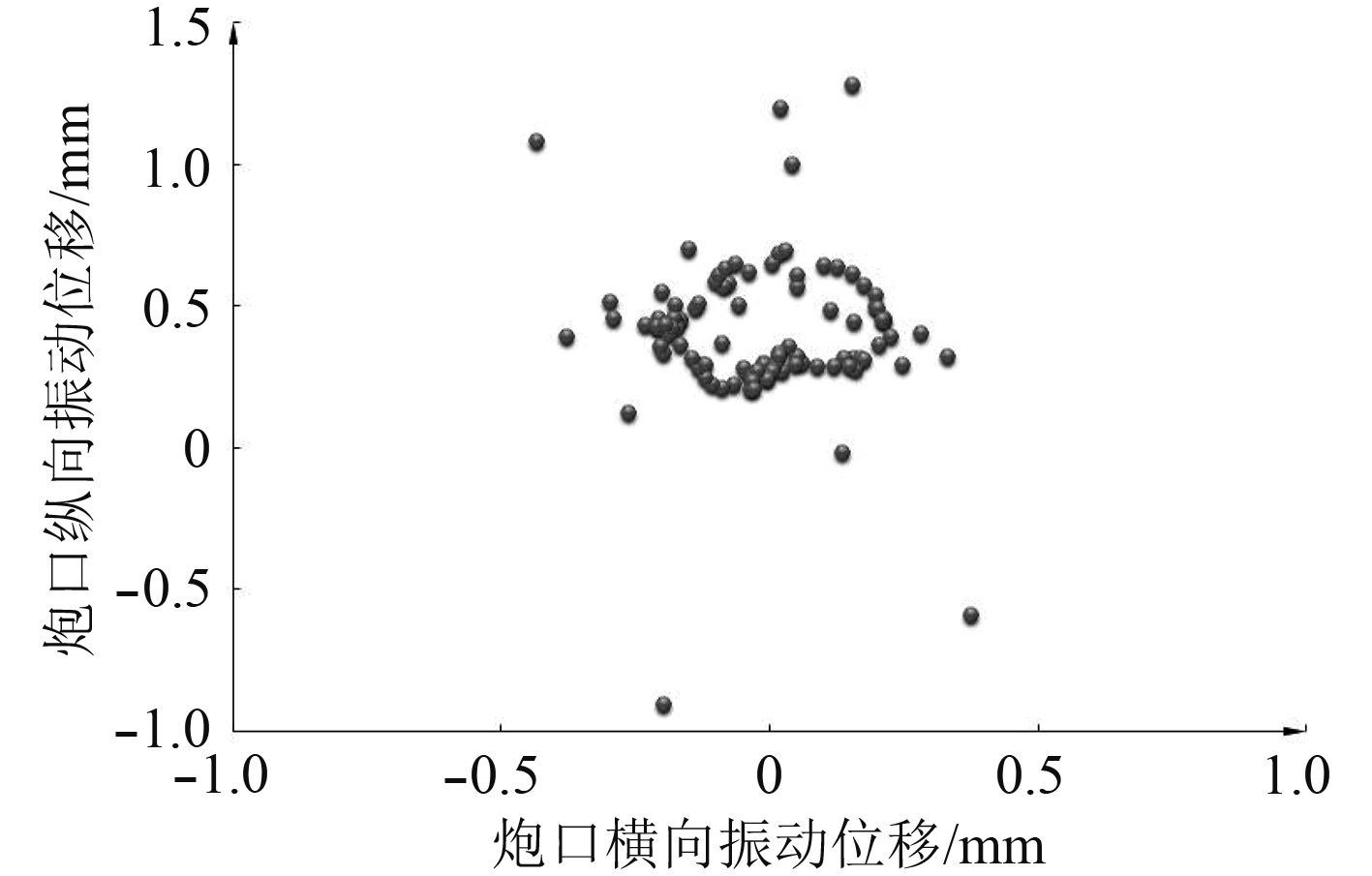
通过计算每发弹丸出炮口的时间，计算得到每发弹丸在此刻的振动线位移、线速度以及角度。从而求得每发弹丸在炮口处膛口中心相对膛底中心振动位移的坐标值。

根据设计要求，设置初始条件为：立靶距离200 m，弹丸初速为890 m/s。将每次火炮发射时炮口扰动的位移值代入外弹道计算软件中，可以得到100连发的立靶坐标值。

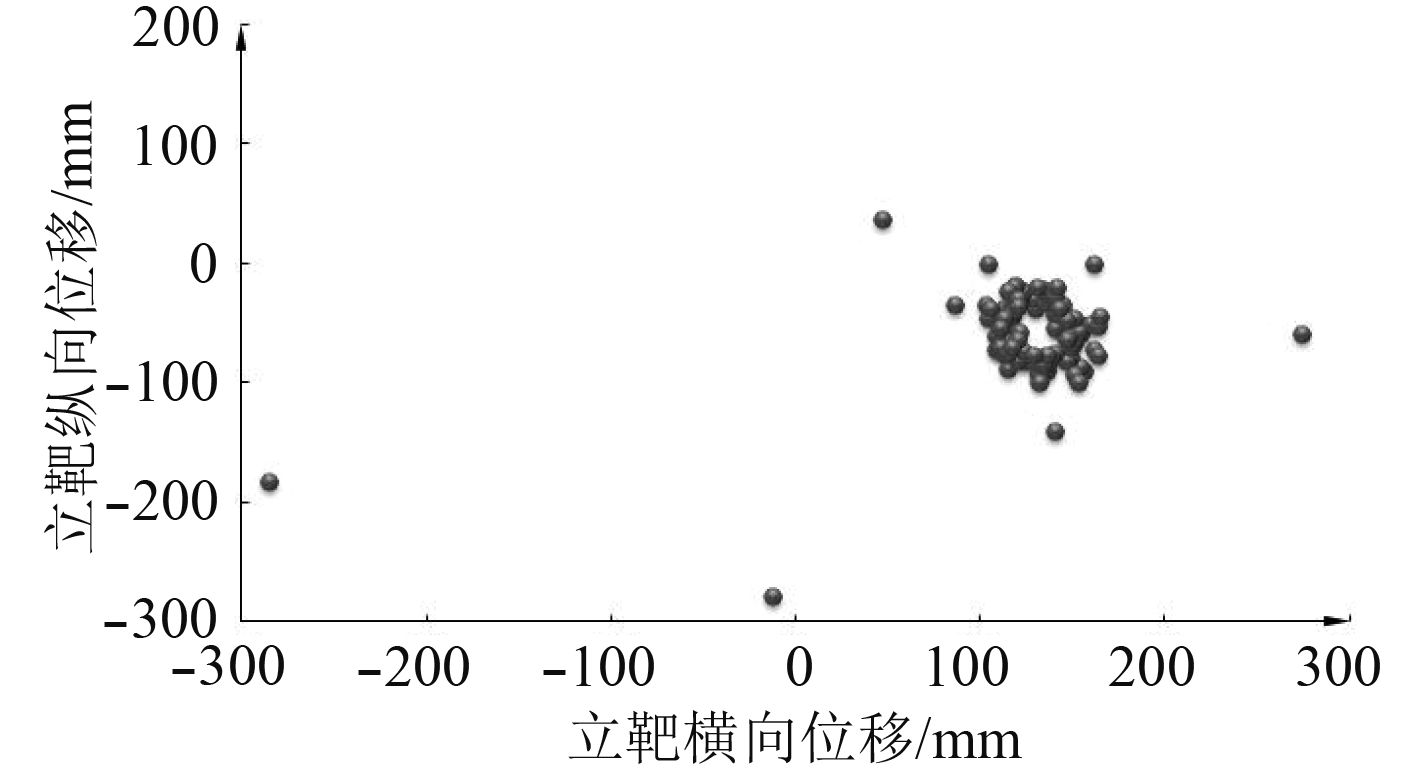
由图8可以看出：有2发弹的位置偏差比较大，绝大部分弹位置相对集中。根据立靶坐标值的数据利用方位和高低立靶密集度公式求得方位立靶密集度为0.58 mrad，高低立靶密集度为0.43 mrad，结果良好。由此可以看出转管火炮射击稳定，振动对立靶密集度影响较小，满足技术指标要求。

3 结　语

炮口振动是引起炮口扰动的主要原因，进而又影响转管火炮射击密集度。本文对一定的研究对象先进行随机振动分析，得出了炮口点的位移和速度，进而代入外弹道计算软件中，得出200 m处立靶密集度，虽然仿真得出的立靶密集度较小，满足转管火炮规定的指标技术要求，但是通过分析可以得出结论如下：

1）通过仿真分析可得炮口振动固有频率，如果固有频率与转管火炮发射率相同时，会发生共振现象，随着射弹发数的增加，射击时间的持续，炮口振动位移将逐渐变大，导致较大的射击密集度，所以在进行转管火炮结构设计时，要避开共振频率，达到振动固有频率和发射率的良好匹配。

2）为了减少振动位移，需要增加转管炮自动机本身和与其配合的摇架、回转前支撑等零部件的装配间隙，提高转管炮的刚性。

3）加强身管和摇架的自身刚度，也可降低振动的影响。

4）提高转管火炮控制系统的性能与随动精度，也可提高射击密集度。