0 引　言

现代新型舰船、舰船雷达和实时通信等系统对数据采集提出了越来越高的要求。采样率作为数据采集领域当中一个非常重要的指标，直接决定了采集系统的水平与使用范围。但是目前国内集成电路工艺的水平远远落后于欧美发达国家，这使得在高速数据采集系统方面国内外差距很大，从而限制了舰船电力系统监控、舰船雷达与通信系统的进步。故此，研究为提高实时采样率而采用的时间交替采集系统结构的意义重大，对于打破国外技术垄断与封锁具有十分重要的现实意义。但是多片模数转换器（ADC）之间失配带来的增益误差、偏置误差和时间误差却降低了时间交替采集系统的性能,因此时间交替采集系统中误差的校正是非常重要的研究内容。

关于时间交替采集系统的误差校正，有大量学者进行研究，并有若干研究成果。文献[1 – 2]使用自适应的误差校正方法，但是多次的迭代计算带来非常大的运算量，工程中的实用性不强；文献[3 – 8]通过各种滤波器进行数字后校正，尽管精度较高，但是同时滤波器的设计复杂度较高；文献[9]使用正弦拟合的时间交替采集系统误差校正方法，该方法工程中实现较简单，但是也存在一些缺点。

本文中频域内的误差校正方法适用于时间交替采集系统中增益误差和时间误差的校正。其基本思路是以某个子模数转换器作为基准，即认为它是无误差的。对各个子模数转换器采样的数据进行频域分析，增益误差和时间误差的估计值可以通过对特定频率点上的幅度、相位值计算得到，进一步可以得到相应的增益误差、时间误差的校正值。该方法思路清晰、实现简单，免去了复杂的计算过程，适合工程中应用，且校正精度高。

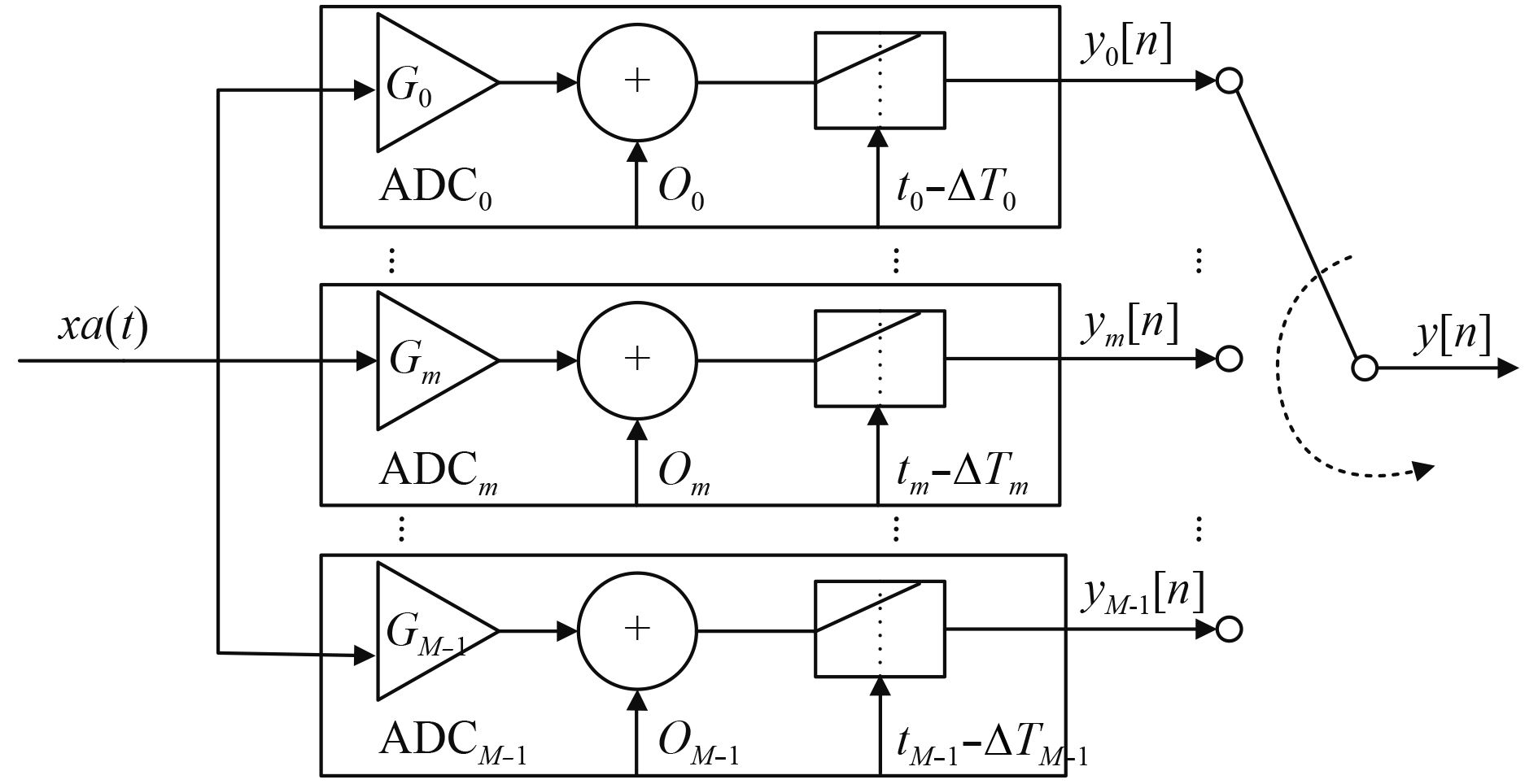
1 时间交替并行采集系统误差建模分析

图1为时间交替采集系统误差模型，图中， $M$ 为构成时间交替并行采集系统的子模数转换器的个数， $m$ 表示第 $m$ 个子模数转换器。 ${G_m}$ ， ${O_m}$ 分别为第 $m$ 个子模数转换器的增益和偏置，如果以第 $0$ 个模数转换器为参考通道，那么第 $m$ 个子模数转换器的增益与偏置误差就体现在 ${G_m}$ ， ${O_m}$ 与 ${G_0}$ ， ${O_0}$ 的差异上。由时间交替采样原理可知，理想情况下第 $m$ 个子模数转换器的采样时刻为：

${t_m} = (nM + m){T_s}{\text{，}}$

(1)

其中： ${T_s}$ 为整个时间交替采集系统的采样周期， ${T_s}$ 对应的采样率为 ${f_s}$ 。时间交替采集系统中也会存在时间误差 $\Delta {T_m}$ ，则实际的采样时刻变成了 ${t_m} - \Delta {T_m}$ 。

由式（1）及图1可得在误差的影响下，第 $m$ 个子模数转换器的量化输出为：

${y_m}[n] = {G_m}{x_a}((nM + m){T_s} - \Delta {T_m}) + {O_m}{\text{，}}$

(2)

从模拟信号 ${x_a}(t)$ 与采样序列 $x(n) = {x_a}(t){|_{t = n{T_s}}} = $ $ {x_a}(n{T_s})$ 频域之间的关系式：

$X({{\rm{e}}^{{\rm{j}}\omega }}) = \frac{1}{{{T_s}}}\sum\limits_{k = - \infty }^\infty {{X_a}} \left[ {{{j}}\left( {\frac{{\omega - 2{\rm{{\text{π}}}}k}}{{{T_s}}}} \right)} \right]{\text{，}}$

(3)

以及离散时间傅里叶变换的线性性质可以得到误差存在时，第 $m$ 个子模数转换器量化输出的离散时间傅里叶变换为：

$\begin{split}{Y_m}({{{e}}^{{{j}}\omega }}) = & \frac{1}{{M{T_s}}}\sum\limits_{k = - \infty }^\infty {\left\{ {{G_m}{X_a}\left[ {{{j}}\left( {\frac{{\omega - 2{\text{π}}k}}{{M{T_s}}}} \right)} \right]} \right.} \times \\ &\left. {{{{e}}^{{{j}}\left( {\frac{{\omega - 2{\text{π}}k}}{{M{T_s}}}} \right)(m{T_s} - \Delta {T_m})}} + 2{\text{π}}{O_m}\delta \left( {\frac{{\omega - 2{\text{π}}k}}{{M{T_s}}}} \right)} \right\}{\text{，}}\end{split}$

(4)

其中，ω为子模数转换器的 $M{T_s}$ 采样周期对应的数字频率，则 ${\omega _0} = {\varOmega _0}M{T_s}$ 。由奈奎斯特采样定理，模拟信号的最高频率为 ${f_s}/2$ 。那么当 $\varOmega > |{\text{π}}{f_s}|$ 时， ${X_a}({{j}}\varOmega ) = 0$ 。进而，式(4)可以改写为：

$\begin{split}{Y_m}({{{e}}^{{\rm{j}}\omega }}) = & \frac{1}{{M{T_s}}}\sum\limits_{k = - M/2 + 1}^{M/2} {\left\{ {{G_m}{X_a}\left[ {{{j}}\left( {\frac{{\omega - 2{\text{π}}k}}{{M{T_s}}}} \right)} \right]} \right.} \times\\ &\left. {{{{e}}^{{{j}}\left( {\frac{{\omega - 2{\text{π}}k}}{{M{T_s}}}} \right)(m{T_s} - \Delta {T_m})}} + 2{\text{π}}{O_m}\delta \left( {\frac{{\omega - 2{\text{π}}k}}{{M{T_s}}}} \right)} \right\}{\text{。}}\end{split}$

(5)

当输入信号 ${x_a}(t) = A\sin ({\varOmega _{\rm{0}}}t)$ ，即它的相位为0时，则第 $0$ 个子模数转换器采样点的初相也为0。把正弦信号的傅里叶变换 ${X_a}({{j}}\varOmega ) = A{\text{π}}(\delta (\varOmega - {\varOmega _0}) -$ $ \delta (\varOmega + {\varOmega _0}))/j$ 代入到式（5），得到第 $m$ 个子模数转换器量化输出的频谱为：

$\begin{split}{Y_m}({{{e}}^{{{j}}\omega }}) = & \frac{1}{{M{T_s}}}\sum\limits_{k = - M/2 + 1}^{M/2} {\left\{ {{G_m}\frac{{A{\text{π}}}}{j}\left[ {\delta \left( {\frac{{\omega - 2{\text{π}}k}}{{M{T_s}}} - {\varOmega _0}} \right)} \right.} \right. - } \\ &\left. {\delta \left( {\left( {\frac{{\omega - 2{\text{π}}k}}{{M{T_s}}}} \right. + {\Omega _0}} \right)} \right]{{{e}}^{{{j}}\left( {\frac{{\omega - 2{\text{π}}k}}{{M{T_s}}}} \right)(m{T_s} - \Delta {T_m})}}{\rm{ + }}\\ &\left. {2{\text{π}}{O_m}\delta \left( {\frac{{\omega - 2{\rm{\pi }}k}}{{M{T_s}}}} \right)} \right\}{\text{，}}\end{split}$

(6)

当 $\omega = {\omega _0} = {\varOmega _0}M{T_s}$ 时，得到存在误差时， ${\omega _0}$ 处的频谱值为：

$\begin{split}{Y_m}({{{e}}^{{{j}}{\omega _0}}}) = & \frac{1}{{M{T_s}}}\!\!\!\sum\limits_{k = - M/2 + 1}^{M/2} \!\!\!{\{ {G_m}\frac{{A{\text{π}}}}{j}\left[ {\delta \left( {\frac{{ - 2{\text{π}}k}}{{M{T_s}}}} \right) \!-\! \delta \left( {2{\varOmega _0} \!-\! \frac{{2{\rm{{\text{π}} }}k}}{{M{T_s}}}} \right)} \right]} \times \\ &\left. {{{{e}}^{{{j}}\left( {{\varOmega _0} - \frac{{2{\text{π}}k}}{{M{T_s}}}} \right)(m{T_s} - \Delta {T_m})}}{\rm{ + }}2{\text{π}}{O_m}\delta \left( {{\varOmega _0} \!-\!\! \frac{{2{\text{π}}k}}{{M{T_s}}}} \right)} \right\}{\text{。}}\;\;\end{split}$

(7)

如果 ${\varOmega _{\rm{0}}} < {\rm{{\text{π}}}}{f_s}/M$ ，即模拟信号的频率使子模数转换器也满足奈奎斯特采样定理，则式（7）进一步简化为：

${Y_m}({{{e}}^{{{j}}{\omega _0}}}) = \frac{{{G_m}A{\text{π}}}}{{M{T_s}}}{{{e}}^{{{j}}\left( {m{\varOmega _0}{T_s} - {\varOmega _0}\Delta {T_m} - \frac{\text{π}}{2}} \right)}}{\text{。}}$

(8)

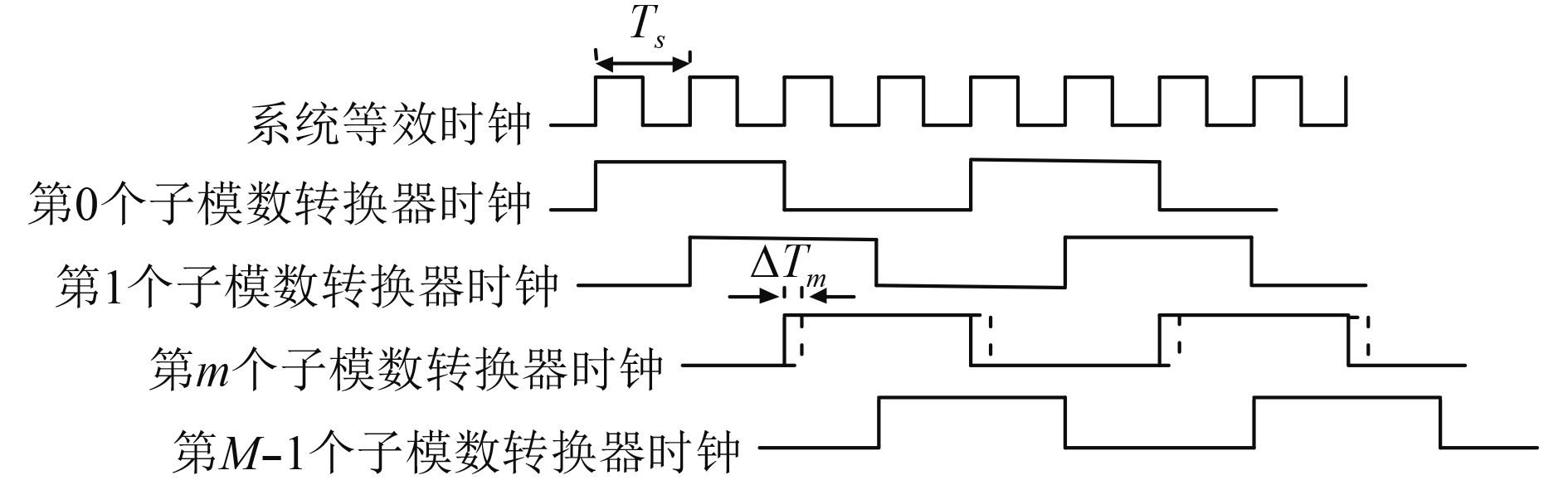
式（8）清晰地展示了 ${G_m}$ ， $\Delta {T_m}$ 与 ${\omega _0}$ 处频谱的幅度、相位关系，从 ${\omega _0}$ 处的幅度、相位信息可以得到第 $m$ 个子模数转换器的增益时间误差的估计值。时间交替采集系统的时间误差如图2所示。

2 算法验证硬件平台简介

算法验证平台中采用的子模数转换器采样率为1.25 GSPS， $M$ 的值为4，这样构成的时间交替采集系统的等效采样率为5 GSPS。

每个子模数转换器有相应的偏置、增益、相位控制单元，采用SPI通讯方式在相应的寄存器写入不同的控制字，可以调整每个子模数转换器的偏置、增益和相位值。而如何计算出时间交替采集系统中的误差，如何计算出相应的校正值是本文研究的关键。

图3给出了整个5 GSPS时间交替采集系统的原理框图，系统采用 ${\rm FPGA}$ 作为高速数据的缓存与处理， ${\rm DSP}$ 用作显示与顶层控制。在 ${\rm FPGA}$ 中可以并行实时的进行快速傅里叶变换，从而迅速的获得频谱信息。它的增益和时间调节寄存器可以调节的范围是0～0x3ff，初始默认控制字DefaultCtrWord是 $0{\rm{x2}}00$ 。增益的调节步进是0.02%，可以调节的范围是 $ \pm 10\% $ 。设置增益调节寄存器为0x200（默认值）表示调整量为0，设置为大于0x200的值表示使调整量变大。时间调节寄存器的调节步进是 ${\rm{3}}0\;{\rm{ fs}}$ ，调节范围是 $ \pm 15{\rm ps}$ 。设置时间调节寄存器0x200（默认值）表示时间调整量为0，设置大于0x200的值表示时间调整量变大。

3 频域内的增益误差和时间误差的估计与校正 3.1 增益和时间误差的估计

从式（8）可以得到，在时间交替采集系统中，当输入信号固定角频率为 ${\varOmega _{\rm{0}}}$ 的单一正弦信号并且 ${\varOmega _{\rm{0}}} < {\text{π}}{f_s}/M$ 时，第 $m$ 个子模数转换器在 ${\varOmega _{\rm{0}}}$ 处的输出频谱幅度与其增益 ${G_m}$ 成比例关系，因此通过 ${\varOmega _{\rm{0}}}$ 处的频谱幅度来估算 ${G_m}$ 的值。从而得到第 $m$ 个子模数转换器增益误差的表达式为：

$\Delta {G_m}{\rm{ = }}\frac{{{G_m}}}{{{G_0}}}{\rm{ = }}\frac{{{G_m}A{\rm{{\text{π}}}}/M{T_s}}}{{{G_0}A{\rm{{\text{π}} }}/M{T_s}}}{\rm{ = }}\frac{{{\rm{Amplitud}}{{\rm{e}}_m}}}{{{\rm{Amplitud}}{{\rm{e}}_0}}}{\text{，}}$

(12)

式中： ${\rm{Amplitud}}{{\rm{e}}_m}$ 和 ${\rm{Amplitud}}{{\rm{e}}_0}$ 分别为第 $m$ 个子模数转换器和第 $0$ 个子模数转换器在频率 ${\varOmega _{\rm{0}}}$ 处的幅度值。

对于时间误差，设定第 $0$ 个子模数转换器的采样点对应的相位为0，那么第 $m$ 个子模数转换器在 ${\varOmega _{\rm{0}}}$ 处频谱的相位值是 $m{\varOmega _0}{T_s} - {\varOmega _0}\Delta {T_m} - {\text{π}}/2$ 。从而得到第 $m$ 个子模数转换器时间误差的表达式为：

$\Delta {T_m}{\rm{ = }}\frac{{{\rm{phas}}{{\rm{e}}_{{\rm{AD}}{{\rm{C}}_m}}} - {\rm{phas}}{{\rm{e}}_{{\rm{AD}}{{\rm{C}}_{\rm{0}}}}} - m{\varOmega _0}{T_s}}}{{{\varOmega _{\rm{0}}}}}{\text{。}}$

(13)

式中： ${\rm{phas}}{{\rm{e}}_{{\rm{AD}}{{\rm{C}}_m}}}$ 和 ${\rm{phas}}{{\rm{e}}_{{\rm{AD}}{{\rm{C}}_{\rm{0}}}}}$ 为第 $m$ 个子模数转换器和第 $0$ 个子模数转换器在频率 ${\varOmega _{\rm{0}}}$ 处的相位值。

由于快速傅里叶变换的精度及截断误差等的影响，对第 $m$ 个子模数转换器的采样数据作频域分析时，每次得到的频谱幅度会略有差异，为了提高校正精度，本文采用做10次快速傅里叶变换，去掉2个最大值和最小值，然后求平均的处理方法。

3.2 增益误差和时间误差的校正

对增益和时间误差的校正是通过发送相应的校正控制字到第 $m$ 个子模数转换器：首先由式（12）计算出增益误差，根据增益误差控制步进值，计算出相应的校正控制字。在算法验证平台中，增益的控制字步进 ${\rm{ste}}{{\rm{p}}_{{\rm{gain}}}}$ 是0.02%，计算增益误差校正控制字的公式为：

${{GainCtrWor}}{{\rm{d}}_m} \!\!=\!\! {{DefaultGainWord}} \!\!+\!\! \frac{{1 - \Delta {G_m}}}{{{{ste}}{{{p}}_{{{gain}}}} \times \Delta {G_m}}}{\text{。}}$

(14)

另外，由于增益误差体现在 ${\varOmega _{\rm{0}}}$ 频点的幅度上，当误差校正完毕时，各个子ADC在 ${\varOmega _{\rm{0}}}$ 频点上的幅度相等。也可以通过不断遍历的方式来校正，直到第 $m$ 个子模数转换器在 ${\varOmega _{\rm{0}}}$ 频点上的幅度值与第 $0$ 个子模数转换器相应幅度值相等，则校正结束。

在ADC没有增益控制器的特殊情况中，利用式（12）求出增益误差，可以通过乘上相应的比例因子的方法来校正增益误差。

接下来是时间误差的校正，因为偏置和增益误差的存在会影响时间误差的估计，时间误差校正前需要先保证时间交替采集系统已经校正好偏置和增益误差。然后根据式（13）计算出第 $m$ 个子模数转换器的时间误差估计值，根据时间控制器的步进值计算出相应的校正值。计算时间误差的校正值公式为：

${{PhaseCtrWor}}{{\rm{d}}_m} = {{DefaultCtrWord}} - \frac{{\Delta {T_m}}}{{{{ste}}{{{p}}_{{{phase}}}}}}{\text{。}}$

(15)

类似的，当不存在时间误差 $\Delta {T_m}$ 时，第 $m$ 个子模数转换器与第 $0$ 个子模数转换器输出的频谱在 ${\varOmega _{\rm{0}}}$ 处的相位差为确定值 $m{\varOmega _{\rm{0}}}{T_s}$ ，也可以通过遍历的方式，不断发送不同的时间控制字，直到第 $m$ 个子模数转换器与第 $0$ 个子模数转换器在 ${\varOmega _{\rm{0}}}$ 处的相位差为 $m{\varOmega _{\rm{0}}}{T_s}$ ，校正结束。

在子模数转换器没有时间控制器的特殊情况中，仍是利用式（13）求出时间误差，可以通过数字处理的方法，设计分数延迟滤波器来校正。

4 实验验证及结果分析

算法验证平台中子模数转换器的采样率为1.25 GSPS，需要设置输入模拟信号的频率小于625 MHz，试验中选择输入信号的频率为156.25 MHz。这种采样率是输入信号整数倍的情况下，输入信号的能量集中在一根谱线上，避免了频谱泄漏，增加了校正的精度，也可以直观的比较校正效果。

将第 $0$ 个子模数转换器作为参考通道，进行增益误差和时间误差的校正，通过对比校正前后频谱的差异来证明算法的有效性。由文献[10]，如果存在增益和时间误差，则在 $n{f_s}/M \pm {f_{{\rm{in}}}}$ 处会存在误差谱。在本试验下，会在1.09，1.40，2.34 GHz频点处出现误差谱。

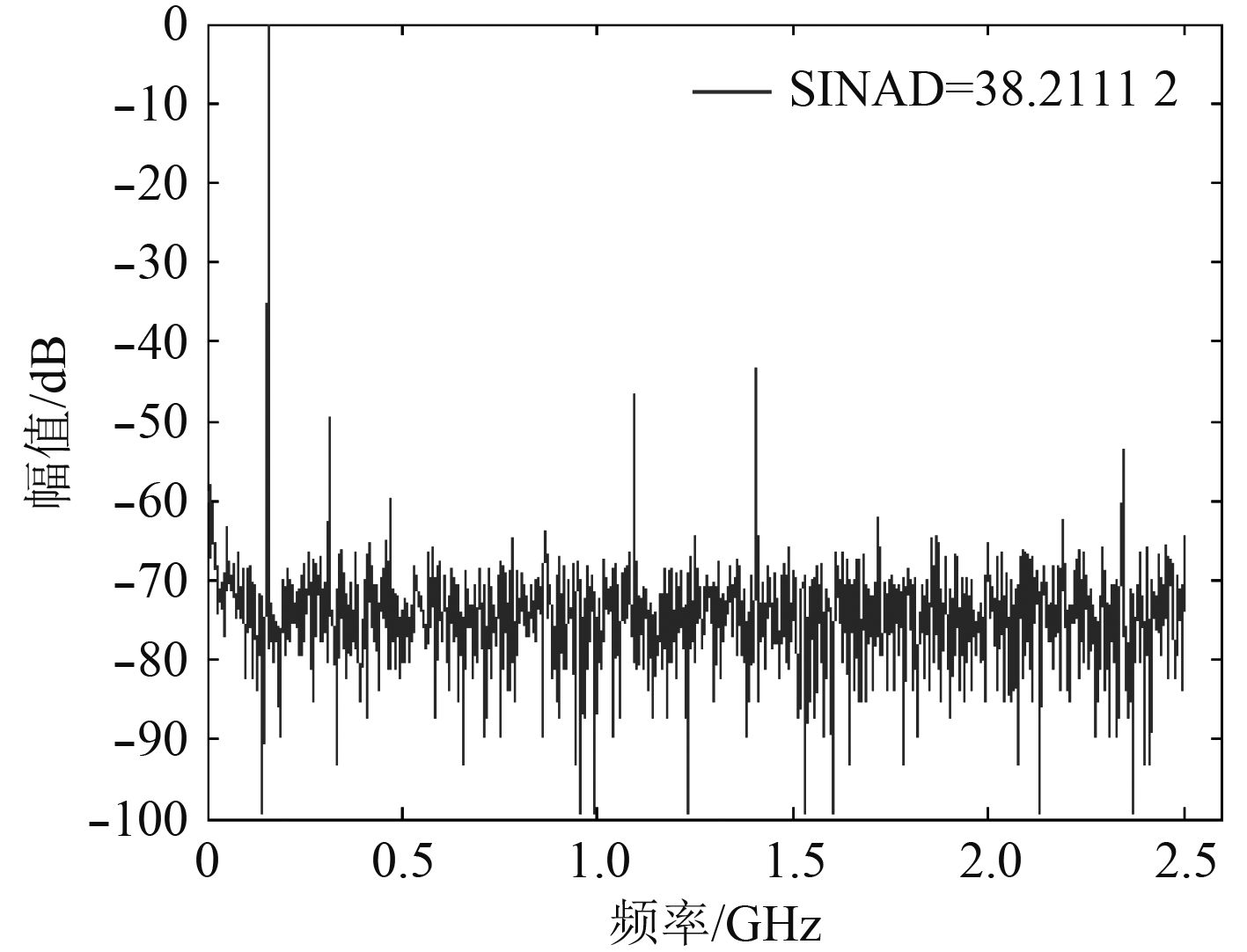
为了清楚比较增益与时间误差，首先校正好时间交替采集系统的偏置误差。图4是校正以前，时间交替采集系统输入为156.25 MHz时的量化输出频谱，可以看出增益和时间的误差的存在使得，1.09，1.40，2.34 GHz频点出现了比较明显的误差频谱，这会影响系统的性能。通过计算得到此时系统的SINAD为38.212 dB，有效位数为6.05 bit。

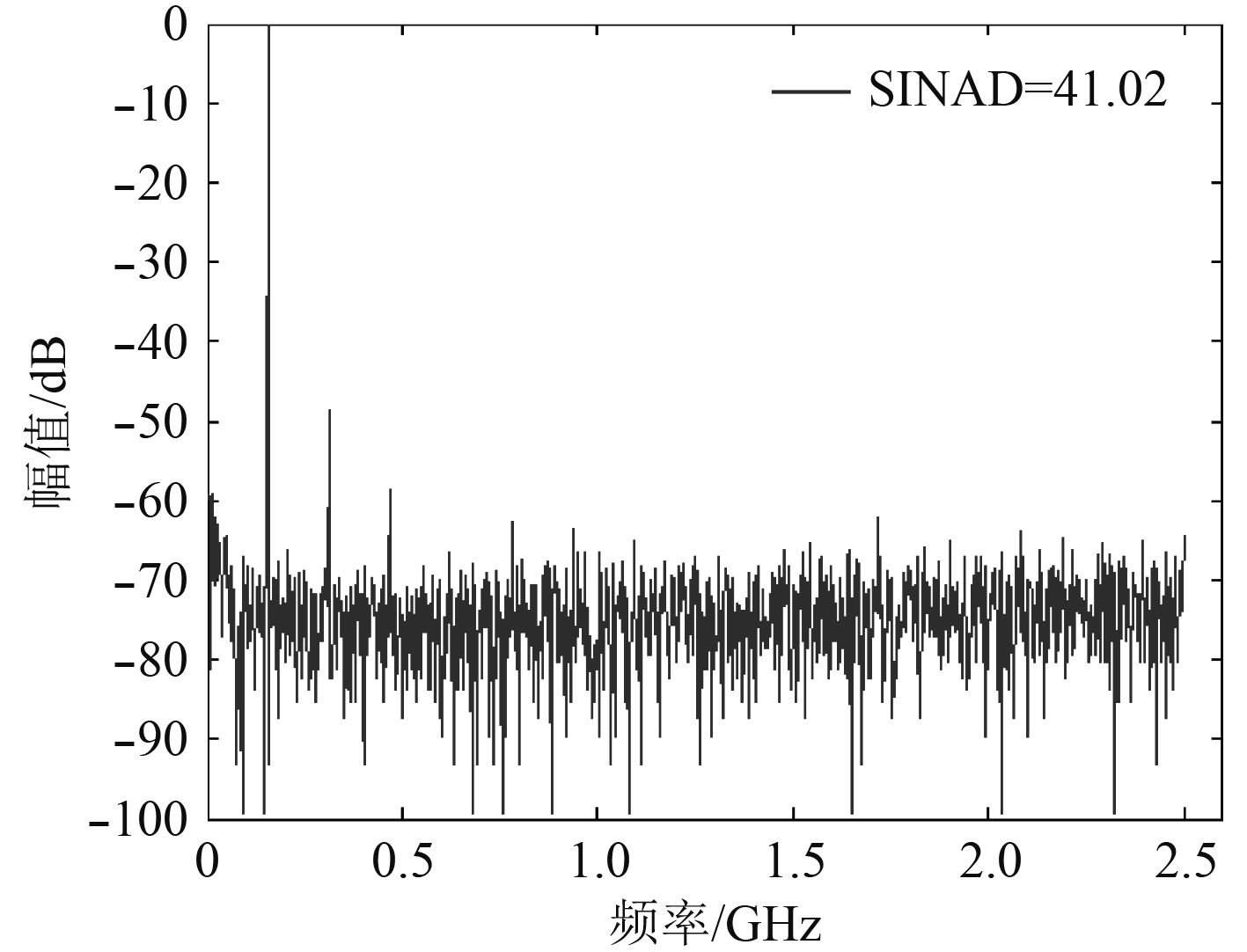
通过频域内误差的估计与校正后，得到图5所示的校正后的频谱图，可以看到各个频点的误差谱得明显降低。计算得到校正后时间交替采集系统的SINAD提高到了41.02 dB，有效位数也提高到了6.52 bit。通过对比得到，时间交替采集系统的频域校正方法能够起到很好的作用，明显降低误差谱，提高了系统的SINAD和有效位数。

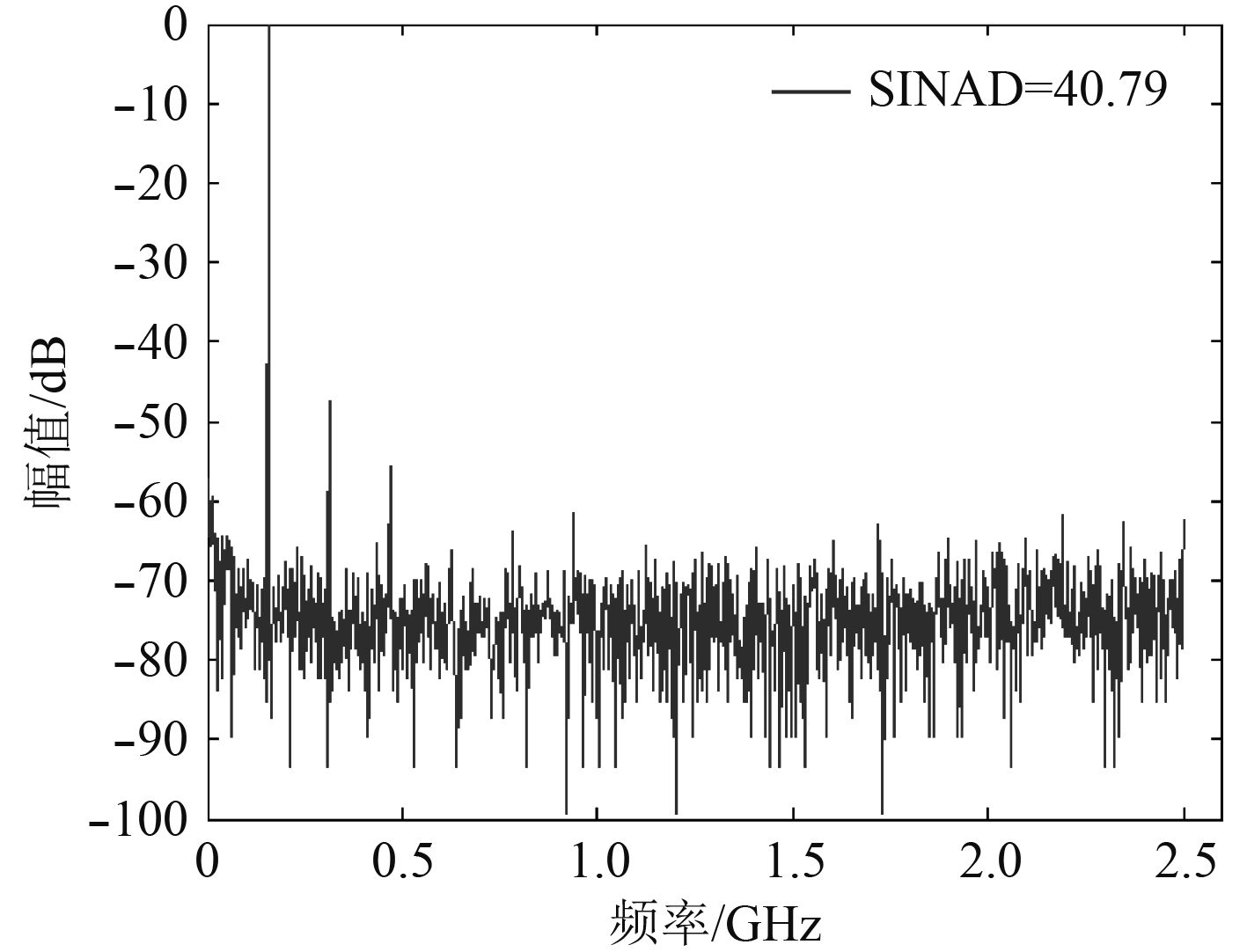
将频域校正算法与文献[9]中的正弦拟合算法做对比。将2种算法采用相同的处理方式，即输入相同频率和幅度的正弦信号，控制系统的偏置误差都一致。图6是采用正弦拟合算法校正后的得到的信号频谱，从中看出在 $n{f_s}/M \pm {f_{{\rm{in}}}}$ 频点处同样可以很好的校正误差，最后得到系统的SINAD为40.79，与文献[9]中的结果相当。对比可以看出，时间交替采样系统的频域校正方法效果不差于传统的正弦拟合算法。

5 结　语

本文特点是讲究实用性，一切从工程实用角度出发。时间交替采集系统误差的频域校正方法思路清晰、实现容易，校正精度不低于传统的正弦拟合算法。虽然需要做快速傅里叶变换，来获取子模数转换器的量化输出频谱信息，看似降低了时效性，但是 ${\rm FPGA}$ 内部的IP核可以并行处理数据，大大减少了设计难度和运算时间。这使得时间交替采集系统误差的频域校正方法优势明显，特别适用于工程应用。对于舰船电力系统监控、舰船雷达和实时通信系统的发展有重要的现实意义。