在舰船水下辐射噪声测量的过程中,安全、可靠地引导被测目标通过测量区域,并保证被测目标与测量系统之间的有效距离以满足测试需求是极其重要的,也是一直关心的问题。现有的被测目标引导方法,往往依靠单一导航信标配合测距系统实现,通常仅提供被测目标与导航信标之间的单点距离信息,缺乏方位信息,使得目标实际航行轨迹与试验要求轨迹有一定的偏差,造成测量单程无效,从而降低了测试效率,延长了试验时间[1]。
目前方位估计算法的通常假设目标在观测时间内为静止状态,即静态方位算法,同时采用大计算量和多快拍数的批处理形式进行方位估计[2]。然而在实际情况下,目标通常为运动状态,批处理方式的静态方位估计方法不适用于实时连续跟踪。同时,静态方位估计方法是互不相关地估计2个连续时刻的方位信息,并没有考虑到2个连续时刻状态的关联性,进而造成动态方位估计偏差较大。随着对运动目标的测向精确度和实时处理的要求越来越高,静态方位估计算法已不能满足日益增长的需求,因此研究适用于动态目标的方位跟踪算法成了一个新趋势。本文将静态方位估计中的MUSIC算法和粒子滤波跟踪算法相结合,既提高了方位估计的精度更减小了计算量以适用于对目标的实时方位跟踪。
1 AVS和MUSIC方位估计算法 1.1 AVS接收信号模型假设AVS接收窄带目标声源信号
通常在实际应用中矢量水听器接收的水下目标辐射声场为平面波声场,因此假设声源为平面波。则矢量水听器接收的声压
| $v(t) = p(t) \cdot {u_t}/\left( {{\rho _0}c} \right){\text{,}}$ | (1) |
其中,
| ${u_t}\left( {{\phi _t},{\varphi _t}} \right) = {[\cos {\varphi _t}\cos {\phi _t},\cos {\varphi _t}\sin {\phi _t},\sin {\varphi _t}]^{\rm T}}{\text{,}}$ | (2) |
则单矢量水听器的接收信号模型为[3]
| $y(t) = \left[ \begin{array}{l}1\\\displaystyle\frac{{{u_t}\left( {{\phi _t},{\varphi _t}} \right)}}{{{\rho _0}c}}\end{array} \right]s\left( t \right) + \left[ \begin{array}{l}{n_p}\left( t \right)\\{n_v}\left( t \right)\end{array} \right]{\text{。}}$ | (3) |
其中:
实际应用中处理的信号为离散信号,一般采用快拍数对每时刻数据进行批处理。假设快拍数为N在k时刻的声源信号为
| $s(k) = \left[ {s\left( {kN + 1} \right), \cdots ,s\left( {kN + N} \right)} \right]{\text{,}}$ | (4) |
则噪声和接收数据为
| $N(k) = \left[ {n\left( {kN + 1} \right), \cdots ,n\left( {kN + N} \right)} \right]{\text{,}}$ | (5) |
| $Y(k) = \left[ {y\left( {kN + 1} \right), \cdots ,y\left( {kN + N} \right)} \right]{\text{,}}$ | (6) |
则接收信号的离散化接收模型为
| $Y(k) = a\left( {{\phi _k},{\varphi _k}} \right)s(k) + N(k){\text{。}}$ | (7) |
其中:
| $a\left( {{\phi _k},{\varphi _k}} \right) = {\left[ {1,{u_k}/{\rho _0}c} \right]^{\rm T}}{\text{。}}$ | (8) |
接收信号包含方位角和俯仰角信息,进而可以对数据进行方位估计。
1.2 MUSIC方位估计MUSIC算法作为子空间特征分解相关算法的代表,实现了方位估计技术向高分辨的发展。MUSIC算法的核心思想是利用数据的自相关矩阵的内在结构特性,将数据的协方差矩阵分解为和阵列流形一致的信号子空间,以及与信号子空间正交的噪声子空间,并利用2个子空间的正交性,通过对谱峰进行搜索来估计信源的方位。
工程实际中,为提高信号处理的精度,采用多快拍数的观测数据。设快拍数为L,则接收数据的自相关矩阵可表示为
| ${{{R}}_k} = \frac{1}{N}{\bf{Y}}(k){\bf{Y}}{(k)^H}{\text{,}}$ | (9) |
对
| ${{{R}}_k} = {{U}}\sum {{{U}}^H} = {{S}}{\sum _S}{{{S}}^H} + {{G}}{\sum _n}{{{G}}^H}{\text{。}}$ | (10) |
则可得MUSIC算法为[4]
| ${P_{MUSIC}}({\phi _k},{\varphi _k}) = \frac{1}{{{a^H}({\phi _k},{\varphi _k}){{G}}{{{G}}^H}a({\phi _k},{\varphi _k})}}{\text{。}}$ | (11) |
其中,G为与噪声相关的特征值矩阵对应的噪声子空间。
因此,通过谱估计式(11)的峰值搜索估计和峰值相对应的角度值即为入射的方向信息。
在信噪比(SNR)相对较高的噪声环境中,MUSIC方法能够通过如图1所示的尖锐峰值来呈现声源DOA。声源真实方位为(20.5°,40.5°),然而,当SNR低时,峰值可能失真并且估计的DOA可能远离真实位置,如图2所示。
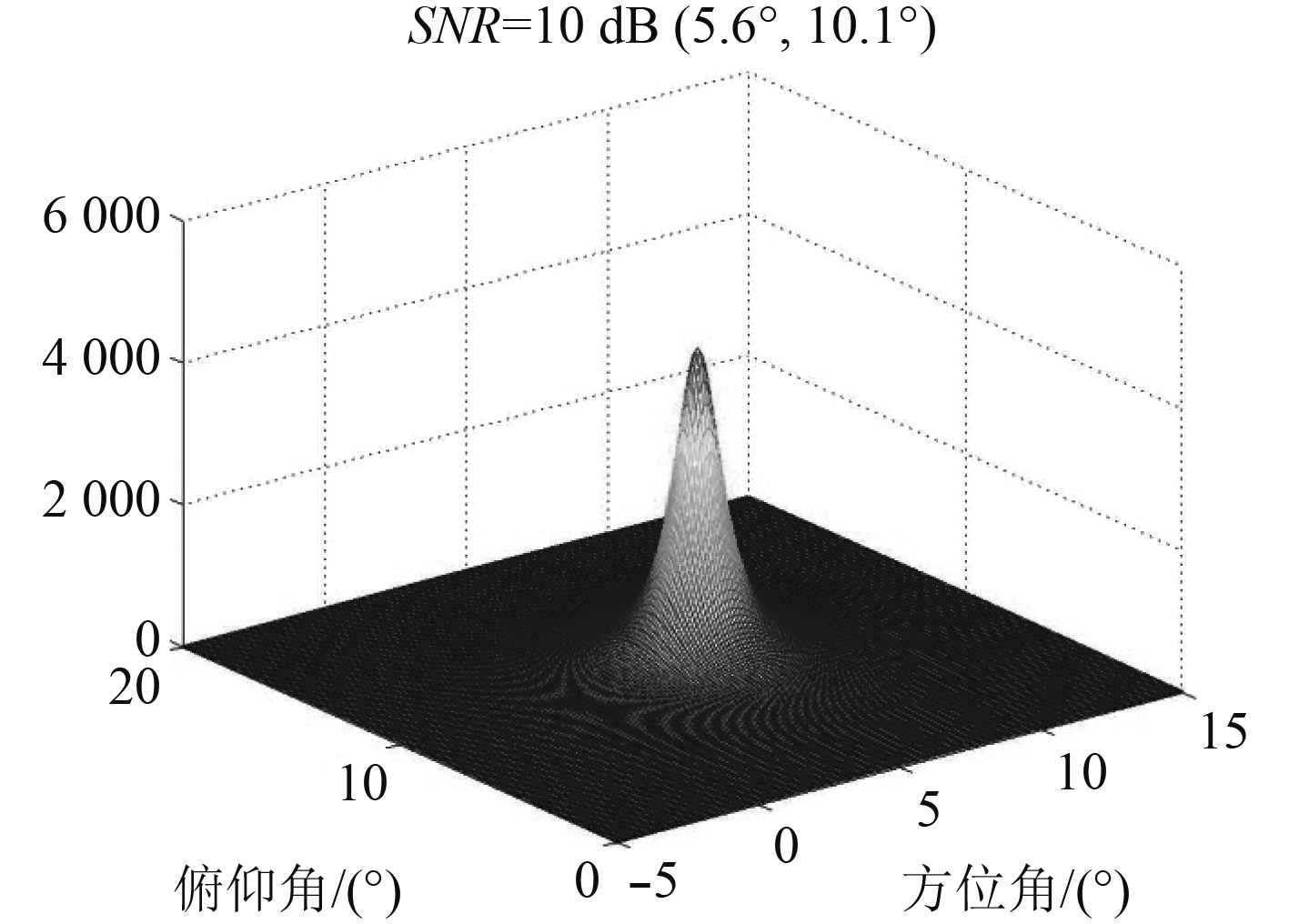
|
图 1 MUSIC方法DOA估计性能SNR=10 dB Fig. 1 DOA estimated performance based on the MUSIC algorithm SNR=10 dB |
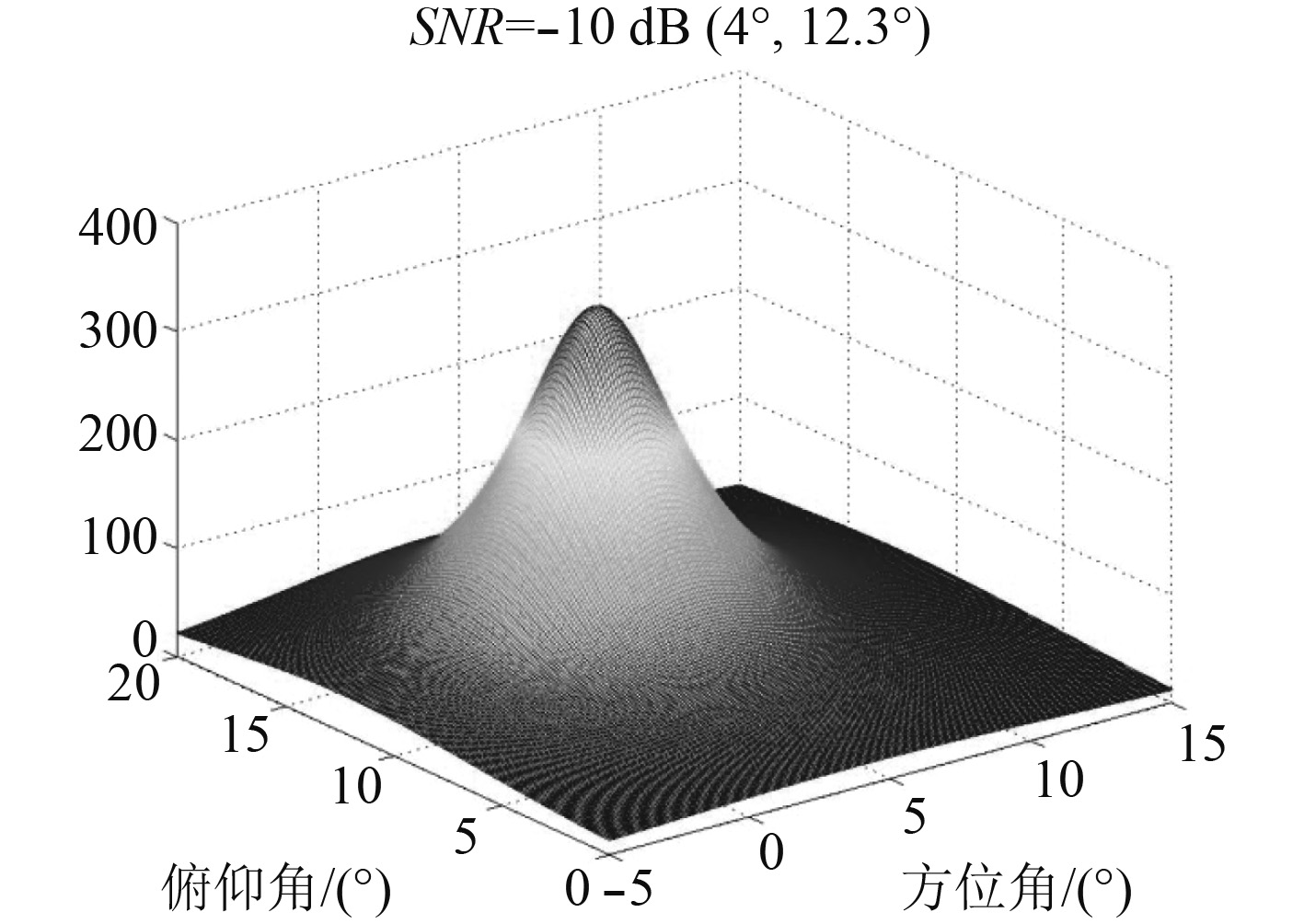
|
图 2 MUSIC方法DOA估计性能SNR=–10 dB Fig. 2 DOA estimated performance based on the MUSIC algorithm SNR=–10 dB |
为了给出DOA跟踪问题的总体框架,首先定义状态空间模型。假设目标声源当前方位为
| ${x_k} = {{A}}{x_{k - 1}} + {{B}}{v_k}{\text{,}}$ | (12) |
其中,A,B为系数矩阵。
| ${{A}} = \left[ \begin{array}{l}{I_2},\Delta T{I_2}\\0,{I_2}\end{array} \right];{{B}} = \left[ \begin{array}{l}\Delta {T^2}{I_2}/2\\\Delta T{I_2}\end{array} \right]{\text{。}}$ | (13) |
其中:
矢量水听器的输出矩阵是天然的观测模型,即为式(7)。采用基于递归方式的贝叶斯重要性采样,并以预测和更新的方式实现状态估计[6]。
在递归过程中,
| ${x_k}(i) \sim p\left( {{x_k}(i)|{x_{k - 1}}(i)} \right){\text{,}}$ | (14) |
当前时刻粒子权重的重要性为[8]
| $w_k^*\left( {{x_k}(i)} \right) = w_{k - 1}^*\left( {{x_{k - 1}}(i)} \right)\frac{{p\left( {{{{Y}}_k}|{x_k}(i)} \right)p\left( {{x_k}(i)|{x_{k - 1}}(i)} \right)}}{{q\left( {{x_k}(i)|{x_{0:k - 1}}(i),{{{Y}}_{1:k - 1}}} \right)}}{\text{,}}$ | (15) |
其中
| $q\left( {{x_k}(i)|{x_{0:k - 1}}(i),{{{Y}}_{1:k - 1}}} \right) = p\left( {{x_k}(i)|{x_{k - 1}}(i)} \right){\text{,}}$ | (16) |
因此,粒子权重为
| ${\kern 1pt} w_k^*\left( {{x_k}(i)} \right) = {\kern 1pt} {\kern 1pt} w_{k - 1}^*\left( {{x_{k - 1}}(i)} \right){\kern 1pt} p\left( {{{{Y}}_k}|{x_k}(i)} \right){\text{,}}$ | (17) |
对粒子权重进行归一化处理:
| $w_k^{}\left( {{x_k}(i)} \right) = \frac{{w_k^*\left( {{x_k}(i)} \right)}}{{\displaystyle\sum\limits_{i = 1}^L {w_k^*\left( {{x_k}(i)} \right)} }}{\text{,}}$ | (18) |
则得当前时刻
| ${\hat x_k} = \sum\limits_{i = 1}^L {{w_k}(i){x_k}(i)}{\text{。}}$ | (19) |
因此粒子权重在算法的滤波性能上具有重要的作用。当粒子接近真实位置时,粒子的似然函数具有较大的权重,则为了让粒子在更新时使权重大的粒子能够在重采样时取代权重小的粒子,由式(20)可知似然函数
| $\hat p\left( {{Y_k}|{x_k}(i)} \right) \!=\! \left\{ {\frac{1}{{{e^N}{\text{π}^4}}}} \right\} \!*\! {\left( {\det \left\{ {\left( {I \!-\! a{{\left( {{a^H}a} \right)}^{ \!-\! 1}}{a^H}} \right){R_k}} \right\}} \right)^{ \!-\! 1}}\!\!{\text{。}}$ | (20) |
似然函数的主瓣通常比较平缓,尤其在低信噪比的条件下,因此不能有效的通过权重衡量真实状态周围的粒子并且可能出现虚假峰值。同时当快拍数很大时,将会导致粒子的权重接近于0,进而导致对粒子的权重估计失效。
因此引入MUSIC方法作为似然函数,即
| $\begin{split}\hat p\left( {{Y_k}|{x_k}(i)} \right) = & {P_{MUSIC}}({\phi _k},{\varphi _k}) = \\ &\frac{1}{{{a^H}({\phi _k},{\varphi _k}){{{G}}_k}{{G}}_k^Ha({\phi _k},{\varphi _k})}}{\text{。}}\end{split}$ | (21) |
则似然函数被重塑,以增强在高似然区域采样粒子的权重。这一步非常重要,因为它能够帮助后续重采样算法更有效地选择和复制粒子。
给出最终PF-MUSIC方法的流程为
步骤1 初始化:采用随机方法估计初始角度,从均匀分布中采样,粒子数为N,
步骤2 在k时刻,按照式(14)进行抽样得
步骤3 计算接收数据协方差矩阵
步骤4 按照式(17)计算粒子权重
步骤5 按照式(18)归一化权重
步骤6 按照式(19)计算状态的的估计值
步骤7 令k=k+1,重复步骤2~步骤7。直到k>T时,终止计算。
3 方位跟踪方法性能验证分析 3.1 仿真分析方位跟踪方法性能设矢量水听器位置为坐标原点;声源是频率为
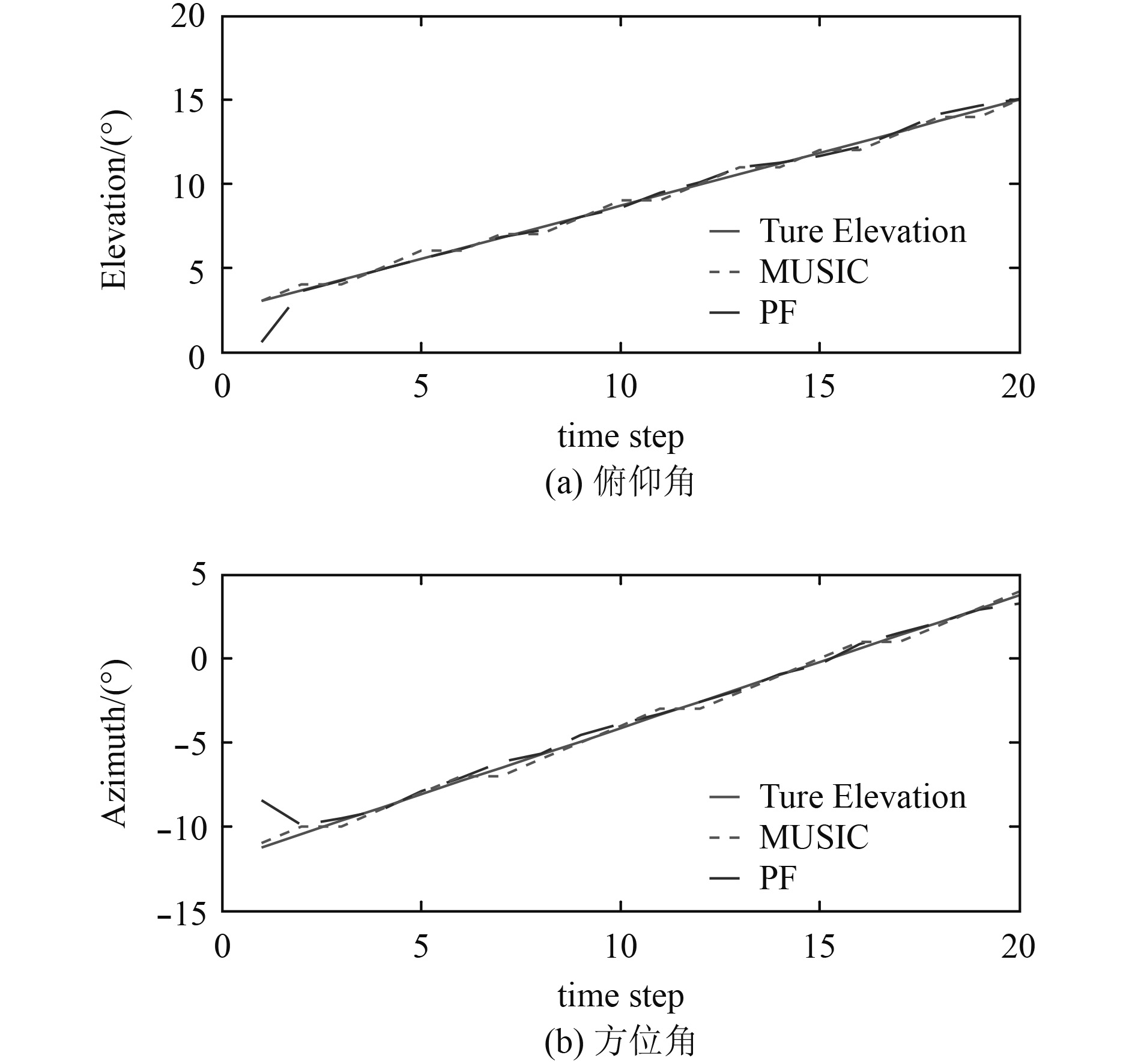
|
图 3 SNR=10条件下的方位跟踪 Fig. 3 DOA tracking under the condition of SNR=10 dB |
图3给出了MUSIC方法和PF-MUSIC跟踪方法的DOA跟踪性能。MUSIC方法的性能在多个时间步长处,DOA估计结果远离真实轨迹。然而,PF-MUSIC方法能够结合来自声源的动力学模型的时间信息以及来自当前测量时刻的空间信息,从而能够一致地跟踪声源方位。它能始终锁定声源,并呈现令人满意的DOA跟踪。另外,虽然初始DOA对于PF-MUSIC方法是未知的并且被假定为均匀分布,但PF-MUSIC跟踪方法能够快速地收敛到真实轨迹。
为了充分评估跟踪性能,采用50次蒙特卡罗平均模拟均方根误差(RMSE)。如果绝对误差小于1°,则被认为是正确的估计。图4给出不同SNR下对RMSE的影响。采用从–10 dB~0 dB的不同SNR,以2 dB的增量产生噪声环境。
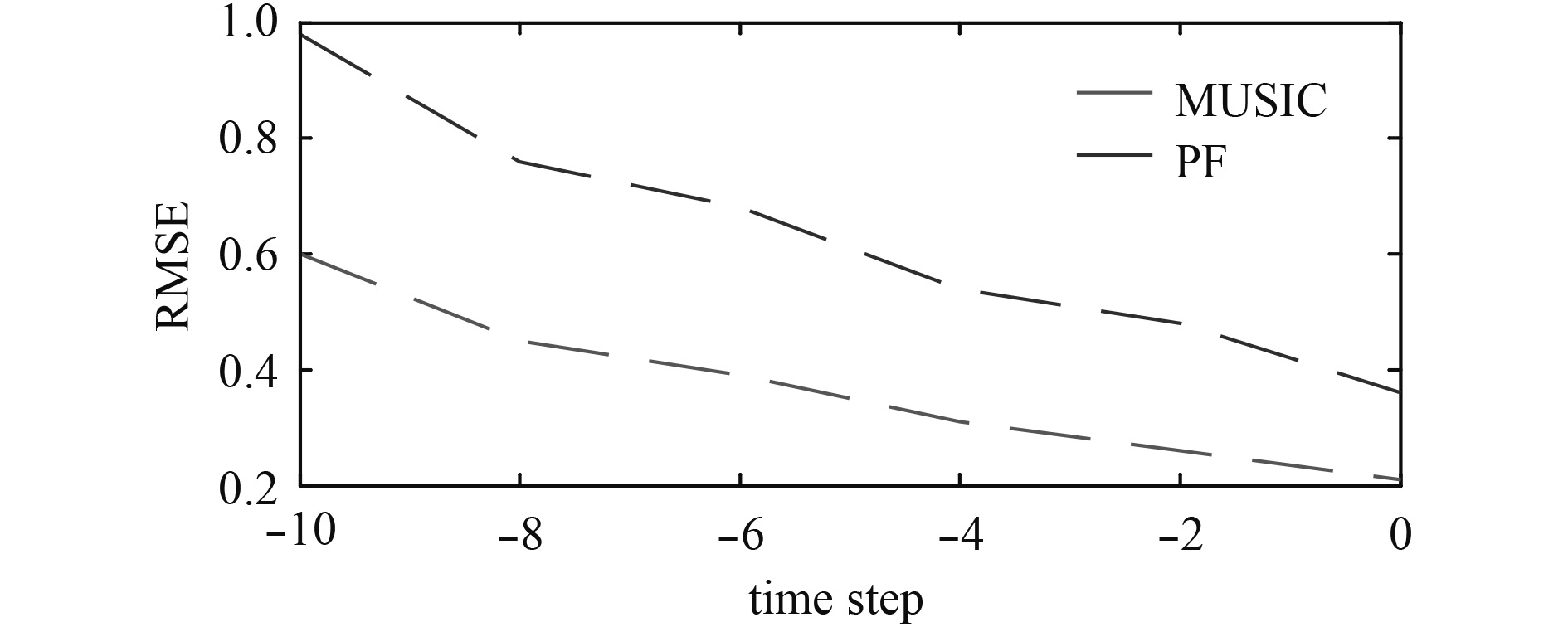
|
图 4 不同快拍数和SNR下的RMSE Fig. 4 RMSE under the conditions of different snapshots and SNR |
由于结合了时间信息,所提出的PF-MUSIC跟踪算法在估计DOA方面比MUISC方位方法执行得更好。PF-MUSIC跟踪算法即使在非常低的SNR环境下(例如,SNR=–10 dB),依然能够保持对声源DOA的锁定。同时,PF-MUSIC方法不需要对角度进行三维搜索,在计算量上远低于MUSIC方法,更适用于对目标的实时方位跟踪的需求。
3.2 海上试验验证2017年8月,在大连海域水深60 m区域,试验验证实时方位跟踪方法的性能。信标的导航信号为
为验证方位跟踪方法的实际性能,这里采用短基线方位方法作为对比方案。分别在目标首部和尾部各安装2个接收器,用以接收导航信标信号。基线长度为53 m。
截取分析200 s的试验数据,即
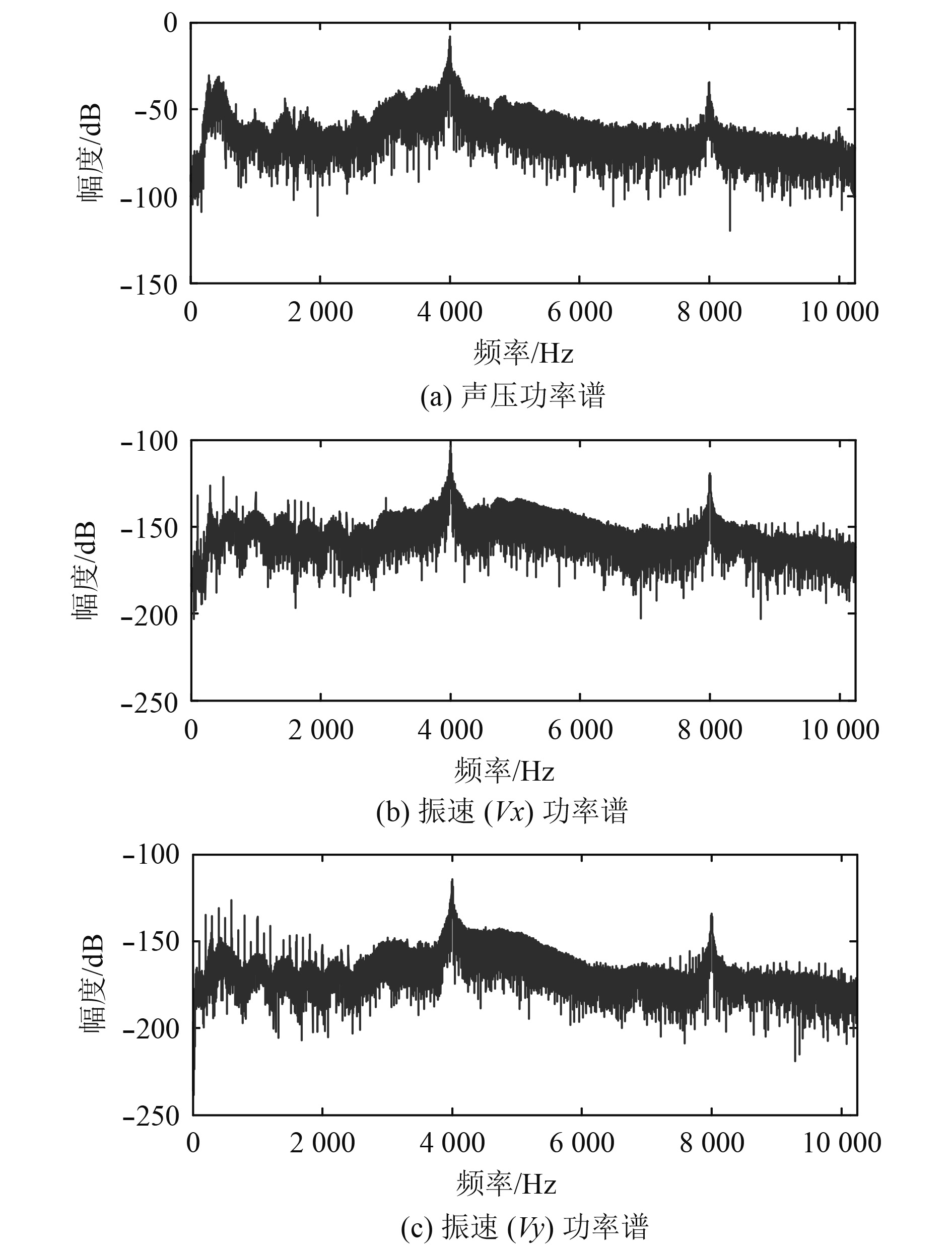
试验所采用的矢量水听器为二维球型,典型的矢量水听器接收的声压及振速的功率谱如图5所示。
|
图 5 矢量水听器接收声压和振速信号的频谱 Fig. 5 Spectrums of Sound pressure and vibration speed received by the vector hydrophone |
短基线和PF-MUSIC方法的跟踪效果如图6所示。

|
图 6 方位跟踪效果 Fig. 6 The effect of DOA tracking |
可知PF-MUSIC方法的方位跟踪效果良好,并且与短基线方位相比曲线更平滑,适用于水下目标的实时方位跟踪。同时,仅需在舰船上加装单矢量水听器即可满足测试要求,更适用于工程实际。
4 结 语将粒子滤波算法和MUSIC方法相结合,应用于矢量水听器接收的水下运动目标数据的处理,有效地对运动目标的方位进行跟踪。采用CV模型对声源运动状态进行建模,将MUSIC方法的估计函数作为粒子滤波算法中的似然函数,有效改进了在低信噪比条件下的跟踪性能。通过结合时间和空间信息,PF-MUSIC跟踪方法在二维DOA跟踪中优于传统的MUSIC方法,并且不需要空间搜索降低了计算量,适用于对目标的实时跟踪,同时在较低信噪比的条件下也能够获得较好的精度,对水下目标的实时方位跟踪上有较好的应用前景。
| [1] |
王之程, 陈宗岐, 于沨, 等. 舰船噪声测量与分析[M]. 北京: 国防工业出版社. 2004.
|
| [2] |
KRIM H, VIBERG M. Two decades of array signal processing research: the parametric approach[J]. IEEE Signal Process. Mag., 1996, 13(4): 67–94.
|
| [3] |
NEHORAI A, PALDI E. Acoustic vector-sensor array processing[J]. IEEE Trans. Signal Process, 1994, 42(9): 2481–2491.
|
| [4] |
WONG K T, ZOLTOWSKI M D. Self-initiating MUSIC-based direction finding in underwater acoustic particle velocity-field beamspace[J]. IEEE J. Ocean. Eng., 2000, 25(2):262–273.
|
| [5] |
LI X RONG, JILKOV V P. Survey of maneuvering target tracking. part 1: Dynamic models[J]. IEEE Trans. Aerosp. Electron. Syst., 2003, 39(4): 1333–1364.
|
| [6] |
ZHONG Xionghu, PREMKUMAR A B, MADHUKUMAR A S. Particle filtering and posterior cramér-rao bound for 2-D direction of arrival tracking using an acoustic vector sensor[J]. IEEE Sensors Journal, 2012, 12(2).
|
| [7] |
ARULAMPALAM M, MASKELL S, GORDON N, et al. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking[J]. IEEE Trans. Signal Process., 2002, 50(2): 174–188.
|
| [8] |
ZHONG Xionghu, PREMKUMAR A B, MADHUKUN A S. Particle filtering and posterior Cramér-Rao Bound for 2-D direction of arrival tracking using an acoustic vector sensor[J]. IEEE Sensors Journal, 2012: 363–377.
|
| [9] |
ZHONG Xionghu, PREMKUMAR A B, WANG W. Direction of arrival tracking of an underwater acoustic source using particle filtering: Real data experiments[C]//Sydney, NSW: IEEE Tencon Spring Conference, April 17–19, 2013: 420–424.
|
 2018, Vol. 40
2018, Vol. 40
