近年来国内对发电机励磁控制系统有较多研究,并提出不少新控制方法,如:线性最优控制、非线性控制、自适应控制、专家控制和模糊PID控制等[1 – 3],但对船舶同步发电机励磁控制系统研究相对较少,采用的控制方法仍是经典PID控制。经典PID控制具有算法简单,不依赖系统精确模型,易实现等优点,但其存在快速性与超调相互矛盾和抗干扰能力不强的缺点。船舶电力系统频繁突加突卸大功率负载,导致在经典PID控制下船舶同步发电机输出电压波动较大。ADRC(Active Disturbance Rejection Controller)能解决经典PID快速性和超调相互矛盾的问题,并通过非线性误差反馈律实时估计和补偿扰动,在系统发生扰动时,具有较好的控制效果。因此,提出采用ADRC代替经典PID控制器,以减少突加突卸大功率负载下船舶同步发电机输出电压的波动。
自抗扰控制技术是对经典PID控制技术的继承及完善,其继承了经典PID算法简单,不依赖于系统精确模型的优点,通过对输入量安排过渡过程降低系统受到扰动后控制量变化太大,用非线性反馈律代替经典PID中对比例、积分、微分三者简单加权求和,提高系统的稳定性[4 – 5]。
本文从船舶发电机励磁系统数学模型出发,考虑到励磁系统是个串级系统的特性,设计基于自抗扰控制技术的励磁控制系统。其次在Simulink平台上搭建船舶发电机励磁系统仿真模型,对ADRC和经典PID控制器做仿真对比实验。
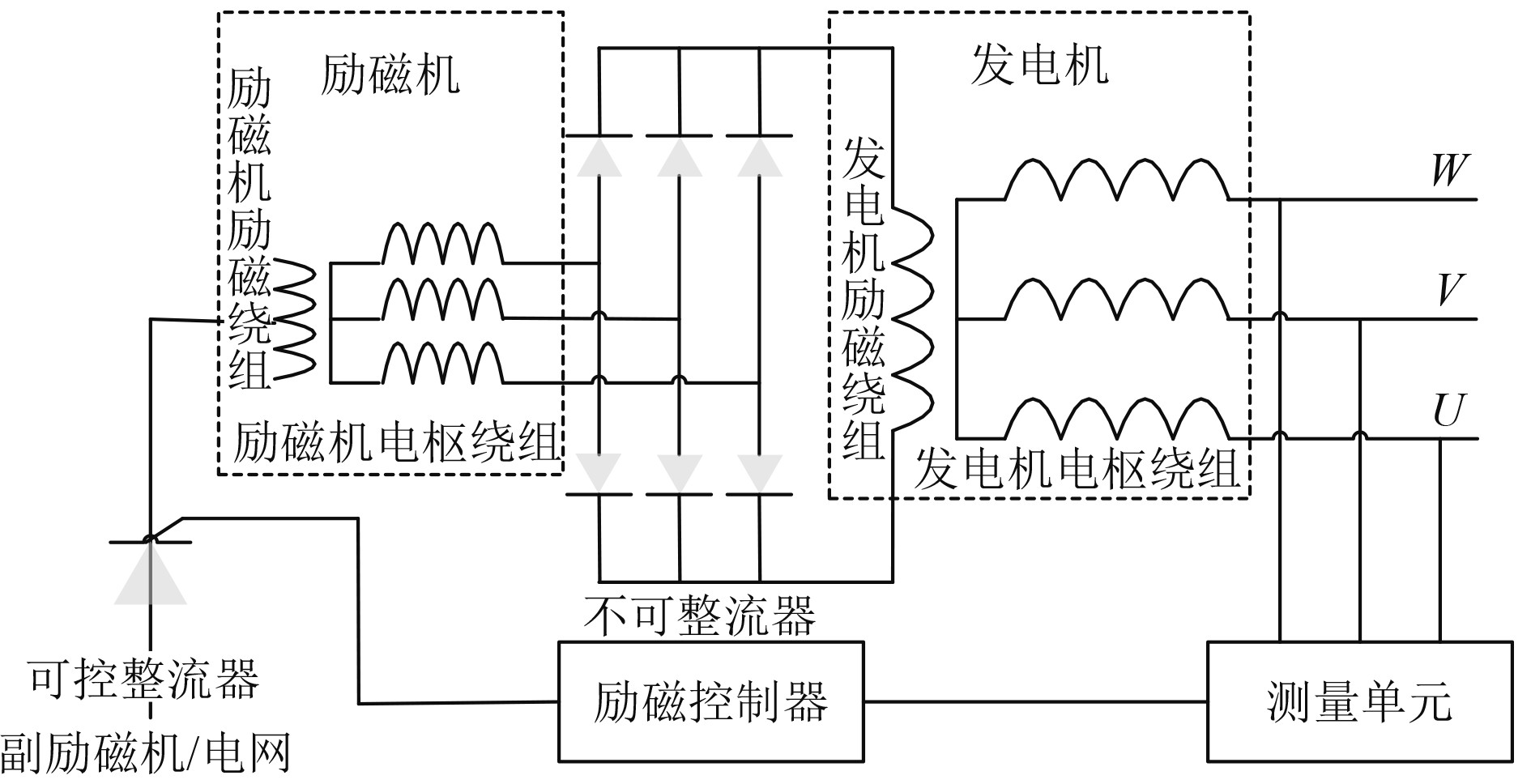
1 船舶无刷同步发电机励磁系统的结构原理船舶无刷同步发电机励磁系统由发电机、励磁机、可控整流器、不可控整流器、控制器及测量单元这几个部分组成,如图1所示。发电机为旋转磁极式同步发电机,励磁机为旋转电枢式同步发电机[6]。励磁机电枢绕组、不可控整流器及发电机励磁绕组由原动机带动同轴旋转,省去电刷和滑环,提高发电机运行的安全性。测量单元检测发电机的电压、电流值,输入给励磁控制器产生控制信号,控制可控整流器调节输入到励磁机励磁绕组的励磁电流,形成励磁机的励磁回路。励磁机电枢绕组输出的交流电流经不可控整流器整流为直流输入给发电机励磁绕组,形成发电机的励磁回路[7]。
|
图 1 无刷同步发电机励磁系统结构 Fig. 1 Structure of excitation system of synchronous generator |
励磁机本身是一个发电机,数学模型较为复杂,在设计励磁系统时,文中仅考虑励磁机的饱和效应、去磁反应和不可控整流器的换向压降,可得交流励磁机带不可控整流器的数学模型[8]:
| $\left\{ \begin{aligned}& {U_{fe}} = {U_E}\left( {1 + {S_E}} \right) + {K_D}{I_{FD}} + {T_e}\displaystyle\frac{{{\rm d}{U_E}}}{{{\rm d}t}}{\text{,}}\\& {E_{FD}} = {F_{EX}}{U_E}{\text{。}}\end{aligned} \right.$ | (1) |
式中:Ufe为励磁机励磁绕组电压;EFD为发电机励磁电压;Se为励磁机励磁绕组空载饱和系数;Te为励磁机随着励磁机饱和程度变化的时间常数;UFD为发电机励磁绕组电压;UE为励磁机电枢绕组电压;FEX为整流器的整流系数;IFD为发电机额定励磁电流。
由式(1)可知交流励磁机是由时间常数、饱和特性、电枢反应和整流换相压降共同作用的,也决定了励磁机是一个非线性时变的系统[9]。
2.2 励磁系统其他单元传递函数根据实际应用和一般的分析情况,对图1所示励磁系统,本文给出各单元的传递函数如下:
1)电压检测单元
| ${G_A}\left( s \right) = \frac{{{U_{of}}\left( s \right)}}{{{U_G}\left( s \right)}} = \frac{{{K_{of}}}}{{1 + {T_d}S}}{\text{,}}$ | (2) |
式中:Uof(s)为控制器的反馈电压;UG(s)为发电机的输出电压;Kof为比例系数;Td为滤波回路的时间常数。
2)电流检测单元
| ${G_R}\left( s \right) = \frac{{{K_H}}}{{1 + {T_H}s}}{\text{,}}$ | (3) |
式中:KH为比例系数;TH为检测单元的时间常数。
3)不可控整流单元
| ${G_m}\left( s \right) = {K_m}{\text{,}}$ | (4) |
式中:Km为整流器增益。
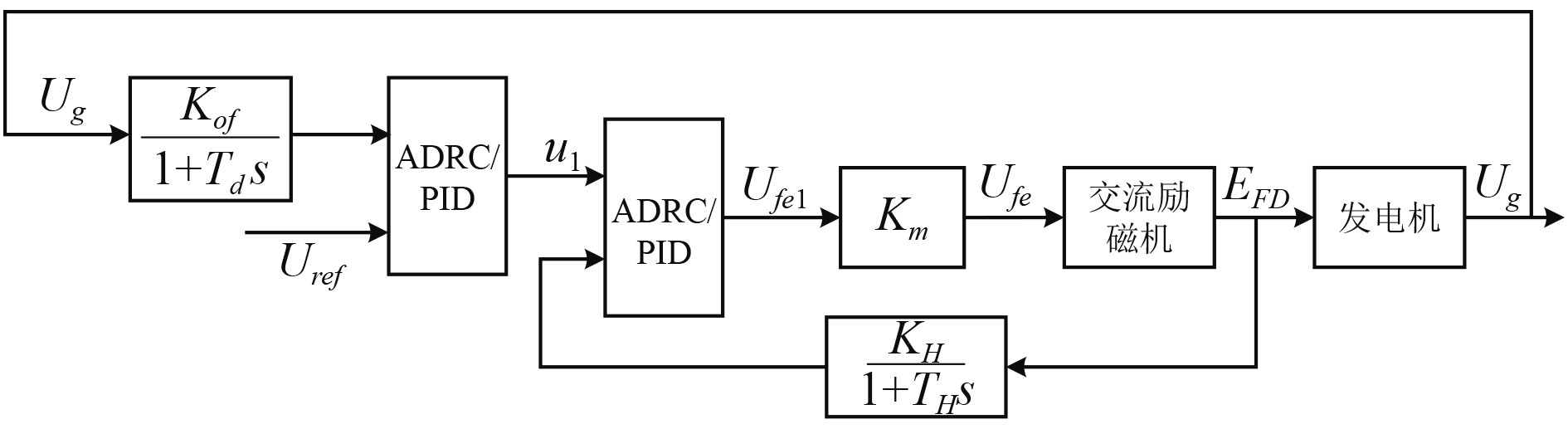
3 自抗扰控制器原理及控制系统设计结合上节所给出的励磁系统各部分单元的数学模型和传递函数,设计励磁系统控制框图,如图2所示。
|
图 2 励磁系统控制框图 Fig. 2 Excitation system control block diagram |
电压检测单元采集发电机输出电压信号作为外环ADRC/PID输入信号,外环ADRC/PID输出信号作为内环ADRC/PID输入信号,构成励磁系统控制环路。
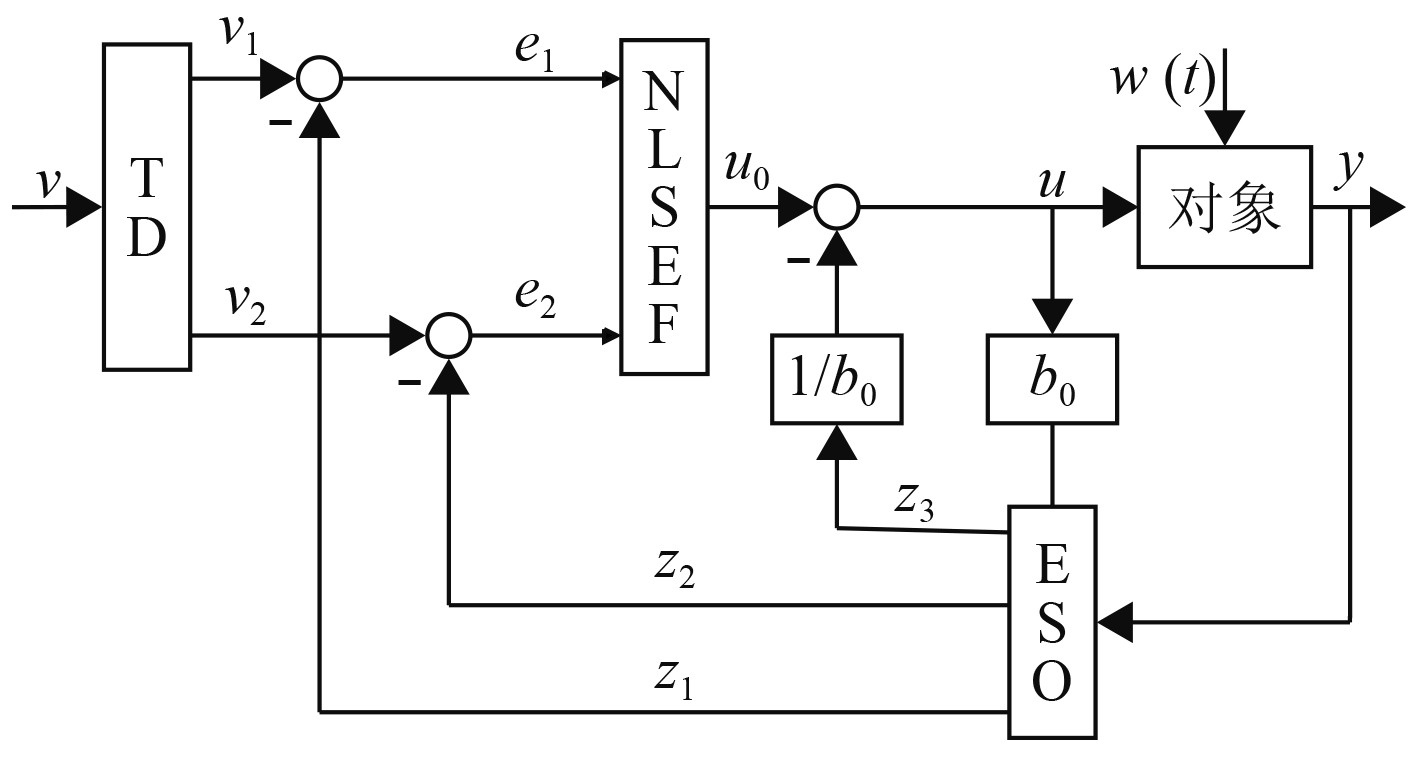
3.1 ADRC的结构ADRC由3个部分组成,分别是微分跟踪器(TD)、扩张状态观测器(ESO)和非线型误差反馈控制律(NLSEF),这里给出二阶ADRC的结构图,如图3所示。
|
图 3 ADRC结构图 Fig. 3 ADRC structure diagram |
图3中跟踪微分器(TD)的输入量为v,2个输出量分别为v1,v2,其中v1跟踪输入信号v,用于控制需要以及根据控制对象的能力安排光滑过渡过程,v2为v1的微分信号;扩张状态观测器的输入信号是系统的输入信号y,输出信号分别为z1,z2,z3,z1为系统输出信号y的跟踪信号,z2为z1的微分信号,z3为对系统模型和扰动的总估计;偏差信号e1=v1–z1与微分信号的偏差e2=v2–z2两者非线性组合产生控制量u0,再通过z3来补偿扰动产生最终的控制信号u=u0–z3/b0。
3.2 ADRC的实现算法1)跟踪微分器(TD):以设定值v为输入,安排过渡过程。
| $\left\{ \begin{array}{l}{z_1}\left( {t + 1} \right) = {z_1}\left( t \right) + h{z_2}\left( t \right){\text{,}}\\{z_2}\left( {t + 1} \right) = {z_2}\left( t \right) + hfhan\left( {{z_1}\left( t \right) - v\left( t \right),{z_2},r,h} \right){\text{。}}\end{array} \right.$ | (5) |
其中,
| $\left\{ \begin{array}{l}d = rh,{d_0} = dh,y = {z_1}\left( t \right) - v\left( t \right) + h{z_2}{\text{,}}\\{a_0} = \sqrt {{d^2} + 8r\left| y \right|}{\text{,}}\\a = \left\{ \begin{array}{l}{z_2} + \frac{y}{h},\left| y \right| \leqslant {d_0}{\text{,}}\\{z_2} + 0.5\left( {{a_0} - d} \right)sign\left( y \right),\left| y \right| > {d_0}{\text{,}}\end{array} \right.\\fhan = \left\{ \begin{array}{l} - \frac{{ra}}{d},\left| a \right| \leqslant d{\text{,}}\\ - rsign\left( a \right),\left| a \right| > d{\text{。}}\end{array} \right.\end{array} \right.$ | (6) |
式中:v(t)为控制器输入信号;h为积分步长,其值越大滤波效果越好;r为速度因子,其值越大控制器的响应速度越快。
2)扩张状态观测器(ESO):以系统输入信号y来跟踪估计系统状态,以系统输出信号u来估计系统总扰动。
| $\left\{ \begin{array}{l}{z_1} = {z_2} + {\beta _1}fa{l_1}\left( e \right){\text{,}}\\e = {z_1} - y{\text{,}}\\ \vdots \\{z_n} = {z_{n + 1}} - \beta {}_nfa{l_n}\left( e \right) + {b_0}u{\text{,}}\\{z_{n + 1}} = - {\beta _{n + 1}}fa{l_{n + 1}}\left( e \right){\text{。}}\end{array} \right.$ | (7) |
其中,
| $fal\left( {e,\alpha ,\delta } \right) = \left\{ \begin{array}{l}\displaystyle\frac{e}{{{\delta ^{\alpha - 1}}}},\left| e \right| \leqslant \delta{\text{,}}\\{\left| e \right|^\alpha }sign\left( e \right),\left| e \right| > \delta {\text{。}}\end{array} \right.$ | (8) |
式中:zn+1为对总扰动的实时估计;b0为控制量系数的估计值。
3)状态误差的非线性反馈律(NLSEF):对跟踪微分器输出量和扩张状态观测器的状态变量估计之间的误差进行非线性组合,并与由扩张状态观测器对总扰动的补偿量一起组成控制量。
TD的输出量v1,v2和ESO输出的状态观测量z1,z2做差得到误差值e1,e2通过NLSEF进行非线性组合得到控制量u0。
| ${u_0} = - fhan\left( {{e_1},{e_2},r,h} \right){\text{。}}$ | (9) |
如图2所示,交流励磁机提供发电机励磁电流,无刷同步发电机的调压器(即励磁机的调压器)提供的是励磁机的励磁电流,所以励磁系统是一个串级系统。在发电机数学模型中励磁电压和输出电压之间存在耦合,不容易分析,在此将发电机的励磁电压和输出电压之间的函数关系当成一个未知函数f(Ug),发电机和励磁机共同作为励磁系统的控制对象,代入励磁机微分方程式(1)得控制对象的微分方程如下:
| $\left\{ \begin{array}{l}{{\dot U}_g} = f\left( {{U_g}} \right) + {E_{FD}}{\text{,}}\\{{\dot E}_{FD}} = - \displaystyle\frac{{1 + {S_e}}}{{{T_e}}}{E_{FD}} + {F_{EX}}\displaystyle\frac{{{U_{fe}}}}{{{T_e}}} - \displaystyle\frac{{{K_D}{I_{FD}}{F_{EX}}}}{{{T_e}}}{\text{,}}\\y = {U_g}{\text{。}}\end{array} \right.$ | (10) |
针对式(10)所示的串级系统,把状态EFD当作控制状态变量Ug的“虚拟控制量”,用ADRC来确定让Ug跟踪目标Uref的控制量
对于该串级系统外环ADRC,取给定电压Uref作为输入,通过跟踪微分器(TD)可以得到一个合适的过渡信号
| ${U_{ref1}} = {U_{ref1}} - hrfal\left( {{U_{ref1}} - {U_{ref}},\alpha ,h} \right){\text{。}}$ | (11) |
通过二阶扩张状态观测器(ESO)来估测系统外环的测量值Ug和外环输出量u1:
| $\left\{ \begin{array}{l}e = {z_{11}} - {U_g},fe = fal(e,\alpha ,h){\text{,}}\\{z_{11}} = {z_{11}} + h\left( {{z_{12}} - {\beta _{11}}e + {u_1}} \right){\text{,}}\\{z_{12}} = {z_{12}} + h\left( { - {\beta _{12}}fe} \right){\text{。}}\end{array} \right.$ | (12) |
式中,β11,β12为可调参数,fal函数在上节中已经给出。
状态误差的非线性反馈律(NLSEF):
| $\left\{ \begin{array}{l}{e_1} = {U_{ref1}} - {z_{11}}{\text{,}}\\{u_1} = {k_1}fal\left( {{e_1},\alpha ,\delta } \right) - {z_{12}}{\text{。}}\end{array} \right.$ | (13) |
式中:k1为可调参数。
对于该串级系统中内环ADRC,输入量为u1,不需要使用微分跟踪器(TD),通过二阶扩张状态观测器(ESO)来估测系统内环的测量值EFD和内环输出量Ufe1:
| $\left\{ \begin{array}{l}e = {z_{21}} - {E_{FD}},fe = fal\left( {e,\alpha ,h} \right){\text{,}}\\{z_{21}} = {z_{21}} + h\left( {{z_{22}} - {\beta _{21}}e + {U_{fe1}}} \right){\text{,}}\\{z_{22}} = {z_{22}} + h\left( { - {\beta _{22}}fe} \right){\text{。}}\end{array} \right.$ | (14) |
式中:β21,β22为可调参数。
状态误差的非线性反馈律(NLSEF):
| $\left\{ \begin{array}{l}{e_2} = {u_1} - {z_{21}}{\text{,}}\\{U_{fe1}} = \displaystyle\frac{{{k_2}fal\left( {{e_2},{\alpha _2},{\delta _2}} \right) - {z_{22}}}}{{{b_0}}}{\text{,}}\\{U_{fe}}{\rm{ = }}{K_m}{U_{fe1}}{\text{。}}\end{array} \right.$ | (15) |
式中:k2为可调参数;b0为控制量系数的估计值。
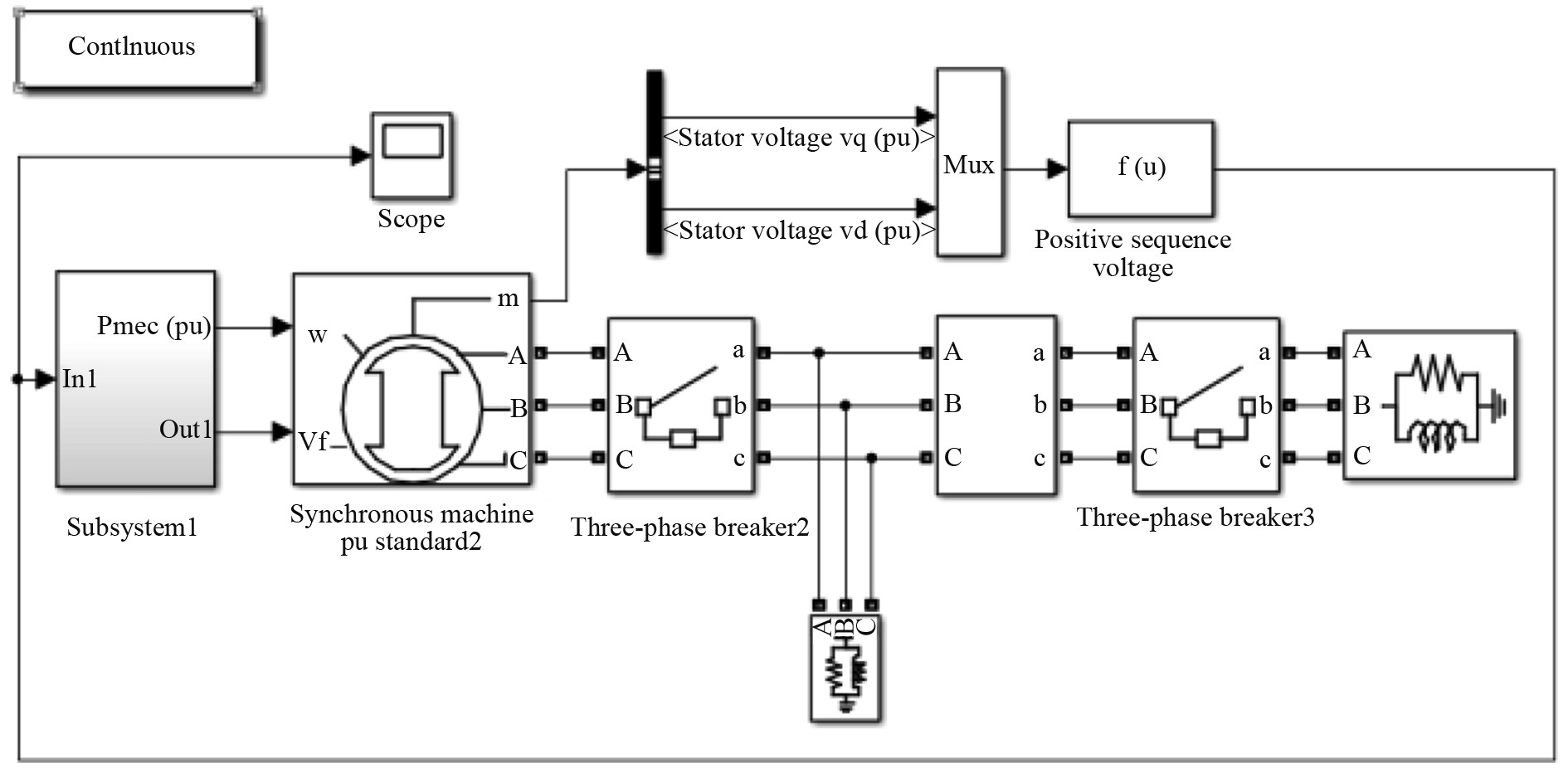
4 励磁系统的仿真及结果分析为了验证文中所设计的ADRC的可行性和控制效果,在Matlab/Simulink平台上搭建同步发电机励磁系统的仿真模型,并将ADRC和PID控制器进行仿真对比实验。仿真模型中发电机是选取Simulink自带的同步电机模块,输入是原动机的机械功率,发电机额定容量为2 MVA,额定电压为400 V,额定频率为50 Hz,励磁机模型是通过数学模型(式(3))设计,其中参数分别为:整流器换相压降系数KC=0.033 42;励磁机不饱和励磁时间常数TE=1.86;励磁机增益KE=1;交流励磁机的电枢反应系数KD=1.863 9;励磁机的饱和函数系数C1,C2分别为0.508和0.001 24。电压检测单元(式(4))中比例系数Kof=1;滤波回路的时间常数Td=0.02;电流检测单元式(5)中比例系数KH=0.2;检测单元式(6)中的时间常数TH=0.006;整流单元中增益Km=4.6。船舶同步发电机励磁系统仿真模型如图4所示。
|
图 4 船舶同步发电机励磁系统仿真模型 Fig. 4 Simulation model of ship synchronous generator excitation system |
控制器参数设置如下:
PID参数:通过Zieler-Nichol整定法整定后取内环参数KP=4.9,KI=1.1,KD=0.78;电压外环参数KP=1.5,KI=1.8,KD=0.43。
ADRC参数:取内环控制器的参数β21=100,β22=300,b0=12,k1=19;外环控制器的参数h=0.001,r=100,β21=100,β22=300,b0=10,k2=15。
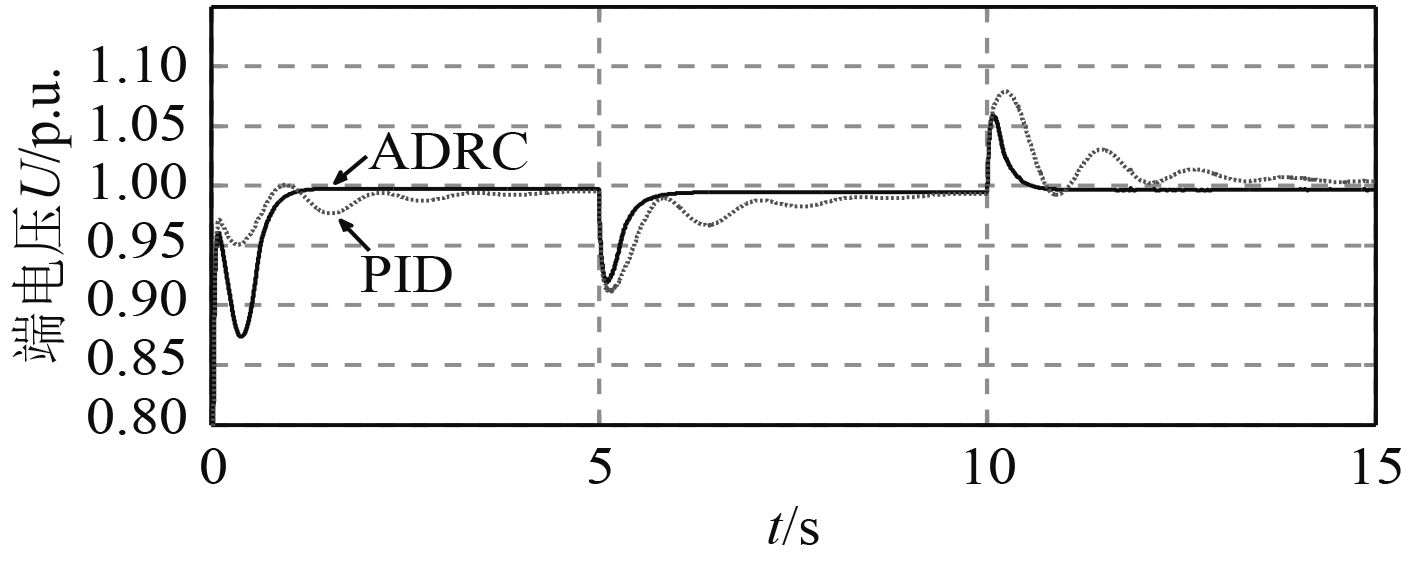
针对船舶电力系统特点,做了突加突减大负载的仿真实验,在第5 s时加入阻感性负载,功率为发电机容量的50%,其功率因数为0.63。在第10 s时卸掉所加负载,得到如图5所示的发电机输出电压曲线图。
|
图 5 突加突卸负载 Fig. 5 Sudden lifting load |
船舶同步发电机励磁系统在2种不同控制策略下的性能比较如表1所示。
|
|
表 1 两种控制器突加突卸负载性能对比 Tab.1 Comparison of the performance of the two controllers |
由表1可知,5 s时刻突加50%的负载,发电机的输出电功率不能及时改变,所以突加的负载会使发电机输出电压值突降,PID控制器突变量达到8.9%,ADRC为7.9%,反映ADRC较PID控制器更能拟制扰动。在调节发电机输出电压值恢复稳定过程中,PID控制器调节时间为1.32 s,ADRC调节时间为0.36 s,PID控制器最后达到稳定时的稳态误差值为0.9%,ADRC为0.5%。当系统卸载时,ADRC较PID控制器波动值小,调节时间短,静态误差小,反应ADRC较PID控制器具有更好的调节性能。使用2种控制器的励磁系统动态特性都能满足船级社规范“瞬态电压值应不低于额定电压的85%”并且满足船级社规范中要求“输出电压恢复到与额定值相差3%以内的时间不超过1.5 s”得要求。通过突加突卸负载的实验表明ADRC比PID控制器的动作要迅速,静态误差小,更能保障船舶电力系统的稳定性。
5 结 语本文针对船舶电力系统具有频繁突加突卸大功率负载,会对船舶电力系统的稳定性造成影响的特点,为提高船舶电力系统的稳定性,提出了基于自抗扰控制技术的发电机励磁系统控制策略。通过仿真实验对比了ADRC和经典PID控制器在突加突卸大功率负载下的控制效果,仿真结果表明ADRC具有更好的快速性和稳定性,具有一定的工程应用价值。
| [1] |
陈家伟, 陈杰, 陈冉, 等. 变速风力发电机组自适应模糊控制技术[J]. 中国电机工程学报, 2011, 31(21): 93-101. |
| [2] |
陈杰, 陈冉, 陈家伟, 等. 变速风力发电机组的模糊-单神经元PID控制[J]. 中国电机工程学报, 2011, 31(27): 88-94. |
| [3] |
刘乐星, 马克雄, 毛宗源. 基于遗传算法的发电机线性最优励磁控制研究[J]. 三峡大学学报(自然科学版), 2001(03): 216-219+238. |
| [4] |
韩京清. 从PID技术到" 自抗扰控制”技术[J]. 控制工程, 2002(03): 13-18. DOI:10.3969/j.issn.1671-7848.2002.03.003 |
| [5] |
王超, 王刚. 非线性特性在船舶电力系统中的研究及仿真[J]. 舰船科学技术, 2015, 37(01): 161-164. DOI:10.3404/j.issn.1672-7649.2015.01.034 |
| [6] |
周左晗, 施伟锋. 船舶无刷发电机励磁控制系统的数字仿真[J]. 计算机仿真, 2013, 06: 152-156. DOI:10.3969/j.issn.1006-9348.2013.02.035 |
| [7] |
IRMAK E, GÜLER N, ERSAN M, " PI controlled solar energy supported static excitation system desing and simulation for synchronous generators”[C]// 2016 IEEE International Conference on Renewable Energy Research and Applications (ICRERA), Birmingham, United Kingdom, 2016, pp. 1024–1028.
|
| [8] |
NUZZO S, GALEA M, GERADA C, et al. " An analytical and genetic-algorithm-based design tool for brushless excitation systems of low-medium rated synchronous generators”[C]//2016 19th International Conference on Electrical Machines and Systems (ICEMS), Chiba, 2016, pp. 1–7.
|
| [9] |
张灵杰, 孙建波, 郭晨. 船舶电力系统暂态稳定性的混合分析法[J]. 船舶工程, 2015, 37(05): 45-49. |
| [10] |
韩京清. 自抗扰控制技术[J]. 前沿科学, 2007(01): 24-31. DOI:10.3969/j.issn.1673-8128.2007.01.004 |
 2018, Vol. 40
2018, Vol. 40
