根据国际海事组织提出的船用柴油机NOX排放要求,2016年1月1日起建造的船舶应满足TierⅢ排放标准。我国作为《MARPOL公约》缔约国,应积极应对该规则内容,大力发展船舶对大气污染控制的先进技术。
选择性催化还原(SCR)技术是目前研究最广泛的排气净化技术。控制策略是SCR系统的核心,在SCR系统中提高尿素溶液喷射量可提高NOX的转化效率,但同时也会增加NH3的泄漏量及装置成本,这就需要采取合适的控制策略,在保证高NOX转化效率的前提下,将NH3的泄漏量控制在限值之下,同时具有较好的经济性。目前国内外在SCR控制策略研究方面都已取得一定的成果,如文献[1–2]中采用的开环控制策略,文献[3–4]中采用的闭环控制策略,罗啸[5]分析研究了基于离散 PID 控制的5种控制模式,并通过样机试验对控制系统功能进行验证[5]。
为了满足排放法规要求,本文针对某型船用柴油机的SCR系统分别采用开环和闭环控制策略对NOX转化效率和NH3泄漏量进行控制,并在Matlab中对催化器及控制系统进行仿真,在此基础上对SCR系统控制策略进行研究。
1 尿素理论喷射量计算SCR的催化还原基本原理为通过催化剂作用,用还原剂(NH3)有选择性地与柴油机排气NOX 进行化学反应,使得有害的排放物NOX转化成无害的氮气和水蒸气。催化还原过程中涉及到的主要化学反应如下:
1)氨气的生成
步骤1 尿素水溶液蒸发析出尿素颗粒:
| ${({\rm{N}}{{\rm{H}}_2})_2}{\rm{CO}}({\text{水溶液)}} \to {{\rm{(N}}{{\rm{H}}_{\rm{2}}}{\rm{)}}_{\rm{2}}}{\rm{CO}}({\text{固态}})+{{\rm{H}}_{\rm{2}}}{\rm{O}}({\text{气态}}){\text{,}}$ | (1) |
步骤2 尿素热解生成等摩尔的氨气和氰酸(HNCO):
| ${({\rm{N}}{{\rm{H}}_2})_2}{\rm{CO}}({\text{固态}}) \to {\rm{N}}{{\rm{H}}_3}({\text{气态}}) + {\rm{HNCO}}({\text{气态}}){\text{,}}$ | (2) |
步骤3 氰酸进一步水解生成等摩尔的氨气和二氧化碳:
| ${\rm{HNCO}}({\text{气态}}) \to {\rm{N}}{{\rm{H}}_3}({\text{气态}}) + {\rm{C}}{{\rm{O}}_2}({\text{气态}}){\text{。}}$ | (3) |
2)NOX的催化还原
| $4{\rm{N}}{{\rm{H}}_3} + 4{\rm{NO}} + {{\rm{O}}_2} = 4{{\rm{N}}_2} + 6{{\rm{H}}_2}{\rm{O}}{\text{,}}{\text{标准反应}}{\text{,}}$ | (4) |
| ${\rm{2N}}{{\rm{H}}_{\rm{3}}} + {\rm{NO}} + {\rm{N}}{{\rm{O}}_{\rm{2}}} = {\rm{2}}{{\rm{N}}_{\rm{2}}} + {\rm{3}}{{\rm{H}}_{\rm{2}}}{\rm{O}}{\text{,}}{\text{快速反应}}{\text{。}}$ | (5) |
其中,快速反应的反应速度是标准反应的大约10倍,但由于排气中NO2的含量较少,SCR催化器中主要发生的催化还原反应为标准反应。
3)NH3的氧化
| $4{\rm{N}}{{\rm{H}}_3} + 3{{\rm{O}}_2} = 2{{\rm{N}}_2} + 6{{\rm{H}}_2}{\rm{O}}{\text{,}}{\text{氧化反应}}{\text{。}}$ | (6) |
4)NH3的吸附与解吸附
| ${\rm{N}}{{\rm{H}}_{\rm{3}}} + {\rm{S}} = {\rm{NH}}_3^*{\text{,}}{\text{吸附反应}}{\text{,}}$ | (7) |
| ${\rm{N}}{{\rm{H}}_{\rm{3}}}^* = {\rm{N}}{{\rm{H}}_{\rm{3}}} + {\rm{S}}{\text{,}}{\text{解吸附反应}}{\text{。}}$ | (8) |
其中,S为催化剂上的活性位,NH3*为被吸附的氨分子。
根据以上化学反应方程式,可计算得到发动机某稳定工况下降低排气中NOX所需的理论尿素喷射量。
对于稳定工况i,柴油机排气流量、原机NOX排放浓度及NOX的最大转化效率都可以通过相应的脉谱图进行确定。
排气中单位时间内需要降低的NOX的物质量为:
| $De{N}{O_{X(i)}} = \frac{{{m_{EXH(i)}}}}{{{M_{EXH}}}} \cdot { N}{ O_{X(i)}} \cdot {C_{conv(i)}} \times {10^{ - 6}}{\text{,}}$ | (9) |
其中,DeNOX(i)为单位时间内需要降低的NOX的物质量,kmol/h;
由反应(1)~反应(3)可知,1 mol尿素可分解为2 mol氨气,由NOX的催化还原反应,氮氧化物与氨气之间的反应系数比为1:1。因此对于工况i,氮氧化物浓度值降到最低所需尿素的摩尔流量为:
| ${W_{(i)}} = 0.5\frac{{{m_{EXH(i)}}}}{{{M_{EXH}}}} \cdot N{O_{X(i)}} \cdot {C_{conv(i)}} \times {10^{ - 6}}{\text{,}}$ | (10) |
式中:W(i)为使工况i的NOX最低所需尿素的摩尔流量,kmol/h。
尿素的摩尔质量为60 g/mol,配制的尿素水溶液质量浓度为32.5%,则使排气中氮氧化物排放最低所需尿素水溶液的体积流量为:
| ${V_{Adblue(i)}} = 3.183 \cdot {m_{EXH(i)}} \cdot N{O_{X(i)}} \cdot {C_{conv(i)}} \cdot {10^{ - 3}}/\rho {\text{,}}$ | (11) |
其中,VAdblue(i)为使工况i的氮氧化物最低所需尿素水溶液的体积流量,ml/h;ρ为尿素水溶液的密度,kg/l。
应用式(9)~式(11),即可获得每一发动机工况对应的理论尿素喷射量。
在Matlab中进行仿真,得尿素理论喷射量模块模型如图1所示。
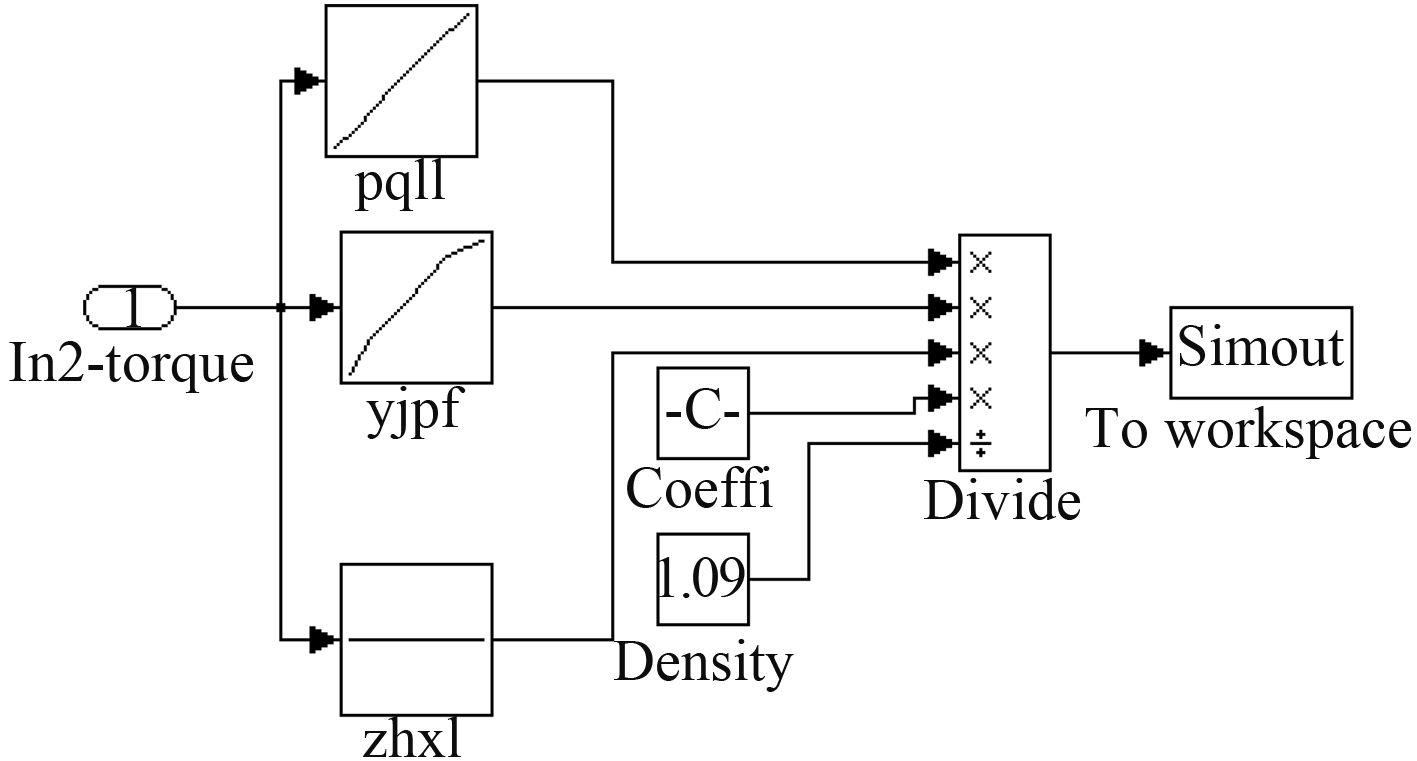
|
图 1 尿素理论喷射量模块 Fig. 1 Urea theoretical injection quantity model |
根据SCR催化器中的4个主要化学反应(4)~反应(8)建立催化器的三阶模型[6],方程如下:
| ${\dot C_{NOx}} = - \bar Q{C_{NOx}} - {k_2}\varOmega \theta {C_{NOx}} + \bar Q{C_{NOx, in}} + {k_4}\varOmega \theta{\text{,}}$ | (12) |
| $\dot \theta = - ({k_4} + {k_6})\theta + {k_5}{C_{NH3}} - {k_2}\theta {C_{NOx}} - {k_5}\theta {C_{NH3}}{\text{,}}$ | (13) |
| $\begin{array}{l} {{\dot C}_{NH3}} = {k_6}\Omega \theta - ({k_5}\Omega + \bar Q){C_{NH3}} + {k_5}\Omega \theta {C_{NH3}} + \\ \bar Q{C_{NH3,in}}. \end{array}$ | (14) |
其中:Ci为物质i的浓度;θ为催化剂表面氨覆盖率;
| ${k_i} = {A_i}{e^{ - {E_i}/RT}}{\text{。}}$ | (15) |
| $\bar Q = Q/V{\text{。}}$ | (16) |
其中,Q为排气体积流量,m3/s;V为催化器内排气体积。
将式(12)~式(14)在平衡点处线性化,可得状态空间模型如下:
| $\begin{array}{l}\left[ {\begin{array}{*{20}{c}}{{{\dot C}_{NOx}}}\\{\dot \theta }\\{{{\dot C}_{NH3}}}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{{A_{11}}} & {{A_{12}}} & 0\\{{A_{21}}} & {{A_{22}}} & {{A_{23}}}\\0 & {{A_{32}}} & {A{}_{33}}\end{array}} \right]{\rm{ }}\left[ {\begin{array}{*{20}{c}}{{C_{NOx}}}\\\theta \\{{C_{NH3}}}\end{array}} \right] + \\\left[ {\begin{array}{*{20}{c}}{\bar Q} & 0 & 0\\0 & 0 & 0\\0 & 0 & {\bar Q}\end{array}} \right]{\rm{ }}\left[ {\begin{array}{*{20}{c}}{{C_{NOx,in}}}\\{{\theta _{in}}}\\{{C_{NH3,in}}}\end{array}} \right]{\text{,}}\\{{Y}} = \left[ {\begin{array}{*{20}{c}}1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\end{array}} \right]{\rm{ }}\left[ {\begin{array}{*{20}{c}}{{C_{NOx}}}\\\theta \\{{C_{NH3}}}\end{array}} \right]{\text{。}}\end{array}$ |
其中:
| ${A_{11}} = - (\bar Q + {k_2}\varOmega {\theta _0}){\text{,}}$ |
| ${A_{12}} = - {k_2}\varOmega {C_{NOx, 0}} + {k_4}\varOmega{\text{,}}$ |
| ${A_{21}} = - {k_2}{\theta _0}{\text{,}}$ |
| ${A_{22}} = - ({k_6} + {k_4} + {k_5}{C_{NH3, 0}} + {k_2}{C_{NOx, 0}}){\text{,}}$ |
| ${A_{23}} = {k_5}(1 - {\theta _0}){\text{,}}$ |
| ${A_{32}} = {k_5}\varOmega {C_{NH3, 0}} + {k_6}\varOmega{\text{,}}$ |
| ${A_{33}} = {k_5}\varOmega {\theta _0} - {k_5}\varOmega - \bar Q{\text{。}}$ |
利用该状态空间模型对催化器进行仿真,设定输入的NOX值为固定值,初始NH3浓度与输入NOX值比例为1:1,保持5 s后,开始随时间逐渐下降,氨覆盖率初始值为0,如图2所示。
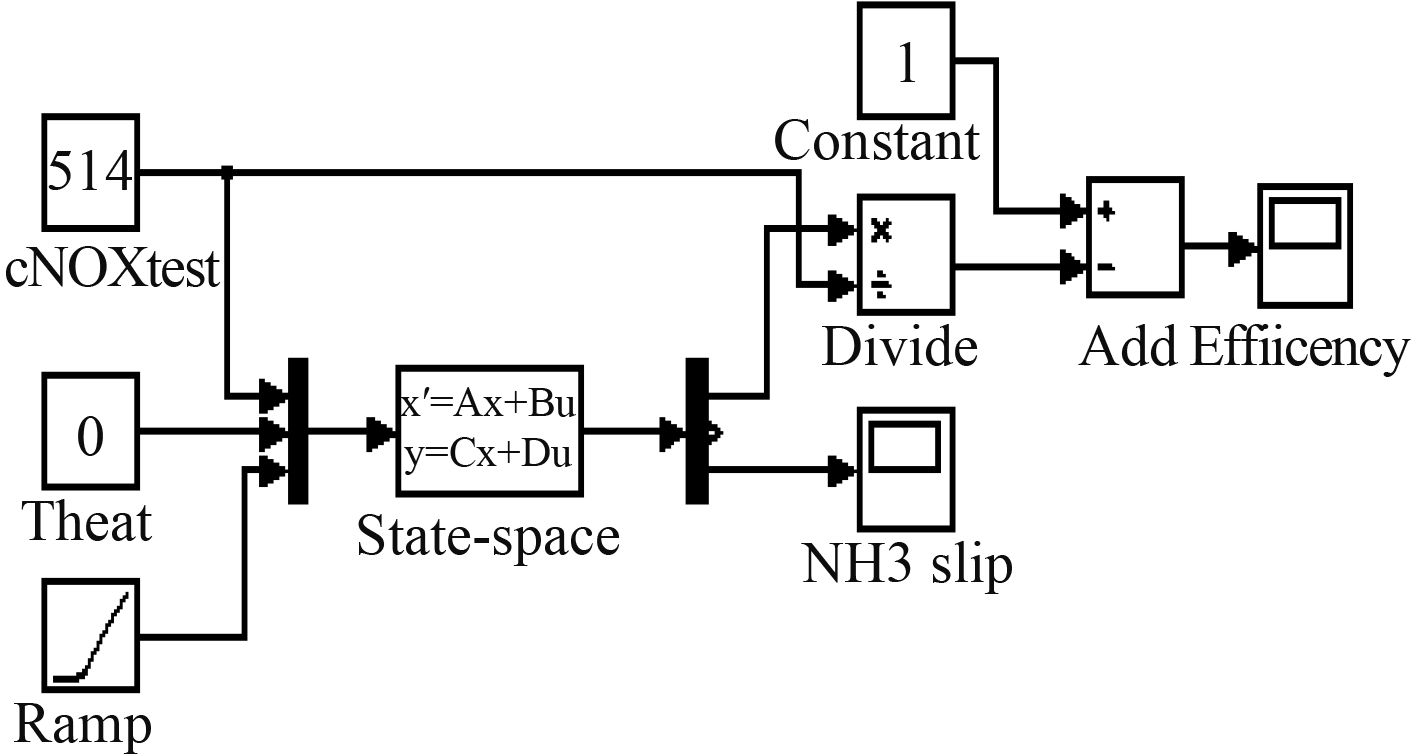
|
图 2 催化器仿真模型 Fig. 2 Catalyst simulation model |
仿真结果如图3所示。在输入NH3浓度与输入NOX值比例为1:1时,NOX转化效率稳定在94.6%,NH3泄漏量稳定在27.8 ppm,随后,在原机排放不变的情况下,二者皆随着输入NH3浓度的下降而减小。该仿真模型可模拟真实催化器性能。
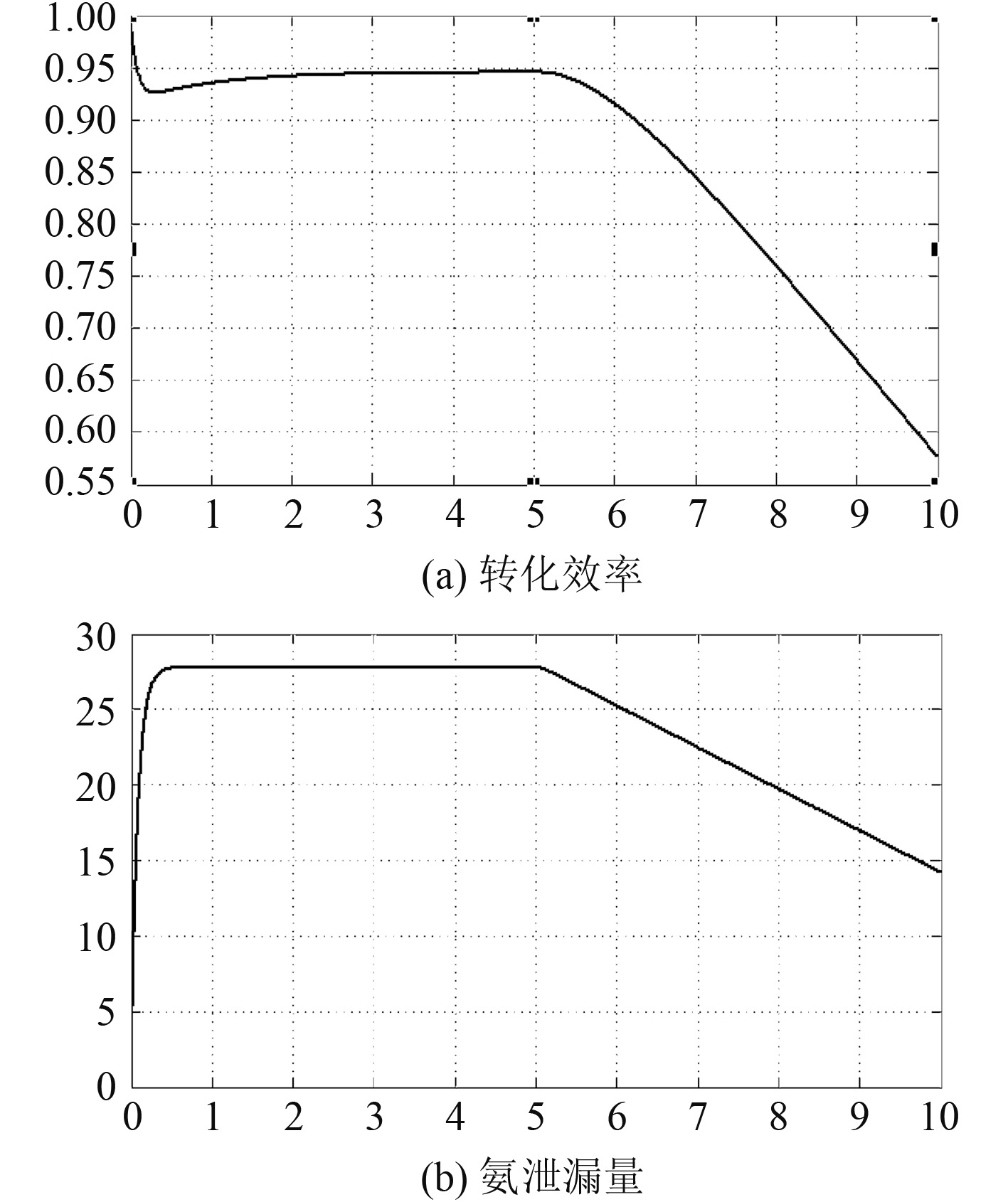
|
图 3 仿真结果 Fig. 3 Simulation results |
选择某型船用柴油机进行台架试验,获得原机排放脉谱图以及排气流量脉谱图如图4所示。
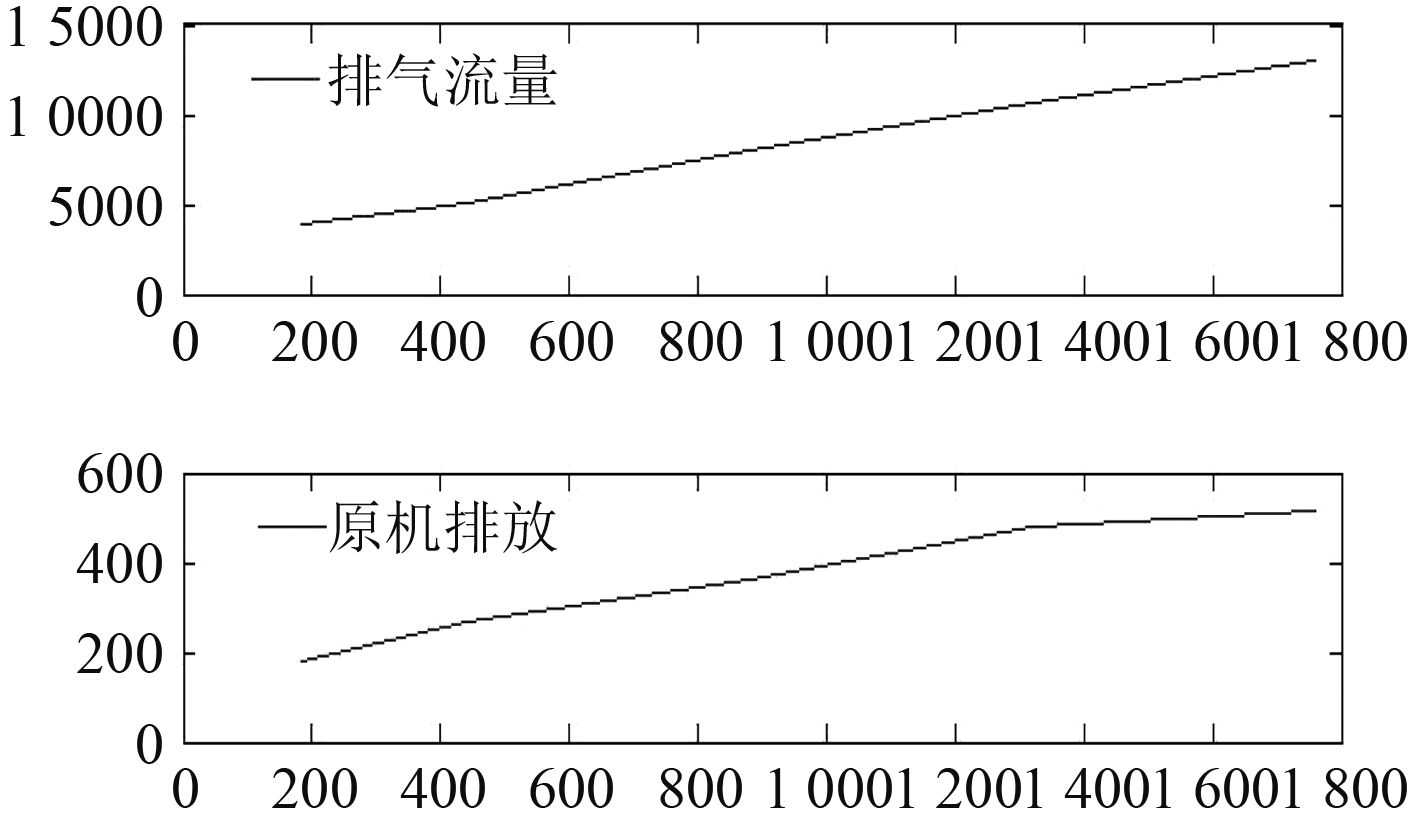
|
图 4 原机排放及排气流量脉谱图 Fig. 4 Maps of primary emission and extraction flow |
该型船用柴油机加权比排放为9.4 g/kWh,若要满足TierⅢ排放标准,则NOX加权转化效率需达到77.9%以上。目前,我国对船用柴油机SCR系统的氨泄漏量尚无规定[7],同时NOX加权转化效率应有一定裕量,本文设定最大转化效率为85%时,NOX降到最低,且氨泄漏恰好为超标,即加权转化效率为85%。
将原机排放、排气流量脉谱图及最大转化效率带入尿素理论喷射量模块,可得不同工况下的理论尿素喷射量如表1所示。
|
|
表 1 理论尿素喷射量 Tab.1 Urea theoretical injection quantity |
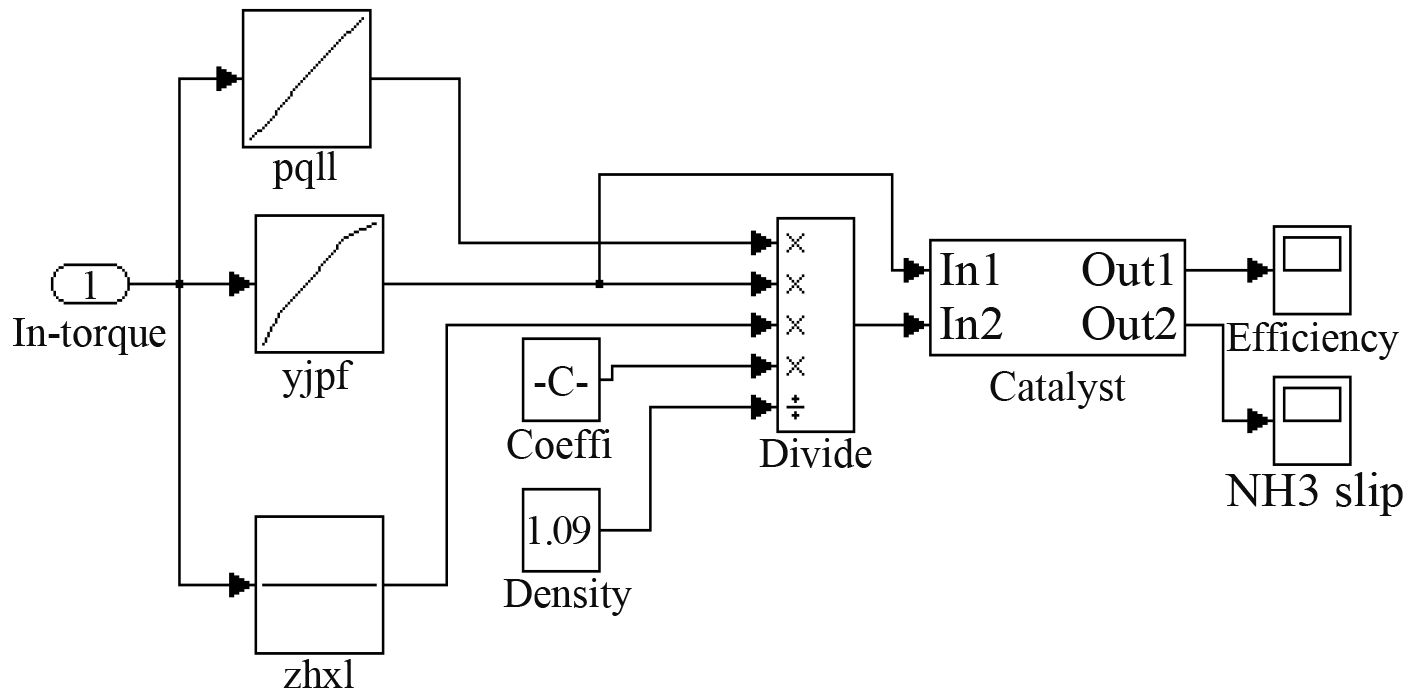
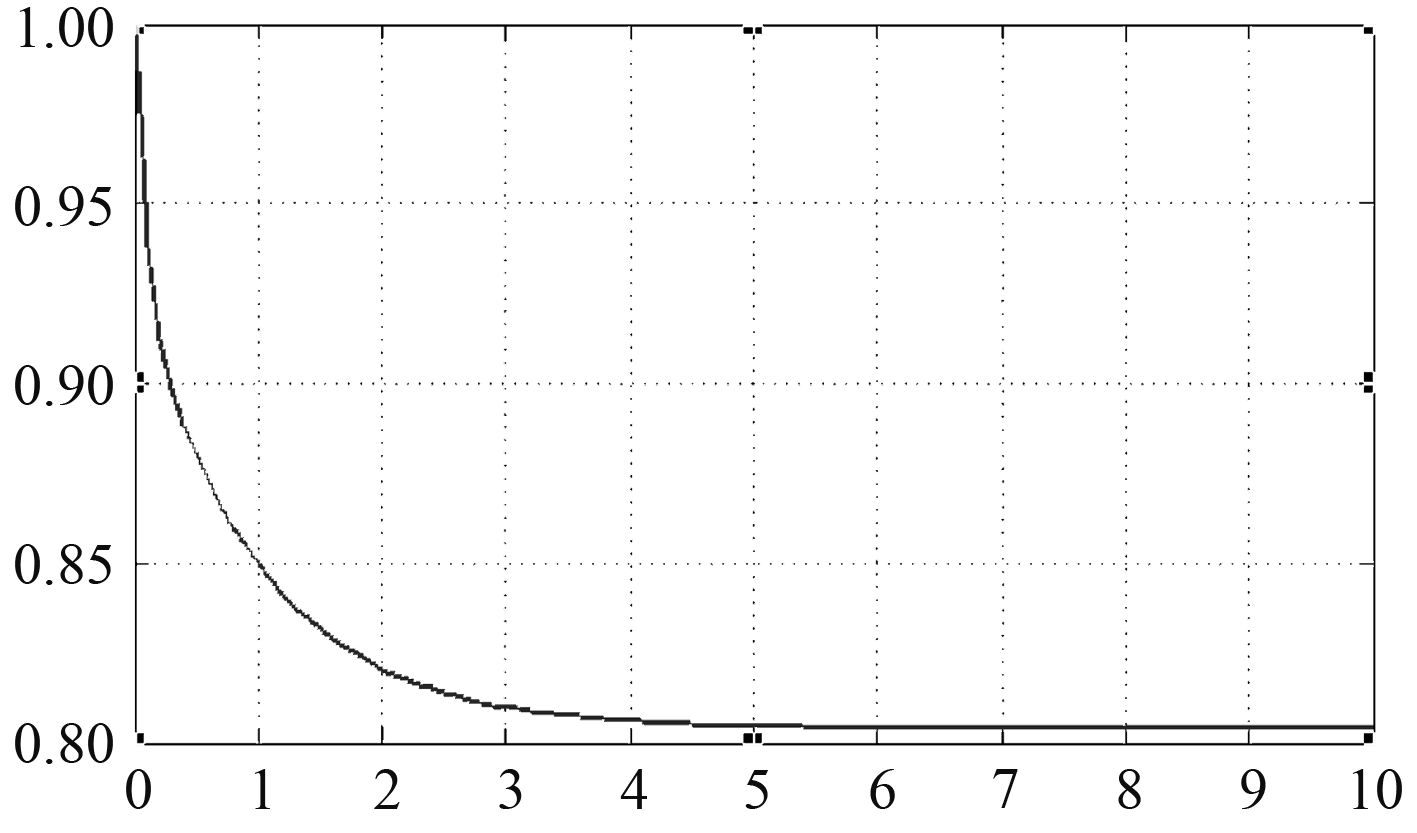
将尿素理论喷射量模块与催化器模块相连,可得前馈控制模型如图5所示,按工况1~工况5的顺序改变输入功率值,阶跃输入,输出NOX加权转化效率为80.4%,氨泄漏量分别为23.6 ppm,21.9 ppm,16.7 ppm,12.3 ppm,8.1 ppm。从仿真结果中可以看出,与设定的转化效率85%相比,开环控制的转化效率偏低,氨泄漏量最大为23.6 ppm。工况1的仿真结果如图6和图7所示。
|
图 5 开环控制模型 Fig. 5 Open-loop control model |
|
图 6 开环控制NOX转化效率仿真结果(工况1) Fig. 6 NOX efficiency of open-loop control (condition1) |

|
图 7 开环控制氨泄漏量仿真结果(工况1) Fig. 7 NH3 leakage of open-loop control (condition 1) |
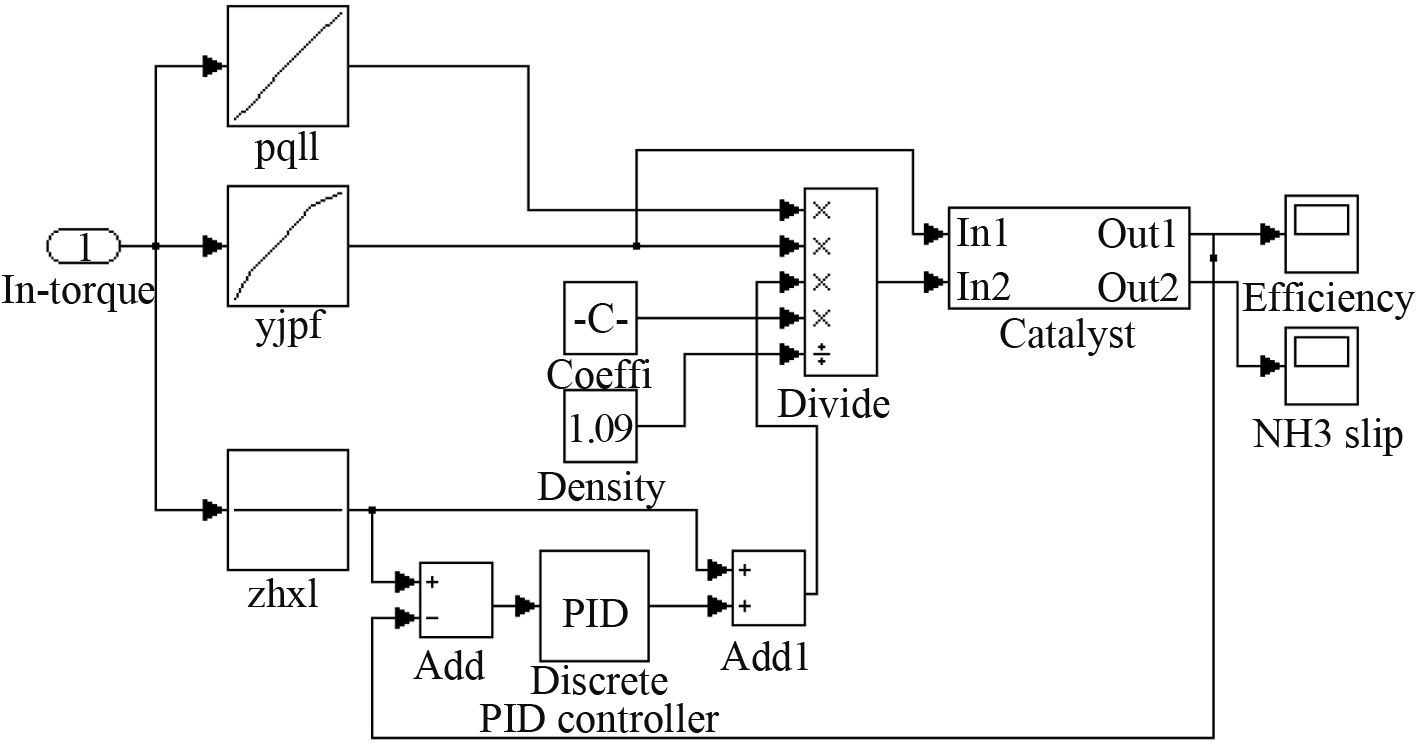
采用PID控制策略,建立闭环控制仿真模型,如图8所示。
|
图 8 闭环控制模型 Fig. 8 Closed-loop control model |
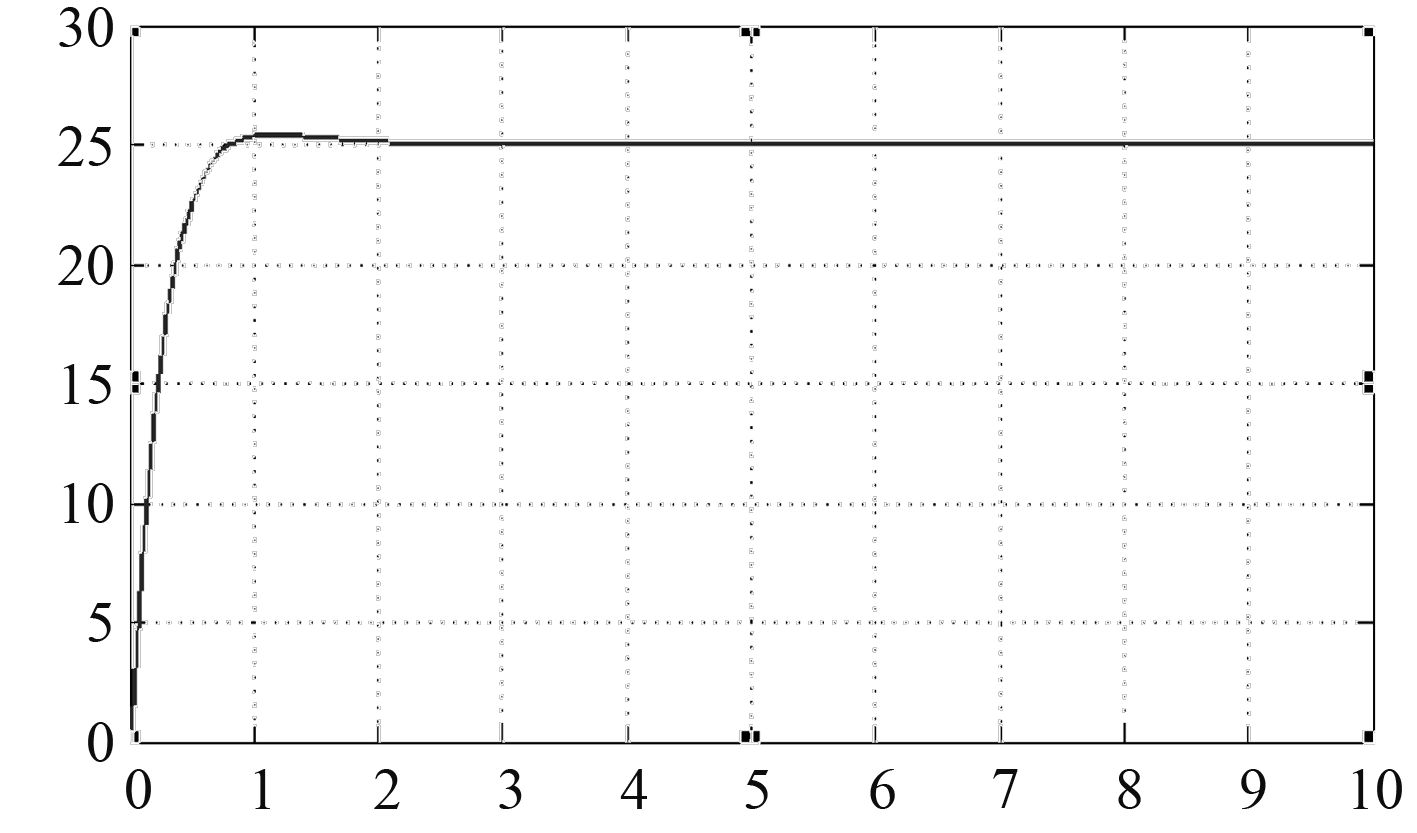
按工况1~工况5的顺序改变输入功率值,阶跃输入,输出NOX加权转化效率为85%,氨泄漏量分别为25 ppm,23.2 ppm,17.6 ppm,13 ppm,8.6 ppm。从仿真结果中可以看出,NOX加权转化效率为0.85,为设定的最大转化效率。氨泄漏量最大为25 ppm,为临界值。工况1的仿真结果如图9和图10所示。

|
图 9 闭环控制NOX转化效率仿真结果(工况1) Fig. 9 NOX efficiency of closed-loop control (condition 1) |
|
图 10 闭环控制氨泄漏量仿真结果(工况1) Fig. 10 NH3 leakage of closed-loop control (condition 1) |
本文对基于SCR的船用柴油机排放控制策略进行研究。首先对尿素喷射量模块及催化器进行建模,接着分别建立了开环控制与闭环控制仿真模型,对某型船用柴油机加装SCR后处理装置后的NOX转化效率及氨泄漏量进行仿真。
根据仿真结果,开环控制策略由于缺乏控制目标的反馈环节,控制精度不高,无法达到预设的最大转化效率。闭环控制策略可令NOX转化效率稳定在最大转化效率,与开环控制策略相比,可以达到更为理想的控制目标。但在实际应用中,开环控制具有结构简单、反应时间短的优点,在控制精度要求不高,且有经济性要求时可考虑采用开环控制策略。
| [1] |
胡杰, 颜伏伍, 苗益坚, 等. 柴油机Urea-SCR系统控制模型[J]. 内燃机学报, 2013, 31(2): 148-153. HU Jie, YAN Fu-wu, MIAO Yi-jian, et al. Control model of urea-SCR system for diesel engine[J]. Transacrions of CSICE, 2013, 31(2): 148-153. |
| [2] |
刘传宝. 柴油机氨基SCR系统控制策略与匹配研究[D]. 武汉: 武汉理工大学, 2013.
|
| [3] |
FRANK W, ROBERT C. Expe-rimental demonstration of a new model-based SCR control strategy for cleaner heavy-duty diesel engines[J]. Ieee Transactions on Con-trol Systems Technology, 2011, 19(5): 1305-1313. DOI:10.1109/TCST.2010.2057510 |
| [4] |
TAN Pi-qiang, CHEN Fei, HU Zhi-yuan, et al. Closed-loop control strategy of NH3-SCR for diesel engines[J]. International Conference on Electric Information & Control Engineering, 2011, 5748-5752. |
| [5] |
罗啸. 船舶柴油机SCR控制系统研究[D]. 北京: 中国舰船研究院, 2013.
|
| [6] |
DEVESH U, MICHIEL V N. Model based analysis and control design of a Urea-SCR deNOX aftertreatment system
[J]. Journal of Dynamic Systems, Measurement and Control, 2006, 128(3): 737-741. DOI:10.1115/1.2234494 |
| [7] |
徐月明. 船用柴油机SCR催化剂选型及性能评价研究[D]. 武汉: 武汉理工大学, 2012. XU Yu-ming. Study on design and performance evaluation of SCR[D]. Wuhan: Wuhan University of Technology, 2012. |
 2018, Vol. 40
2018, Vol. 40
