中国拥有较为丰富的近海风力资源,据中国气象科学研究院统计评估,我国近海可开发的风能资源储量约750 GW。海上风能具有海面粗糙度小、风湍流强度小、主导风向稳定等特点。这有利于增大装机容量,减轻风机疲劳,降低塔架高度,并且不涉及土地征用、噪声扰民等问题[1]。因此在这些方面都较陆地风力发电有更多优势。
尽管从世界范围来看,未来海上风电会由近海固定式基础向深远海漂浮式基础发展,但当前我国的海上风力发电依然以近海固定式基础为主。使用这种基础有较高的可靠性和成熟度,而由于装机容量的不断提高,对基础的承载能力也提出了更高要求,因此近海风机基础正向单桩大直径发展。随着桩径增大,传统的在工程中广泛应用于细长体结构的Morison公式不再适用。本文工作围绕单桩大直径基础所受波浪载荷展开,通过CFD软件的数值模拟,研究在不同波浪作用下基础的受载情况,进而对结构设计提供一些参考和建议。
1 固定式单桩大直径基础计算示例使用STAR-CCM+软件建立单桩基础的几何模型和物理模型。
1.1 几何模型以静水面为基准确定各高程,桩基础几何参数如表1所示。
|
|
表 1 桩基础几何参数 Tab.1 Geometrical parameters of the foundation |
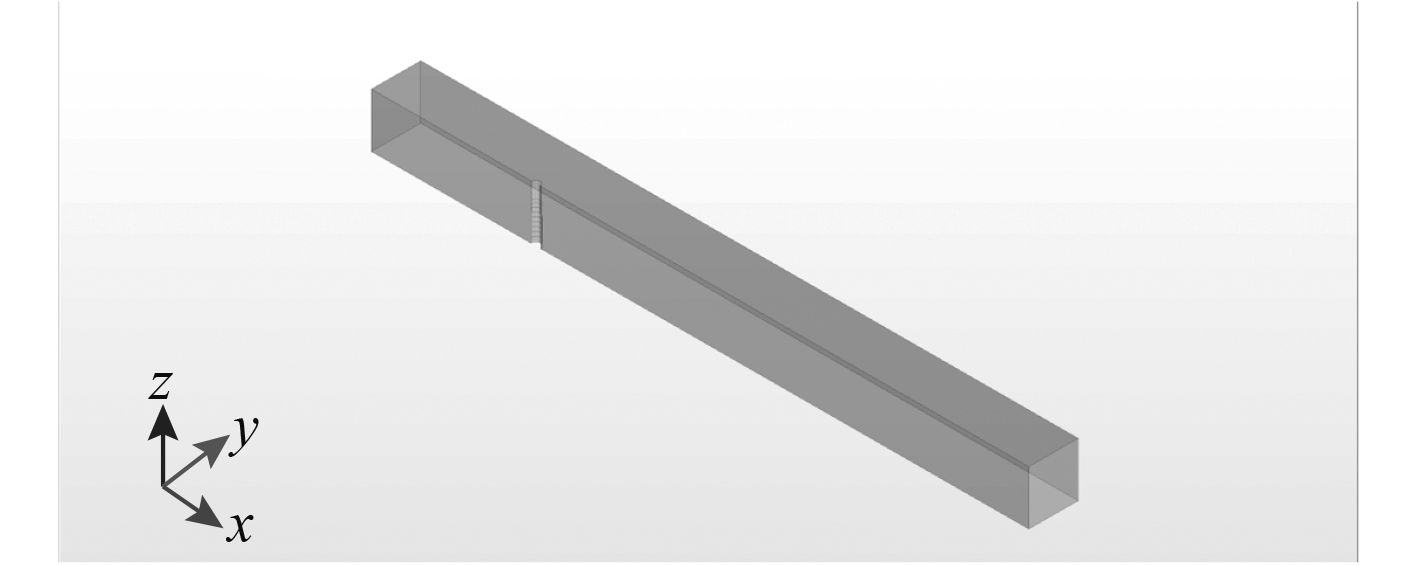
依照上述参数建立了桩基础和流体域几何外形。由于流场为对称结构,因此仅分析半个流域,以节省计算资源。计算域长宽高分别设置为400 m,30 m,33 m,用布尔运算减去桩基础半体,得到如图1所示的流体计算域。
|
图 1 流体域几何外形 Fig. 1 Configuration of fluid domain |
其中桩基础轴线与Z轴重合,浪向沿X轴正向。速度入口位于x=–100 m处,压力出口位于x=300 m处,即留有300 m尾流区。由于涉及气液两相流的自由液面问题,因此初始设置静水面(z=0)以上有10 m的空气区,以下23 m均为液体区。
在计算泥面下降前(水深20 m)工况时,将上述流体计算域设置为高为30 m的长方体,其他设置保持不变。即水面以上10 m空气区,水下20 m为液体区。
另外,真实的海洋环境中,海床并不平整,尤其在桩基础与泥面交界处随着时间推移会出现冲刷坑。水流的冲刷作用一般包括自然演变冲刷、局部冲刷和一般冲刷。本文对冲刷的研究主要集中于局部冲刷产生的冲刷坑,这是造成桩基事故发生的重要原因。由于桩基础的存在对水流的行进形成阻碍,改变了周围的局部流场,引起附近急剧的泥沙运动,长此以往形成局部冲刷坑[2]。它不仅会减小桩基础周围的土侧抗力,引起基底应力的重新分布,而且会直接影响流场,从而带来波浪载荷的改变。为研究在形成冲刷坑后,桩基础根部的水质点流动情况和桩体受载荷情况,本文以20 m水深为基础设置一个深度为3 m的冲刷坑。尽管土木工程领域有一些计算冲刷深度的相关规范[3 – 4],但本文限于研究其造成的水动特性。因此为方便建模,冲刷坑几何形状设置为旋转抛物面,深度3 m,最大开口直径为桩底端直径3倍。有冲刷坑的流体域几何外形如图2所示。

|
图 2 有冲刷坑流体域几何外形 Fig. 2 Configuration of fluid domain with scour pit |
坐标系设置如图2所示。对于长方体流体计算域,其左端(x=–100 m)、上面(z=10)、背面(y=30)均设置为速度入口,右端(x=300)设置为压力出口,前面(y=0)设置为对称面,其余如底面和桩基础表面均设置为无滑移壁面。在x=200~300 m范围内设置阻尼消波区,防止波浪反射。所有算例的浪向均沿X轴正向方向,不规则波模拟时长600 s,规则波模拟时长100 s。
使用STAR-CCM+内置的VOF方法跟踪自由表面,湍流模型选用k-ε模型,数值方法采用非稳态隐式算法。k-ε模型模拟大的流动结构令人较为满意,而小尺度的湍流对我们关心的结果影响较小,且该模型已被许多工程师接受的一种模型并得到了广泛应用,故而选用k-ε湍流模型[5]。
1.3 网格划分网格划分需要平衡精度和计算量,如果网格过密,则会显著增大计算时间。由于对长方形计算域6个表面上的情况关心较少,网格可适当稀疏。在靠近桩基础壁面处需重点研究,网格应适当加密。此外,该问题涉及自由表面,由于自由表面对问题的影响较大,且变化较为剧烈。因此对自由表面附近的网格进行了进一步加密的处理。按此思路,对该模型进行网格划分。得到划分后的体网格如图3所示。

|
图 3 网格划分 Fig. 3 Mesh generation |
本文的模拟计算包含4种典型的波浪工况,其中2组不规则波,2组规则波,具体波浪参数如表2所示。
|
|
表 2 各工况波浪参数 Tab.2 Parameters of waves in different conditions |
4种波浪条件分别施加于1.1节描述的3种海床条件下的桩基础,共计12种不同算例。
2 数值模拟结果及分析 2.1 波浪载荷强度分析由于桩基础为对称结构,除波浪传播方向所受载荷较大外,其他方向受载较小,因此以下所有载荷分析均为波浪传播方向上的载荷。
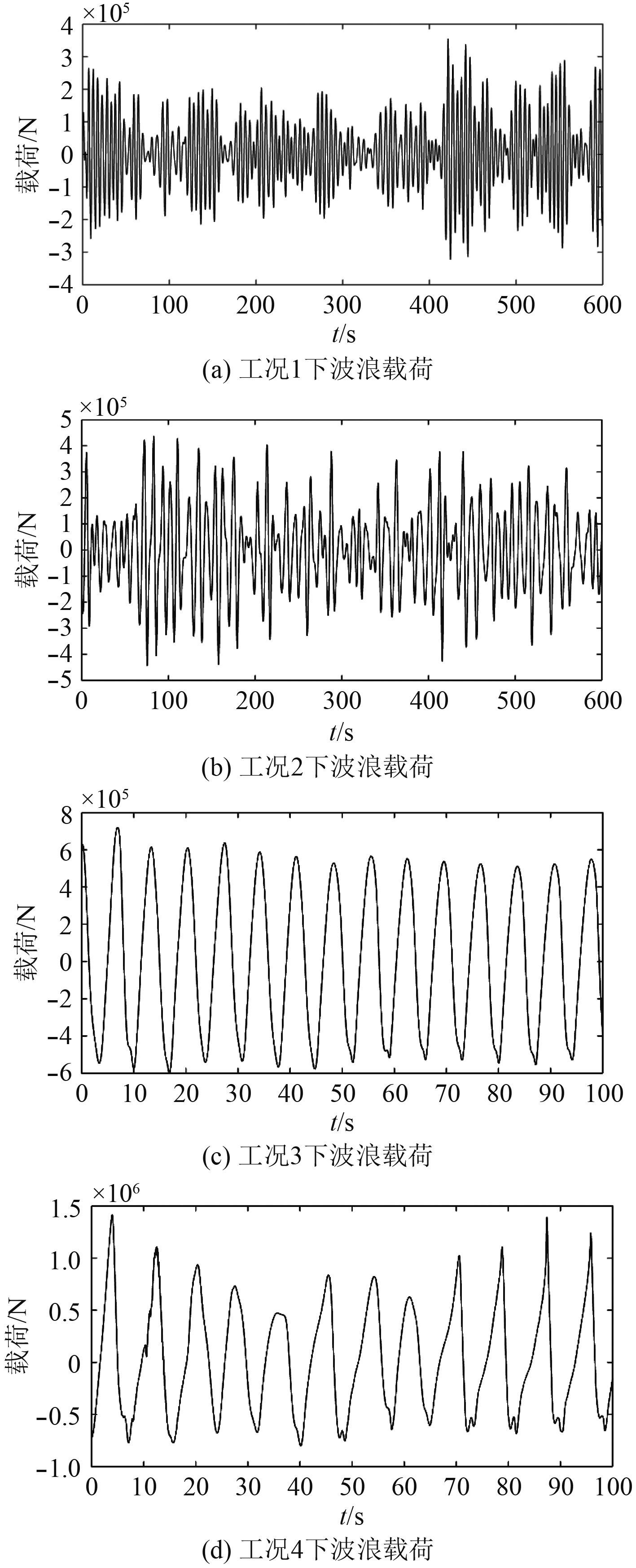
经过数值计算,获取了不同海床条件、各个工况下载荷的时程数据。图4~图6为12种条件下波浪载荷的时程数据。
|
图 4 水深20 m各工况载荷时历曲线 Fig. 4 Time-history curve under the depth of 20 meters |

|
图 5 水深23 m各工况载荷时历曲线 Fig. 5 Time-history curve under the depth of 23 meters |

|
图 6 有冲刷坑各工况载荷时历曲线 Fig. 6 Time-history curve with scour pit |
从图中可见,由于波陡的增大和水深的减小,会加大波浪的畸变,生成的规则波亦产生变形,趋于形成波浪破碎。这对CFD软件和VOF方法造成了一定的困难,如果进一步增大波陡则应考虑使用其他数值模拟方法。
根据以上各种情况下的时程数据,统计并获得各种工况下载荷的幅值,结果如表3所示。
|
|
表 3 各工况下载荷的幅值 Tab.3 Maximum loads in different conditions |
桩基础在23 m水深情况下,其水线面下表面积大于20 m水深情况,而与有冲刷坑情况表面积十分接近。因此表3中比较23 m无冲刷坑和有冲刷坑2列数据较有意义,从表中可明显发现有冲刷坑存在时载荷幅值均呈增大趋势。通过CFD数值模拟方法可发现冲刷坑的存在会增大载荷,而冲刷坑在工业界传统使用的基于势流理论的Morison公式等方法中未被考虑进来。因此传统方法对载荷的计算具有一定风险。
2.2 波浪载荷频率分析将时程数据通过Fourier变换进行频域分析,可获得不同频率载荷的占比情况,其中占比最高的频率对结构影响最大,在结构设计时应尽量避开,以免发生共振。将这些占比最高的幅值频率列出,得到各种工况下各载荷对应的幅值频率如表4所示。
|
|
表 4 各工况下频率的幅值 Tab.4 Frequencies of highest proportion in different conditions |
从表4 中可见无冲刷坑情况下,水深23 m与水深20 m的幅值频率差异不大,在不规则波条件下均接近谱峰频率,在规则波条件下均接近波浪频率。但有冲刷坑情况下频率均较无冲刷坑情况有所上升。对应4种工况23 m水深时幅值频率分别升高了32.76%,18.67%,19.11%,19.24%,对泥面位于水深20 m时4种工况下的载荷频率幅值分别提高了28.45%,11.02%,19.02%,19.14%。因此在结构设计时应考虑到桩基础在安置一段时间,形成冲刷坑后其所受载荷频率会有所上升。为防止共振造成结构破坏,应将这种变化考虑在内。
3 与绕射理论的对比分析在工程领域,对小尺度直径圆柱广泛使用Morison公式[6]计算所受波浪载荷。由于Morison公式忽略了波浪的绕射作用,而对大直径圆柱,如本文涉及的单桩大直径基础,波浪绕射作用明显,因此R.C. MacCamy和R.A. Fuchs[7]提出了平面规则波对单个圆柱的作用问题。基于微幅波假设,应用势流理论,假定流体无粘、无旋,对不同几何外形的纯圆柱形桩进行计算,从而对Morison公式进行修正。由于计算能力受限,在计算中将Bessel函数做了近似处理。实际上以现今的计算机技术可直接对Bessel函数进行计算,本文即不采用简化近似。根据势流理论,圆柱形桩在垂向位置高度为z处,单位长度上受到的横向载荷Fz可由以下方程得到:
| ${F_z} = \frac{{2\rho gH}}{k}\frac{{\cosh k(d + z)}}{{\cosh kd}}A\left(\frac{D}{L}\right)\cos (\sigma t - \alpha ){\text{,}}$ |
其中:
| $A\left(\frac{D}{L}\right) = \frac{1}{{\sqrt {J{{_1'}^2}\left(\text{π} \frac{D}{L}\right) + Y_1^{'2}\left(\text{π} \frac{D}{L}\right)} }}{\text{。}}$ |
式中:H为波高;k为波数;d为水深;D为桩径;L为波长。对Fz沿垂向进行积分,得到圆柱桩总体受力。由于本文涉及的桩基础并非纯圆柱,而是直径在5.2~6 m之间变化的圆台。因此分别对直径5.2 m和6 m的圆柱桩按照MacCamy和Fuchs的方法进行计算,并与上述CFD计算结果进行对比。
绕射理论计算得到的是周期性载荷的幅值,而CFD方法得到一个幅值有小变化的周期性载荷。由于理论限制,因此只对比分析无冲刷坑规则波工况下的载荷数据。表5列出了规则波工况下2种方法计算的载荷幅值结果,其中CFD方法幅值为模拟时长内载荷极值的平均数。
|
|
表 5 规则波下载荷对比结果 Tab.5 The comparison of loads under regular waves |
从上述对比中可见,通过绕射理论计算所得载荷均大于使用CFD方法计算所得平均载荷。因此,采用绕射理论进行设计,对于保证安全有一定的效果。但同时应注意,计算的载荷如果高于实际载荷过多,会带来材料的大量浪费,于成本节约不利。
4 总结与展望本文使用STAR-CCM+软件,使用CFD方法对一种固定式风机桩基础在波浪中受到的载荷进行分析,并与传统应用势流理论的工程方法进行对比,结果主要为以下3个方面。
1)Morison公式以及MacCamy和Fuchs的绕射理论均未考虑海床条件,本文分析了桩基础根部形成冲刷坑后的波浪载荷,发现同等条件下均较无冲刷坑情况下有所增大,因此在结构设计时应注意这种趋势。
2)冲刷坑的存在对载荷的频率也造成了一定程度的影响,使得频率上升。为避免共振造成的结构破坏,在实际设计时应予考虑。
3)通过与MacCamy和Fuchs的绕射理论计算结果进行对比,发现CFD计算结果较小,因此采用绕射理论设计可带来较高的安全性,但同时易造成材料浪费,提高成本。
通过上述分析以及结论,本文给出了近海风机单桩大直径基础设计的一些建议。本文将CFD结果作为基准,与工业界常用经验公式进行对比分析,实际上尽管CFD能够给出更为细致的结果,但由于当前相关技术水平的限制,依然不能取代实验结果。而且以当前技术水平,CFD计算仍要消耗大量计算资源,工程上的时间成本较大。因此未来可进行相关模型实验,以进一步校正结果,证实结论,为工程上使用的经验公式提供指导。
此外,本文中的冲刷坑假设为旋转抛物面,而实际的冲刷坑外形并不规则,因此未来可模拟其他形状冲刷坑并比较分析不同外形带来的差异。
| [1] |
肖运启, 贾淑娟. 我国海上风电发展现状与技术分析[J]. 华东电力, 2010, 38(2): 277-280. |
| [2] |
王成华, 高洋, 李全辉. 冲刷条件下既有桥梁桩基础工作性状研究进展[J]. 铁道标准设计, 2016, 60(1): 59-65. |
| [3] |
齐梅兰. 采砂河床桥墩冲刷研究[J]. 水力学报, 2005, 36(7): 835-838. |
| [4] |
张玉娥. 桥渡设计[M]. 北京: 中国铁道出版社, 2008.
|
| [5] |
邓军, 许唯临, 杨忠超, 等. 基岩冲刷的数值模拟[J]. 水科学进展, 2005, 16(1): 47-51. DOI:10.3321/j.issn:1001-6791.2005.01.010 |
| [6] |
MORISON J R, JOHNSON J W, SCHAAF S A. The force exerted by surface waves on piles[J]. Journal of Petroleum Technology, 1950, 2(5): 149-154. DOI:10.2118/950149-G |
| [7] |
MACCAMY R C, FUCHS R A. Wave forces on piles: a diffraction theory[J]. Wave Forces on Piles A Diffraction Theory, 1954. |
 2018, Vol. 40
2018, Vol. 40
