0 引　言

我国风能储存总量极其丰富，风能清洁环保无污染，因此风力发电是当今新能源开发价值最高的领域。相比陆地发电，我国拥有18 000千米长的大陆海岸线，可利用海域面积300多万平方千米。海上发电空间广阔，风速波动小，工作时间长。我国海上发电多建造在东南部沿岸滩涂和近海领域，沿海省份人口稠密，经济发展快，用电量大，同时发电运输更加便利。

现今主流的变速恒频双馈感应发电系统，在电网与发电机之间加入变流器，由此使得风轮可以变速运行。在主齿轮箱和发电机之间加入一个无级调速的行星齿轮调速装置适应风轮的变速运行工况，并且使用了和常规火电、水电机组一样的恒速恒频同步发电机，采取了与早期恒速风力发电机组感应发电机同样的直联电网的方式。这种新型液力调速装置实现变速输入恒速输出，具有发电品质更高、对电网冲击小的优点。

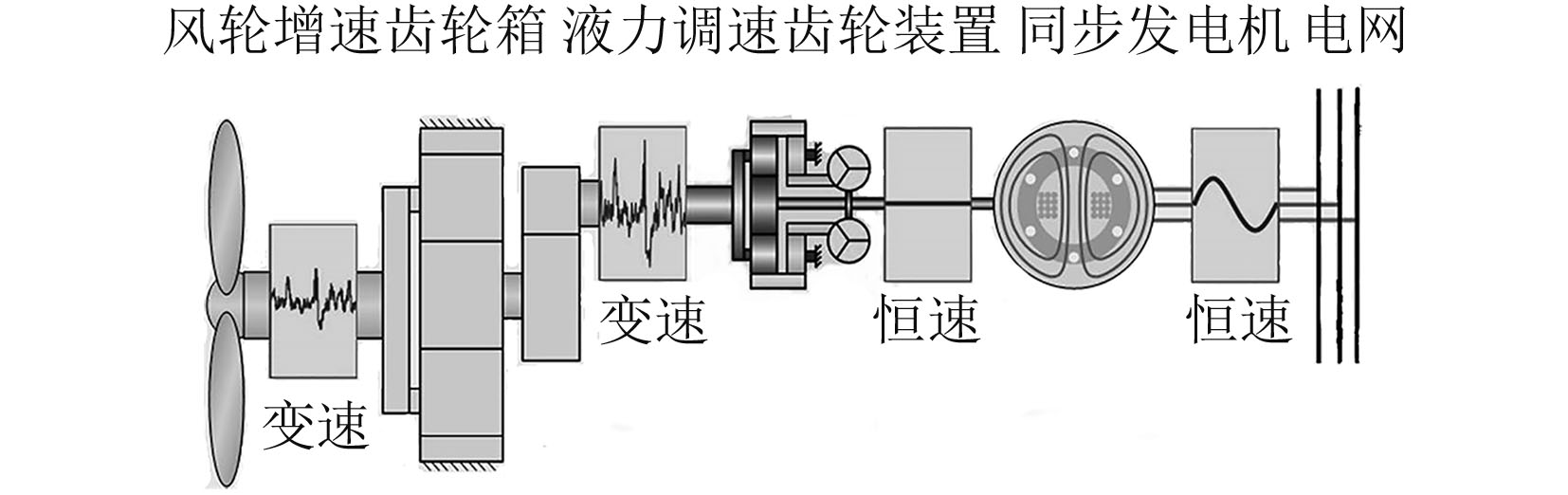
1 海上风力发电机械传动系统匹配关系

采用液力调速装置海上发电并网机组的工作模式一般分为4个环节，如图1所示。A到B段：风速达到切入发电风速，风力机起动加速直到并网同步；B到C段：风速低于额定发电风速，调节风轮转速获得最佳叶尖速比，跟踪最佳风能利用系数；C到D段：接近额定功率风速区的恒速控制，调节液力变矩器的导叶开度使得行星液力调速装置恒速输出；D到E段：随着功率增大，发电机和变流器达到其功率极限，调节桨矩角，限制输出功率^{[1 – 2]}。

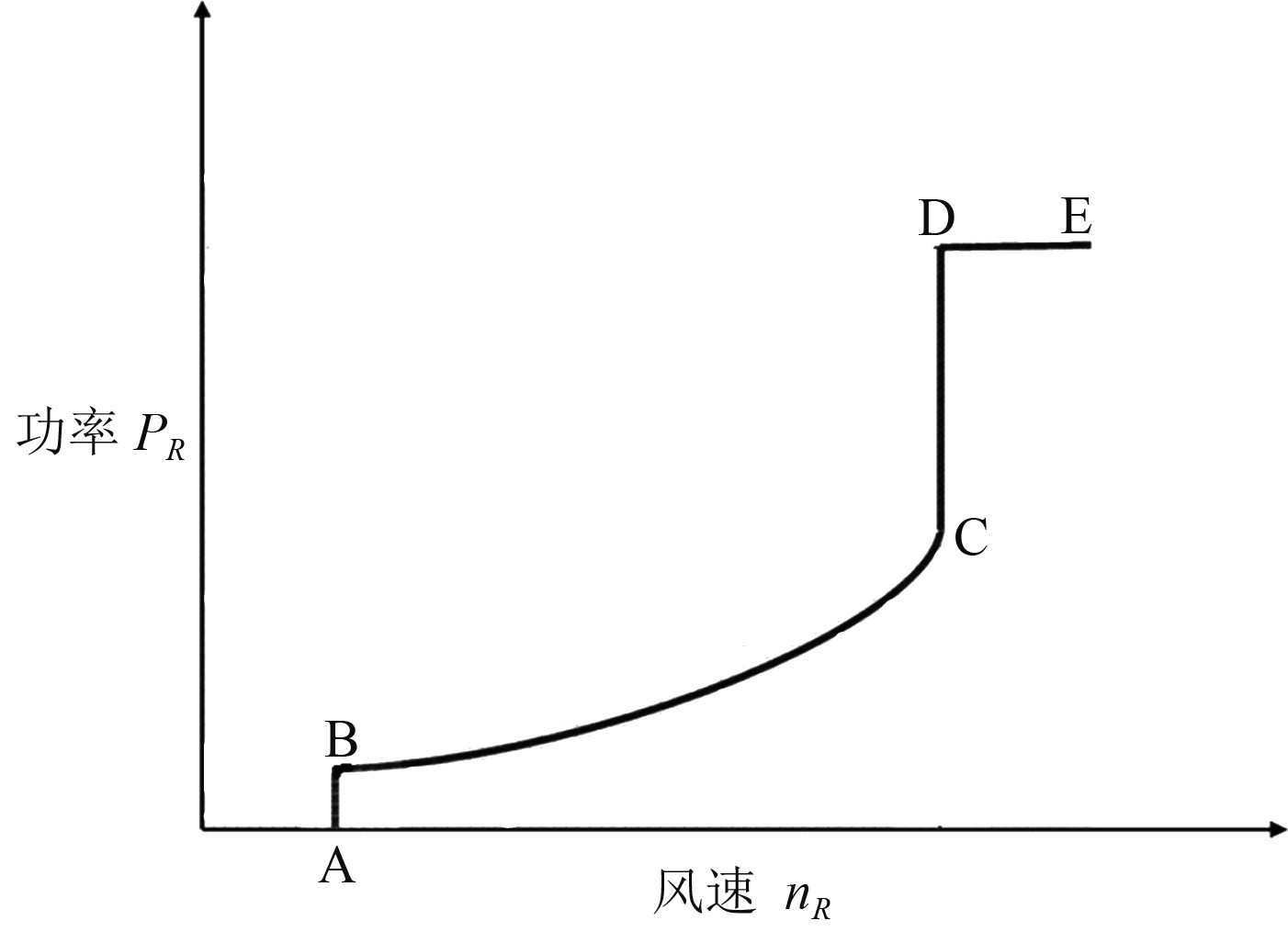
在海上风力发电机组中，输出到发电机组恒速1 500 r/min，风力发电机组叶轮转速允许在一定范围内进行变化，发电机组只需控制载荷转矩。在最佳叶尖速比下，风能利用系数最大，就是说叶轮可以实现最大风能捕获。这用来说明具有同直径的变速风力发电机组可以比恒速风力发电机组获得更多能量^[3]。液力调速传动系统原理如图2所示。

1.1 运动学关系

1）装置的输出转速

旋转轮系运动方程

${n_{t1}} + {\alpha _1}{n_{q1}} - (1 + {\alpha _1}){n_{j1}} = 0 {\text{。}}$

(1)

式中： ${n_{t1}}$ 为旋转轮系中心（太阳）轮转速； ${n_B}$ 为变矩器泵轮输入转速； ${n_{{{out}}}}$ 为装置的输出转速，也是发电机的输入转速（ ${n_G}$ ）， ${n_{t1}} = {n_B} = {n_{{{out}}}} = {n_G}$ ； ${n_{q1}}$ 为旋转轮系齿圈转速； ${n_{q2}}$ 为固定轮系齿圈转速， ${n_{q1}} = {n_{q2}}$ ； ${n_{j1}}$ 为旋转轮系行星架转速； ${n_{{{in}}}}$ 为风轮转速经过装置前端增速箱后的装置输入转速， ${n_{j1}} = {n_{{\rm{in}}}}$ ； ${n_{{\rm{in}}}} = {n_R} \cdot {\alpha _3}$ ； ${n_R}$ 为风轮转速； ${\alpha _3}$ 为增速箱传动比； ${\alpha _1}$ 为旋转轮系结构参数； ${\alpha _2}$ 为固定轮系的结构参数^{[4 – 5]}。

固定轮系运动方程

${n_{t2}} + {\alpha _2}{n_{q2}} - (1 + {\alpha _2}){n_{j2}} = 0 {\text{，}}$

(2)

固定轮系行星架固定， ${n_{j2}} = 0$ ，太阳轮转速为变矩器涡轮输出转速 ${n_T}$ ，即 ${n_{t2}} = {n_T}$ ，由此可得固定轮系齿圈转速为

${n_{q2}} = - \frac{{{n_T}}}{{{\alpha _2}}} {\text{，}}$

(3)

固定轮系的齿圈转速即为旋转轮系齿圈的转速为

${n_{q1}} = {n_{q2}} = - \frac{{{n_T}}}{{{\alpha _2}}} {\text{，}}$

(4)

固定轮系运动方程变为

${n_{{{out}}}} - \frac{{{\alpha _1}}}{{{\alpha _2}}}{n_T} - (1 + {\alpha _1}){n_{{\rm{in}}}} = 0 {\text{，}}$

(5)

由此可得装置的输出转速

${n_{{{out}}}} = \frac{{{\alpha _1}}}{{{\alpha _2}}}{n_T} + (1 + {\alpha _1}){n_{{{in}}}} {\text{。}}$

(6)

2）液力变矩器转速比与装置传动比的关系

由固定轮系运动方程（5）可得：

$1 - \frac{{{\alpha _1}}}{{{\alpha _2}}} \cdot \frac{{{n_T}}}{{{n_{{{out}}}}}} - (1 + {\alpha _1})\frac{{{n_{{{out}}}}}}{{{n_{{{in}}}}}} = 0 {\text{，}}$

(7)

${i_{CR}} = \displaystyle\frac{{{n_{out}}}}{{{n_{in}}}}$ 为装置传动比； ${i_{TB}} = \displaystyle\frac{{{n_T}}}{{{n_B}}} = $ $ \displaystyle\frac{{{n_T}}}{{{n_{out}}}}$ 为液力变矩器转速比；得到：

$1 - \frac{{{\alpha _1}}}{{{\alpha _2}}} \cdot {i_{TB}} - \frac{{1 + {\alpha _1}}}{{{i_{CR}}}} = 0 {\text{，}}$

(8)

$\left\{ \begin{array}{l}\text{液力变矩器转速比}:{i_{TB}} = \left( {1 - \frac{{1 + {\alpha _1}}}{{{i_{CR}}}}} \right) \cdot \displaystyle\frac{{{\alpha _2}}}{{{\alpha _1}}} {\text{，}}\\\text{装置传动比}:{i_{CR}} = \displaystyle\frac{{(1 + {\alpha _1}) \cdot {\alpha _2}}}{{{\alpha _2} - {\alpha _1} \cdot {i_{TB}}}} {\text{。}}\end{array} \right.$

(9)

1.2 液力变矩器的基本关系式

1）液力变矩系数

$K = \frac{{ - {M_T}}}{{{M_B}}} {\text{。}}$

(10)

式中： $ - {M_T}$ 为涡轮输出转矩； ${M_B}$ 为泵轮输入转矩。

2）液力变矩器传动效率效率

$\eta = \frac{{ - {M_T}{\omega _T}}}{{{M_B}{\omega _B}}} = K \cdot {i_{TB}} {\text{。}}$

(11)

1.3 传动系统转矩平衡关系

1）固定轮系

${\text{齿圈转矩}}\quad {M_{q2}} = {\alpha _2} \cdot {M_{t2}} {\text{，}}$

(12)

${\text{行星架转矩}}\quad {M_{j2}} = - (1 + {\alpha _2}) \cdot {M_{t2}} {\text{，}}$

(13)

${\text{太阳轮转矩}}\quad {M_{t2}} = - {M_T} {\text{，}}$

(14)

${\text{转矩平衡方程}}\quad {M_{t1}} + {M_{q1}} + {M_{j1}} = 0 {\text{。}}$

(15)

2）旋转轮系

${\text{齿圈转矩}}\quad {M_{q1}} = {\alpha _1} \cdot {M_{t1}} {\text{，}}$

(16)

${\text{行星架转矩}}\quad {M_{j1}} = - (1 + {\alpha _1}) \cdot {M_{t1}} {\text{，}}$

(17)

${\text{太阳轮转矩}}\quad {M_{t1}} = - ({M_B} + {M_G}) {\text{，}}$

(18)

${\text{转矩平衡方程}}\quad {M_{t1}} + {M_{q1}} + {M_{j1}} = 0 {\text{。}}$

(19)

式中： ${M_G}$ 为发电机轴上的作用转矩，也是装置输出轴对外负载（发电机）的作用转矩。

根据固定轮系和旋转轮系构件间的连接关系，固定轮系齿圈和旋转轮系的齿圈作用转矩之间有如下关系：

${M_{q1}} = - {M_{q2}} = - {\alpha _2} \cdot {M_{t2}} = - {\alpha _2} \cdot ( - {M_T}) = {\alpha _1} \cdot {M_{t1}} {\text{，}}$

(20)

由此可得

${M_{t1}} = - ({M_B} + {M_G}) = - \frac{{{\alpha _2}}}{{{\alpha _1}}} \cdot ( - {M_T}) = - \frac{{{\alpha _2}}}{{{\alpha _1}}} \cdot K \cdot {M_B} {\text{，}}$

(21)

${M_B} = \frac{{{\alpha _1}}}{{{\alpha _1} - {\alpha _2} \cdot K}} \cdot ( - {M_G}) {\text{，}}$

(22)

${M_{j1}} = - (1 + {\alpha _1}) \cdot {M_{t1}} = \frac{{(1 + {\alpha _1}) \cdot {\alpha _2}}}{{{\alpha _1}}} \cdot ( - {M_T}) {\text{。}}$

(23)

3）装置输入轴转矩

装置输入转矩为

$\begin{split}&{M_{{{in}}}} = {M_{j1}} = \frac{{(1 + {\alpha _1}) \cdot {\alpha _2}}}{{{\alpha _1}}} \cdot ( - {M_T}) = \\&\frac{{(1 + {\alpha _1}) \cdot {\alpha _2} \cdot K}}{{{\alpha _1} - {\alpha _2} \cdot K}} \cdot ( - {M_G}) {\text{。}}\end{split}$

(24)

4）功率关系

${M_{j1}} \cdot {n_{j1}} + {M_{q1}} \cdot {n_R} + {M_{t1}} \cdot {n_{t1}} = 0{\text{。}}$

(25)

1.4 分流功率比及总体传动机械效率

1）液力变矩器泵轮输入功率占装置输入功率的比例

${\bar P_B} = \frac{{{M_B}{\omega _B}}}{{{M_{in}}{\omega _{in}}}} = \frac{{{M_B}}}{{{M_{in}}}} \cdot {i_{CR}} = \frac{{{\alpha _1} \cdot {i_{CR}}}}{{(1 + {\alpha _1}) \cdot {\alpha _2} \cdot K}}{\text{，}}$

(26)

液力变矩系数： $K = \eta /{i_{TB}}$ ，可得：

${\bar P_B} = \frac{{{\alpha _1} \cdot {i_{TB}} \cdot {i_{CR}}}}{{(1 + {\alpha _1}) \cdot {\alpha _2} \cdot \eta }}{\text{。}}$

(27)

2）液力变矩器涡轮功率占装置输入功率的比例

${\bar P_T} = \frac{{ - {M_T} \cdot {n_T}}}{{{M_{in}} \cdot {n_{in}}}} = \frac{{{\alpha _1} \cdot {i_{TB}} \cdot {i_{CR}}}}{{(1 + {\alpha _1}) \cdot {\alpha _2}}}{\text{。}}$

(28)

3）装置总体传动机械效率

${\eta _{YJ}} = \frac{{{M_G}{n_{out}}}}{{{M_{in}}{n_{in}}}} = \frac{{{M_G}}}{{{M_{in}}}} \cdot {i_{CR}} = \frac{{({\alpha _2} \cdot K - {\alpha _1}) \cdot {i_{CR}}}}{{(1 + {\alpha _1}) \cdot {\alpha _2} \cdot K}}{\text{，}}$

(29)

同样根据 $K = \eta /{i_{TB}}$ ，结合 ${i_{TB}} = - \displaystyle\frac{{({i_{CR}} + {\alpha _1}) \cdot {\alpha _2}}}{{1 + {\alpha _1}}}$ ，得到：

${\eta _{YJ}} = \frac{{(\eta \cdot {\alpha _2} - {i_{TB}} \cdot {\alpha _1}) \cdot {i_{CR}}}}{{(1 + {\alpha _1}) \cdot {\alpha _2} \cdot \eta }}{\text{。}}$

(30)

对于变矩器的反转工况，效率应按 $\eta = K \cdot {i_{TB}}$ 所得的负值来计算，不能取 $\eta = 0$ 。或者直接代入对应工况点的变矩系数值，由式（26）和式（29）计算。

2 液力变矩器自适应特性功能体现

根据前面对风轮与液力调速装置匹配工作的分析，得到液力变矩器涡轮输出转矩与风轮转矩间的关系为：

$ - {M_T} = \frac{{{\alpha _1}}}{{(1 + {\alpha _1}) \cdot {\alpha _2} \cdot {\alpha _3}}}{M_R}{\text{，}}$

(31)

涡轮转速与风轮转速、发电机转速间的关系为：

${n_T} = \left[ {{n_G} - (1 + {\alpha _1}) \cdot {\alpha _3} \cdot {n_R}} \right] \cdot \frac{{{\alpha _2}}}{{{\alpha _1}}}{\text{。}}$

(32)

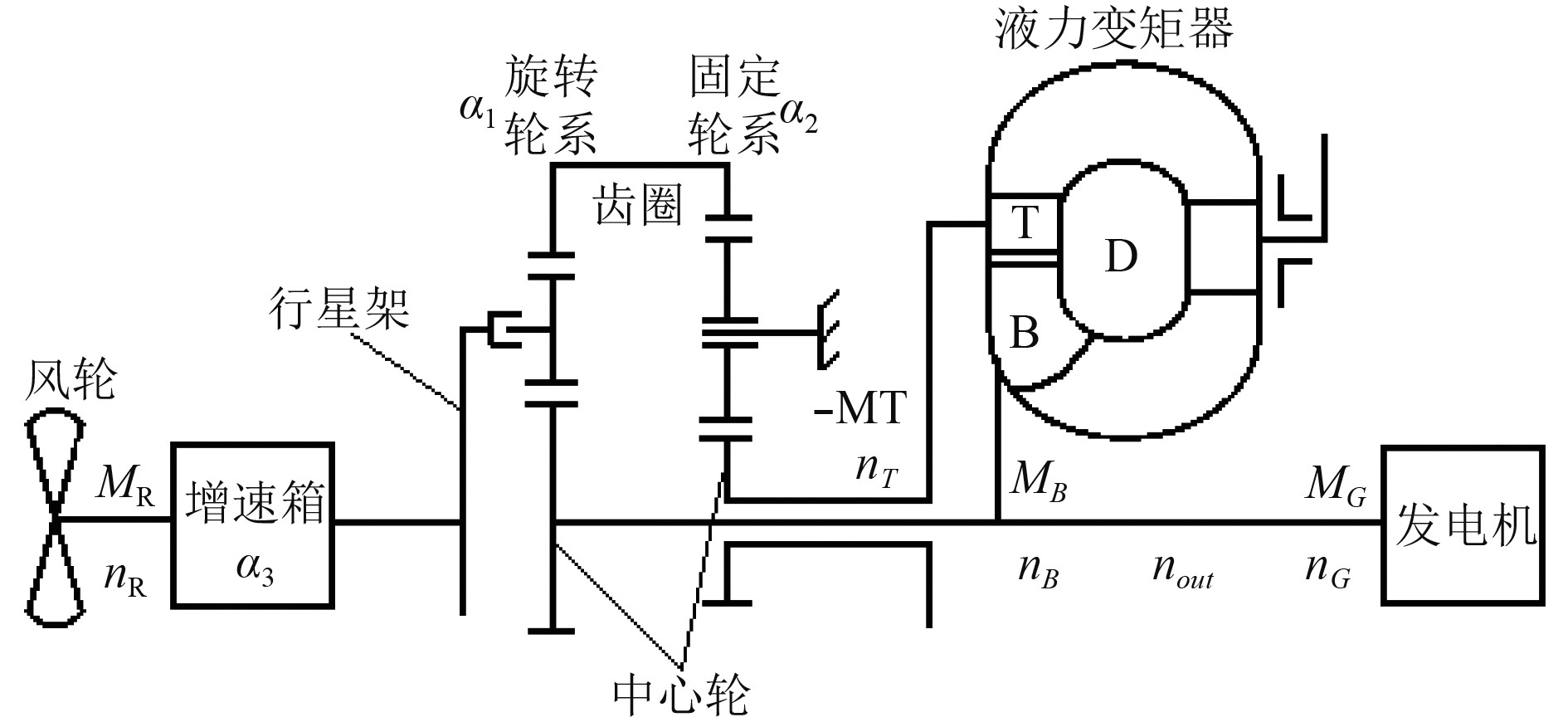
变矩器涡轮输出转矩与风轮转矩是标准的比例关系，而涡轮转速与风轮转速的关系则是一条负斜率直线的关系，即随着风轮转速的增大，风轮转矩增大，而液力变矩器涡轮输出转速则降低，涡轮输出转矩也增大。参考某典型的海上风轮特性曲线，采用以上关系式可以计算对应的液力变矩器输出工况点参数。得到适应风力机工况的液力变矩器输出特性曲线如图3所示。

这种典型工况计算得到的特性曲线正是液力变矩器近似双曲线特性的特征，也正是液力变矩器本身自动适应性的体现。作为流体机械，液力变矩器的输出特性与风轮转子转速—转矩特性相吻合，将两者配合起来使用再理想不过。

3 海上发电液力调速装置控制系统分析 3.1 同步发电机的恒速控制

采用液力调速装置技术的海上风力发电系统的同步发电机直接接入电网，恒速风电机组的异步发电机没有任何的附加控制系统，其特性完全是由其自身的电磁转矩转速特性决定的。采用液力调速装置技术的机组也是一类发电机恒速的风力发电形式，保持同步发电机的恒速运行也不会附加其他的控制环节，依靠的是同步发电机自身的工作特性及励磁调节特性。通过液力调速齿轮系统的运动学分析可以得出同步发电机转速与变矩器涡轮输出转速和风轮转速的关系：

${n_G} = \frac{{{\alpha _1}}}{{{\alpha _2}}}{n_T} + (1 + {\alpha _1}) \cdot {\alpha _3} \cdot {n_R}{\text{。}}$

(33)

从这个关系式出发，实时调节变矩器涡轮输出转速变化的风轮转速保持恒定的发电机输入转速是很自然的控制思路，并且液力调速装置的主控回路要有涡轮输出转速的采样反馈。实际的液力调速装置中，液力变矩器的导叶开度则专设一个位移传感器，主控回路为导叶开度的反馈控制，变矩器涡轮输出转速不是采样值而是一个计算值。涡轮转速的关系：

${n_T} = \left[ {{n_G} - (1 + {\alpha _1}){n_{in}}} \right] \cdot \frac{{{\alpha _2}}}{{{\alpha _1}}}{\text{。}}$

(34)

因此，以系统运动分析得出的发电机转速关系为根据而认为的直观控制思路应该放弃。可以这样讲，同步发电机或感应发电机直接接入电网是恒速运行的风力发电机组。在采用液力调速齿轮技术的风力发电机组中，液力变矩器的导叶调节并不参与同步发电机的恒速控制。

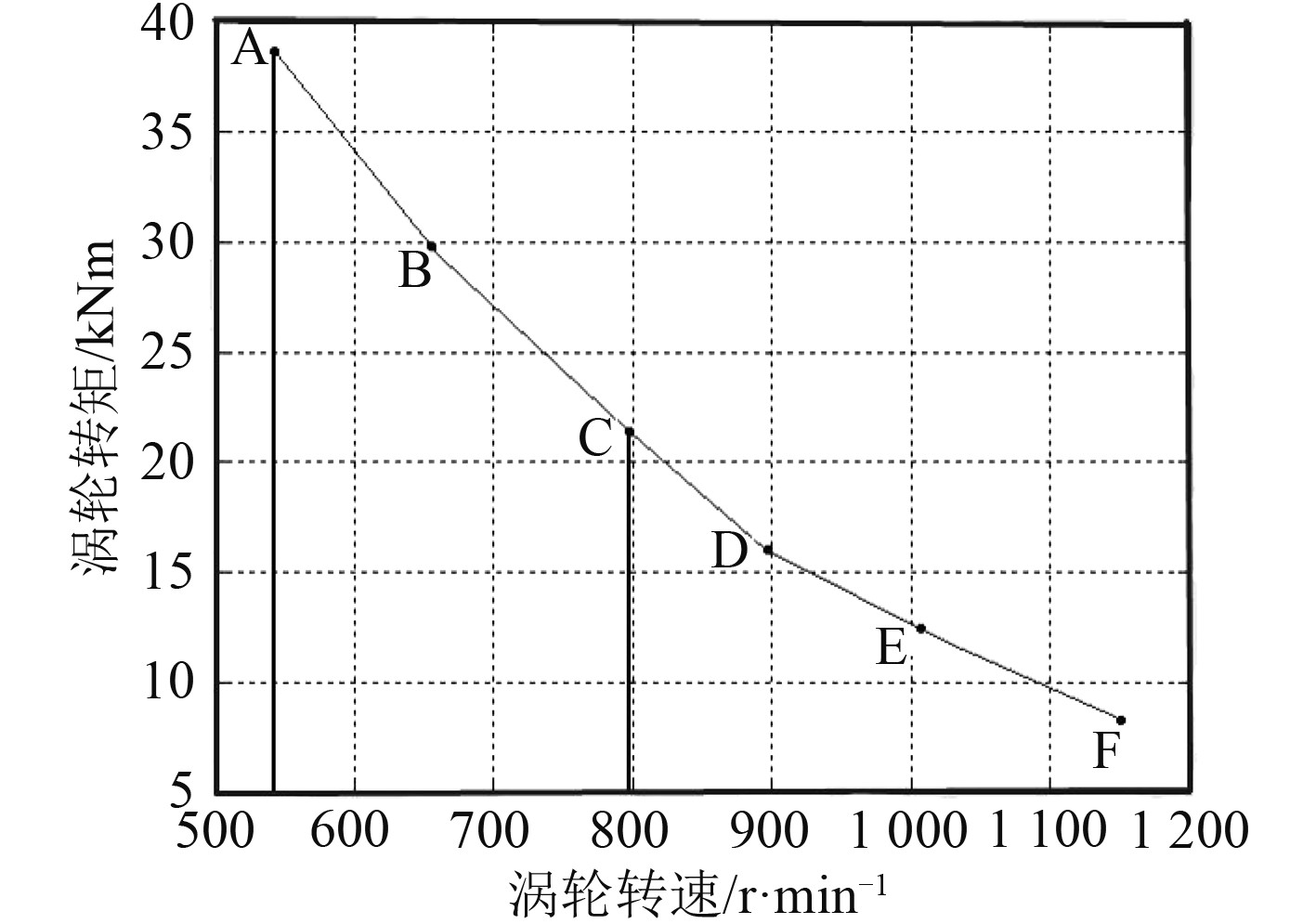
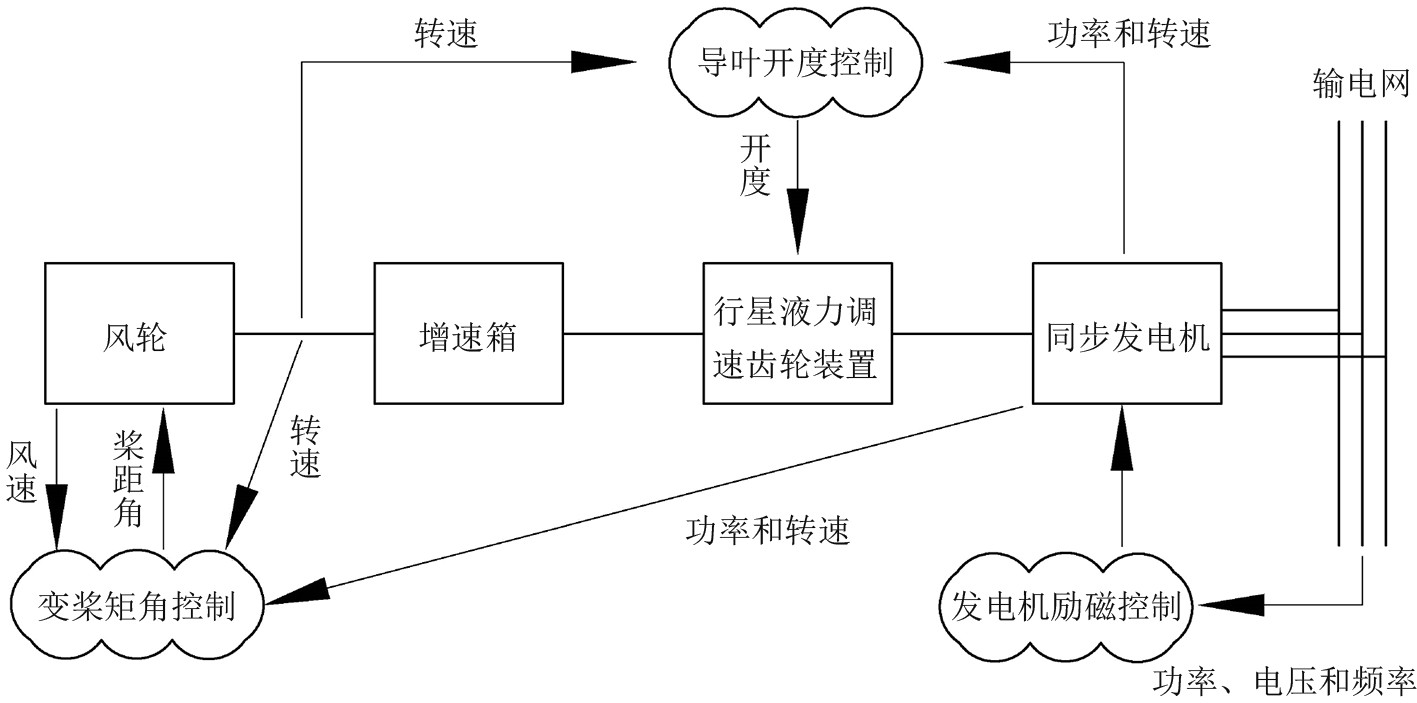
3.2 系统控制回路

液力调速装置的海上风电控制系统主要控制3套回路：变桨距角调节、液力变矩器导叶开度调节和发电机励磁调节。变桨距角调节是额定风速以下优化桨距角运行，额定风速以上，变桨距控制限制风能获取，维持额定发电功率；相关控制信号有风速、风轮转速、桨距角、功率和发电机转速。液力变矩器导叶开度调节是调节变矩器涡轮输出特性（转矩、转速），适应跟踪发电机组目标功率曲线风轮工况的调整；相关控制信号有导叶开度、风轮转速、功率和发电机转速。发电机励磁调节是提供发电机转子线圈励磁电流，保持发电机输出端电压稳定，调节系统无功功率；相关控制信号有励磁电压、电网电压、发电机频率^[6]。原理如图4所示。

4 海上风电液力调速系统控制策略

采用液力调速齿轮技术的海上风电系统属于风轮变速运行的风力发电机组，其控制的基本思想理论上仍然是取得最佳叶尖速比，获得最大风能利用系数，跟踪目标功率曲线的控制策略。液力变矩器的导叶调节并不参与同步发电机的恒速运行控制，液力变矩器导叶开度参考信号是基于平衡输出端扭矩给出的。

4.1 海上风力机工作特性

根据海上风能最大捕获原理，对某一风速风轮 ${v_1}$ ，风轮存在某一转速 ${n_R}^ * $ ，取得最佳叶尖速比 ${\lambda _{{{opt}}}}$ ，获得最佳风能利用系数 ${C_{p{\rm{max}}}}$ ，风力机目标（最佳）转矩—转速特性如图5所示。风轮获得最佳机械功率输出：

${P_{{{opt}}}} = \frac{1}{2}\rho {\text{π}} {R^2}{C_{p{\rm{ma}}x}}{v_1}^3 = \frac{1}{2}\rho {\text{π}}{R^2}{C_{p\max }}{\left( {\frac{{R{\omega _R}^ * }}{{{\lambda _{{{opt}}}}}}} \right)^3}{\text{，}}$

(35)

最佳叶尖速比：

${\lambda _{{{opt}}}} = \frac{{R{\omega _R}^ * }}{{{v_1}}} = \frac{R}{{{v_1}}} \cdot \frac{{2{\text{π}}{n_R}^ * }}{{60}}{\text{，}}$

(36)

海上风轮功率：

${P_{{{opt}}}} = {M_{R,{{opt}}}} \cdot \frac{{2{\text{π}}{n_R}^ * }}{{60}}{\text{。}}$

(37)

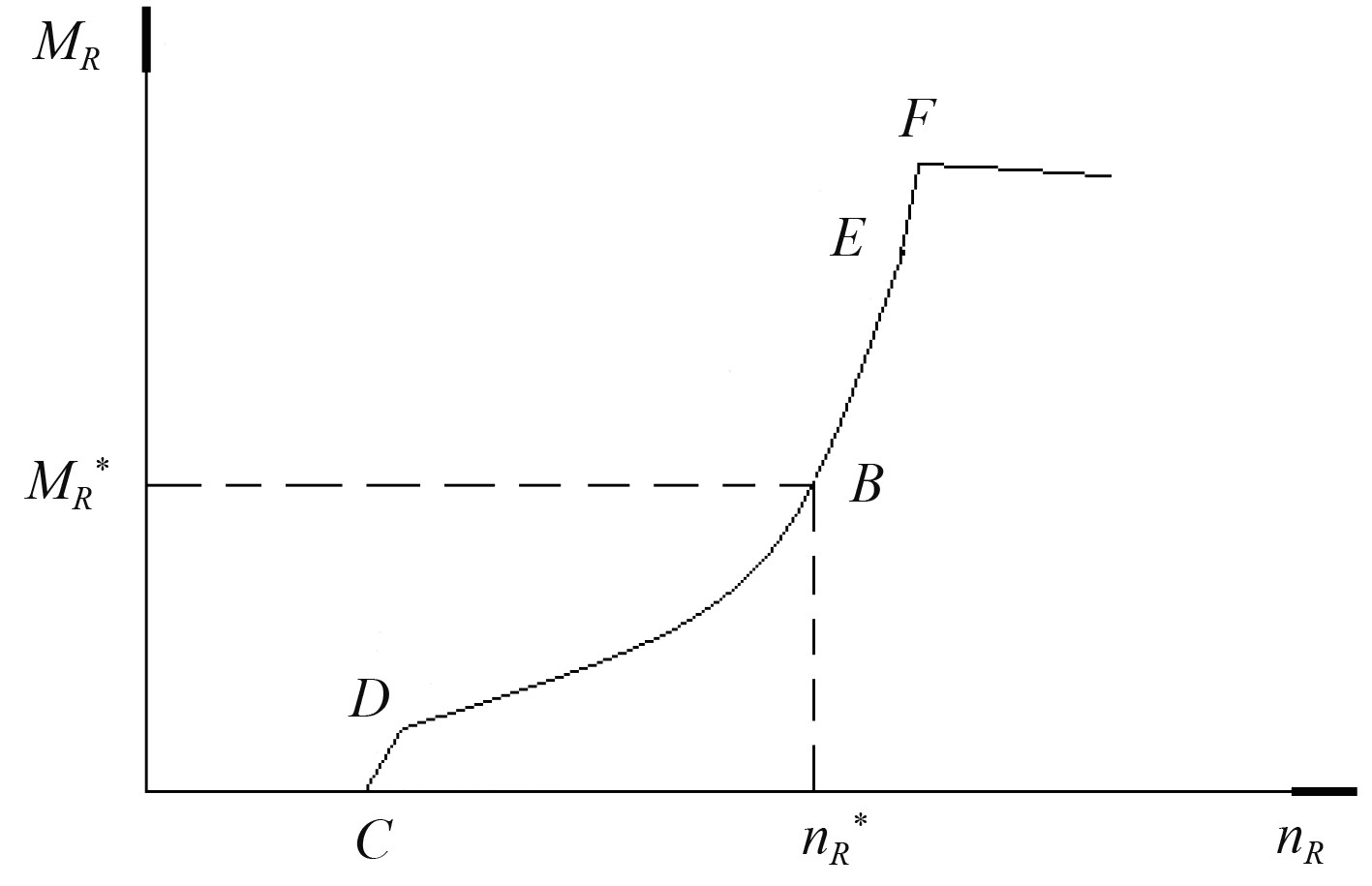
由此可得最优转矩模型： ${M_{R,{\rm{opt}}}} = {K'_{{\rm{opt}}}}{\left( {{n_R}^ * } \right)^2}$ ，如图5所示的DE段转矩曲线。理论上，系数 ${K'_{{\rm{opt}}}} = \displaystyle\frac{1}{2}\rho {\text{π}} {R^5}\frac{{{C_{p\max }}}}{{{\lambda _{{\rm{opt}}}}^3}} \cdot {\left( {\displaystyle\frac{{2{\text{π}} }}{{60}}} \right)^2}$ 。

对于系统检测到的风轮转速 ${n_R}^ * $ ，最优转速模型对应的风轮目标转矩为 ${M_R}^ * $ 。

4.2 液力变矩器外特性曲线上的工况点

导叶可调式液力变矩器外特性如图6所示。由风力机与液力调速装置匹配工作分析得到液力变矩器涡轮转速（ ${n_T}$ ）与发电机转速（ ${n_G}$ ）和风轮转速（ ${n_R}$ ）的关系为：

${n_T} = \left[ {{n_G} - (1 + {\alpha _1}) \cdot {\alpha _3} \cdot {n_R}} \right] \cdot \frac{{{\alpha _2}}}{{{\alpha _1}}}{\text{，}}$

(38)

涡轮输出转矩与风轮转矩的关系为：

$ - {M_T} = \frac{{{\alpha _1}}}{{(1 + {\alpha _1}) \cdot {\alpha _2} \cdot {\alpha _3}}}{M_R}{\text{。}}$

(39)

发电机的转速由电网、同步发电机工作特性确定同步，针对风力机运行工况采样得到的液力调速装置输入转速（ ${n_{in}}^ * $ ）可确定风轮转速 ${n_R}^ * $ ： ${n_R}^ * = {n_{in}}^ * /{\alpha _3}$ ，从而液力变矩器涡轮输出转速可定：

${n_T}^ * = \left[ {{n_G} - (1 + {\alpha _1}) \cdot {\alpha _3} \cdot {n_R}^ * } \right] \cdot \frac{{{\alpha _2}}}{{{\alpha _1}}}{\text{。}}$

(40)

适应风力机运行工况液力变矩器的涡轮输出转矩可由风轮目标转矩 ${M_R}^ * $ 确定：

$ - {M_T}^ * = \frac{{{\alpha _1}}}{{(1 + {\alpha _1}) \cdot {\alpha _2} \cdot {\alpha _3}}}{M_R}^ * {\text{。}}$

(41)

工况点（ ${n_T}^ * $ ， $ - {M_T}^ * $ ）位于可调液力变矩器某一导叶开度下的外特性曲线上，如图6所示的导叶开度 ${\bar \delta _2}^ * $ ， ${\bar \delta _2}^ * $ 则可作为液力调速装置控制器中导叶调节的参考目标给定值。在液力调速装置控制器开发工作中，一项重要的工作就是针对导叶可调式液力变矩器导叶开度 ${\bar \delta _i} = f({n_{Ti}}, - {M_{Ti}})$ 或者原始特性曲线 ${\bar \delta _i} = f({i_{TBi}},{K_i})$ 的编程。

液力调速装置运行中液力变矩器导叶开度的调节控制类似于做导叶可调式液力变矩器的特性试验，导叶调至某一开度，风轮对液力变矩器涡轮实施加载操作，在调节涡轮输出转速 ${n_T}^ * $ 的情况下，“读出”液力变矩器涡轮输出转矩 $ - {M_T}^ * $ 。

4.3 液力变矩器的泵轮输入转矩

对于海上风力机的某一目标工况（ ${n_R}^ * $ ， ${M_R}^ * $ ），液力变矩器转速比工况参数为：

${i_{TB}}^ * = \frac{{{n_T}^ * }}{{{n_B}}} = \frac{{{n_T}^ * }}{{{n_G}}}{\text{，}}$

(42)

${i_{TB}}^ * $ 此处并非代表液力变矩器的计算（设计）工况转速比。导叶可调式液力变矩器原始特性如图7所示。

在液力变矩器原始特性曲线上，根据 ${i_{TB}}^ * $ 可以得到对应的液力变矩系数 ${K^ * }$ ，如图7所示，由此可确定泵轮输入转矩：

${M_B}^ * = - {M_T}^ * /{K^ * }{\text{。}}$

(43)

4.4 液力调速装置的输出转矩

液力调速装置的输出转矩（ ${M_{out}}$ ）是发电机输入轴上的作用转矩（ ${M_G}$ ），也是同步发电机的拖动转矩： ${M_G} = {M_0} + M$ 。 ${M_0}$ 为同步发电机的空载制动转矩； $M$ 则为与发电机电磁功率PM对应的电磁制动转矩，也就是需要由发电机定子磁场与转子磁场相互作用产生的电磁制动转矩。

稳定工况下，旋转轮系中太阳轮上的转矩平衡关系为：

${M_{t1}} + {M_B} + {M_G} = 0{\text{。}}$

(44)

由液力调速装置传动系统的旋转轮系中心中太阳轮转矩与涡轮转矩之间的关系式

${M_{t1}} = - \frac{{{\alpha _2}}}{{{\alpha _1}}} \cdot ( - {M_T}){\text{，}}$

(45)

得到发电机轴上的作用转矩：

$\begin{split}& {M_G} = \left( {\frac{{{\alpha _2}}}{{{\alpha _1}}} - \frac{1}{K}} \right) \cdot ( - {M_T}) = \\& \left( {\frac{{{\alpha _2}}}{{{\alpha _1}}} - \frac{1}{K}} \right) \cdot \frac{{{\alpha _1}}}{{(1 + {\alpha _1}) \cdot {\alpha _2} \cdot {\alpha _3}}} \cdot {M_R}{\text{。}}\end{split}$

(46)

风力机目标转矩特性： ${M_{R,{{opt}}}} = {K'_{{{opt}}}}{\left( {{n_R}^ * } \right)^2}$ ， ${K'_{{{opt}}}} = $ $\displaystyle\frac{1}{2}\rho {\text{π}} {R^5}\frac{{{C_{p\max }}}}{{{\lambda _{{{opt}}}}^3}} \cdot {\left( {\displaystyle\frac{{2{\text{π}} }}{{60}}} \right)^2}{\text{。}}$

采用液力调速齿轮技术的风力发电机组，风轮转速与发电机转速的关系为

${i_{RG}} = \frac{{{n_R}}}{{{n_G}}} = \frac{{(1 + {\alpha _1}){\alpha _2}{\alpha _3}}}{{{\alpha _2} - {\alpha _1}{i_{TB}}}}{\text{，}}$

(47)

由以上关系推导得到发电机转矩与发电机转速（ ${n_G}$ ）的关系为

${M_G} = \frac{{({\alpha _2} \cdot K - {\alpha _1})(1 + {\alpha _1}) \cdot {\alpha _2} \cdot {\alpha _3} \cdot {{K'}_{{\rm{opt}}}}}}{{{{({\alpha _2} - {\alpha _1}{i_{TB}})}^2} \cdot K}} \cdot {n_G}^2 = {K''_{{\rm{opt}}}}{\omega _G}^2{\text{，}}$

(48)

式中， ${K''_{{{opt}}}} = \displaystyle\frac{{({\alpha _2} \cdot K - {\alpha _1})(1 + {\alpha _1}) \cdot {\alpha _2} \cdot {\alpha _3} \cdot {{K'}_{{{opt}}}}}}{{{{({\alpha _2} - {\alpha _1}{i_{TB}})}^2} \cdot K}}{\text{。}}$

对于变速恒频恒速风力发电机组，发电机的转速是恒定的，但 ${K''_{{{opt}}}}$ 是变化的。

5 结　语

1）液力调速装置的旋转行星齿轮叠加了2种可变转速来实现恒定的输出转速，应用在同步发电机中，实现变化的风速输入恒速1 500 r/min输出并网发电。

2）海上风力发电机组在风速达到切入风速时开始发电，桨叶角跟随最佳风能利用系数开始变化，接近额定风速开始恒速控制。到达海上风力发电功率极限时，调节桨叶角使得实际发电功率不超过发电机组极限。

3）同步发电机或感应发电机直接接入电网就是恒速运行的海上风力发电机组。在采用液力调速齿轮技术的海上风力发电机组中，液力变矩器的导叶调节并不参与同步发电机的恒速控制。

4）通过数学模型分析出海上风电风力机特性、同步发电机功角特性与液力变矩器输出参数、液力调速装置输出参数的数学关系。