超大型浮体(VLFS)尺度巨大,由多个结构形式相同的单一模块构成,单一模块长度可达300~400 m,可作为海洋开发研究基地、海上中转基地以及海上机场等,是我国海洋权益保障的重要依靠。对超大型浮体研究较早的国家包括日本和美国,日本于20世纪90年代对超大型浮式机场进行了系统性的研究,研究内容包括浮式机场构型、水弹性响应基本特征、结构应力分析、功能性要求、综合安全评估(FSA)以及维护管理等,并于1999年建立了海上浮式机场,进行飞机起降试验后拆除。美国90年代也开展了移动式离岸基地(MOB)理论和试验研究,并于1991年和1999年在夏威夷召开了超大型浮式结构国际会议[1]。近年来,我国对超大型浮体开展了大量理论和试验研究,包括浮体流固耦合响应研究、极值载荷研究、系泊系统及多模块连接器研究、风险评估与结构安全可靠性研究等。
超大型浮体风险评估和安全可靠性研究是设计建造过程中的关键技术之一,可靠性研究首要解决的问题是确定可靠度的衡量标准,即确定结构目标可靠度,其代表了结构的最大可容许失效概率,既可用来校核结构的实际安全水平是否符合相关要求,又可作为确定载荷和抗力因数设计(LRFD)方法中分项安全系数(PSF)的依据[2]。传统结构可靠性校核所依据的目标可靠度一般是参考现行规范或相似结构的相关要求,例如DNV[3]针对失效类型和后果严重程度的不同建议了不同的失效概率要求;不同规则通过对失效后果的定性描述来确定目标失效概率,缺少针对失效后果严重程度的定量评估。一些学者考虑结构寿命、结构冗余度、结构失效后果等指标建议了计算目标失效概率的经验公式[4 – 5],这些经验公式对于确定现存同类结构物的安全裕度具有一定的指导意义,但超大型浮体是一种新颖结构,针对此种结构设计衡准未有直接经验可借鉴,对于容纳大量人员的超大型浮体空港或海港应用经验公式进行目标可靠度标定的合理性和适用性有待商榷,因此需对浮体失效后果进行理性评估后再确定目标可靠度。
由于风险分析方法可对结构失效后果进行定性或定量分析,国际上一些学者开始采用风险分析方法确定超大型浮体的目标可靠度,Suzuki[6]对超大型浮体致命失效模式进行分析,采用日本铁路致命事故发生率(FAR)标定超大型浮体的目标失效概率。Baidurya B.[7]对不同国际组织提出的目标可靠度进行汇总,探索将风险理论应用于超大型浮体目标可靠度的选取过程中,提出了应用风险分析方法确定移动式离岸基地目标可靠度的流程。上述文献从风险的角度对结构目标可靠度进行分析,但在确定目标可靠度取值时,未考虑结构失效概率占总体事故概率的比例。
本文首先根据风险分析方法确定了适用于超大型浮体的结构目标可靠度,应用简化逐步破坏分析方法确定了半潜式超大型浮体典型剖面的极限承载能力,基于三维线性势流理论对处于我国南海海况下的超大型浮体波浪载荷进行预报,最后根据选定的目标可靠度对超大型浮体极限强度可靠性进行分析。
1 浮体目标可靠度的选取 1.1 风险理论基础风险可表示为危害发生频率与后果严重性的组合,用公式表示为:
| $R = L \times C{\text{。}}$ | (1) |
其中:
| ${R_{reliability}} = 1 - {p_f}{\text{。}}$ | (2) |
其中:
结构失效概率可作为风险理论中危害的发生频率,结构失效概率用可靠度指数
| $\beta = {\Phi ^{ - 1}}\left( {1 - {p_f}} \right){\text{。}}$ | (3) |
致命事故发生率(FAR)表达个体风险。FAR表示1个群体每1亿小时的死亡数,其计算公式如下:
| $FAR = \frac{{PLL \times {{10}^8}}}{{PO{B_{av}} \times 8\;760}}{\text{,}}$ | (4) |
式中:
社会风险是指能够引起大于等于N人伤亡的事故累积频率,也即单位时间内(通常为年)的伤亡人数。通常用社会风险曲线(F-N曲线)表示[8]:
| $PL{L_A} = r \cdot EV{\rm{ = }}{F_1} \cdot \left(1 + \sum\limits_{N = 1}^{{N_u} - 1} {\frac{1}{{N + 1}}}\right) = {F_1} \cdot \sum\limits_{N = 1}^{{N_u}} {\frac{1}{N}} {\text{。}}$ | (5) |
式中:
选取碰撞(CN)、火灾/爆炸(FX)、搁浅(GR)、恶劣天气导致的浮体破坏(包括沉没)(HD)典型事故作为超大型浮体总体事故,分析恶劣天气导致的浮体结构失效概率占总体事故概率的比例。各事故造成的PLL表示如下:
| $PL{L_i} = POB \cdot {c_i} \cdot {p_{f(i)}}{\text{。}}$ | (6) |
其中:
| ${c_i} = \frac{{\displaystyle\sum\limits_{N = 1}^{{N_u}} {N \cdot {f_N}} }}{{POB \cdot {p_{f(i)}}}}{\text{。}}$ | (7) |
各类事故导致的PLL如下:
| $\left\{ \begin{array}{l}PL{L_{CN}} = POB \cdot {c_{CN}} \cdot {p_{f(CN)}}{\text{,}}\\PL{L_{FX}} = POB \cdot {c_{FX}} \cdot {p_{f(FX)}}{\text{,}}\\PL{L_{GR}} = POB \cdot {c_{GR}} \cdot {p_{f(GR)}}{\text{,}}\\PL{L_{HD}} = POB \cdot {c_{HD}} \cdot {p_{f(HD)}}{\text{。}}\end{array} \right.$ | (8) |
将四类事故PLL相加得到总PLL如下:
| $\begin{array}{l}PL{L_T} = PL{L_{CN}} + PL{L_{FX}} + PL{L_{GR}} + PL{L_{HD}} =\\ POB \cdot \displaystyle\sum\limits_i {\left( {{c_i} \cdot {p_{f(i)}}} \right)} {\text{。}}\end{array}$ | (9) |
建立了超大型浮体碰撞(CN)、火灾/爆炸(FX)、搁浅(GR)、恶劣天气导致的浮体破坏(包括沉没)(HD)事件树模型,使用英国海洋平台碰撞事故历史数据[9]和全球客滚船火灾/爆炸、搁浅和船体破坏事故历史数据[10]作为初始事故频率,针对不同的事故序列后果进行假设,得到典型事故类型的PLL,如表1所示,可以看出,浮体破坏导致的PLL约占总体PLL的14.5%,由此计算可接受的浮体破坏事故发生概率如下:
|
|
表 1 典型事故的PLL Tab.1 Potential loss of lives for typical accidents |
| $P_{f(i)}^{AC} = \frac{{\displaystyle\frac{{PL{L_i}}}{{PL{L_T}}} \times PL{L^{AC}}}}{{POB}}{\text{。}}$ | (10) |
其中:
应用风险分析方法确定结构目标可靠度首先应确定风险衡准,即可接受风险水平。识别结构失效模式,分析结构风险占总体风险的比例,评估事故后果(人员伤亡、财产),根据事故后果严重程度选择结构的目标可靠度。根据我国民用航空局的统计数据,2016年我国民用机场平均吞吐量约为1.3万人次,因此本文设定超大型浮体空港平均吞吐量为1.3万人次,机场服务人员1 000人,出发乘客和到达乘客各占一半,每个旅客离港时间为3 h,到港时间为2 h,则每年乘客暴露于风险的总小时数为1.19百万小时,相当于1 354乘客年(passenger-year)。同时,作为空港职员1 000人计,将24 h常留,为1 000职员年。
分别基于FAR和F-N曲线2种方法确定目标可靠度,考虑船体破坏PLL占总体PLL的比例。选取Suzuki(2001)推荐的超大型浮体致命事故发生率FAR=2作为标准,计算所得的失效概率为7.48E-06(
| $PLL{\rm{ = }}\frac{{FAR \times PO{B_{av}} \times 8760}}{{{{10}^8}}}{\rm{ = }}{N_T} \times {p_f}{\text{。}}$ | (11) |
其中:
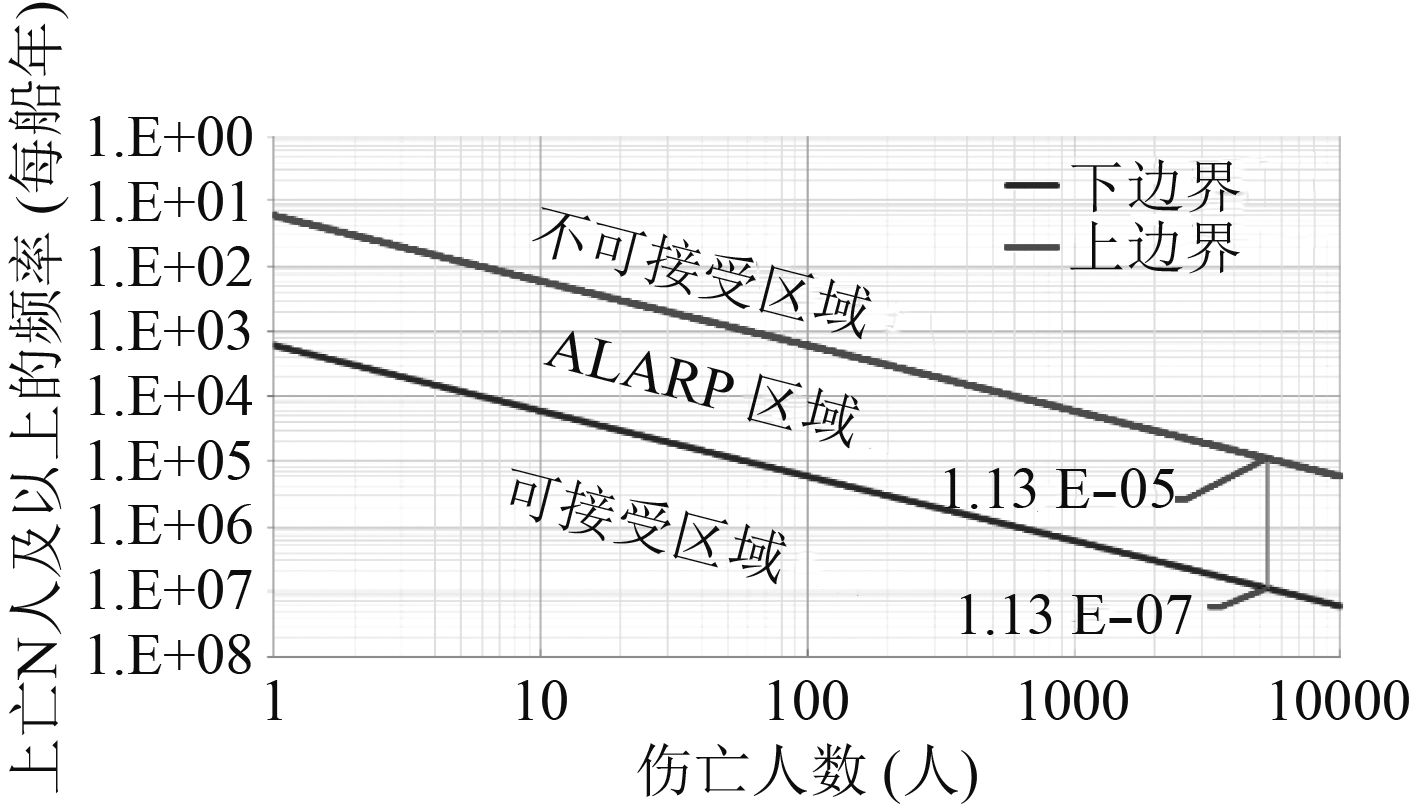
选用世界航空运输业伤亡标准作为F-N曲线衡准,2012年世界航空运输业伤亡人数414人,航空业总回报为5 610亿美元,则r为0.73人/10亿美元。根据2016年某航空公司年报统计,可计算得到每乘客年的收入为0.23百万美元。伤亡1人及以上的频率上边界和下边界为5.99E-02和5.99E-04,则可得到F-N曲线衡准,如图1所示。按照恶劣天气条件下船体破坏导致66%的伤亡假设,选择伤亡人数5 280对应的上边界作为允许的结构失效概率,即为1.13E-05,目标可靠度为4.24。此外,还可划分出目标失效概率的合理可行(ALARP)区域,为1.13E-05~1.13E-07。
|
图 1 基于F-N图的超大型浮体结构目标失效概率范围 Fig. 1 VLFS structure target failure probability based on F-N diagram |
| $PL{L_A} = r \cdot EV = 0.73 \cdot \frac{{0.23}}{{1\;000}} \cdot 2\;354 = 0.395{\text{,}}$ | (12) |
| ${F_1} = \frac{{PL{L_A} \times 14.5{\rm{\% }}}}{{\displaystyle\displaystyle\sum\limits_{N = 1}^{8\;000} {\displaystyle\frac{1}{N}} }} = 5.99 \times {10^{{\rm{ - 3}}}}{\text{。}}$ | (13) |
超大型浮体的目标可靠度随不同的使用年限的变化而变化,对于不同使用年限的目标可靠度可应用下式进行计算[11]:
| ${p_{fN}} = 1 - {(1 - {p_{f1}})^N}{\text{,}}$ | (14) |
式中:N为服役年份;
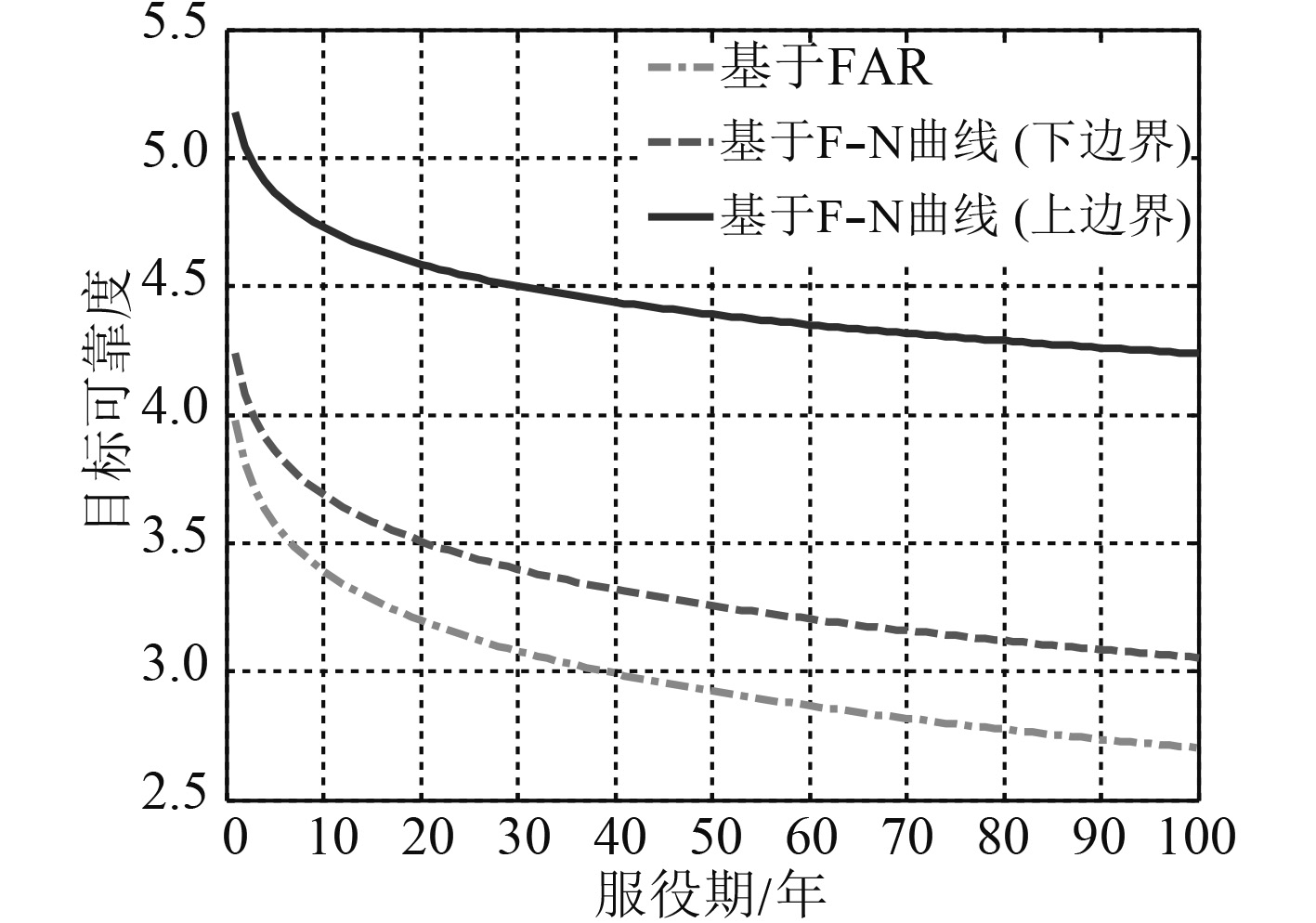
对吞吐量13 000人的超大型浮式机场计算不同服役年限的总纵极限强度目标可靠度,百年服役期内目标可靠度的变化情况如图2所示,可以看出随着服役期的不断增加,目标可靠度逐渐减小。
|
图 2 百年服役期内目标可靠度的变化情况 Fig. 2 Target reliability variance in 100 service year |
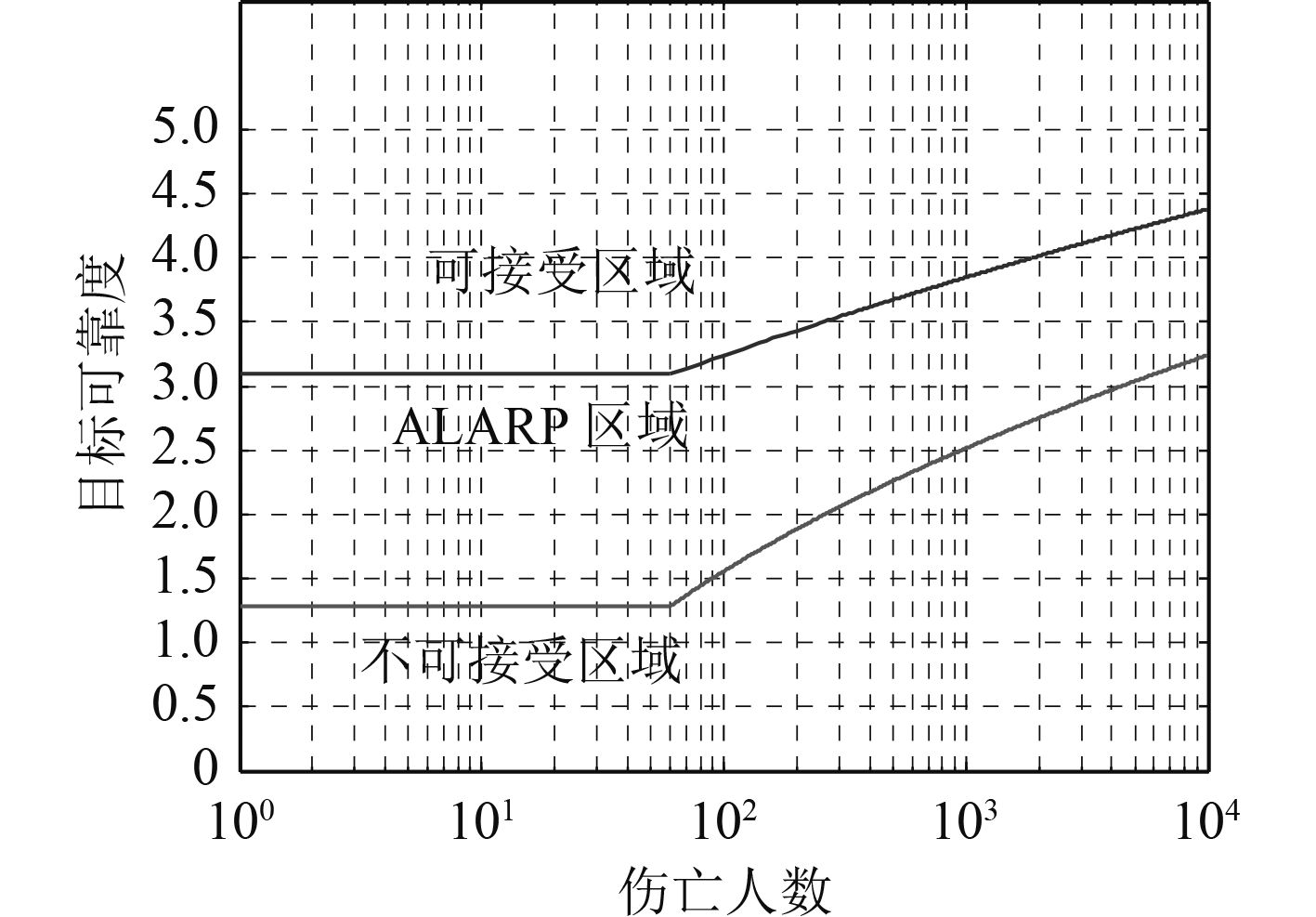
由于随着伤亡人数的减少目标可靠度也会变小,但结构目标可靠度不能无限制变小,结构仍需具有一定的可靠性要求,因此本文对导致不同伤亡后果的结构目标可靠度可设置最低目标可靠度要求,以DNV Note 30.6[3]建议的的目标可靠度3.09(1E-03)作为可接受区域的边界,根据风险分析中对ALARP区域的设定方法,则超大型浮体目标可靠度ALARP区域的下边界为1.28(1E-01),此种设定符合可接受风险水平的要求,避免了由于事故后果较小而导致目标可靠度过低的情况。百年服役期内不同伤亡后果下的目标可靠度如图3所示,整个区域分为可接受区域、ALARP区域和不可接受区域,当结构可靠度处于ALARP区域时,代表结构可靠度合理可行,应采取符合费效比的措施尽可能提高目标可靠度(尽可能降低失效概率)。
|
图 3 百年服役期内目标可靠度选取建议 Fig. 3 Suggestion on target reliability selected for 100 service year |
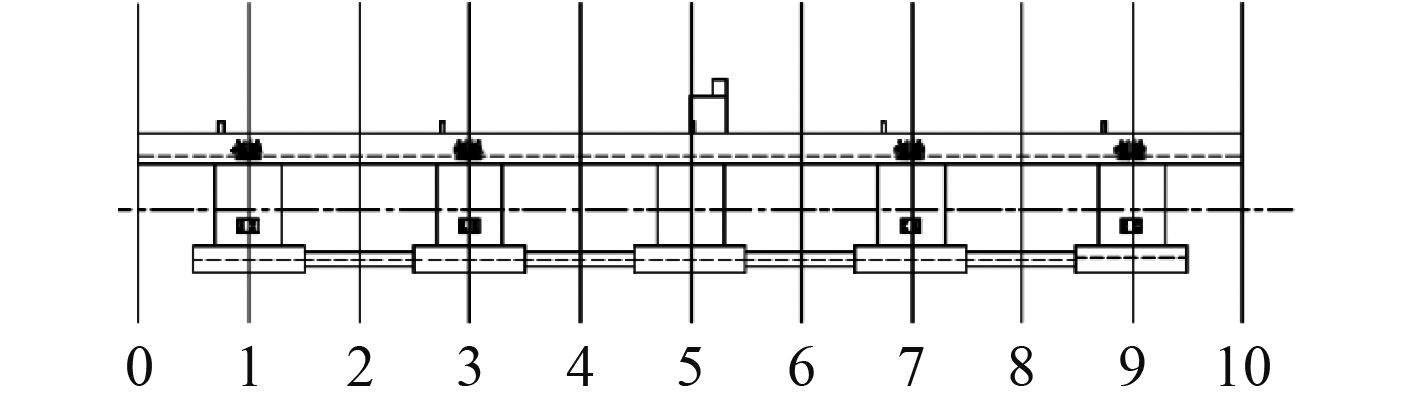
超大型浮体单个模块总长300 m,总宽100 m,由上箱体、立柱、下箱体和撑杆组成,采用横向浮箱结构,各部位的设计参数见表2,超大型浮体各站面分布情况如图4所示,站距为30 m。
|
|
表 2 浮体单模块主要设计参数 Tab.2 Main design parameters of VLFS single module |
|
图 4 浮体分段情况 Fig. 4 Segments of VLFS |
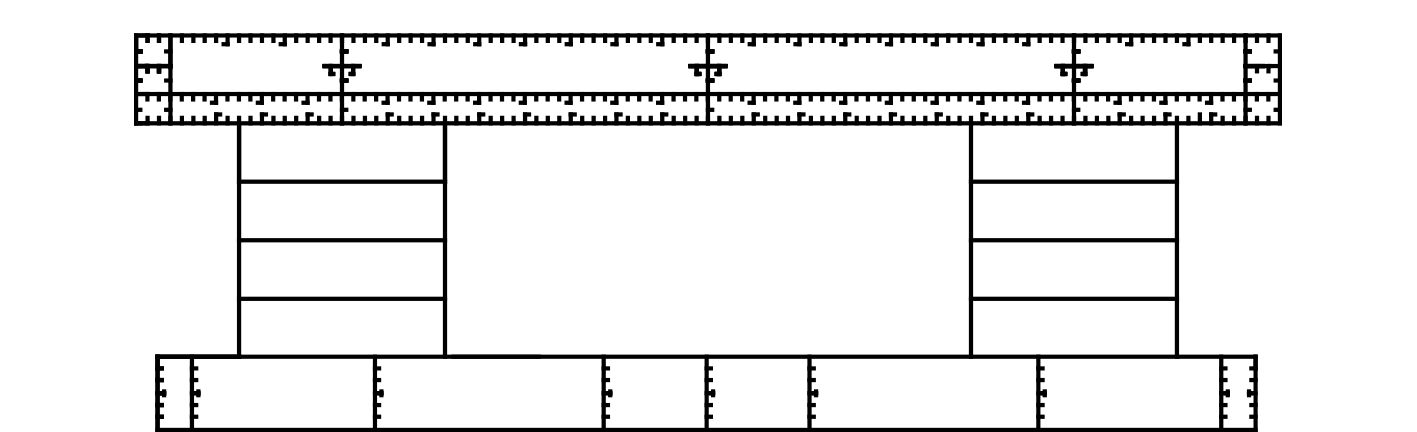
简化逐步破坏分析方法将浮体横剖面离散成为加筋板单元和硬角单元,确定各单元的平均应力应变关系,利用平断面假设,逐步增加曲率,得到结构单元破坏过程中的弯矩极值作为结构极限强度。由于超大型浮体各站面横截面的形式不同,因此本文应用简化逐步破坏分析方法计算了中剖面和第六站面的极限强度。横截面形式如图5和图6所示。
|
图 5 浮体中剖面示意图 Fig. 5 Midship section draft of VLFS |
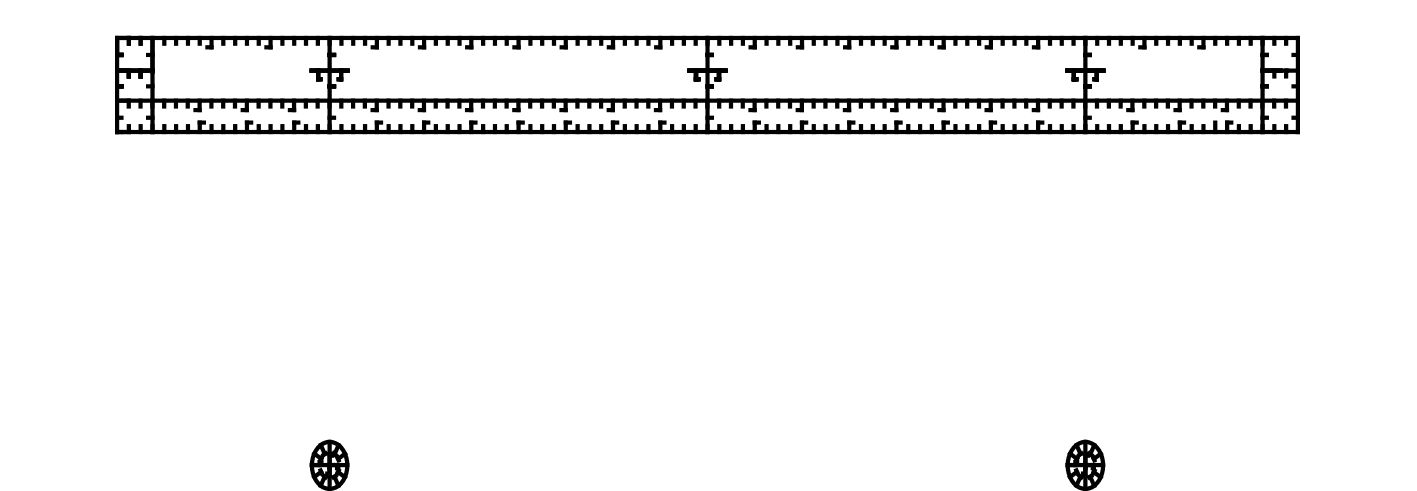
|
图 6 浮体第六剖面示意图 Fig. 6 No.6 Cross section draft of VLFS |
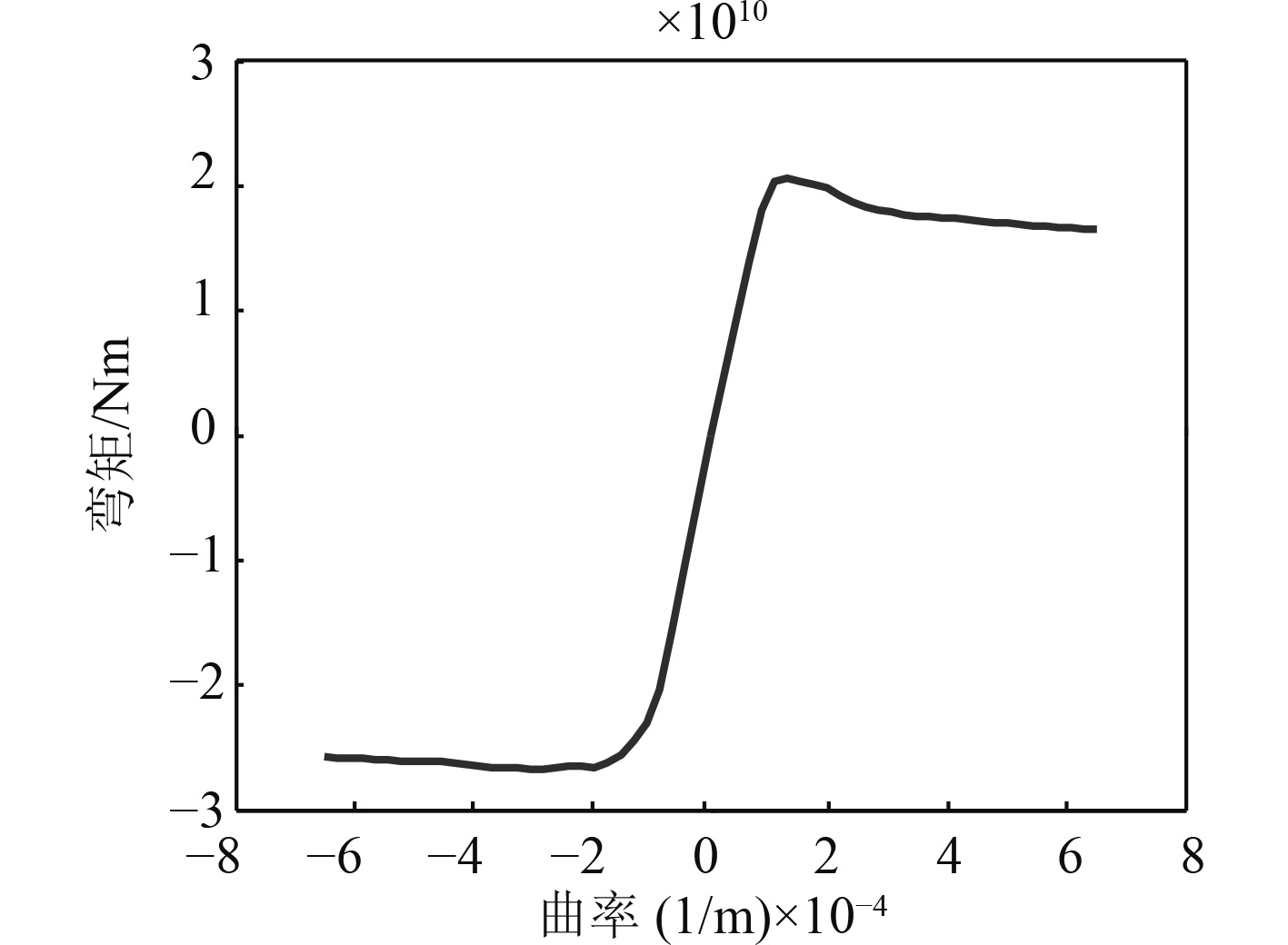
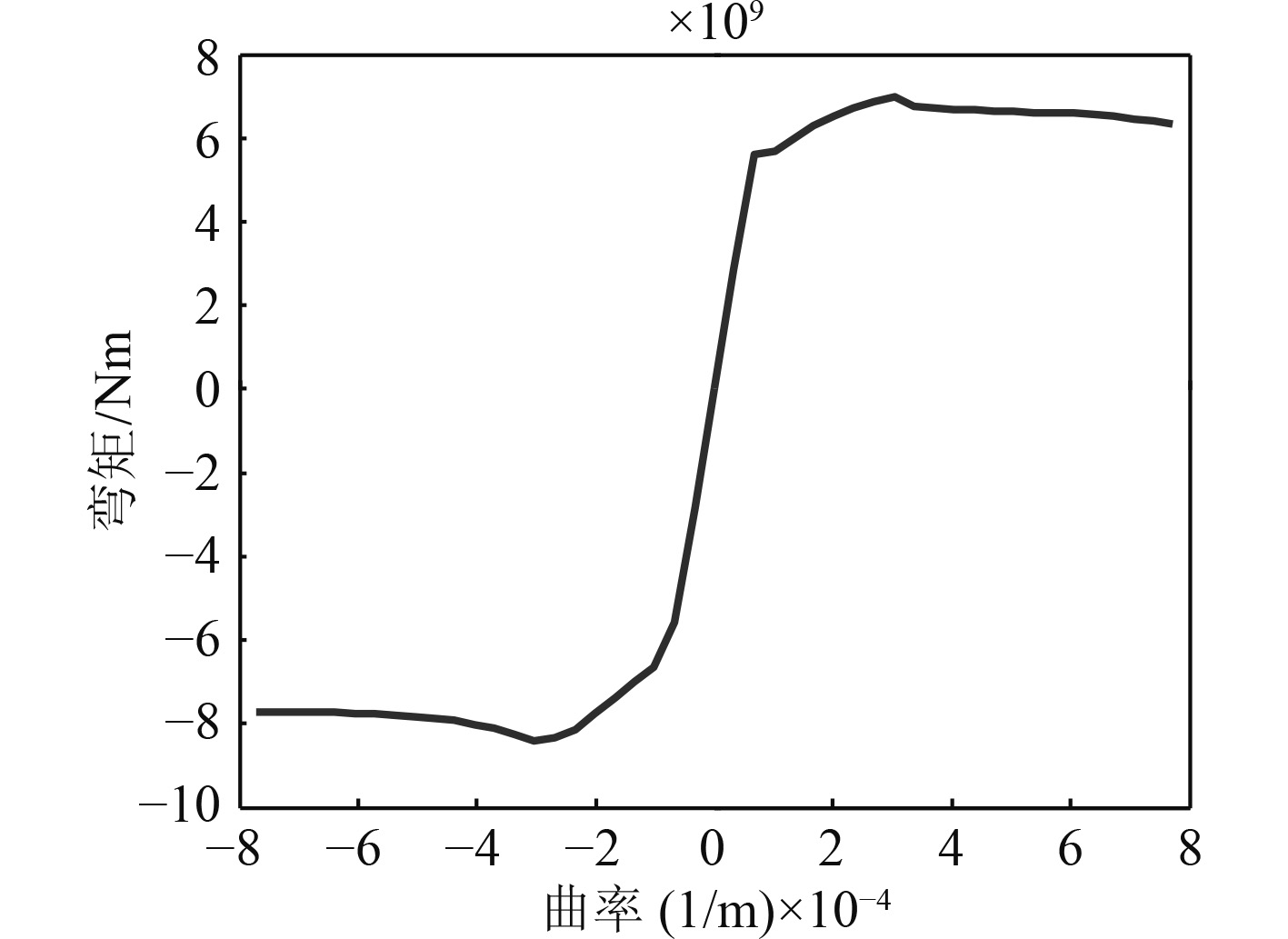
中剖面共划分了458个单元,计算得到中拱状态下的极限强度值为2.06E+10 Nm,中垂状态下的极限强度值为–2.67E+10 Nm(见图7)。第6剖面共划分了381个单元,计算得到中拱状态下的极限强度值为6.97E+09 Nm,中垂状态下的极限强度值为–8.37E+09 Nm(见图8)。中剖面中拱弯矩约为第6剖面的2.96倍,中垂弯矩约为第6剖面的3.19倍,第6剖面强度较弱。
|
图 7 超大型浮体中剖面弯矩-曲率关系 Fig. 7 Moment to curvature relationship of VLFS midship section |
|
图 8 超大型浮体第6剖面弯矩-曲率关系 Fig. 8 Moment to curvature relationship of VLFS NO.6 cross section |
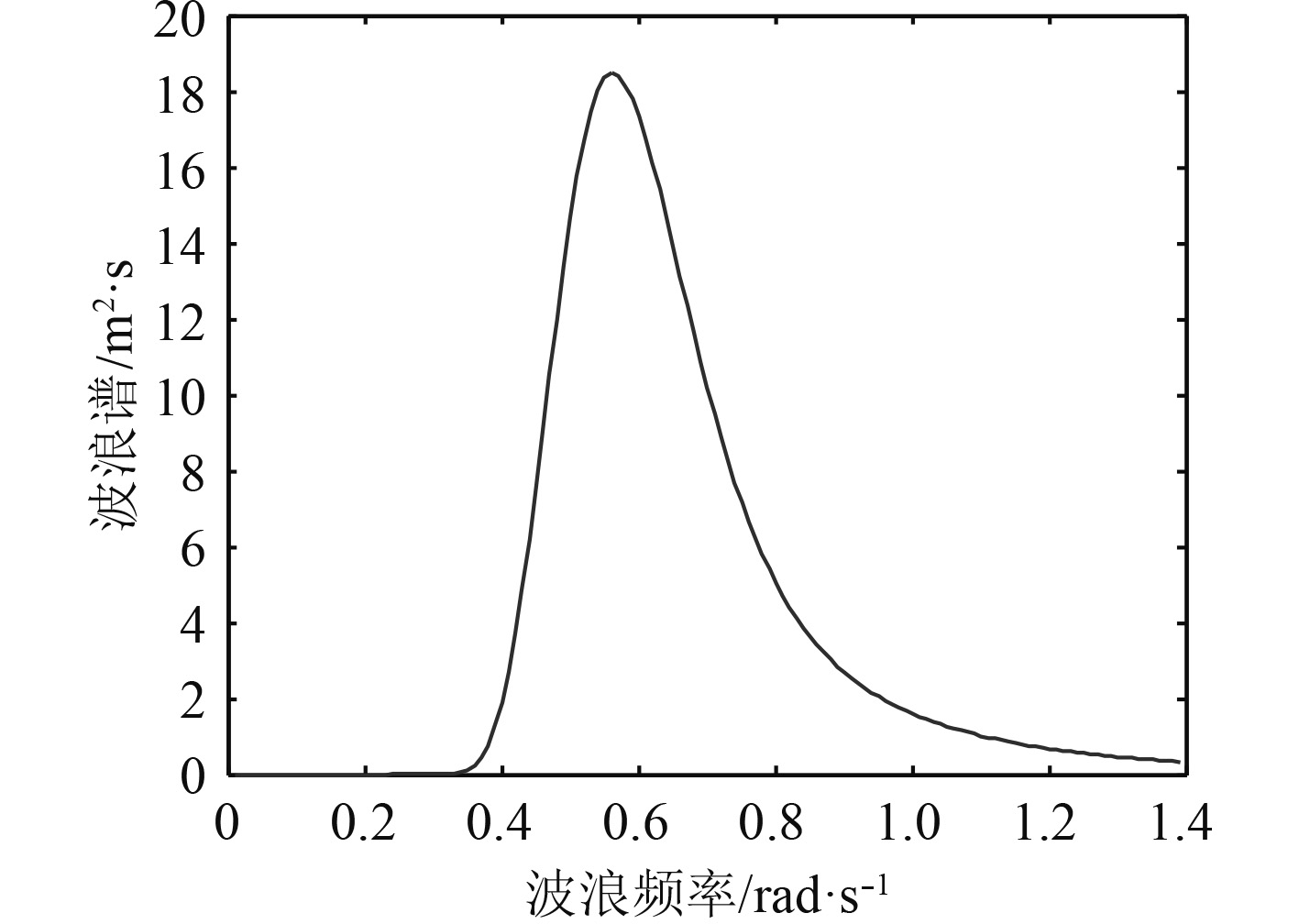
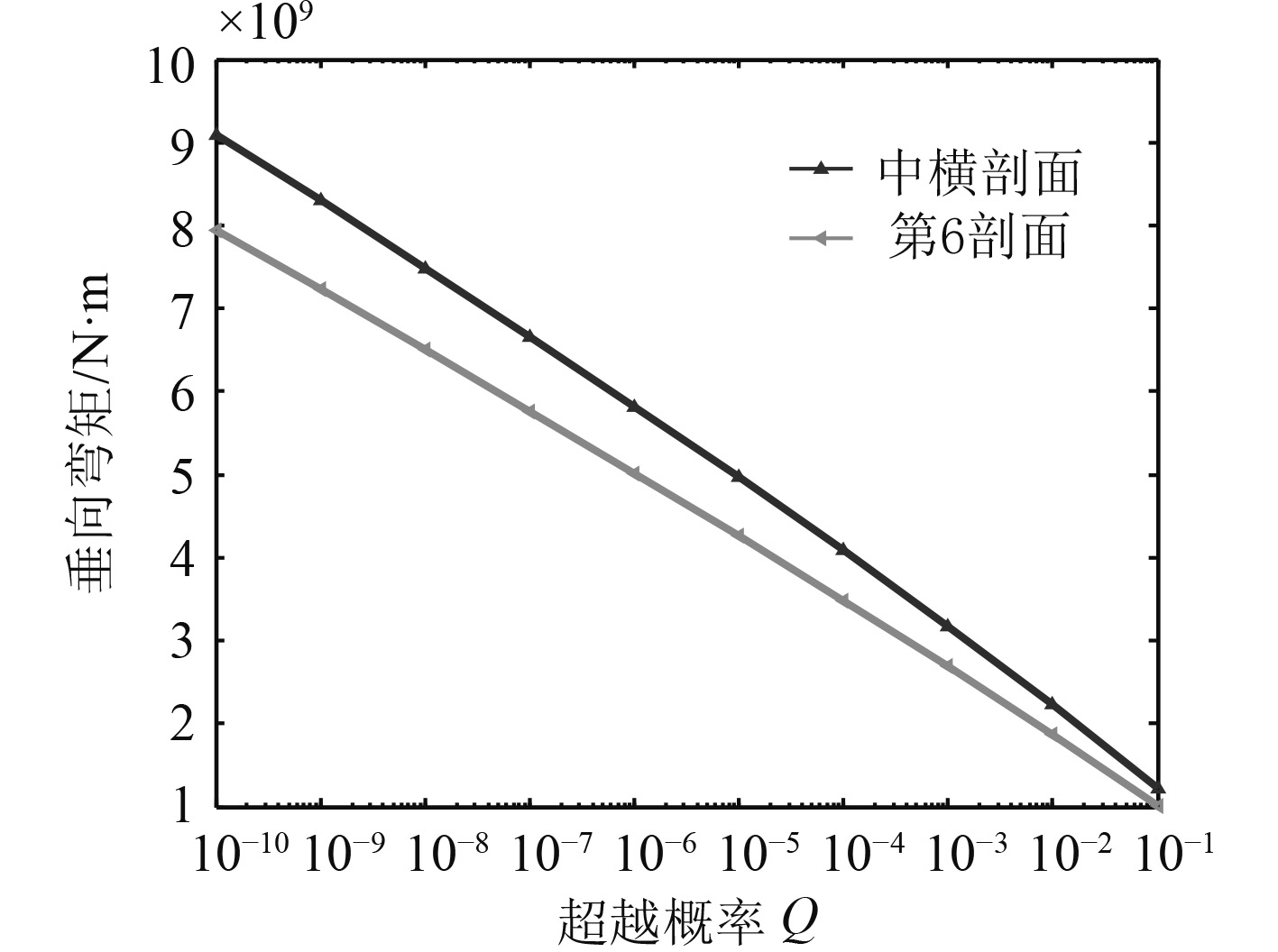
基于三维线性势流理论,利用水动力软件Ansys/AQWA在频域中计算了中剖面和第6剖面在0°,15°,30°,45°,60°,75°和90°浪向下的纵向弯矩传递函数。短期海浪谱选用Jonswap谱(见图9),谱峰提升因子取为2。采用我国南海波浪散布图作为确定波浪长期预报的海况资料,计算波高和跨零周期对应的波浪弯矩短期预报值,波浪载荷长期预报服从Weibull分布,不同超越概率下的波浪载荷长期预报值如图10所示,随着超越频率从
|
图 9 JONSWAP波浪谱(Hs=8.5,Tz=8.5) Fig. 9 JONSWAP wave spectrum (Hs=8.5,Tz=8.5) |
|
图 10 长期波浪弯矩预报结果 Fig. 10 Long-term predicted value of vertical wave moment |
由于存在材料屈服强度、板厚和弹性模量的不确定性,因此浮体结构强度的实际值与名义值不同,本文选取材料屈服应力COV=0.06,服从对数正态分布;板厚COV=0.01,服从正态分布。应用改进的Rosenbluthe方法[13]计算超大型浮体极限强度均值和变异系数,计算结果如表3所示。超大型浮体极限强度服从对数正态分布,变异系数约在0.05~0.06之间。
|
|
表 3 浮体极限强度均值、标准差和变异系数 Tab.3 Mean value, standard deviation and COV of ultimate strength |
波浪载荷极值服从Gumbel(极值I型)分布,计算得到中剖面百年一遇Gumbel分布的均值为8.18E+09 Nm,第6剖面均值为7.12E+09 Nm,变异系数取为0.08。Weibull分布和Gumbel分布概率密度函数如图11所示。

|
图 11 Weibull分布和Gumbel分布概率密度函数 Fig. 11 Weibull and Gumbel distribution probability density function |
对于静水载荷,根据装载工况计算书,超大型浮体舯剖面静水弯矩取为2.55E+07 Nm,第六剖面产生的静水弯矩为1.95E+07 Nm,服从正态分布,变异系数为0.1。
4.2 极限强度校核采用本文设定的目标可靠度合理可行范围对超大型浮体中剖面和第六剖面的极限强度进行校核,令极限强度安全裕度方程为:
| $Z(X) = {M_u} - {M_s} - {M_w}{\text{。}}$ | (15) |
式中:
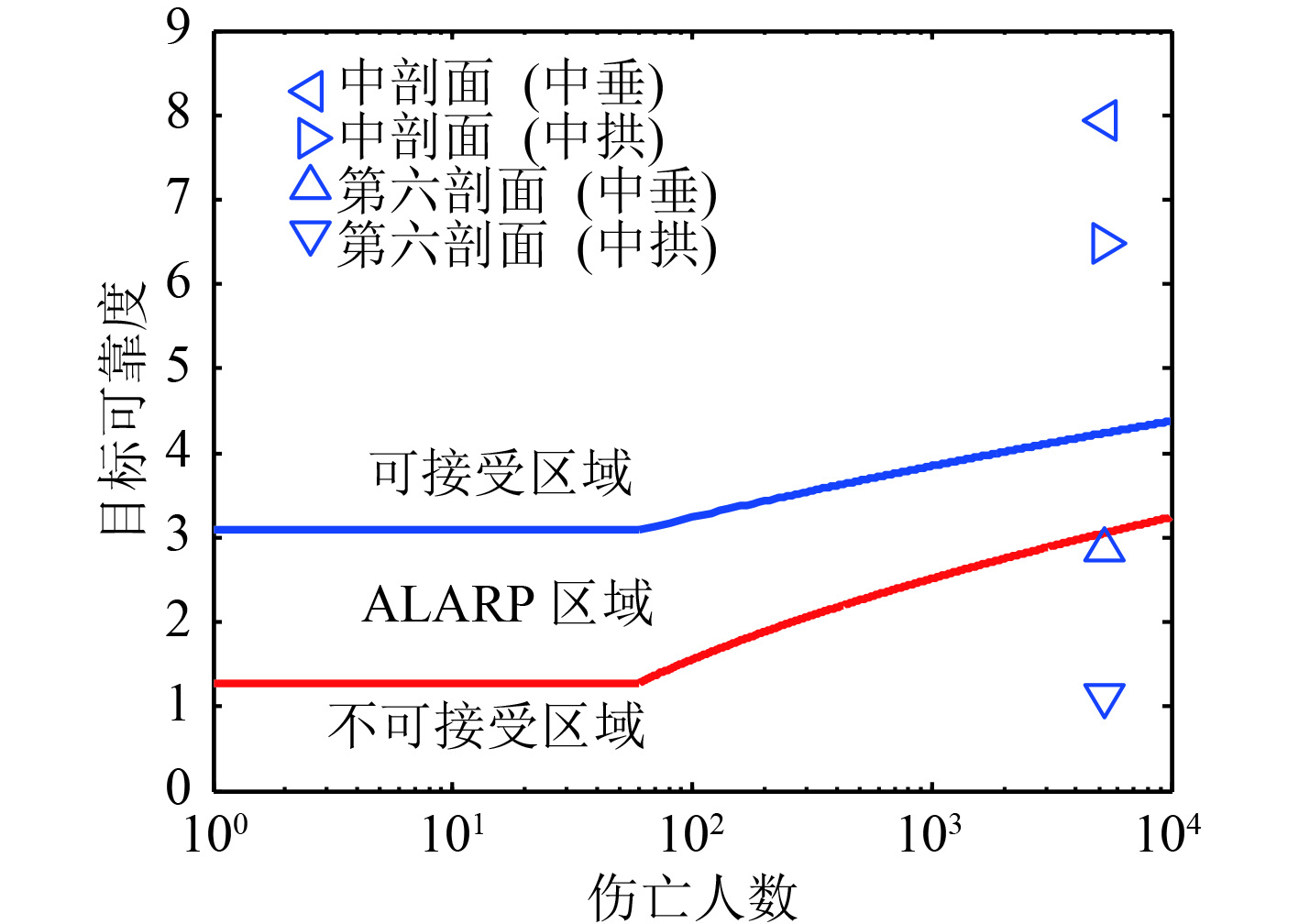
应用验算点法计算百年一遇波浪弯矩极值作用下浮体强度可靠性结果,如表4所示,与本文设定的目标可靠度合理可行范围相比较,如图12所示,可以看出,中剖面的极限强度可靠度处于可接受区域,第6剖面极限强度可靠度处于不可接受区域。可基于本文设定的目标可靠度合理可行区域进行超大型浮体第六剖面极限强度可靠性设计,进而使第六剖面极限强度可靠性满足要求。
|
|
表 4 极限强度可靠性计算结果 Tab.4 Calculation results of ultimate strength reliability |
|
图 12 百年一遇波浪载荷下浮体可靠性 Fig. 12 Reliability of VLFS under a-hundred-year return period wave load |
本文探索性地利用风险分析方法对超大型浮体结构进行了安全可靠性分析,借用其他行业风险衡准和设计原则,确定了超大型浮体的目标可靠度合理可行范围,通过对浮体总纵强度安全可靠性实例分析,得到以下结论:
1)基于风险的结构设计可合理确定超大型浮体结构安全可靠性水平,并能与其他行业风险水平相类比,可供未有直接经验借鉴的新颖结构设计参考使用。
2)在建立超大型浮体安全可靠性衡准的过程中,考虑结构失效概率并计及结构失效后果,可以给出浮体结构目标可靠度合理可行区域(ALARP),作为结构极限强度可靠性分析的判据,用于指导相关准则的编制。
3)通过对浮体典型剖面总纵强度结构可靠性分析,指出了结构设计中的薄弱环节,对指导未来工程设计具有一定的实用意义。
| [1] |
崔维成, 吴有生, 李润培. 超大型海洋浮式结构物开发过程中需要解决的关键技术问题[J]. 海洋工程, 2000, 18(3): 1-7. CUI Wei-cheng, WU You-sheng, LI Run-pei. Technical problems in the development of very large floating structures[J]. Ocean Engineering, 2000, 18(3): 1-7. DOI:10.3969/j.issn.1005-9865.2000.03.001 |
| [2] |
SADEGHI K. An overview of design, analysis, construction and installation of offshore petroleum platforms suitable for Cyprus oil gas fields[J]. Soc Appl Sci, 2007, 2(4): 1-16. |
| [3] |
Det Norske Veritas. Structural reliability analysis of marine structures[R]. Classification Notes no. 30. 6, 1992.
|
| [4] |
Construction Industry Research and Information Association. Rationalization of safety and serviceability factors in structural codes[R]. CIRIA, Report No. 63, London, 1977.
|
| [5] |
BEA RG. Reliability criteria for new and existing platforms[C]//Offshore Technology Conference, OTC6312, 1990.
|
| [6] |
HIDEYUKI S. Safety target of very large floating structure used as a floating airport[J]. Marine Structures, 2001(14): 103-113. |
| [7] |
BAIDURYA B. Developing target reliability for novel structures: the case of the Mobile Offshore Base[J]. Marine Structures, 2001(14): 37-58. |
| [8] |
Norway. Decision parameters including risk acceptance criteria[R]. IMO, MSC 72/16. 2000.
|
| [9] |
DNV and Brazil, Estimation Of Collision Probability And Frequency For Merchant Vessels At The Campos Basin Without The Restricted Zone For Navigation[R]. IMO, NAV 53/INF. 2. 2007. 02
|
| [10] |
European Maritime Safety Agency. Risk Acceptance Criteria and Risk Based Damage Stability. Final Report, part2: Formal Safety Assessment[R]. 2015.
|
| [11] |
MASAHIKO F, TAOYUN X, KAZUHIRO Y. Structural safety assessment of a pontoon-type VLFS considering damage to the breakwater[J]. J Mar Sci Technol, 2003, 7: 119-127. DOI:10.1007/s007730300002 |
| [12] |
吴东伟, 顾学康, 祁恩荣. 半潜式平台全寿命期极值载荷的确定[J]. 舰船科学技术, 2011, 33(4): 39-47. WU Dong-wei, GU Xue-kang, QI En-rong. Determination of extreme wave loads for semi-submersible during the whole life[J]. Ship Science and Technology, 2011, 33(4): 39-47. DOI:10.3404/j.issn.1672-7649.2011.04.007 |
| [13] |
崔维成, 徐向东, 邱强. 一种快速计算随机变量函数均值与标准差的新方法[J]. 船舶力学, 1998, 2(6): 50-60. CUI Wei-cheng, XU Xiang-dong, QIU Qiang. A new method for fast calculating the mean and standard deviation of random variable functions[J]. Journal of Ship Mechanics, 1998, 2(6): 50-60. |
 2018, Vol. 40
2018, Vol. 40
