海面浮体在复杂的自然环境条件下,不可避免地产生六自由度的运动,未知的浮体运动可能对海上作业造成安全隐患,所以对海面浮体的运动进行预报在工程上具有重要的意义。
海面浮体极短期运动预报是指通过建立模型,对海面浮体未来几秒到十几秒的运动进行预测的方法。根据各种方法之间的理论差异,极短期预测模型主要可以分为基于流体力学的物理模型、经典的时间序列模型和基于智能学习理论的非线性预测模型,后两者都是基于统计学理论的预测方法[1]。基于流体动力学的预测模型本质上是线性方法,适用于小振幅波浪引起的船体运动。其性能取决于线性流体动力学方程系数的计算,同时依赖于线性假设、边界条件和非线性波相互作用的简化。与之相比,统计模型具有建模相对简单并且计算量较小的优点。统计模型不需要知道海浪的任何先验信息和浮体的状态方程,仅仅利用浮体本身的历史数据寻求规律进行预报。
Wiener[2]在1949年提出平稳时间序列预报方法,Fleck & Bates等 [3 – 4]将这种方法用于研究波浪频率比较低的浮体运动。1990年,Broome[5]分别采用了AR模型和ARMA模型对浮体运动进行预报,发现可以预报横摇有效时长为7 s。彭秀艳[6]、赵希人[7]等采用AR模型,重点研究了浮体运动在线预报仿真技术及应用,可以预报7~10 s的运动时历。孙李红[8]、杨震[9]等采用支持向量机回归(SVR)方法分别对船舶横摇和纵摇运动进行预测,发现SVR方法更加灵活,但是在处理非平稳数据时仍有局限。
为了解决信号的非平稳问题,信号数据的分解处理就非常重要。在数据分解应用中,傅里叶变换、经验模态分解和小波分析是最常用的方法。黄礼敏[10]、段文洋[11]等采用复合自回归经验模态分解支持向量机回归模型(EMD-SVR)对非线性非平稳船舶运动进行了极短期预报,预测精度较高。但是经验模态分解方法常常受到边界效应的影响,傅里叶变换不能从非平稳信号中提取频率信息。
考虑到小波分解对非平稳信号分析的适应性[12]、对非平稳时间序列中趋势的分离作用及支持向量机较好的泛化能力,本文提出一种复合的小波-SVR模型,对数据的不同频域信息分别建模,而原始序列的预测结果为逼近信号和细节信号预测结果的叠加。通过对一艘钻井船在水池模型试验中运动数据的分析和预报对比,结果证明本文方法有效。
1 基本原理 1.1 小波分解小波变换是一种多尺度的信号分析方法,是分析非平稳信号的有力工具,克服了傅里叶变换没有时域局部化,以及短时傅里叶变换固定分辨率的缺陷。小波变换用一个基函数的平移和伸缩来分解二维空间的函数。设基函数满足容许条件:
| ${C_\phi } = \int {\frac{{\left| {{{\overline \phi }^2}(\omega )} \right|}}{\omega }} {\rm d}\omega < \infty {\text{,}}$ | (1) |
其中,
| $\phi (a,b) = \frac{1}{a}\phi \left(\frac{{t - b}}{a}\right){\text{,}}$ | (2) |
小波变换为:
| $Wf(a,b) = \int {f \cdot \phi (a,b)}{\rm d}t{\text{,}}$ | (3) |
其逆变换为:
| $f(t) = C_\phi ^{ - 1}\int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {\frac{{{\rm d}a{\rm d}b}}{{{a^2}}}} } Wf(a,b)\phi (a,b){\text{。}}$ | (4) |
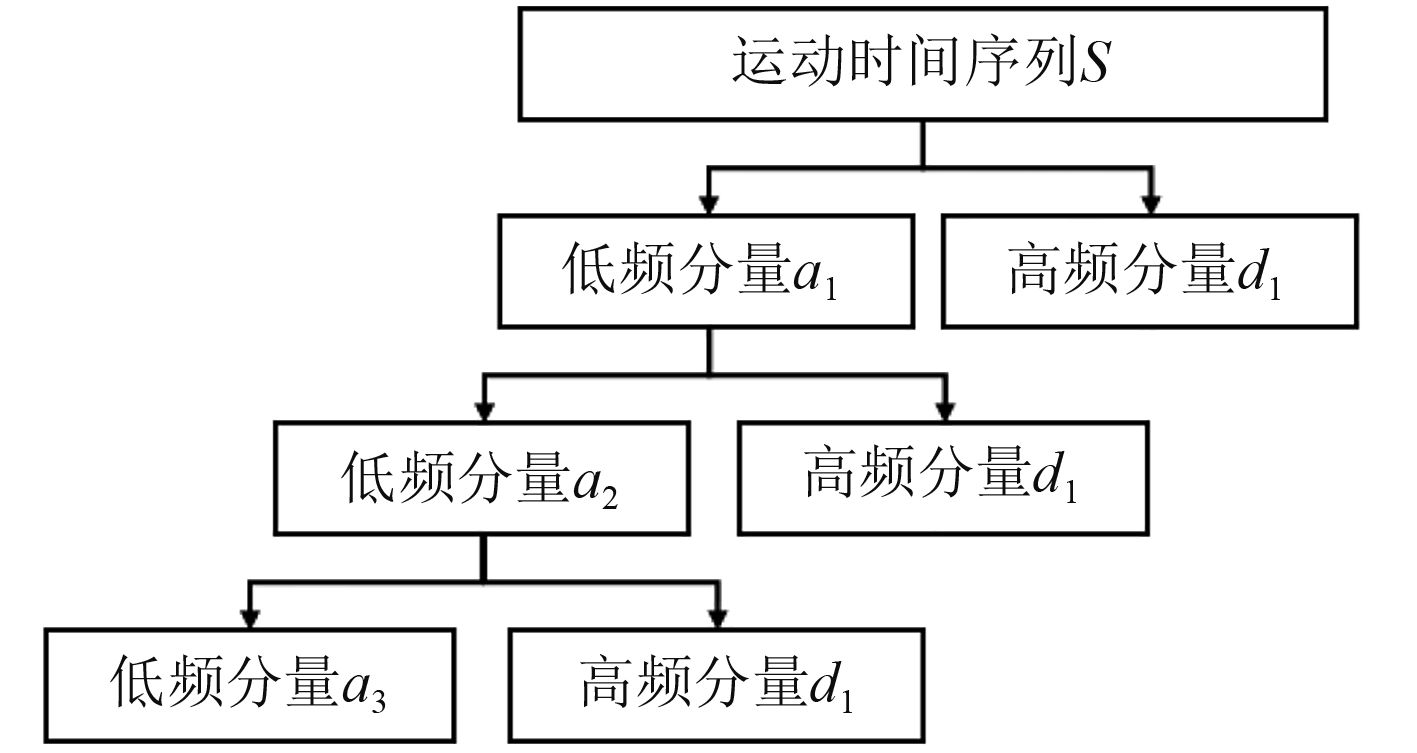
小波分解是把时间序列S分解成低频信息a1和高频信息d1两部分。在分解中,低频a1中失去的信息由高频d1捕获。在下一层分解中,又将a1分解成低频a2和高频d2两部分,低频a2中失去的信息由高频d2捕获,以此类推,可以进行更深层的分解。小波分解过程如图1所示。
|
图 1 时间序列3层小波分解过程 Fig. 1 Three-layer wavelet decomposition for time series |
支持向量机回归(SVR,Support Vector Regression)[13]方法是用基于核函数的支持向量机(SVM,Support Vector Machine)算法进行非线性回归分析的方法。其基本思想是:定义最优线性超平面,并把寻找最优线性超平面的算法归结为求解一个最优化(凸规划)问题。进而基于Mercer核展开定理,通过非线性映射,把样本空间映射到一个高维乃至于无穷维的特征空间,使在特征空间中可以应用线性学习机的方法解决样本空间中的高度非线性分类和回归等问题。简单地说就是实现升维和线性化。
对于给定的一个训练样本集T:
| $T = \{ ({x_1},{y_1}),({x_2},{y_2}), \cdots ,({x_l},{y_l})\} \in {(x \times y)_l}{\text{,}}$ | (5) |
其中
| $\begin{array}{l}\mathop {\min }\limits_{\omega ,b} \displaystyle\frac{1}{2}\left\| \omega \right\|^2,\\s.t.yi((\omega \cdot xi) + b) \geqslant 1,i = 1, \cdots ,l{\text{。}}\end{array}$ | (6) |
由最优解确定的分类面如下式:
| $(\omega * \cdot x) + b* = 0{\text{,}}$ | (7) |
决策函数
将这种方法推广到回归问题,就是所谓的支持向量机回归分析(SVR),引入损失函数,利用SRM准则构造最小化目标:
| $\begin{array}{l}\min \displaystyle\frac{1}{2}{\left\| \omega \right\|^2} + C\sum\limits_{i = 1}^m {({\xi _i} + {\xi _i}*)}{\text{,}}\\{\rm s.t.}\left\{ {\begin{array}{*{20}{c}}{{y_i} - \omega \cdot {x_i} - b \leqslant \varepsilon + {\xi _i}}{\text{,}}\\{\omega \cdot {x_i} + b - {y_i} \leqslant \varepsilon + {\xi _i}}{\text{,}}\\{{\xi _i},{\xi _i}* \geqslant 0}{\text{。}}\end{array}} \right.\end{array}$ | (8) |
最小化目标式中第1部分表示模型的结构信息,这部分越小表示回归函数越平滑,第2部分表示回归函数对于误差的惩罚。C为平衡系数,或称为惩罚参数,是对经验风险和置信范围匹配程度的度量,用于调整上述2个部分的偏重,这样可以对模型的复杂度和经验误差进行适当的调节,从而获得较好的泛化能力。
本文采用复合的小波-SVR方法进行运动预报。
首先,对原始数据进行预处理,包括去除趋势项、季节项和均值归零。然后对数据进行小波分解。这里采用的是3层小波分解,小波函数为Daubechies5小波。对分解出的所有细节信号d1,d2,d3进行整合,得到整合细节信号d。采用SVR模型分别对最低频的逼近信号a3和整合细节信号进行预测,并且对2个预测结果进行叠加,再还原趋势项和均值,得到最终的运动预测结果。
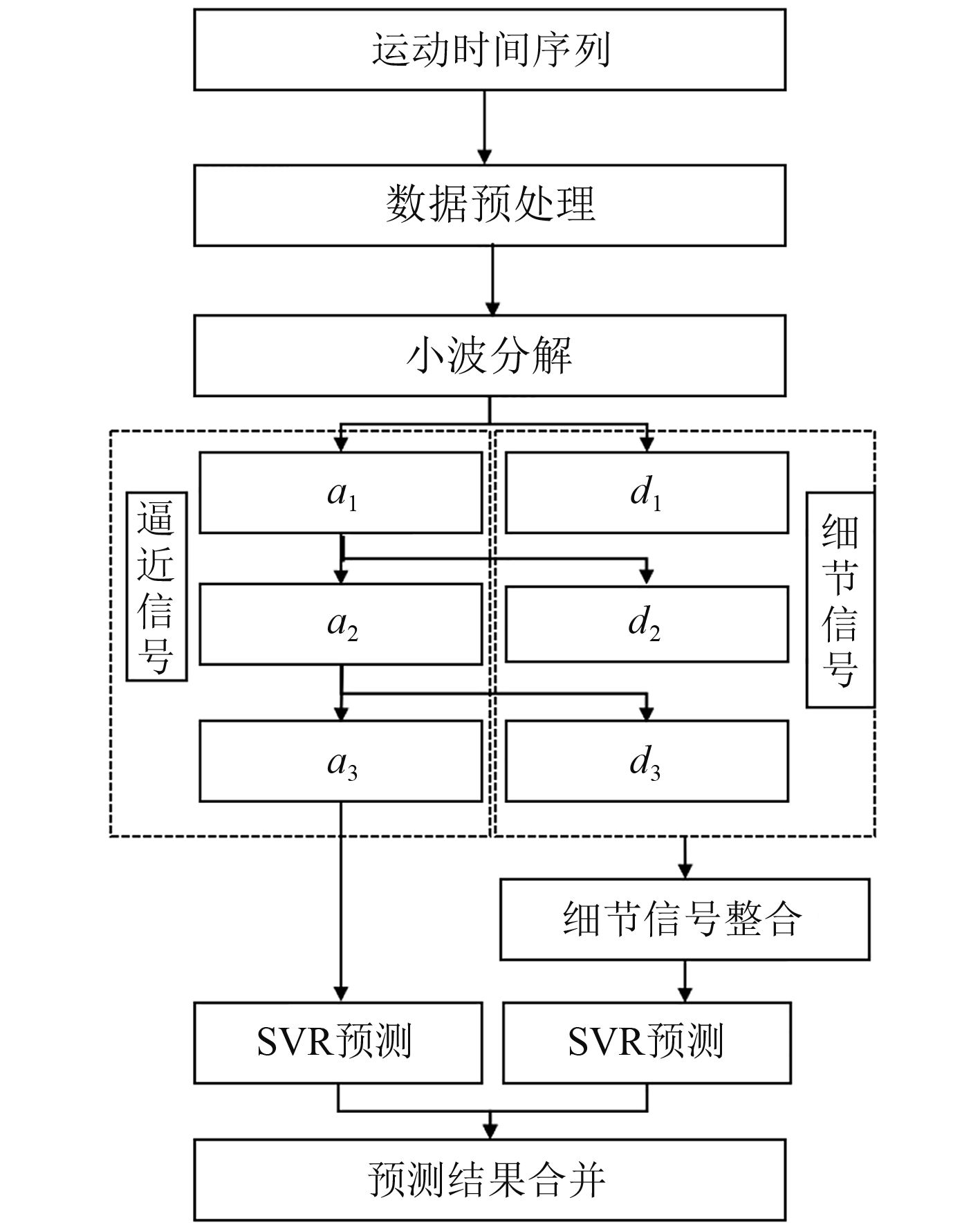
本文对浮体运动的预报方法按照图2进行。
|
图 2 复合的小波-SVR算法流程图 Fig. 2 Algorithm flowchart of the Wavelet-SVR method |
本文对同一浮体运动时间序列分别采用SVR方法和小波-SVR方法进行预测,采用均方根误差作为指标来评价模型对测试样本的预报性能。误差公式如下:
均方根误差
| ${E_{RMS}} = {\left[ {\frac{1}{n}\sum\limits_{t = 1}^n {{{(x(t) - \hat x(t))}^2}} } \right]^{1/2}}{\text{。}}$ | (9) |
本文采用水池模型试验中,某钻井船在轻载横浪条件下的垂荡运动数据进行分析。模型试验中采样频率为25 Hz,缩尺比为1:60,换算成实型采样时间间隔为0.31 s,对未来100步,即31 s进行预测。
|
|
表 1 波浪条件 Tab.1 Wave conditions |

|
图 3 半潜式平台垂荡运动时历 Fig. 3 Heave motion time series of the semi-submersible |
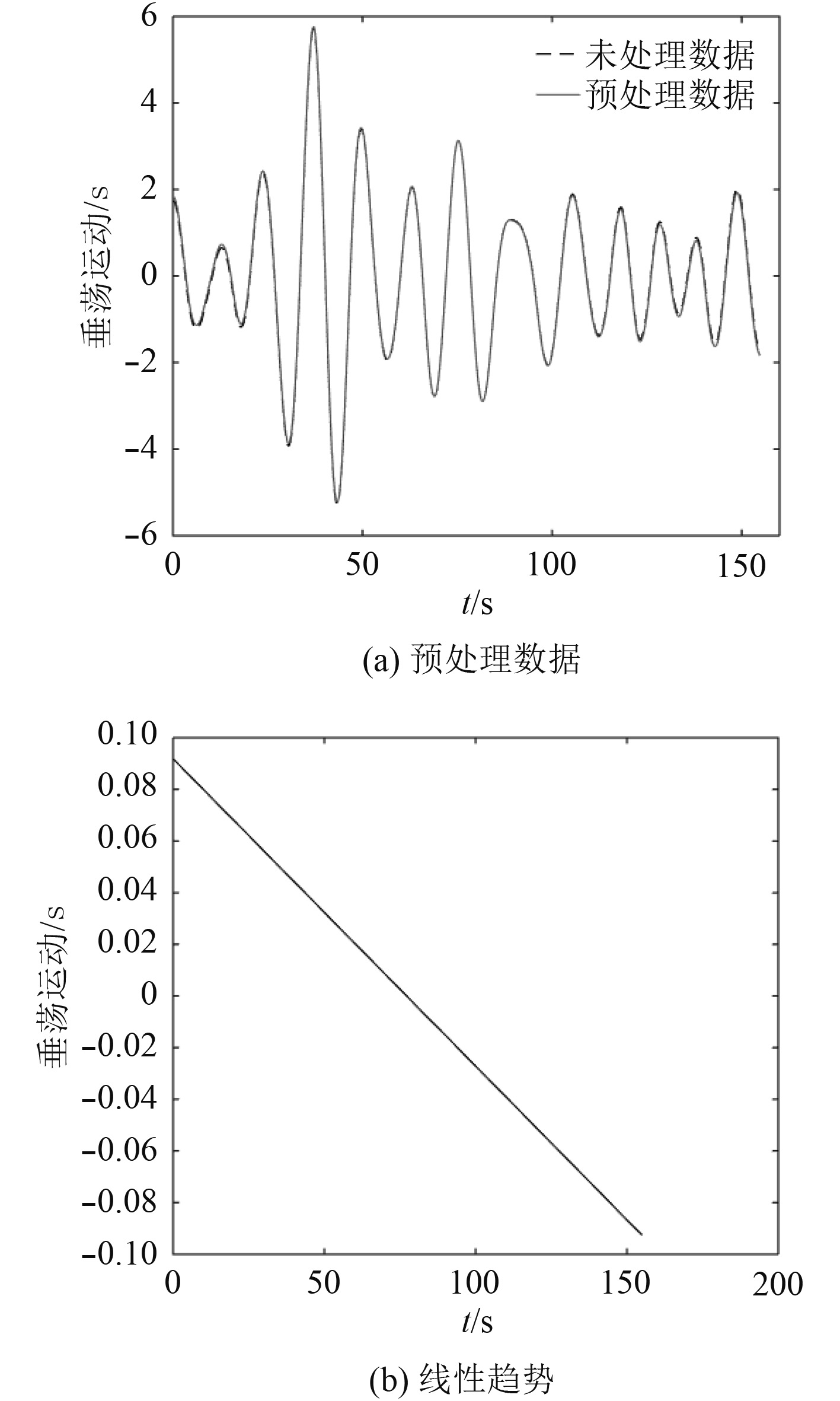
在运动时历中截取部分数据,包括400个数据点,首先对数据进行预处理,包括线性趋势和均值归零,处理结果如图4所示。
|
图 4 垂荡运动数据预处理 Fig. 4 Pretreatment of the original heave motion data |
对处理后的数据进行平稳性分析,计算自相关系数和偏相关系数,结果如图5所示。

|
图 5 原始数据自相关图和偏相关图 Fig. 5 Autocorrelation diagrams and partial correlation diagrams for the original data |
原数据的自相关系数和偏相关系数都没有很快收敛到0,所以数据包含了非平稳的信息,仅仅用SVR模型进行处理是不够的。这里对预处理后的数据进行小波分解。
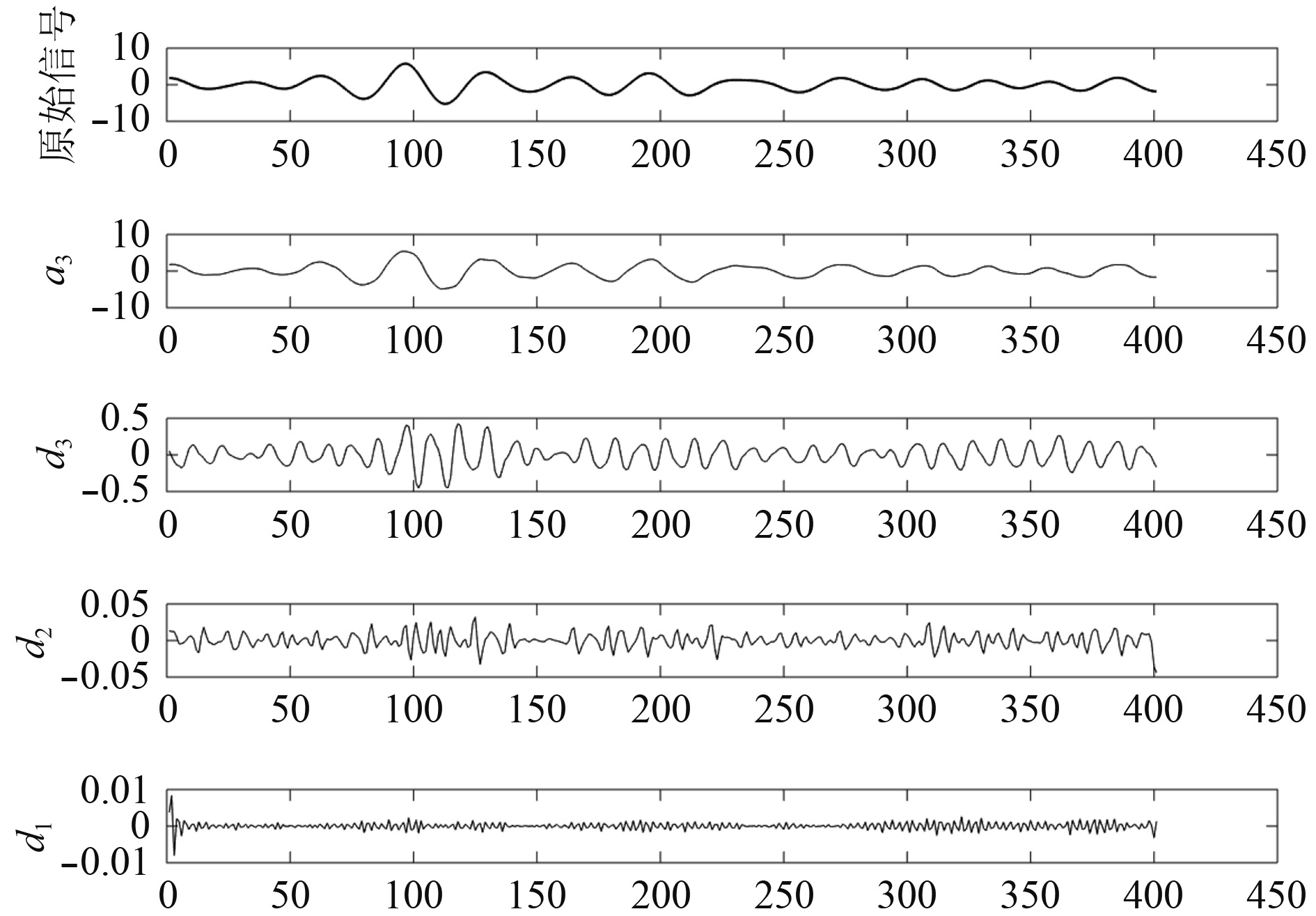
2.2 小波分解预处理后的数据包括400个数据点,在Matlab中采用db5小波对数据进行3层小波分解,分解结果如图6所示。
|
图 6 小波分解结果 Fig. 6 Decomposition results based on wavelet |
将所有的细节信号叠加在一起,得到整合细节信号d,然后采用SVR方法对d和a3分别进行SVR建模。首先设定参数范围。在SVM实现过程中,惩罚参数C和核函数g的选取直接关系最终的预测分类的准确率。目前,关于支持向量机的核函数参数的选取问题还没有一个标准的方法,常用的有实验比较法、梯度下降法、交叉验证法等。本文采取的是交叉验证法,选取前350个数据为训练集,后50个数据为验证集,设定惩罚参数C的范围为
细节信号和逼近信号的SVR预测结果如图7所示。
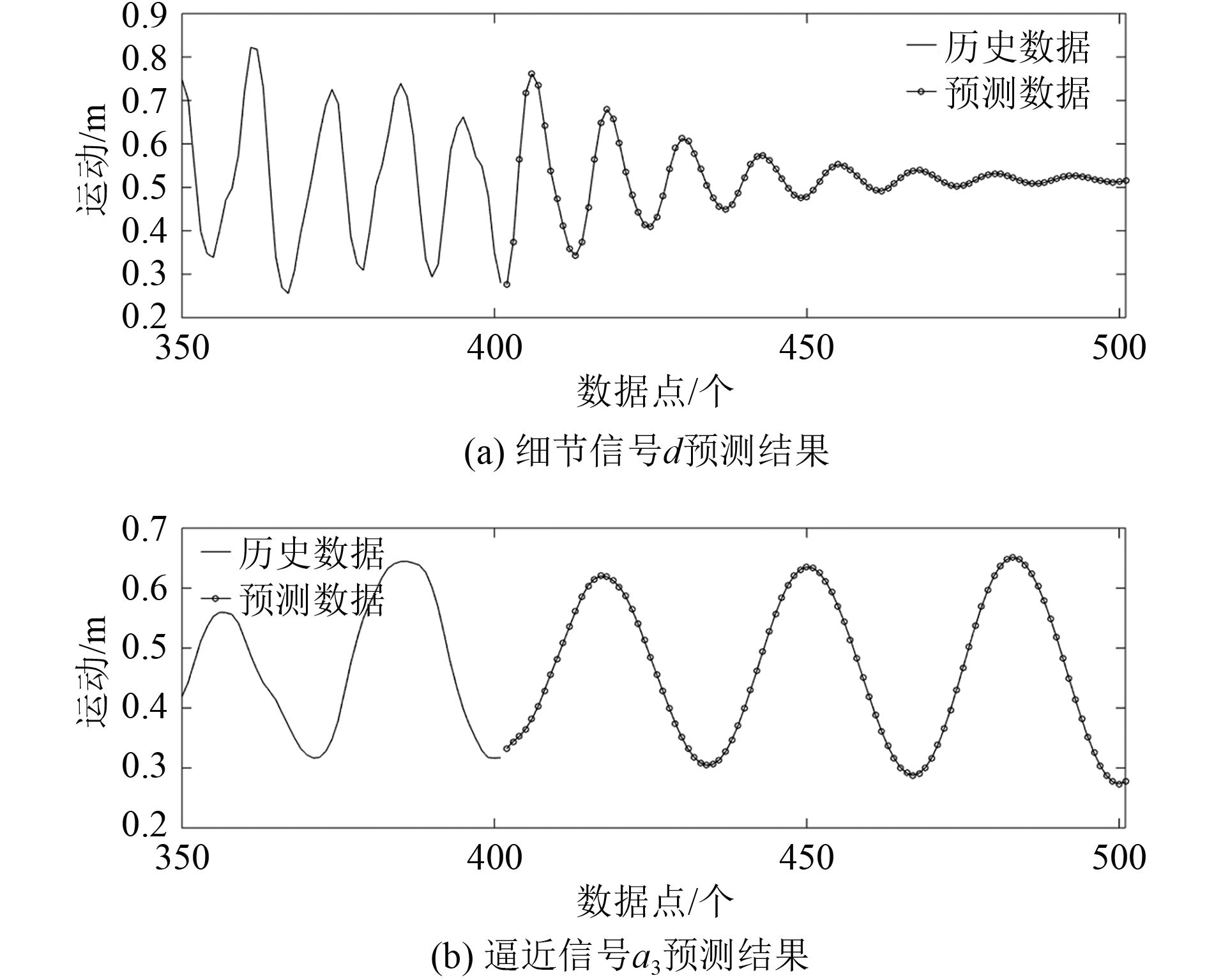
|
图 7 细节信号和逼近信号预测结果 Fig. 7 Forecast results of the detail signal and the approximation signal |
将各个部分的预测结果进行整合,对预测结果进行对比,如图8所示。
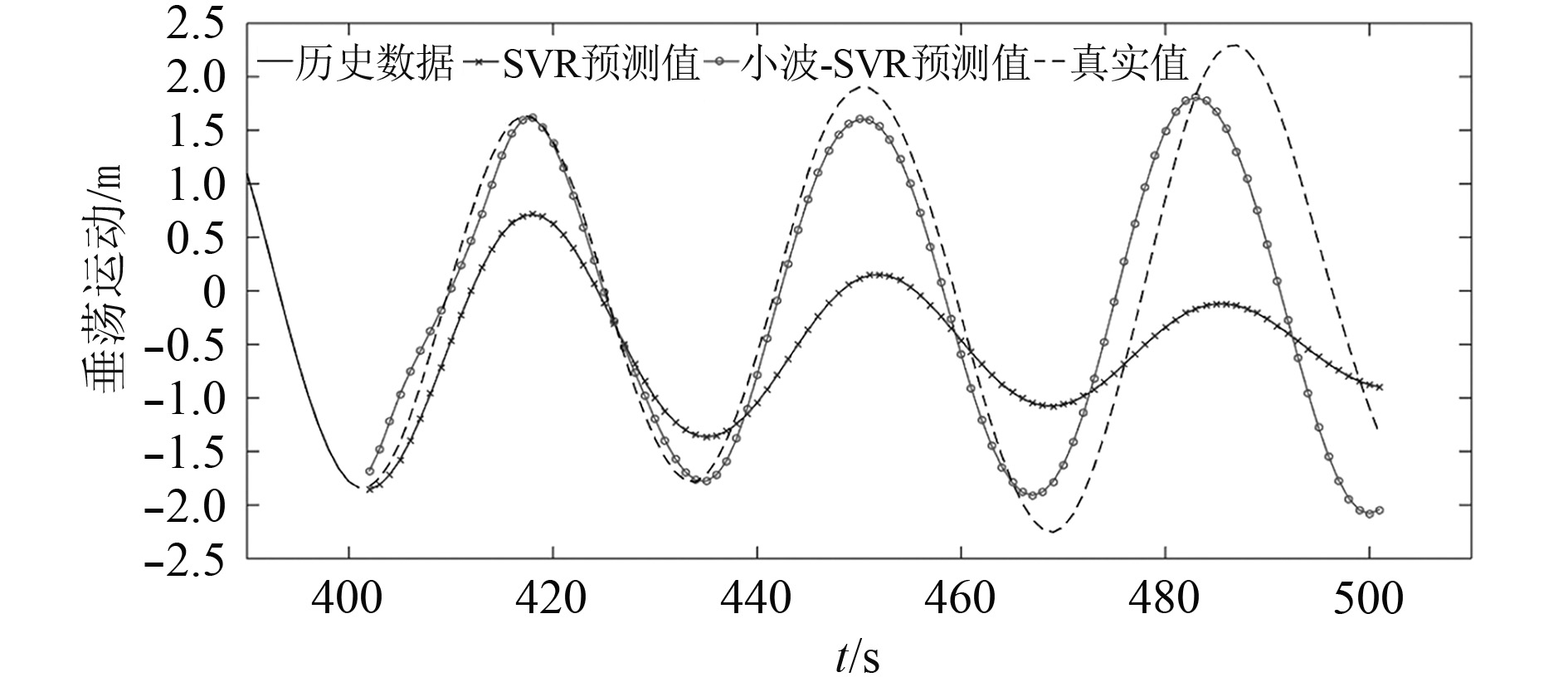
|
图 8 小波-SVR方法、SVR方法预测结果对比(预测前方100步) Fig. 8 Comparison of the forecast results used Wavelet-SVR method and SVR method respectively (100 steps ahead) |
计算不同方法的均方根误差随预测步长变化,得到如图9所示结果。
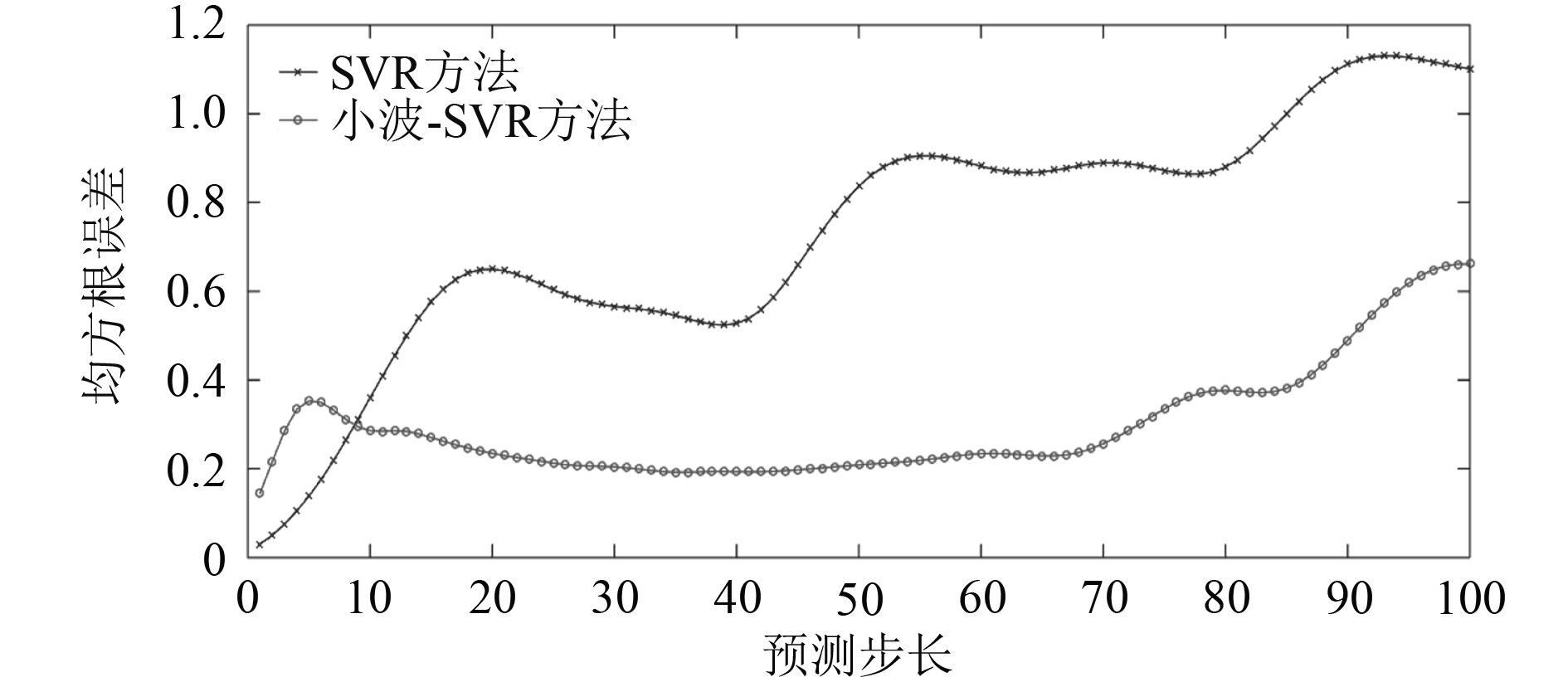
|
图 9 不同方法的均方根误差 Fig. 9 Root mean square error of different methods |
分别计算不同方法的均方根误差,结果如表2所示。
|
|
表 2 不同方法的均方根误差 Tab.2 Root mean square error of different methods |
根据表2和图9的结果,小波-SVR方法均方根误差明显小于直接使用SVR方法。SVR方法的预测误差随着预测步长的增大而迅速增加,而小波-SVR方法的预测误差在一定的预测步长内,可以控制在一定的范围,预测方法的可靠性更好。而从预测结果图形上看,小波-SVR方法虽然从第2个运动周期起,预测误差较大,幅值预测不是很准确,在预测的前10 s,已经可以达到较高的精度,所以在极短期运动预测中,小波-SVR方法可以作为非线性非平稳问题的一个很好的解决方法。
事实上,从图8结果看,结合仿真过程中的尝试,发现SVR方法预测结果幅值通常都是逐渐变小,直到达到一个稳定的值。这就是由于在SVR直接预测中,由于数据的非平稳性,包含了复杂的频域信号,模型训练过程并没有捕捉到足够的细节信息,预测的结果只能反映出低频运动的趋势,而小波分解过程很好的弥补了这一点。
3 结 语本文在SVR模型的基础上,通过小波分解方法将非线性非平稳数据分解成细节信号和逼近信号的组合,然后对不同特征的信号分别进行SVR建模预测,叠加后得到最终结果。预测结果表明,对于有一定非平稳性的数据,小波-SVR方法预测效果更好,并且该方法计算量较小,计算速度较快,适合用于工程实践。
| [1] |
HUANG L M, DUAN W Y, HAN Y, et al. A review of short-term prediction techniques for ship motions in seaway[J]. Journal of Ship Mechanics, 2014, 18(12): 1534-1542. |
| [2] |
WEINER N, EXTRAPOLATION I. Smoothing of stationary time series[J]. 1949.
|
| [3] |
FLECK J T. Short time prediction of the motion of a ship in waves[C]//Proc. Ist Conf. On Ships and Waves. 1954.
|
| [4] |
BATES M R, BOCK D H, POWELL F D. Analog computer applications in predictor design[J]. IRE Transactions on Electronic Computers, 1957(3): 143-153. |
| [5] |
BROOME D R, PITTARAS A. The time prediction of ship motions at sea[C]//Offshore Technology Conference. Offshore Technology Conference, 1990.
|
| [6] |
彭秀艳. 船舶运动姿态在线预报及仿真技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2006.
|
| [7] |
赵希人, 彭秀艳, 沈艳, 等. 舰船运动极短期建模预报的研究现状[J]. 船舶工程, 2002(3): 4-8. ZHAO Xi-ren, PENG Xiu Yan, SHEN Yan. Study status quo of extremely short-time modeling and predicting of ship motion[J]. Ship Engineering, 2002(3): 4-8. DOI:10.3969/j.issn.1000-6982.2002.03.001 |
| [8] |
孙李红. 基于组合预测方法的舰船纵摇运动预报[D]. 哈尔滨: 哈尔滨工程大学, 2009.
|
| [9] |
杨震. 大型船舶横摇运动姿态预报技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2013.
|
| [10] |
HUANG L M, DUAN W Y, HAN Y, et al. Extending the scope of AR model in forecasting non-stationary ship motion by using AR-EMD technique[J]. Journal of Ship Mechanics, 2015, 19(9): 1033-1049. |
| [11] |
DUAN W, HUANG L, HAN Y, et al. A hybrid AR-EMD-SVR model for the short-term prediction of nonlinear and non-stationary ship motion[J]. Journal of Zhejiang University SCIENCE A, 2015, 16(7): 562-576. DOI:10.1631/jzus.A1500040 |
| [12] |
李亚嘉. 小波分析在船舶测试信号中的算法研究[J]. 舰船科学技术, 2017(2): 115-117. LI Y-Jia. Research on the algorithm of wavelet analysis in ship test signal[J]. Ship Science and Technology, 2017(2): 115-117. |
| [13] |
BOSER B E, GUYON I M, VAPNIK V N. A training algorithm for optimal margin classifiers[C]//Proceedings of the Fifth Annual Workshop on Computational Learning Theory. ACM, 1992: 144–152.
|
 2018, Vol. 40
2018, Vol. 40
