Spar平台在海洋开发中的应用已经超过30多年,但在1987之前其主要是作为辅助系统使用比如浮标、海洋科研站、海上通信中转站等。Spar作为钻井平台主要有3种类型[1]:传统Spar平台(Classic Spar)、桁架式Spar平台(Truss Spar)和多柱式Spar平台(Cell Spar)。海洋平台在复杂海域进行工程作业时,在承受环境载荷的同时,还有可能与过往的船只、补给船、守卫船等船舶发生碰撞,根据WOAD数据库对海洋平台给出的严重灾害事故发生频率统计数据,无论是固定式平台还是移动式平台,船舶碰撞都是最主要的风险因素。本文以1艘5000吨级补给船以不同速度(分别为v=0.5 m/s,v=2 m/s,v=4 m/s,v=6 m/s)正碰某Truss Spar平台水面浮体部分,采用有限元软件Ansys/Ls-dyna建立Spar平台和船舶三维有限元模型,并对碰撞过程进行模拟,对碰撞过程中的能量变化、撞击力情况以及应力情况进行分析,得出一般性规律和结论,为Spar平台的设计提供理论参考依据。
1 碰撞基本理论 1.1 碰撞问题的研究方法船舶与海洋结构的碰撞是一个短暂的过程,但是却包含了复杂的非线性过程,包含材料弹塑性变形为典型特征的材料非线性和以接触摩擦为特征的状态非线性。而且,在描述碰撞的状态时,不光具有复杂的空间变量,更包含复杂的时间变量。
目前解决碰撞问题的方法主要有经典的Minorsky方法、汉斯-德鲁彻理论、各种简化解析方法、简化内部机理的数值解法、试验方法和有限方法等[2]。其中,显示动力有限元仿真方法是碰撞领域最常用的数值计算方法。显示动力学采用差分格式,不用求解切线刚度,不需要进行平衡,不存在收敛问题,并且在材料模型、接触算法、并行计算方面也具有优势。因此显示方法特别适用于求解高速动力学事件和复杂的接触问题。
1.2 碰撞运动方程的显示求解在本文所采用的Ansys/Ls-dyna软件中求解船舶与海洋平台碰撞这种具有高度非线性的动力学问题时一般采用显示求解方法,其对于碰撞运动方程的显示求解会用到有条件稳定的中心差分法,具体求解过程如下:
在总体坐标系下,如果当前时间步是步n,显式运动微分方程[3]为
| ${ M}a_n' + { C}v_n' + { K}d_n' = F_n^{ext}{\text{。}}$ | (1) |
式中:M为结构质量矩阵,C为结构阻尼矩阵,K结构刚度矩阵,
| $Ma_n' = F_n^{ext} - F_n^{in}{\text{。}}$ | (2) |
其中,
由式(2)可以得到加速度的表达方式:
| ${a_n} = {{ M}^{ - 1}}{\rm{ }}F_n^{re}{\text{。}}$ | (3) |
式中:
如果单元质量分布在节点上,则M为一对角阵,称为集中质量矩阵,线性方程组将成为一系列关于自由度的独立的一元一次方程,从而可以求得节点加速度为:
| ${a_{ni}} = F_{ni}^{re}/{M_i}{\text{。}}$ | (4) |
进而对时间进行积分即可获得速度vi和位移di。这里采用中心差分的显式格式来进行时间积分,其格式为:
| $\left\{ \begin{gathered} {v_{n + 1/2}} = {v_{n - 1/2}} + {a_n}(\Delta {t_{n + 1/2}} + \Delta {t_{n - 1/2}})/2 {\text{,}} \\ {\rm{ }}{d_{n + 1}}{\rm{ = }}{d_n}{\rm{ + }}{v_{n + 1/2}}\Delta {t_{n + 1/2}}{\rm{ }} {\text{,}}\quad\quad\quad\quad\quad\quad\;\; \\ {\rm{ }}\Delta {t_{n + 1/2}} = (\Delta {t_n} + \Delta {t_{n + 1}})/2 {\text{。}}\quad\quad\quad\quad\quad\quad \\ \end{gathered} \right.$ | (5) |
显示积分,通常情况下不需要对矩阵进行求解或分解,也不需要求解联立方程组,不存在收敛性问题,计算速度比较快,时间积分的精度保证和自动控制计算时间步长的大小,则有稳定性准则来实现。同时,在运用中心差分法求解碰撞问题时需要特别注意时间步长的选取,它不能超过临界时间步长。在实际使用中,临界时间步长一般取近似表示,即以有限单元网格的特征长度除以应力波速,其表达式为:
| $\Delta t \leqslant \Delta {t_{cr}} = \min \left( {{L^e}/c} \right){\text{。}}$ | (6) |
其中:
| $c = \sqrt {\frac{E}{\rho }}{\text{,}} $ | (7) |
| $\Delta t = \frac{l}{c}{\text{。}}$ | (8) |
由式(6)可以知道临界时间步取决于材料特性(音速)和单元长度,而Ls-dyna可以自动计算尺寸,一般不需要用户自己重新定义。
2 有限元模型单元及材料的选取 2.1 有限元模型的建立Truss Spar结构形式分为上部组块、主体硬舱、桁架结构(连接硬舱和软舱,包括垂荡板)、底部软舱、立管系统和系泊系统。平台的底部压载舱有永久的固体压载和可变压载2部分,固体压载用以提升稳定性,而可变压载能够注入海水以便在安装和作业中调节稳性。平台及碰撞船的相关参数如表1所示。
|
|
表 1 Truss Spar主要参数 Tab.1 Main parameters of the Truss Spar platform |
在建立碰撞船模型时,为减少建模工作量节省计算时间,有必要对模型进行一定的简化。本文中平台上层建筑以质量块形式添加,未考虑立管系统和系泊系统。同时,由于主要考虑平台的受力及变形,对于船舶形状也采取了一定的简化,碰撞有限元模型如图1所示。

|
图 1 Truss Spar平台碰撞有限元模型 Fig. 1 Finite element model of ship collision with Truss Spar platform |
在船舶与海洋平台的碰撞中,平台和船舶均会发生一定的塑性变形,因此对于平台采取随动塑性材料模型[4](Plastic kinematics model),该模型是各向同性、随动硬化或各向同性和随动硬化的混合模型,且与应变率相关,能够很好地模拟结构在碰撞中的塑性变形。具体参数如表2所示。
|
|
表 2 平台材料模型主要参数 Tab.2 The main parameters of the material model platform |
此外,在碰撞中船舶的变形主要发生在碰撞体接触的船首部区域,船中后部区域不会发生变形,仅提供刚度和质量的影响[5]。因此,在建模时仅建立船体靠船首的部分船体,船首采用随动塑性材料,其余部分采用刚体材料,材料参数如表3所示。
|
|
表 3 船舶材料参数设置 Tab.3 The main parameters of the material model ship |
在碰撞仿真中需要给模型施加一定的边界条件,以防止在碰撞中发生刚体位移。位移边界条件具体施加情况为:在硬舱浮筒底部平面上选取3个不共线的节点施加位移约束[6],每个节点施加位移边界条件(假设3个节点分别为节点1、节点2和节点3,那么边界条件为:在节点1约束x方向位移,节点2的x、y方向位移,节点3的x、y、z方向位移)。同时,在碰撞过程中流体的影响也不可以忽略。目前对于碰撞过程中流体的处理主要有流固耦合和附加水质量2种方法,本文选取附加水质量法来对流体进行处理。其原因在于附加水质量结果和流固耦合结果相差不大(最大误差不超过10%),计算时间仅为流固耦合的2%[7]。
3 碰撞仿真结果及分析 3.1 碰撞过程中能量的分析为研究碰撞中能量的变化,将平台和碰撞船舶视为一个完整的系统,选取碰撞速度v=2 m/s进行分析,碰撞过程中系统各能量变化如图2所示。

|
图 2 速度v=2 m/s时的能量转化曲线 Fig. 2 The energy conversion curve at velocity v = 2 m/s |
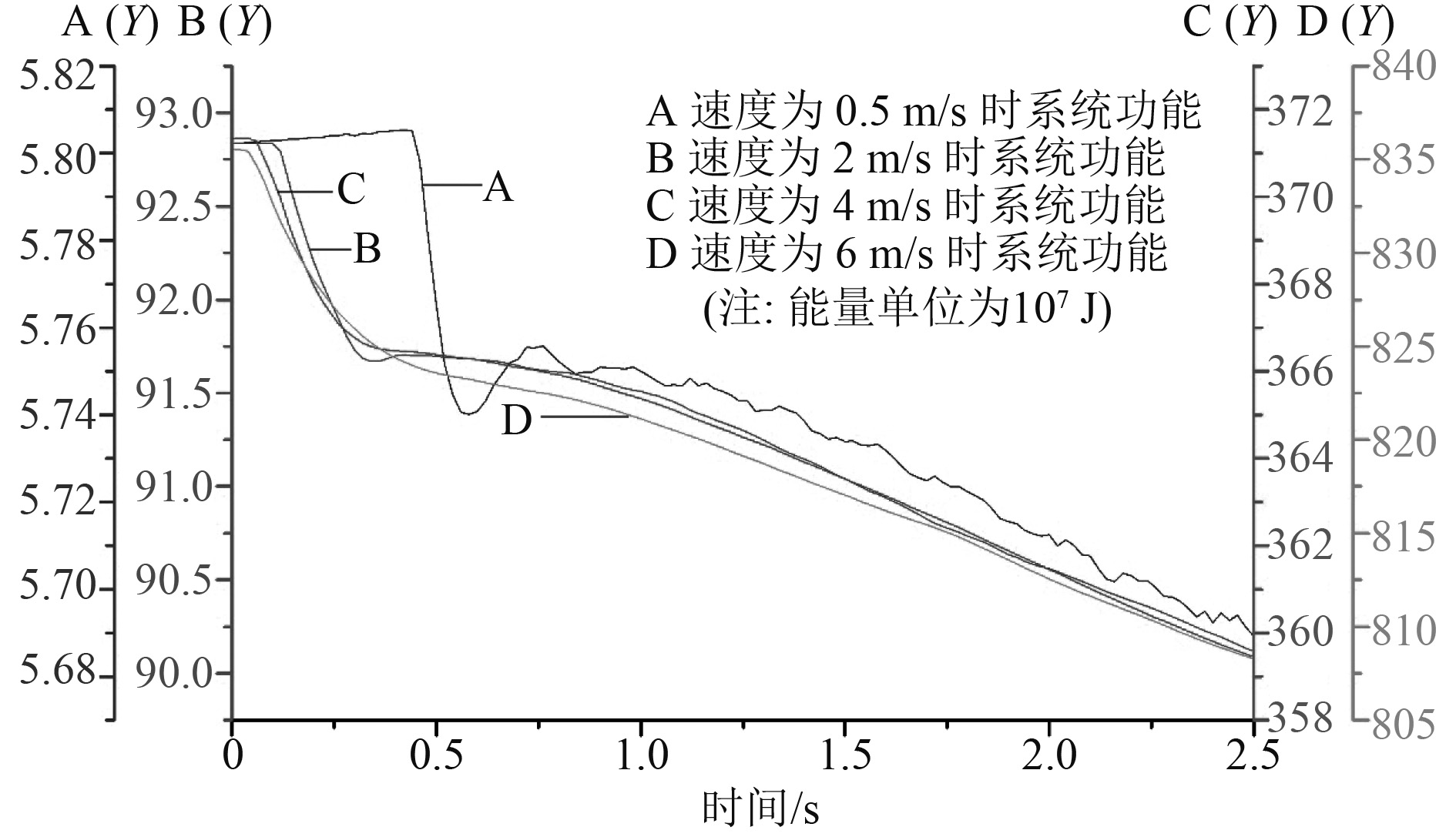
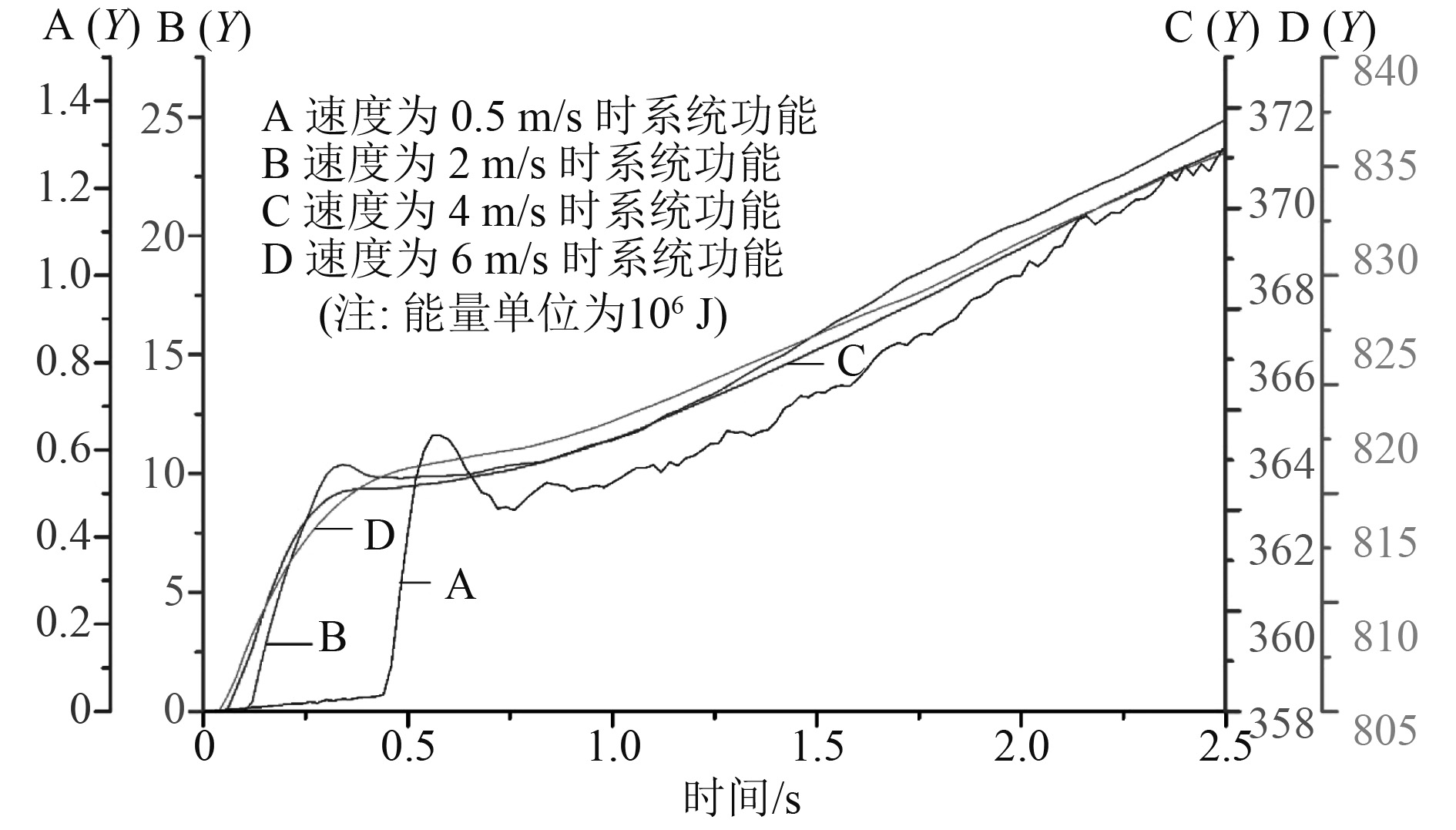
由图2可以得到在整个碰撞过程中,系统的动能在不断减小,内能、沙漏能和摩擦能在不断增加,即系统动能转化为内能,同时产生了少量的沙漏能和滑移能。结合4条曲线变化的趋势可以知道,系统中一部分能量减少,另一部分能量增加,总的能量变化是遵循能量守恒定律的。而从数值上看,系统中动能占主要部分最大时达到了9.28E+08J,其次是内能最大值达到了2.49E+07J,而沙漏能和滑移能相对较少,这说明当船舶撞击Truss Spar平台时,系统中能量的转化主要发生在动能和内能之间发生,为此在研究不同船舶速度撞击平台中的能量变化时可以将精力集中在动能和内能。
图3和图4分别为船舶以不同速度(分别为v=0.5 m/s,v=2 m/s,v=4 m/s,v=6 m/s)撞击Truss Spar平台碰撞系统内动能和内能的变化曲线。由图3可知,在碰撞中速度越大系统动能越大,而在碰撞过程中,不同速度下系统动能都逐渐减少。从曲线变化趋势来看,除了速度在0.5 m/s时系统动能曲线变化趋势略有不同,其他速度下(v=2 m/s,4 m/s,6 m/s)大致相同,在碰撞初期动能急速降低,在运动相对稳定后,降低速度变缓。同样,由图4可知,在碰撞中速度越大系统内能越大,在整个碰撞过程中,系统内能都增加,其增加的速度在碰撞初期较大,随后一段时间内相对平缓,随后将保持在一定的增长速度不变。结合图3和图4来看,在同一速度下随着系统动能的减少,系统内能在不断增加,这在一定程度上印证了上文的结论。
|
图 3 不同速度下系统动能变化曲线 Fig. 3 System kinetic energy curve at different speeds |
|
图 4 不同速度下系统内能变化曲线 Fig. 4 Variation curve of system energy at different speeds |
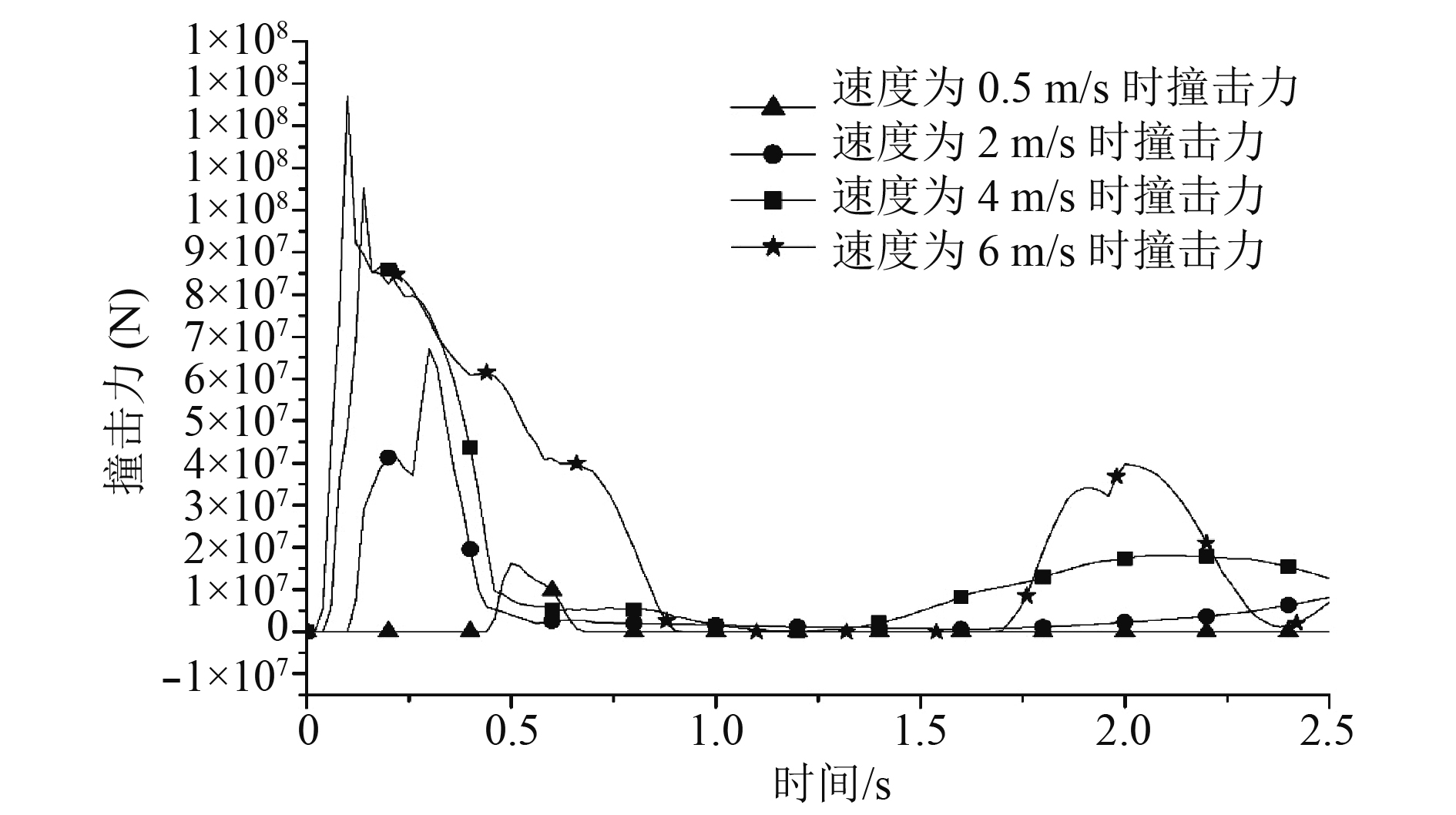
船舶以不同速度(分别为v=0.5 m/s,v=2 m/s,v=4 m/s,v=6 m/s)撞击Truss Spar平台过程中的撞击力时间历程曲线如图5所示。撞击力在一定程度上反映了平台在遭受船舶碰撞时结构受损程度,对碰撞中撞击力时间历程曲线的分析有助于更好地认识在碰撞过程中平台的运动情况。
|
图 5 不同速度下撞击力时程曲线 Fig. 5 Time-course curve of impact force at different speeds |
由图5可以得到,当速度为0.5 m/s时,船舶低速运动一段时间,此时碰撞力为0,在发生碰撞的一瞬间碰撞力达到最大,同时构件发生变形以卸载部分撞击力直至船舶与平台分离,碰撞力再次降为0,碰撞持续时间较短;当速度为2 m/s时,在碰撞船舶运行极短的时间内即发生碰撞,此时碰撞力急剧攀升但未达到最大值,同时结构发生变形卸载部分撞击力,在外围结构变形结束后,碰撞波及平台整体,碰撞力达到最大值,随着运动继续船舶与平台仍会分离,碰撞力趋近与0;当速度为4 m/s和6 m/s时,船舶运动速度相对较大,在碰撞的瞬间撞击力急剧增至最大值,随后结构多次变形,撞击力逐渐减小,在平台和碰撞船分离后为0。但是由于浮动式平台结构柔性较大,在碰撞后会发生回弹,与撞击船舶发生二次碰撞,所以撞击力在归零后又会上升。从数值上看,在速度增大后撞击力也随之增大,而且曲线峰值(即最大撞击力)出现的时间也越来越早(见表4)。总体来看,不同速度下的撞击力时程曲线变化趋势大致相同。
|
|
表 4 不同速度下撞击力最大值及出现时间 Tab.4 The maximum impact force and time of occurrence at different speeds |
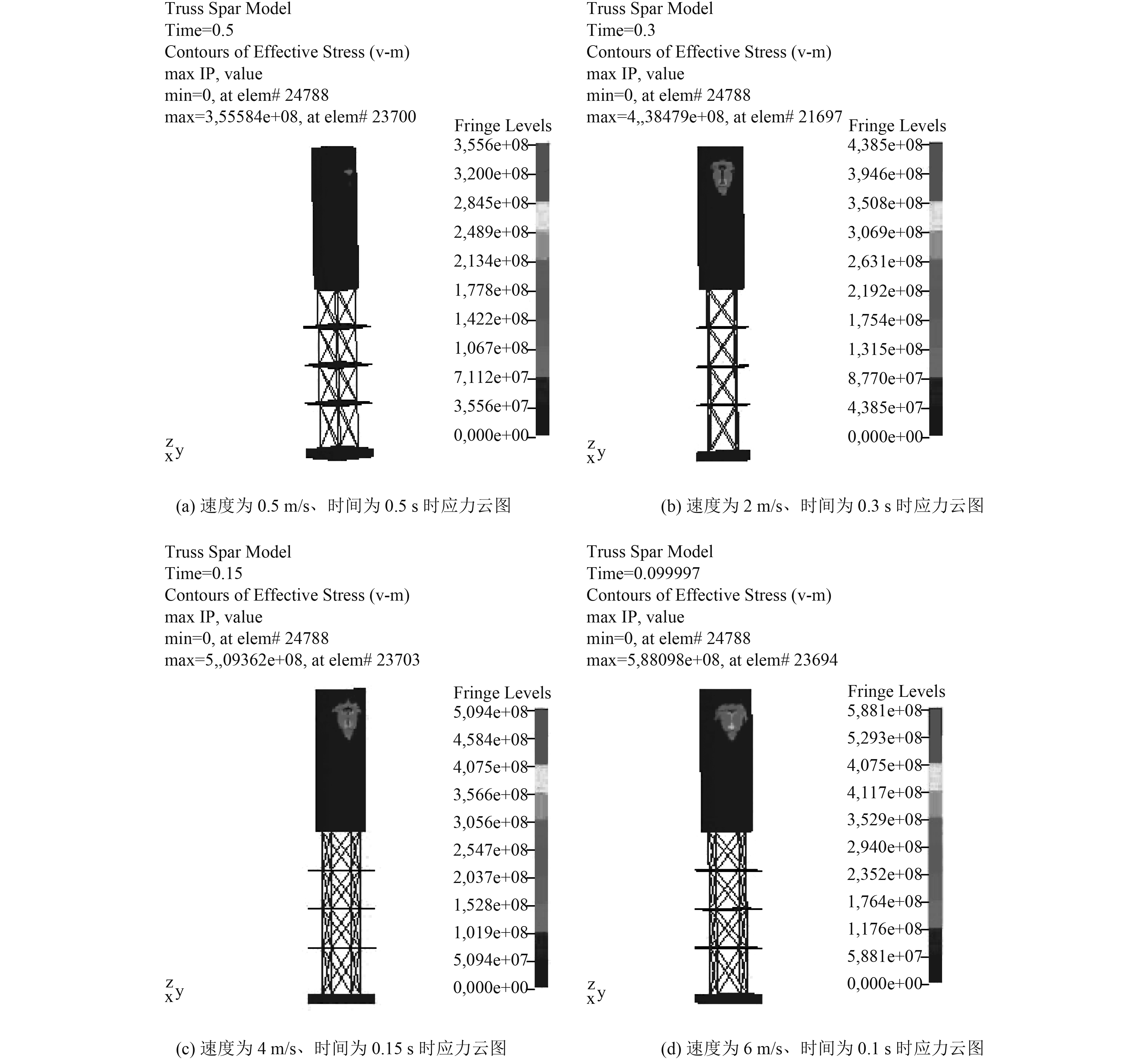
船舶与海洋平台发生碰撞时,巨大的撞击力会使结构产生很高的应力。图6为船舶以0.5 m/s,2 m/s ,4 m/s,6 m/s速度撞击Truss Spar平台结构撞击力达到最大时的应力云图。
|
图 6 不同速度下撞击力达到最大时应力云图 Fig. 6 The stress nephogram at the maximum impact force under different speeds |
由图6可知,随着撞击船舶速度的增大,平台结构产生的高应力的区域也越来越大,同时在撞击接触区域产生的应力也越来越大。但是,当平台结构遭受的船舶撞击力达到最大时,所对应时刻的应力并不一定最大,这可以从结构应力时程曲线得到验证。
结合表4和图7可知,最大应力值不一定在最大撞击力出现的时候出现,在撞击力达到最大后的运动中结构仍会产生较高的应力。从数值来看,随着速度的增大,应力值明显增大,而且除了碰撞速度为0.5 m/s的曲线图外,其余曲线中应力都在极短时间内超出钢材屈服极限。而在曲线变化趋势上,不同速度下应力变化趋势大致相同,都是在碰撞瞬间应力急剧增加,随后应力开始下降,最终上升一段时间后稳定在一定数值。这其中碰撞速度为0.5 m/s的应力曲线变化较为明显,其原因是船舶速度较低在碰撞后船舶与平台在较短时间内分离,应力下降较快,而后平台因获得速度继续运动,结构之间因位移导致应力又开始增大并最终稳定在一定数值。

|
图 7 不同速度下的应力时程图 Fig. 7 Stress time histogram at different speeds |
本文以1艘5 000吨级补给船以不同速度(分别为v=0.5 m/s,v=2 m/s,v=4 m/s,v=6 m/s)正碰某Truss Spar平台水面浮体部分进行数值仿真模拟,通过对仿真结果的分析可以得到如下结论:
1)船舶与海洋平台的碰撞是一个瞬态过程,在碰撞过程中能量转化主要发生在动能和内能之间,同时伴随有沙漏能和滑移能的产生。不同撞击速度对碰撞响应的影响趋势大致一致,随着碰撞速度的增大,能量变化和结构损伤更大。
2)在对撞击力的分析中可以知道,撞击力时程曲线具有很强的非线性特性。在比较不同撞击速度下的撞击力时程曲线时得到,不同速度下的撞击力时程曲线变化趋势大致相同,随着速度的增加撞击力也在不断增加且最大撞击力出现的时间也随着速度的增大出现的时间越来越早。
3)结合应力云图和不同速度下的应力时程曲线可以知道,随着撞击速度的增大,平台结构产生高应力的区域也随之增大,接触区域平台应力也会增大。同时通过应力云图可以得到,应力主要产生在船舶与海洋平台发生碰撞的部位,在碰撞结束后,平台结构会有一定的损坏,因此对于相应的位置在设计以及作业中必须考虑做对应的防撞措施,例如设置缓冲材料或配备守护船等。
| [1] |
张帆, 杨建民, 李润培. Spar平台的发展趋势及其关键技术[J]. 中国海洋平台, 2005, 20(2): 6-11. DOI:10.3969/j.issn.1001-4500.2005.02.002 |
| [2] |
张文明, 王涛, 张华兵, 等. 基于ANSYS/LD-DYNA的船桥碰撞分析[J]. 中国水运, 2006(11): 21-23. |
| [3] |
MSC/DYTRAN USER`S MANUAL. Vsersion 4, 1997.
|
| [4] |
郝好山, 胡仁喜, 康士廷, 等. ANSYS 12.0 LS-DYNA非线性有限元分析从入门到精通[M]. 北京: 机械工业出版社, 2010: 39–46.
|
| [5] |
段金刚. 船舶在失控状态下撞击高桩码头结构的动力响应研究[D]. 镇江: 江苏科技大学, 2015.
|
| [6] |
智广信. 船舶与浮式海洋平台碰撞的动力响应研究[D]. 镇江: 江苏科技大学, 2015.
|
| [7] |
王自力, 蒋志勇, 顾永宁. 船舶碰撞数值仿真的附加质量模型[J]. 爆炸与冲击, 2002, 22(4): 321-326. DOI:10.3321/j.issn:1001-1455.2002.04.006 |
 2018, Vol. 40
2018, Vol. 40
