2. 华中科技大学 能源与动力工程学院,湖北 武汉 430074
2. School of Energy and Power Engineering, Huazhong University of Science and Technology, Wuhan 430074, China
大功率全回转推进器是现代海洋动力定位系统中的重要装备,高性能动力定位系统是大型海洋平台在复杂海况下确保其工作稳定性及实现精确定位的关键。海洋工况十分复杂,海水腐蚀以及风、浪、流等恶劣环境因素对大功率全回转推进器服役性能提出了极高要求。由于我国对大功率推进系统的研制起步较晚,西方国家又一直对这方面的生产技术实行严密封锁。因此,我国目前尚不具备超过3 500 kW大功率级别推进器的制造能力[1]。
推进器服役性能主要包括水动力学性能、可靠性及疲劳寿命等。而水动力学性能是其中最重要的指标,直接影响着推进器其余性能指标。因此,开展大功率全回转推进器水动力学性能研究对保证全回转推进器的服役性能具有非常重要的意义。
1 推进器水动力学性能研究 1.1 几何建模本文以中船重工集团第702研究所设计的某型大功率全回转推进器为研究对象开展相关研究工作。该型推进器结构组成主要包括立柱、导管、螺旋桨以及桨毂等部件,各零部件之间主要以过盈配合、螺纹连接等方式进行装配。在不影响水动力学计算精度的前提下,建立该型全回转推进器三维简化模型,如图1所示。其主要结构参数见表1。

|
图 1 全回转推进器三维简化模型 Fig. 1 3D simplified model of azimuth propulsor |
|
|
表 1 推进器结构参数 Tab.1 Geometric dimension of propulsor |
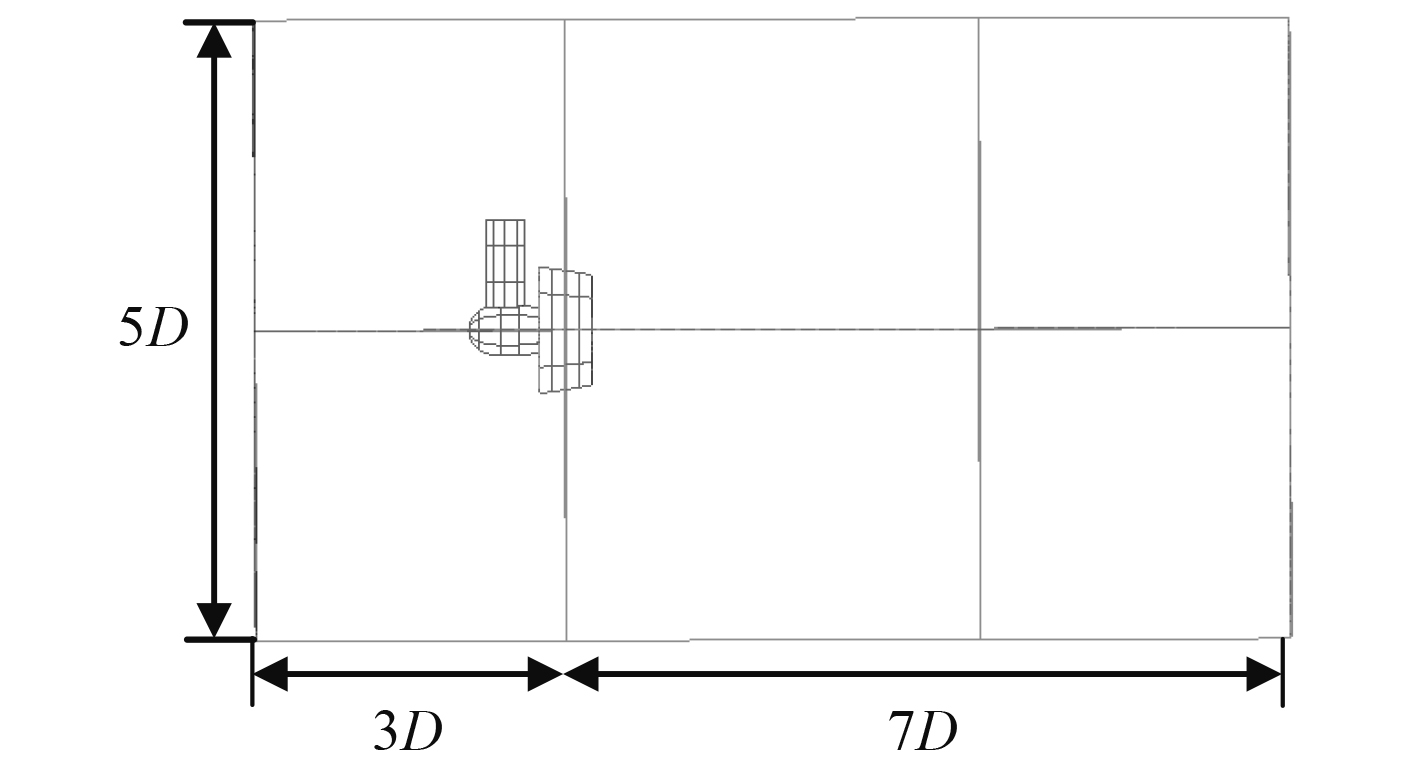
为提高计算精度,减小计算域边界对计算结果的干扰,将计算域设为一长度为10 D、直径为5 D的圆柱体区域,D为螺旋桨直径。为保证螺旋桨尾流可以自由流动,桨叶中心到入口面距离定为3 D,到出口面距离定为7 D[2],如图2所示。
|
图 2 计算域模型 Fig. 2 Computational domain |
计算域模型采用多参考坐标系(MRF)方式建立,即将计算域划分为外部静止域及内部旋转域2部分。静止域包括立柱和导管等部件[3]。旋转域包括螺旋桨及桨毂,并通过螺旋桨坐标系旋转来模拟螺旋桨的旋转。
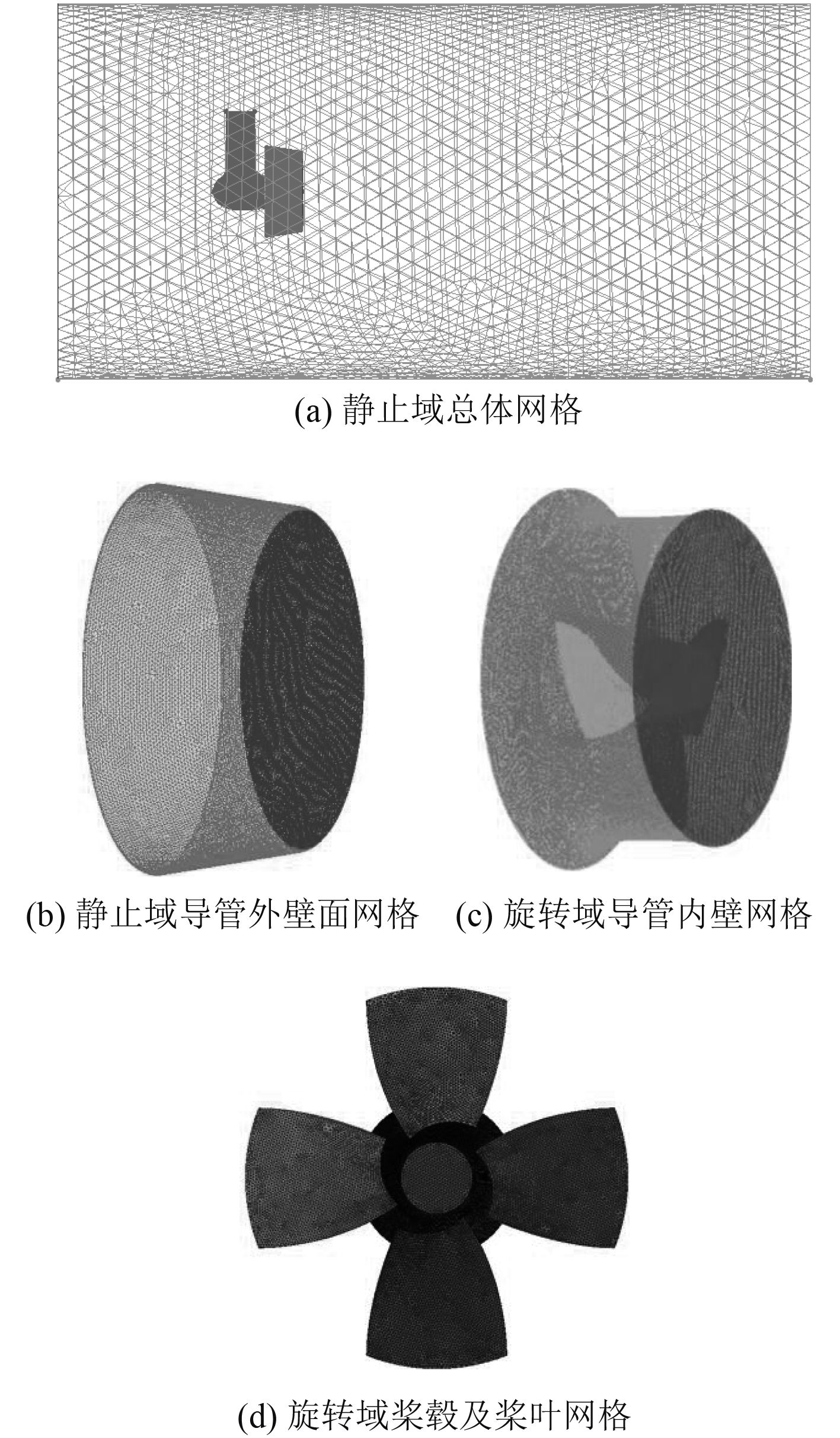
1.3 网格划分计算域网格的划分均采用四面体网格,如图3所示,网格信息如表2所示。由于桨叶叶梢与导管内壁面间距非常小,需将间隙处的网格进行细化,在叶梢和导管内壁面间设置3层边界层网格[4]。
|
图 3 计算域各部分网格 Fig. 3 Grid division of computational domain |
|
|
表 2 计算域网格数和节点数 Tab.2 Grid and node number of computational domain |
计算模型边界条件设置如下:
1)计算域左侧端面设为速度入口边界条件,根据不同的进速系数调整设定来流速度,右侧端面设为压力出口边界条件[5]。
2)推进器部件表面和静止域外边界面,都设为壁面Wall。
3)旋转域和静止域的接触面设为Interface[6]。
湍流模型选用两方程的RNG k-ε模型,近壁面处采用Standard wall functions[7]。推进器最高转速为180 r/min,进速系数J在0.01~0.75区间内取值。
1.5 材料属性计算域内的流体为海水,其物性参数如表3所示。
|
|
表 3 海水物性参数(20 ℃) Tab.3 Property parameters of sea water |
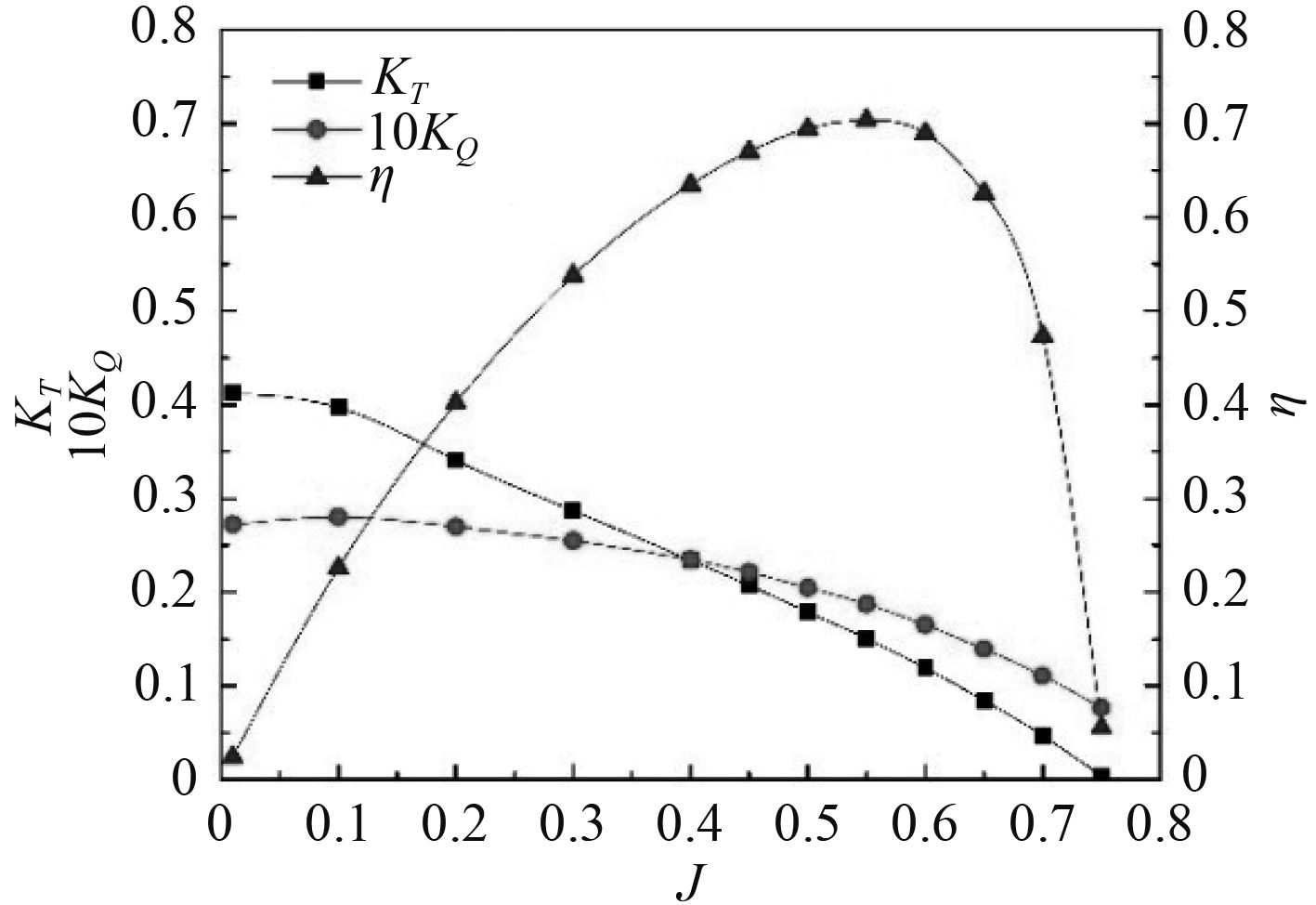
基于上述推进器水动力学数值模型,可得到不同进速系数下螺旋桨和导管推力T,螺旋桨扭矩Q,并进一步计算得到推力系数KT,扭矩系数KQ及敞水效率η,如表4所示。根据表中数据,绘制其敞水性能曲线,如图4所示。
|
|
表 4 不同进速系数下全回转推进器水动力学性能 Tab.4 Hydrodynamic performance of azimuth propulsor with different advance coefficient |
|
图 4 推进器敞水性能曲线 Fig. 4 Open water performance curve of propulsor |
由图4可知,随着进速系数J增大,KT和KQ都随之减小,而推进效率η变化呈抛物线趋势。当J=0.55时,η达到最大值0.704,此时推进器处于最佳工作状况。当J=0.75时,KT为0.004,接近为0,说明此时产生的推力很小。
图5为进速系数J=0.55,即敞水效率最高时,螺旋桨桨叶表面的受力情况。从图中可知,桨叶表面最大压力都出现在桨叶边缘靠近叶根处,桨叶中部受力比较均匀。在此工况下,螺旋桨产生297.154 kN的正推力。

|
图 5 J=0.55吸力面、压力面受力分布 Fig. 5 J=0.55 pressure distribution on suction surface and pressure surface |
为获得推进器360°回转过程中的水动力学特性,将这一动态过程离散为若干个回转角度下进行分析。
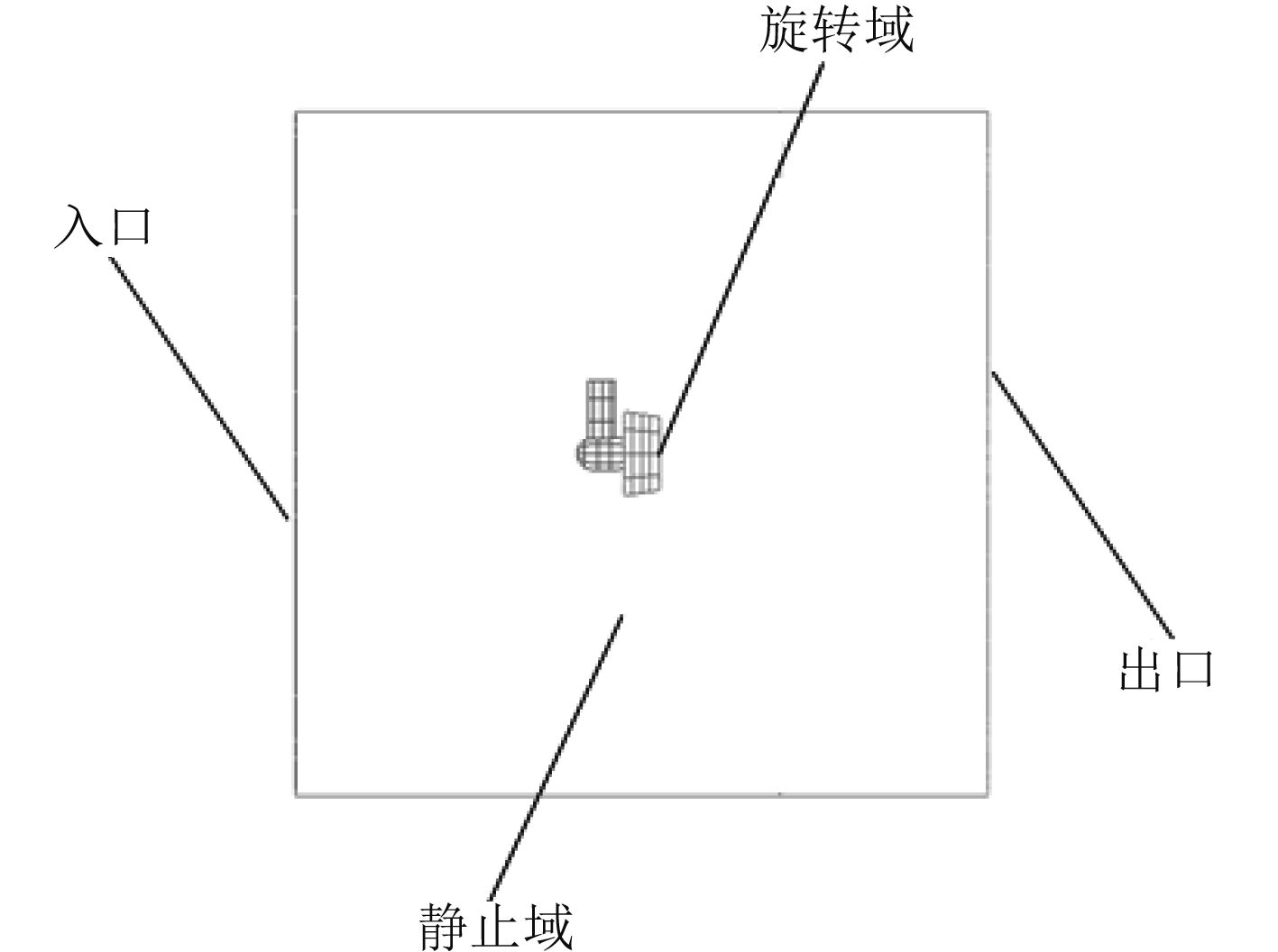
2.1 计算域由于推进器在静止域内作360°转动,将静止域设为一圆柱体,长度和直径都为10 D。入口面和出口面到推进器中心的距离都为5 D。计算域如图6所示。
|
图 6 计算域划分 Fig. 6 Computational domain division |
静止域计算网格选用四面体网格,如图7所示。网格数为659 178,节点数为112 948。旋转域计算网格保持不变。

|
图 7 回转角为60°时静止域网格 Fig. 7 Static domain grid when rotation angle is 60° |
取J=0.087,即来流速度v=1 m/s,螺旋桨转速为180 r/min时,不同回转角度下螺旋桨和导管推力T及螺旋桨扭矩Q在螺旋桨坐标系xoy中表示的计算结果如表5所示,水动力学性能曲线如图8所示。
|
|
表 5 不同回转角下全回转推进器水动力学性能参数 Tab.5 Hydrodynamic performance parameters of azimuth propulsor at different angle of rotation |
|
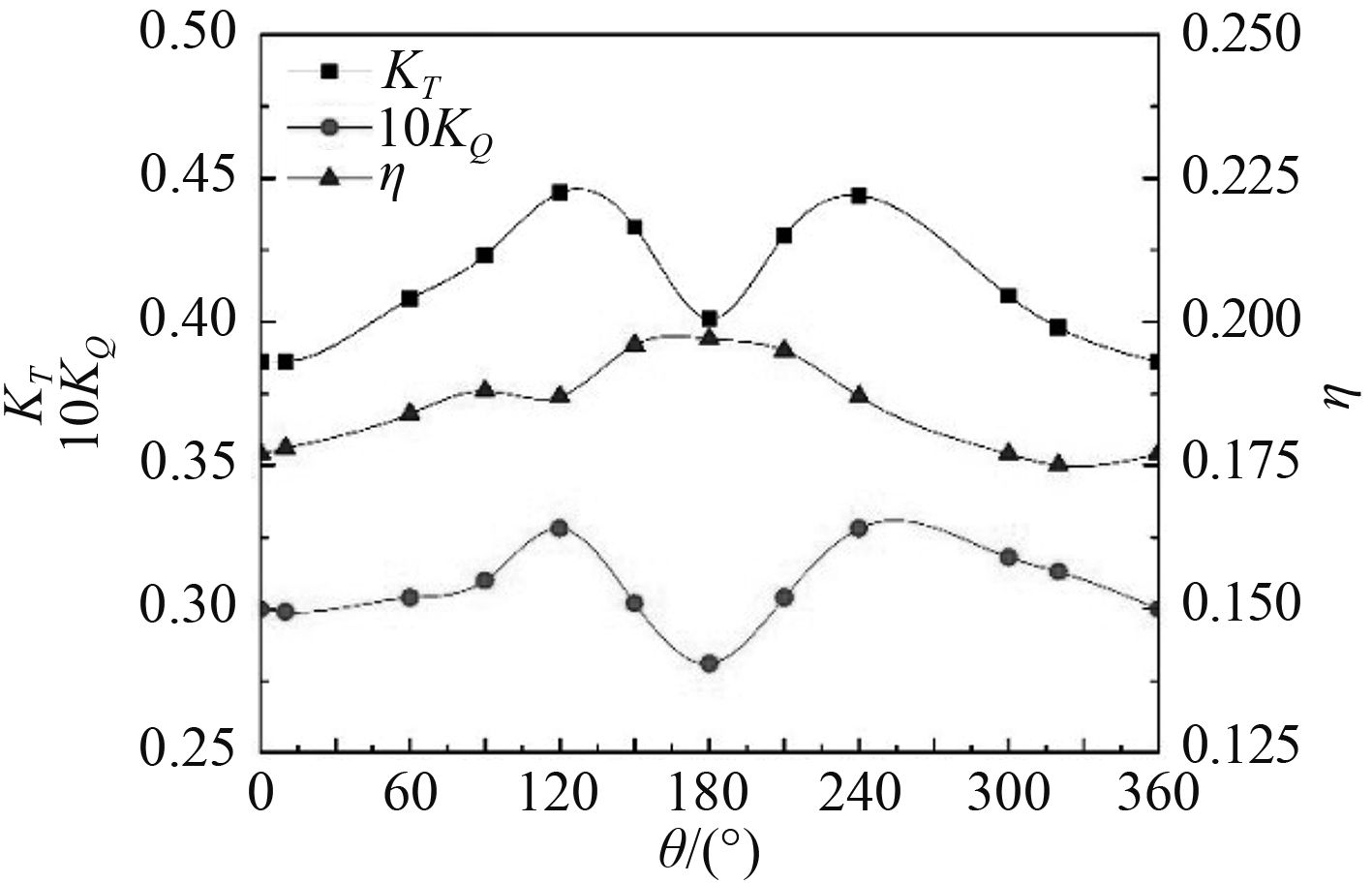
图 8 螺旋桨坐标系xoy下的水动力学性能曲线 Fig. 8 Hydrodynamic performance curve at propulsor coordinates xoy |
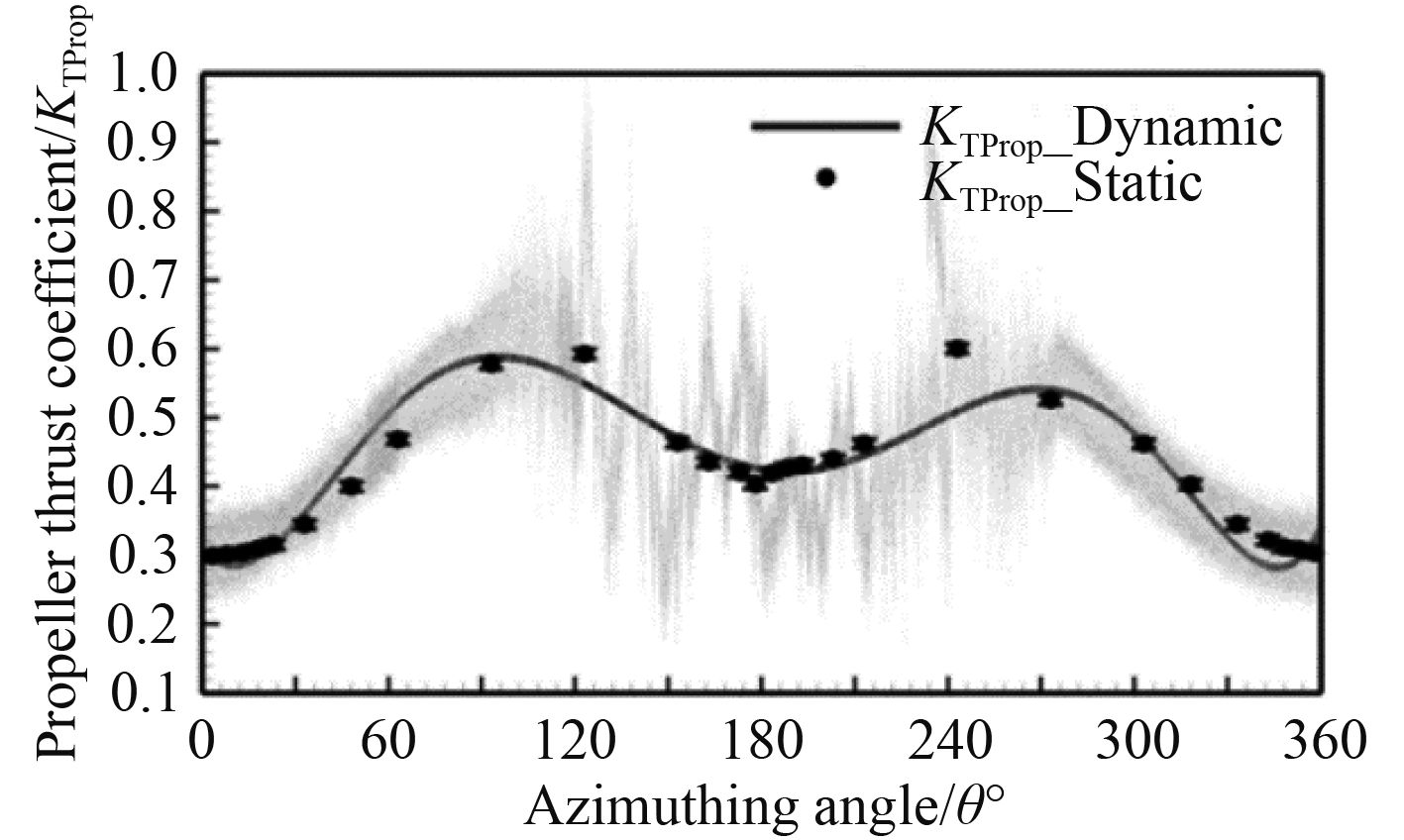
由图8可知,敞水效率η呈抛物线变化趋势,在回转角为180°时达到最大值0.197。图9为国外某机构对某全回转推进器在360°回转时应用六分力天平测得其推力系数变化曲线[8]。
通过对比可知,图8所示计算结果与图9测试结果变化规律基本吻合。在全回转工况下推力系数KT曲线呈“双峰一谷”型变化趋势,在180°时出现波谷,在120°和240°附近出现波峰。
|
图 9 某型推进器全回转推力系数测试值 Fig. 9 Test value of thrust coefficient of a certain propulsor |
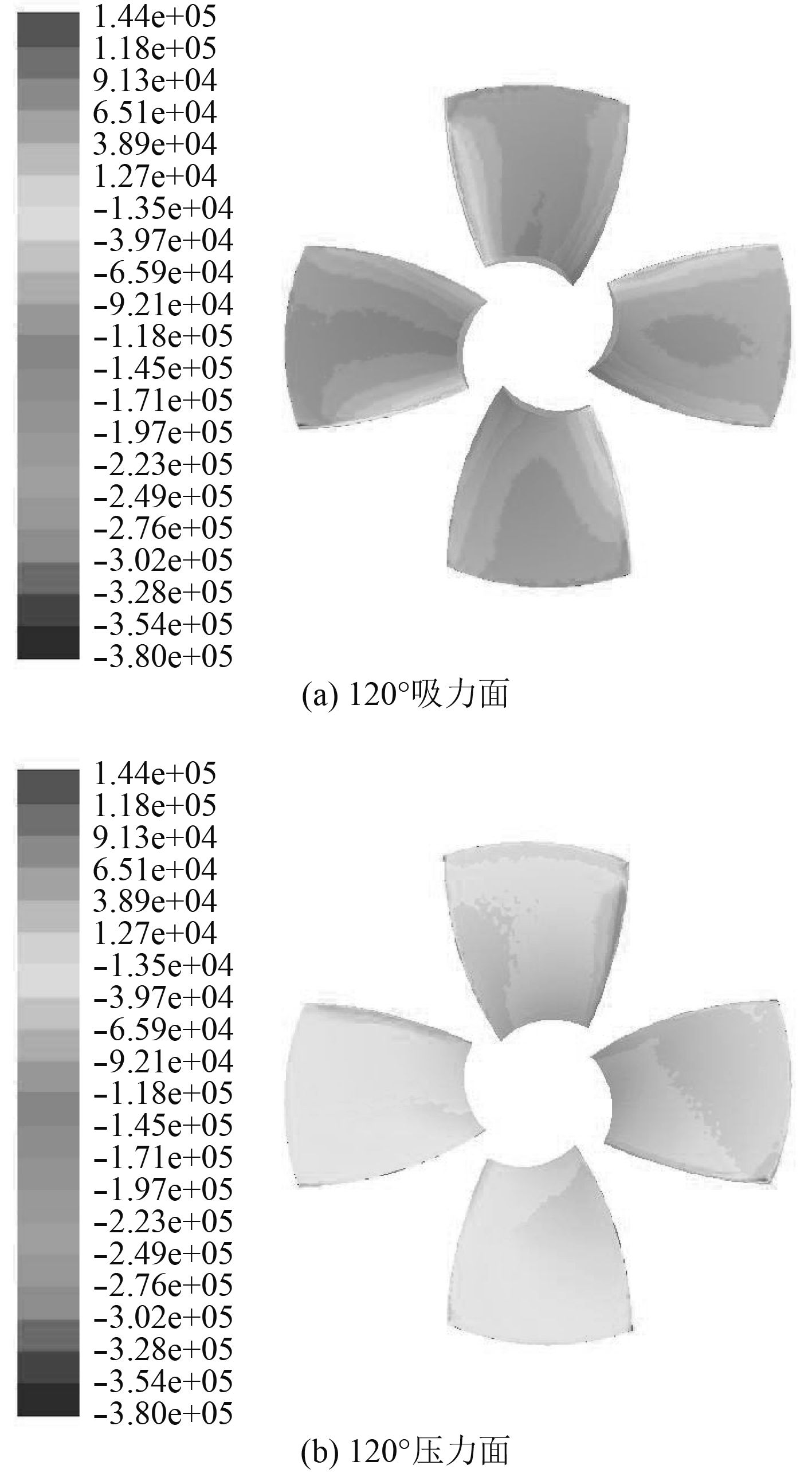
图10为全回转推进器在回转角为120°时,螺旋桨表面的压力分布情况。由图10以及表5可知,在螺旋桨坐标系xoy下转角为120°时,推进器此时输出的推力达到峰值为877.694 kN。此时,桨叶吸力面和推力面间的压差达到最大,造成桨叶上产生较大的应力。
|
图 10 回转角为120°时桨叶表面压力分布 Fig. 10 Pressure distribution on blade surfaces when rotation angle is 120° |
本文建立了某型大功率全回转推进器水动力学数值模型,获得了不同工况下的推力系数、扭矩系数、推进效率等水动力学性能参数。基于对计算结果分析,结论如下。
1)随着进速系数J增大,KT和KQ都减小,在J=0.75时,KT接近为0,说明此时产生的推力很小。
2)随着进速系数J增大,推进效率η变化呈抛物线趋势。当J=0.55时,η达到最大值0.704,此时推进器处于最佳工作状况。
3)在推进器360°回转过程中,推力系数和扭矩系数变化规律一致,都呈M型,且曲线对称。在120°和240°时出现峰值,180°时出现谷值。而推进效率η变化呈抛物线趋势,180°时出现最大值,为0.197。
4)当转角是120°时,推进器输出的推力达到峰值。此时会造成桨叶上产生最大应力,桨叶吸力面、推力面的压力差最大。因此,在设计螺旋桨叶片时,应该着重考虑这一工况下的受力情况。
| [1] |
李巍, 王国强, 汪蕾. 螺旋桨粘流水动力特性数值模拟[J]. 上海交通大学学报, 2007, 41(7): 1200-1203, 1208. LI Wei, WANG Guo-qiang, WANG Lei. The numerical simulation of hydrodynamics characteristic in propeller[J]. Journal of Shanghai Jiaotong University, 2007, 41(7): 1200-1203, 1208. DOI:10.3321/j.issn:1006-2467.2007.07.036 |
| [2] |
NORBERT W. H. B. Numerical analysis of flow around a thruster[C]//Dynamic Positioning Conference, US: 2006. 86–102.
|
| [3] |
朱俊飞, 周瑞平, 林雨, 等. 导管螺旋桨水动力与结构强度计算方法研究[J]. 造船技术, 2012, 4: 39-45. ZHU Jun-fei, ZHOU Rui-ping, LIN Yu, et al. Calculation and analysis of the hydrodynamic and structural strength for ducted propeller[J]. Marine Technology, 2012, 4: 39-45. DOI:10.3969/j.issn.1000-3878.2012.04.009 |
| [4] |
SINGHAL A K, ATHAVALE M M. Mathematical basis and validation of the full cavitation model[J]. Journal of Fluids Engineering, 2002, 124: 617-624. DOI:10.1115/1.1486223 |
| [5] |
张利军. 螺旋桨性能预报的速度势面元法研究[D]. 大连: 大连理工大学, 2006.
|
| [6] |
覃新川, 黄胜, 常欣. 船舶螺旋桨面元法的改进[J]. 华中科技大学学报, 2007, 35(5): 65-68. QIN Xin-chuan, HUANG Sheng, CHANG xin. Improvement of the ship panel method[J]. Journal of Huazhong University of Science and technology, 2007, 35(5): 65-68. DOI:10.3321/j.issn:1671-4512.2007.05.019 |
| [7] |
王超, 黄胜, 解学参. 基于CFD方法的螺旋桨水动力性能预报[J]. 海军工程大学学报, 2008, 20(4): 107-112. WANG Chao, HUANG Sheng, XIE Xue-shen. Hydrodynamic performance prediction of some propeller based on CFD[J]. Journal of Naval University of Engineering, 2008, 20(4): 107-112. |
| [8] |
MOHAMMED F I, Ayhan AKINTURK. Performance characteristics of static and dynamic azimuthing podded propulsor[C]// First International Symposium on Marine Propulsors, Trondheim, Norway, 2009, 6.
|
 2018, Vol. 40
2018, Vol. 40
