2. 中国船舶科学研究中心,江苏 无锡 214082
2. Chinese Ship Scientific Research Center, Wuxi 214082, China
深海潜水器是进行大洋勘查与深海科学研究的重要运载工具,受到世界各国的普遍重视[1]。耐压壳作为潜水器的关键组成部分,在潜水器的设计开发进程中举足轻重,因此在对海洋的认知、开发过程中耐压壳的研究占有重要位置[2 – 3]。
球形耐压壳体具有强度高、稳定性好等特点,已成为潜水器耐压壳体的首选,但是其空间利用率较低,人们在舱内工作时多数空间不易被利用,造成了较高的空间资源浪费;其次由于其横截面积较大从而水阻系数较高,不便于水下流动作业[4]。蛋壳属于薄壳结构,它的母线是一种正高斯曲线,这种结构不仅能给人一种美学的艺术感,还能节约材料,其次蛋形结构还符合圆顶原理,能够很好地分散来自外在的均布载荷[5]。
混凝土具有抗压、抗腐蚀、抗冻以及防渗透等特性,为其运用于海底建筑建设中提供了保障。通过改变混凝土的水灰比,可以得到不同性能的混凝土材料,这更多的体现了其运用的灵活性[6 – 8]。混凝土结构在海洋建筑中的运用已经非常普遍,如桥梁、堤坝、海上工作台,但将混凝土运用于潜水器耐压壳的建设中,至今仍未见报道。因此,综合考虑蛋壳的耐压性能和混凝土的耐久性,研究并设计能在水下工作的耐压壳结构,可大大节约海洋开发、研究的成本,这不仅对未来海洋资源的开发,还对海军军事发展都显得尤为重要。
本文结合蛋形结构和混凝土的耐压特性,完成2 000 m水深耐压壳的结构设计,分析其在承受均布载荷时,理想状态、考虑初始几何缺陷以及考虑蠕变时的失稳形态以及极限载荷,得出了2年内蛋形混凝土耐压壳的蠕变曲线。
1 蛋形混凝土耐压壳的结构设计 1.1 混凝土配料的选择国家混凝土结构建设规范根据混凝土的强度划分若干等级,常用的有C20-C50,设计时根据不同的工作环境,选择合适的混凝土强度等级,其中基础在海水里混凝土标号不能低于C30[9]。本文设计2 000 m水深蛋形耐压壳,工程主体建设材料选用混凝土,计算载荷为:
| ${p_s} = k{\rho _\omega }gh/0.9{\text{,}}$ | (1) |
式中:
通过计算可得需承受静水压力32.67 MPa,因此,混凝土强度等级初选C35,配料比为:水泥209 kg/m3;砂731 kg/m3;石1 144 kg/m3;水152 kg/m3;粉煤灰95 kg/m3;减水剂4.490 kg/m3。
常规建筑中混凝土浇筑之后,有必要进行养护,其原因是刚刚浇筑好的混凝土仍处于熔浆质,不具备较高的强度等力学特性,待其硬化后,才能充分发挥混凝土的力学特性。C35混凝土不同龄期抗压强度见表1。C35混凝土养护28 d后,其抗压强度可达到44.62 MPa,用于2 000 m水深的耐压壳符合要求,其材料基本参数为:弹性模量
|
|
表 1 C35混凝土不同龄期抗压强度 Tab.1 Compressive strength of concrete at different age |
国内外球形耐压壳直径一般为2 m,本文采用等体积的设计方法,设计蛋形耐压壳。通过前期的试验研究分析[10],采用N-R函数[11]作为蛋形耐压壳轮廓设计的数学模型,蛋形耐压壳的体积公式[12]以及蛋形系数公式[12]为:
| $V = \frac{{\text{π}}}{6}L{B^2}{\text{,}}$ | (2) |
| $SI = \frac{L}{B} \times 100\% {\text{。}}$ | (3) |
式中:V为体积;L为蛋形耐压壳长轴尺寸;B为短轴尺寸;SI为蛋形系数。
根据对蛋形系数的统计分析,蛋形系数取0.69为最佳。通过计算可得到蛋形耐压壳的长轴尺寸为2.56 m,短轴尺寸为1.77 m。
根据薄壳理论[13-14],可确定蛋形耐压壳的经向应力
| ${\sigma _\varphi }(x) = - \frac{{{p_s}{R_2}(x)}}{{2t}}{\text{,}}$ | (4) |
| ${\sigma _\theta }(x) = {\sigma _\varphi }(x) \cdot \left( {2{\rm{ - }}\frac{{{R_2}(x)}}{{{R_1}(x)}}} \right){\text{,}}$ | (5) |
式中:Ps为计算载荷;
由于
| $t = \frac{{{p_s}}}{{2\left[ \sigma \right]}}{\left\{ {\frac{{2{R_1}(x){R_2}(x) - R_2^2(x)}}{{{R_1}(x)}}} \right\}_{\max }}{\text{。}}$ | (6) |
蛋形耐压壳的屈曲临界载荷,采用Mushtari方程[15]表述:
| ${p_Q}{\rm{ = }}\frac{{2E{t^2}}}{{\overline {{R_2}} (2\overline {{R_1}} - \overline {{R_2}} )}}\sqrt {\frac{1}{{3(1 - {\mu ^2})}}} {\text{,}}$ | (7) |
式中:PQ为屈曲临界载荷;μ为泊松比;E为弹性模量;
综合考虑极限载荷和屈曲载荷,蛋形耐压壳的厚度可由式(8)确定。通过等厚设计方法确定厚度为t=55.29 mm。
| $\begin{array}{*{20}{l}} {t = }&{\left\{ {\frac{{{p_s}}}{{2\left[ \sigma \right]}}{{\left\{ {\frac{{2{R_1}(x){R_2}(x) - R_2^2(x)}}{{{R_1}(x)}}} \right\}}_{\max }},} \right.}\\ {}&{{{\left. {\sqrt {\frac{{{p_Q}\overline {{R_2}} (2\overline {{R_1}} - \overline {{R_2}} )\sqrt {3(1 - {\mu ^2})} }}{{2E}}} } \right\}}_{\max }}.} \end{array}$ | (8) |
对于耐压壳的力学特性研究,主要集中在强度和屈曲两方面的研究,通过研究2 000 m水深下的蛋形耐压壳最终失稳形式为屈曲失稳[4]。可以认为当耐压壳发生屈曲破坏时,其强度仍未达到极限值,因此本文只对混凝土耐压壳的屈曲展开研究。
2.1 理想状态下蛋形混凝土耐压壳屈曲分析在混凝土薄壳结构力学稳定性验算方法上,国际壳体和空间结构协会(IASS)推荐了半经验的验算方法,其公式如下:
| $\gamma {p_{cr}} = {\alpha _1}{\alpha _2}p_{cr}^{lin}{\text{。}}$ | (9) |
其中:
使用三维建模软件根据N-R方程建立蛋形耐压壳轮廓曲线,抽取模型内部保留规定的厚度,得到蛋形壳体结构,使用Ansa软件进行有限元计算前处理,采用网球划分法进行网格划分。由于耐压壳在2 000 m水深下工作,因此其承受均布载荷,理论上模型是不受任何约束力的,但是为了消除模型的刚性位移,在模型中任意选取3点限制模型6个自由度的刚性位移。通过有限元计算可得屈曲临界载荷
| $p_{cr}^{lin} = \alpha {p_s}{\text{,}}$ | (10) |
式中:α为临界系数;
图1为蛋形耐压壳一阶线弹性屈曲失稳模式图。
由图1可知,蛋形耐压壳在外载荷情况下,失稳部位主要发生在中部区域,且呈现波浪状失稳模式,具有5个波峰值,是一种具有正高斯曲线壳的典型失稳模式,沿纬向呈现有规律的凹进与凸出,波峰与波谷数均为5,最大位移出现在如图所示波谷处,值为1.006 mm。

|
图 1 屈曲失稳模式图 Fig. 1 Buckling model |
壳类结构的稳定性对初始缺陷十分敏感,在求解壳类结构稳定性时,初始缺陷必须予以考虑,它能引起壳体临界载荷的下降,无论是在求解线性还是非线性时,初始几何缺陷的特征将十分明显。对于有限元模型,结构初始缺陷的分布趋势,一般可以假设为结构的某一模态或者某几个模态的组成。特征值屈曲模态,是目前非常普遍的计算壳体初始缺陷的一种方法。即假设初始缺陷按照最低阶特征值屈曲模态形式分布。
从开始的理想状态逐渐增大模型的初始缺陷展开研究,分别设置缺陷值为厚度的0.8,0.6,0.4以及0.2倍,研究随着缺陷的增加,模型的屈曲临界载荷的变化情况。
令
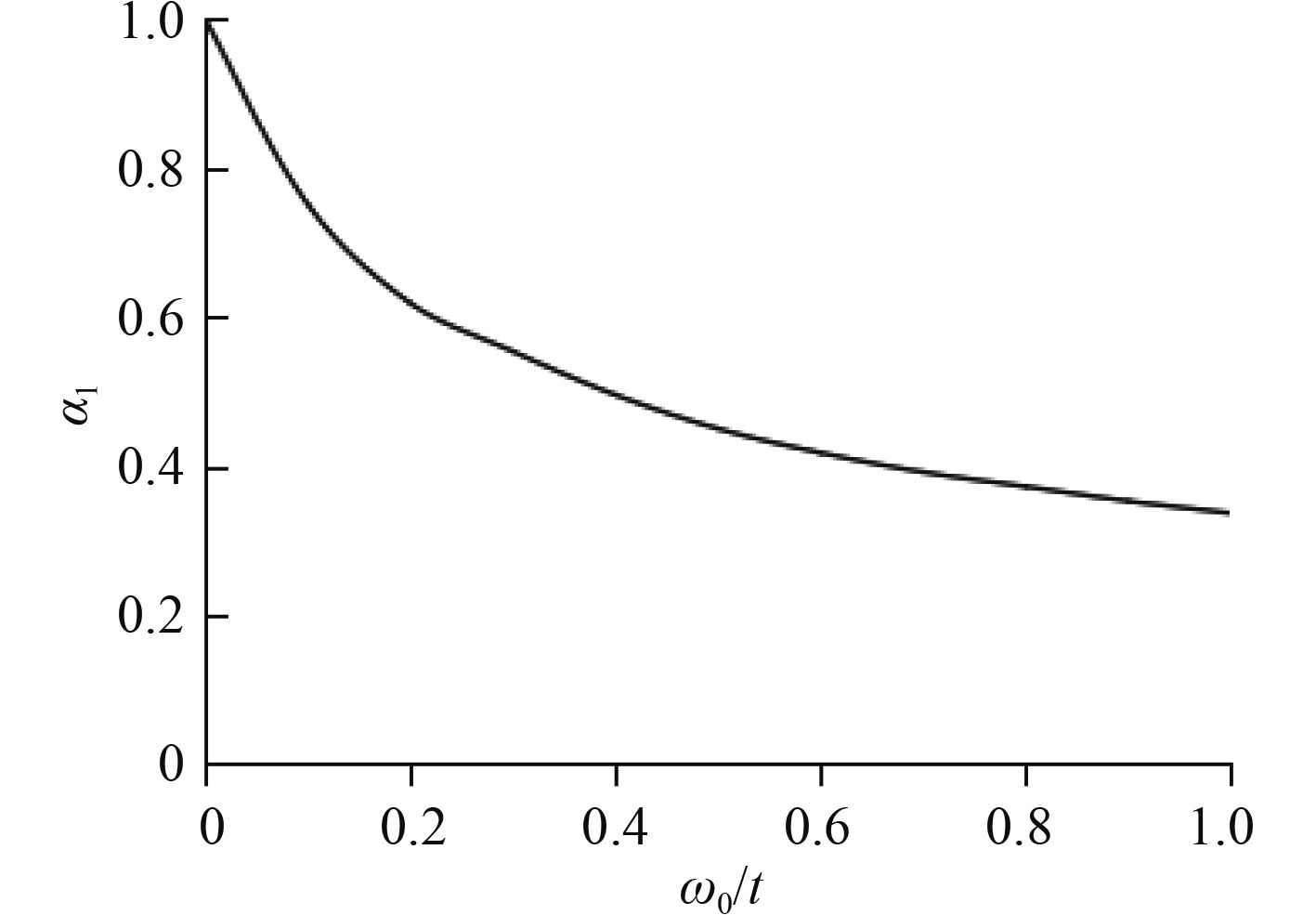
|
图 2 几何缺陷对屈曲的影响 Fig. 2 The effect of geometric imperfections on buckling |
|
|
表 2 缺陷状态下的临界屈曲载荷 Tab.2 Critical buckling load under the condition of imperfections |
通过图2可得随着缺陷的增加,耐压壳结构承载能力逐渐降低,屈曲临界载荷不断下降,只是下降的速率不断减小,说明初始几何缺陷对混凝土耐压壳屈曲有一定的影响,相比而言缺陷发展初期对屈曲的影响较大,后期影响较小,这也就是混凝土在裂缝初期对构件的稳定性影响较为显著的原因。
图3为
图4为图3中平衡路径末端点的后屈曲失稳模式图,由图可见,混凝土蛋形耐压壳后屈曲失稳模式不同于其线弹性失稳模式,其主要呈现局部凹坑失稳,且失稳部位位于混领土蛋形耐压壳的中部区域,表明蛋形耐压壳中部为危险区域,极易发生屈曲失稳。

|
图 4 屈曲失稳模式图 Fig. 4 Buckling model |
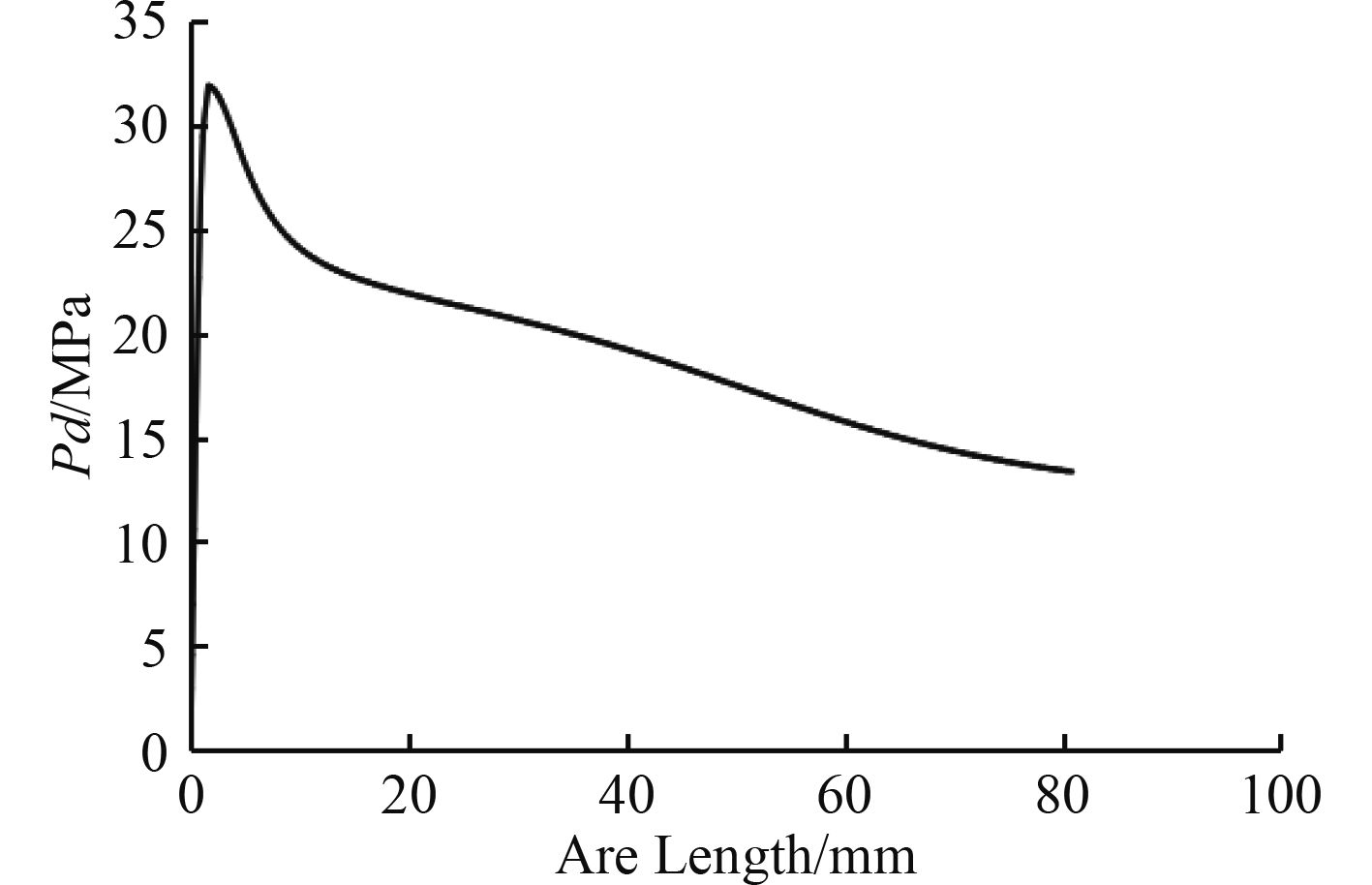
|
图 3 平衡路径图 Fig. 3 Equilibrium path |
本文使用Abaqus模拟混凝土耐压壳在2年时间内恒定温度下,受到恒定载荷的情况下的蠕变全过程,观察其应力分布、应力应变过程以及屈曲临界载荷。在Abaqus中模型的前处理,如单元类型的选择、网格的划分等都与上文相同,但是材料设置添加了混凝土塑性参数的定义。在Abaqus中,混凝土本构关系由三维模型简化为平面模型,因此在计算时只需要定义混凝土单轴受压的应力应变曲线即可,混凝土的应力应变曲线如图5所示。
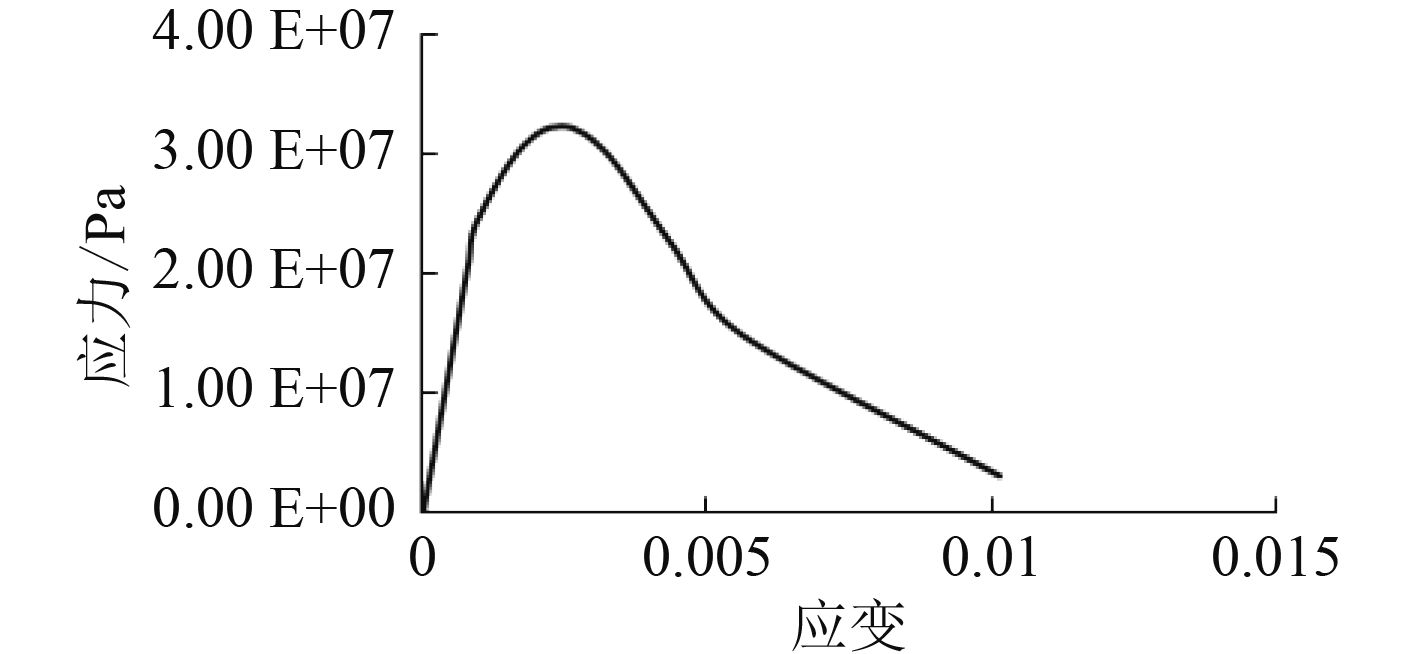
|
图 5 混凝土本构关系曲线 Fig. 5 The stress-strain curve of concrete |
在计算蠕变应变时,容差的设置十分关键,它与增量步的大小有着密切的关系,容差越小,增量步也跟着降低,因此在计算时容差值太大会影响精度,太小则会使计算时间变大导致系统崩溃。一般取1E–4~1E–6左右,容差可根据具体计算作调整。本文沿着经线,取蛋形耐压壳结构赤道与钝端之间中点处取一点A,中间赤道部位取点B,赤道与尖端之间中点处取点C。研究随时间的发展各点处的变形情况,结果如图6所示。
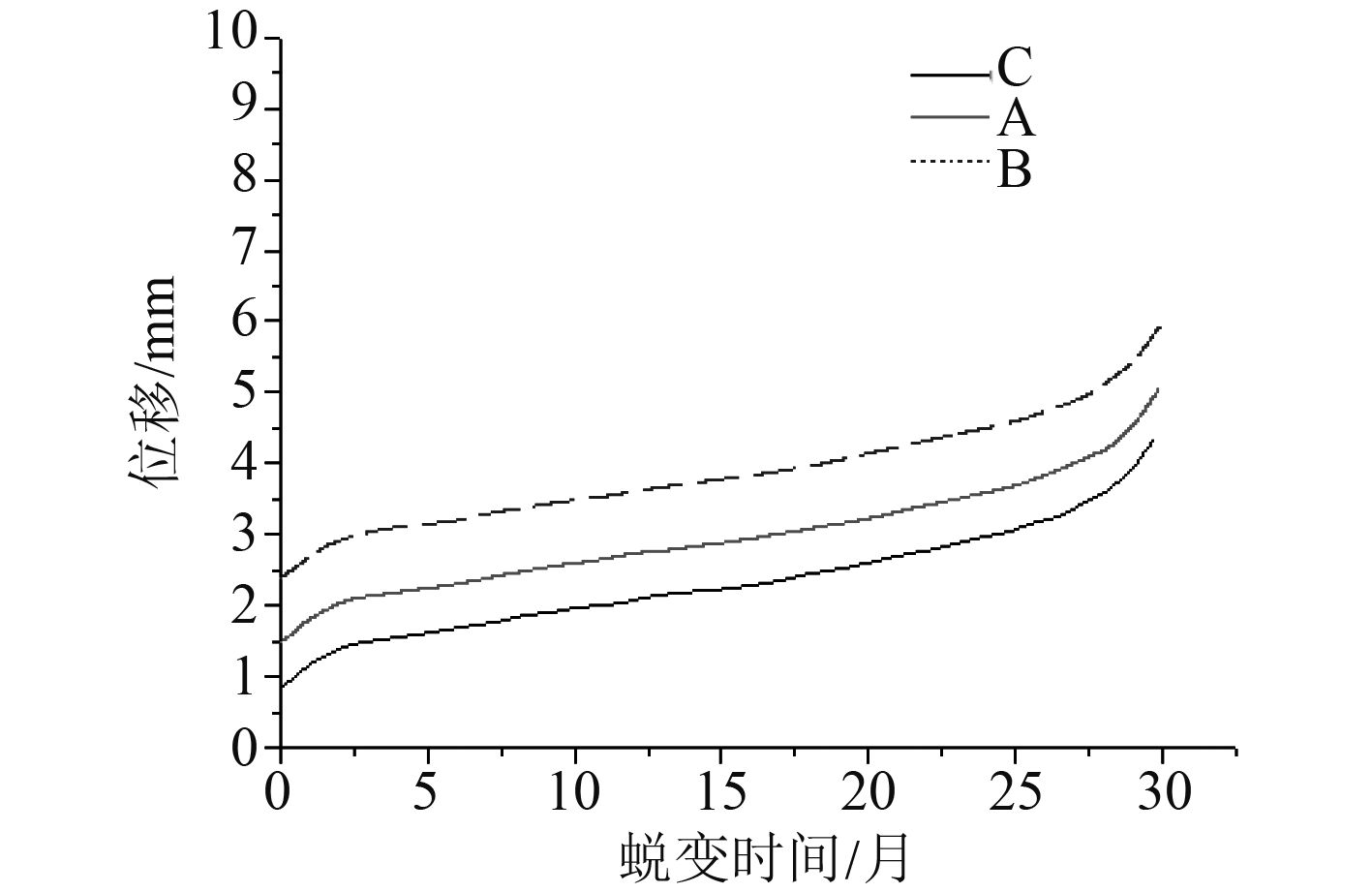
|
图 6 蠕变曲线 Fig. 6 Creep curve |
从图6可看出,随着时间的发展,耐压壳各点处均发生蠕变,但是在相同时间,同等载荷的情况下耐压壳B点处的蠕变发展比A点的大,A点处蠕变比C点大,这也证明了耐压壳内部应力分布规律为赤道处应力比两端大,钝端比尖端应力大;混凝土破坏分为3个阶段,第1阶段为蠕变发展阶段,第2阶段为加速阶段,第3阶段为蠕变破坏阶段,本例在加载2年时间内,混凝土蠕变未发展为第3阶段,因此可以认为未达到破坏极限。最终计算蠕变后屈曲极限载荷为48.34 MPa。
3 结 语结合蛋形结构和混凝土的耐压特性,完成了2 000 m水深耐压壳的结构设计,分析了其在承受均布载荷时,理想状态、考虑初始几何缺陷以及考虑蠕变时的失稳形态以及极限载荷,可得到如下结论:
1)耐压壳结构在承受均布载荷时,纬向应力变化幅度大于经向应力,因此设计耐压壳时应重点考虑纬向应力;蛋形结构两端承受的应力较小,中间段承受的应力较大,相比而言尖端承受应力比钝端大,此结果说明失稳最先发生于耐压壳中部,和实验结果相符合。
2)随着缺陷的增加,耐压壳结构承载能力逐渐降低,屈曲临界载荷下降,但是下降的速率逐渐减小,说明在缺陷发展初期对屈曲的影响较大,后期影响较小,此结果说明混凝土在裂缝初期对构件稳定性影响更为显著。
3)随着时间的增大,耐压壳各点处均发生蠕变,但是在相同时间,同等载荷的情况下耐压壳蠕变进展依次为:赤道处,钝端处,尖端处。发生蠕变后耐压壳屈曲极限载荷与理想状态相比下降了6.88%。
| [1] |
ZHANG J, ZUO X L, WANG W B, et al. Overviews of investigation on submersible pressure hulls[J]. Advances in Natural Science, 2014, 7(4): 54-61. |
| [2] |
STANLEY I W. Department of precision and microsystems engineering on lightweight design of submarine pressure hull[D]. Holland: Delft University Technology, 2012, 10.
|
| [3] |
ZHANG J, WANG M L, WANG W B, et al. Biological characteristics of eggshell and its bionic application[J]. Advance in Natural Science, 2015, 8(1): 1-7. |
| [4] |
张建, 王纬波, 高杰, 等. 深水耐压壳仿生设计与分析[J]. 船舶力学, 2015, 18(11): 1360-1367. DOI:10.3969/j.issn.1007-7294.2015.11.009 |
| [5] |
张建, 王明禄, 王纬波, 等. 蛋形耐压壳的力学特性研究[J]. 船舶力学, 2016, 20(2): 99-109. |
| [6] |
刘秉京. 混凝土结构耐久性设计[M]. 北京: 人民交通出版社, 2007.
|
| [7] |
李英. 沿海地区混凝土耐久问题的思考与建议[J]. 浙江建筑, 2002, 3: 46-47. |
| [8] |
张芳. 基于可靠度的海工混凝土结构耐久性设计及寿命预测参数分析[D]. 烟台: 烟台大学, 2013.
|
| [9] |
强华. 浅谈高标号混凝土设计及施工需要注意的几个问题[J]. 甘肃科技, 2011, 10: 27(20): 89-91. |
| [10] |
张建, 朱俊臣, 王明禄, 等. 蛋形耐压壳设计与分析[J]. 机械工程学报, 2016, 8: 12(8): 79-86. |
| [11] |
NEDOMOVA S, SEVERA L, BUCHAR J. Influence of hen egg shape on eggshell compressive strength[J]. International Agrophysics, 2009, 23: 249-256. |
| [12] |
NEDOMOVA S, BUCHAR J. Goose eggshell geometry[J]. Research in Agricultural Engineering, 2014, 60(3): 100-106. DOI:10.17221/RAE |
| [13] |
VENTSEL E, KRAUTHAMMER T. Thin plates and shells: theory, analysis, and applications[M]. CRC Press. 2001.
|
| [14] |
MC RAE D C, DUFF J W. The measurement of compression stress in eggshells[J]. J Agric. Engng Res, 1969, 14(1): 1-10. DOI:10.1016/0021-8634(69)90060-2 |
| [15] |
BABICH D V. Stability of shells of revolution with multifocal surfaces[J]. International Applied Mechanics, 1993, 29(11): 935-938. DOI:10.1007/BF00848278 |
 2018, Vol. 40
2018, Vol. 40
