目前船舶行业中,为了提高钢结构的力学性能,钢板结构的组合形式已经成为如今研究的重点,在船体结构中,上层板、下层板、中间加筋形成双层板的结构形式较为普遍,目的是为了提高结构的力学性能,比如抗冲击性能等[1 – 5]。但是,当双层板结构上层板承受压力时,由于层间加强筋的不连续性产生局部载荷,使得结构受力不均匀,容易产生应力集中现象,不利于改善结构的承压性能。本文为了解决上述问题,提出了在双层板结构内填充液体介质(非腐蚀性液体),能够大大提高双层结构的受力均匀性,增大双层板结构的截面抗弯性能,很好地改善双层板加筋结构的抗压性能。在国内外学者的研究中,主要针对夹层板或梁结构受液体压缩时的振动传递特性作了大量的研究,为结构的降振减噪提供了有力的依据[6 – 13]。很少有学者对双层板填充液体结构作静力学承载能力分析。
本文分析的对象是上、下层板形成密闭的空间内填充液体,在保证与双层板加筋结构重量不变的情况下进行抗压力学性能的比较。在上层板受到压力的作用时,压力从上层板经过液体介质传递到下层板,本文用压力传递系数C [14]来描述。
本文主要研究内容为:
1)通过理论计算,导出双层板内填充液体时该介质压力传递系数的具体表达式,并分析了双层板最大应力随着液体体积弹性模量K的变化规律,给出K的最佳取值范围。
2)通过数值模拟计算,对双层板填充液体结构与双层板加筋结构抗压性能进行比较,验证双层板填充液体结构的优势。
3)通过数值模拟计算,比较了双层板填充液体结构的抗压性能与填充液体厚度之间的变化规律,为双层板结构的优化设计提供依据。
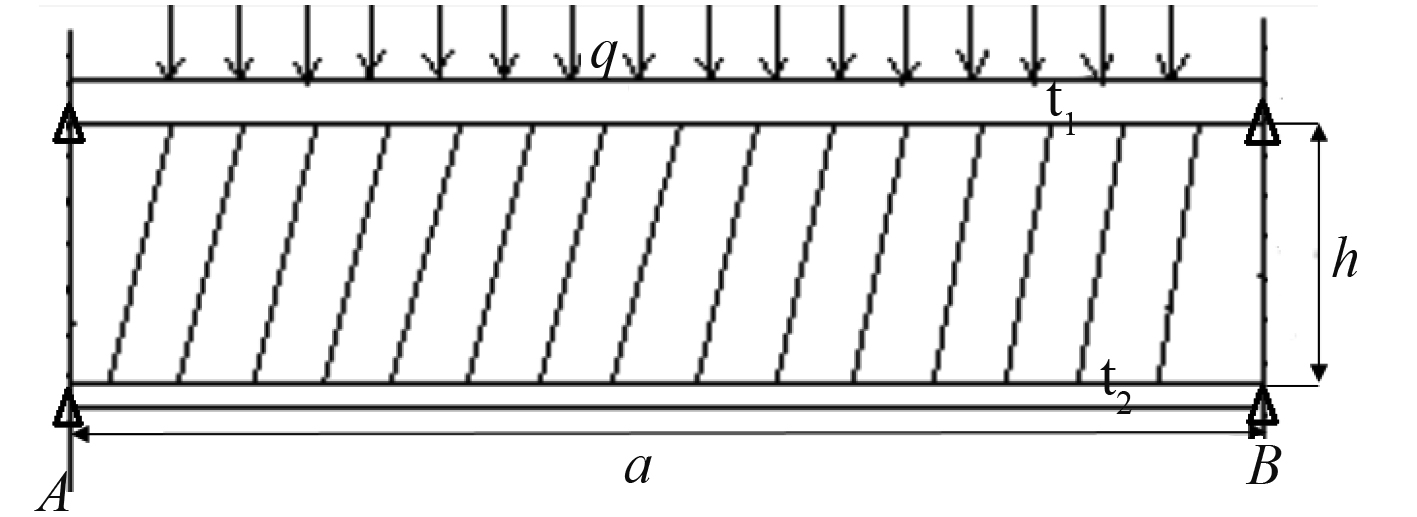
1 双层板填充液体结构的理论研究在理论分析中,为了简化计算,双层板填充液体的结构简化为在同一深度平面的二维截面形式,其截面形式为两端简支约束,上层板受均布载荷q,如图1所示。
|
图 1 双层板填充液体结构简化理论模型 Fig. 1 Simplified theoretical model of double-layer plate filled liquid |
采用液体的可压缩性质导出结构所受压力与液体介质的体积弹性模量之间的关系,其中液体体积模量的数学模型为
| $K = - V(\Delta P/\Delta V)\text{。} $ | (1) |
式中:
压力传递系数[14]即为在上层板受压力的作用下,压力经过上层板再经过液体介质作用到下层板上压力的系数,即
由于研究的是静压力作用,此双层板结构是密封结构,故液体介质压力大小在同一深度平面各个方向上均相等,设为
由材料力学的知识可知,上层板在受均压为q-Q,则挠度方程可表示为
| ${\omega _1} = \frac{{q - Q}}{{E{I_1}}}\left( - \frac{1}{{24}}{x^4} + \frac{a}{{12}}{x^3} - \frac{{{a^2}}}{{24}}{x^2}\right)\text{,} $ | (2) |
下层板受压为Q,则其挠度方程可表示为
| ${\omega _2} = \frac{Q}{{E{I_2}}}\left( - \frac{1}{{24}}{x^4} + \frac{a}{{12}}{x^3} - \frac{{{a^2}}}{{24}}{x^2}\right)\text{,} $ | (3) |
单位长度内上、下板的变形导致内充液体体积变化量为
| $\Delta V = \int_0^a {({\omega _2} - {\omega _1})} {\rm d}x\text{,} $ | (4) |
代入式(1)可求得
| $\Delta V = \frac{{{a^5}}}{{720}}\left( - \frac{Q}{{E{I_2}}} + \frac{{q - Q}}{{E{I_1}}}\right)\text{。} $ | (5) |
上、下板变形前,单位长度内液体的初始体积为
| ${V_0} = a \cdot h\text{,} $ | (6) |
联立可求得,压力传递系数C为
| $C = \frac{Q}{q} = \frac{{{a^4}{I_2}}}{{{a^4}({I_1} + {I_2}) + 720E{I_1}{I_2}h/K}}\text{。} $ | (7) |
从压力传递系数C的表达式可知,当钢板的结构尺寸、材料参数确定,则压力传递系数仅是液体体积弹性模量K的函数。随着K值的增加,压力传递系数呈递增的趋势。因此,为了保证下层板结构不发生变形破坏,压力传递系数应尽可能小,K应尽量较小。
若将双层板内的加强筋等效为板内填充的固体介质,其体积弹性模量大于液体体积弹性模量,则固体介质的压力传递系数大于液体介质的压力传递系数,因此填充液体结构的承压性能高于加筋结构的承压性能。
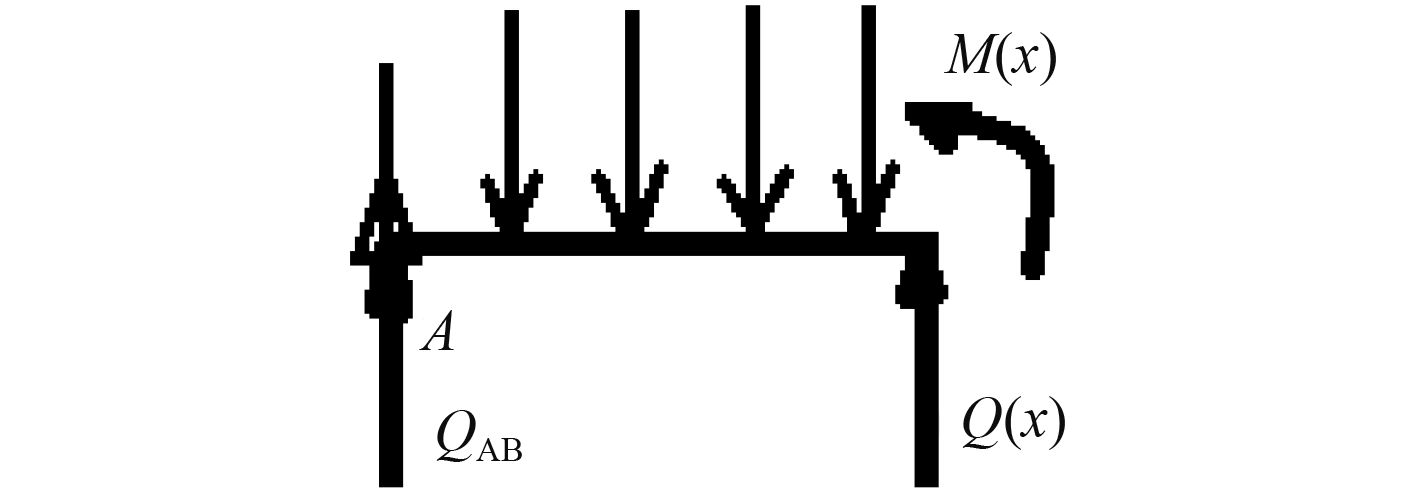
3 双层板最大弯曲应力的计算设图1中任意截面的弯矩为
由结构力学的知识可知挠度曲线微分方程为
| $\omega '' = \frac{{M(x)}}{{EI}}\text{,} $ | (8) |
可得
| ${M_1}(x) = (q - Q)\left( - \frac{1}{2}{x^2} + \frac{a}{2}x - \frac{{{a^2}}}{{12}}\right)\text{,} $ | (9) |
| ${M_2}(x) = Q\left( - \frac{1}{2}{x^2} + \frac{a}{2}x - \frac{{{a^2}}}{{12}}\right)\text{,} $ | (10) |
由此可得钢板的截面弯曲应力为
| $\sigma = \frac{{My}}{I}\text{。} $ | (11) |
对于上层板,当
| ${\sigma _{1\max }} = \frac{{{M_{1\max }}{y_{1\max }}}}{{{I_1}}} = \frac{{(q - Q)\left( - \displaystyle\frac{{{a^2}}}{{12}}\right)}}{{{I_1}}} \cdot \frac{{{t_1}}}{2}\text{。} $ | (12) |
同理,对于下层板,当
| ${\sigma _{2\max }} = \frac{{{M_{2\max }}{y_{2\max }}}}{{{I_2}}} = \frac{{Q\left( - \displaystyle\frac{{{a^2}}}{{12}}\right)}}{{{I_2}}} \cdot \frac{{{t_2}}}{2}\text{。} $ | (13) |
本文取
|
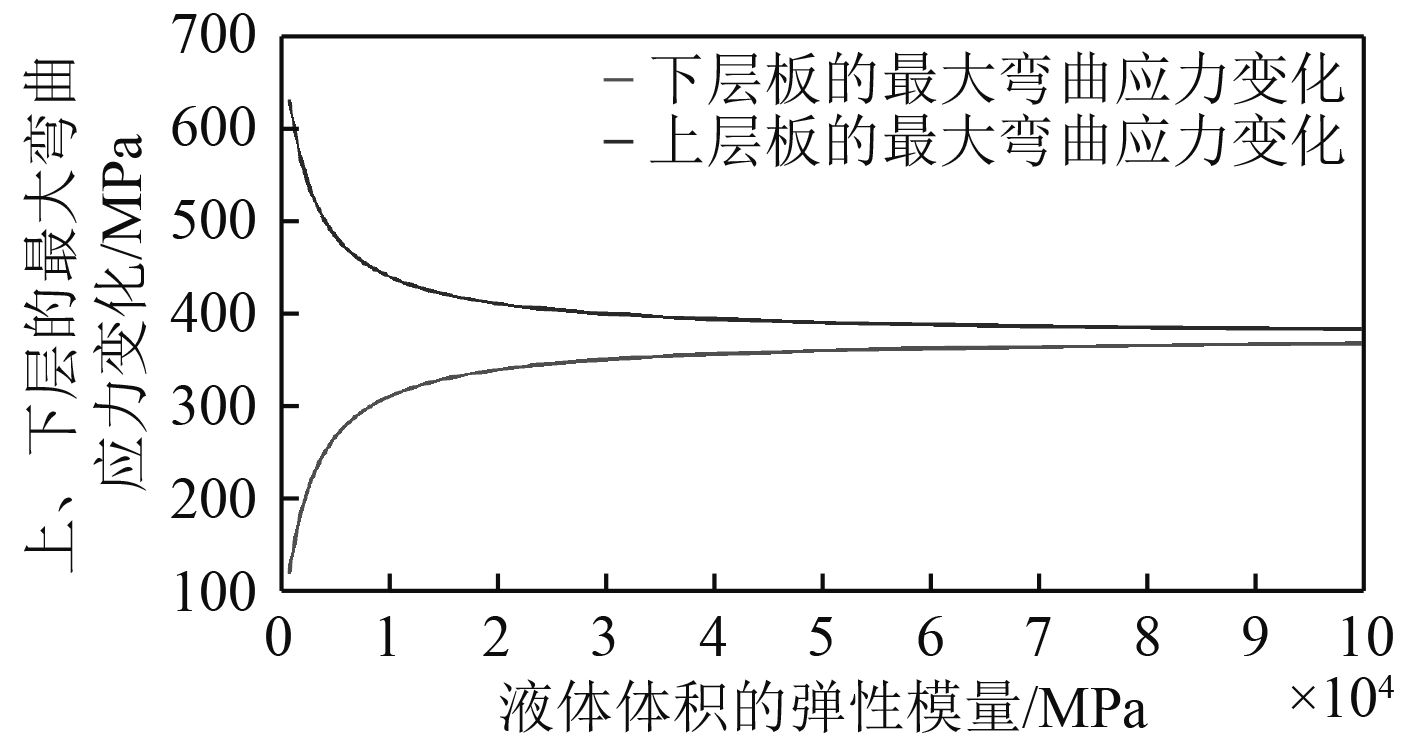
图 3 上、下板最大弯曲应力解析解随液体体积弹性模量变化 Fig. 3 The analytical solution of the maximum bending stress of the upper and lower plates vary with the bulk modulus of the liquid |
当
通过有限元方法模拟,在保证填充液体结构与加筋结构重量不变的情况下,比较其抗压性能,以此来验证理论推导的准确性。通过计算取加筋结构上、下层板厚度均为20 mm,加强筋厚度为36 mm,填充液体结构上、下层板厚度均为16 mm,加筋结构与填充液体结构上、下层板间距均为300 mm,长度、宽度均为3 000 mm。双层板加筋结构的布置形式为两板之间布置横纵交叉的加强筋,如图4所示。

|
图 4 双层板加筋结构的布置形式 Fig. 4 The layout form of double-layer plate reinforced structure |
按照第四强度理论进行比较,加筋结构整体Mises应力分布以及上、下层板的Mises应力分布如图5~图7所示。

|
图 5 双层板加筋结构整体Mises应力 Fig. 5 The whole Mises stress of double-layer plate reinforced structure |

|
图 6 双层板加筋结构上层板Mises应力 Fig. 6 The Mises stress of the upper plate of double-layer plate reinforced structure |

|
图 7 双层板加筋结构下层板Mises应力 Fig. 7 The Mises stress of the lower plate of double-layer plate reinforced structure |
可以看出,上、下层板与加筋板连接处出现较明显的应力集中,主要是由于上、下层板不均匀受压导致;下层板的应力分布大小较上层板小近80%,主要是由于加筋板的变形导致上层板承受的压力不会直接由下层板承受,这样就大大减少了整体结构的材料利用率。
填充液体结构整体Mises应力以及上、下层板的Mises应力如图8~图10所示。

|
图 8 填充液体结构整体Mises应力 Fig. 8 The whole Mises stress of the structure filled liquid |

|
图 9 填充液体结构上层板Mises应力分布 Fig. 9 The Mises stress of the upper plate of the structure filled liquid |
|
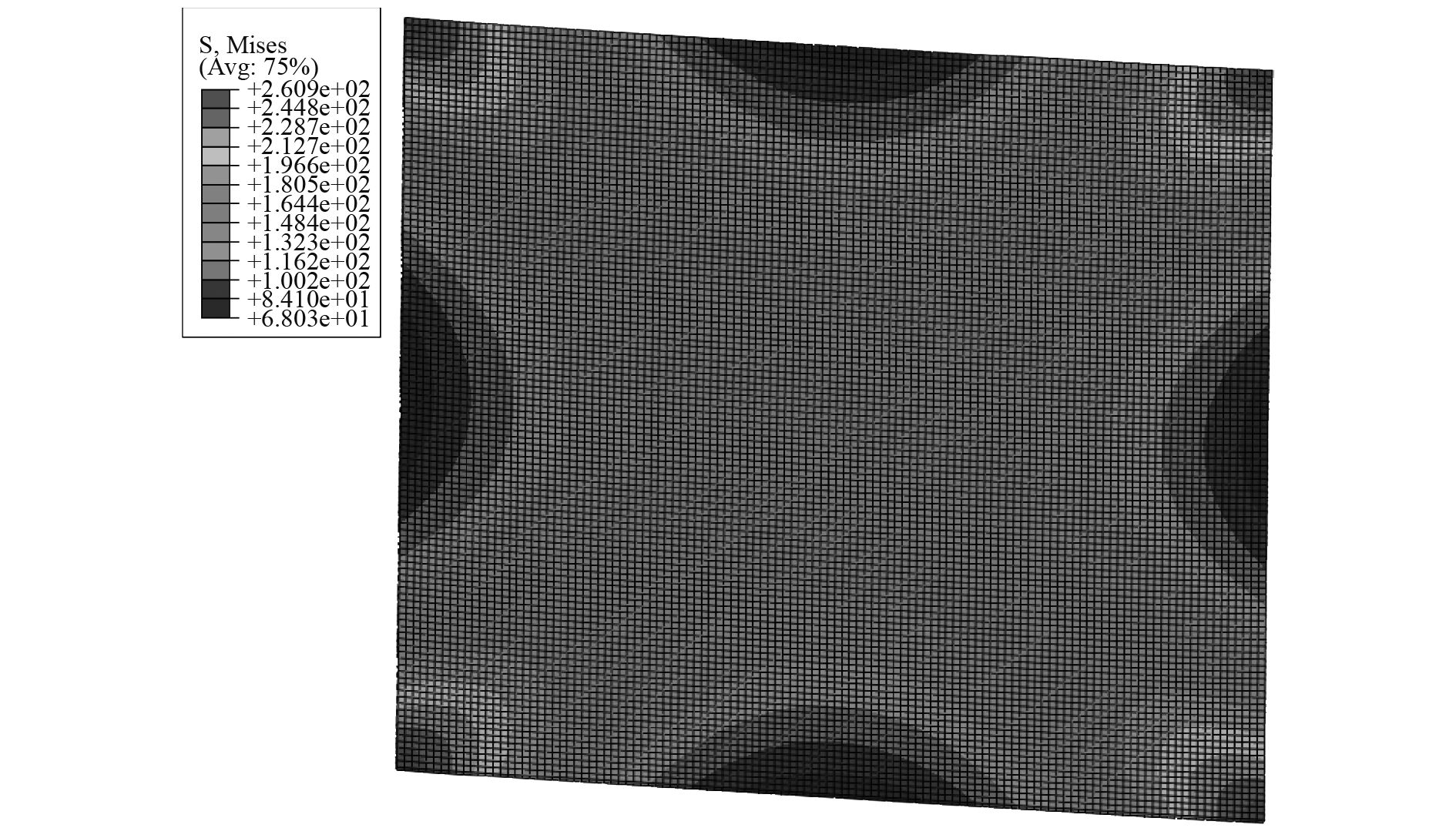
图 10 填充液体结构下层板Mises应力分布 Fig. 10 The Mises stress of the lower plate of the structure filled liquid |
可以看出,在不考虑边界效应的情况下,上、下层板应力分布比较均匀,不同单元间应力连续过渡,主要是由于液体受压均匀变形,使上、下层板承受均匀压力;下层板的应力分布大小较上层板小近18%,说明上层板承受的压力能有效的传递给下层板,起到很好的承压效果,相应增加了整体结构的材料利用率。
综上比较,对比于双层板加筋结构,填充液体结构充分利用了液体受压均匀变形的理论,增加了下层板结构的材料利用率,从而提高了整体结构的承压性能。
5 填充液体结构抗压性能随液体厚度的变化规律图11为双层板填充液体结构的上、下板最大应力随着液体厚度的变化曲线。

|
图 11 上、下板最大应力随着液体厚度的变化曲线 Fig. 11 The maximum bending stress of the upper and lower plates vary with the thickness of the liquid |
由图11可知,上、下层板最大应力随着填充液体厚度的增加呈逐渐减小的趋势,上下层板的承压性能会逐渐升高,由此说明,填充液体厚度的增大对结构的承压性能有利。
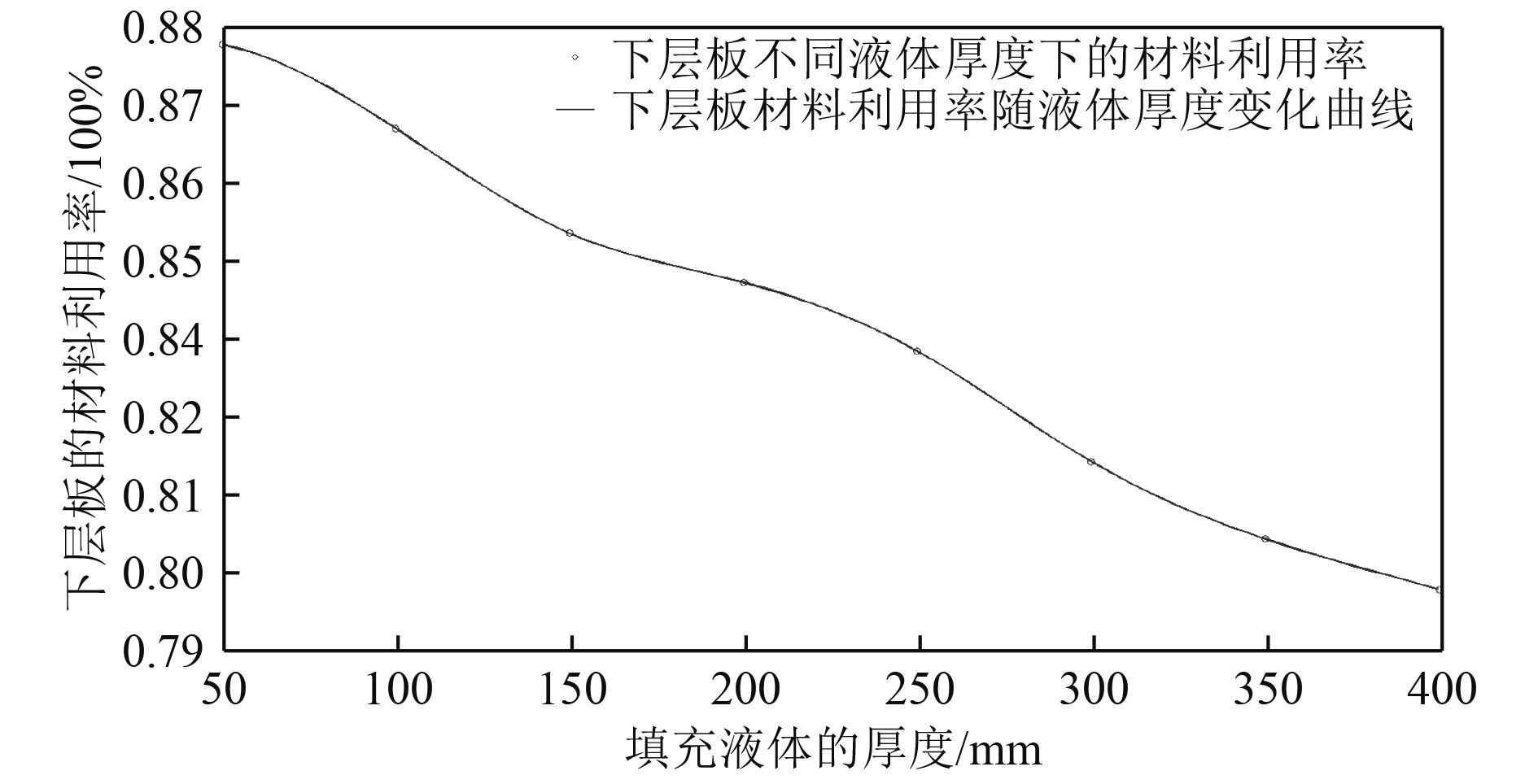
考虑到结构的规模和经济性,填充液体厚度不可能太小,也不可能无限增大,因此,本文引出了材料利用率这一指标,即材料利用率为下层板最大应力与整个结构的最大应力的比值,以此来衡量填充液体厚度的最佳取值范围。图12为材料利用率随填充液体厚度的变化曲线。
|
图 12 材料利用率随液体厚度的变化 Fig. 12 Material utilization rate varies with liquid thickness |
由图12可知,材料利用率随填充液体厚度的增加呈减小的趋势,填充液体厚度在150~250 mm范围内,曲线斜率变化较为平缓,材料利用率也相对较高,当填充液体厚度在50~150 mm或250~400 mm范围内,曲线斜率变化较大,即下层板材料利用效率突变较为明显,材料利用效率不够经济,因此,当填充液体厚度在150~250 mm范围内取值时,能有效的提高整体结构的承压性能。
6 结 语本文对双层板填充液体结构进行了理论简化分析及有限元模拟分析,得到如下结论:
1)针对双层板填充液体结构,由压力传递系数的推导公式可知,为了保证下层板不发生变形破坏,压力传递系数应可能小,液体体积模量应尽可能小,并且由此可以推导出双层板填充液体结构的承压性能高于双层板加筋结构。
2)随着液体体积模量K的增加,上、下层板最大弯曲应力向相反的方向变化,即最大弯曲应力的大小相互转移,当
3)通过有限元分析可知,双层板加筋结构承压时会出现较大的应力集中现象,不利于结构的承压,而双层板填充液体结构液体受压均匀变形,增加了下层板结构的材料利用率,从而提高整体结构的抗压性能。
4)考虑到结构的规模和经济性,本文引用材料利用率这一指标进行衡量,分析可知,材料利用率随双层板填充液体厚度的增加呈减小的趋势,填充液体厚度在150~250 mm范围内,曲线斜率变化较为平缓,材料利用率也相对较高。因此,当填充液体厚度在150~250 mm范围内取值时,能有效地提高整体结构的承压性能。
本文提出了一种新型的双层板结构,相比传统的结构能够得到较为有利的效果,本文研究为船舶行业中双层板密闭结构的设计提供一定的指导意义。
| [1] |
王自力, 顾永宁. 双层舷侧结构碰撞损伤过程研究[J]. 船舶工程, 2000(1): 17-20. DOI:10.3969/j.issn.1000-6982.2000.01.004 |
| [2] |
刘元丹, 刘敬喜. 双壳船内壳和外壳结构耐撞性能的分析和比较[J]. 中国造船, 2012, 53(3): 121-128. |
| [3] |
PAIK J K, CHUNG J Y, PEDERESEN P T, el al. On rational design of double hull tanker structures against collision [C]// The Society of Naval Architectures and Marine Engineers 1999 Annual Meeting Preprints, 1999.
|
| [4] |
KUROIWA T. Dynamic experiments and numerical simulations of failure of ships side structure [C]// 1993.31–37.
|
| [5] |
SANO A, MURAGISHI O, YOSHIKAWA T. Strength analysis of a new double hull structure for VLCC in collision and grounding[J]. Protection of Ships, San Francisco, Califonia, USA, 1996, 22-23. |
| [6] |
周叮. 考虑液面波动和液体压缩时一侧受液作用悬臂梁的横振分析[J]. 应用力学学报, 1994, 11(2): 111-119. |
| [7] |
周叮. 两侧受液时悬臂梁的自由振动分析[J]. 工程力学, 1991, 8(3): 107-115. |
| [8] |
J. Natural vibration of a beam-water interaction system[J]. Journal of Sound and Vibration, 1997, 199: 491-512. DOI:10.1006/jsvi.1996.0662 |
| [9] |
J. Natural vibration of two-dimensional slender structure interaction systems subject to Somerfield radiation condition[J]. Journal of Sound and Vibration, 2007, 308: 67-79. DOI:10.1016/j.jsv.2007.07.009 |
| [10] |
李增, 张志谊. 含弹性连接和层间流体的双梁结构的耦合振动分析[J]. 振动与冲击, 2010, 29(7): 189-193. DOI:10.3969/j.issn.1000-3835.2010.07.041 |
| [11] |
Kyeong-Hoon JEONG, Gye-Hyoung YOO. Hydroelastic vibration of two identical rectangular plates[J]. Journal of Sound and Vibration, 2004, 272: 539-555. DOI:10.1016/S0022-460X(03)00383-3 |
| [12] |
Kyeong-Hoon JEONG. Hydroelastic vibration of two annular plates coupled with a bounded compressible fluid[J]. Journal of Fluid and Structure, 2006, 22: 1079-1096. DOI:10.1016/j.jfluidstructs.2006.07.001 |
| [13] |
王自力, 张延昌. 基于夹层板抗水下爆炸舰船底部结构设计[J]. 舰船科学技术, 2010, 32(1): 23-27. |
| [14] |
练章华, 赵国珍. 双层组合套管内填充液体介质的力学分析[J]. 石油钻采工艺, 1997, 19(5): 1-5. |
 2018, Vol. 40
2018, Vol. 40