复合材料具有轻质、高强、耐海洋环境侵蚀等众多优势,随着复合材料技术的快速发展更新,复合材料在船舶领域中的应用越来越广泛[1 – 3]。
层合板是复合材料结构的主要形式之一[4],在船舶领域,船舶与海洋结构物相对于航空航天结构物而言,构件尺度较大,成本控制要求较高。目前船用复合材料主要的增强纤维体系仍以玻纤为主,然而,在某些关键部位使用时,构件弯曲刚度特性往往无法满足设计要求。若通过提高板厚,则无法体现复合材料结构的重量优势,且会增加工艺难度;若大量使用高模量碳纤维,则由于成本控制要求,在工程上往往无法实现,因此,混杂层合薄板结构形式已成为目前船舶结构实现结构刚度、强度、成本以及轻量化综合要求的重要技术途径。
复合材料层合结构材料种类众多,力学性能较为复杂[5 – 7],对于一定厚度的复合材料层合薄板,混杂形式通常有夹层混杂、层间混杂和层内混杂3种[8],不同混杂形式弯曲刚度系数分布特征存在差异,且对于一定厚度的某种混杂形式层合薄板,其弯曲刚度系数也将随混杂比的变化而变化。关于混杂比对层合结构力学性能的影响,目前国内对这方面的研究较少。陈汝训[9]曾研究过混杂结构受拉构件的最优混杂比,洪彬等[10]对不同混杂比下竹木复合纤维板的弹性模量做过一定研究,以上学者的研究对象与本文的研究对象不同,但是其研究方法对于本文有一定的指导意义。因此重点针对夹层混杂、层间混杂2种混杂形式、选取不同混杂比的层合薄板进行理论研究和试验分析,着重探讨混杂比对层合薄板弯曲刚度系数的影响及层合薄板弯曲刚度系数的理论预报方法,并给出相应的理论计算公式。
1 矩形层合薄板弯曲刚度特性的理论分析 1.1 正交各向异性板刚度系数影响规律对于承受均布载荷
| ${w_{\max }} = 0.003\;418\frac{{q{a^4}}}{{{D_{11}} + 0.5714{D_3}{C^2} + {D_{22}}{C^4}}}{\text{。}}$ | (1) |
式中:
| ${w_{\max }} = 0.003\;418\frac{{q{a^4}}}{{2{D_{11}} + 0.5714({D_{12}} + 2{D_{66}})}}{\text{。}}$ | (2) |
分析可知:板中心挠度主要与a,
根据层合薄板弯曲经典理论,正交层合薄板弯曲刚度系数计算公式[12]为:
| ${D_{ij}} = \frac{1}{3}\sum\limits_{k = 1}^N {{{({Q_{ij}})}_k}} (z_k^3 - z_{k - 1}^3){\text{。}}$ | (3) |
式中:N为层数,
对于夹层混杂和层间混杂2种结构形式,若将夹层混杂结构高模量材料置于最外层,则夹层结构的抗弯刚度明显大于层间混杂结构,由于层间混杂层合薄板的弯曲刚度系数推导较为复杂,故给出如图1(b)所示层合薄板形式与夹层混杂层合薄板进行比较。
考虑2种材料,其工程常数为,材料1:

|
图 1 两种不同混杂形式的层合薄板 Fig. 1 Laminated plates with two different types of hybrid |
可推导夹层混杂层合薄板弯曲刚度系数的计算公式如下:
| $\begin{split}{D_{11}} = & \frac{{{h^3}}}{{12}} \cdot \frac{{{E_{11}}^1}}{{1 - {\nu _{12}}^1{\nu _{21}}^1}} - \frac{{{h^3}}}{{12}}{\text{×}} \\& \left(\frac{{{E_{11}}^1}}{{1 - {\nu _{12}}^1{\nu _{21}}^1}} - \frac{{{E_{11}}^2}}{{1 - {\nu _{12}}^2{\nu _{21}}^2}}\right) \frac{1}{{{{(\xi + 1)}^3}}}{\text{,}}\end{split}$ | (4) |
层间混杂层合薄板弯曲刚度系数的计算公式如下:
| $\begin{split}{D_{11}} = & \frac{{{h^3}}}{{12}} \cdot \frac{{{E_{11}}^1}}{{1 - {\nu _{12}}^1{\nu _{21}}^1}} - \frac{{{h^3}}}{{36}} {\text{×}}\\& \left(\frac{{{E_{11}}^1}}{{1 - {\nu _{12}}^1{\nu _{21}}^1}} - \frac{{{E_{11}}^2}}{{1 - {\nu _{12}}^2{\nu _{21}}^2}}\right){\text{×}} \\& \left[ {\frac{1}{{(\xi + 1)}} + \frac{1}{{{{(\xi + 1)}^2}}} + \frac{1}{{{{(\xi + 1)}^3}}}} \right]{\text{。}}\end{split}$ | (5) |
由于
| ${D_{11}} = \frac{{{E_{11}}^2 \cdot {h^3}}}{{12}} \cdot \left[ {k - \frac{{k - 1}}{{{{(\xi + 1)}^3}}}} \right]{\text{,}}$ | (6) |
| $\begin{split}{D_{11}} =& \frac{{{E_{11}}^2 \cdot {h^3}}}{{36}} {\text{×}}\quad\quad\\&\left\{ {3k \!-\! {\rm{(}}k \!-\! {\rm{1}}) \cdot \left[ {\frac{1}{{(\xi + 1)}} \!+\! \frac{1}{{{{(\xi + 1)}^2}}} \!+\! \frac{1}{{{{(\xi + 1)}^3}}}} \right]} \right\}{\text{。}}\quad\quad\!\!\end{split}$ | (7) |
对式(6)进一步分析可知,
由于弹性模量E和k对弯曲刚度系数

|
图 2
|
由图2分析可知,在不同混杂比时,弯曲刚度系数
为进一步说明上述特性,结合典型船用复合材料体系进一步加以阐述。选取材料体系1为T700/350环氧,增强体为正交T700碳纤维单向带,取材料体系2为E800/350环氧,其增强体为正交E800玻璃纤维多轴向带,真空成型,其参数分别为
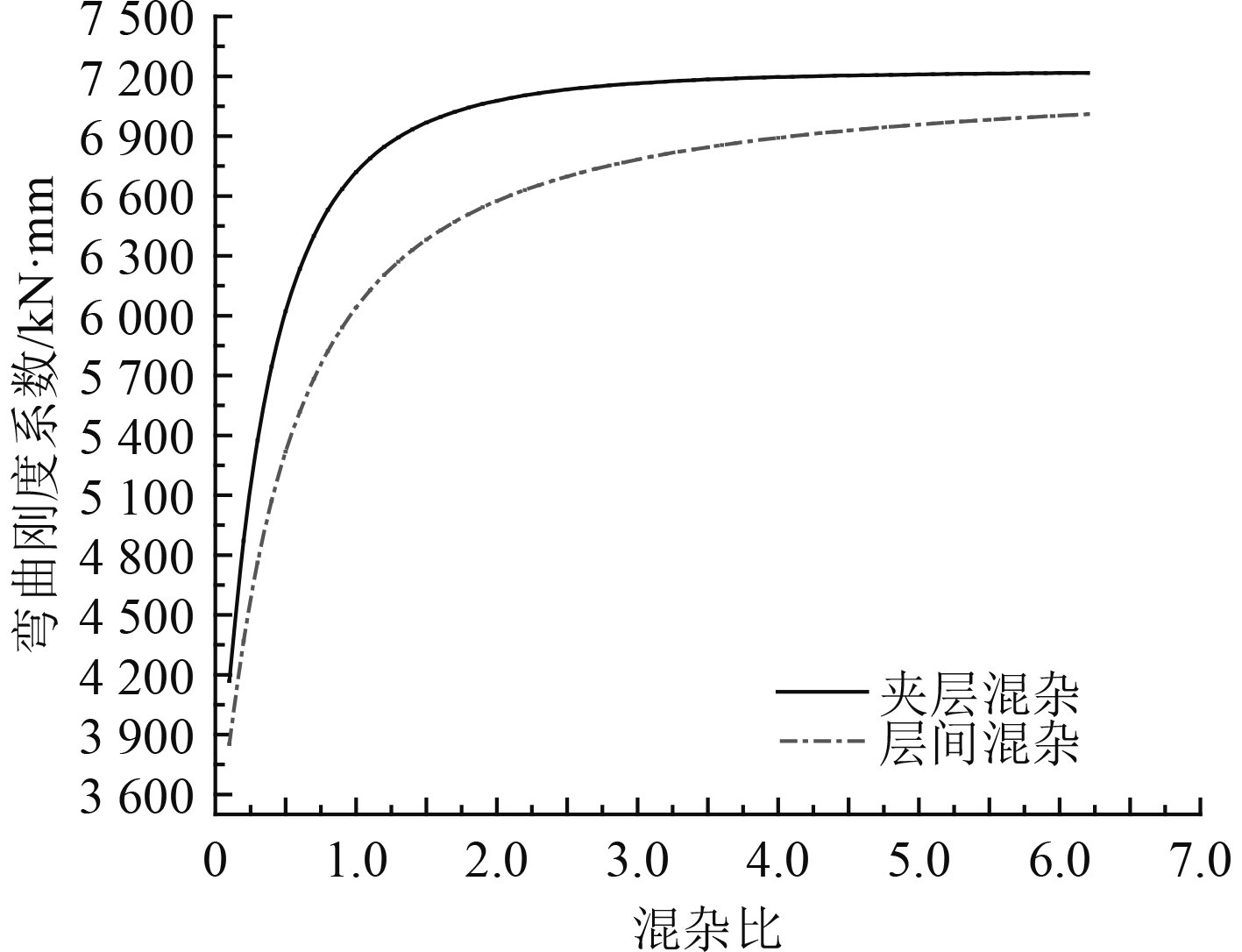
|
图 3 两种混杂结构混杂比对弯曲刚度系数的影响 Fig. 3 Effect of hybrid ratio on bending stiffness coefficient about two different types of hybrid |
分析可知,对于以上2种材料,夹层混杂结构弯曲刚度明显大于层间混杂结构,夹层混杂结构的弯曲性能优良。混杂比在1.5附近之间出现增速拐点,具有较好的弯曲特性和经济性。故对混杂比为1.0~3.5的范围开展试验研究,以验证理论计算的合理性。
2 试验研究对于混杂正交各向异性层合薄板可以视为某种特性材料具有正交各向异性的单层板,因此采用试验测得混杂层合梁的表观弯曲模量[8],认为该弯曲模量即为构成混杂层合薄板材料的表观弯曲模量,进而通过正交各向异性单层板弯曲理论求得其弯曲刚度系数。
考虑到试验的可行性,制作纯碳纤维、纯玻纤维和碳/玻混杂层合梁,开展静力学试验研究,以测试其表观弯曲模量,进而得到该碳/玻混杂比下层合薄板弯曲刚度系数。
2.1 试验工况本试验所用材料体系参数如表1所示。
|
|
表 1 试验所用材料体系参数 Tab.1 Parameters of materials used in the experiment |
试件制作参照标准GB/T 1449-2005《纤维增强塑料弯曲性能试验方法》[13],主要用于测试复合材料的表观弯曲模量,参数如表2所示,部分典型试件及试验过程如图4所示。
|
|
表 2 弯曲试验试件参数 Tab.2 Parameters of bending test specimens |

|
图 4 层合梁试件及弯曲试验过程 Fig. 4 The laminated beam specimen and bending test procedure |
试验参照标准GB/T 1449-2005《纤维增强塑料弯曲性能试验方法》[13]进行,弯曲模量按下式计算:
| ${E_f} = \frac{{{l^3} \cdot \Delta P}}{{4b \cdot {h^3} \cdot \Delta S}}{\text{。}}$ | (8) |
式中:
该试验的位移载荷曲线除初始点由于在试件安装、工装间隙、试件滑动等因素引起的非线性之外,在上升阶段呈现出良好的线性特征。各混杂比下的8个试件表观弯曲模量取均值作为该混杂比试件的表观弯曲模量。
试验测得的结果如表3所示。
|
|
表 3 层合梁厚度值及表观弯曲模量 Tab.3 Thickness values and apparent bending modulus of laminated beams |
由于混杂层合结构没有泊松比的概念,故引用复合材料细观力学中泊松比混合定律[8]的概念并加以变形,根据泊松比混合定律可求得不同混杂比下各试件的表观泊松比;由于泊松比是小量,对计算结果的影响可忽略。将上述试验参数代入单层板弯曲刚度系数计算公式可求得不同混杂比下的层合薄板弯曲刚度系数。泊松比混合定律计算公式及单层板弯曲刚度系数计算公式如式(9)及式(10)所示[12]:
| $\nu = {c_1}{\nu _1} + {c_2}{\nu _2},$ | (9) |
| $D = \frac{{E \cdot {h^3}}}{{12 \cdot (1 - {\nu ^2})}}{\text{。}}$ | (10) |
式中:
不同混杂比材料的表观泊松比及层合薄板弯曲刚度系数试验结果如表4所示,其中纯碳纤维和纯玻璃纤维材料的泊松比由试验测得。利用式(6)可计算不同混杂比以及不同厚度下混杂层合薄板的弯曲刚度系数,理论计算结果见表4。
|
|
表 4 层合薄板弯曲刚度系数理论值及试验值 Tab.4 Theoretical values and experimental values of bending stiffness coefficient of laminated thin plates |
通过混杂层合梁弯曲试验得到不同混杂比下层合薄板的弯曲刚度系数,并与理论计算进行对比认为:
1)在碳/玻混杂比为1.0~3.5之间时,通过理论计算能够较为准确地得到混杂层合薄板的弯曲刚度系数,理论计算值与试验值差别较小,最大差值仅为2.39%。可以认为理论计算的层合梁弯曲刚度系数有效且较为准确;
2)试件厚度对弯曲模量的影响较小,对弯曲刚度系数的计算影响也较小,随着试件的增厚或者减薄,层合梁的表观弯曲模量不会发生显著变化;理论计算不同厚度的层合薄板弯曲刚度系数与试验吻合较好,可以认为厚度不会影响理论计算层合薄板的弯曲刚度系数。
3 结 语基于层合薄板经典弯曲理论,推导了夹层及层间混杂层合薄板弯曲刚度系数计算公式,并进行对比分析研究,认为夹层混杂合板弯曲刚度系数优于层间混杂层合薄板弯曲刚度系数。通过进一步研究,还认为通过混杂层合梁的表观弯曲模量对层合薄板弯曲刚度系数进行计算,可以校核层合梁弯曲刚度理论计算的准确性;通过进行不同混杂比层合梁的弯曲试验测得层合梁表观弯曲模量,通过上述关系求得层合薄板的弯曲刚度系数与理论计算值进行比较,认为理论计算可以较为准确地预测混杂层合薄板的弯曲刚度系数,并可以指导层合壳板结构的工程设计。
通过理论分析,给出了式(6)和式(7),可以通过构成混杂层合薄板的基本材料的弯曲模量直接求出一定厚度的混杂层合薄板的弯曲刚度系数,具有较高的实用价值。
| [1] |
PERI D, CAMPANA E F. Multidisciplinary design optimization of a naval surface combatant[J]. Journal of Ship Research, 2003, 47(1): 1-12. |
| [2] |
EEFSEN T, WALREE F V, PERI D. Development of frigate designs with good sea keeping characteristics [C]//9th Symposium on Practical Design of Ships and Other Floating Structures. Luebeck-Travemuende, Germany, 2004.
|
| [3] |
冯佰威. 基于多学科设计优化方法的船舶水动力性能综合优化研究[D]. 武汉: 武汉理工大学, 2011.
|
| [4] |
石小红, 李成友, 王婷婷, 等. 复合材料层合板力学性能试验研究[J]. 工程与试验, 2014(1): 39-41+81. SHI Xiao-hong, LI Cheng-you, WANG Ting-ting, et al. Experimental study on mechanical properties of composite laminates[J]. Engineering & Test, 2014(1): 39-41+81. DOI:10.3969/j.issn.1674-3407.2014.01.011 |
| [5] |
STEEVES CA, FLECK NA. Material selection in sandwich beam construction[J]. Scripta Materialia, 2004, 50: 1335-1339. DOI:10.1016/j.scriptamat.2004.02.015 |
| [6] |
MARTENS K, CASPEELE R, BELIS J. Development of composite glass beams—a review[J]. Engineering Structures, 2015, 101: 1-15. DOI:10.1016/j.engstruct.2015.07.006 |
| [7] |
CHENG QH, LEE HP, LU C. A numerical analysis approach for evaluating elastic constants of sandwich structures with various cores[J]. Composite Structures, 2006, 74: 226-236. DOI:10.1016/j.compstruct.2005.04.007 |
| [8] |
沈林观, 胡更开, 刘彬. 复合材料力学[M]. (第2版). 北京: 清华大学出版社, 2013.
|
| [9] |
陈汝训. 混杂纤维复合材料受拉构件的最优混杂比研究[J]. 固体火箭技术, 2005, 3(3): 219-221. CHEN Ru-xun. Study on optimal hybrid ratio of hybrid fiber composite tension member[J]. Journal of Solid Rocket Technology, 2005, 3(3): 219-221. DOI:10.3969/j.issn.1006-2793.2005.03.018 |
| [10] |
洪彬, 朱一辛, 关明杰. 不同混杂比下竹木复合纤维板的弹性模量[J]. 世界竹藤通讯, 2009(6): 9-11. HONG Bin, ZHU Yi-xin, GUAN Ming-jie. MOE of bamboo-wood composite fiberboard with different hybrid ratios[J]. World Bamboo and Rattan, 2009(6): 9-11. DOI:10.3969/j.issn.1672-0431.2009.06.003 |
| [11] |
沃丁柱, 李顺林, 王业兴, 等. 复合材料大全[M]. 北京: 化学工业出版社, 2000: 539–550.
|
| [12] |
陈建桥. 复合材料力学概论[M]. 北京: 科学出版社, 2006: 48–57.
|
| [13] |
中华人民共和国国家质量监督检验检疫总局. GB/T 1456.-2005夹层结构弯曲性能试验方法[S]. 北京: 中国标准出版社, 2005.
|
 2018, Vol. 40
2018, Vol. 40
