2. 江苏现代造船技术有限公司,江苏 镇江 212003;
3. 广州船舶及海洋工程设计研究院,广东 广州 510250
2. Jiangsu Modern Shipbuilding Technology., Ltd., Zhenjiang 212003, China;
3. Guangzhou Marine Engineering Corporation, Guangzhou 510250, China
船舶在波浪中的快速性和耐波性是衡量船舶性能的重要指标,一般而言,与静水中的船舶阻力相比,波浪中阻力增加了约15%~30%[1],导致船舶产生额外的燃料消耗和失速现象,而船舶在波浪中所产生的纵摇和垂荡运动对船舶安全性和舒适性等造成了不利影响,鉴于目前国际海事组织已经推出了船舶能效设计指数(EEDI)和船舶能效营运指数(EEOI),准确预报船舶在波浪中航行的阻力增值和运动响应十分必要。
目前研究波浪增阻的方法主要有船模试验、势流理论计算和全粘流CFD软件数值模拟等。船模试验因其复杂性与成本较高等原因,往往仅作为对最终计算结果的验证。而势流理论计算相对较为简单高效,但没有考虑粘性的影响。势流理论主要包括切片法、三维面元法等,最早开始研究波浪增阻的是Havelock[2],其通过研究零航速的圆柱体在波浪中的受力,提出一个简单的公式计算船舶在波浪中的阻力增值。Maruo[3]提出了利用势流方法进行求解,并指出主要是由船舶在波浪中的垂荡和纵摇运动引起的阻力增加。而随着计算机技术与计算流体动力学的高速发展,CFD方法因其充分考虑粘性作用,且对非线性船舶运动和力的响应能够作出较为准确的预报,已越来越多地应用到船舶与海洋工程水动力学领域。国外的Orihara和Miyata[4]采用了WISDAM-X软件和overset mesh方法分析了SR-108船舶的阻力增值,结果表明该船首能够有效减小波浪中的阻力。Simonsen等[5]利用URANS代码计算了KCS船模(缩尺比为52.667)在规则波中的增阻与运动响应,并进行了相应的模型试验研究。Seonguk Seo等[6]利用开源代码Open FOAM平台对KCS船模(缩尺比为37.9)在规则波中迎浪航行进行模拟,同时评估了网格的不确定性影响,并和模型试验数据进行比较。而国内的吴乘胜等[7]建立了数值波浪水池,并对高速三体船波浪中航行进行数值模拟。沈志荣等[8 – 10]利用Open FOAM工具箱计算分析了Wigley III型、DTMB5415、S175等船型的阻力与耐波性能。查若思[11]使用naoe-FOAM-SJTU求解器分别对单体船和双体船在典型规则波海况下航行进行数值模拟。曹阳等[12]利用重叠网格方法研究了KVLCC2船模在规则波中的增阻与运动响应,分析了波浪增阻成分,并同势流理论计算结果及试验结果进行对比。
本文基于CFD软件对KSC船模在规则波中迎浪航行进行数值模拟,首先建立了数值波浪水池,利用入口处设置波速函数的方法和强迫消波技术,成功模拟了5个不同波长规则波的生成与传播;然后结合重叠网格方法,对航速为2.017 m/s、缩尺比为37.9的(带舵的)KCS船模在静水和波浪中的阻力与运动响应进行数值计算,并将计算结果与试验数据进行对比分析,最后对舰船在规则波中航行模拟的CFD方法进行了初步探讨。
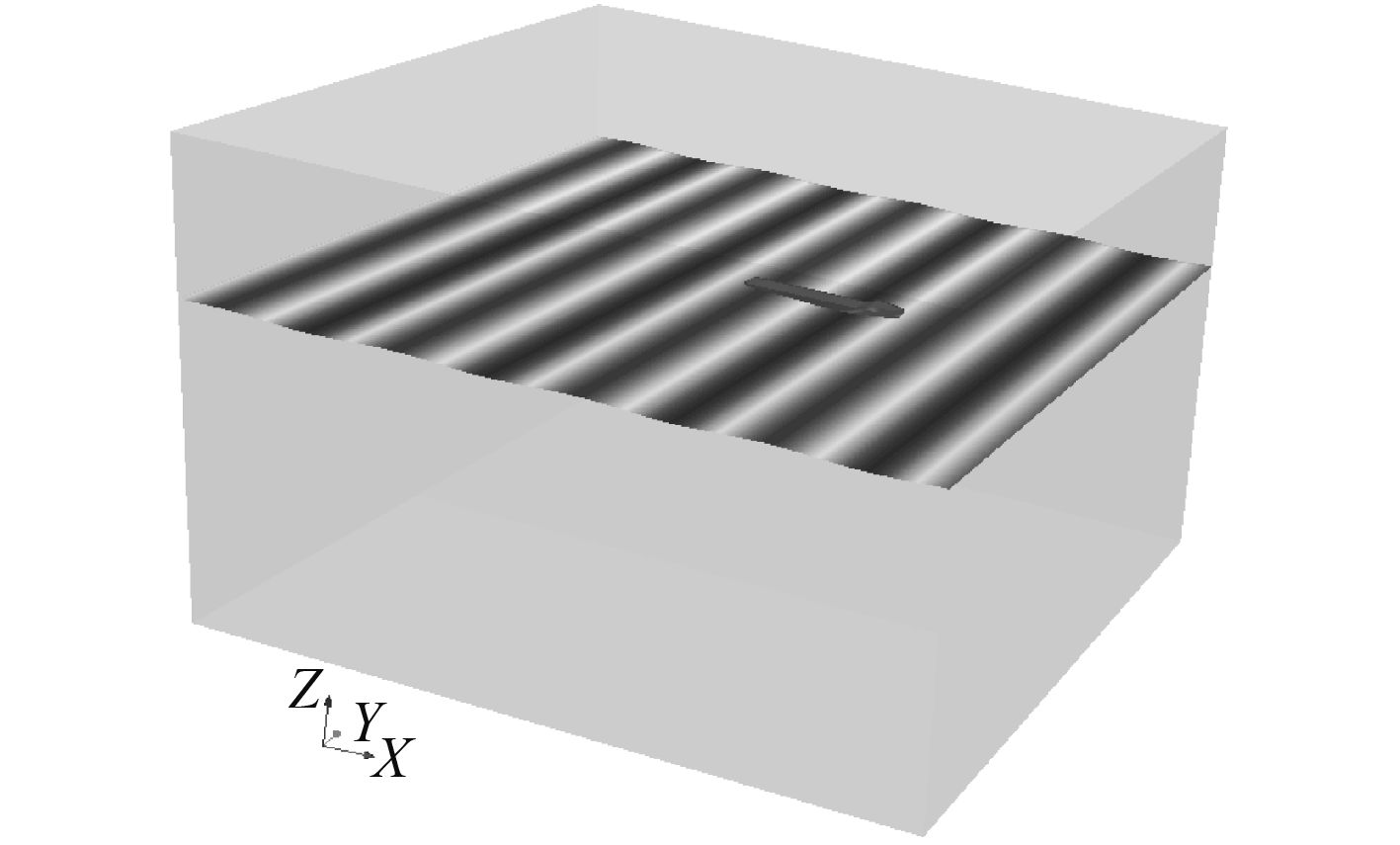
1 数值波浪水池本文的数值模拟是在长方形的三维数值波浪水池中进行,其入口距离船首约1倍船长,出口距离船尾约2.5倍船长(距离随着入射波的波长变化),侧边界距离舷侧约2倍船长,上边界距离波面约1倍船长,下边界距离波面约2倍船长。如图1所示,上部为空气,下部为水,两者间的交界面即为自由波面,波浪沿着x轴的负方向传播。
|
图 1 三维数值波浪水池 Fig. 1 3D numerical wave tank |
数值波浪水池的数学模型以连续性方程和N-S方程为控制方程:
| $\frac{{\partial \rho }}{{\partial t}} + \frac{{\partial (\rho {u_i})}}{{\partial {x_i}}} = 0\text{,}\;\;\;(i = 1,2,3)\text{,}$ | (1) |
| $\begin{split}& \frac{{\partial (\rho {u_i})}}{{\partial t}} + \frac{{\partial (\rho {u_i}{u_j})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[\mu \left(\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}\right)\right]-\\& \frac{{\partial p}}{{\partial {x_i}}} + \rho {f_i}\text{,}\;\;\;\;(i,j = 1,2,3)\text{。}\end{split}$ | (2) |
式中:ui为流体质点在i方向的速度分量;p为流体压力;fi为质量力;
本文使用Realizable k-ε湍流模型,数值计算中采用有限体积法离散控制方程,选择三维非定常分离隐式求解器和欧拉多项流模型,对流项采用二阶迎风格式,扩散项为中心差分格式,采用半隐式方法(SIMPLE法)求解压力耦合方程组;自由波面的追踪使用VOF(Volume of Fluid,流体体积)方法处理,VOF方法主要采用网格单元中流体的体积与网格总体积的比值函数来确定自由波面的位置和形状,其方程为
| $\frac{{\partial {a_q}}}{{\partial t}} + \frac{{\partial ({u_i}{a_q})}}{{\partial {x_i}}} = 0\text{,}\;\;\;(q = 1,2)\text{。}$ | (3) |
式中:a1和a2分别为空气相和水相的体积分数,并定义aq=0.5处为自由波面。
1.2 造波与消波目前常见的造波方法主要包括源造波方法和边界模拟方法。本文采用在入口处给定波速函数的方法进行造波,根据线性理论,考虑无限水深的情况,规则波的波面方程和速度场可表示为:
| $\eta = A\cos (kx - \omega t)\text{,}$ | (4) |
| $\left\{ {\begin{array}{*{20}{l}} {u = A\omega {e^{kz}}\cos (kx - \omega t)} \text{,}\\ {v = 0}\text{,} \\ {w = A\omega {e^{kz}}\sin (kx - \omega t)} \text{。}\end{array}} \right.$ | (5) |
式中:A为波幅;k为波数(
通过在离散的N-S方程中添加源项,可以实现强迫消波[13]。
| ${q_\varphi } = - \gamma \rho (\varphi - {\varphi ^ * })\text{,} $ | (6) |
式中:
| $\gamma = - {\gamma _0}{\cos ^2}({\text{π}} {x^ * }/2) \text{。}$ | (7) |
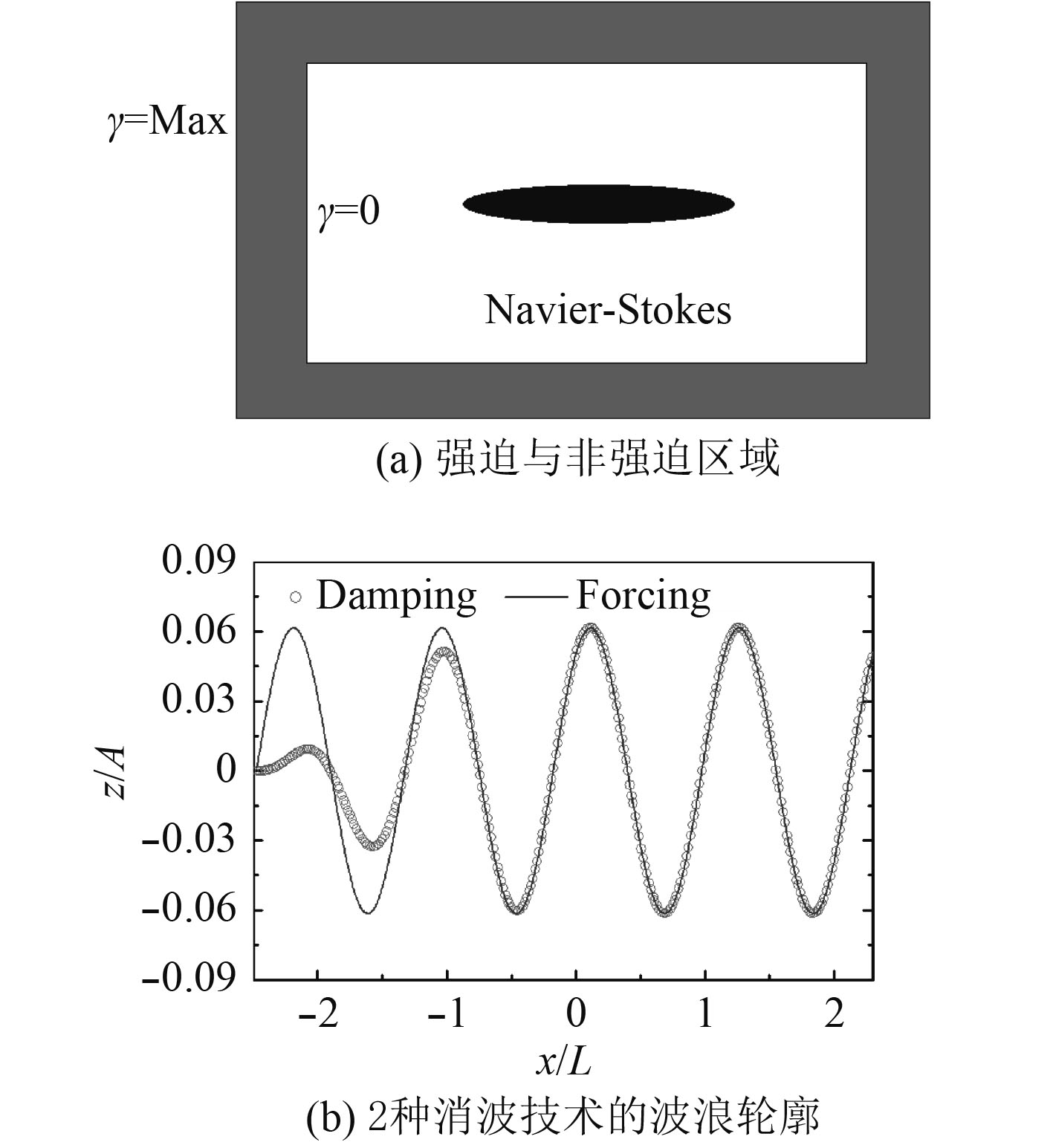
由图2(b)可见,阻尼消波方法是逐渐消除靠近出口的波浪,而强迫消波方法是将强迫区域内的波浪强迫保持原来的轮廓;强迫消波方法的边界条件设置与阻尼消波有所不同:一般入口、出口以及侧面的边界条件都设置为速度入口,而顶部边界条件设置为压力出口。
|
图 2 强迫消波技术 Fig. 2 Wave-forcing technology |
进行波浪中船模航行模拟前,需要在数值水池中实现波浪的生成与传播。本文共模拟了5个不同波长的规则波,包括短波长(Case 1,Case 2)、中波长(Case 3)、长波长(Case 4,Case5),波高比波长(H/λ)固定为1/60,水深认为是无限的,各方案波浪要素如表1所示。
|
|
表 1 各方案波浪要素 Tab.1 Wave conditions of each case |
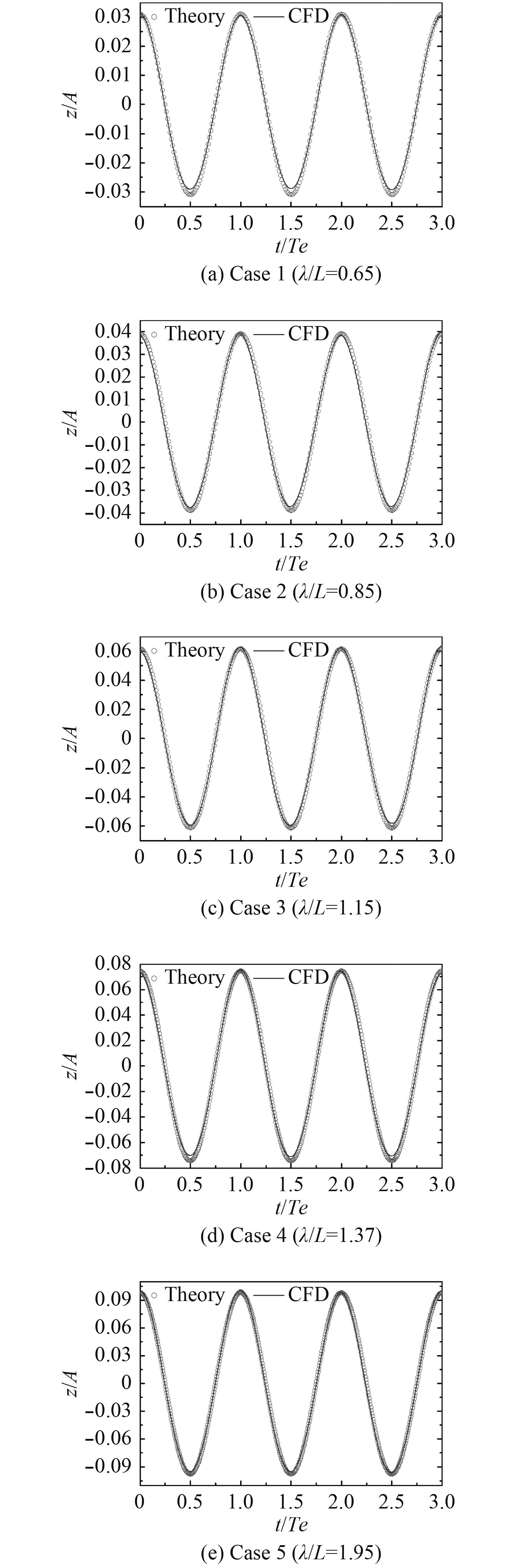
本文是在三维数值水池中对规则波进行模拟,为避免数值耗散引起波浪幅值的沿程衰减较大,在波高范围内需要设置足够的网格数,一般设置10~20个网格单元,而在波长范围内网格单元一般不少于80个,网格单元尺寸的比例取为:
|
图 3 各方案监测点波高的时间历程 Fig. 3 Time history of wave elevation for various wavelengths |
本文采用CFD方法计算了不同波长的规则波中带舵的KCS船模迎浪增阻与运动响应(纵摇和垂荡),并将计算结果与试验结果[14]进行对比分析。由于整个流场和船体几何关于船舶中纵剖面对称,因此本文计算域仅采用流场的一半进行模拟。
KCS船是由韩国船舶与海洋工程研究所(KRISO)设计的3 600 TEU集装箱船,该KCS船模(包括舵)主尺度参数如表2所示,船体几何如图4所示。
|
|
表 2 KCS船模的主尺度参数 Tab.2 Main dimensions of KCS model |

|
图 4 带舵的KCS船型计算模型 Fig. 4 KCS ship computational model with rudder |
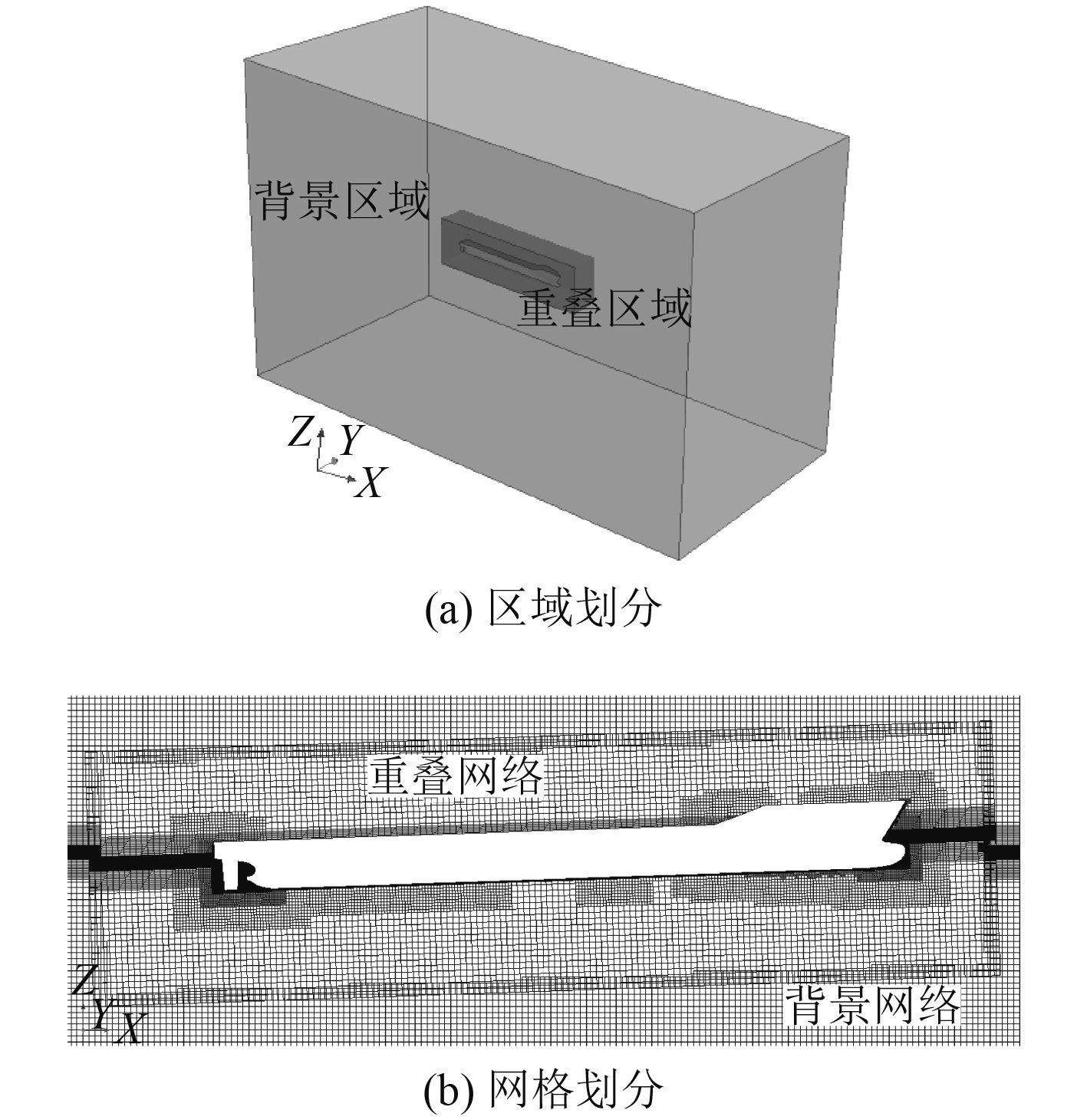
本文采用重叠网格方法求解船模在波浪中的运动响应。重叠网格(overset mesh,又称为嵌套网格),是一种区域分割与网格组合的策略,其包含2种区域:背景区域和重叠区域,如图5(a)所示,整个计算域为背景区域,嵌套在其中的小区域为重叠区域,重叠区域包裹着船体并随船体同步运动;背景区域内产生的网格称为背景网格,同样,重叠区域内产生的网格称为重叠网格,如图5(b)所示;该套网格包含2种类型的单元:有效单元和无效单元。有效单元是指参与离散求解控制方程的网格单元,而不参与计算的即为无效单元。沿着有效单元的第1层无效单元被称为受者单元,而贡献单元和受者单元相邻却位于不同区域。2套网格之间通过形成交界面(Interface)进行信息交换,通过受者单元和贡献单元之间插值来完成,一般采用拉格朗日插值的思想,进行线性插值,具有以下形式[13]:
|
图 5 重叠网格方法 Fig. 5 Overset mesh method |
| ${\phi _r} = \sum {{\xi _i}} {\phi _i}\text{,}$ | (8) |
式中:
船舶在规则波中迎浪航行时,受到波浪的扰动,船舶将产生摇荡运动,而其中纵摇和垂荡运动对波浪增阻的影响较大,因此本文仅考虑纵摇和垂荡运动,其运动方程为:
| $\left\{ {\begin{array}{*{20}{c}} {\displaystyle\frac{\rm d}{{{\rm d}t}}(m \cdot \nu ) = {F_z}} \text{,}\\ {\displaystyle\frac{\rm d}{{{\rm d}t}}({I_{yy}} \cdot \omega ) = {M_\theta }} \text{。}\end{array}} \right.$ | (9) |
式中:m为船体质量;v为船体平均速度;
本文采用软件中切割体网格技术和棱柱层网格技术进行网格生成,在船体近壁面处设置有5层棱柱层网格,平均y+取60左右,而舵附近仅设置2层,为了减少计算量,甲板可以不设置棱柱层网格;对于船体曲率变化大、流场变化比较剧烈的局部区域,例如球首、球尾和舵等,需要进行局部的网格加密;在船身周围和开尔文兴波区域内物理量随着空间位置的变化梯度较大,因此在这一范围内网格要精细一些,而远场的网格可以稀疏一些;而尾部消波区的网格设置为沿纵向逐渐变稀,这样可以起到数值消波的作用;由于采用重叠网格技术实现船模在波浪中的纵摇和垂荡运动,背景区域与重叠区域网格密度要相互匹配,以保证两区域网格之间的信息交换更加精确。图6为各区域网格和船体表面网格。
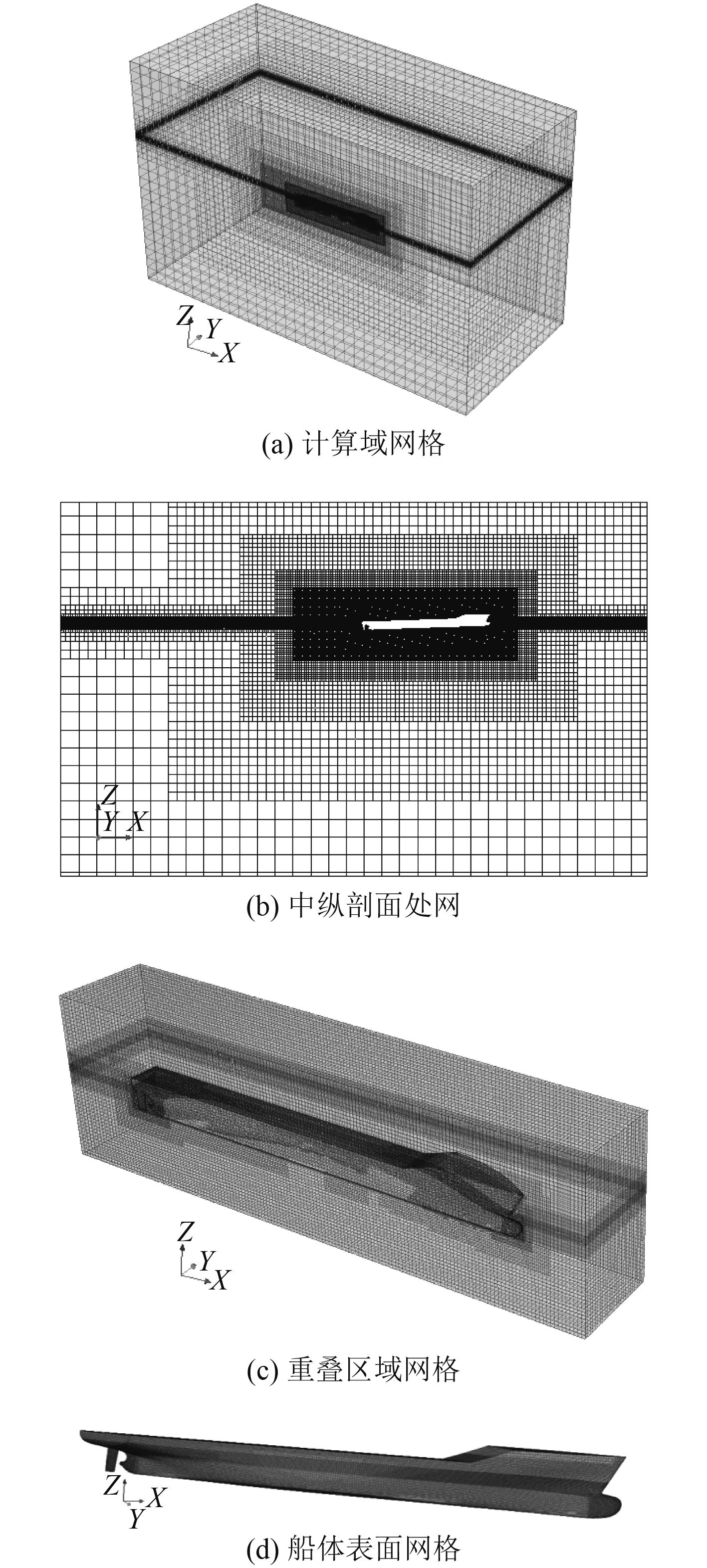
|
图 6 区域与船体网格划分 Fig. 6 Meshing of overlap and hull |
为了方便结果分析,对试验结果进行无量纲化处理,船舶在规则波中迎浪航行的垂荡与纵摇方程[15]:
| $z = {z_a} \cdot {\rm cos}({w_e}t + {\varepsilon _z})\text{,}$ | (10) |
| $\theta = {\theta _a} \cdot {\rm cos}({w_e}t + {\varepsilon _\theta })\text{,}$ | (11) |
式中:
无量纲化垂荡与纵摇幅值表达式:
| $\left\{ {\begin{array}{*{20}{c}} {z_a^{''} = \frac{{{z_a}}}{A}}\text{,} \\ {\theta _a^{''} = \displaystyle\frac{{{\theta _a}}}{{Ak}}} \text{。}\end{array}} \right.$ | (12) |
船舶阻力系数计算公式:
| ${C_T} = \frac{R}{{0.5\rho S{U^2}}}\text{。}$ | (13) |
式中:R为船舶阻力;S为湿表面积;U为船速。
船舶在波浪中增加的阻力系数表示为:
| ${\sigma _{aw}} = \frac{{{R_{aw}}}}{{\rho g\frac{{{B^2}}}{L}{A^2}}}\text{。}$ | (14) |
式中:
如图7所示,由于计算工况较多,本文仅显示了当船体运动稳定后Case 3三个周期的阻力系数、垂荡与纵摇时历曲线。

|
图 7 Case 3三个周期的阻力系数、垂荡与纵摇时间历程 Fig. 7 Time history for resistance coefficient, heave and pitch motions over 3 wave periods of Case 3 |
波浪中船舶阻力的平均值通过对阻力时间历程取平均得到,而静水中船舶阻力可以通过静水中自由船模阻力与运动响应数值计算获得,Case 0(静水中工况)的计算结果如表3所示。
|
|
表 3 静水中船模阻力系数与垂荡、纵摇幅值 Tab.3 Resistance coefficient and heave and pitch motions in calm water |
图8给出了不同波长的规则波中KCS船模的阻力系数、垂荡和纵摇的时历曲线,并将CFD计算结果与船模试验(EFD)数据进行对比。由图8可见,在短波长(Case 1,Case 2)中,垂荡运动响应与实验数据略有不同,特别是在Case 2中,阻力计算结果与实验数据差异较大;中、长波长(Case 3,Case 4,Case 5)中的运动响应与实验数据相对一致。由于Case 3模型试验的阻力值存在较大变化,因此其阻力系数取为平均值。数值计算与试验结果存在差异的潜在原因可能是模型试验存在不确定性,模型试验与数值计算存在不同初始条件,以及反射波的影响等。

|
图 8 各方案阻力系数、垂荡和纵摇的时间历程 Fig. 8 Time history for resistance coefficient, heave and pitch motions of each case |
图9给出了KCS船模波浪增阻系数以及垂荡、纵摇传递函数曲线,并与试验数据进行对比。由于波高比波长(H/λ)固定为1/60,波幅很小,因此船模阻力增加相对较小。从图9可以看出,在短波范围内波浪增阻系数较小,随着波长增大到稍大于船长(λ/L=1.15附近),波浪增阻出现峰值,而对于长波长的规则波,其垂荡运动的幅值接近于相应规则波的波幅,此时船舶处于“随波逐流”状态,尽管运动响应较大,而增加的阻力却较小。总的来讲,静水中阻力计算的差异和生成的波幅差异增加了波浪增阻的计算误差,而垂荡与纵摇传递函数随波长与船长比(λ/L)的变化与试验结果具有相同的变化趋势。
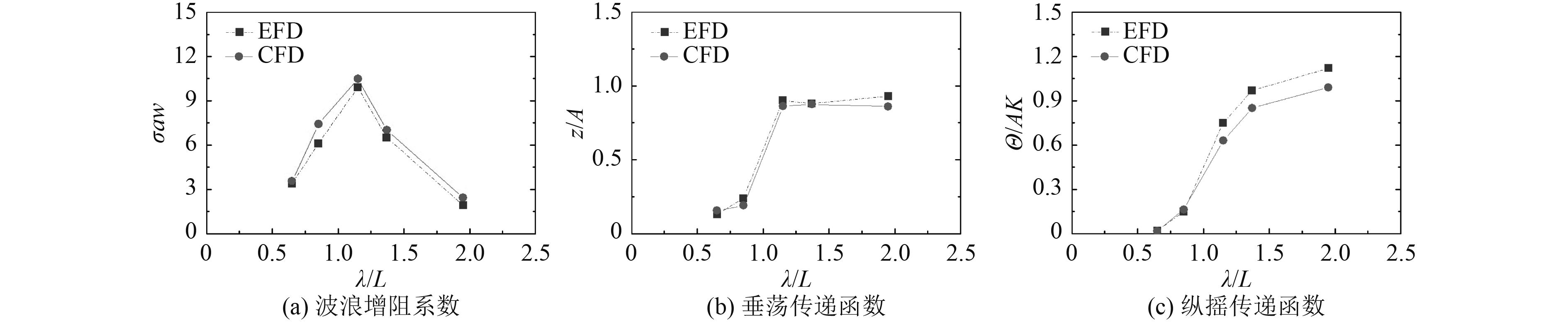
|
图 9 波浪增阻系数、垂荡与纵摇传递函数 Fig. 9 Added resistance coefficient, heave and pitch motions in head waves |
图10给出了计算稳定后KCS船模在静水和5个不同波长的规则波中的瞬时自由波面波形图,从图中可以看出波浪与船行波的相互作用随波长与船长比(λ/L)的变化。

|
图 10 各方案瞬时自由波面波形图 Fig. 10 Instantaneous wave figure of each case |
本文基于CFD软件建立了数值波浪水池,生成的规则波波幅与理论波幅吻合良好,并结合重叠网格技术与强迫消波技术对带舵的KCS船模在静水和5个不同波长的规则波中迎浪航行进行了数值模拟,计算了其在静水和波浪中的阻力、垂荡与纵摇运动响应。本文数值计算结果与试验数据总体上吻合良好,说明了CFD方法预报船舶在静水或波浪中的阻力和运动的可靠性,并得出如下结论:
1)为避免数值耗散引起波浪幅值的沿程衰减较大,在波高范围内可以设置10~20个网格单元,而在波长范围内网格单元一般不少于80个,网格单元尺寸的比例(
2)研究表明重叠网格技术可以准确处理波浪中船模的运动问题,能够获得较为精确的预报结果;
3)所采用的强迫消波技术获得了较好的效果,能够有效消除边界的波浪反射,缩短了模拟时间,同时可以实现计算域入口处的消波。
| [1] |
ARRIBAS F. Some methods to obtain the added resistance of a ship advancing in Waves[J]. Ocean Engineering, 2007, 34(7): 946-955. DOI:10.1016/j.oceaneng.2006.06.002 |
| [2] |
HAVELOCK T H. The drifting force on a ship among waves[J]. Phil. Mag. 1942.
|
| [3] |
MARUO. The excess resistance of a ship in rough seas[J]. International Shipbuiding Progress, 1957, 4(35): 337-345. DOI:10.3233/ISP-1957-43501 |
| [4] |
ORIHARA H. Evaluation of added resistance in regular incident waves by computational fluid dynamics motion simulation using an overlapping grid system[J]. Journal of Marine Science and Technology, 2003, 8(2): 47-60. DOI:10.1007/s00773-003-0163-5 |
| [5] |
SIMONSEN C, STERN F. CFD simulation of KCS sailing in regular head waves[C]//In Proceedings from Gothenburg-A Workshop on Numerical Ship Hydrodynamics, Gothenburg, 2010.
|
| [6] |
SEO S. Effect of wave periods on added resistance and motions of a ship in head sea simulations[J]. Ocean Engineering, 2017, 137: 309-327. DOI:10.1016/j.oceaneng.2017.04.009 |
| [7] |
吴乘胜, 朱德祥, 顾民. 数值波浪水池及顶浪中船舶水动力计算[J]. 船舶力学, 2008, 12(2): 168-79. WU Cheng-sheng, ZHU De-xiang, GU Min. Computation of hydrodynamic forces for a ship in regular heading waves by a viscous numerical wave tank[J]. Journal of Ship Mechanics, 2008, 12(2): 168-79. DOI:10.3969/j.issn.1007-7294.2008.02.002 |
| [8] |
SHEN Z, JIANG L, MIAO S, et al. RANS simulations of benchmark ships based on open source code[C]//In Proceedings of the Seventh International Workshop on Ship Hydrodynamics, Shanghai, China, 2011: 76–82.
|
| [9] |
YE H. Numerical prediction of added resistance and vertical ship motions in regular head waves[J]. Journal of Marine Science and Application, 2012, 11(4): 410-416. DOI:10.1007/s11804-012-1150-1 |
| [10] |
沈志荣, 叶海轩, 万德成. 船舶在迎浪中运动响应和波浪增阻的RANS数值模拟[J]. 水动力学研究与进展A辑, 2012, 27(6): 621-633. SHEN Zhi-rong, YE Hai-xuan, WAN De-cheng. Motion response and added resistance of ship in head waves based on RANS simulations[J]. Chinese Journal of Hydrodynamics (Series A), 2012, 27(6): 621-633. |
| [11] |
查若思. 单体船和双体船波浪增阻的数值计算分析[D]. 上海: 上海交通大学, 2015.
|
| [12] |
曹阳, 朱仁传, 蒋银, 等. 波浪中KVLCC2运动与阻力增加的CFD计算验证及波阻成分分析[J]. 哈尔滨工程大学学报, 2017. CAO Yang, ZHU Ren-chuan, JIANG Yin, et al. CFD verification of added resistance and motions of KVLCC2 in head waves and analysis about the constituents of wave resistance[J]. Journal of Harbin Engineering University, 2017. DOI:10.11990/jheu.201603028 |
| [13] |
CD-adapco.User guide STAR-CCM+ version 8.04[EB/OL], 2014.
|
| [14] |
http://www.t2015.nmri.go.jp/Instructions_KCS/Case_2.10/Case_2-10.html. [Z]. 2015.
|
| [15] |
方昭昭, 赵丙乾, 朱仁传. 顶浪中船舶运动的数值模拟与波浪增阻计算[J]. 中国造船, 2014(2): 8-17. FANG Zhao-zhao, ZHAO Bing-qian, ZHU Ren-chuan. Numerical simulation of ship motion and calculation of added resistance in heading waves[J]. Shipbuilding of China, 2014(2): 8-17. DOI:10.3969/j.issn.1000-4882.2014.02.002 |
 2018, Vol. 40
2018, Vol. 40
