桁架结构可设计性强、重量轻,安装方便快捷,在水面舰艇装备中得到广泛应用。随设计方法和手段的更新,对结构性能要求越来越高,必须对结构进行优化设计。对于桁架结构的优化设计,通常包扩结构拓扑优化和杆件参数优化两方面内容。1904年和1977年,Michell,Prager分别提出了Michell桁架与经典布局理论[1]。结构设计工程应用方面,以经验为导向设计方法比较常见,或者应用单一形式的结构优化设计,如拓扑优化或参数优化设计,而采用结构拓扑-参数联合优化的工程应用相对较少。采用单一形式优化设计方法,在方法上容易实现,但结构容易陷入局部最优解。本文以舰载某型装置桁架式承载结构为应用背景,采用拓扑-参数联合优化设计方法开展结构设计,即在结构初始设计阶段,根据水面舰艇空间安装要求以及载荷约束情况,采用连续结构连拓扑优化策略,获取桁架式承力结构的拓扑布局,然后利用其结果建立结构参数化模型,进行结构参数优化设计,最终得到优化后详细模型。
1 拓扑与参数联合优化策略桁架式结构强度高,形式简单,易于实现模块化,可设计性强。对于承载式桁架结构,通过调整杆件空间布局,使杆件位置与载荷沿路径一致,能够最大限度发挥杆件力学性能,减少结构总体重量,提高舰载某型装置结构性能。为了获得最优桁架结构,需要借助优化设计方法。结构的拓扑优化,本质是通过一系列数值计算方法来得到最佳的传力路径。根据对象和类型不同,优化种类可以分为连续体和离散体拓扑优化。连续体拓扑优化是在指定二维或三维连续区域,通过移除低效率材料的方法获取最优结构;离散体拓扑优化通常采用基结构方法,即在基结构中移除低效率构件获取最优结构。其中,基结构设定,从一开始便限制了优化解的范围,经过优化后最优解只是基空间一个子集,有可能真正最优解并没有在初始基结构范围内 [2 – 3]。
为消除基结构设定的缺陷,本文在桁架结构概念设计阶段,采用连续体拓扑优化方法,获取结构最优传力路径。该方法避免了在设定基结构时主观因素局限,最大限度扩展了桁架结构最优解空间范围。之后,根据连续体拓扑优化方法获取的最优结构,设计桁架结构杆件空间布局,确保杆件沿传力路径方向布置。确立桁架结构拓扑结构形式后,建立以杆件截面尺寸为变量的参数化模型,使用拉格朗日乘数法,开展以重量为目标,应力应变为约束条件的参数化优化[4 – 6]。优化流程如图1所示。

|
图 1 桁架结构优化流程 Fig. 1 Optimization process of truss structure |
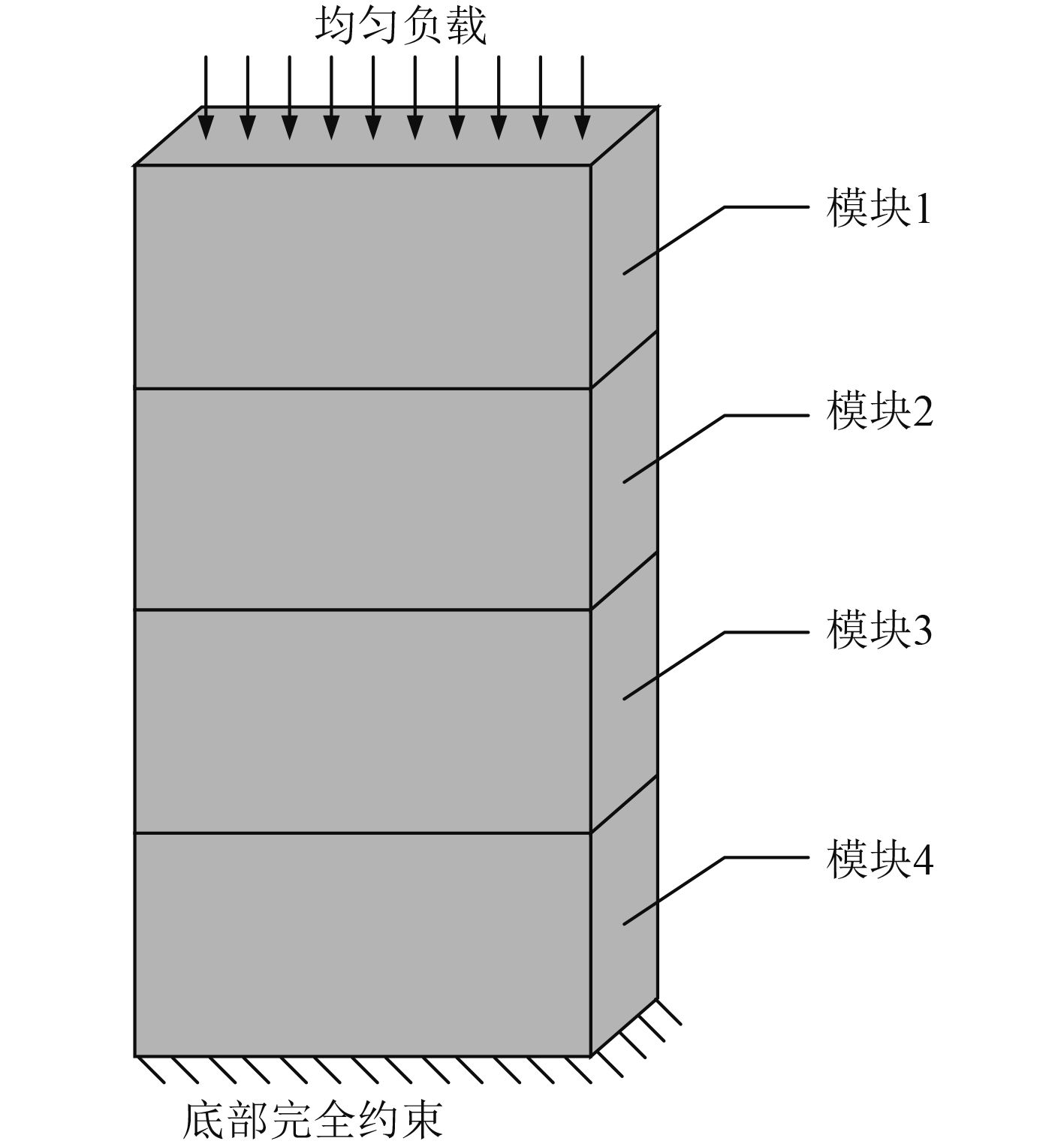
该桁架式承载结构采用模块化设计,整个结构分4个模块,在竖直方向承受大质量负载,模块结构如图2所示。桁架结构安装在浮动平台上,需要承受摇摆载荷。在满载荷负重情况下,桁架结构需要满足一定刚度要求,变形位移不能超出限定范围。
|
图 2 桁架结构空间模型 Fig. 2 Spatial model of struss structure |
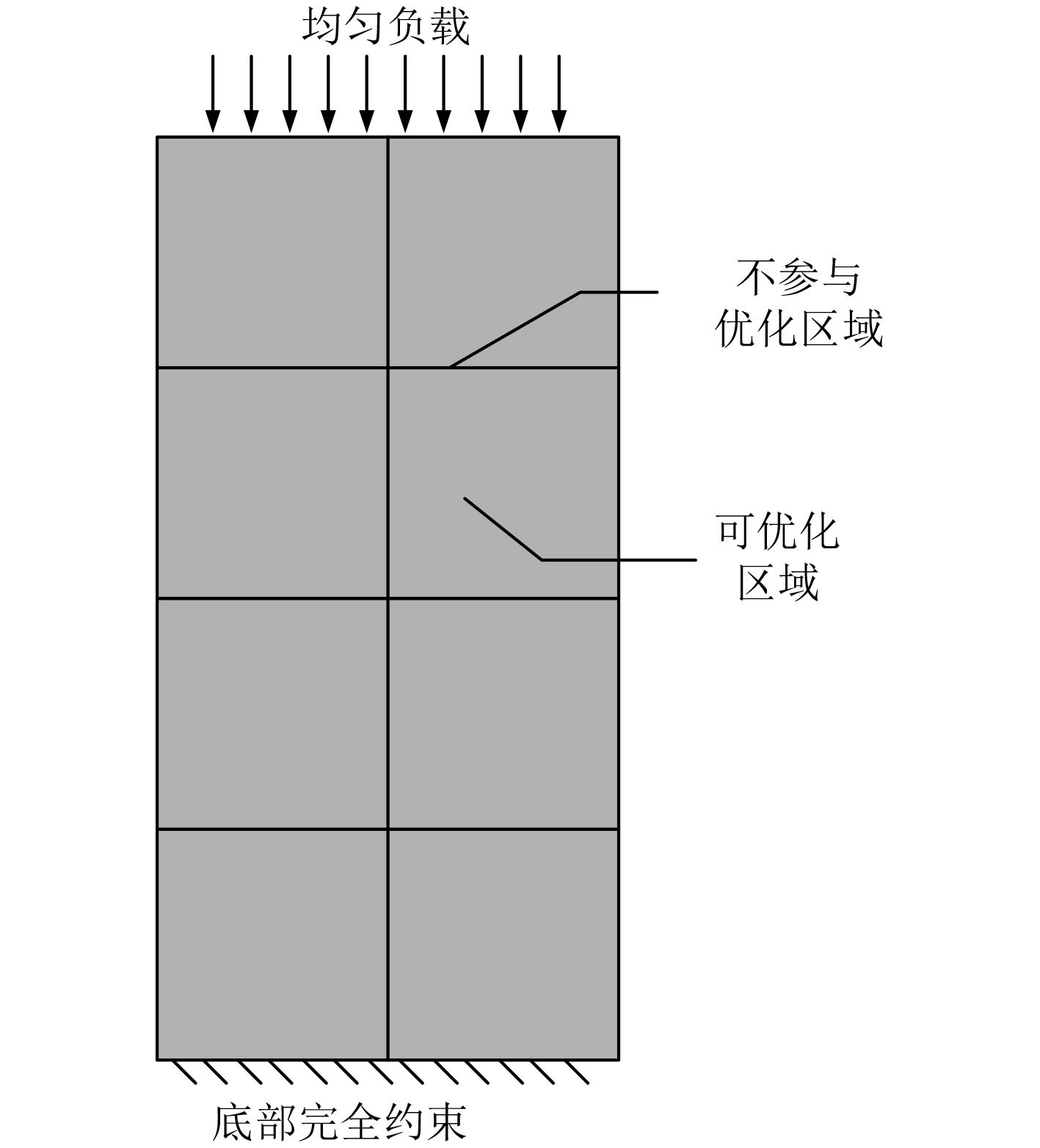
根据实际工况,将摇摆载荷简化成x,y,z方向加速度载荷。考虑到桁架结构内部承载物的包络尺寸限制,确定基本轮廓尺寸;考虑桁架上外挂设备安装,与外部接口对接以及模块化设计要求,部分横梁、竖直梁必需保留,不参与拓扑优化。考虑到在z方向载荷以及轮廓尺寸非常小,为了模型简洁高效,将载荷及结构均简化到x-y平面内,简化后模型如图3所示。
|
图 3 简化拓扑优化模型 Fig. 3 Simplified topology optimization model |
其中,结合实际工程情况及整个模型尺寸,不参与优化区域的横、竖直梁采用2个单元厚度建立。连续体拓扑优化结果与几何空间要求、边界约束条件、载荷加载矢量方向及载荷步密切相关,对其他参数,如设计区域材料特性、载荷大小等无特殊要求,只要保持载荷比例值相同即可。
2.2 连续体拓扑优化数学模型连续体结构拓扑优化应用仿真转件Ansys中的拓扑优化模块,使用变密度法优化,固体各向同性惩罚微结构模型(SIMP),材料模型将结构设计域离散成若干有限单元,各单元弹性模量和其相对密度的关系如下:
| ${E_i} = x_i^p{E_0}\text{,}$ |
式中:xi指单元i相对密度;E0指实体材料弹性模型;Ei指单元i材料弹性模量;p指惩罚因子。
本优化方法,建立在小位移、力平衡前提下,即结构在受力过程中始终保持平衡,无动能和非机械能改变。结构在载荷作用下,外力所做的功等于变形势能的增加。由于结构应变能和外力势能在数值变化保持一致,应变能能够作为结构静刚度的一个标量响应。
所以,优化问题能够表述为:受加速度载荷时,桁架结构与设计区域体积分数在变形位移约束下的结构静态应变能最小,其设计变量是结构有限元模型中设计区域内每单元的相对密度值。连续体结构拓扑优化问题的数学模型为[7 – 8]:
| $\begin{align}&{\rm{find}} \quad {X = ({x_1},{x_2}, \cdot \cdot \cdot ,{x_n})}\text{,}\\&{\min } \quad {C(X) = \sum\limits_{i = 1}^n {U_i^{\rm{T}}{{{K}}_i}{U_i}} }\text{,}\\&{\rm{s.t.}} \quad {V(X) = \sum\limits_{i = 1}^n {{x_i}{u_i} \leqslant {f_V} \cdot \sum\limits_{i = 1}^n {{u_i}} } }\text{,}\\&\;\;\;\;\;\;\;\;{f_{\min }}(X) \geqslant \overline f\text{,} \\& \;\;\;\;\;\;\;\;0 < \delta \leqslant{x_i},i = 1, \cdot \cdot \cdot ,n\text{。}\end{align}$ |
式中:X=(x1,x2,...,xn)指拓扑优化设计变量向量,xi为第i个单元相对密度;C(X)反映结构静态应变能量;Ui为单元i位移向量;Ki为单元i刚度矩阵;V(X)为设计区域结构总体积;fmin与
根据已确定的边界条件,将空间结构简化成平面模型,在平面结构上对桁架结构进行拓扑优化。基于已建立的优化模型与有限元模型,利用不断调整模型中的结构变形位移约束与体积分数开展多次试算。在优化过程中,迭代步数均设置为50,当分别设定减少体积比例为65%,70%,75%,80%时,对应优化结果如图4所示。

|
图 4 拓扑优化结果 Fig. 4 Topology optimization results |
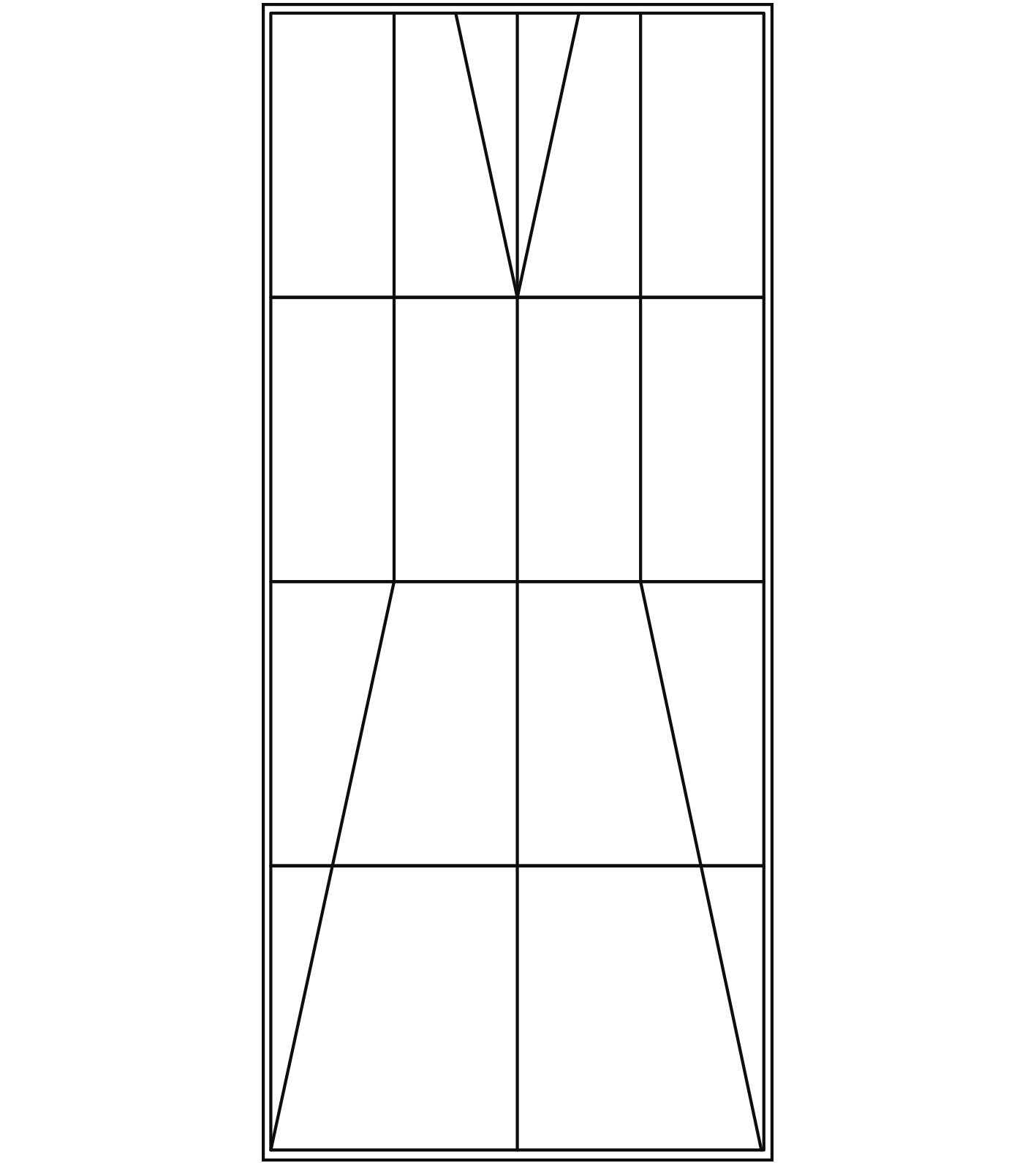
随着拓扑优化的目标体积减少百分比提高,结构越来越接近工程上桁架结构形式。以减少体积比例为80%的拓扑优化结果参考,确定桁架结构拓扑形式如图5所示。
|
图 5 桁架结构拓扑形式 Fig. 5 Topological form of truss structure |
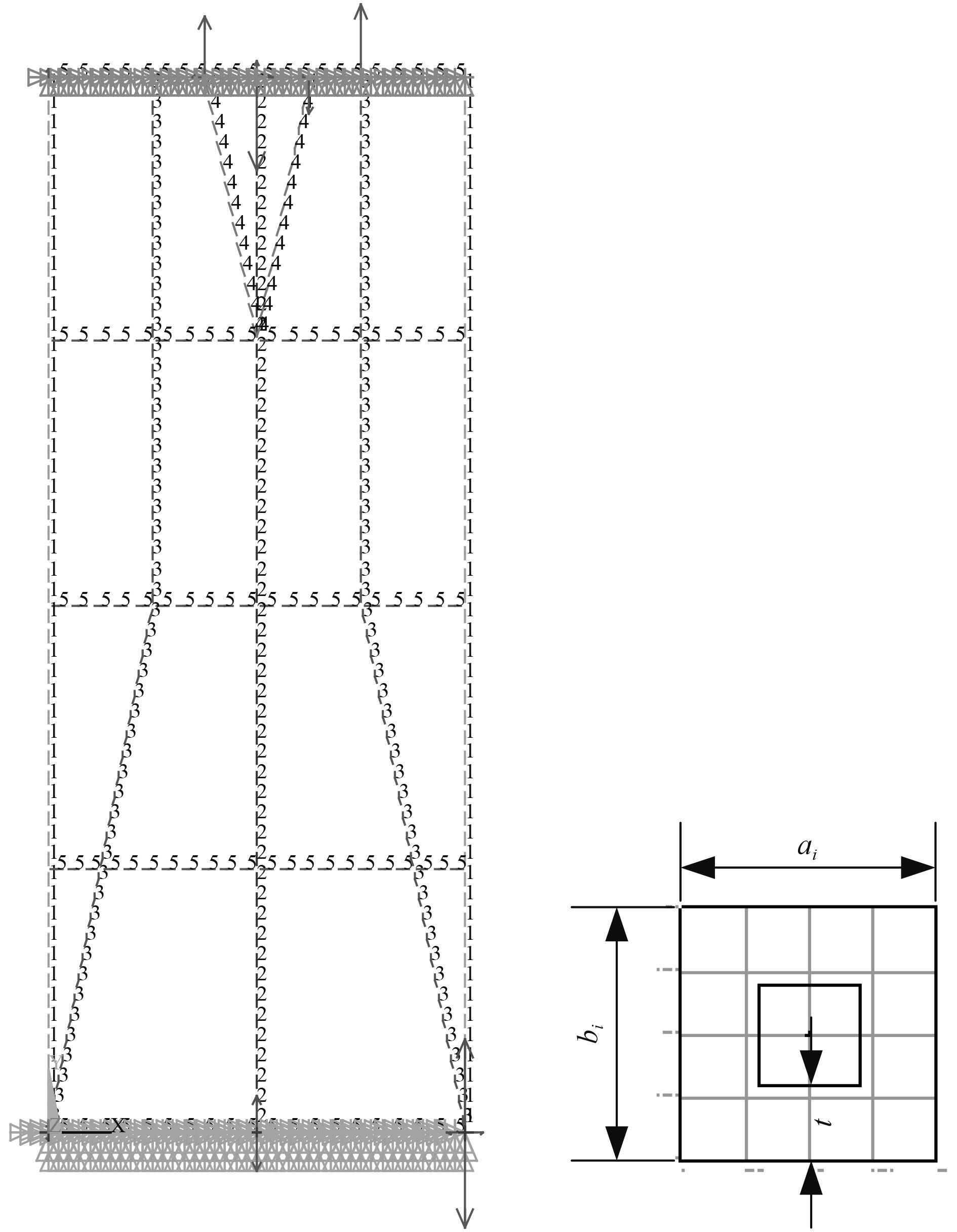
建立桁架结构参数化有限元模型。所有杆件均采用空心方管结构,每个空心方管的参数有长a、宽b和壁厚t,为了减少变量,将所有杆件壁厚均设置为t=0.003。确定后桁架结构为左右对称形式,根据其结构,将杆件分为5类,同一类型杆件具有相同尺寸参数ai,bi和t,桁架结构杆件类型分布及杆件横截面如图6所示。
|
图 6 杆件类型分布及横截面形式 Fig. 6 Member type distribution and cross section |
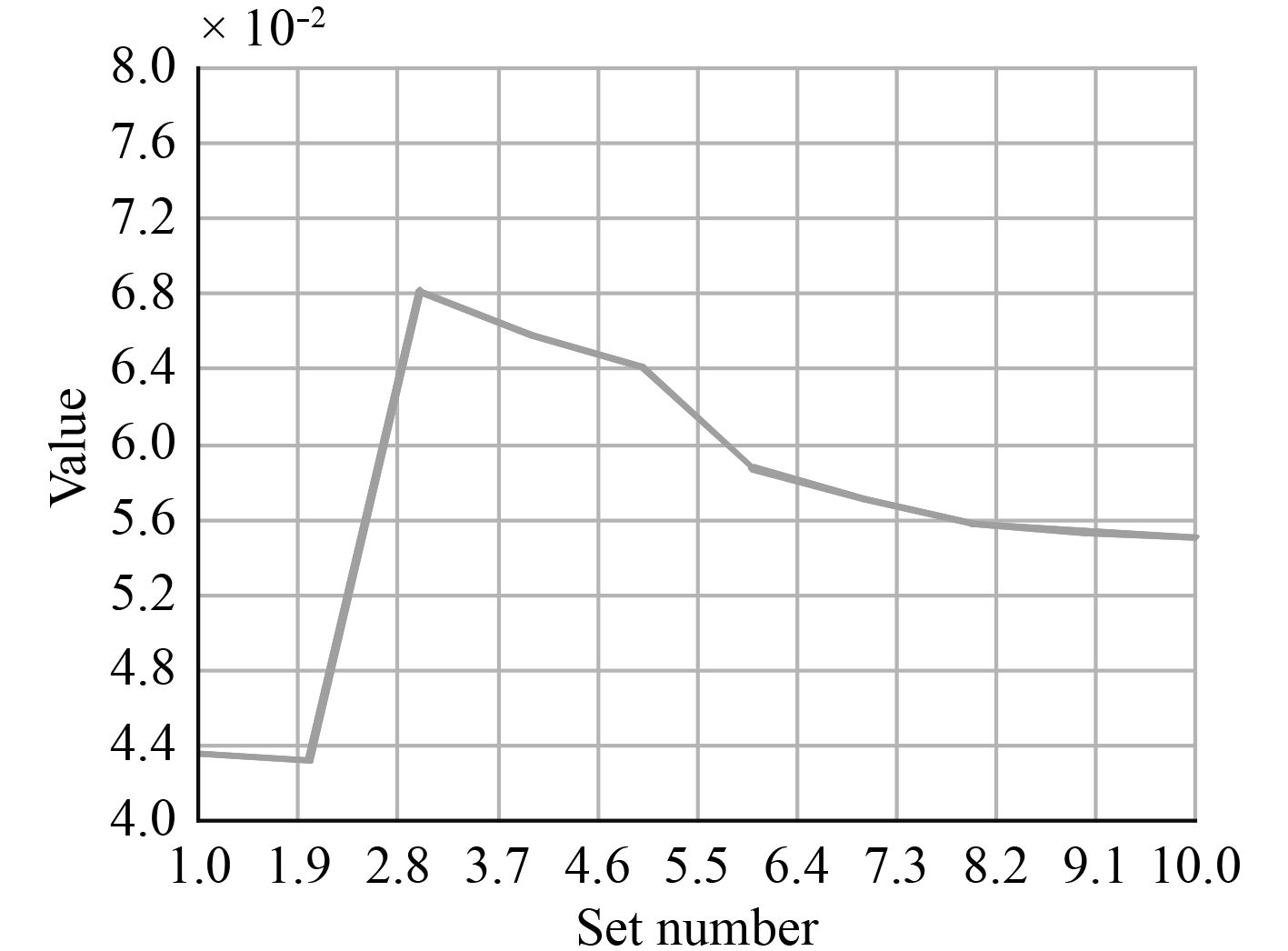
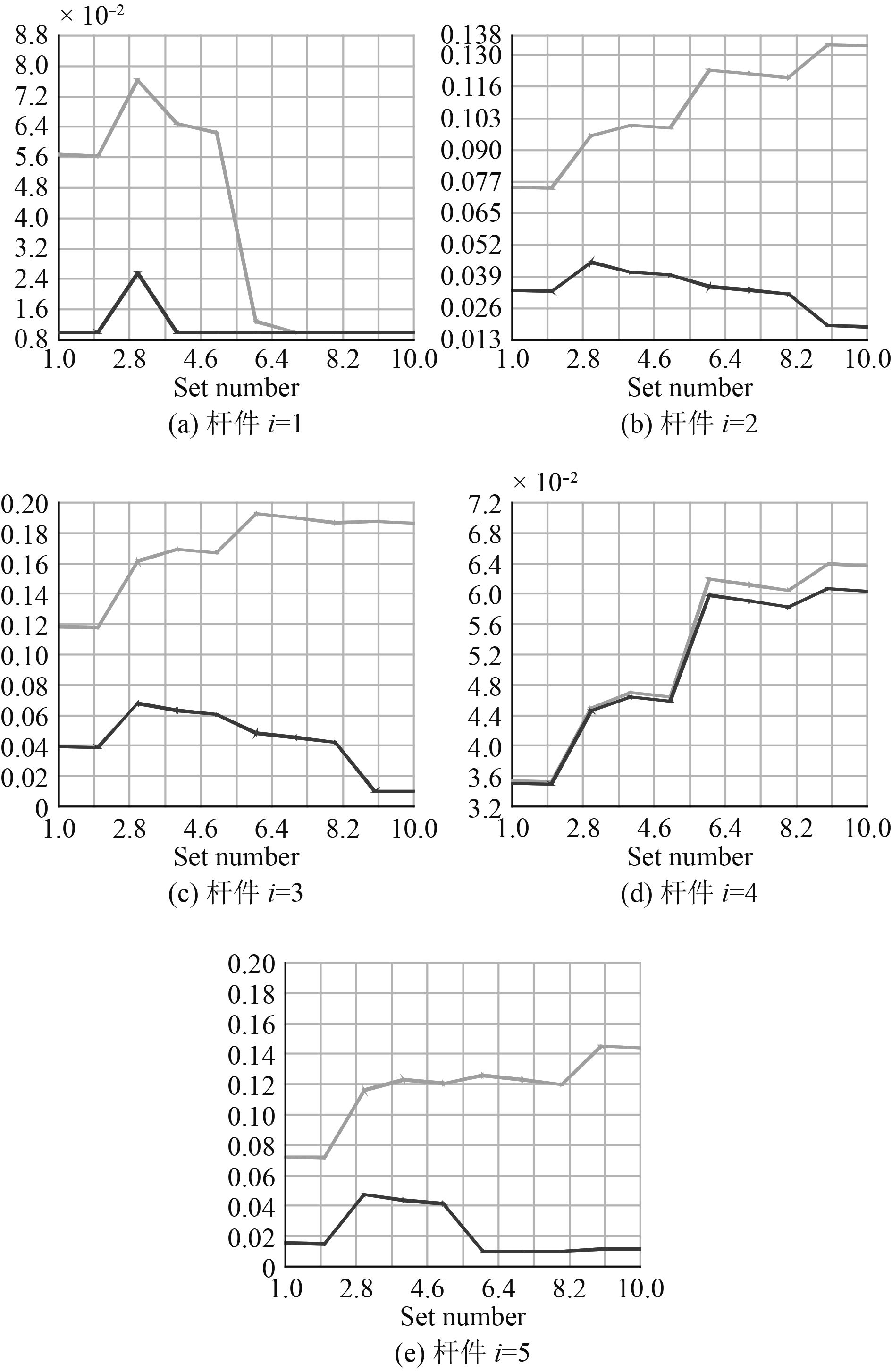
在参数优化中,桁架底部节点完全约束,顶部所有节点全自由度耦合,竖直方向和摇摆方向载荷简化到桁架平面内,其载荷比例保持与拓扑优化施加载荷比例相同。所有杆件截面初始参数设置为ai=0.08,bi=0.08,t=0.003(i=1,2,...,5)。经过计算,初始状态桁架结构在该约束条件下变形位移dis=0.396。在参数优化中,将桁架结构位移约束设置为初始位移的1/4,即dis≤0.1;截面参数限定范围为0.01≤ai≤0.2,0.01≤bi≤0.2;优化目标为体积最小。参数优化的体积变化历程如图7所示。各杆件横截面尺寸变化历程如图8所示。最终优化后桁架结构详细情况如图9所示。
|
图 7 体积变化历程 Fig. 7 Volume evolution process |
|
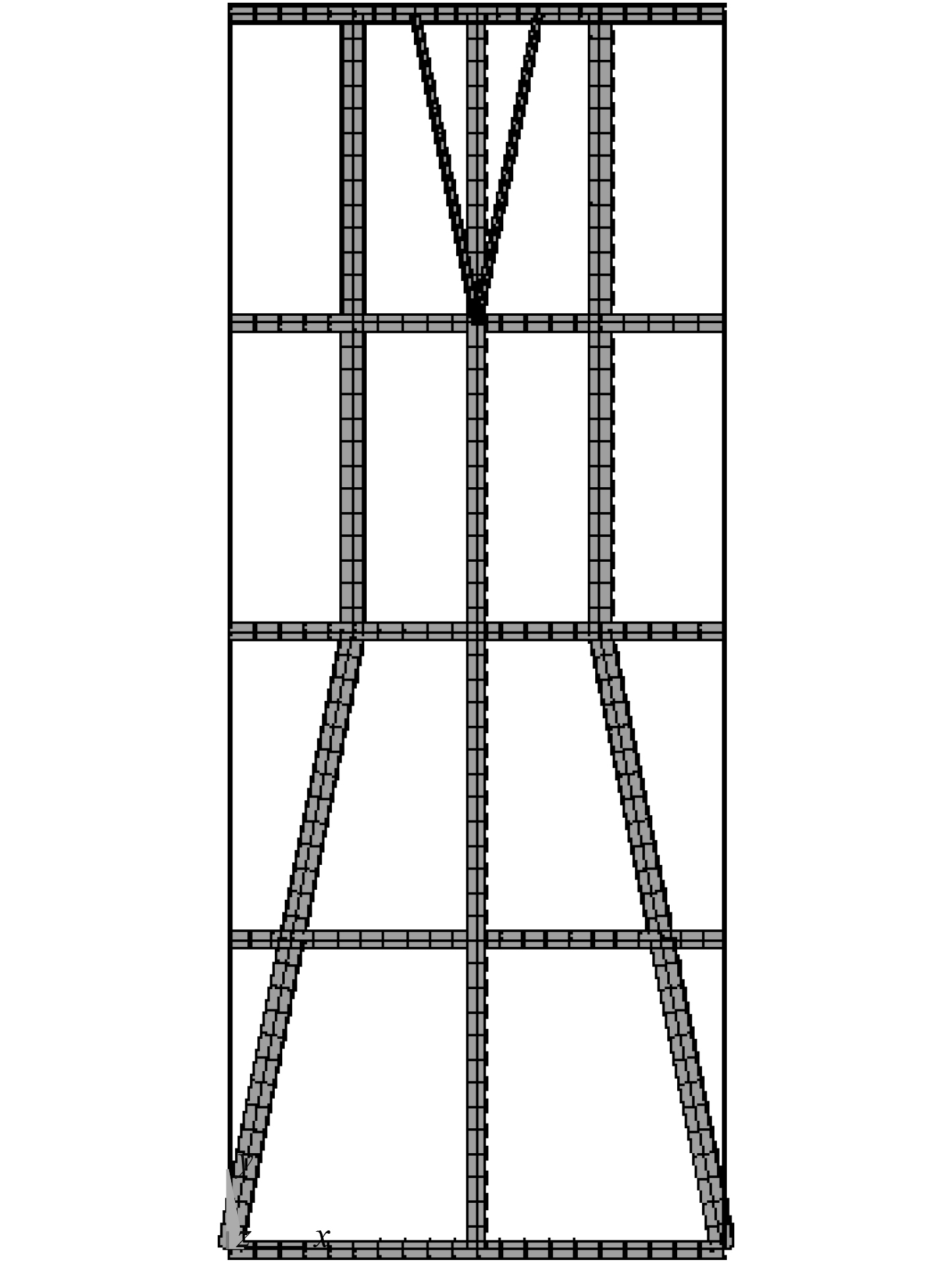
图 9 最终优化结果 Fig. 9 Final optimization results |
|
图 8 杆件截面尺寸变化历程 Fig. 8 Evolution of bar section size |
经过优化,结构呈现对称结构形式,这与载荷对称加载形式相符,说明优化程序对结构产生作用且满足预期效果。经过优化,桁架式结构承载杆件主要集中在靠中间位置,平面桁架上两边竖直杆件,即类型1截面尺寸减小;中间竖直杆件,即类型2、类型3和类型5,截面尺寸增大。这说明中间杆件对结构刚度和稳定性起重要作用。桁架结构顶部为载荷施加部分,为了保证结构上部刚度,支撑顶部横梁,优化结果保留辅助支撑杆件,即类型4截面杆件。同时对辅助支撑杆截面参数进行优化,减少截面尺寸。
4 结 语目前结构优化设计方法应用越来越普遍,针对工程应用中采用单一的拓扑或者参数优化方法,不易获得全局最优解情况,本文以舰载某型装置桁架式承载结构为应用背景,提出桁架结构设计的拓扑与参数联合优化方法。首先通过拓扑优化得到桁架结构构型,然后在此基础上进一步开展结构参数优化,确定桁架结构中最优截面尺寸。通过联合优化方法,获得桁架结构拓扑和截面参数最优结构形式,在保证结构刚度,满足安全的前提下,减轻结构重量。该方法易于工程实现,能为桁架式承载结构设计提供理论依据和有益参考,提高设计效率。
| [1] |
周奇才, 吴青龙, 熊肖磊, 等. 桁架结构拓扑及截面尺寸优化设计方法[J]. 西安交通大学学报, 2016, 50(9): 1-9. ZHOU Qi-cai, WU Qing-long, XIONG Xiao-lei, et al. Optimal design of topology and section size of truss structures[J]. Jouunal of Xi'an Jiaotong University, 2016, 50(9): 1-9. |
| [2] |
郝宝新, 周志成, 曲广吉, 等. 大型航天器桁架式主承力结构构型拓扑优化研究[J]. 航天器工程, 2014, 23(2): 44-51. HAO Bao-xin, ZHOU Zhi-cheng, QU Guang-li, et al. Research on configuration topology optimization for main truss structure of large spacecraft[J]. Spacecraft Engineering, 2014, 23(2): 44-51. DOI:10.3969/j.issn.1673-8748.2014.02.008 |
| [3] |
黄玉兰, 刘剑. 基于ANSYS Workbench的FAST天线背架结构的优化算法[J]. 中国工程机械学报, 2016, 14(4): 342-346. HUANG Yu-lan, LIU Jian. Algorithmic optimization design on FAST antenna frame based on ANSYS Workbench[J]. Chinese Journal of Construction Machinery, 2016, 14(4): 342-346. |
| [4] |
杨博, 金仁和. 基于满应力法的平面桁架优化[J]. 钢结构, 2015, 30(3): 18-20. YANG Bo, JIN Ren-he. Optimization of plane truss based on full stress method[J]. Steel Structure, 2015, 30(3): 18-20. |
| [5] |
徐芝纶. 弹性力学[M]. 北京: 高等教育出版社, 2006: 257–260.
|
| [6] |
ESCHENAUER H A, OIHOFF N. Topology optimization of structures: a review[J]. Appl Mech Rev, 2001, 54(4): 331-390. DOI:10.1115/1.1388075 |
| [7] |
李东泽, 于登云, 马兴瑞. 基频约束下的桁架结构半定规划法拓扑优化[J]. 工程力学, 2011, 28(2): 182-185. LI Dong-ze, YU Deng-yun, MA Xing-rui. Truss topology optimization with fundamental frequency constrains via semidefinite programming[J]. Engineering Mechanics, 2011, 28(2): 182-185. |
| [8] |
代鸿, 曹波. 多目标模糊优化在船舶结构设计中的应用[J]. 舰船科学技术, 2017, 39(7A): 4-6. DAI Hong, CAO Bo. Application of multi objective fuzzy optimization method in ship structure design[J]. Ship Science and Technology, 2017, 39(7A): 4-6. |
 2018, Vol. 40
2018, Vol. 40
