海水作为一种导电媒质,对电磁波衰减很大,目前,水下通信的有效手段仍然以甚低频和超低频通信为主,低频通信是在舰船等军用领域具有重要应用前景。低频电磁波经海水衰减,信号十分微弱。因此,其接收设备高灵敏低频磁性天线[1]必须具有很高的灵敏度及很强的抗干扰能力。
但是,高灵敏低频磁性天线对磁场十分敏感,随舰船振动会切割磁力线形成感应电流,使高灵敏磁性天线的信噪比降低、产生信号失真,甚至无法完成正确的通信任务,其中以垂向振动影响最为显著。消除低频磁性天线的运动感应噪声具有十分重要的意义。由于低频磁性天线对电磁场的敏感度过高,因此必须选用一种合适的、不会产生多余电磁噪声的减振方式对高灵敏低频磁性天线安装位置的振动进行衰减。
隔振分为被动隔振和主动隔振[2 – 5],前者依赖元器件的刚度、阻尼特性实现隔振,而主动隔振则依赖主动驱动器产生驱动力从而达到抑制振动的目的。国内外研究表明[6 – 7],被动隔振通过增加层数的方式能够有效地增强隔振性能,但当层数增加时系统的稳定性会下降,且较主动隔振技术而言,被动隔振的无源特性不会对设备本身产生额外电磁干扰。
本文从磁性天线运动感应噪声产生原理出发,分析振动对通信信号的影响,并采取双层隔振方式实现天线振动抑制,通过仿真对比掌握系统隔振特性,然后从有限元仿真及试验的角度出发完成隔振系统性能验证。
1 天线振动分析及建模 1.1 舰船天线运动感应噪声原理舰船低频磁性天线产生运动感应噪声的原因是天线振动引起磁场与天线实际轴线之间夹角θ的变化,产生了随时间变化的磁感线切割,造成了线圈磁通量的变化,引起了磁性天线的收发噪声信号电压,其原理如图1所示[8]。
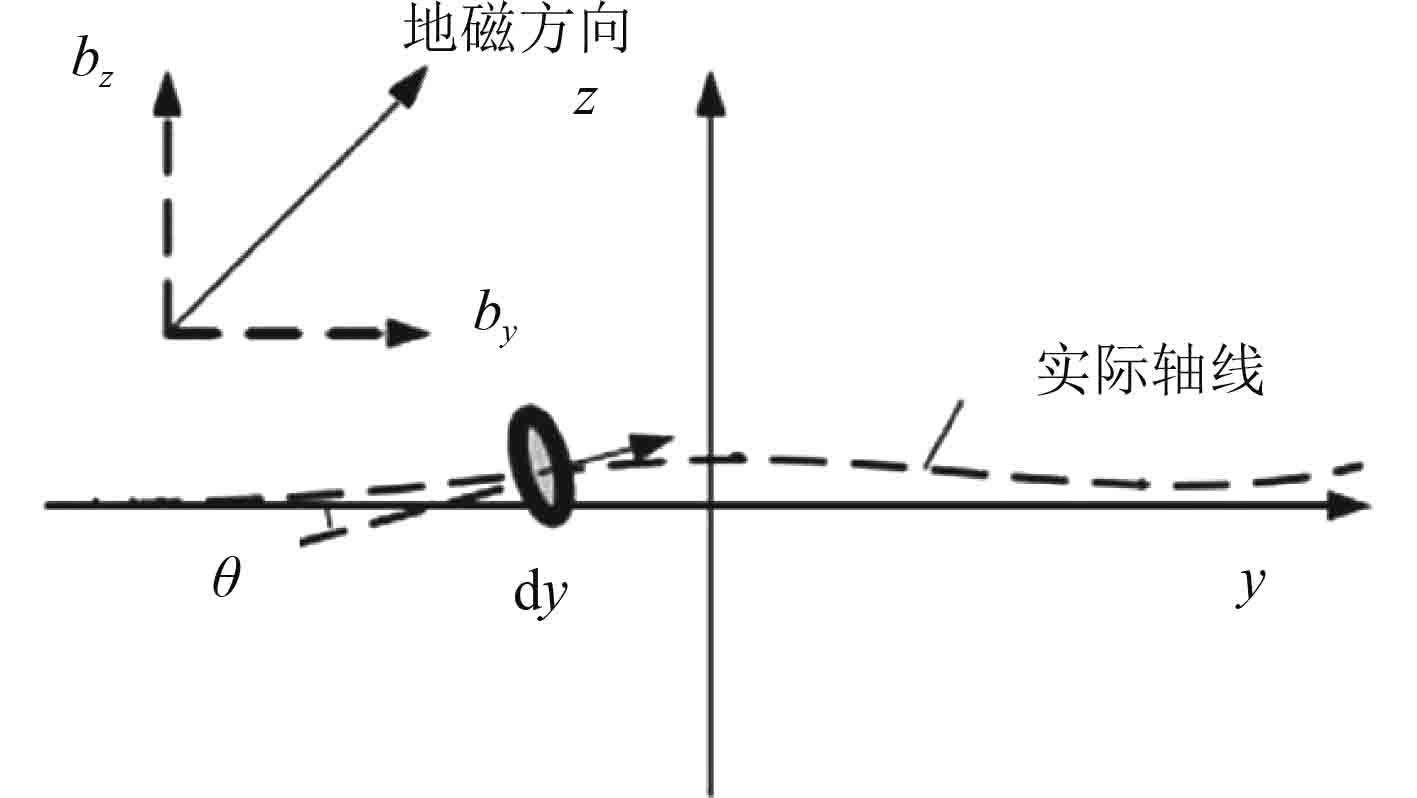
|
图 1 运动感应噪声原理 Fig. 1 Principle of motion induced noise |
通过微元天线的磁通量为:
| ${\rm d}\varPhi = \mu (y)\cos \theta ({B_y} + {B_z}{{\partial z} / {\partial y}}){\rm d}y{\text{,}} $ | (1) |
式中
| $ v(t) = \int {\frac{{{\rm d}\varPhi }}{{{\rm d}t}}} {\rm d}y = {B_z}\int {\mu (y)} \frac{{{\partial ^2}z(y,t)}}{{\partial y\partial t}}{\rm d}y{\text{。}} $ | (2) |
式中运动感应噪声电压大小与磁性天线的振动强度息息相关,因此采取适宜的隔振方法,减弱通信天线的振动强度,可以减小天线运动感应电压,提高通信系统的信噪比
1.2 低频天线被动隔振建模多级被动隔振技术在获取优异隔振性能的同时意味着需要增加多个没有实际用途的中间层质量,因此需要综合掌握系统的隔振特性,从而获得最优设计结果,理想情形下,多级被动隔振系统动力学模型如图2所示,可以得到多级被动隔振系统动力学方程表达式:
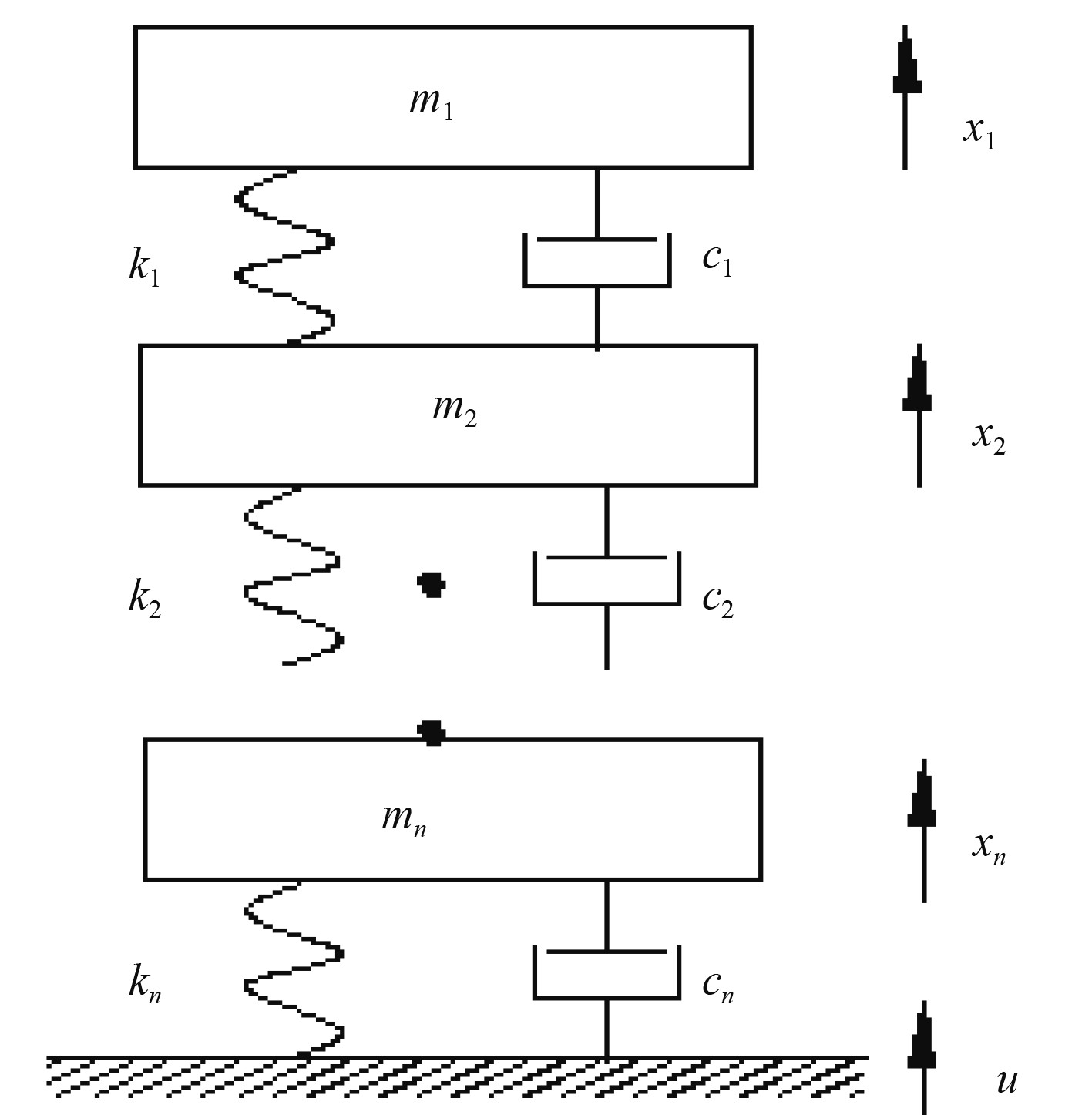
|
图 2 多级被动隔振系统动力学模型 Fig. 2 Multi-stage passive vibration isolation system dynamics model |
| $ {{M}}\ddot {{X}} + {{C}}\dot {{X}} + {{KX}} = {{A}}\dot u + Bu {\text{,}}$ | (3) |
其中M,C,K分别为系统的质量矩阵、阻尼矩阵和刚度矩阵。当隔振级数n=2时,为双级隔振系统,即
| $ \begin{array}{l}\left[ {\begin{array}{*{20}{c}}{{m_1}}&{}\\{}&{{m_2}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{\mathop {{x_1}}\limits^{..} }\\{\mathop {{x_2}}\limits^{..} }\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}{{c_1}}&{ - {c_1}}\\{ - {c_1}}&{{c_1} + {c_2}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{\mathop {{x_1}}\limits^. }\\{\mathop {{x_2}}\limits^. }\end{array}} \right]+\\ \left[ {\begin{array}{*{20}{c}}{{k_1}}&{{k_1}}\\{ - {k_1}}&{{k_1} + {k_2}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{{x_1}}\\{{x_2}}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}0\\{{k_2}}\end{array}} \right]u + \left[ {\begin{array}{*{20}{c}}0\\{{c_2}}\end{array}} \right]\mathop u\limits^. {\text{。}}\end{array} $ | (4) |
令
| $\displaystyle\left\{ \begin{aligned}& {\omega _{1,2}}^2 = \displaystyle\frac{{{k_{1,2}}}}{{{m_{1,2}}}},\lambda = \frac{\omega }{{{\omega _1}}},{\xi _1} = \frac{{{c_1}}}{{2\sqrt {{k_1}{m_1}} }}{\text{,}}\\& {\xi _2} = \displaystyle\frac{{{c_2}}}{{2\sqrt {{k_2}{m_2}} }},{a_1} = \frac{{{\omega _2}}}{{{\omega _1}}},{\mu _1} = \frac{{{m_1}}}{{{m_2}}}{\text{。}}\end{aligned} \right.$ | (5) |
双级隔振系统幅值衰减的无量纲表达式为:
| $\displaystyle\left\{ \begin{aligned}& L = - 10 \cdot \log \left(\frac{{{C^2} + {D^2}}}{{{A^2} + {B^2}}}\right){\text{,}}\\& A = {\lambda ^4} - {\lambda ^2}(\displaystyle{a_1}^2 + 4{\xi _1}{\xi _2}{a_1} + {\mu _1} + 1) + {a_1}^2{\text{,}}\\& B = 2{\lambda ^3}({\xi _1}{a_1} + {\xi _1}{\mu _1} + {\xi _1}) - 2\lambda ({\xi _1}{a_1}^2 + {\xi _2}{a_1}){\text{,}}\\& C = {a_1}^2 - 4{\xi _1}{\xi _2}{a_1}{\lambda ^2};D = 2\lambda ({\xi _1}{a_1}^2 + {\xi _2}{a_1}){\text{。}}\end{aligned} \right.$ | (6) |
依照单一变量原则可以依次得到不同
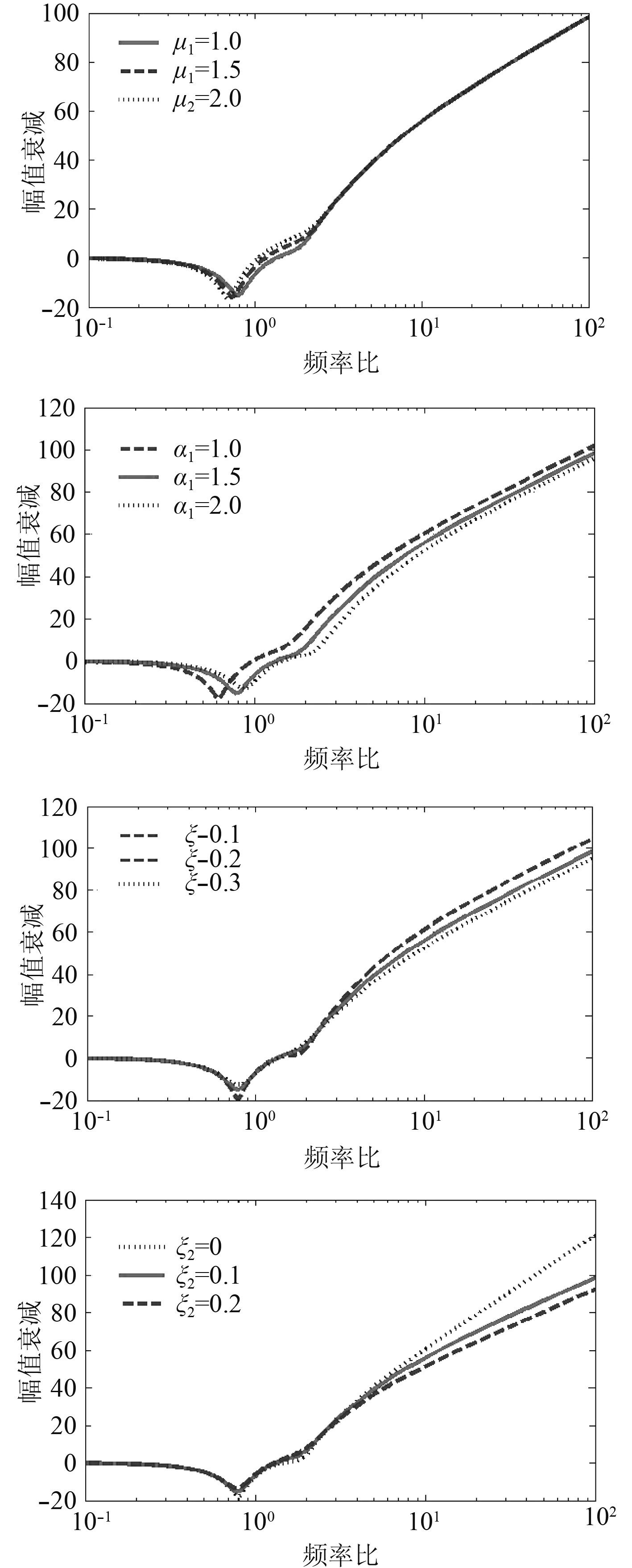
|
图 3 系统参数影响特性 Fig. 3 System parameter influence characteristics |
根据图中特性曲线可以得出以下结论:
1)增加质量比或减小上下级固有频率比,能够略微扩宽系统的隔振频带,但无法提高工作频段内幅值衰减的增长速率;
2)增加上、下级阻尼比能够有效地抑制共振,降低系统发生共振时的振幅,但在隔振频段内,上下级阻尼的增加会对系统幅值衰减性能产生负面影响;
3)阻尼比不同时的隔振系统谐振频率相近,弱阻尼条件下,系统谐振频率近似等于无阻尼固有圆频率。
2 双级被动隔振的结构有限元仿真 2.1 隔振系统结构方案设计在满足隔振元件选取原则[9]:刚度合适、形状合适、阻尼比合适、材料合适的前提下,选取了BE型橡胶隔振器,该隔振器在橡胶内固连着金属框架,能够保证足够的结构强度,避免橡胶长期受载情况下的疲劳断裂致使装置意外脱落。
双级隔振系统中各自由度之间的耦合严重影响系统的隔振性能,一般在隔振元件安装时应满足对称于中心主惯性坐标轴的垂直平面的原则,并保证各隔振元件承受的载荷一致,且上、下级之间的隔振元件应该不对齐布置从而能够减小传递到隔振对象的振动。在满足三维空间尺寸要求前提下,依照安装布置原则的隔振结构如图4所示。
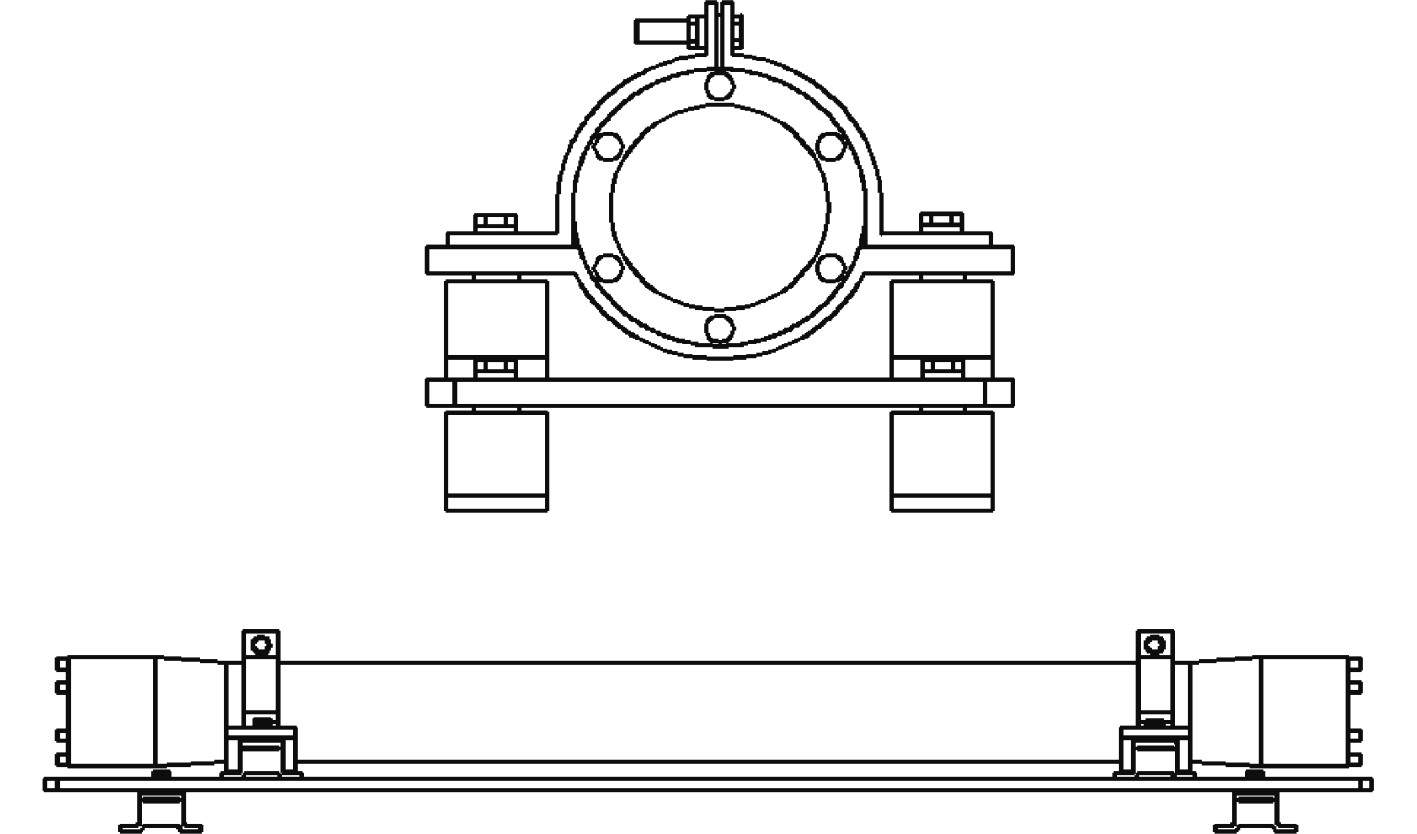
|
图 4 隔振样机结构示意图 Fig. 4 Vibration isolation prototype structure diagram |
Ansys位移谐响应分析可以确定线性结构在承受简谐载荷时的稳态响应,分析过程中只计算结构的稳态受迫振动,不考虑激振开始时的瞬态振动,本文位移谐响应分析通过0~150 Hz内取15个频率点在给定位移激励下计算得到的磁性天线某频率下表面振幅最大值,从而完成仿真性能验证。各个频率点仿真计算结果拟合曲线如图5所示。
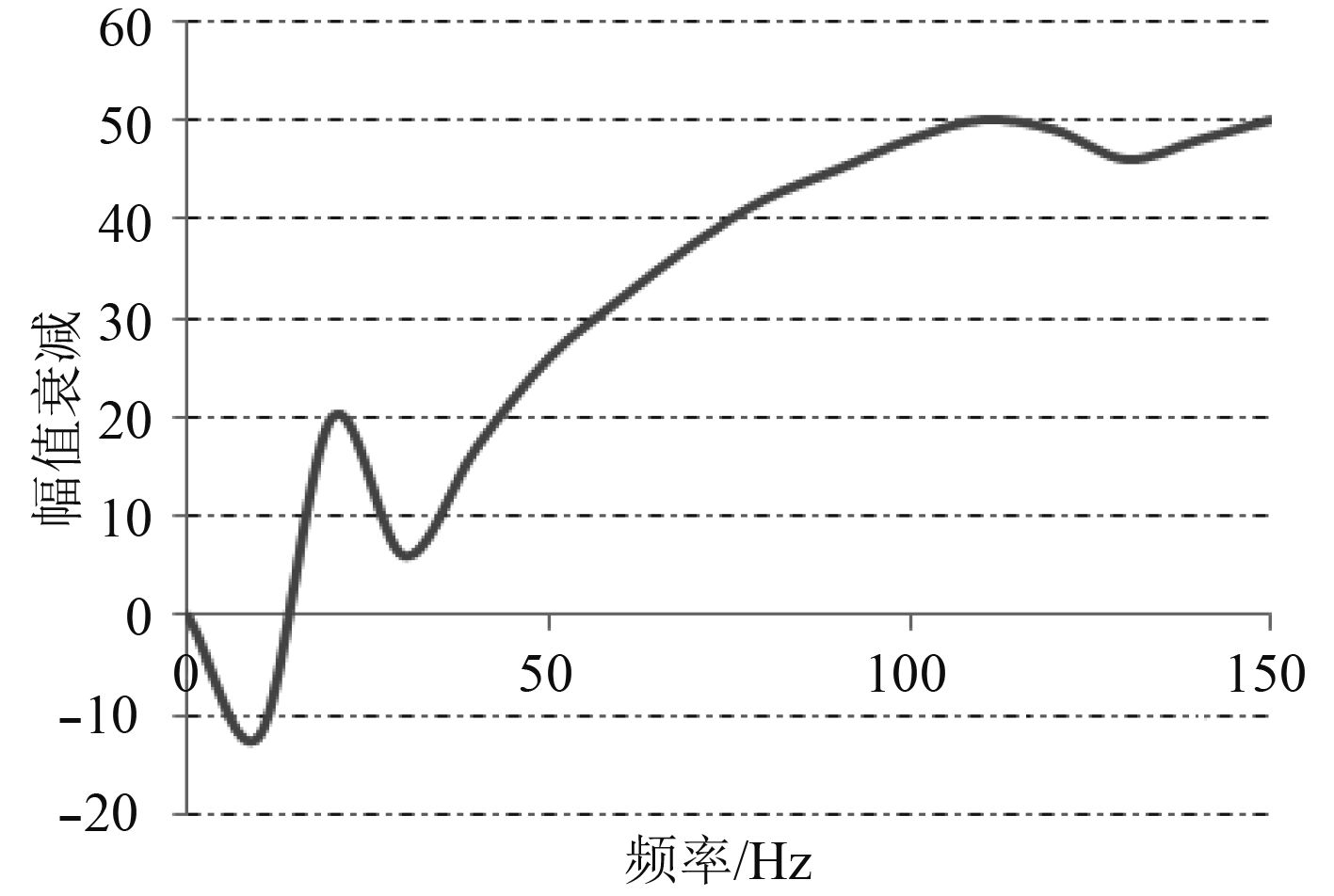
|
图 5 幅值衰减有限元仿真结果 Fig. 5 Amplitude attenuation finite simulation results |
根据图示结构有限元仿真结果可以得到以下结论:
1)共振频段内,振动抑制作用较差,并在第1个谐振频率,振幅达到最大,但此时共振振幅不超过结构允许最大幅值,满足隔振需求;
2)工作频段内幅值衰减性能能够达到25 dB以上,且随频率的增加,隔振性能呈上升趋势,满足隔振需求。
3 低频天线隔振系统试验测试为进一步明确系统隔振性能,在仿真基础上搭建如图6所示双级被动隔振结构试验装置。

|
图 6 试验测试装置 Fig. 6 Test device |
试验基本流程为计算机给出振动控制指令使振动台产生不同的振动激励,并完成定频试验、扫频试验测试。磁性天线上从固定端到中心处等距分布测点1~测点4,加速度传感器分别测量振动台、天线的加速度响应,经过信号调理以及数据采集设备后,传递到计算机进行数据处理和分析,通过对比并计算加速度传感器测量信号幅值差异,验证磁性天线隔振装置的隔振性能是否满足幅值衰减要求。振动试验需要在满足表1所示定频、扫频国军标GJB150.16A-2009[10]振动试验条件要求下定义装置激励条件。如图7为不同测点幅值衰减测试性能曲线。
|
|
表 1 国家标准的振动试验条件 Tab.1 National standard vibration test conditions |
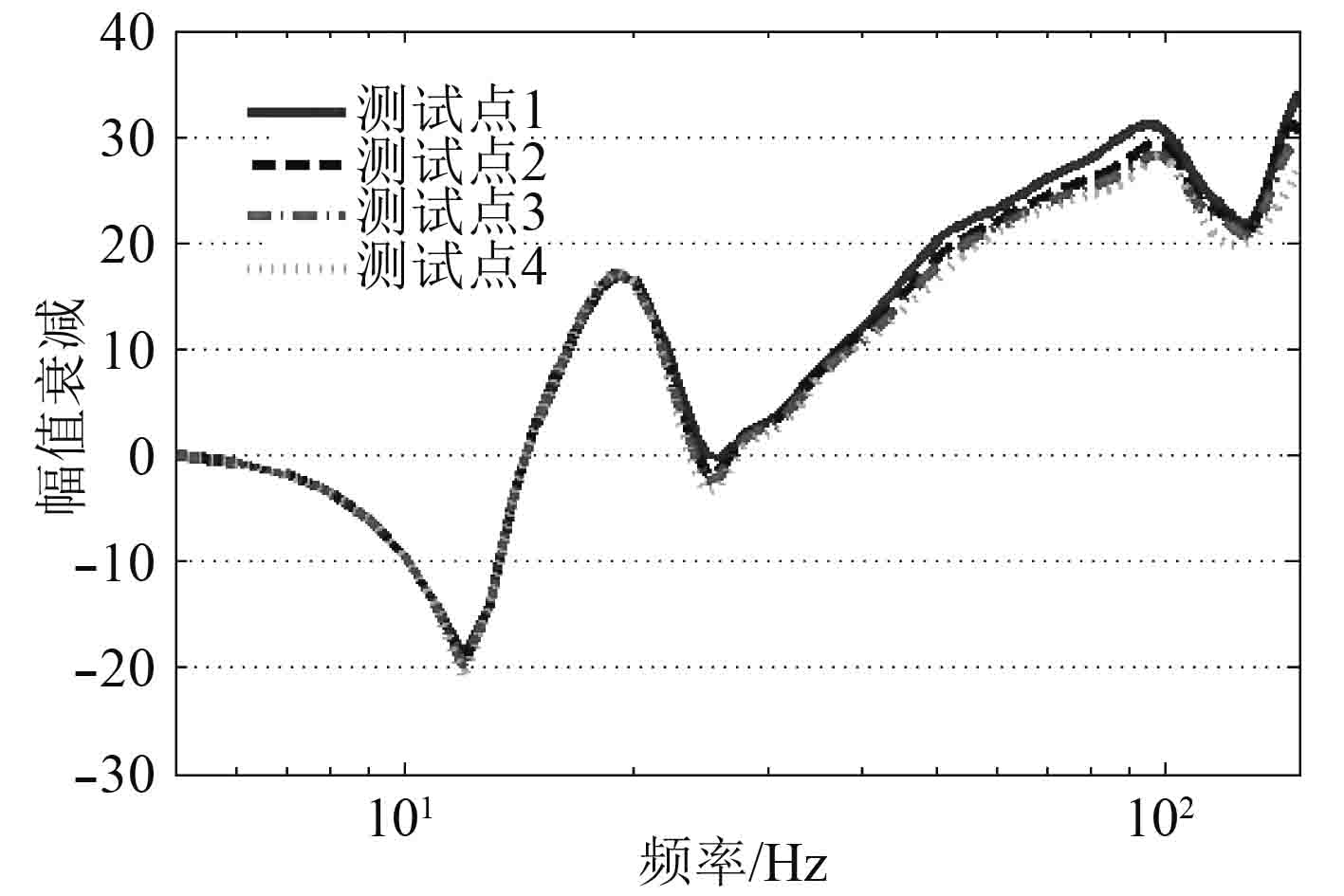
|
图 7 不同测点幅值衰减测试性能 Fig. 7 Different measurement points amplitude attenuation test performance |
从图中的测试性能可以得到以下结论:
1)该隔振设计合理可靠,工作频段内隔振样机幅值衰减能够大致满足20 dB的隔振需求,靠近固定端隔振效果最佳时能够达到31 dB;
2)共振区域内,测试曲线近似重合,但在工作频段内,由于隔振装置无法视为理想刚体,靠近固定处隔振性能显著优于磁性天线中心处,且在工作频段内存在额外的谐振点此时天线刚性对性能的影响最为显著。
4 总 结本文在掌握天线振动影响规律的基础上,采用双级隔振方式完成了低频磁性天线隔振设计研究,其仿真性能在工作频段内达到至少25 dB,然而在实际情形下,由于隔振元件的刚度不能视为恒定值,伴随着激励频率升高,隔振元件会硬化,刚度增加,因此实际测试往往达不到仿真预估值。该隔振装置在工作频段内实际能够达到至少18 dB的衰减性能,基本满足低频磁性天线幅值衰减需求,为低频天线上艇应用奠定基础。
然而仿真及试验结果中,结构刚性对系统幅值衰减性能的影响十分显著,在后续工作中,需利用有限元仿真完成系统结构优化,进一步获得更佳的隔振性能,从而更加完善解决舰船运动过程中天线信噪比较低的问题。
| [1] |
KIMURA, Tetsuya, Otake Plant TODA KOGYO CORP. MAGNETIC ANTENNA: EP, EP1901394[P]. 2008.
|
| [2] |
RIVIN E I. Passive vibration isolation[J]. Applied Mechanics Reviews, 2003, 57(6): B31-B32. |
| [3] |
顾海明, 周勇军. 机械振动理论与应用[M]. 南京: 东南大学出版社, 2007.
|
| [4] |
孙玉华. 内燃动车动力包双层隔振设计方法研究[D]. 成都: 西南交通大学, 2013.
|
| [5] |
张士峰, 张辉. 高精度测量的被动隔振研究[J]. 现代机械, 2006(4): 3-5. DOI:10.3969/j.issn.1002-6886.2006.04.002 |
| [6] |
张志, 张兆会, 董森, 等. 橡胶双层减振与隔振系统冲击响应研究[J]. 振动与冲击, 2013, 32(23): 126-129. DOI:10.3969/j.issn.1000-3835.2013.23.023 |
| [7] |
WU Hao, ZHANG Fu-tao. Research on mass ratio in the secondary vibration isolation[J]. Coal Mine Machinery, 2015, 36(12). |
| [8] |
杨路刚. 超低频磁场拖曳天线技术研究[D]. 武汉: 华中科技大学, 2007.
|
| [9] |
吴祺. 室内配变电设施双层隔振设计研究[D]. 成都: 西南交通大学, 2016.
|
| [10] |
GJB 150.16A-2009军用装备实验室环境试验方法[S]. 北京:中国标准出版社, 2009: 32.
|
 2018, Vol. 40
2018, Vol. 40
