2. 国家水运安全工程技术研究中心 可靠性工程研究所,湖北 武汉 430063;
3. 船舶动力工程技术交通行业重点实验室,湖北 武汉 430063
2. Reliability Engineering Institute, National Engineering Research Center for Water Transport Safety (WTS), Wuhan 430063, China;
3. Key Laboratory of Marine Engineering and Technology (Ministry of Transport), Wuhan 430063, China
波浪能作为一种清洁、无污染的可再生能源,分布广阔、储量巨大。据估算,全世界波浪能的理论值约为109 kW量级,是目前世界发电量的数百倍,其作为可预测的丰富海洋能源,有能力对世界日益增长的电力需求做出贡献,因此成为各国海洋能研究开发的重点[1 – 3]。目前,世界上提出的波浪能发电技术根据捕获方式分为点吸收式、振荡水柱式、鸭式、摆式、越浪式等。其大部分是以建设在近海的岸式或固定式电站的形式收集波能并达到发电的目的。英国波浪能量公司在苏格兰伊斯莱岛建立的500 kW岸式振荡水柱波浪能发电站LIMPET500,站址选择在已有岸线的陡峭岸壁处并装备2台功率为250 kW威尔斯透平发电机 组,目前已进入商业化运营阶段,其电力可供400户居民使用[4];芬兰AW-Energy公司开发了一种运用海底波浪动能来发电的近岸摆式波浪发电设备WaveRoll,平均捕获功率可达13 kW,并于2012年在葡萄牙Peniche安装运行[5]。
漂浮式波浪发电装置作为一种方便高效的海上移动平台,已经削弱了严格要求的海域和水域的深度,已经在海洋波能装置备受关注。国外开发的漂浮式波浪发电装置的典型装置包括Pelamis Wave Power(750 kW),PowerBuoy(150 kW),Dexawave(5 kW)等[6]。中国科学院广州能源所研制了100 kW一基多体鹰式波浪能发电装置[7]和10 kW漂浮点吸收直线发电波能装置[8],并完成了实海况试验;哈尔滨工程大学设计了一种陀螺式波浪能发电装置通过实物水槽试验验证了其发电可行性[9]。现阶段的波能装置很大一部分能量的捕获利用浮体上下垂荡,而波浪作用于浮体时,使浮体摇荡的能量巨大。因此,对这部分能量的收集和利用便显得非常有必要[10]。针对漂浮式波能装置的获能方式,本文提出一种基于双浮筒浮体在波浪中横摇的新型波浪能发电装置。通过CFD方法对双浮筒浮体运动规律及水动力性能进行分析,其结果为下一步装置的优化及实海况试验提供了理论基础。
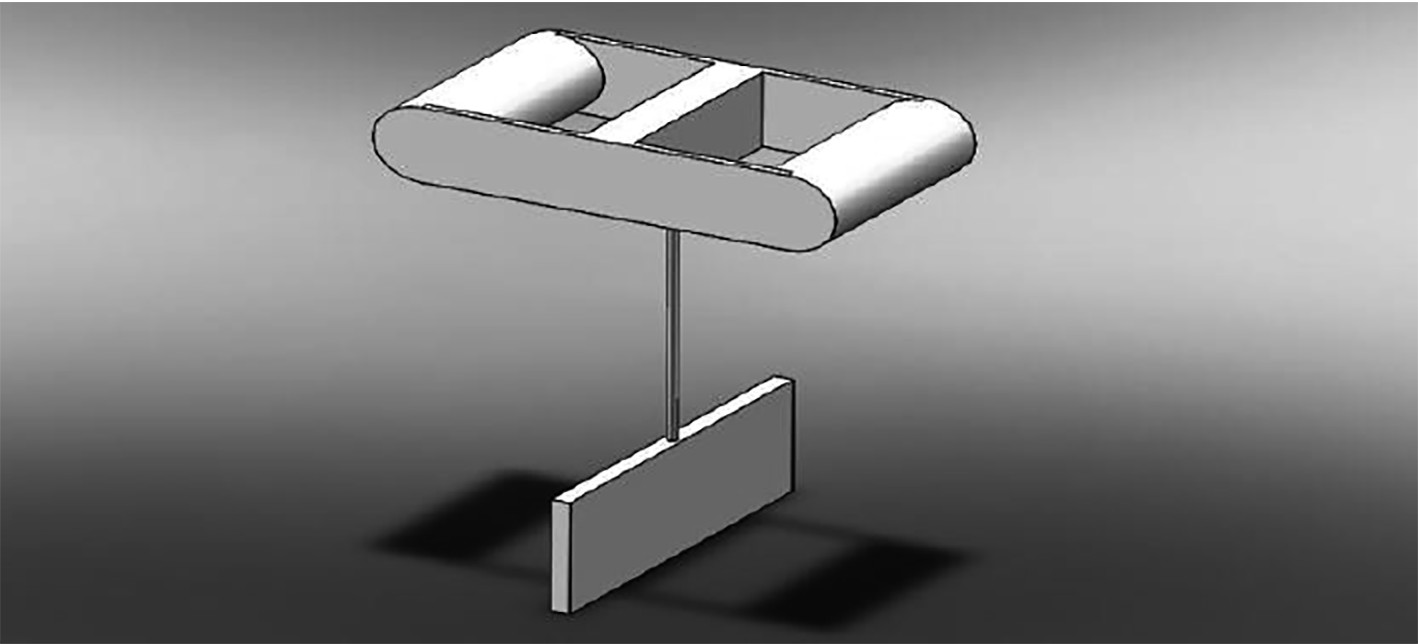
1 波浪能发电装置方案设计双浮筒式波浪能发电装置主要由双浮筒浮体和阻尼竖板构成。其中双浮筒浮体包括2个横向浮筒以及工作舱,三者由两侧的浮箱连接,装置结构如图1所示。与波浪传播方向垂直布置的水下竖直阻尼板通过连杆与置于工作舱内的电力输出装置(PTO,Power Take Off)输入端相连接。双浮筒浮体在波面随海浪进行横摇运动,阻尼板由于受到深水的巨大阻力产生微幅摆动或几乎保持不动,从而便与浮体产生相对转动。工作舱内的PTO系统将输入的旋转机械能进行传递和利用,达到发电目的。
|
图 1 装置设计方案 Fig. 1 The WEC device design |
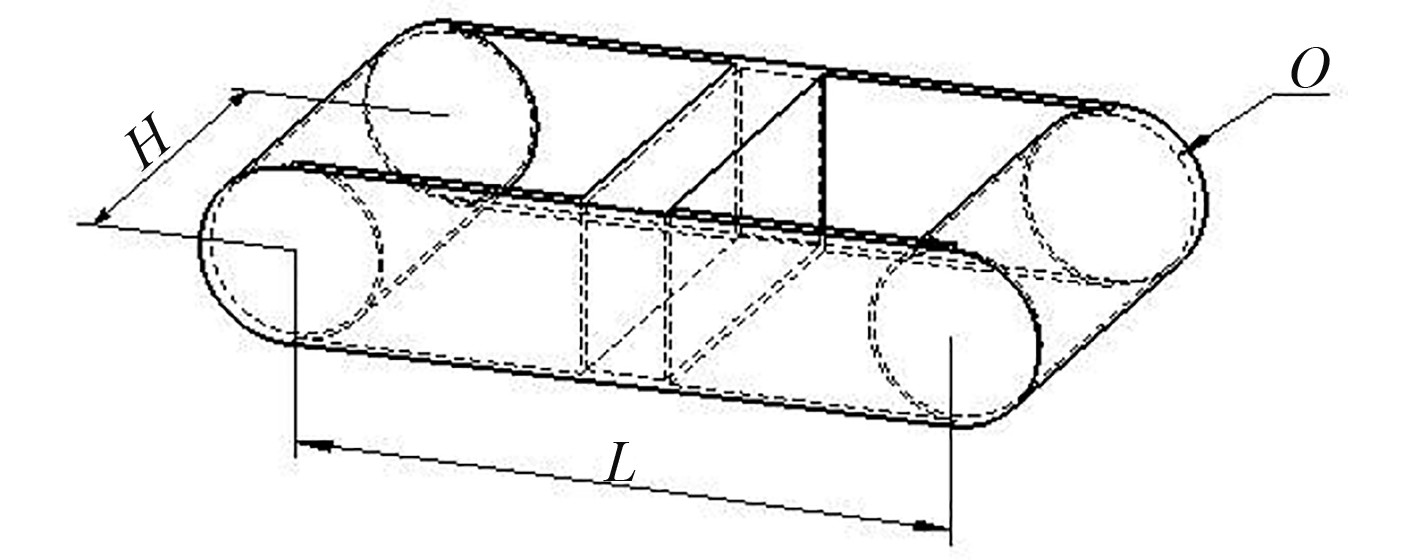
作为获能的载体双浮筒浮体成为影响装置能量吸收及效率转换的关键,因此对其进行研究和分析显得尤为必要。根据浮体运动特性,设计双浮筒浮体结构如图2所示,尺寸参数见表1。
|
图 2 双浮筒浮体结构 Fig. 2 The structure of float in twin-pontoon WEC |
|
|
表 1 双浮筒浮体尺寸参数 Tab.1 The size parameters of float in twin-pontoon WEC |
首先对无阻尼板状态下的双浮筒浮体进行分析,浮体在波浪中受到各种力的影响进行摇摆运动,针对其横摇运动特性,本文首先做出假设:1)双浮筒浮体为一般刚体;2)浮体为时间恒定的线性系统。
根据耐波性原理,双浮筒浮体在波浪中的横摇运动方程可表示为:
| $M\left( {\ddot \theta } \right) + M\left( {\dot \theta } \right) + M\left( \theta \right) = M\left( \alpha \right)\text{,}$ | (1) |
其中:θ为浮体的横摇角度;α为海浪波倾角。
式(1)从左到右分别为横摇惯性力矩、横摇阻尼力矩、横摇恢复力矩以及波浪的扰动力矩。
1)横摇惯性力矩
| $M\left( {\ddot \theta } \right) = - \left( {I + \delta I} \right)\ddot \theta \text{,}$ | (2) |
其中:I为双浮筒浮体绕横摇轴的转动惯量;δI为双浮筒浮体绕横摇轴的转动引起的周围流体质量对横摇轴的附加转动惯量。
2)横摇阻尼力矩
| $M\left( {\dot \theta } \right) = - 2N\dot \theta \text{,}$ | (3) |
式中:2N为双浮筒浮体的横摇阻尼系数。
横摇阻尼力矩主要由流体的势流阻尼组成,当横摇角度较小时,阻尼力矩与横摇角速度近似认为呈线性关系。
3)横摇恢复力矩
| $M\left( \theta \right) = - Dh\theta \text{,}$ | (4) |
式中:D为双浮筒浮体排水量;h为初稳性高。恢复力矩代表浮体在静水中作角位移引起的力矩。
4)波浪扰动力矩
| $M\left( \alpha \right) = - \left( {\delta I\ddot \alpha + 2N\dot \alpha + Dh\alpha } \right)\text{,}$ | (5) |
波浪扰动力矩是浮体摇荡方程中起摇动作用的力矩,它与波浪的运动有关。其中α为海浪波倾角。
整理可得,双浮筒浮体的运动方程为:
| $I\ddot \theta + \delta I\left( {\ddot \theta - \dot \alpha } \right) + 2N\left( {\dot \theta - \ddot \alpha } \right) + Dh\left( {\theta - \alpha } \right) = 0\text{。}$ | (6) |
由于装置的波能捕获依赖双浮筒浮体与水下竖直阻尼板的相对运动,因此阻尼板在水下的运动形式便影响装置的工作能力。为了实现波浪能吸收过程的稳定,当浮体在波面进行摇荡运动时,水下的竖直阻尼板需要保持良好的稳定性,其可以通过阻尼板设计的深度、形状以及质量来实现。本文设计水下阻尼板的运动幅度很小或几乎不动,因此双浮筒阻尼竖版波浪能发电装置可以简化为双浮筒浮体和PTO系统的模型的耦合。
PTO装置的力矩数学模型通常被简化为线性阻尼器与线性弹簧的组合[11]。本文设计装置的PTO系统为旋转线性阻尼器,故PTO的数学模型可表示为:
| ${M_P} = {\rm{g}}{B_P}\dot \theta \text{,}$ | (7) |
其中:BP为PTO系统旋转阻尼系数,kg∙m∙s;其取值与PTO装置的设计及浮体模型本身有关。
令
| ${B_P} = \frac{{{b_P}\left( {I + \delta I} \right)}}{{\rm{g}}}\text{,}$ | (8) |
其中:bP为PTO等效旋转阻尼系数,s–1。
结合上述模型,波浪能装置的浮体除在受到波浪提供的力和力矩外,还受PTO提供的阻尼力矩的影响,可以得到装置中双浮筒浮体的运动方程
| $I\ddot \theta + \delta I\left( {\ddot \theta - \dot \alpha } \right) + 2N\left( {\dot \theta - \ddot \alpha } \right) + Dh\left( {\theta - \alpha } \right) = {b_P}\left( {I + \delta I} \right)\dot \theta \text{。}$ | (9) |
附加转动惯量随着横摇角度变化,难以通过理论计算准确得出,只能通过试验和经验获取。船舶中附加转动惯量大致占船体转动惯量的10%~30%[12 – 13]。因此,本文选择附加转动惯量为双浮筒浮体转动惯量的20%,即δI=0.2I。
定义浮体的PTO系统阻尼单位时间内消耗的能量即为装置所获得的平均功率,因此双浮筒式波浪能装置的平均输出功率为:
| ${{\bar P}_a}\!\! =\!\! \frac{1}{T}\int_0^T \left| {{M_P} \cdot \dot \theta } \right|{\rm d}t\!\! =\!\! \frac{{{b_P}}}{T}\int_0^T \left( {I + \delta I} \right) \cdot {{\dot \theta }^2}{\rm d}t\!\! =\!\! \frac{{1.2I{b_P}}}{T}\int_0^T {{\dot \theta }^2}{\rm d}t \text{。}$ | (10) |
本文设计的装置考虑适用海域为我国的南海海域,其海况受季风气候和天气系统的影响较大,主要为风海流。在冬季,海流基本是稳定的西南流;在夏季,流向基本为东北向或偏东向漂流[14]。南海冬季平均波高在0.4~1.8 m之间,最大值为2.5~6.5 m,周期在4.8~8.6 s之间;南海夏季平均波高在0.4~1.4 m之间,最大值为1.5~5 m,周期在3.2~7.6 s之间[15]。本文取保守海况波高0.6 m,波浪周期3 s,波速0.5 m/s2为计算工况。
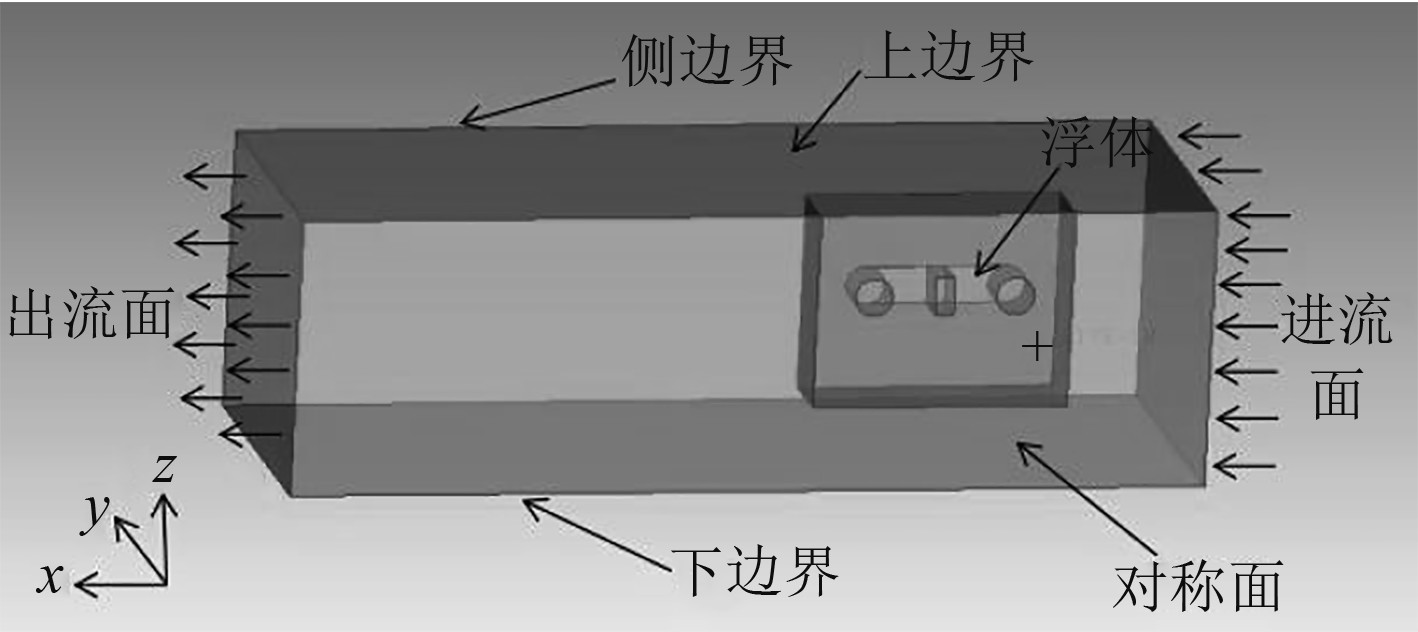
3.2 CFD计算设置 3.2.1 计算域划分双浮筒浮体为对称结构,数值计算取模型流场一半区域,根据给定模型尺寸其边界设置如下:1)进流方向,浮体前约2.0LWL(LWL为双浮筒浮体水线长);2)出流方向,浮体后约5.0LWL;3)下边界,浮体上方约2.0LWL;4)上边界,水线以上约1.0LWL;5)侧边界,浮体侧方约2.0LWL;6)对称面,浮体模型中剖面的延展面。计算域及边界设置如图3所示。
|
图 3 计算域示意图 Fig. 3 The schematic of calculation domain |
建立总体坐标系O-XYZ,以浮体重心为坐标原点,X轴正方向为波浪传播方向,Z轴为浮体垂荡方向,Y轴为浮体横摇轴。利用动网格技术实现浮体在波面上的运动,基于SST k-ω湍流模型,采用VOF方法捕捉自由液面变化,利用Fluent及其二次开发功能建立可有效模拟线性波的三维数值计算域。初定浮体重量180 kg,吃水0.2 m,绕Y轴转动惯量为64 kg∙m2。
3.2.2 网格划分计算域网格划分采用混合网格。流体域采用结构网格,网格数目约460 000,并在浮体域附近进行网格加密;浮体域采用非结构网格,网格数目约270 000。
3.2.3 UDF编写为定义双浮筒浮体在横摇过程中PTO系统提供的阻尼力矩,利用Fluent中的UDF宏DEFINE_SDOF_PROPERTIES(sdof_properties,prop,dt,time,dtime)编写程序实现阻尼力矩符合式(7)和式(8),并在程序中定义浮体的质量及转动惯量。
3.2.4 边界条件设置进流面为velocity-inlet,出流面为pressure-outlet,并打开Open Channel设置自由面和底部坐标,xy面设置为Symmetry,流体域与浮体域的交界面设为interface,其他边界条件设为Wall边界。
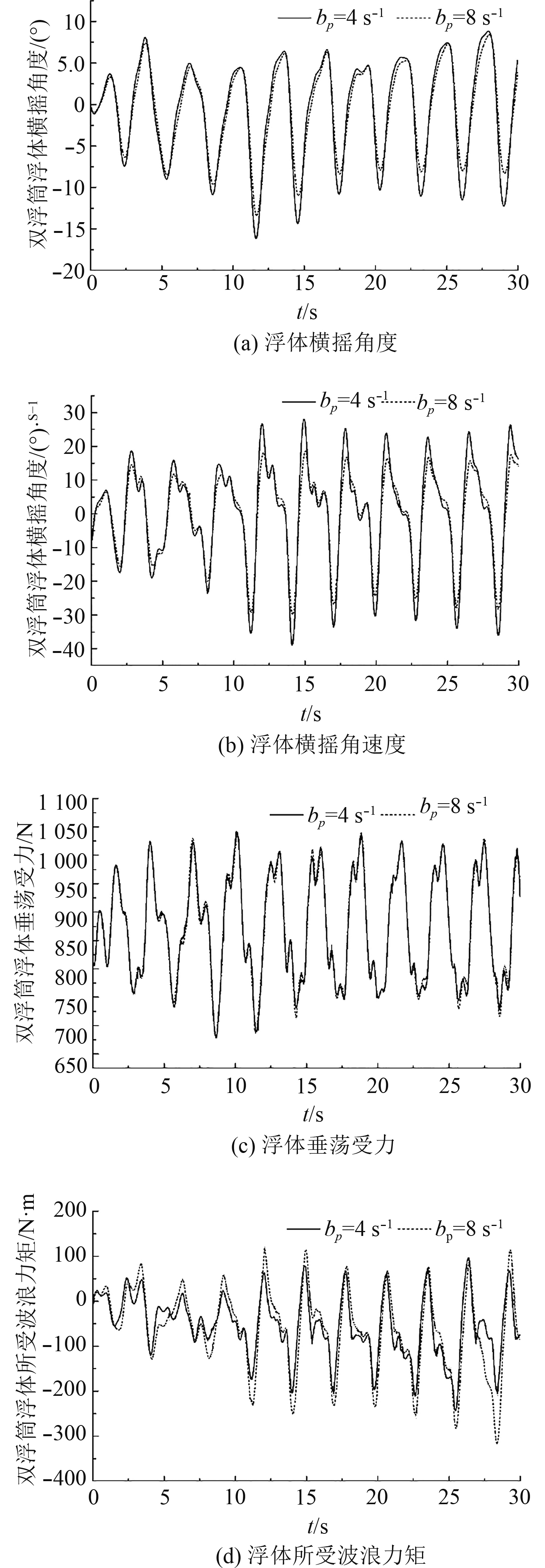
3.3 仿真结果分析 3.3.1 阻尼系数对浮体的影响分析PTO装置的阻尼系数影响着PTO产生的阻尼力矩,从而影响双浮筒浮体的运动状况及波能的吸收能力。本文选取装置的PTO等效旋转阻尼系数bP取值范围为0~10 s–1,选取并对比4 s–1和8 s–1两种工况下浮体运动及载荷状况,结果如图4所示。
|
图 4 浮体运动及受力 Fig. 4 The motion and force of the floater |
图4(a)和图4(b)为不同阻尼系数下浮体横摇角度和横摇角速度随时间的变化曲线。当横摇阻尼系数较大时,浮体的横摇角度幅值相对较小。这是因为阻尼系数越大,浮体在运动过程需要克服的外力做越多的功,PTO系统消耗的能量也越多,从而造成浮体的运动幅度减小,浮体转动速度也相应减小。
图4(c)为浮体的垂荡受力随时间的变化曲线。由图可知2种工况下浮体的垂荡受力基本重合,这表明依靠浮体横摇获能的方式,由PTO系统阻尼系数的变化对浮体的垂荡受力影响较小。
图4(d)为浮体所受波浪力矩随时间的变化曲线。由图可见,横摇阻尼系数越大,浮体所受的波浪力矩也越大,主要原因是横摇阻尼系数越大,由波浪引起的浮体横摇运动响应越小,浮体与波面位置相差越大,从而造成波浪力矩也越大。
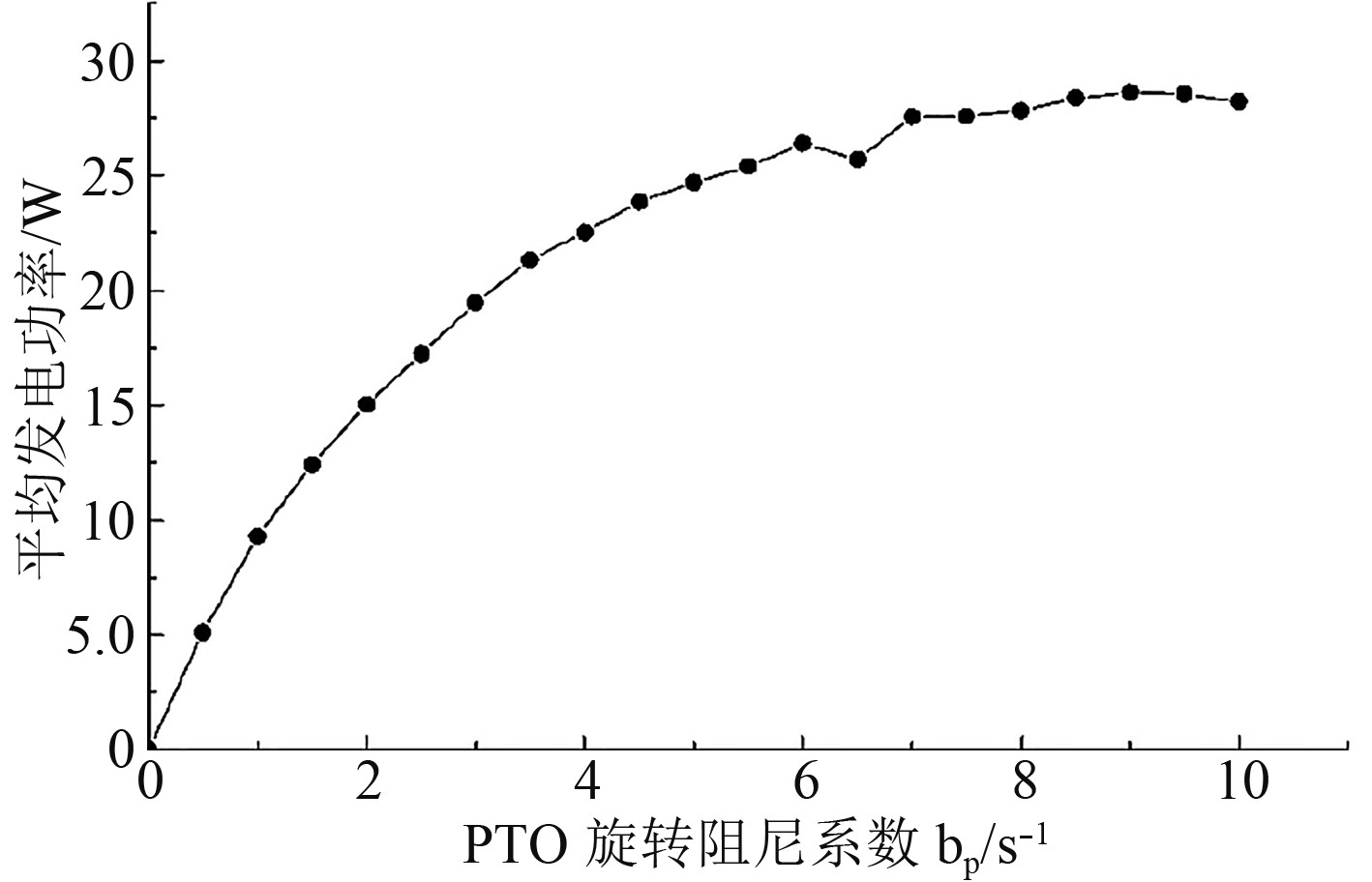
图5所示为装置在不同PTO旋转阻尼系数工况的平均发电功率变化曲线。当横摇阻尼系数bP=9 s–1时,即对应最佳旋转阻尼系数BP为70.46 kg∙m∙s时,装置能量吸收的平均功率
|
图 5 装置平均输出功率 Fig. 5 Average power of the device |
由于浮体在波浪中周期性的运动形态,需要对浮体在不同定攻角下的载荷及水动力特性的进行研究,从而得到浮体的运动机理。根据上节分析得到的横摇角度结果,采用全模型方式,在相同波浪参数下本文选取0°,5°,10°,15°四种攻角工况进行仿真分析。
不同攻角下双浮筒浮体速度矢量图如图6所示。

|
图 6 不同攻角下浮体速度矢量及压力分布(左列为速度矢量分布,右列为压力分布) Fig. 6 Velocity and pressure distribution around the floater when attack angle is different (the left is vector distribution and the right is pressure distribution) |
从图6的速度矢量图可以看出,波浪来流由右向左冲向双浮筒浮体,浮体背浪面存在较明显的速度矢量变化。这是因为来流由于受到浮体阻碍,速度急剧下降,绕流在浮体背表面形成涡流区。当逐渐接近横摇角度幅值时,涡流区逐渐减弱。
从图6压力分布图可见,前后端浮筒表面存在较大的压力差,且随着攻角增大,前端浮筒压力增加,后端浮筒压力下降甚至出现负压。同时,浮体迎浪面与背浪面也存在较大的压力差,表现为迎浪面所受压力大于背浪面压力。当浮体攻角接近横摇角度幅值时,2组压力差均出现减小趋势。
因此当波浪传播至浮体时,处于迎浪面和背浪面的上下表面由于压力差的存在,推动浮体进行垂荡运动。同时前后端浮筒间的压力差推动浮体绕中间轴向波浪前进方向转动。当波浪传播通过浮体时,后端浮筒表面压力大于前端浮筒,从而产生反向转动。
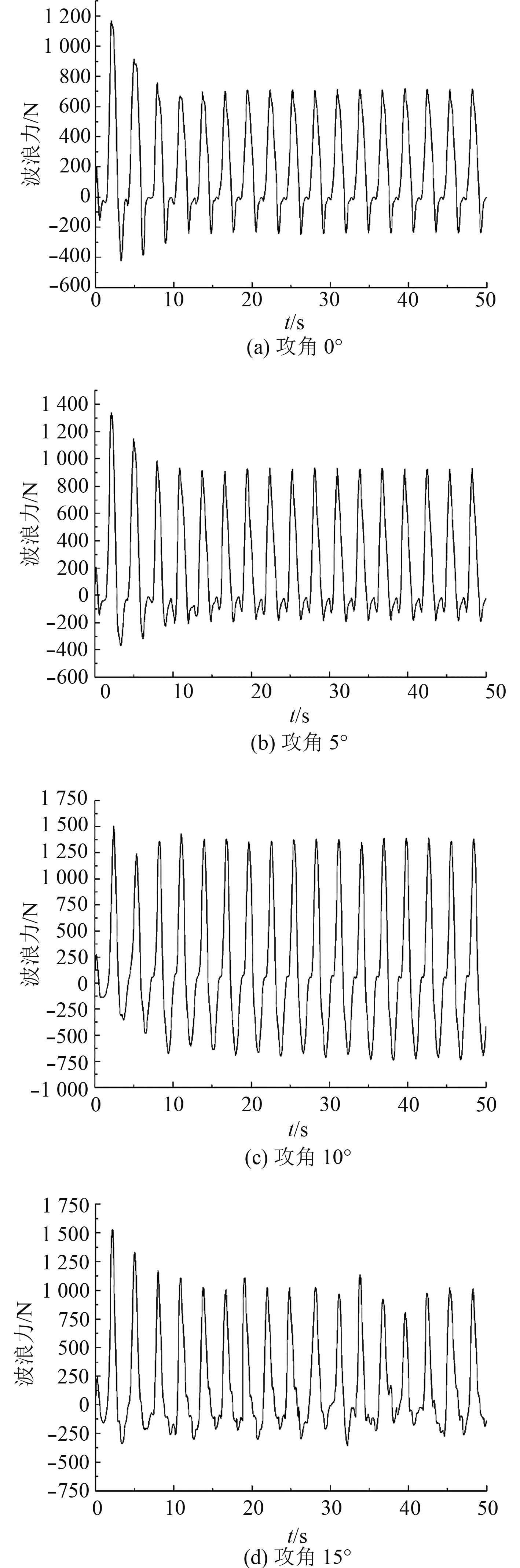
由于不用攻角下浮体迎浪面和背浪面的压力分布不同,因此浮体所受波浪力也随着变化,图7显示了各攻角下浮体所受波浪力随时间变化曲线。
|
图 7 不同攻角下浮体所受波浪力 Fig. 7 The wave force of the floater with different attack angle |
从图7可以看出,浮体所受波浪力随时间呈周期性变化。随着攻角的增大,浮体所受波浪力呈先增后减的趋势,对比4种攻角工况,当攻角为10°时,浮体所受波浪力最大,其幅值达1 500 N。因此,攻角角度对双浮筒浮体所受波浪力有重要影响。
4 模型简易试验基于装置结构设计的要求,结合以上CFD数值分析结果,为验证双浮筒式波浪能发电装置的发电可行性,制作了小尺度样机模型并设计了简易水池试验。
4.1 模型制作实物模型如图7所示,模型缩尺比按4:1制作,整体包括2个浮筒、浮箱以及阻尼板。
1)浮筒:直径为0.1 m,长度为1 m,浮筒内部空心且壁厚3 mm。两侧浮筒轴心距0.8 m并通过U型紧固螺栓固定在装置钢结构骨架上;
2)浮箱:采用合金铝板拼制,长0.6 m,宽0.3 m,高0.25 m,重30 kg。整个发电系统安置于浮箱内,如图8所示,包括换向齿轮箱、增速箱以及发电机组成。

|
图 8 样机实物 Fig. 8 WEC prototype |
3)阻尼板:长1 m,宽0.3 m,通过刚性轴与发电系统的输入端相连接。
4.2 简易水池试验由于试验条件限制,模型试验在长3 m,宽2 m,高1.5 m的简易水池中进行,试验水深0.8 m。发电装置输出端通过电缆线连接至岸边的测量回路用于实验数据测量。测量回路由10个2 W白炽灯、电阻、稳压模块以及万用表组成。
试验过程在由造波机产生波高H=0.3 m、周期T=3 s的波浪中进行,利用回路中万用表测量装置发电过程电压、电流等数据。万用表显示在装置于波浪中发电过程中电压峰值保持在U=10 V左右,电流峰值I=0.4 A左右,并可持续点亮白炽灯,从而证明整个发电装置具备一定的发电能力。
5 结 语本文设计了一种水面双浮筒浮体和水下竖直阻尼板的构成的波浪能发电装置,其依靠在波浪中进行横摇运动的双浮筒浮体与水下微幅摆动的竖直阻尼板的相对运动将波浪能吸收并转换为电能。基于装置的数学模型,运用CFD方法分析了双浮筒浮体在波浪中的运动响应,得到了不同PTO系统阻尼系数工况下装置的运动及载荷。在此基础上,研究了不同定攻角下浮体的水动力特性及载荷变化。最后通过制作的模型及简易水池试验,验证了装置的发电可行性,为今后装置的优化和实海况试验提供了理论基础。
| [1] |
ORAZOV B, OREILLY O M. Savas on the dynamics of a novel ocean wave energy converter[J]. Journal of Sound and Vibration, 2010(329): 5058-5069. |
| [2] |
LOPEZ I, ANDREU J, CEBALLOS S, et al. Review of wave energy technologies and the necessary power-equipment[J]. Renewable & Sustainable Energreviews, 27, 2013, 413-434. |
| [3] |
马克•科拉正格著, 高健, 陈林生, 等译. 海洋经济——海洋资源与海洋开发(引进版)[M]. 上海: 上海财经大学出版社有限公司, 2011: 68.
|
| [4] |
闫耀保. 海洋波浪能综合利用—发电原理与装置[M]. 上海: 上海科学技术出版社, 2013: 154–163.
|
| [5] |
PECHER A, KOFOED J P, ESPEDAL J, et al. Result of an experimental study of the langlee wave ennergy converter[C]//Proceedings of the Twentieth(2010) International Offshore and Polar Engineering Conference Beijing, China, 2010, 6: 20–25.
|
| [6] |
A. F. O. Hydrodynamic optimization of an axisymmerric floating oscillating water column for wave energy conversion[J]. RENEWABLE ENERGY, 44, 2012: 328–339.
|
| [7] |
张亚群, 盛松伟, 游亚戈. 100 kW一基多体漂浮鹰式波浪能发电装置模型试验研究[J]. 海洋技术学报, 2014, 33(4): 73-79. |
| [8] |
吴必军, 刁向红, 王坤林. 10 kW漂浮点吸收直线发电波力装置[J]. 海洋技术, 2012, 31(3): 68-73. DOI:10.3969/j.issn.1003-2029.2012.03.018 |
| [9] |
周宇英, 李炳强, 蔡宗举. 陀螺式波浪能发电装置浮子运动及载荷分析[J]. 船海工程, 2016, 45(3): 90-97. DOI:10.3963/j.issn.1671-7953.2016.03.022 |
| [10] |
王志波, 马春翔, 郑茂琦. 一种新型海浪发电装置的设计及分析[J]. 机械设计与研究, 2013, 29(2): 29-32. DOI:10.3969/j.issn.1006-2343.2013.02.008 |
| [11] |
Alexandra Anne Elizabeth Price. New perspective on wave energy converter control[D]. The University of Edinburgh, 2009, 211–216.
|
| [12] |
邳帅. 起重船对南海海况的适用性研究[D]. 天津: 天津大学, 2011: 2–4.
|
| [13] |
王晓明, 尚建忠, 张志雄. 双浮体波浪能转换装置中重心布置对波浪能吸收影响分析[J]. 国防科技大学学报, 2013, 35(4): 57-61. |
| [14] |
宗芳伊. 近20年南海波浪及波浪能分布、变化研究[D]. 青岛: 中国海洋大学, 2014: 35–38.
|
| [15] |
孙湘平. 中国近海区域海洋[M]. 北京: 海洋出版社, 2006: 168–191.
|
 2018, Vol. 40
2018, Vol. 40
