2. 海洋工程国家重点实验室,上海 200240;
3. 高新船舶与深海开发装备协同创新中心,上海 200240
2. State Key Laboratory of Ocean Engineering, Shanghai 200240, China;
3. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China
为了保证风机结构的完整性,国际电工委员会发布的陆上风机标准IEC 61400-1[1]和海上风机标准IEC 61400-3[2],对风机的多个部分均提出了极限强度分析的要求,需要计算构件在一年或多年重现周期下可能承受的最大载荷。
夏一青等[3]利用区组模型和超越门槛值法联合Gumbel分布求解了某5 MW单桩型和浮式型风机叶片根部的极端面外弯矩;张友文等[4]以分块法联合Gumbel分布求解了某5 MW陆上风机和海上风机的极端塔筒基底侧向弯矩等载荷;李昕雪等[5]比较了广义极值分布和广义帕累托分布在风机极端载荷预报中的差别。但是上述研究工作主要集中在短期载荷极值的求解上,对载荷的长期超越概率分布考虑较少。
P.J. Moriarty等[6]使用超越门槛值法选取WP_Baseline 1.5 MW陆上风机叶片根部的短期载荷极值,然后运用多种类型的分布进行拟合,求解了具有1年和50年重现周期的极端载荷。为了对比验证,进行了时长1年的直接仿真,获取了相应载荷的“真实数据”。但是对比之后,发现外推结果与“真实数据”相差较大。P.J. Moriarty等分析其主要原因是短期载荷分布对数据尾部的拟合效果不佳,建议采用拟合效果更好的分布来减少估计高分位数时的误差。
本文承接P.J. Moriarty的建议,以经典极值理论为基础,采用分块法选取样本点,以广义极值分布进行拟合,由线性矩法估计分布参数,得到了与“真实数据”贴近的外推值,并且对外推的稳定性进行检验,从而证实了P.J. Moriarty想法的可行性。此外,Korn Saranyasoontorn等[7]另辟蹊径,利用环境等值线法直接求取长期载荷,避开了拟合分布的问题,同样得到了较好的效果。
1 基本原理 1.1 经典极值理论设
| $\mathop {\lim }\limits_{n \to \infty } Pr \left( {\frac{{{M_n} - {b_n}}}{{{a_n}}} \leqslant x} \right) = H\left( x \right), \; x \in {R}{}{\text{,}}$ | (1) |
成立,其中
Ⅰ型分布:
| ${H_1}\left( x \right) = \exp \left\{ { - {e^{ - x}}} \right\}, \; - \infty < x < + \infty; $ |
Ⅱ型分布:
| ${H_2}\left( {x;\alpha } \right) = \left\{{\begin{aligned}& {0,\;\;\;\;\;\;\;\;\;\;\;\;\;x \leqslant 0}\text{,}\\& {\exp \left\{ { - {x^{ - \alpha }}} \right\},\;\;x > 0\text{,}}\end{aligned}} \right.\;\;\;\alpha > 0;$ |
Ⅲ型分布:
| ${H_3}\left( {x;\alpha } \right) = \left\{ {\begin{aligned}& {\exp \left\{ { - {{\left( { - x} \right)}^\alpha }} \right\}{\rm{, }}x \leqslant 0}\text{,}\\& {1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x > 0}\text{,}\end{aligned}} \right.\;\;\;\;\alpha > 0\text{。}$ |
其中:
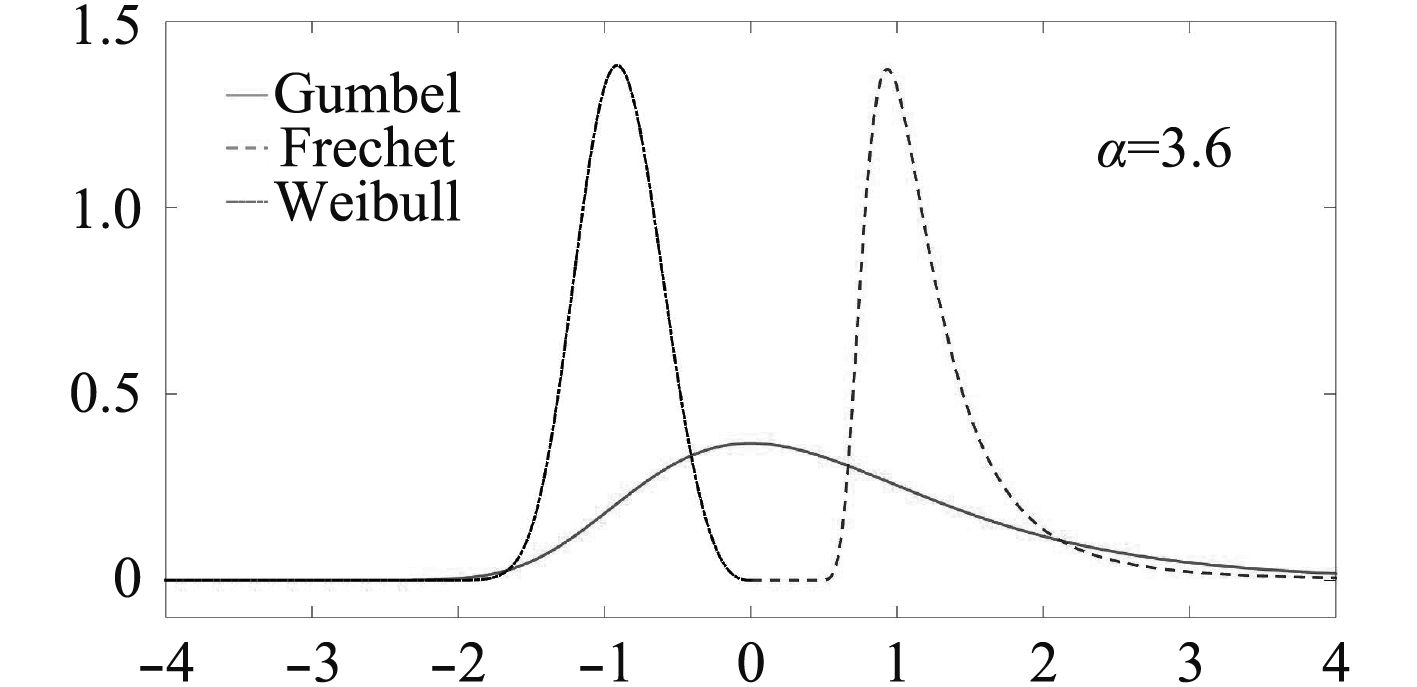
|
图 1 3种极值分布的概率密度函数 Fig. 1 Probability density functions of 3 extreme value distributions |
进一步引进位置参数
| ${H_1}\left( {x;\mu ,\sigma } \right) = \exp \left\{ { - {e^{ - \frac{{x - \mu }}{\sigma }}}} \right\}, \; - \infty < x < + \infty{\text{;}}$ |
| ${H_2}\left( {x;\mu ,\sigma ,\alpha } \right) = \left\{ {\begin{aligned}& {0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x \leqslant \mu }{\text{,}}\\& {\exp \left\{ { - {{\left( {\frac{{x - \mu }}{\sigma }} \right)}^{ - \alpha }}} \right\},x > \mu }{\text{,}}\end{aligned}} \right.\;\;\;\alpha > 0{\text{;}}$ |
| ${H_3}\left( {x;\mu ,\sigma ,\alpha } \right) = \left\{ {\begin{aligned}& {\exp \left\{ { - {{\left( { - \frac{{x - \mu }}{\sigma }} \right)}^\alpha }} \right\},x \leqslant\mu }{\text{,}}\\& {1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x > \mu }{\text{,}}\end{aligned}} \right.\;\;\;\alpha > 0{\text{。}}$ |
则可以用统一的形式表示上述3种不同类型的极值分布
| $H\!\left( {x;\mu ,\sigma ,\xi } \right) \!\!=\!\! \exp \left\{ { \!\!-\! {{\left( \!{1 \!\!+\! \xi \frac{{x - \mu }}{\sigma }} \right)}^{ - 1/\xi }\!}} \right\},\! 1 \!\!+\! \xi {{\left( {x \!-\! \mu } \right)} / {\sigma \!\!>\!\! 0}}{\text{,}}$ | (2) |
其中
设独立同分布序列
| ${F^{ - 1}}\left( p \right) = \inf \left\{ {x \in {R}:F\left( x \right) \geqslant p} \right\}, \; 0 < p < 1{\text{,}}$ | (3) |
为它的分位数函数。
假设
| $E\left( {\sum\limits_{i \leqslant T} {I\left\{ {{X_i} > u} \right\}} } \right) = 1{\text{,}}$ | (4) |
显然,由
| $Pr \left\{ {{X_i} > u} \right\} = \displaystyle\frac{1}{T}=1 - Pr \left( {{X_i} \leqslant u} \right)= 1 - F\left( u \right){\text{,}}$ | (5) |
即可得
| $u\left( T \right) = {F^{ - 1}}\left( {1 - {1 / T}} \right){\text{,}}$ | (6) |
为式(1)–式(5)的解。由此可知一方面
在风机极值载荷的求解中,仿真时长通常设为10 min。现考虑重现周期
| ${1 / {\left( {1 - p} \right)}} = N\text{,}$ | (7) |
得
| $p = 1 - {1 / N}\text{,}$ | (8) |
称
在直接积分法中,要求的重现周期
| ${P_T} = Pr \left\{ {L > {l_T}} \right\} = \int\nolimits_X {Pr \left\{ {L > {l_T}\left| {X = x} \right.} \right\}{f_X}\left( x \right){\rm d}x} {\text{,}}$ | (9) |
其中:
| ${P_T} \!=\! Pr \left\{ {{L_{10\min }} > {l_T}} \right\} \!= \!\int_{{V_{in}}}^{{V_{out}}} {Pr \left\{ {{L_{10\min }} > {l_T}\left| {V \!=\! v} \right.} \right\}{f_V}\left( v \right){\rm d}v}\text{。} $ | (10) |
其中:
在求解
线性矩法由Hosking[12]于1990年定义,目前在水文、气象等领域已广泛应用。陈元芳等[13 – 14]利用线性矩法分别研究了在P-Ⅲ型分布和GEV分布下可考虑历史洪水信息的参数估计问题。梁玉音等[15]、吴俊梅等[16]利用线性矩法研究了太湖流域暴雨频率的问题。上述研究工作均通过线性矩法取得了不错的成效。
设
| ${\lambda _r} \equiv {r^{ - 1}}\sum\limits_{k = 0}^{r - 1} {{{\left( { - 1} \right)}^k}\left( {\begin{array}{*{20}{c}} {r - 1} \\ k \end{array}} \right)} E{X_{r - k:r}}, \; r = 1,2, \cdot \cdot \cdot \text{。}$ | (11) |
其中:
| $\left\{ \begin{aligned}& {\lambda _1} = EX\text{,}\\& {\lambda _2} = \frac{1}{2}E\left( {{X_{2:2}} - {X_{1:2}}} \right)\text{,}\\& {\lambda _3} = \frac{1}{3}E\left( {{X_{3:3}} - 2{X_{2:3}} + {X_{1:3}}} \right)\text{,}\\& {\lambda _4} = \frac{1}{4}E\left( {{X_{4:4}} - 3{X_{3:4}} + 3{X_{2:4}} - {X_{1:4}}} \right)\text{。}\end{aligned} \right.$ | (12) |
样本的线性矩可表示为:
| $\begin{align} & {{l}_{r}}={{\left( \begin{matrix} n \\ r \\\end{matrix} \right)}^{-1}}\sum\limits_{1\le {{i}_{1}}}{\sum\limits_{<{{i}_{2}}<}{\underset{_{_{_{_{_{_{\ \cdot \cdot \cdot}}}}}} }{\mathop{\cdot \cdot \cdot }}\,\sum\limits_{<{{i}_{r}}\le n}{{{r}^{-1}}}\sum\limits_{k=0}^{r-1}{{{\left( -1 \right)}^{k}}\left( \begin{matrix} r-1 \\ k \\\end{matrix} \right){{x}_{{{i}_{r-k}}:n}},\text{ }}}} \\ & r=1,2,\cdot \cdot \cdot ,n {\text{。}}\end{align}$ | (13) |
则前4阶样本线性矩计算公式为:
| $\left\{\!\! \begin{aligned}& {l_1} = {n^{ - 1}}\sum\limits_{i = 1}^n {{x_{i:n}}} \text{,}\\& {l_2} = \frac{1}{2}{\left( {\begin{array}{*{20}{c}}n\\2\end{array}} \right)^{ - 1}}\sum\limits_{i = j + 1}^n {\sum\limits_{j = 1}^{n - 1} {\left( {{x_{i:n}} - {x_{j:n}}} \right)} } \text{,}\\& {l_3} = \frac{1}{3}{\left( {\begin{array}{*{20}{c}}n\\3\end{array}} \right)^{ - 1}}\sum\limits_{i = j + 1}^n {\sum\limits_{j = k + 1}^{n - 1} {\sum\limits_{k = 1}^{n - 2} {\left( {{x_{i:n}} - 2{x_{j:n}} + {x_{k:n}}} \right)} } }\text{,}\quad\quad (14) \\ & {l_4} = \frac{1}{4}{\left( {\begin{array}{*{20}{c}}n\\4\end{array}} \right)^{ - 1}}\sum\limits_{i = j + 1}^n {\sum\limits_{j = k + 1}^{n - 1} \!\!{\sum\limits_{k = l + 1}^{n - 2} {\sum\limits_{l = 1}^{n - 3} {\left( {{x_{i:n}} - 3{x_{j:n}} + 3{x_{k:n}} - {x_{l:n}}} \right)} } } } \text{。}\end{aligned} \right.$ |
为了更好地描述统计曲线的分布特征,类似常规矩法中的变异系数、偏态系数、峰度系数,定义线性矩系数如下:
| $\left\{\begin{split}& {\text{样本线性变异系数}}\left( {L - {C_V}} \right):\;\;\tau = {{{l_2}} / {{l_1}}}\text{,}\\& {\text{样本线性偏态系数}}\left( {L - {C_S}} \right):\;\;{\tau _3} = {{{l_3}} / {{l_2}}}\text{,}\\& {\text{样本线性峰度系数}}\left( {L - {C_K}} \right):\;\;{\tau _4} = {{{l_4}} / {{l_2}}}\text{。}\end{split}\right.$ | (15) |
广义极值分布的线性矩及其系数与分布参数之间的关系如下:
| $\left\{ \begin{aligned}& {\lambda _1} = \mu + {\sigma / {\left( {1 - \xi } \right)}}\text{,}\\& {\lambda _2} = {\sigma / {\left( {1 - \xi } \right)\left( {2 - \xi } \right)}}\text{,}\\& {\tau _3} = 2{{\left( {1 - {3^\xi }} \right)} / {\left( {1 - {2^\xi }} \right)}} - 3\text{,}\\& {\tau _4} = {{\left( {1 - {{6.2}^\xi } + {{10.3}^\xi } - {{5.4}^\xi }} \right)} / {\left( {1 - {2^\xi }} \right)}}\text{。}\end{aligned} \right.$ | (16) |
尺度参数
| $\hat \sigma = {{ - {l_2}\hat \xi } / {\left( {1 - {2^{\hat \xi }}} \right)}}\Gamma \left( {1 + \hat \xi } \right)\text{,}$ | (17) |
| $\hat \mu = {l_1} + {{\hat \sigma \left\{ {1 - \Gamma \left( {1 - \hat \xi } \right)} \right\}} / {\hat \xi }}\text{。}$ | (18) |
首先由式(1)~式(16)用数值方法求出形状参数
本文的仿真工具以美国国家可再生能源实验室开发的湍流风仿真软件TurbSim和风机仿真软件FAST为基础。风机模型为WP_Baseline 1.5MW陆上风机,基本参数见表1。
|
|
表 1 风机基本参数 Tab.1 Basic parameters of wind turbine |
风机等级IECⅠ-A。计算工况为IEC 61400-1中正常发电工况类的DLC 1.1。假定平均风速服从瑞利分布。
| $\begin{aligned}& {f_V}\left( v \right) = \frac{{2v}}{{{\alpha ^2}}}\exp \left[ { - {{\left( {\frac{v}{\alpha }} \right)}^2}} \right]\text{,}\\& \alpha = \frac{{2{\mu _V}}}{{\sqrt {\text{π}} }}\text{。}\end{aligned}$ | (19) |
其中
| $\begin{aligned}& {F_V}\left( v \right) = \frac{{G\left( v \right) - G\left( {{V_{in}}} \right)}}{{G\left( {{V_{out}}} \right) - G\left( {{V_{in}}} \right)}}\text{,}\\& G\left( v \right) = \exp \left[ { - {{\left( {\frac{v}{\alpha }} \right)}^2}} \right]\text{。}\end{aligned}$ | (20) |
将工作风速区间按照2 m/s的分辨率划分成11个子区间,各子区间的平均风速为5 m/s,7 m/s,…,25 m/s。对每一个子区间进行8次随机仿真,单次仿真时长630 s,其中前30 s是为了消除风机启动时的影响,在选取极值点时会被忽略。湍流谱为IEC Kaimal谱,幂指数风切。
3 极限载荷求解 3.1 短期载荷极值采用分块法选取短期载荷极值,即将短期载荷数据分为若干块,然后从每一块中选取各自的最大值。设定输出步长0.05 s,则单次仿真输出12 000个有效数据。以风速11 m/s,块容量400为例,选取的短期极值点如图2所示。
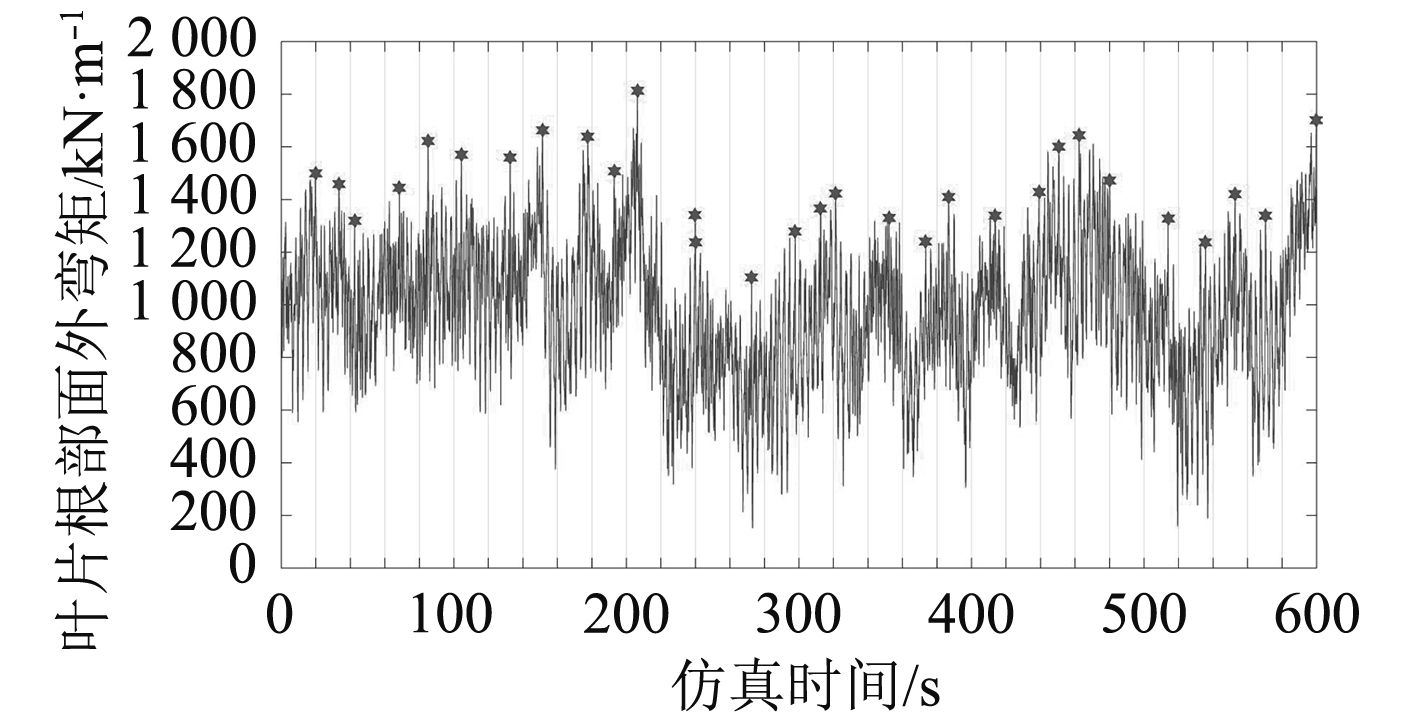
|
图 2 短期载荷极值点 Fig. 2 Short-term load extremes |
设分块数为m,则在累积分布函数上,分块极值点与全局极值点的关系如下:
| $\begin{aligned}& {F_{L10\min \left| V \right.}}\left( {l\left| v \right.} \right) = Pr \left\{ {{L_{10\min }} \leqslant l\left| {V = v} \right.} \right\}=\\& \quad Pr \left\{ {{L_{block1}} \leqslant l\left| {V = v},{L_{block2}} \leqslant l \right| {V = v} , \cdot \cdot \cdot ,} {L_{blockm}} \leqslant l \left| V =\right.\right. \\ & \quad \left\{v \right\} {F_{L - block\left| V \right.}}^m\left( {l\left| v \right.} \right)\text{。}\end{aligned}$ | (21) |
选取了短期载荷极值点后,即可根据前述原理对样本点进行拟合。风速11 m/s,块容量400时,拟合分布的概率密度函数和累积分布函数如图3和图4所示。
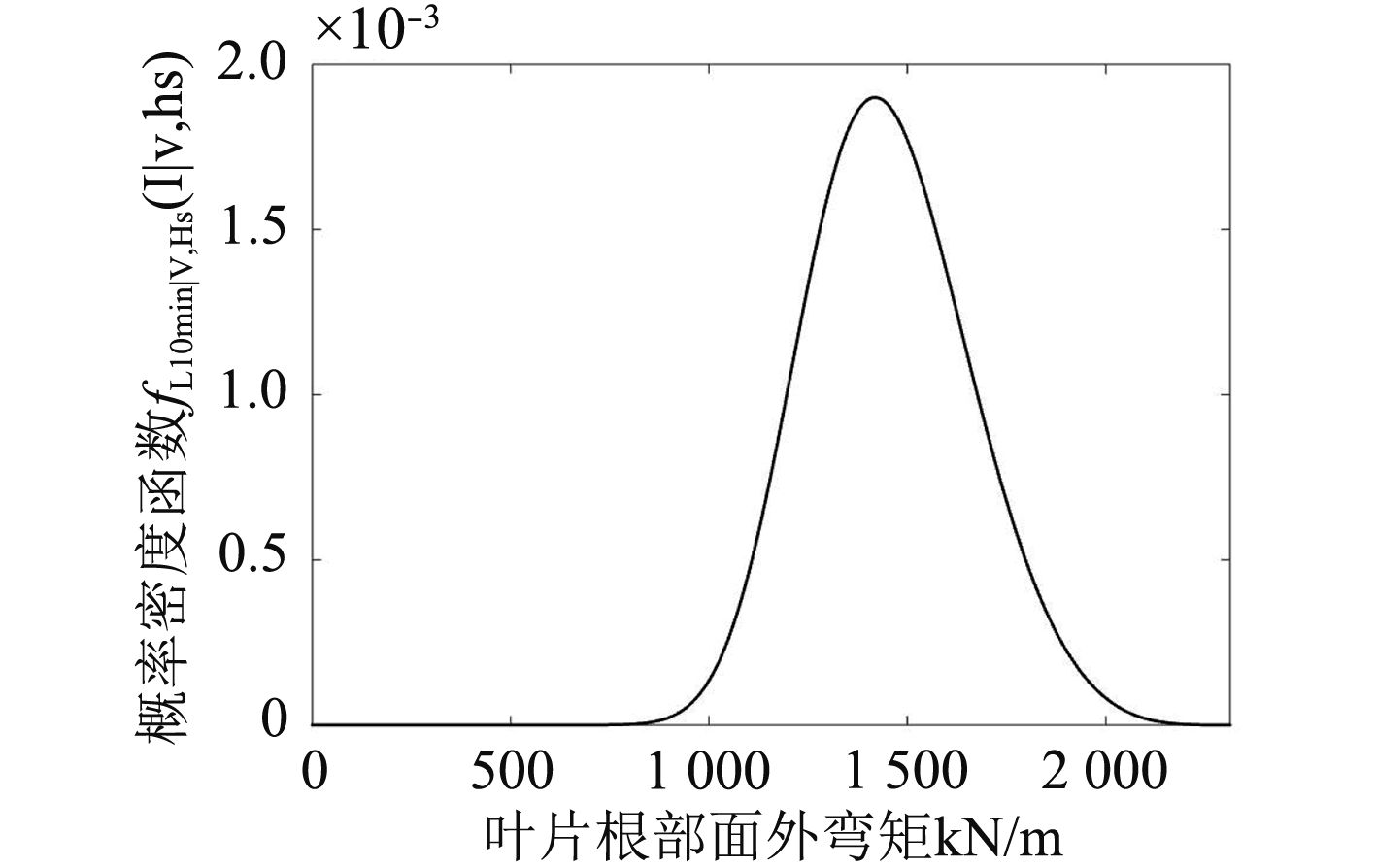
|
图 3 拟合分布概率密度函数 Fig. 3 Probability density function of fitted distribution |
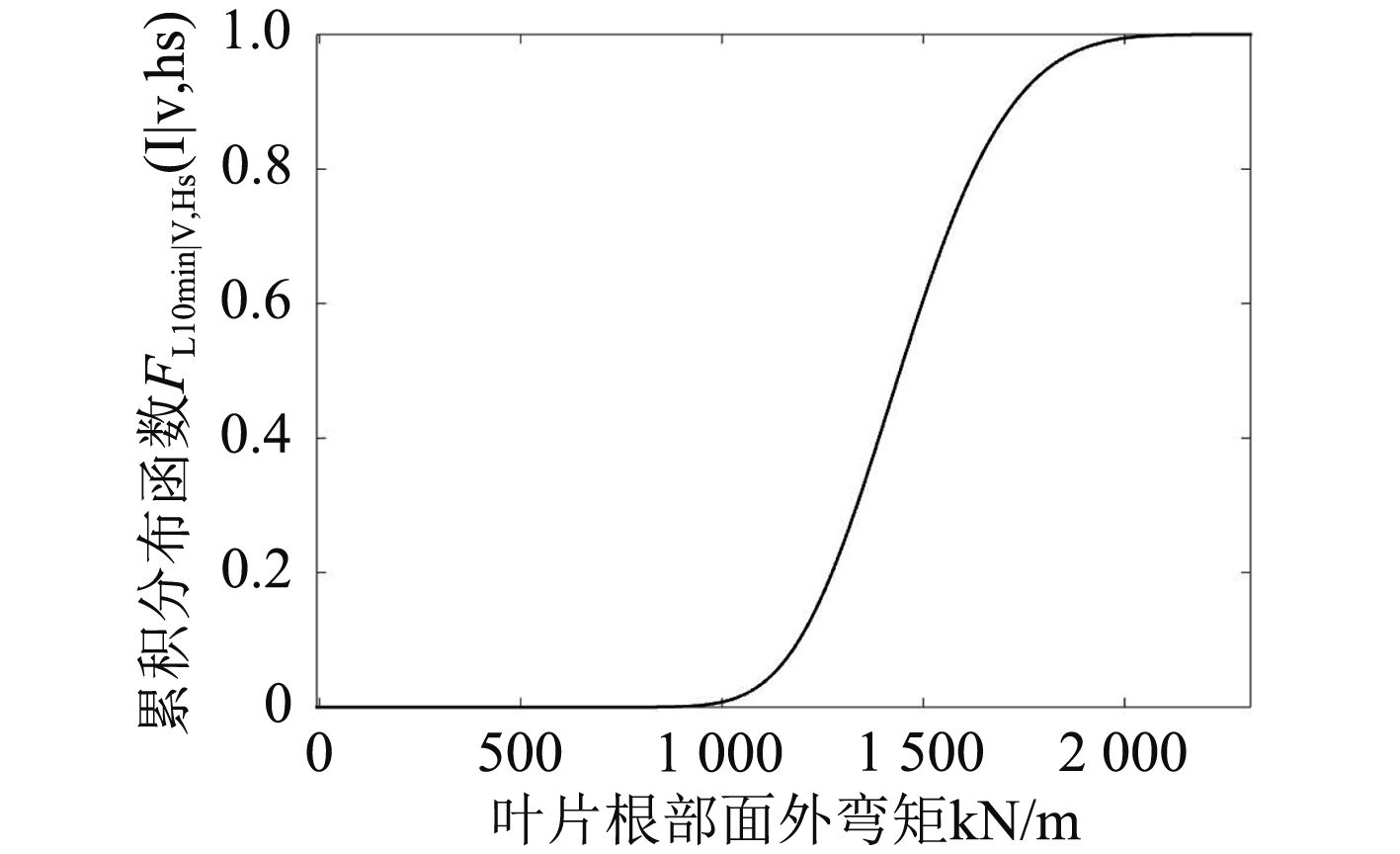
|
图 4 拟合分布累积分布函数 Fig. 4 Cumulative distribution function of fitted distribution |
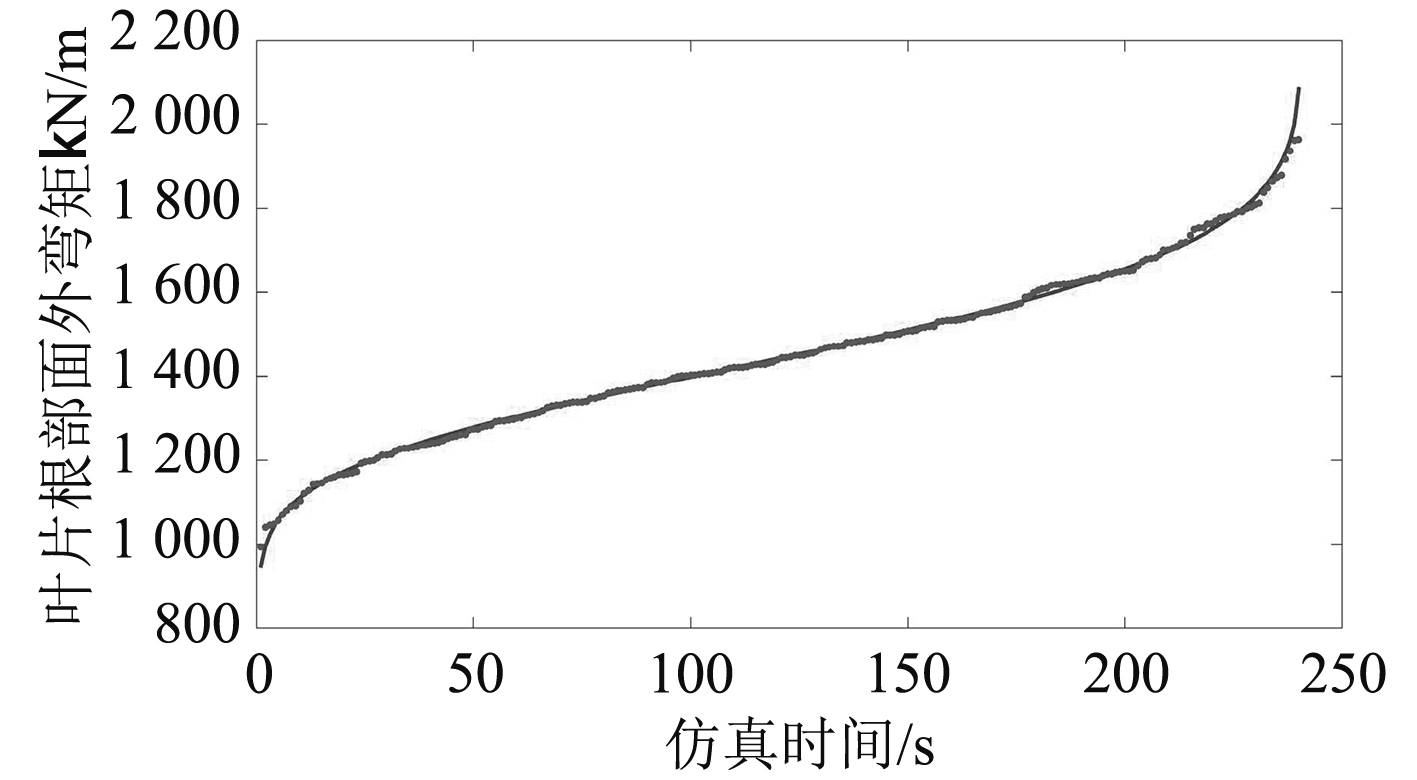
在统计分析中,Q-Q图是检验模型分布最常用也是最直观的方法。同样以风速11 m/s,块容量400为例,经验分布函数和拟合分布函数所形成的Q-Q图如图5所示,其中经验频率公式为中值公式。
|
图 5 短期载荷极值Q-Q图 Fig. 5 Quantile-Quantile plot of short-term load extremes |
由图可知,拟合分布与经验分布总体较接近,曲线右侧高分位数之间的误差较小,这对提高外推精度无疑是有利的。因为总体的超越概率是由多个子区间的超越概率累加起来的,因此每个子区间误差的细微减小,也能在总体上较大地减少误差。
3.2 长期载荷分布利用1.3节原理对选取的短期载荷极值进行统计分析,得到不同风速下的形状参数
|
|
表 2 拟合分布参数估计 Tab.2 Estimated parameters of fitted distribution |
由表可知,各平均风速下的形状参数均为负数,因此所有的短期载荷分布均为广义极值Ⅲ型分布。
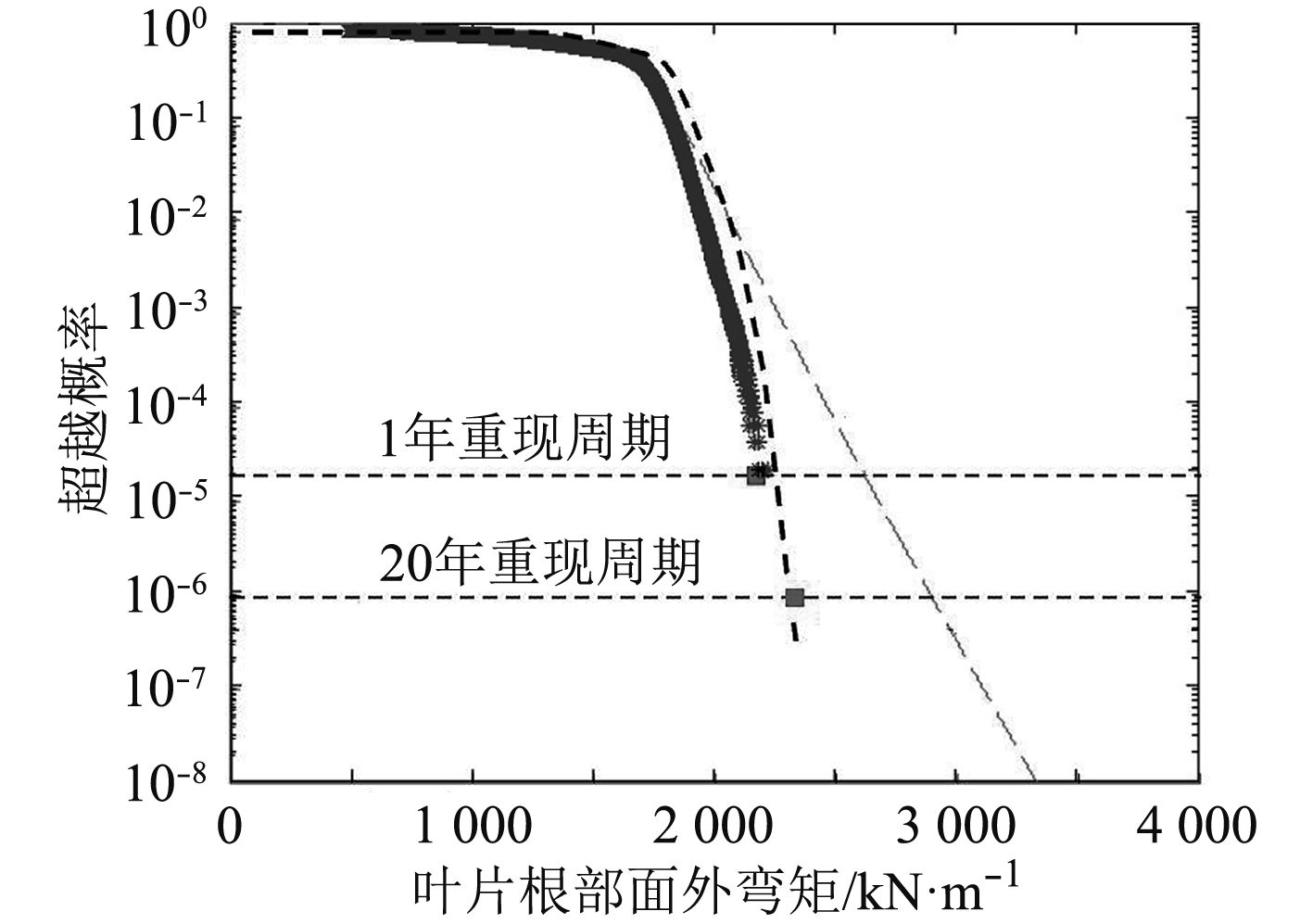
将载荷短期分布和平均风速分布联合起来,即可求得叶片根部面外弯矩的长期分布。选取不同的
|
图 6 外推结果与“真实数据”对比 Fig. 6 Comparison of extrapolation results and real data |
图6中实线部分为“真实数据”,短虚线为本文外推结果,长虚线为P.J. Moriarty外推结果,方形点为Korn Saranyasoontorn外推结果。由图6可知,本文计算出的超越概率曲线与“真实数据”整体较接近,两者在500~2 500 kN·m的区间内,都具有相似的形态。P.J. Moriarty计算出的超越概率曲线在1 750 kN·m之前与“真实数据”差别不大,但是在该点之后曲线斜率出现了较大的偏差,以致在1年和20年重现周期时较远的偏离了“真实数据”点。Korn Saranyasoontorn的计算结果没有超越概率曲线,是通过环境等值线法外直接外推1年和20年重现周期时的极端载荷,由图可知,其结果与“真实数据”较吻合。同时由表3可知,在20年重现周期时,本文的外推结果与环境等值线法也大致相当。
|
|
表 3 1年和20年重现周期外推结果对比 Tab.3 Comparison of extrapolation in 1 year and 20 years return periods |
为了检验外推结果的稳定性,将仿真时长分别增加至20 min和40 min,同时保持其他设置参数不变。多个分块容量下不同仿真时长在1年重现周期时的结果对比如表4所示。
|
|
表 4 多个分块容量及仿真时长下的外推结果 Tab.4 Extrapolations of multiple simulation times and block capacities |
当仿真时长增加后,外推结果仍然具有较好的稳定性。在多个块容量下,外推值都集中在2 300 kN·m左右,波动幅度5%以下。同时,对于每个仿真时长,块容量的变化对外推值的影响也较小。
4 结 语以经典极值理论和积分法为基础,采用分块法选取短期载荷极值,广义极值分布进行样本拟合,线性矩法估计分布参数,外推求解了WP_Baseline 1.5 MW陆上风机叶片根部面外弯矩的长期分布,得出以下结论:
1)采用广义极值分布对短期载荷极值进行拟合,解决了P.J. Moriarty使用其他分布时遇到的拟合问题,减少了估计高分位数时的误差,最终在极端载荷长期分布的外推上获得了更好的效果。
2)利用线性矩法估计分布参数,得到了较好的参数估计值,并且经过了分位数对比图的检验。
3)从仿真时长及分块容量两方面检验了外推数据的稳定性,证明了本文所述方法不仅具有良好的外推结果还具有较高的可靠性。
| [1] |
IEC 61400-1: 2005, Wind turbines - Part 1: Design requirements, Edition 3.0, 2005 [S].
|
| [2] |
IEC 61400-3: 2009, Wind turbines - Part 3: Design requirements for offshore wind turbines, Edition 1.0, 2009 [S].
|
| [3] |
夏一青, 王迎光. 应用统计外推求解近海风机面外叶根部弯矩最大值[J]. 上海交通大学学报, 2013, 47(12): 1968-1973. |
| [4] |
张友文, 王迎光. 浮式风机极限载荷与疲劳载荷对比分析[J]. 海洋工程, 2015, 33(3): 57-62. |
| [5] |
李昕雪, 王迎光. 不同外推方法求解近海风机的极限载荷[J]. 上海交通大学学报, 2016, 50(6): 844-848. |
| [6] |
MORIARTY PJ, HOLLEY W, BUTTERFIELD CP. Extrapolation of extreme and fatigue loads using probabilistic methods [EB/OL]. (2004-11) [2017-02]. http://www.nrel.gov/docs/fy05osti/34421.pdf.
|
| [7] |
SARANYASOONTORN K, MANUEL L. Design loads for wind turbines using the environmental contour method[J]. Journal of Solar Energy Engineering, 2006, 128(4): 554-61. DOI:10.1115/1.2346700 |
| [8] |
段忠东, 周道成. 极值概率分布参数估计方法的比较研究[J]. 哈尔滨工业大学学报, 2004, 36(12): 1605-1609. DOI:10.3321/j.issn:0367-6234.2004.12.006 |
| [9] |
陈子燊, 刘曾美, 路剑飞. 广义极值分布参数估计方法的对比分析[J]. 中山大學學報 (自然科學版), 2010, 49(6): 105-109. |
| [10] |
卢安平, 赵林, 郭增伟, 等. 基于Monte Carlo法的极值分布类型及其参数估计方法比较[J]. 哈尔滨工业大学学报, 2013(2): 88-95. |
| [11] |
罗纯, 王筑娟. Gumbel分布参数估计及在水位资料分析中应用[J]. 应用概率统计, 2005, 21(2): 169-175. DOI:10.3969/j.issn.1001-4268.2005.02.007 |
| [12] |
HOSKING JR. L-moments: analysis and estimation of distributions using linear combinations of order statistics[J]. Journal of the Royal Statistical Society Series B (Methodological), 1990, 105-24. |
| [13] |
陈元芳, 沙志贵. 具有历史洪水时P—Ⅲ分布线性矩法的研究[J]. 河海大学学报: 自然科学版, 2001, 29(4): 76-80. |
| [14] |
陈元芳, 李兴凯, 陈民, 等. 可考虑历史洪水信息的广义极值分布线性矩法的研究[J]. 水文, 2008, 28(3): 8-13. DOI:10.3969/j.issn.1000-0852.2008.03.002 |
| [15] |
梁玉音, 刘曙光, 钟桂辉, 等. 线性矩法与常规矩法对太湖流域降雨频率分析的比较研究[J]. 水文, 2013, 33(4): 16-21. DOI:10.3969/j.issn.1000-0852.2013.04.003 |
| [16] |
吴俊梅, 林炳章, 邵月红. 地区线性矩法在太湖流域暴雨频率分析中的应用[J]. 水文, 2015, 5: 004. |
 2018, Vol. 40
2018, Vol. 40
