海洋工程船为了满足作业要求,需要装备能够控制其位置或航行轨迹的动力装置,常见的有柴油机推进、电力推进以及柴电混合推进装置。柴电混合推进装置结合了柴推和电推的优点,既具备动力强劲、经济性好的优点,又能保证在低速航行中的灵活性及定位能力。但装备柴电混合推进装置的船舶拥有多组推进器及多台柴油机,当控制器发送总的推力命令,如何通过某种逻辑对推进器的推力以及柴油机的功率进行分配,会对海洋工程船的能耗、排放和磨损产生很大影响。目前针对推力分配优化问题的解决主要分为线性约束分配和非线性约束分配两类,文献[1 – 5]分别使用序列二次规划、拉格朗日法、遗传算法及模拟退火算法对动力定位系统的推力进行分配,并限制了每个推进器的最大推力,推力变化及全回转推进器方向角的变化。通过优化算法得出各个推进器的输出推力后,还需要对主机和副机进行动力分配以满足推进器的功率需求。船舶的柴电混合推进系统通常有3种动力输出方式:主柴油机单独运行的纯机械推进,1台或多台副机运行的电力推进,主柴油机和副机共同运行的混合推进。周奇勋等[6]对混合动力汽车的工作模式进行分析,提出了在各种模式下的能量管理策略,并制定了模式切换策略。凌斌等[7]建立了混合动力汽车的功率分配模型,并利用离散动态规划算法对实际运行时的功率分配进行优化控制,达到了节省燃油消耗和提髙燃油经济性的目的。
本文以某海洋工程船为研究对象,使用改进的遗传算法对控制器发出的推力进行分配,得到严格满足等式约束的仿真结果。之后对船舶在不同工况下的动力进行分配,得到海洋工程船在不同功率下的最佳混合度。本文所做的研究工作及相应结论可为海洋工程船的推力及动力分配控制器的设计提供参考。
1 建立优化模型海洋工程船配备2台主柴油机,并配有轴带发电机,编号分别为G5和G6;4台柴油发电机,编号分别为G1~G4;7台推进器,其中包括2部可以由主柴油机和电机驱动的调距桨,1台尾侧推,2台首侧推,2台全回转推进器,如图1所示。
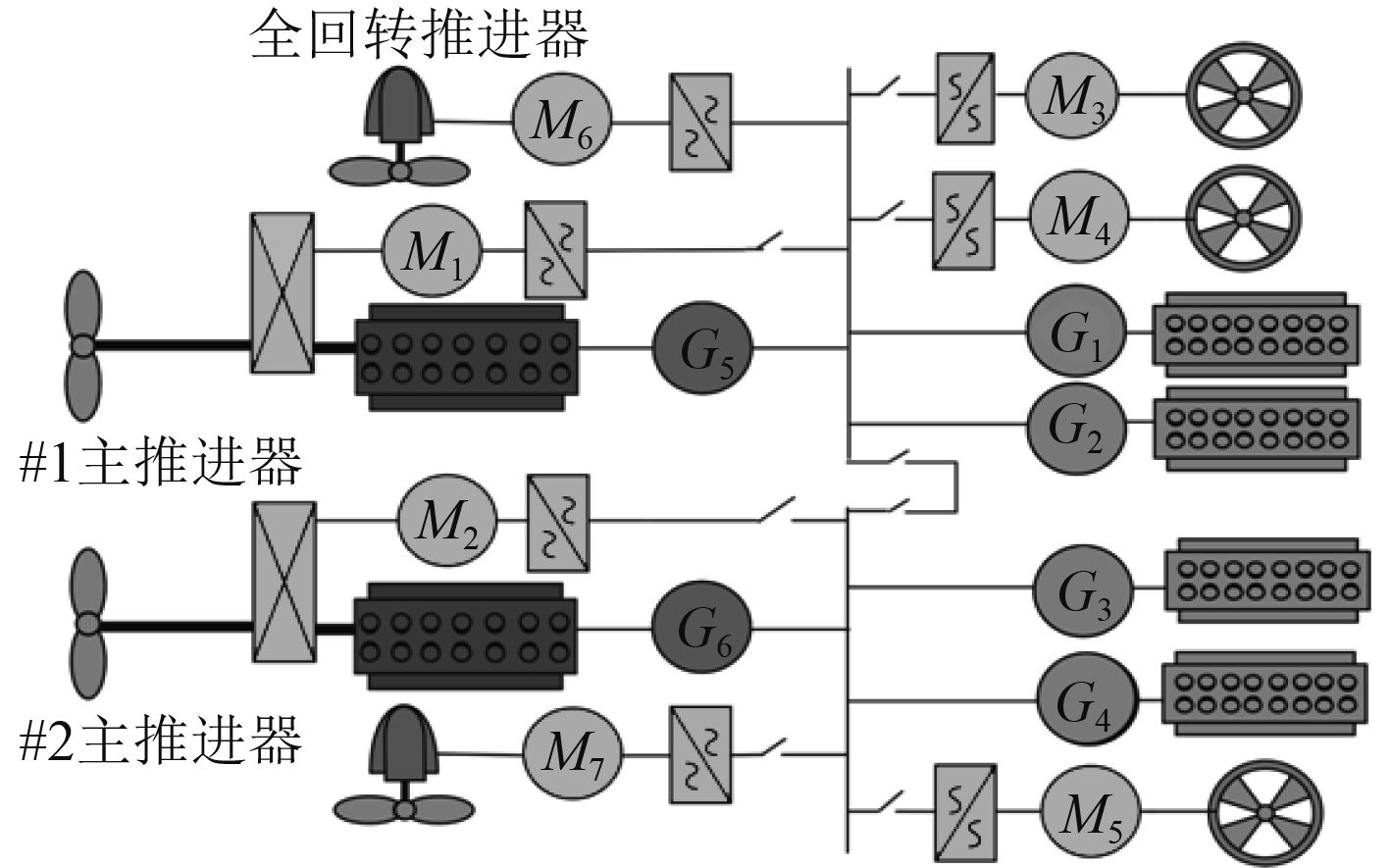
|
图 1 海洋工程船推进系统结构图 Fig. 1 Propulsion system structure of the ocean engineering ship |
通过7个控制器对海洋工程船的3个自由度进行控制,这是过驱动控制问题。当控制器发出对横荡、纵荡方向上的合力及首摇方向上的控制力矩时,需要对7台推进器进行协同控制,在多种推力分配的结果中选取能耗最低、推进器磨损最小的一组。同时还要约束推进器所能提供的最大推力、全回转推进器推力角的变化速率以及推进器之间水动力干涉等问题。因此得出推力分配的目标函数为:
| ${\rm{Min}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} J = \sum\limits_{i = 1}^7 {{P_i}({u_i})} + {(\Delta \alpha )^{\rm T}}\Omega (\Delta \alpha ) + {s^{\rm T}}Qs\text{,}$ | (1) |
约束条件为:
| ${F_x} = \sum\limits_{i = 1}^n {{u_i}\cos {\alpha _i}}\text{,} $ |
| ${F_y} = \sum\limits_{i = 1}^n {{u_i}\sin {\alpha _i}}\text{,}$ |
| $M = \sum\limits_{i = 1}^n {{u_i}\cos {\alpha _i}} {l_{yi}} + \sum\limits_{i = 1}^n {{u_i}\sin {\alpha _i}} {l_{xi}}\text{,}$ |
| ${u_{\min }} \leqslant u \leqslant {u_{\max }}\text{,}$ |
| $\Delta {u_{\min }} \leqslant {u_t} - {u_{t - 1}} \leqslant \Delta {u_{\max }}\text{,}$ |
| $\Delta {\alpha _{\min }} \leqslant {\alpha _t} - {\alpha _{t - 1}} \leqslant \Delta {\alpha _{\max }}\text{。}$ |
目标函数第1项表示所有推进器的消耗功率;第2项通过推进角的变化率表示推进器的磨损,Ω为权值矩阵;第3项引入松弛变量s,用来保证在不满足输入指令的情况下也能得到一组最优解。约束条件中,Fx,Fy,M分别为控制器在纵荡、横荡及首摇方向的输入指令;ui为第i个推进器提供的推力,αi为第i个推进器的推力角,lxi和lyi分别为推进器的横坐标和纵坐标;Δumin,Δumax,Δαmin,Δαmax分别为推力及推力角变化的最大值和最小值。
式(1)通过对等式约束进行松弛解决等式约束的优化问题,但是松弛法会导致拓扑空间发生变化,使等式无法严格满足。本文采用文献[8]提出的基于降维和排序的约束遗传算法,解决拥有等式约束的推力分配问题。经过降维处理的优化问题可以使等式约束严格满足,进而将等式约束转化为不等式约束。因为存在等式约束,所以待优化的变量之间并不独立。假设待优化的变量有n个,而等式约束有m个,相当于有n–m个变量相互独立,另外m个变量可以由剩余n–m个变量表达,进而在保证等式成立的前提下降低了变量数目。假设优化函数的等式约束为:
| $\left\{ {\begin{aligned} & {{a_{11}}{x_1} + {a_{12}}{x_2} + \cdots {\rm{ + }}{a_{1n}}{x_n} = {b_1}} \text{,}\\ &\quad\quad\quad\quad\quad\quad \vdots \\ & {{a_{m1}}{x_1} + {a_{m2}}{x_2} + \cdots {\rm{ + }}{a_{mn}}{x_n} = {b_m}} \text{,} {m \leqslant n} \text{。}\end{aligned}} \right.$ | (2) |
移项后为:
| $\left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{a_{11}}{x_1} + {a_{12}}{x_2} + \cdots {\rm{ + }}{a_{1m}}{x_m} = {b_1} - } \\ { ({a_{1,m + 1}}{x_{m + 1}} + \cdots {\rm{ + }}{a_{1n}}{x_n})} \text{,}\end{array}} \\ \vdots \\ {{a_{m1}}{x_1} + {a_{m2}}{x_2} + \cdots {\rm{ + }}{a_{mm}}{x_m} = {b_m} - } \\ { ({a_{m,m + 1}}{x_{m + 1}} + \cdots {\rm{ + }}{a_{mn}}{x_n})} \text{。}\end{array}} \right.$ | (3) |
通过解线性方程组,x1,x2,…,xm很容易被求解出来。
因此可将优化函数简化为:
| ${\rm{Min}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} J = \sum\limits_{i = 1}^7 {{P_i}({u_i})} + {(\Delta \alpha )^{\rm T}}\Omega (\Delta \alpha )\text{。}$ | (4) |
位于上游的全回转推进器尾流会对处在同一直线上的下游螺旋桨产生水动力干扰,使下游螺旋桨的水流速度增大,导致推力减小。在推力分配的优化中,通常设置推力禁区、推力衰减、在推力禁区内限制最大推力等方法来避免或减小全回转推进器的水动力干扰问题。但设置推力禁区或者在推力禁区内限制前一个螺旋桨的最大推力可能会降低优化效果,因此采用在推力禁区内设置推力减额系数的方法。推力减额系数与螺旋桨的推力大小以及方向有关,前一个推进器的推力越大,则后一个螺旋桨受水动力干扰的影响越大,2个螺旋桨在x轴方向上的重叠角度越大,则影响越大。推力减额系数的表达式为:
| $b = t \times \frac{{\theta - \left| \alpha \right|}}{\theta } \times \frac{{u - \bar u}}{{u{}_{\max }}}\text{。}$ | (5) |
式中:b为推力减额系数,是全回转推进器单位功率下的推力衰减量;t为一个极限减额系数,其大小决定了推进器在推力禁区内的最大推力衰减量,全回转推力器之间的水动力干扰最大可造成60%的推力损失[9];
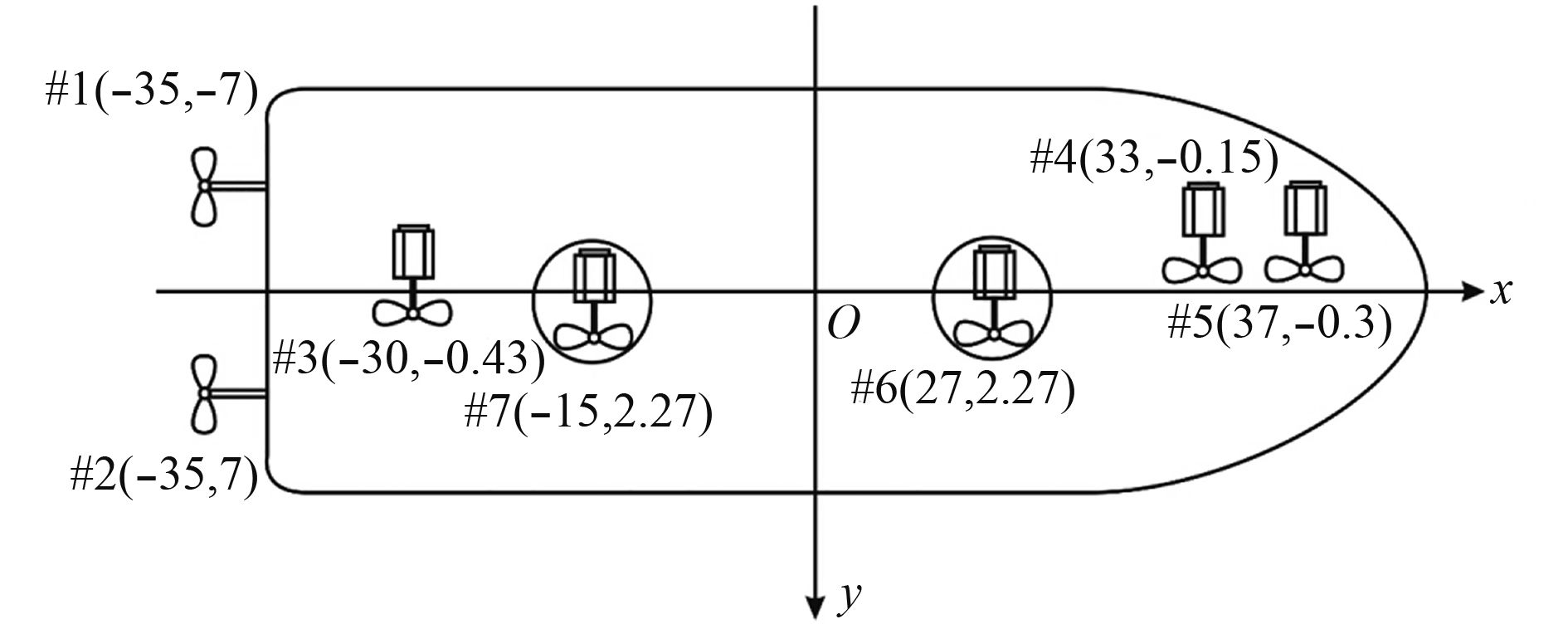
|
图 2 推进器布置图 Fig. 2 The propeller layout |
各推进器最大推力及额定功率如表1所示。
|
|
表 1 推进器参数 Tab.1 Propeller parameters |
一般来说,全回转推进器的推力禁区通过其推力衰减系数图来确定,但也可以采用文献[10]提出的公式确定:
| $\theta = \pm \frac{{500}}{{{L / D} + {{20{\rm{^\circ }}}}}}\text{。}$ | (6) |
式中:L为全回转推进器之间的距离;D为上游螺旋桨的直径。
因为海洋工程船的2个全回转推进器距离较远,选定推力减额系数为0.4。海洋工程船的2个全回转推进器的距离是42 m,螺旋桨直径为1.5 m,所以推力禁区界限θ=±10.42°。
2 改进遗传算法遗传算法具有很强的全局搜索能力及很好的鲁棒性能,适用于求解推力分配这种超静定约束的优化问题。但是标准遗传算法的局部搜索能力较弱,并且后期由于个体间的高相似度会导致种群停止进化。而本文提出的推力分配优化方案以基于降维和排序的约束算法为基础,从2个方面对遗传算法进行改进,进而提高其优化精度及收敛速度:1)采用基于上一时刻精英个体的均匀分布种群生成方法;2)在标准遗传算法中结合自适应算法。
2.1 初始种群的生成方法遗传算法的时效性很大一部分取决于初始种群的精英程度。一般来讲,初始种群如果拥有较高的精度和多样性时,遗传算法的搜索效率及收敛速度能够得到很大的提升。但标准遗传算法的初始种群是随机生成的,无法保证其精英程度及多样性。在推力分配的目标函数中,存在着对推进器推力及推力角的约束,这就导致下一时刻的推力及推力角的取值范围必须在上一刻推力及推力角最优值的附近,本文采用遗传算法的种群数目设为p。将上一时刻适应度最高的q(q<p)个个体作为下一时刻初始种群的一部分,另外p–q个初始个体采用平均分布的方法生成,每个个体由n个变量组成。设Ui为初始种群的第i个个体,uij为Ui的第j个变量,aj和bj分别为变量uij的上限和下限,即
| ${U_i} = [{u_{i1}} , \; {u_{i2}} , \; \cdots , \; {u_{in}}]\text{。}$ | (7) |
令rij为对应初始种群第i个个体第j个分量在[0,1]内满足均匀分布几率的随机数,则初始种群其他个体Ui为:
| ${U_i} = {{A}} + \frac{{({{{R}}_i} + i - 1) \otimes ({{B - A)}}}}{{20}}\text{。}$ | (8) |
式中:A=[a1,a2,…,an]T;B=[b1,b2,…,bn]T;Ri=[ri1,ri2,…,rin]T,i=q+1,q+2,…,p。
2.2 自适应局部搜索算法遗传算法的性能好坏很大程度上取决于交叉算子和变异算子。交叉算子的作用是生成新的个体,对遗传算法的全局搜索能力具有很大影响;而变异算子只是用来辅助生成新个体,但它能改变个体编码串的结构,维持种群的多样性,防止早熟现象的出现,并对遗传算法的局部搜索具有很大影响。但是随着进化代数的增加,种群的个体相似度会越来越大,交叉算子很难产生新的个体,这时应该动态调整交叉和变异算子,增大变异概率,减小交叉概率。所以本文使用结合自适应调整交叉和变异算子的算法来提高遗传算法的局部搜索能力,进而提高推力分配的优化精度。
在进化中,以适应度的变化来改变交叉和变异的概率。设群体的最佳适应值为gmax,当代最佳的适应值为fmax,当代的平均适应值为favg;设定2个交叉概率和2个变异概率,分别为Pcmax,Pcmin和Pmmax,Pmmin,则具体算法为:
if g > k
| $Pc = P{c_{\max}} \times {{\left( {g_{\rm max} - f_{\rm avg}} \right)} / {\left( {f_{\rm max} - f_{\rm avg}} \right)}}\text{,}$ | (9) |
| $Pm = P{m_{\max}} \times {{\left( {f_{\rm max} - f_{\rm avg}} \right)} / {\left( {g_{\rm max} - f_{\rm avg}} \right)}}\text{,}$ | (10) |
otherwise
| $Pc = P{c_{\max}} - {i / m} \times \left( {P{c_{\max}} - P{c_{\min}}} \right)\text{,}$ | (11) |
| $Pm = P{m_{\max}} + {i / m} \times \left( {P{m_{\max}} - P{m_{\min}}} \right)\text{。}$ | (12) |
式中:g为fmax与gmax的比值;k为设定的阈值;i为进化代数;m为总的进化代数。
3 推力分配优化以海洋工程船的初始位置为坐标原点建立北东坐标系,目标位置为[100,20],流速为0.2 m/s,方向为正西,风速为30 m/s,方向为北偏东40°,使用自抗扰控制器得出的需求推力及需求力矩如图3所示。
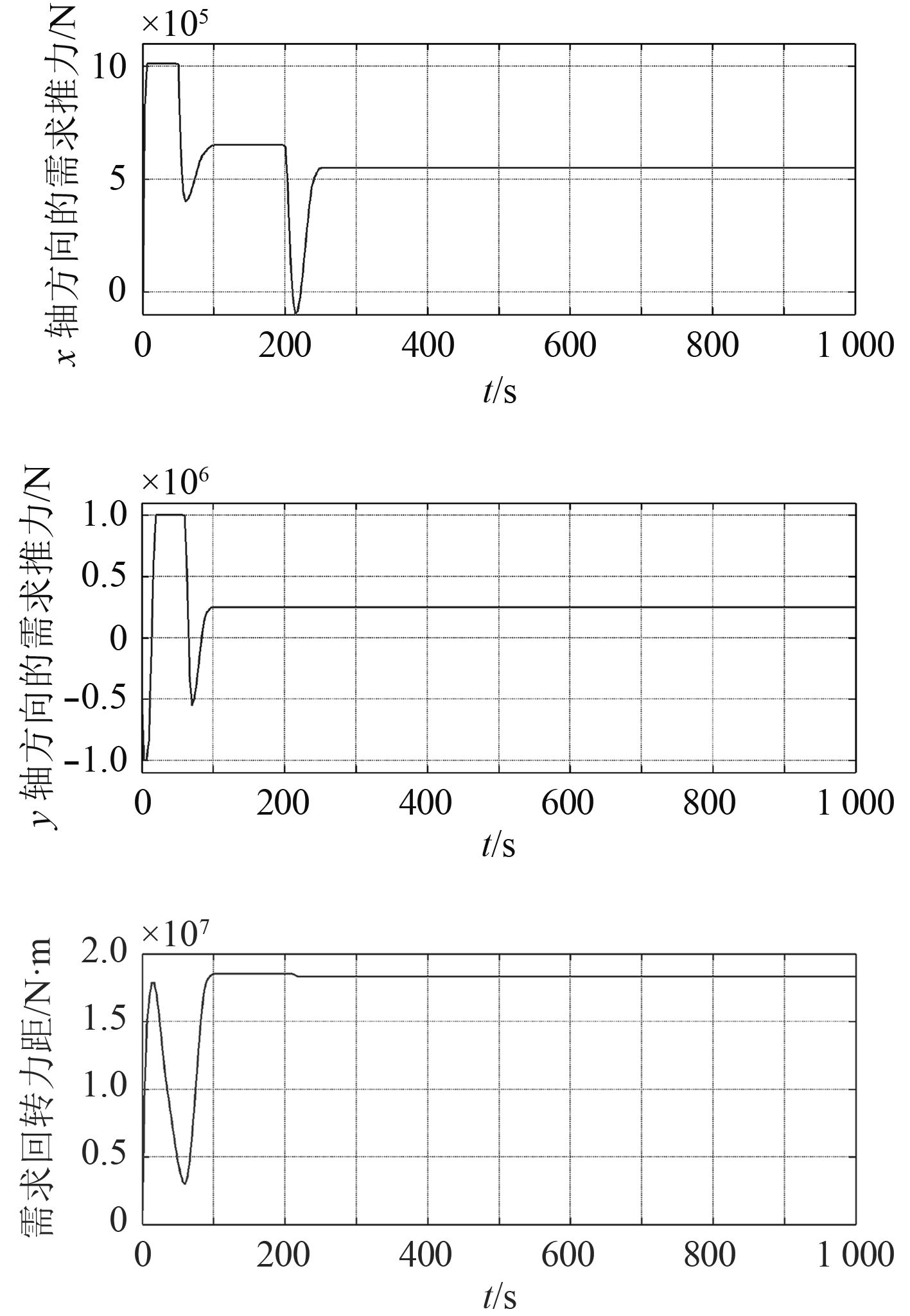
|
图 3 控制器输出的推力及力矩 Fig. 3 The output thrust and torque of controller |
海洋工程船有7台推进器,包括2个全回转推进器,目标函数的自变量为9个,但经过式(2)和式(3)的降维处理,1~3号推进器的推力可由其他变量表示,所以目标函数的最终变量个数为6个。遗传算法的最大进化代数为100,种群数量为30,将上一时刻最优的10个个体作为下一时刻初始种群的一部分。k为0.9,Pcmax为0.8,Pcmin为0.6,Pmmax为0.04,Pmmin为0.02,自变量离散精度eps为0.1。
将建立的推力分配模型导入改进的遗传算法中,得出的推力分配结果如图4所示。
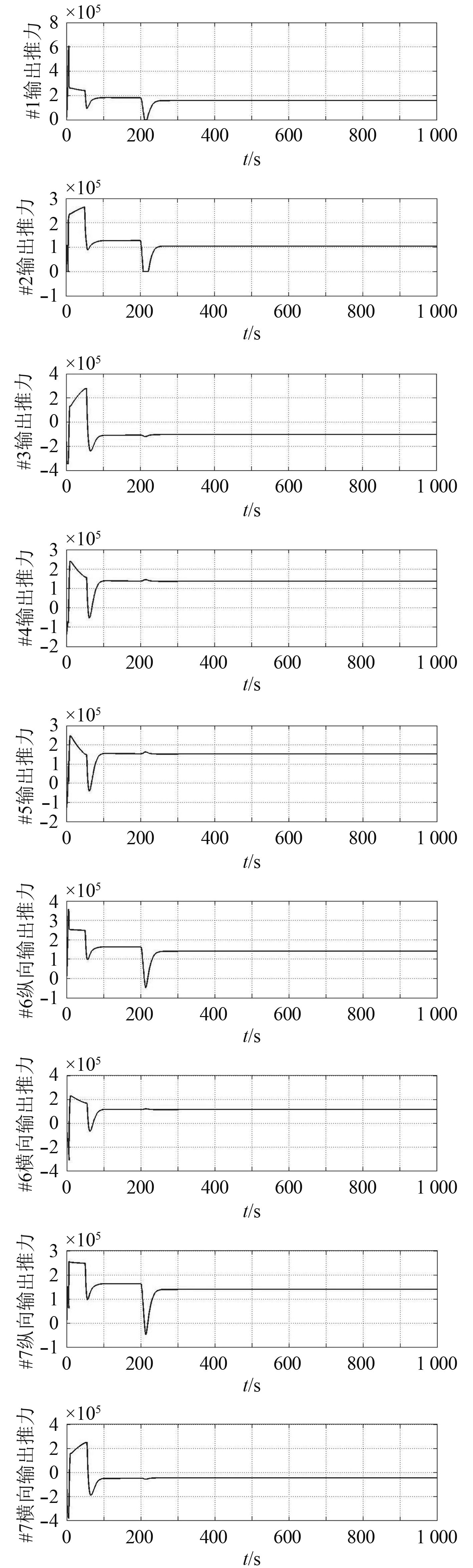
|
图 4 推进器的推力分配结果 Fig. 4 The thrust distribution results of propeller |
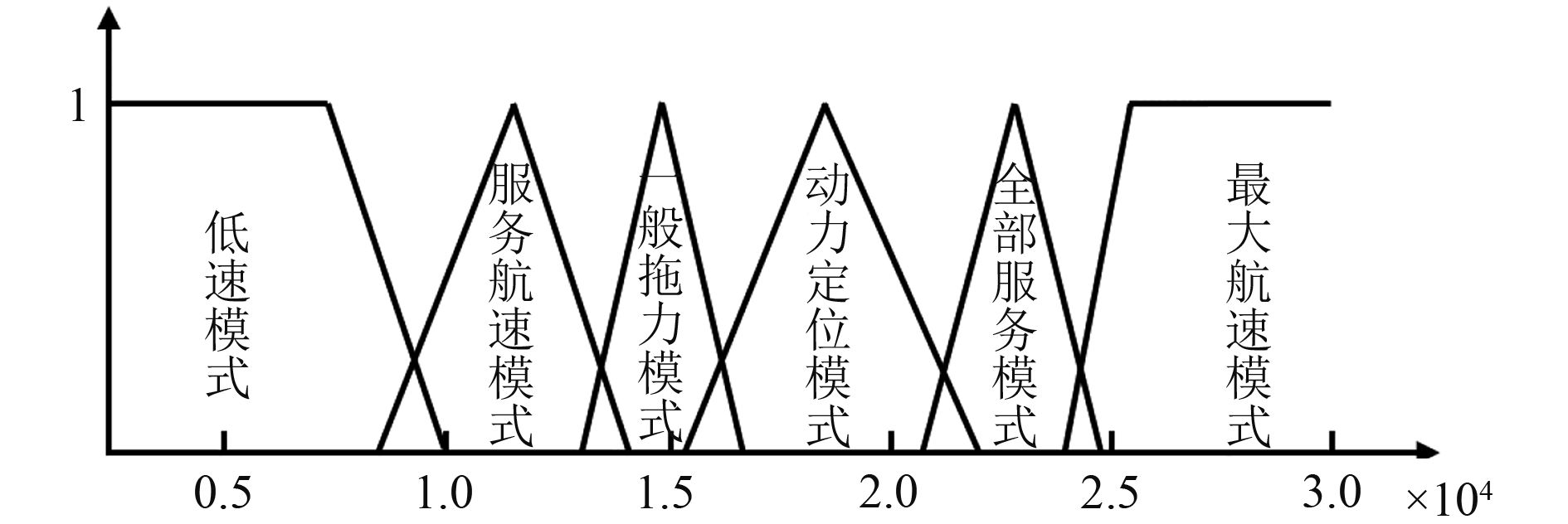
在不同的工况下,海洋工程船的功率输出可以分为低速模式、服务航速模式、一般拖力模式、动力定位模式、全部服务航速模式和最大航速模式。但在实际运行中相邻2种模式的判定非常模糊,使用最小模糊度法,根据经验对数据进行采集,最终得到6个模式的三角形隶属度函数,如图5所示。
|
图 5 模式识别的隶属度函数图 Fig. 5 The pattern recognition membership function graph |
对海洋工程船舶动力进行分配的目的是用最少的燃油消耗使船舶输出给定的动力,进而提高工程作业的经济性。
将主机的输出功率与船舶动力系统发出的总功率之比定义为功率混合度,即
| $H = \frac{{{P_1}}}{{{P_1} + {P_2}}} = \frac{{{P_1}}}{P}\text{。}$ | (13) |
式中:P1为主机的输出功率;P2为副机的输出功率。
以海洋工程船的燃油经济性为动力定位的评价指标,其可以表示为:
| $G = {g_1}PH + \frac{{{p_1}}}{{{p_2}}}{g_2}P(1 - H)\text{。}$ | (14) |
式中:g1和g2分别为主机和副机在对应负荷下的燃油消耗率;p1和p2分别为主机和副机使用燃油的价格。
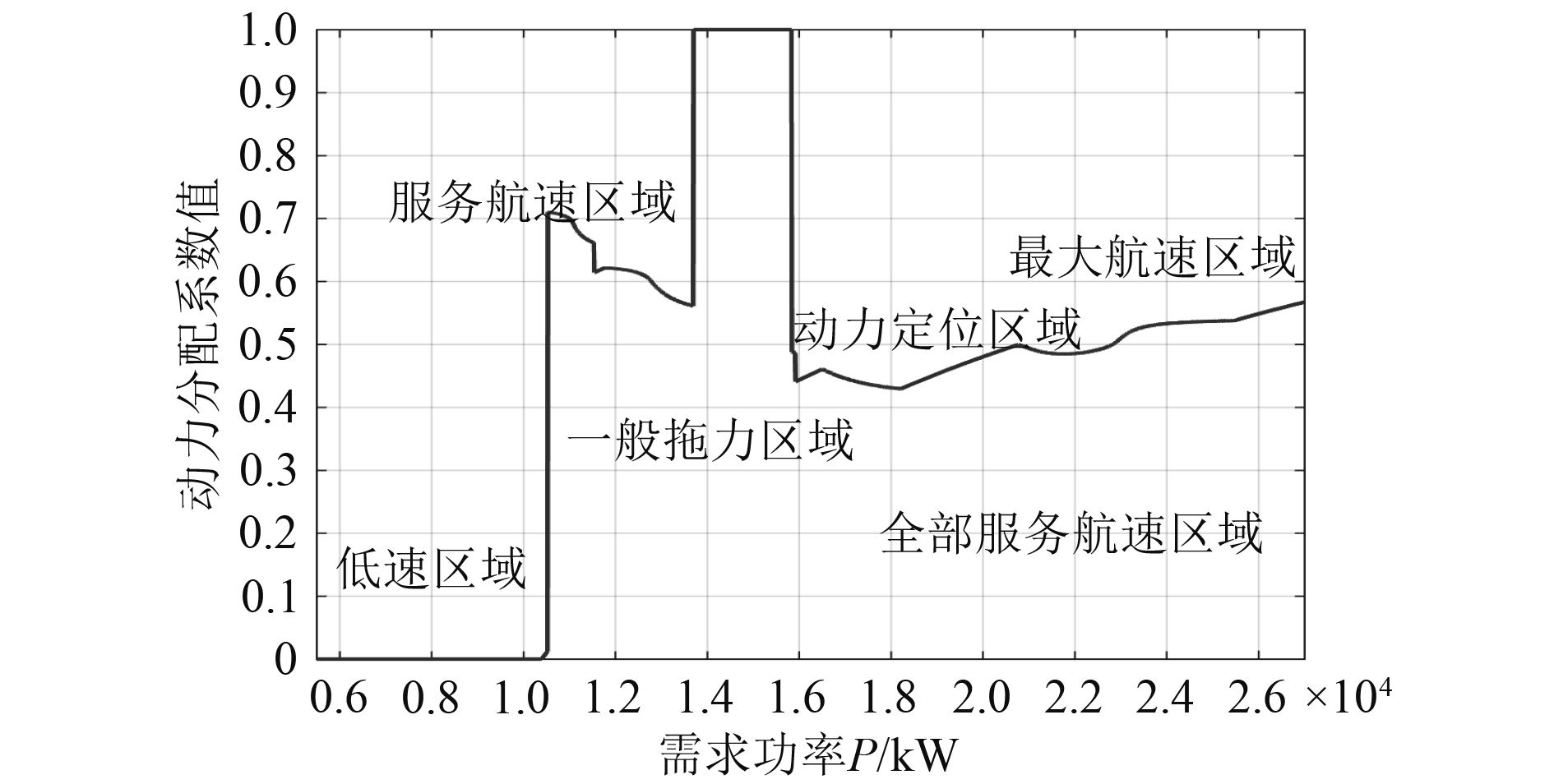
在Matlab中建立海洋工程船燃油经济性G与功率混合度H的关系模型,求解不同功率下的最佳混合度,如图6所示。
|
图 6 不同功率下的最佳动力分配 Fig. 6 The best power distribution under different power |
本文提出一种基于降维和排序的改进遗传算法对海洋工程船进行推力分配。该方法解决了优化算法对等式约束的求解问题,并具有较高的优化速度及收敛精度。使用在推力禁区内设置推力减额系数的方法解决全回转推进器的水动力干扰问题。最后对海洋工程船的动力分配问题进行求解,提高船舶运行的经济性。本文所做的研究工作及相应结论可为海洋工程船的推力及动力分配控制器的设计提供参考。
| [1] |
CALABRO V, CAITI A. Parametric control allocation for a class of marine vessels[J]. Ocean Engineering, 2013, 58: 275-283. DOI:10.1016/j.oceaneng.2012.11.005 |
| [2] |
王芳, 潘再生, 万磊, 等. 深水钻井平台动力定位的推力分配研究[J]. 船舶力学, 2013, 17(2): 19-28. WANG Fang, PAN Zai-sheng, WAN Lei, et al. Optimal thrust allocation for a dynamically positioned deepwater drilling rig[J]. Journal of Ship Mechanics, 2013, 17(2): 19-28. |
| [3] |
袁伟, 俞孟蕻, 朱艳. 动力定位系统舵桨组合推力分配研究[J]. 船舶力学, 2015, 19(4): 397-404. YUAN Wei, YU Meng-hong, ZHU Yan. Research on thrust allocation of dynamic positioning vessels with propeller-rudder pairs[J]. Journal of Ship Mechanics, 2015, 19(4): 397-404. DOI:10.3969/j.issn.1007-7294.2015.04.007 |
| [4] |
曹建春, 李聪. 推力分配优化算法在船舶动态控制中的应用研究[J]. 舰船科学技术, 2017, 39(3A): 43-45. CAO Jian-chun, LI Cong. Research on the application of thrust allocation optimization algorithm in ship dynamic control[J]. Ship Science and Technology, 2017, 39(3A): 43-45. |
| [5] |
刘正峰, 刘长德, 匡晓峰, 等. 模拟退火算法在动力定位能力评估中的应用[J]. 船舶力学, 2013, 17(4): 376-381. LIU Zheng-feng, LIU Chang-de, KUANG Xiao-feng, et al. Application of simulated annealing algorithem in dynamic positioning capability analysis[J]. Journal of Ship Mechanics, 2013, 17(4): 376-381. |
| [6] |
周奇勋, 曹世宏, 季新杰. ISG混合动力汽车控制规则优化与转矩分配策略研究[J]. 汽车工程, 2015, 37(7): 751-756. ZHOU Qi-xun, CAO Shi-hong, JI Xin-jie. Research on the control rules optimization and torque distribution strategy for ISG hybrid electric vehicles[J]. Automotive Engineering, 2015, 37(7): 751-756. DOI:10.3969/j.issn.1000-680X.2015.07.003 |
| [7] |
凌滨, 王博强, 卢晓琳. 混合动力汽车功率分配管理优化研究[J]. 计算机仿真, 2017, 34(5): 156-161. LING Bin, WANG Bo-qiang, LU Xiao-lin. Study on hybrid electric vehicle power allocation management optimization[J]. Computer Simulation, 2017, 34(5): 156-161. DOI:10.3969/j.issn.1006-9348.2017.05.033 |
| [8] |
金鸿章, 苏晓宇, 于安才, 等. 基于锚链切换的平台自动锚泊定位系统设计[J]. 电机与控制学报, 2017, 34(5): 156-161. JIN Hong-zhang, SU Xiao-yu, YU An-cai, et al. Design of automatic mooring positioning system based on mooring line switch[J]. Electric Machines and Control, 2017, 34(5): 156-161. |
| [9] |
LI B, WANG L. Thrust allocation with dynamic forbidden sectors in dynamic positioning system[J]. Journal of Ship Mechanics, 2014, 18(9): 1025-1034. |
| [10] |
祝庆庆, 俞孟蕻, 卢佳佳, 等. 海洋工程船推力分配策略[J]. 舰船科学技术, 2013, 35(5): 21-24. ZHU Qing-qing, YU Meng-hong, LU Jia-jia, et al. Research on thrust allocation strategy for ocean engineering vehicles[J]. Ship Science and Technology, 2013, 35(5): 21-24. DOI:10.3404/j.issn.1672-7649.2013.05.005 |
| [11] |
张春来, 俞孟蕻, 袁伟. 基于功率管理的动力定位系统推力分配方法研[J]. 舰船科学技术, 2017, 39(7): 89-93. ZHANG Chun-lai, YU Meng-hong, YUAN Wei. Studies of the thrust allocation methods of dynamic positioning system based on power management[J]. Ship Science and Technology, 2017, 39(7): 89-93. DOI:10.3404/j.issn.1672-7649.2017.07.018 |
 2018, Vol. 40
2018, Vol. 40
