流载荷是开敞水域内海洋工程船舶受到主要环境扰动之一,其影响主要体现在水平面内对船体的作用力及力矩,流速以及流向角的大小对船舶的流载荷有着重要影响。OCIMF通过水池实验获得15~50万吨VLCC船舶的流载荷计算图谱[1],文献[2]采用平板升力理论和二维横流理论分析流载荷作用的特性。与之相比,近年来兴起的CFD(Computational Fluid Dynamics)仿真技术采用数值计算的方法模拟不可压缩流体湍流运动的速度、压力场,进而实现对船舶水动力性能(阻力、伴流、波形)的预报[3]。对比水池试验与半经验公式,该方法所需的时间及费用成本较低、效率高,针对不同船型具有更可靠的计算精度。
Vaz[4]研究了位置保持状态下半潜式海洋平台单桩体流载荷预报问题,将CFD方法与水池模型测试数据及半经验公式进行比较并讨论偏差出现的原因。Toxopeus[5]应用CFD仿真了不同水深下运动船舶周围的粘性流体流场分布情况,发现浅水区域粘性流体对船舶阻力的影响系数更大。Shi等[6]通过CFD方法研究了船舶凹陷对其阻力的影响。Wang等[7]则采用基于RANS方法的SST k–ω模型进行了二维平板摩擦阻力计算,在不同输入条件设定分别对比了CFD仿真与ITTC-1957等方法提出的摩擦阻力线计算结果,实验结果充分证明了其计算方法有效。CFD仿真也广泛应用于其他流体领域的数值仿真与计算中[8]。
已有研究工作表明,应用CFD方法进行流体动态分布及载荷特性研究已建立了相对成熟的理论方法。本文在已有研究基础上,采用RANS方法的RNG k–ε湍流模型研究海洋工程船舶的流载荷特性,重点讨论了不同傅汝德数及不同入口流场条件下船体周围形成的流体速度场及压力场的分布情况,并分别分析了不同船型对应的流场以及船体表面受到的压力分布,得到了关于海洋工程船舶流体载荷分布及特性的一般规律。
1 基础理论 1.1 流载荷计算模型船舶在流场中所受到的波浪和流载荷作用需要遵守守恒方程,即连续方程、动量守恒方程和能量守恒方程。由于流场中流载荷的运动机理比较复杂,为能准确地模拟出流场特性,该模型与标准k–ε模型类似,但其数值不是通过实验数据得到的,而是由理论分析获得。与k–ε模型不同的是,为了进一步提高计算的精度,RNG k–ε方程修正了湍流旋涡带来的影响。
RNG k–ε模型基本形式如下:
| $\frac{\partial }{{\partial t}}(\rho k) + \frac{\partial }{{\partial xi}}(\rho kui) = \frac{\partial }{{\partial xj}}\left[ {\alpha k\mu eff\frac{{\partial k}}{{\partial xj}}} \right] + Gk + \rho \varepsilon{\text{,}} $ | (1) |
| $\begin{aligned}& \frac{\partial }{{\partial t}}(\rho \varepsilon ) + \frac{\partial }{{\partial xi}}(\rho \varepsilon ui) = \\&\frac{\partial }{{\partial xj}}\left[ {\alpha \varepsilon \mu eff\frac{{\partial \varepsilon }}{{\partial xj}}} \right] + C_{1\varepsilon }^*\frac{\varepsilon }{k}Gk - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k}{\text{。}}\end{aligned}$ | (2) |
式中:Gk和Gb分别为由平均速度梯度以及浮力引起的湍动能,Ym为可压缩湍流脉动膨胀对总耗散率的影响。其余各系数计算如下:
相关参数意义可参见文献[9]。
1.2 阻力预报根据国际拖曳水池会议(ITTC)所提出的ITTC-1957公式,船舶摩擦阻力系数的估算方法如下:
| ${C_f} = \frac{{0.075}}{{{{({\rm{lg}} {Re} - 2)}^2}}}{\text{,}}$ | (3) |
式中,Re为雷诺数。相应的粗糙度补贴系数为:
| $\Delta {C_f} = \left[105{({k_s}/L)^{\frac{1}{3}}} - 0.64\right] \times {10^{ - 3}}{\text{,}}$ | (4) |
式中,Ks表示船舶粗糙度,这里取Ks=150×10–6 m。总摩擦阻力可表示为:
| ${R_f} = \frac{1}{2}({C_f} + \Delta {C_f})\rho {U^2}S{\text{。}}$ | (5) |
式中:
本文研究对象为某海洋工程船舶,船长Loa为93.4 m,型宽B为22 m,型深D为9.5 m,设计吃水T为6.5 m。按照船体型线图,采用SolidWorks软件进行1:1的几何建模,这样做的目的是为了避免尺寸效应引起的计算偏差。建模过程中,为了节省计算机资源,简化计算,同时又不影响计算精度,对上层建筑形状过于复杂部分进行一定的模型简化,最终采用的船舶模型以及型线如图1所示。
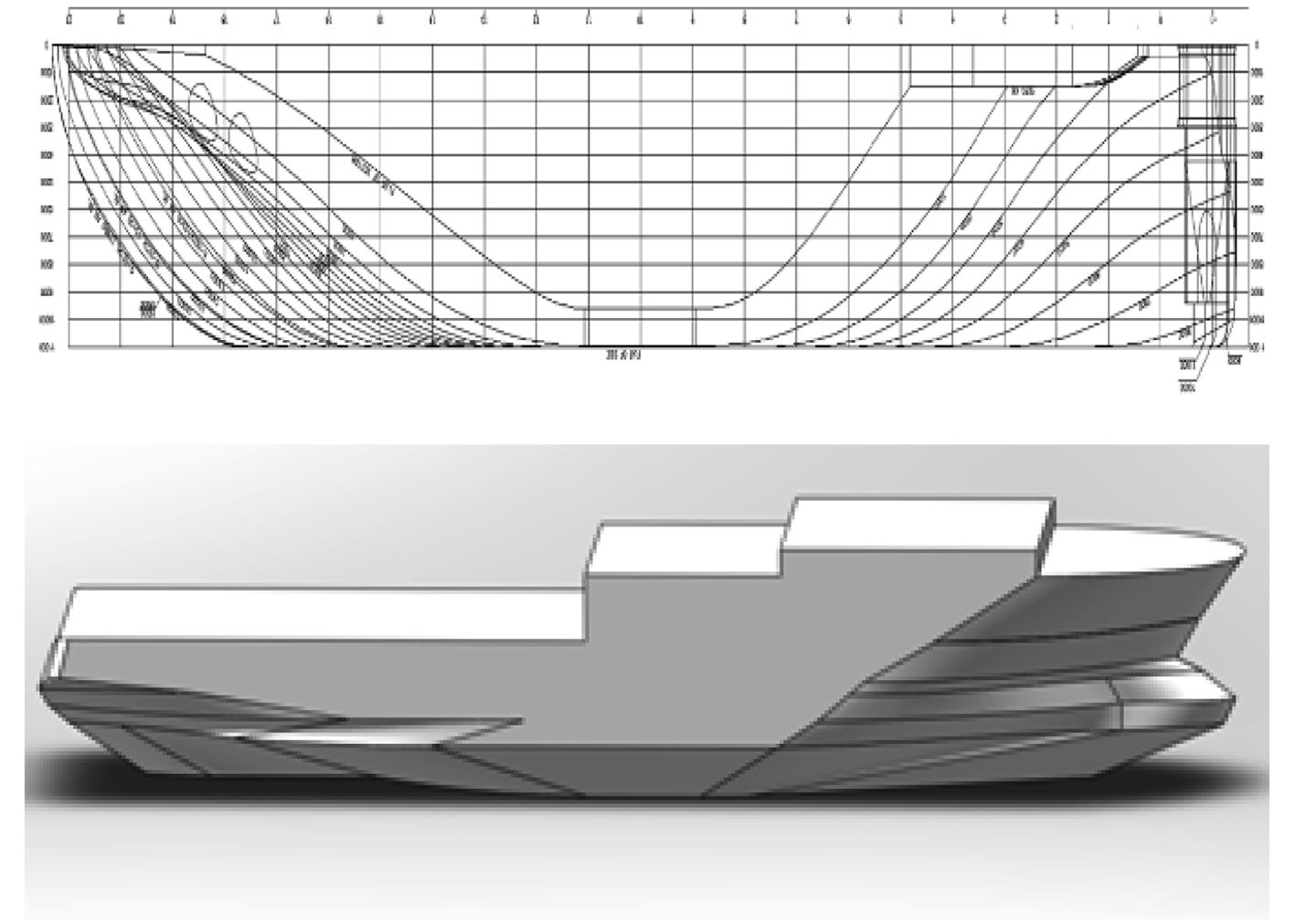
|
图 1 海洋工程船线图及其三维模型 Fig. 1 Hull profile and its 3D model of ocean engineering ship |
计算域大小关系到仿真结果的精度,若流体域过小会对船舶造成二次扰动,流体域过大,则划分的网格数量较多,数值计算耗时增加。通常计算域按照以船舶为中心,计算域进口与船首的间距为船长的1倍,计算域出口与船尾的间距为船长的3倍,计算域的上表面与下表面之间的距离为船舶吃水的5倍,计算域的宽度为船体宽度的6.5倍,依据上述标准所建立的计算域如图2所示。

|
图 2 计算域选取 Fig. 2 Computational domain selection |
采用ICEM CFD前处理软件对计算域进行网格划分,网格质量的优劣将影响接下来采用Fluent进行数值计算的准确性。为同时提高计算精度和计算效率,采用混合网格结构可以在不影响网格质量的前提下降低网格数量,在计算域的表面及其附近区域划分结构性网格,而船体与计算域壁面之间的其余区域划分为非结构性网格,划分结果如图3所示。由于所研究的是流载荷对船舶的影响,因此在模型创建后,截取了设计水线以下的船体部分作为主要研究目标。
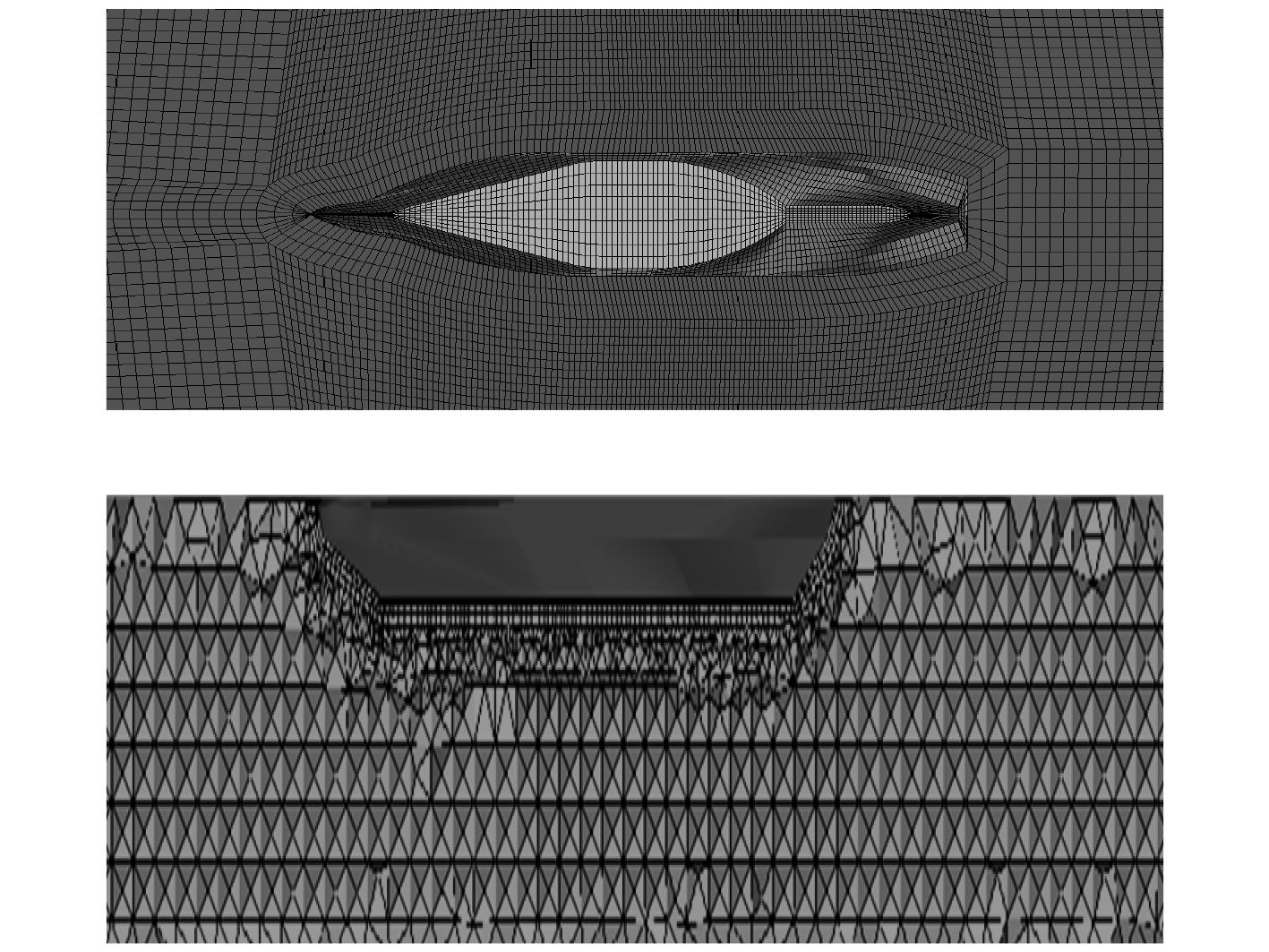
|
图 3 混合网格 Fig. 3 Hybrid mesh |
船舶绕流流场的数值模拟是在有限区域中进行的,为了使模拟条件更接近船舶航行的实际环境,需要在求解前设置流场计算域的边界条件,计算域进口类型为Velocity,出口类型为Outflow,流场上、左、右面类型为Stationary wall,流场底面类型为Moving wall,船体的类型为Wall,具体如图4所示。
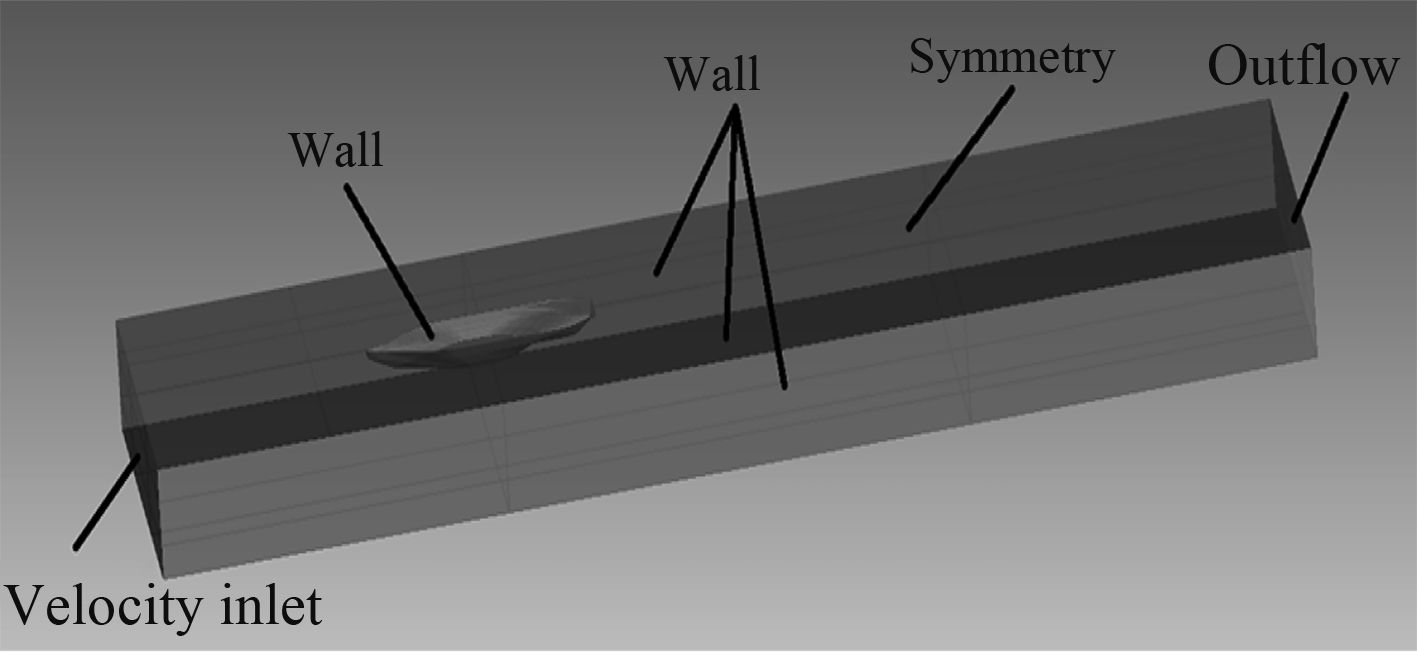
|
图 4 边界条件定义 Fig. 4 Boundary condition setting |
对比经验公式(ITTC-1957公式)与CFD两种方法计算出船舶阻力的差别,6种不同工况下的傅汝德数分别为0.05,0.1,0.15,0.2,0.25和0.3,2种计算方法得到的船舶阻力曲线如图5所示。
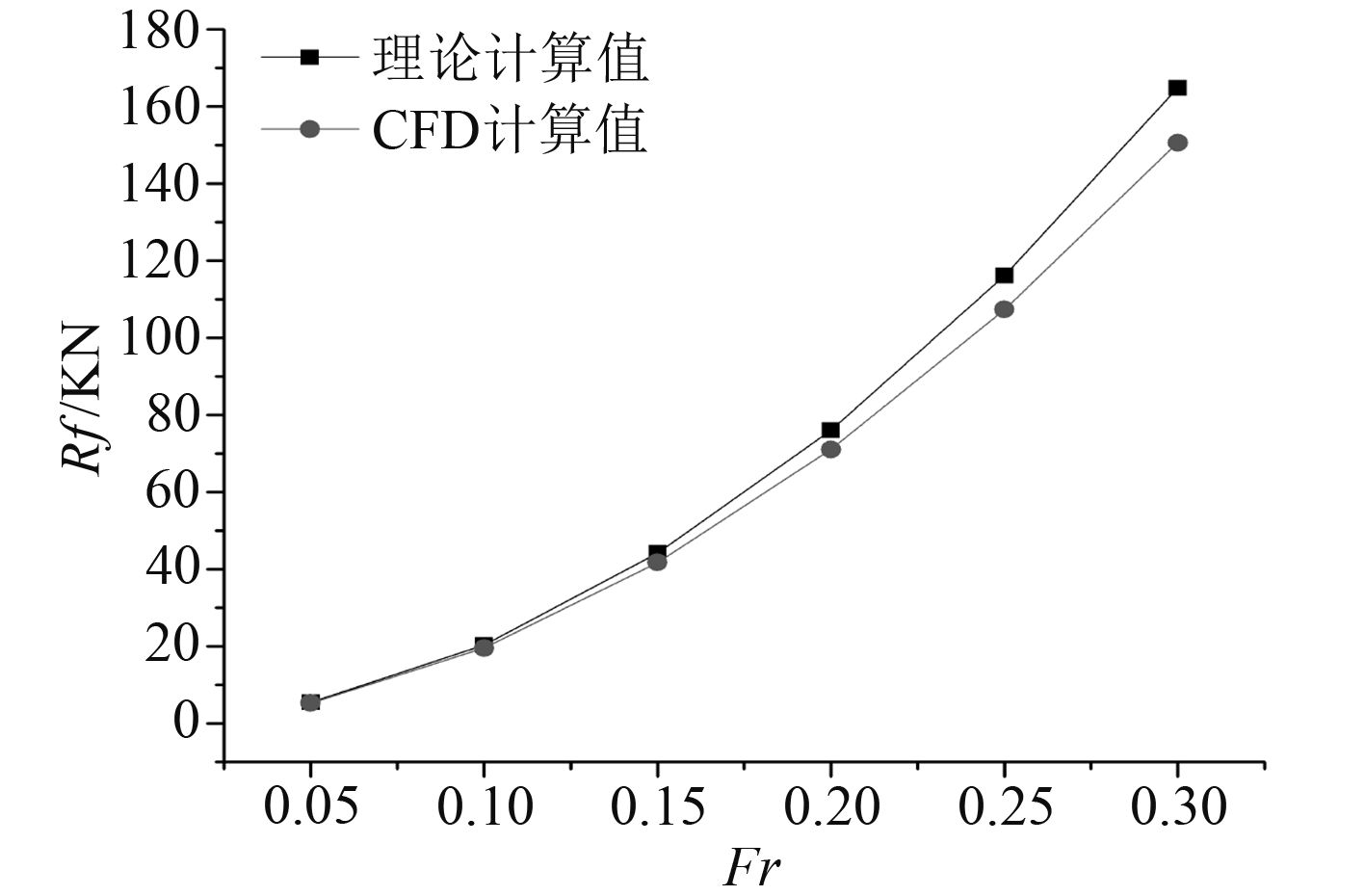
|
图 5 经验公式与CFD阻力计算结果对比 Fig. 5 Resistance result comparison of empirical formula and CFD |
由图可知,经验公式方法和CFD方法计算出的船舶阻力的总体趋势相同,即随着傅汝德数的增加,船舶阻力增加且增加的越来越快。同时,由经验公式得出的船舶阻力值略大于CFD方法的计算结果,并且二者的差值与傅汝德数成正比。造成这种现象的原因是,不同于CFD方法,传统的经验公式法计算船舶阻力忽略了粘性产生的影响,由此导致的阻力偏差在允许的量级范围内,可以判断所建立的模型、网格划分方法及边界条件设定符合船舶在实际流场中的情况。
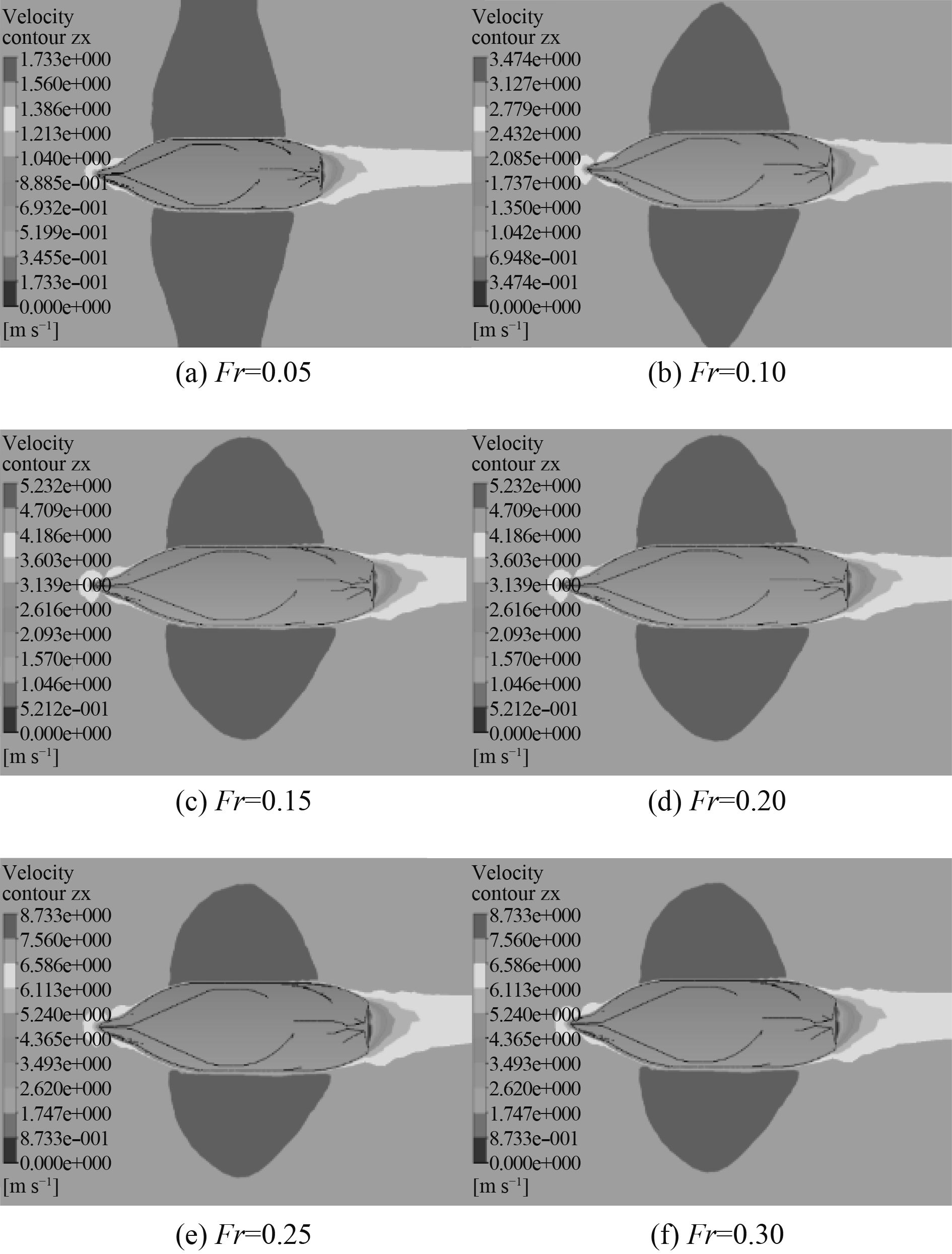
3 数值仿真分析 3.1 傅汝德数影响分析当傅汝德数分别取0.05,0.1,0.15,0.2,0.25和0.3时,船舶周围流体的速度场以及压力场的特点。
图6和图7分别展示了不同傅汝德数时船舶周围流体的速度云图和压力云图。由图可知,船首周围的流体由于船首的阻塞作用,速度减小而压力增大。船体的侧面由于没有了阻碍以及船体与流体的相对运动,流体的速度增大而压力降低。船尾附近的流体由于船体形状的突然变化,速度减小压力增大,但是由压力云图可知,船首受到的压力大于船尾的压力,这个压力差是船舶的粘压阻力,是由于流体的粘性产生的。由图6和图7还可以看出,傅汝德数的不同不会改变船舶周围流体的速度场与压力场的分布特点,但是船舶周围流体的速度与压力随着傅汝德数的增加而增大。

|
图 7 不同傅汝德数Fr压力场分布 Fig. 7 Pressure profile with different Fr number |
|
图 6 不同傅汝德数Fr流场速度分布 Fig. 6 Current profile with different Fr number |
为研究不同来流攻角对船舶的作用特性,取计算域进口流速为5 m/s,改变船舶中纵剖面与流体来流方向的夹角即流向角的大小,取流向角为0°,30°,60°,90°,120°,150°和180°,研究不同流向角对船舶周围流体的速度场和压力场的影响。
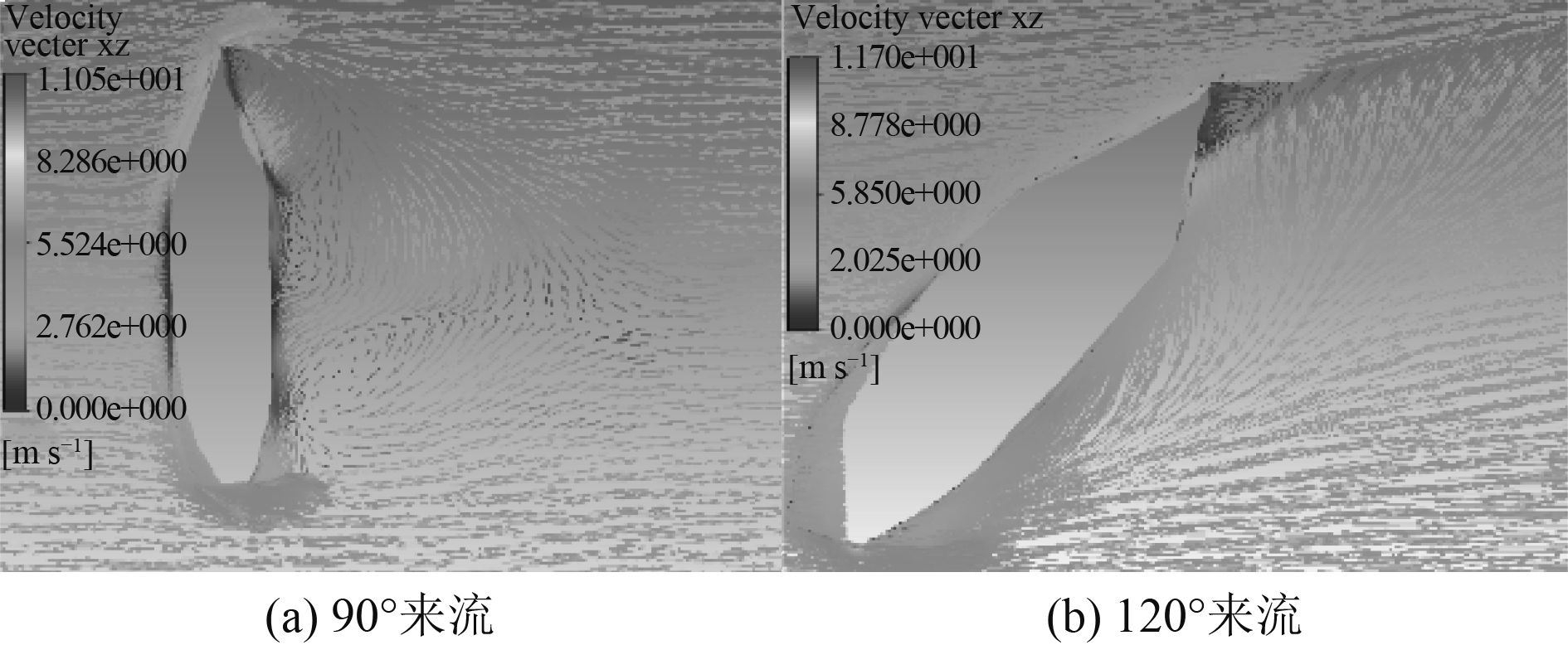
从图8、图10可以看出,在来流速度相同的情况下,流向角变化对船舶周围流场速度分布及船体压力分布有较大影响。当船舶的流向角由低到高变化时,船体受到压力最大的位置均位于船体与来流直接接触的一侧,而该位置流体的速度降低。造成这种现象的原因是船体对水流的壅塞作用。由于流体的绕流现象,船体迎着来流方向一侧的压力随着与受力点的距离增加而降低,流体速度的变化则相反。与来流方向相反一侧的船体受到的压力较低,基本为负值。由图8(c)和图8(d)可以看出,当船舶处于90°和120°流向角时,周围流场收到船体的影响与其他角度时相比尤为强烈,产生旋涡(见图9),在旋涡处流体的速度增大,增加了船舶的阻力。
|
图 9 背侧向来流旋涡图 Fig. 9 Vortex figure of lateral flow direction |

|
图 10 不同攻角船体压力分布 Fig. 10 Pressure profile with different attack angle |

|
图 8 不同攻角流场速度分布 Fig. 8 Current velocity profile with different attack angle |
设定流体的初始速度为5m/s,使流体分别以0.05 m/s2,0.025 m/s2和0.017 m/s2的速度变化率达到速度10 m/s,研究流体速度变化率对船舶阻力的影响,如表1所示。由仿真结果得知,船舶的粘压阻力随着流体速度变化率的减小而减小,摩擦阻力随着流体速度变化率的减小而增大,而船舶的总阻力随着流体速度变化率的减小而减小。由此可知,流体速度变化率对船舶粘压阻力的影响大于对摩擦阻力的影响,同时,船舶阻力随流体速度变化率的增大而增大。
|
|
表 1 不同变化速率时船舶受到的阻力值 Tab.1 The ship's resistance value of different velocity |
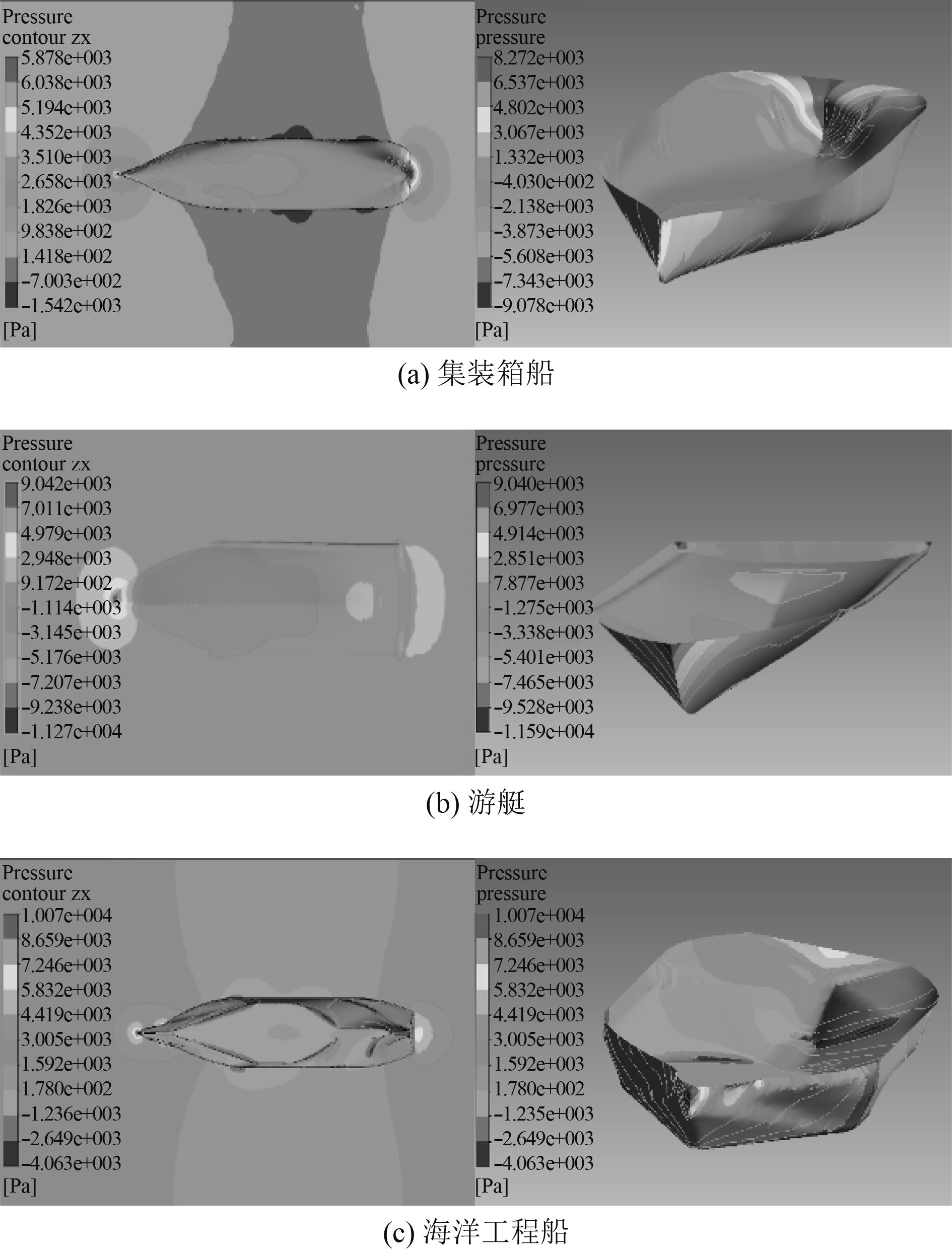
分别选取了300 m长的集装箱船和17 m长游艇作为参照,集装箱船主尺度为:船长Loa=300 m,船宽B=48.2 m,型深D=24.6 m,设计吃水T=12.5 m。游艇主尺度为:船长Loa=17 mm,船宽B=4.7 m,型深D=2.8 m,设计吃水T=1.3 m。建模方法、计算域以及边界条件的选取与上文相同,划分网格后在Fluent仿真软件中进行水动力学数值仿真,当流速为5 m/s时船体周围的流场分布及压力分布结果如图11所示。
|
图 11 不同船型流场与船体压力分布对比图 Fig. 11 Compare diagram of current profile and hull pressure profile with different vessel shape |
由图11可知,虽然3种船船型结构不同,但是船体周围流体的速度场与压力场分布情况有着相似的趋势,即船首周围的流体压力较高、速度低,船体侧面周围流体的流速增大、压力降低,船尾周围的流体压力增加、速度降低。同时大尺度船舶对船体周围流场的影响程度要高于小尺度船舶结构。不难看出,船舶周围流体的速度和压力的变化规律具有相同的特点,不以船型的改变而不同。
4 结 语本文以某海洋工程船为主要研究对象,分别对不同海流作用下船舶受到的流场作用力及其分布进行仿真研究,得到如下结论:
1)海洋流场经过船体时,因受到船体阻力作用,在船舶首、尾形成不同的流场分布,由此形成的压差是海流对船体作用力的主要成因。随着傅汝德数增加相同船体对流场的影响范围有减小的趋势,相同的变化趋势也存在于船体周围的流体压力场中。
2)不同流向角作用下由于在来流方向和背流方向形成不同形式的流场,尤其当流向角为90°和120°时背流侧将形成明显的涡流区,由此导致船舶所受的流场作用力激增。可见航行过程中侧向来流对船舶的稳性和操纵性能影响较大,实际船舶操控时要尽量避免此种情况发生。
4)船舶的形体增加对流场作用力的分布规律有一定的影响,大尺度船舶对水域内船体周围的流场影响相应增强。
本文所做研究主要针对开敞水域下流载荷对船舶的影响,研究结果表明本文所采用CFD方法研究流体对船舶载荷及船体周围流场分布情况基本可行,所做工作对于改善船舶的型线设计,减小航行阻力及船舶操纵控制具有一定的意义。
| [1] |
OCIMF. Prediction of wind and current loads on VLCCs[M]. Bermuda: Oil Companies International Marine Forum, 1994.
|
| [2] |
LEITE A J P, ARANHA J A P, UMEDA C, et al. Current force in tankers and bifurcation of equilibrium of turret systems, hydraodynamic model and experiments[J]. Applied Ocean Research, 1998, 20: 145-156. DOI:10.1016/S0141-1187(98)00002-9 |
| [3] |
高秋新. 船舶CFD研究进展[J]. 船舶力学, 1999, 3(4): 74-78. |
| [4] |
GUILHERME V, OLAF J W, HARALD O, Current affairs: model tests, semi-empirical predictions and CFD computations for current coefficients of semi-submersibles[C]//Proceedings of the 28th International Conference on Ocean, Offshore and Arctic Engineering(OMAE2009–80216), Honolulu, Hawaii, USA, 2009.
|
| [5] |
S L TOXOPEUS, Viscous-flow calculations for KVLCC2 in deep and shallow water[C]//Marine 2011, IV International Conference on Computational Methods in Marine Engineering, Barcelona, Spain, 2011.
|
| [6] |
SHI X, CHEN X Q, TAN J H. Study of resistance performance of vessels with notches by experimental and computational fluid dynamics calculation methods[J]. Journal of Shanghai Jiaotong University, 2010, 15(3): 340-345. DOI:10.1007/s12204-010-1014-2 |
| [7] |
WANG Z Z, XIONG Y, SHI L P, et al. A numerical flat plate friction line and its application[J]. Journal of Hydrodynamics, 2015, 27(3): 383-393. DOI:10.1016/S1001-6058(15)60496-6 |
| [8] |
KIM J J, BAIK J J. A numerical study of the effects of ambient wind direction on flow and dispersion in urban street canyons using the RNG κ-ε turbulence model[J]. Atmospheric Environment, 2004, 38: 3039-3048. DOI:10.1016/j.atmosenv.2004.02.047 |
| [9] |
YAKHOT V, ORSZAG S A. Renormalized group analysis of turbulence: I. basic theory[J]. Journal of Scientific Computing, 1986, 1(1): 3-50. |
 2018, Vol. 40
2018, Vol. 40
