随着科学技术的发展,AUV在海洋资源开发、环境质量监测、水下作战等领域发挥着越来越重要的作用。面对复杂多变的水域环境,三维路径规划是保证AUV安全完成任务的关键技术之一。全局路径规划和局部路径规划是复杂多变环境下的AUV根据障碍物类型进行的分类,由于全局路径规划主要针对环境中静止不变且信息已知的障碍物,能够更好地提供路径规划的解决方案,也因为如此近年来,AUV三维空间下的全局路径规划成为大家研究的热点之一。目前,人工势场法、A*算法、神经网络算法、遗传算法、人工免疫算法、模糊推理算法、粒子群算法等是最常用的路径规划算法。
本研究在蚁群算法的基础上对该算法进行优化,融合了粒子群算法和人工势场法,并在多目标环境路径规划中增加了路径代价的函数,使在融合算法下得到最优路径长度基础上充分考虑外界环境及探测干扰和自身能源的消耗问题。
1 路径规划相关模型建立 1.1 环境模型建立环境模型是AUV路径规划的首要环节,将三维现实环境特征进行提取和解析,并转化为计算机模拟路径规划过程中的地图模型数据。环境建模的方法很多,如可视图法、自由空间法、栅格法等。由于栅格法的地图创建和维护比较容易,主要内容是以栅格为基础单位,离散化三维环境模型,所以本研究采用栅格法。设置三维空间为:水平面与XY平面重合,AUV的运动主方向定位X轴且机身头为X轴的正方向(起点与终点分别对应对应X轴的最大值和最小值),垂直于水平面方向定位Z轴。这样三维空间就可以分为若干基本单位栅格,以AUV开始运动的点作为空间的零点位置,其他障碍物及空位区域也就进行了相应的方位坐标确定。栅格[1]在计算时可选择使用坐标法或是序号法,本研究为了直观地判断点与点的位置关系将采用坐标法。
在路径规划过程中对环境模型建立的要求:
1)将AUV的中心位置用质点表示,同时对障碍物的尺寸按AUV的半径作适当扩展,以保证AUV能够无碰撞地运动;
2)AUV每次运动只能在所有栅格的中心位置(也就是栅格体的中心),不可在边界或是端点处;
3)AUV的下一个位置只能是相邻的26个栅格体的自由栅格体中;
4)为避免没有必要的局部最优,某一个栅格体的上下左右前后有5个是障碍栅格,则此栅格体就默认为障碍栅格体;
5)不考虑环境中海流、潮流等对路径规划的干扰。
1.2 干扰模型建立 1.2.1 障碍模型AUV在障碍环境下进行路径规划,可使用人工势场法计算AUV与障碍间的障碍代价,对AUV的运动路径进行调整。AUV在运动过程中,始终远离障碍代价函数值大的点运动,以实现避障。在此过程中还需要不断朝目标点运动,因此建立目标代价函数,越趋近于目标点则目标代价函数值越小,AUV会始终寻找趋近目标代价函数值小的点运动,以实现趋向目标点的运动。
1)障碍代价函数
障碍代价函数是采用人工势场法的思想建立,将AUV所识别的障碍物看作斥力势场,其势能函数为:
| $U(q) = \left\{ \begin{aligned}& 0,{\rho _0} < \rho \left( {q,{q_{ob}}} \right)\text{;}\\& k \frac{1}{{{r_0}^2}} \left( {\frac{1}{{{r_0}}} - \frac{1}{{{\rho _0}}}} \right) \left( {1 - \frac{{\rho \left( {q,{q_{ob}}} \right) - {r_0}}}{{{\rho _0} - {r_0}}}} \right)\text{,}\\ & \quad {r_0} < \rho \left( {q,{q_{ob}}} \right) \leqslant {\rho _0}\text{;}\\& k \! \left( {\frac{1}{{\rho \left( {q,{q_{ob}}} \right)}} \!- \!\frac{1}{{{\rho _0}}}} \right) \! \frac{1}{{{\rho ^2}\left( {q,{q_{ob}}} \right)}},\,\rho \left( {q,{q_{ob}}} \right)\! < {r_0}\text{。}\end{aligned} \right.$ |
其中:
由上式可知当AUV越靠近障碍物时其势能越高,其障碍代价函数值越大,令其为
2)目标代价函数
AUV在空间中运行,在其一段路径中目标点只有一个,暂定离目标点距离越远其目标代价函数值越大,相反当离目标点距离越近其目标代价函数值越小,从而建立目标代价函数公式为:
| ${f_2} = \sigma E\left( {\rho {{\left( {{q_i},{q_{goa}}} \right)}^{ 2}}} \right)\text{,}$ |
其中,
3)障碍总代价函数
| $f = {k_1}{\sum {{f_1} + k} _2}{f_2}\text{,}$ |
式中,
AUV在水下运动过程中,除了躲避可见的障碍之外,还需要躲避来自人为因素的影响,其中最主要的是雷达的探测,其主要来自水面及水上探测雷达和水下潜艇及其他AUV的探测雷达。根据雷达回波强度与位置的关系,得到雷达探测威胁如下:
| ${J_{radar}} = \sum\limits_{i = 1}^n {\int_0^{{l_i}} {\frac{1}{{{d_i}^{ \wedge 4}(l)}}} }{\rm{d}}l \text{。}$ |
其中,
AUV在水下某点收到第
| $H(x) = \left\{ \begin{aligned}& \frac{{{\beta _i}{K_i}}}{{d_i^{ 4}}},{\text{被威胁}}i{\text{覆盖}}\text{,}\\& 0,{\text{未被威胁}}i{\text{覆盖}}\text{。}\end{aligned} \right.$ |
式中:
由障碍模型中的目标代价函数可知,当AUV在路径规划过程中,虽然目标点确定,但是还是存在多个路线去选择的情况,如图1所示。
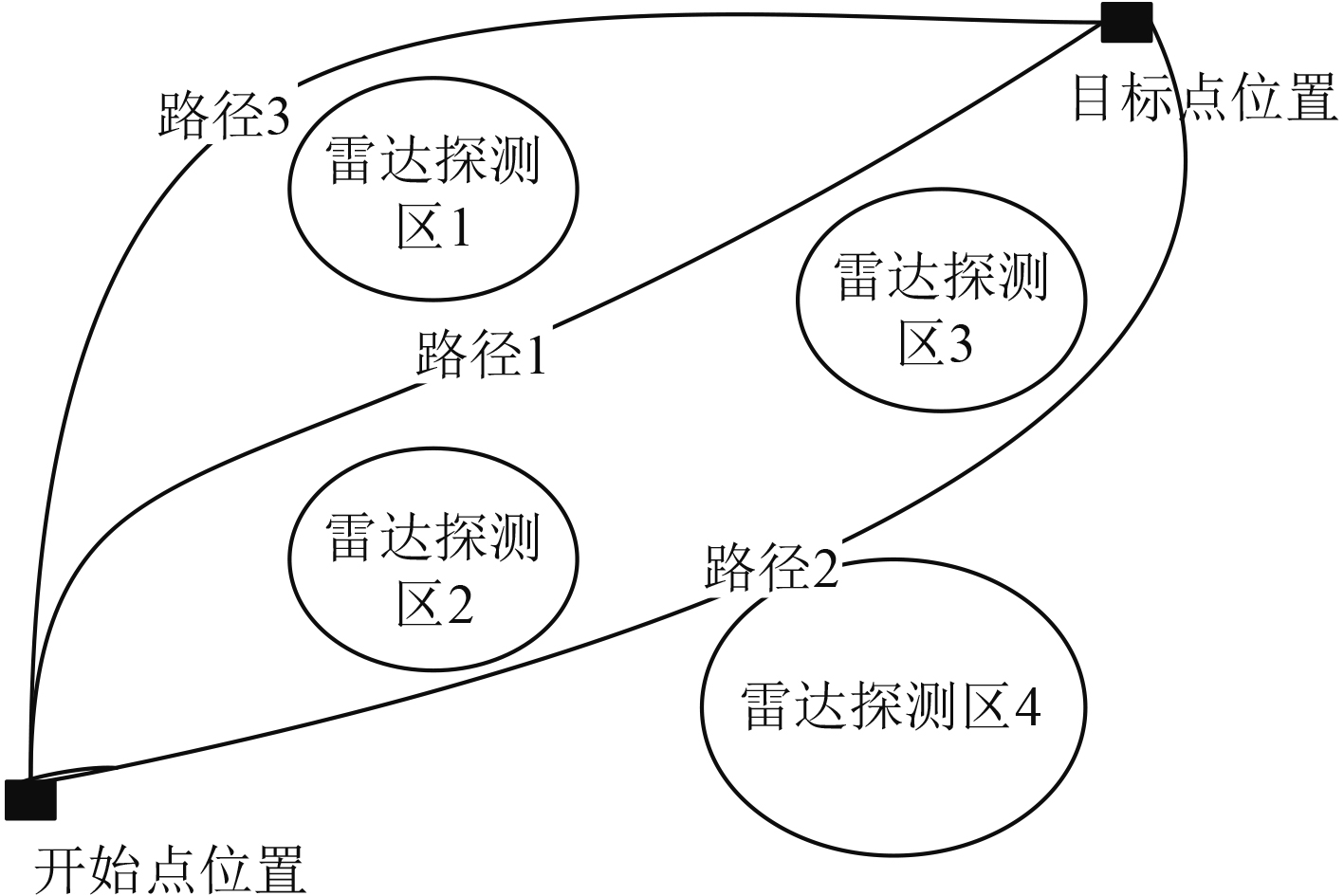
|
图 1 AUV路径规划目标点确定 Fig. 1 Determine the AUV path planning target point |
AUV在路径规划过程中始终需要满足其物理性能要求和任务约束,保证其稳定安全的完成任务,多条路径必定有长度和安全的差异,因此建立路径代价函数为:
| $g = \sum\limits_{i = 1}^n {({\omega _1}} l_i^2 + {\omega _2} h_i^2 + {\omega _3} {\left| l \right|^2} + {\omega _4} H)\text{。}$ |
式中:
在AUV的路径规划过程中必定优先在环境模型的基础上进行,考虑到外界环境的干扰,AUV在航行过程中总代价函数为障碍模型和探测模型的总和,也就是其干扰模型下AUV为获得最优路径所作出的决策和付出的代价,公式为:
| $D = \sum\limits_{i = 1}^n {f + \sum\limits_{i = 1}^n g } \text{。}$ |
在路径规划过程中,将AUV看作一只蚂蚁,设有
| ${P_{ij}} = \left\{ \begin{aligned}& \frac{{{{\left( {{\tau _{ij}}(t)} \right)}^\alpha }\cdot {{\left( {{\eta _{ij}}(t)} \right)}^\beta }}}{{\displaystyle\sum\limits_{s \in {\rm{allow}}M} {{{\left( {{\tau _{ij}}(t)} \right)}^\alpha }\cdot {{\left( {{\eta _{ij}}(t)} \right)}^\beta }} }},j \in {\rm{allow}}M \text{;}\\& 0,j \notin {\rm{allow}}M\text{。}\end{aligned} \right.$ |
式中:
信息素浓度是衡量路径规划过程中路径价值,为蚂蚁的运动作引导依据。信息素只要涉及3个基本概念,分别是初始信息素、信息素更新、信息素挥发。初始信息素由蚂蚁
1)信息素更新的优化
蚂蚁每移动一次称为一次搜索,当蚂蚁完成一次搜索后,就会对路径上的信息素进行局部更新,更新公式如下:
| ${\tau _{ij}}(t + 1) = (1 - \varepsilon )\tau (t) + \varepsilon \Delta \tau \text{。}$ |
式中:
由此可见,当路径最优时,其总代价函数越小,局部更新中信息素的增量
当所有蚂蚁完成一次迭代后,对路径的全局信息素进行更新,公式如下:
| ${\tau _{ij}}(t + 1) = (1 - \rho ){\tau _{ij}}(t) + \rho \Delta {\tau _{ij}}\text{。}$ |
式中:
| $\Delta {\tau _{ij}} = \left\{ \begin{aligned}& \frac{{\left| {{L_B} - L} \right|}}{{{L_B}}},\left| {L - {L_B}} \right| > \sigma \text{;}\\& \frac{{\left| {L - {L_B}} \right|}}{{{L_B}}},\left| {L - {L_B}} \right| < \sigma \text{;}\\& 0,{\text{其他}}\text{。}\end{aligned} \right.$ |
式中:
2)信息素挥发的优化
在一次搜素路径结束后,路径还是那个的信息素会进行一定的挥发,这样可以使信息素不会积累过多,对于提高路径规划效率和全局搜索能力有一定的作用。在信息素挥发时最重要的是保留最佳路劲优势的同时也不能影响后续算法的进行,也就是不影响后面蚂蚁对路径的选择。
为了能有更好的最初决策,对路径上的信息素进行不同的挥发,将以通过路径蚂蚁数量
| ${\tilde \tau _{ij}} = \left\{ \begin{aligned}& 1 - \frac{{{L_b}}}{{{L_B}}} \rho ,s > \frac{m}{2}\text{;}\\& 1 - \frac{L}{{{L_B}}} \rho ,s < \frac{m}{2}\text{。}\end{aligned} \right.$ |
式中:
在路径规划相关模型建立的过程中,可以发现常规蚁群算法中,启发因子
| $\eta {}_{ij}(t) = {\left( {\frac{1}{{{d_{ij}} + {d_{jE}}}}} \right)^{{q_1}}}{f_1}^{{q_2}} {g^{{q_3}}}\text{。}$ |
式中:
在三维栅格地图中,当一只蚂蚁从当前位置向下移位置运动过程中可能都是遍历过的栅格体时,它将无法选择下一位置进行运动转移,此时,它可能陷入死循环或死锁状态[3]。因此,在计算转移概率时在考虑距离和信息素浓度的同时也需要考虑栅格体区域的安全性。在一个栅格体的周围障碍体占大多数,那么在运动到这个栅格体后,其运动方向的可能性会变得很小,也就是其栅格体区域内附件的安全性相对较差。那么,优化后的公式为:
| ${B_{grid}} = \frac{{A{B_{grid}}}}{{{A_{grid}}}}\text{。}$ |
式中:
在转移概率公式中加入区域安全信因素后的公式为:
| ${P_{ij}} = \left\{ \begin{aligned}& \frac{{{{\left( {{\tau _{ij}}(t)} \right)}^\alpha } {{\left( {{\eta _{ij}}(t)} \right)}^\beta }{{\left( {1 - {B_{grid \cdot j}}} \right)}^\mu }}}{{\displaystyle\sum\limits_{s \in {\rm{allow}}M} {{{\left( {{\tau _{ij}}(t)} \right)}^\alpha } {{\left( {{\eta _{ij}}(t)} \right)}^\beta }{{\left( {1 - {B_{grid \cdot s}}} \right)}^\mu }} }},j \in {\rm{allow}}M\text{;}\\& 0,j \notin {\rm{allow}}M\text{。}\end{aligned} \right.$ |
其中,
由公式可以看出,当一个栅格体附近的栅格体中障碍数越多,
粒子群算法是一种群体的迭代算法,通过群体性性能在解空间进行结果的优化计算[5]。其公式为:
| $\!\!\!\!$v_{id}^{k + 1} \!=\! w(k) v_{id}^k \!+\! {c_1}{r_1} \left(p_{id}^k \!-\! x_{id}^k\right)\! +\! {c_2} {r_2}\left(p_{gd}^k \!- \!x_{id}^k\right)\text{,}$$ |
| $x_{id}^{k + 1} = x_{id}^k + v_{id}^{k + 1}\text{。}$ |
式中:
由公式可以看出,粒子群算法在每次迭代过程中通过粒子跟踪2个最优解来更新自己。
为提高粒子群算法的收敛能力,因为在其公式中存在
| $w(k) = {w_{\max }} - \frac{{{w_{\max }} - {w_{\min }}}}{{{\lambda _{\max }}}} \lambda \text{。}$ |
式中:
蚁群算法是启发式优化算法中比较常用和经典的算法,具有较强的鲁棒性与正反馈机制,但是由于其初期信息素信息匮乏,搜索比较盲目容易陷入局部最优和过早收敛,为了追求搜索精度使其整个算法的搜索速度慢。而粒子群算法虽然其搜索精度不高,但却具有较强的全局搜索能力和较快的搜索速度。将蚁群算法和粒子群算法进行融合,先利用粒子群算法较强的全局搜索能力和搜索速度对整个区域空间进行路径搜索得到最优解或是次优解。接下来,将得到的最优解或是次优解转化为蚁群算法中的初始信息素,并进行重新分布,利用优化后的蚁群算法的正反馈机制对次优解进行精确搜索,得到当前路径信息素丰富的最优解。这样不仅解决了蚁群算法容易陷入局部最优、搜索盲目的缺点,也通过粒子群算法加快了路径规划搜索的速度。
改进型蚁群—粒子群融合算法中2种算法的衔接点为利用粒子群算法产生蚁群算法的初始信息素分布,也就是利用蚁群算法中根据外界环境信息等确定的信息素的初始值
| $\tau {}_{ij} = \tau {{}_{ij}^c} + \tau {{}_{ij}^p}\text{。}$ |
算法流程框架图如图2所示。
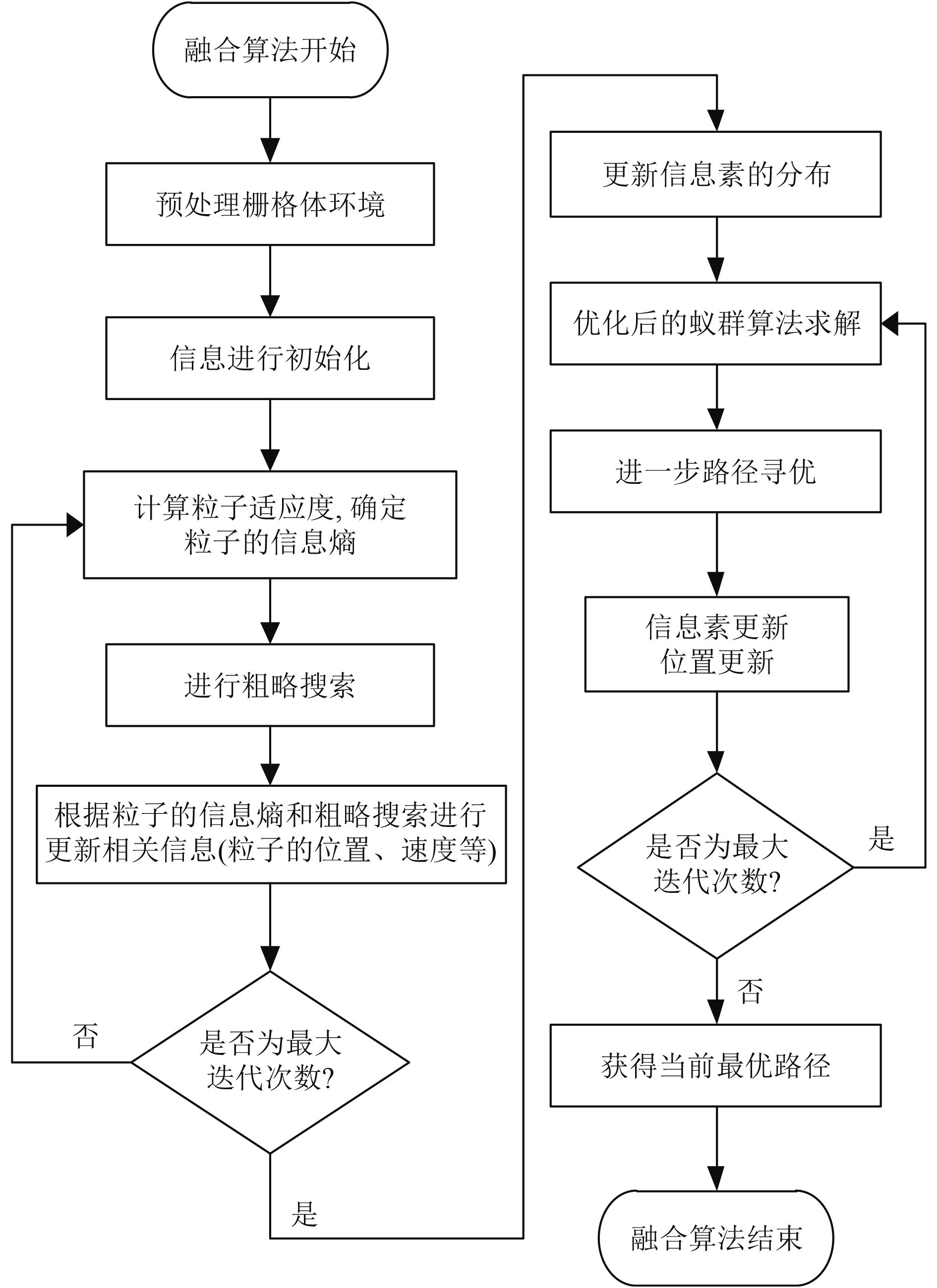
|
图 2 算法流程框架图 Fig. 2 Framework of the algorithm flow |
在Matlab环境下编程对AUV三维路径规划进行仿真实验,实验环境在跨度为21×21 km的一片海域中搜索从起点到目标终点并且避开所有障碍物及干扰的路径。为了方便问题的求解,取该片区域内最深的点的高度为0,其他高度根据最深点来确定。起点坐标为(1,0,800),目标终点坐标为(21,4,100)。粒子群算法参数设置为:
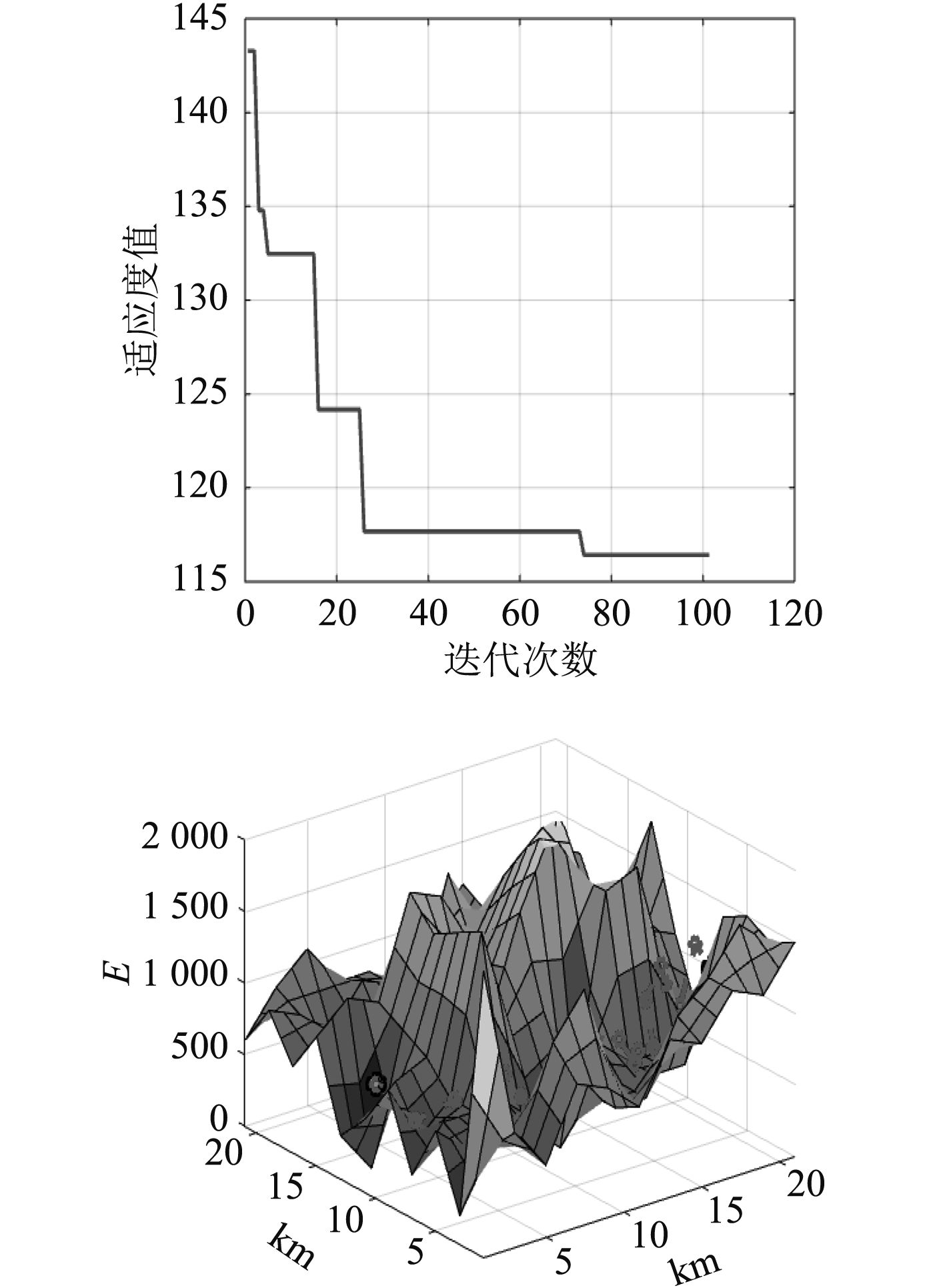
|
图 3 未采用融合优化算法的路径规划; Fig. 3 The path planning without fusion optimization algorithm |
可以看出融合后的算法在路径规划时适应度值较小,且响应时间较快,而且在优化后的融合算法中效果更加明显。
4 结 语本文提出了基于改进型蚁群—粒子群融合算法对AUV在水下三维空间的路径规划进行研究。首先利用粒子群算法较强的全局搜索能力和搜索速度对整个区域空间进行路径搜索得到最优解或是次优解,然后再利用蚁群算法的正反馈机制对次优解进行精确搜索,得到当前路径信息素丰富的最优解。根据仿真结果显示分析可知,改进型蚁群—粒子群融合算法获得的最终结果优于单一以蚁群算法或粒子群算法以及传统蚁群—粒子群融合算法进行路径规划寻优的结果。该算法对于AUV路径规划的应用研究以及多AUV水下环境协调路径规划方法的研究具有一定的参考意义。
| [1] |
周兵, 杨凡, 徐琪. 基于ADAMS的转向机构的优化设计[J]. 湖南大学学报(自然科学版), 2008, 35(12): 23-26. ZHOU Bing,YANG Fan,XU Qi. Optimization design of steering linkage based on ADAMS[J]. Journal of Hunan University(NaturalSciences), 2008, 35(12): 23-26. |
| [2] |
陈岩, 苏菲, 沈林成. 概率地图UAV航线规划的改进型蚁群算法[J]. 系统仿真学报, 2009, 21(06): 1658-1662, 1666. CHEN Yan,SU Fei,SHEN Lin-cheng. Improved ant colony algorithm based on PRM for UAV route planning[J]. Journal of System Simulation, 2009, 21(06): 1658-1662, 1666. DOI:10.16182/j.cnki.joss.2009.06.002 |
| [3] |
屈鸿, 黄利伟, 柯星. 动态环境下基于改进蚁群算法的机器人路径规划研究[J]. 电子科技大学学报, 2015, 44(02): 260-265. QU Hong,HUANG Li-wei,KE Xing. Research of improved ant colony based robot path planning under dynamic environment[J]. Journal of University of Electronic Science and Technology of China, 2015, 44(02): 260-265. DOI:10.3969/j.issn.1001-0548.2015.02.017 |
| [4] |
喻环. 改进蚁群算法在机器人路径规划上的应用研究[D]. 合肥: 安徽大学, 2017.
|
| [5] |
周岩, 王盛, 高传善, 等. 基于改进粒子群算法的模糊神经网络及其在短时天气预报中的应用[J]. 计算机应用与软件, 2010, 27(05): 234-237. ZHOU Yan,WANG Sheng,GAO Chuan-shan,et al. An improved pso-based fuzzy neural network and its application in short-term weather forecast[J]. Computer Applications and Software, 2010, 27(05): 234-237. DOI:10.3969/j.issn.1000-386X.2010.05.070 |
| [6] |
邱莉莉. 基于改进蚁群算法的机器人路径规划[D]. 上海: 东华大学, 2015.
|
| [7] |
李心. 基于改进粒子群蚁群融合算法的智能移动机器人路径规划研究[D]. 沈阳: 东北大学, 2014.
|
| [8] |
高敏. 基于粒子群蚁群算法的路径规划研究[D]. 南昌: 南昌航空大学, 2013.
|
| [9] |
胡荟. 基于改进蚁群算法的机器人三维路径规划技术的研究[D]. 金华: 浙江师范大学, 2012.
|
 2018, Vol. 40
2018, Vol. 40
