2. 大连测控技术研究所,辽宁 大连 116013
2. Dalian Scientific Test and Control Technology Institute, Dalian 116013, China
随着计算机辅助设计的发展,三维船舶模型建立软件层出不穷。同时由于虚拟现实技术的发展以及OPENGL图形库可提供强大的底层命令,为船舶设计可视化提供了程序支撑。源于实船在随机海况中运动的可视化可以使船舶设计人员能够更直观地了解实船的运动性能[1 – 2],同时,随着飞速发展的计算机技术,可视化技术越来越逼真,近年来,计算机辅助设计和科学计算的可视化已在船舶设计领域屡见应用,发展成为船舶在随机海况中运动机理研究的重要手段之一。由于船舶在随机海况中运动的复杂性,计算机仿真研究已成为必然,即可以直观再现船舶运动过程,又可以研究极端海况下实船的运动情况,总结运动规律,为设计人员提供参考,为操作人员提供建议,因此实船运动仿真研究越来越得到学术上的关注。
在实船运动仿真的研究中,首先要建立数学模型,并求解。在此过程中会需要大批量的矩阵计算,并对分析结果实时图形化显示。Matlab是MathWorks公司开发的科学计算环境,具有强大的计算绘图能力,提供大量的函数库、工具箱,几乎涵盖了所有的工程计算领域,被誉为“演算纸”式的工程计算工具[3 – 5]。Visual Basic作为一门简单易学易用的编程语言,在工程上有诸多应用,其界面友好且执行速度相对较快[6]。因此将VB与Matlab混合编程,不仅会大大提高开发效率[7],对于解决工程问题十分有意义,而且可为科研工作以及工程应用提供有力的技术支持。
1 环境建模实船在极不规则的随机海况环境下航行,为了研究实船在海上的运动模型,需首先对海上环境进行建模研究,因海浪对实船的作用力矩主要与海浪波倾角有关,所以,环境建模转化为对海浪波倾角的仿真研究[8 – 9]。
波倾角的仿真模型参考文献[10]取为:
| $\begin{split} {\alpha _{\theta e}}(t) =& \sum\limits_{i = 1}^n {{\alpha _{\theta ei}}(t)} = \hfill \\& \sum\limits_{i = 1}^n {\left[ {\sqrt {2S({\omega _i})\vartriangle \omega } \cos ({\omega _{ei}}t + {\varepsilon _i})} \right]} {K_\theta }\sin \beta \hfill \text{,}\quad\quad\;(1)\end{split} $ |
| $\begin{split} {\alpha _{\phi e}}(t) =& \sum\limits_{i = 1}^n {{\alpha _{\phi ei}}(t)} \hfill = \\ &\sum\limits_{i = 1}^n {\left[ {\sqrt {2S({\omega _i})\vartriangle \omega } \cos ({\omega _{ei}}t + {\varepsilon _i})} \right]} {K_\phi }\sin \beta \hfill\text{。} \quad\quad(2)\end{split} $ |
式中:
近年来,船舶运动模型方程的建立分为以下几种:时域或频域方程、基于操纵性理论、基于源汇分布法或STF切片法,以及基于控制理论建立运动方程。本文基于控制理论建立数学模型。以单自由度横摇运动为例,首先根据Conolly理论,建立微分方程,再对其进行Laplace变换,最后得到船舶单自由度横摇运动系统的状态方程[11 – 13]
| $\left[ \begin{gathered} \dot x{}_1 \hfill \\ \dot x{}_2 \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} 0 \hfill \\ - {a_0} \hfill \\ \end{gathered} \right.\left. \begin{gathered} 1 \hfill \\ - {a_1} \hfill \\ \end{gathered} \right]\left[ \begin{gathered} {x_1} \hfill \\ {x_2} \hfill \\ \end{gathered} \right] + \left[ \begin{gathered} {\beta _1} \hfill \\ {\beta _0} \hfill \\ \end{gathered} \right]u\text{,}$ | (3) |
| $y = \left[ {\begin{array}{*{20}{c}} 1&0 \end{array}} \right]\left[ \begin{gathered} {x_1} \hfill \\ {x_2} \hfill \\ \end{gathered} \right] + {\beta _2}u\text{。}$ | (4) |
式中:x1,x2为状态变量;输入信号为
| $\begin{split} &{a_0} = {\omega _\theta }^2,{a_1} = 2{\xi _\theta }{\omega _\theta },{a_2} = 1, \\& {b_0} = {\omega _\theta }^2,{b_1} = 2{\xi _\theta }{\omega _\theta },{b_2} = \frac{{{\omega _\theta }^2\Delta {J_\theta }}}{{Dh}}\text{,}\\& {\beta _2} = {b_2} = \frac{{{\omega _\theta }^2\Delta {J_\theta }}}{{Dh}}\text{,} \\& {\beta _1} = {b_1} - {a_1}{\beta _2},{\beta _0} = {b_0} - {a_0}{\beta _2} - {a_1}{\beta _1} \text{。}\end{split} $ | (5) |
式中:ωθ为船舶的横摇固有角频率
| ${\omega _\theta }^2 = \frac{{Dh}}{{{J_\theta } + \Delta {J_\theta }}}\text{,}$ | (6) |
ξθ为船舶的横摇阻尼因子
| ${\xi _\theta } = \frac{{{N_\theta }}}{{\sqrt {({J_\theta } + \Delta {J_\theta })Dh} }}\text{。}$ | (7) |
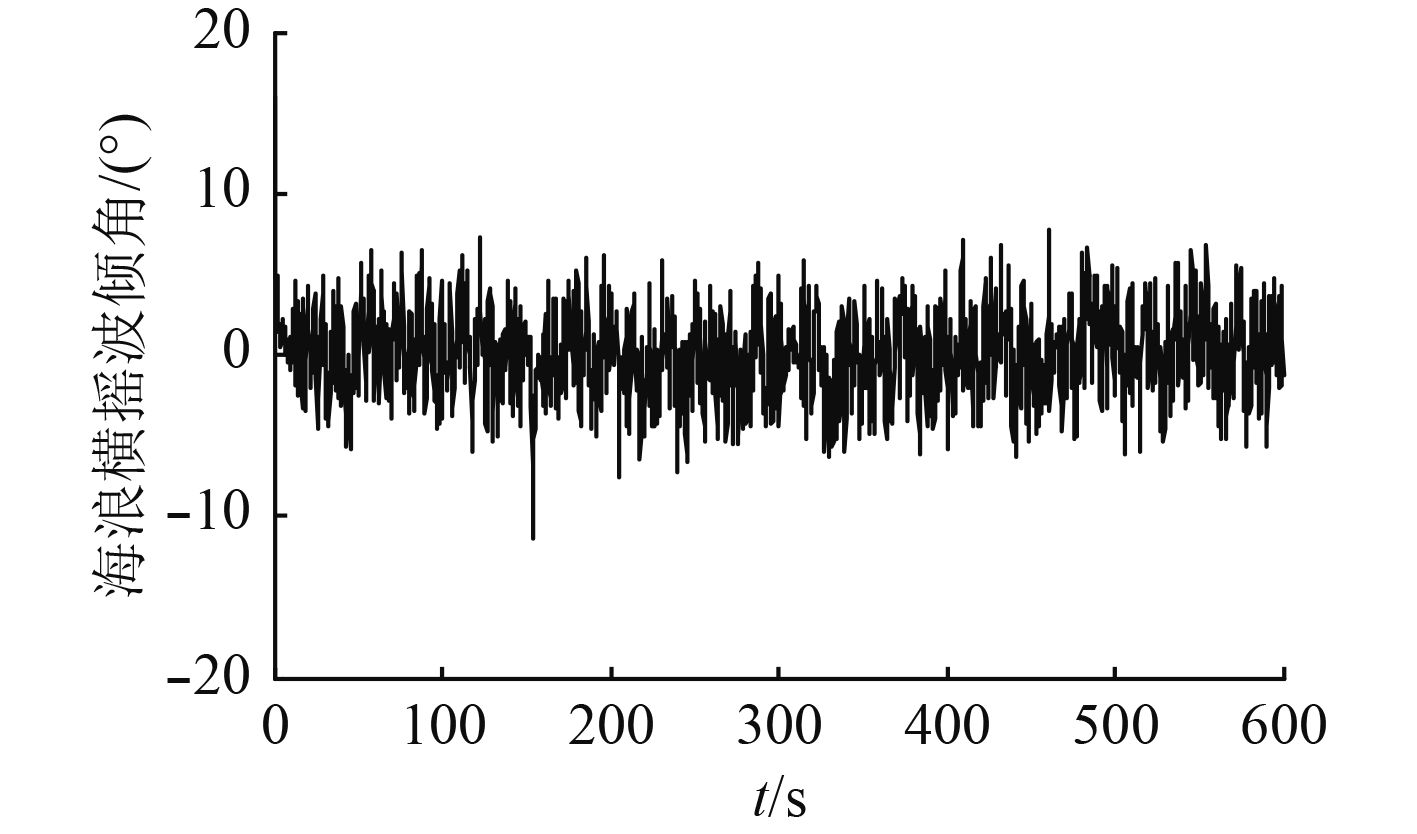
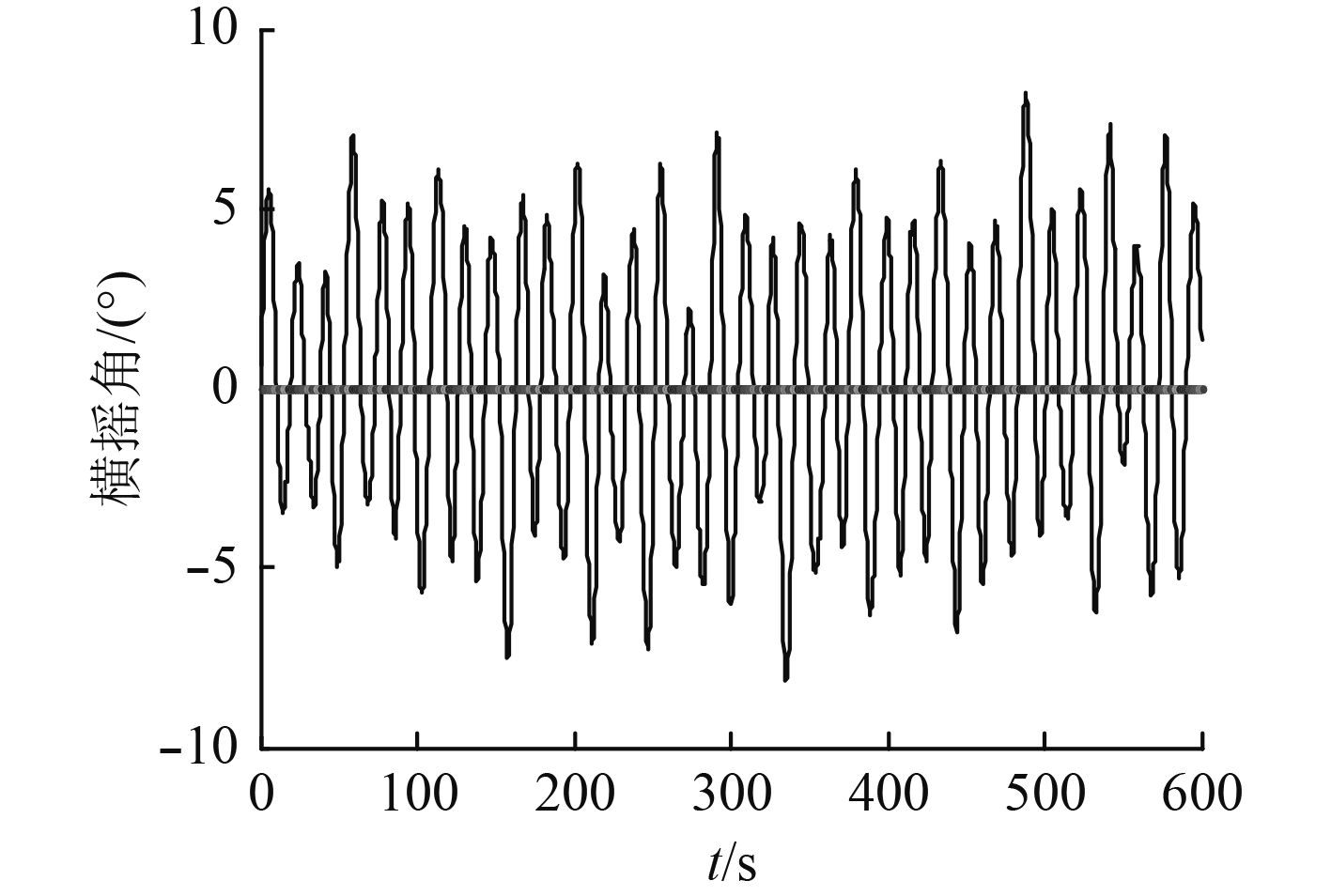
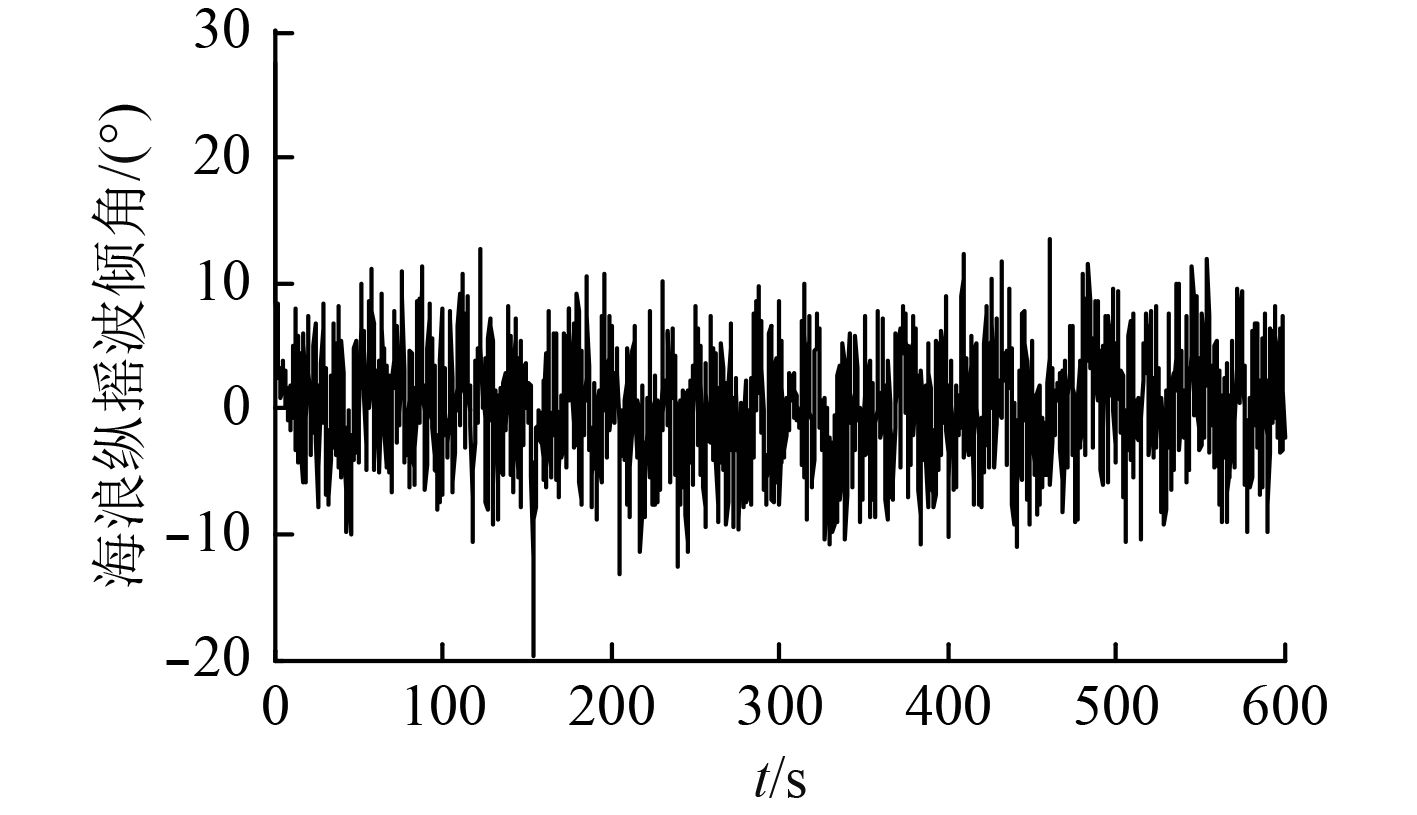
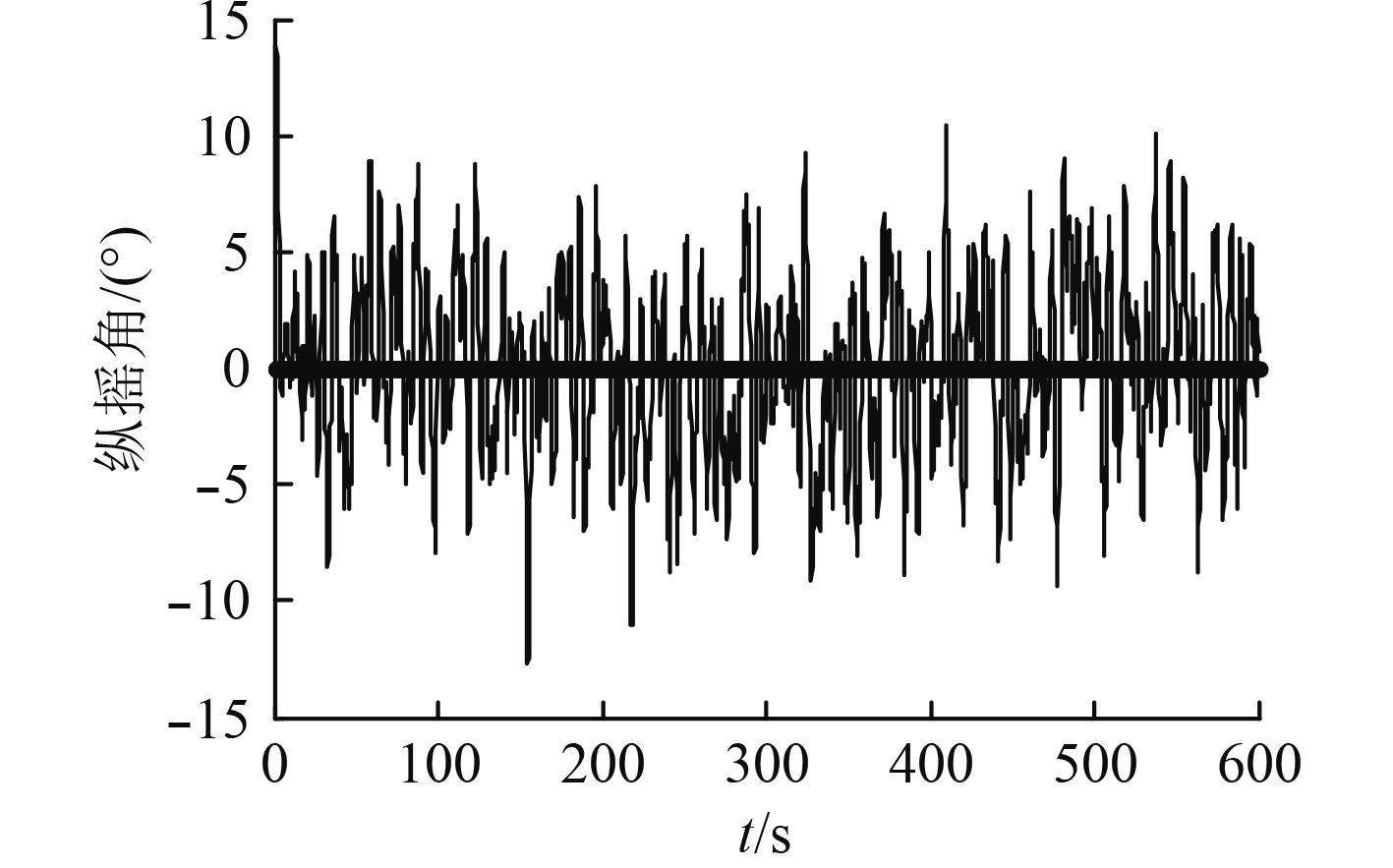
在船舶横摇运动仿真中输入参数如图2所示,输出数据如图3和图4所示。船舶纵摇运动仿真研究亦可同理获得,输出数据如图5和图6所示。
|
图 3 横摇波倾角角仿真 Fig. 3 Rolling wave inclination angle simulation |
|
图 4 横摇角仿真 Fig. 4 Rolling angle simulation |
|
图 5 纵摇波倾角仿真 Fig. 5 Pitching wave inclination angle simulation |
|
图 6 纵摇角仿真 Fig. 6 Pitching angle simulation |
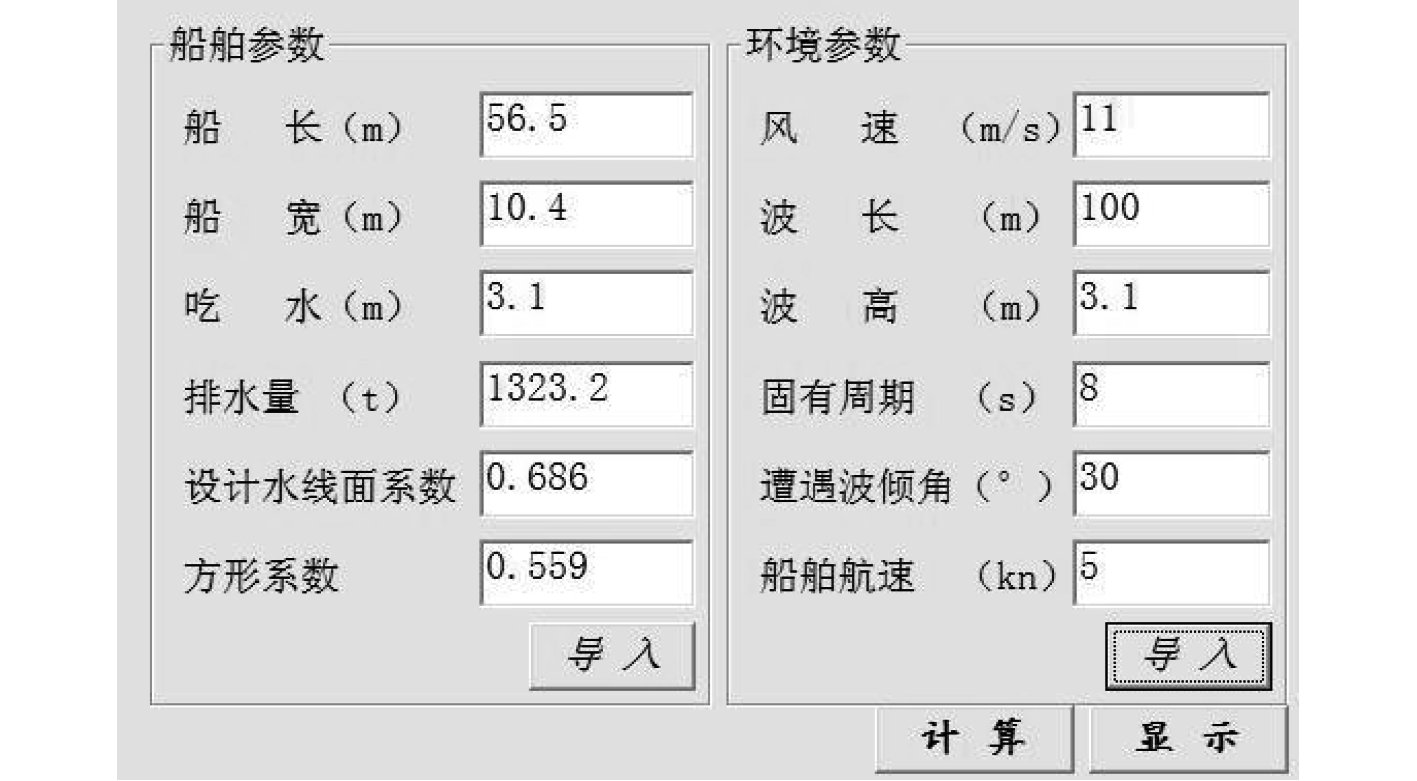
|
图 2 船舶横摇运动仿真输入参数界面 Fig. 2 Input parameters interface of the ship's rolling motion |
|
图 1 船舶摇荡运动仿真平台界面 Fig. 1 Interface of ship swaying motion simulation |
在单自由度横摇、纵摇运动仿真研究基础上,本文尝试了基于时域求解实船横摇与垂荡耦合的运动方程的求解,输入参数详见图7所示,输出数据如图8和图9所示。
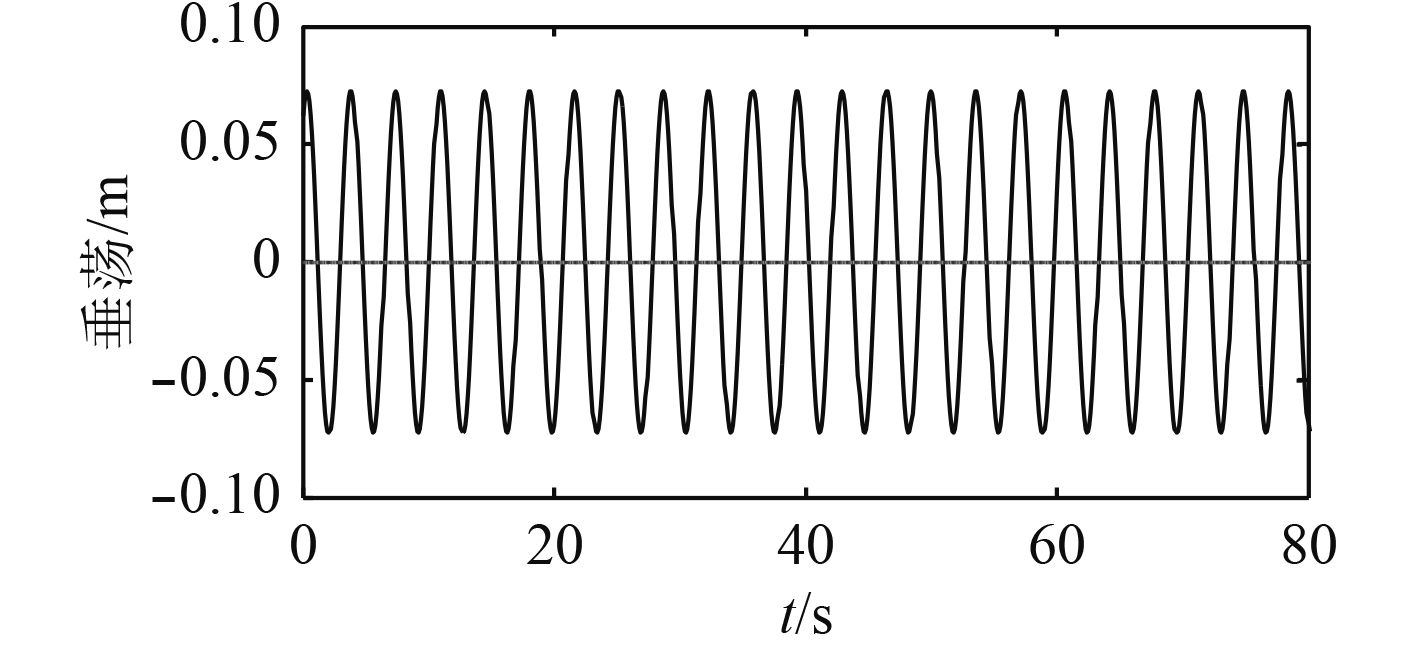
|
图 9 耦合运动中垂荡运动 Fig. 9 Heaving angle simulation of coupling motions |
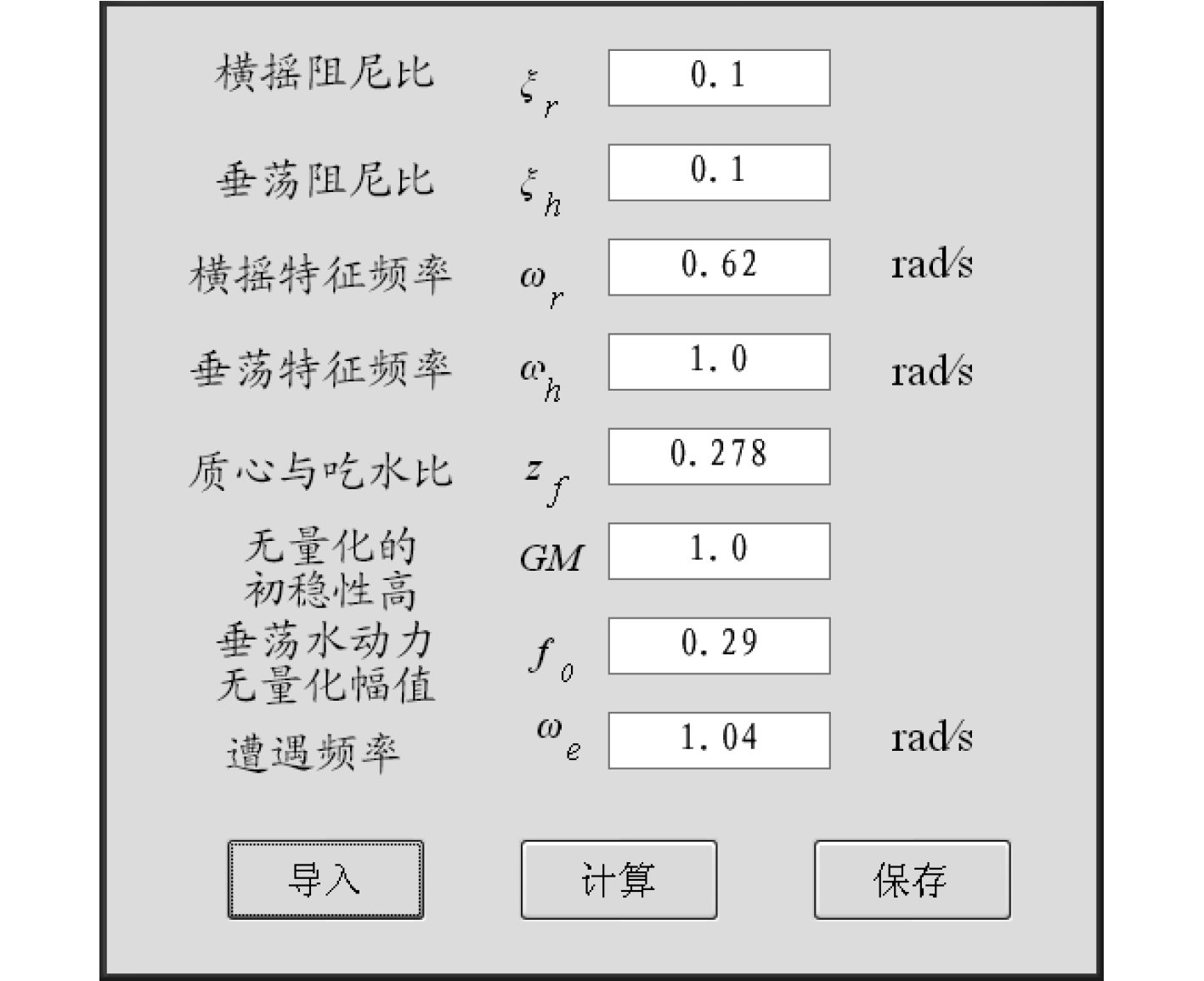
|
图 7 船舶横摇垂荡耦合运动的仿真界面 Fig. 7 Simulation interface of the ship's rolling and heaving coupling motion |
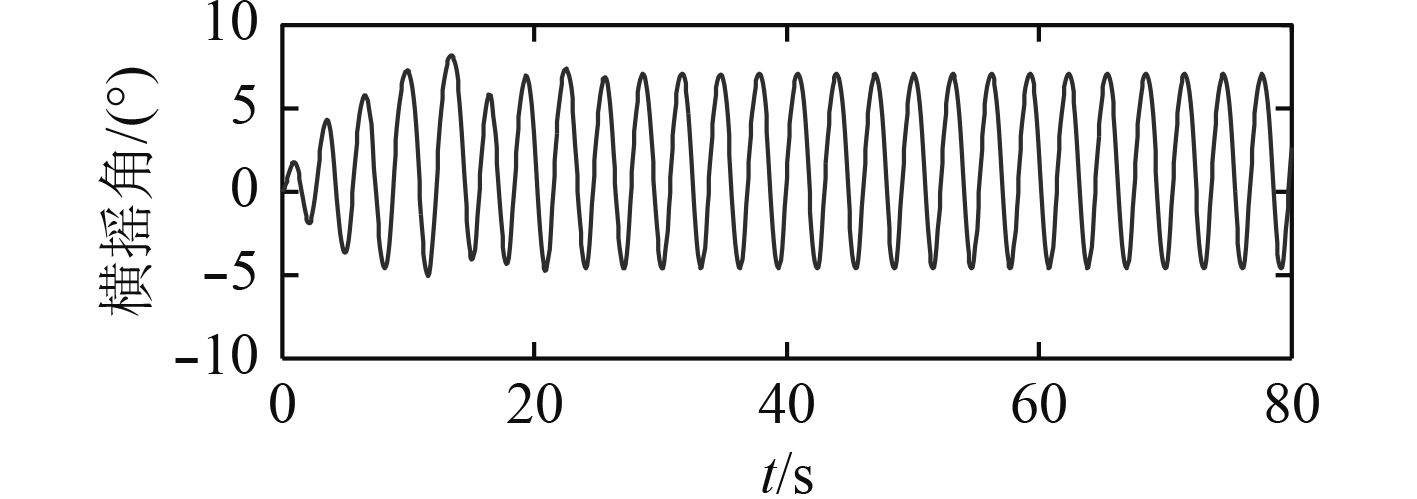
|
图 8 耦合运动中横摇角 Fig. 8 Rolling angle simulation of coupled motions |
在仿真基础上,应用SQLServer数据库存储实船的基本参数信息、海浪环境参数信息以及实船运动的仿真数据。同时,总结实船摇荡运动规律,设计者可按查询条件查询得出相应船型的运动规律数据信息,从而为实船设计者或实船操纵提供更为直观的参考。将这些仿真数据导入到三维模型的运动控制中,驱动三维模型实现运动显示。
3 仿真显示OPENGL图形库提供了强大的底层命令,其高层渲染都通过底层命令来完成,且对VB,VC等编程语言是开放的。基于本文的研究是针对不同的实船进行运动分析,因此为了快速地建立仿真模型,放宽对模型真实性的要求,仅反映出正确的几何外形即可。建模过程如下:首先读取实船型值表数据,按绘图要求选取部分型值后再次存储数据,然后将其转化为对应的多个多边形图形的绘制,计算出对应多边形的顶点坐标、法向量、光照等重要数据,更新以上数据快速生成实船简化模型[8 – 14]。如图10所示。

|
图 10 船舶摇荡运动三维仿真演示截图 Fig. 10 The 3D simulation interface of the ships′ swaying motions |
通过仿真计算可归纳出以下几点结论:
1)对于单自由度运动而言,横摇运动对实船的设计和操纵起着关键作用;对于耦合运动,横摇运动与其他自由度的耦合也是以横摇运动响应为重。因此,横摇运动响应的研究成果,是船舶摇荡运动的基础。
2)在本文仿真研究中,可以通过不同船型、不同海况的参数输入计算出运动响应,从而总结出运动规律:船舶质量越大,摇摆周期就越长,振幅则减小;航速相同、遭遇角相同条件下,有义波高越高,作用在船舶上的海浪横摇力矩越大;相同有义波高、相同遭遇角条件下,作用在实船上的海浪横摇力矩与航速成反比;有义波高和航速都相同,遭遇角小于90°的情况下,实船上的波浪横摇力矩与遭遇角成正比,遭遇角大于90°时成反比,90°遭遇角时最大。
3)预防船舶倾覆事故是一项安全管理的系统工程,应对“人、机、环境、管理”各要素采取本质化的安全措施。为减少倾覆危险事故的发生,预先研究实船运动的情况显得十分重要。
利用Matlab和VB的混合编程,使所收集到的数据更快速、直观、形象地反映出了实船运动的特性,便于更快捷、准确地对运动特性进行分析;此程序在运行时由于未脱离Matlab运行环境,这样会占用内存,从而对程序的执行速度有一定的影响。另外,本文模型是简化模型,可以借用成熟的应用软件,如3DMAX,3DSTUDIO等,与OPENGL结合建立更为精细的实船模型。
| [1] |
耿东升. 随机海浪中船舶非线性横摇的可视化方法研究[D]. 天津: 天津大学, 2005. GENG Dong-sheng. Study on the visualization method of nonlinear roll of ship in the random seas.[D]. Tianjin: Tianjin University, 2005. |
| [2] |
耿东升. 船舶海浪中非线性随机运动的可视化技术[J]. 计算机仿真, 2007, 24(3): 210-214. GENG Dong-sheng. Visualization techniques for ship motion in waves[J]. Conputor Simulation, 2007, 24(3): 210-214. DOI:10.3969/j.issn.1006-9348.2007.03.056 |
| [3] |
张志涌, 杨祖樱. Matlab教程: R2010a[M]. 北京: 北京航空航天大学出版社, 2010.
|
| [4] |
林永秋. MatrixVB在测量数据处理中的应用[J]. 《福建建设科技》, 2010(3): 68-71. LIN Yong-qiu. The application of MatrixVB in measurement data processing[J]. Fujian Construction Science & Technology, 2010(3): 68-71. |
| [5] |
卢峰. 基于ARM的体外反搏控制系统的研究[D]. 赣州: 江西理工大学, 2007. LU Feng. Study on the control system of extracorporeal counter pulsation based on ARM[D]. Ganzhou: Jiangxi University of science and technology, 2007. |
| [6] |
钱永胜, 王殿夫, 于化东. VB 6.0入门与应用[M]. 大连: 大连理工大学出版社, 1999.
|
| [7] |
李延平. 利用Visual Basic开发平面曲柄摇杆机构可视化图谱[J]. 微计算机应用, 2003, 24(3): 378-380. LI Yan-ping. Visualization of planar crank rocker mechanism using visual Basic[J]. Microcomputer Applications, 2003, 24(3): 378-380. |
| [8] |
宋杨. 船舶减摇无模型自适应控制技术研究[D]. 大连: 大连理工大学, 2013. SONG Yang. Research on ship anti-rolling control techniques with model free learning adaptive control method[D]. Dalian: Dalian University of Technology, 2013. |
| [9] |
马洁. 船舶运动姿态预报与控制方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2006. MA Jie. Research on ship movement prediction and anti-roll control method[D]. Harbin: Harbin Engineering University, 2006. |
| [10] |
张显库, 贾欣乐. 船舶运动控制[M]. 北京: National Defense Industrial Press, 2006.
|
| [11] |
马洁, 韩蕴涛, 李国斌. 不同航态下船舶运动规律仿真研究[J]. 舰船科学技术, 2016, 38(1): 32-36. MA Jia, HAN Yun-tao, LI Guo-bin. The simulation studies on a ship′s movement pattern under the various sailing situations[J]. Ship Science and Technology, 2016, 38(1): 32-36. |
| [12] |
余音, 朱航彬, 夏利娟. 基于小波理论的舰船非线性横摇运动特性分析[J]. 上海交通大学学报, 2005, 38(5): 682-685. YU Yin, ZHU Hang-bin, XIA Li-juan. Analysis on the nonlinear dynamical character of ship rolling based on warelet theory[J]. Journal of Shanghai Jiaotong University, 2005, 38(5): 682-685. DOI:10.3321/j.issn:1006-2467.2005.05.005 |
| [13] |
朱航彬. 基于小波理论的分析方法及其在船舶工程中的应用[D]. 上海: 上海交通大学, 2005. ZHU Hang-bin. Analytical method based on the theory of wavelet and its application on ship engineering.[D]. Shanghai: Shanghai Jiaotong University. 2005. |
| [14] |
JACKIE NEIDER, TOM DAVIS, MASON WOO. OpenGL Programming Guide[M]. Addison-Wesley Press 1994.
|
 2018, Vol. 40
2018, Vol. 40
