随着各国对领海环境要求的不断提高,船舶振动噪声作为航运船舶一项重要的性能指标,越来越受到船舶使用各方的重视[1 – 2]。受限于使用条件和设计背景的制约,在进行船舶系统设计之初,船舶总体结构、附体结构以及推进器等都会被基本固化,因而由这些设计因素引起的船舶声学设计量被基本确定,控制船舶各功能系统运行时的振动噪声,就成为船舶低噪声设计的关键[3]。如何在船舶众多功能设计参数中提取出制约系统声学性能的设计参数,并建立这些设计参数与系统声学性能的量化关系,进而有针对性的来开展系统参数设计,达到控制系统运行噪声的目的,是船舶系统设计的核心技术内容。
在船舶机械噪声控制方面,一般做法是通过机械设备的减振、隔振,以及系统管路上的消声等技术措施来实现[4 – 5],没有能够从船舶总体声学设计和运行工况的需要方面考虑,对系统声学设计进行统筹性的分析和系统设计参数的权衡设计,因而系统声学设计往往花费代价高却难以达到总体平衡设计的需求[6 – 7]。
1 系统声学性能的表征若船舶某系统运行时的总功率为P,有效功率为Pe,系统运行时由机械做功损失的功率为ΔPm,由系统中管路及附件泄漏引起的流量损失为ΔPQ,由系统附件阻力导致的扬程损失为ΔPH,这样,船舶中某机械系统运行时有:
| $P = {P_e} + \Delta {P_m} + \Delta {P_Q} + \Delta {P_H}{\text{。}}$ | (1) |
对于密度为ρ的流体介质,Pe用系统中的流量Q和扬程H表示为ρgQH;ΔPQ用系统中的泄漏量qd表示为ρgqdH;ΔPH用系统中的扬程损失量hd表示为ρgQhd,g为重力加速度。
对于结构型式确定的船舶系统,其工作时引起的辐射噪声PW可以表示为[4]
| ${P_W} = A + \mu \log \left( P \right){\text{,}}$ | (2) |
式中μ为常数系数,A为与系统布置型式有关的常数。这样,由式(1)和式(2)可知,对于船舶各功能系统而言,系统噪声由系统的总功率和系统总体的布置型式确定。
系统总功率决定系统噪声源的特性而系统总体布置决定系统噪声传递的途径以及对系统噪声传递途径的控制。
在系统噪声源方面,主要是控制系统中泵源和系统介质在管路中运行时产生的二次噪声[3];在传递路径方面,主要是控制介质向船体的振动传递或介质直接向海水中的传递。对于总功率需求一定的船舶系统,为了有效控制噪声源对系统声学性能的影响,很大程度上在于根据船舶运行状态对系统运行状态进行调节上;而系统噪声的传递控制方面,则依赖于系统自身的结构形式、整体布置以及对系统各噪声传递路径的声学平衡等技术措施上。因此,对于船舶机械系统而言,应用系统工况调节方式、构造型式、整体布置以及系统噪声传递通道的量化平衡等方面的参数,能够将其声学性能进行全面的表征。
2 系统噪声的影响因素分析对船舶液体介质系统,泵是系统中的主要动力设备,也是系统中的主要噪声源,本文以船舶中应用较多的离心泵为例,分析系统声学性能的影响因素。
对于船舶中的各个功能系统,系统运行时应按照船舶总体和其他关联系统的需求,满足以下3个方面的要求,即提供满足一定功能要求的介质,提供满足系统运行要求的流量和扬程(或称压力)。一定功能要求的介质由系统中的各个功能性附件来实现,而系统运行要求则由系统的泵和管路来实现。因此,系统中流量Q和扬程H是系统的主要输入参数。
对转速n一定的离心泵,设备机脚上的振动加速度可以表示为:
| $\ddot q\left( \omega \right) = \frac{{{F_\varPhi }\left( \omega \right)\omega }}{{\left| {Z\left( \omega \right)} \right|}}{\text{。}}$ | (3) |
式中:
| ${L_q}\left( {{f_k}} \right) = 20\lg \left( {\frac{{{t_u}{R_{\max }}}}{{{m_W}QH}}} \right) + 4 + R\left( {{t_u},{f_0},{f_{ik}}} \right){\text{。}}$ | (4) |
式中:Q和H为对应转速n时的流量和扬程;tu为泵内流体通过叶轮的时间;Rmax为泵体内脉冲力函数的幅值;mW为泵的比质量;f0为设备机脚减振器的固有振动频率;fik为振动幅值脉冲函数中心频率fk对应的第i个计算点。
同理,对于出口管道内径为D的泵,可以得到离心泵管内声压Lp(fk)的估算公式为
| ${L_P}\left( {{f_k}} \right) = 20\lg \left( {\frac{{{t_u}{R_{\max }}}}{{{D^2}}}} \right) + 63 + G\left( {{t_u},{f_{ik}}} \right){\text{。}}$ | (5) |
对离心泵而言,在不同的转速n1和n0下,其转速比为k = n1/n0,这样,泵机脚振级的变化量ΔLp可以表示为
| $\begin{split}\Delta {L_p} =& 10\lg \frac{{{Q_0}{H_0}}}{{QH}} + 70\lg \frac{{{n_0}}}{n} - 10\lg {\left( {\frac{n}{{{n_0}}}} \right)^\gamma } =\\ & - 10\left( {10 + \gamma } \right)\lg k{\text{,}}\end{split}$ | (6) |
式中,γ为通过泵转速调节泵流量时的振级变化因子。
从式(4)~式(6)可以看出,当满足系统功能约束的泵确定后,Q、H和n三个参数直接决定了泵在对应运行工况下的声学性能。
系统中附件工作的噪声与其流体阻力有关,附件流体阻力Δf与流量Q的关系可以表示为
| $\Delta f = \psi {Q^2}{\text{,}}$ | (7) |
式中,ψ为附件的阻力系数。从式(7)可以看出,为了控制非调节用附件工作时引起的噪声,需要控制附件的流阻系数和通过附件的流量。
对于船舶系统中应用较多的调节阀门等附件,理论研究和试验表明,其声学性能与阀门前后的压力差,阀门所在位置的压力、流量以及阀门是否空化有关,可以通过这几个参数得到不同状态下阀门的声学性能估算公式。
从上面分析可以看出,在船舶系统运行的诸多参数中,流量、压力以及设备运行状态是影响系统声学性能的关键因素,对于附件而言,还要控制附件所在部位的该局部参数。
3 系统声学性能影响因素分析 3.1 系统工况调节方式对声学性能的影响根据船舶系统管路的运行特点,运行工况的调节方法可以概括为改变装置特性曲线和改变泵的特性曲线2类。改变装置特性曲线通过调节系统参数来实现系统运行状态的改变,技术措施包括改变系统中管路和附件的流阻特性,改变管路的布置型式等;改变泵的特性曲线通过改变泵的运行状态和泵自身的设计参数来实现,技术措施包括调节泵的转速,改变泵的叶型角等。
根据相似定律[8],对同一台离心水泵,当转速n从n0变化到n1时,其流量Q和扬程H满足
| $\frac{{{H_0}}}{{{H_1}}} = {\left( {\frac{{{Q_0}}}{{{Q_1}}}} \right)^2} = {\left( {\frac{{{n_0}}}{{{n_1}}}} \right)^2}{\text{,}}$ | (8) |
根据泵额定运转条件下流量和扬程的关系,可以得到泵的流量-扬程曲线为
| $H = a{k^2} + bkQ + c{Q^2}{\text{。}}$ | (9) |
同样,对于在系统中运行的泵,若管路需要的静压力参数Hst,则得到系统的装置曲线为
| $H = {H_{st}} + s{Q^2}{\text{,}}$ | (10) |
式中,s为整个系统的流阻参数。
离心泵的运行工况点是扬程—流量特性曲线和装置特性曲线的交点。为了使得泵在系统规定工况下具有较好的声学性能,应该使得流量、扬程参数与系统在对应工况下的相应参数相适应。
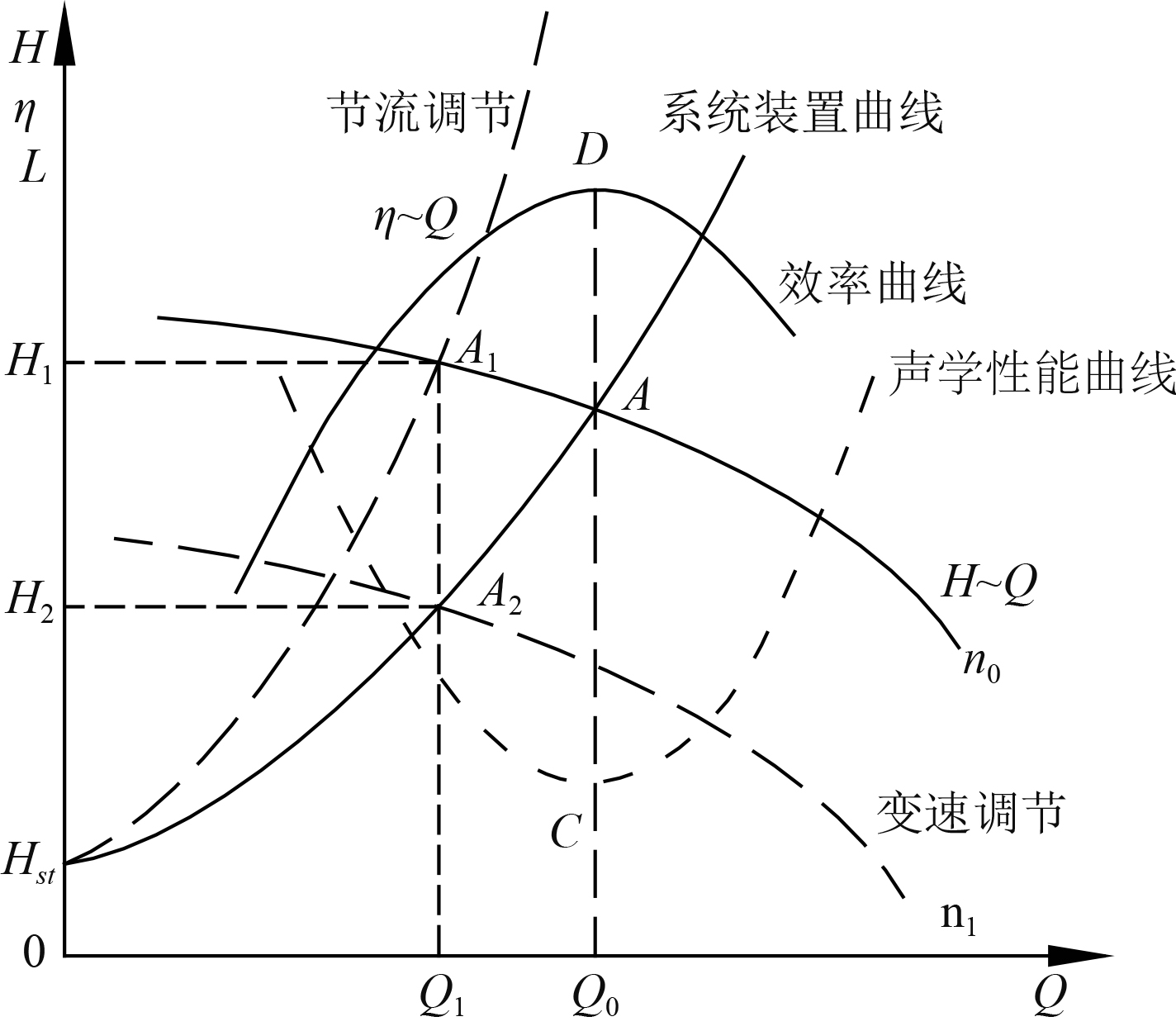
根据系统运行的参数关系,对于船舶系统中的2种工况调节方式,其对应的流量—扬程曲线、流量—效率曲线和流量—声学效果曲线如图1所示。这样,若系统的装置曲线能够使得泵的工作点在点A处,则泵的效率位于高点D,声学性能曲线对应最优点C。
|
图 1 系统工况调节性能曲线 Fig. 1 Performance curve of system working condition |
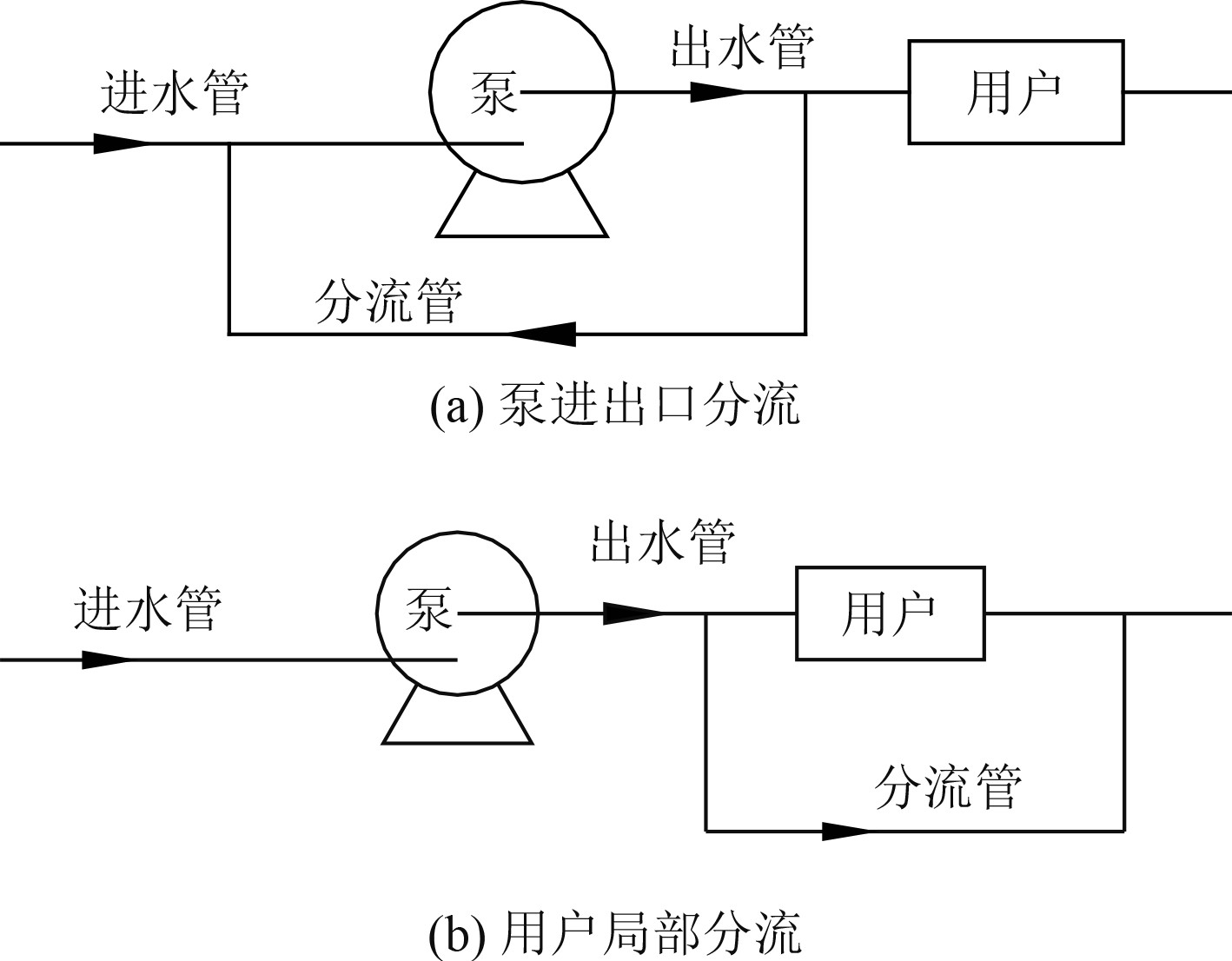
改变装置特性曲线的工况调节办法可以分为通过系统附件的节流调节、通过增加系统管路的分流调节2种。对于节流调节,依据式(10)并结合图1所示的曲线可以看出,系统工作点将稳定在A1点,其噪声量级呈增大趋势。对这种调节方式还要注意附件声学性能与所在位置运行参数的关系,避免二次噪声的产生。对于图2中的分流调节方式,系统在扬程需求不变的条件下,流量增大,使得系统的工作点重新稳定在A点的右侧,引起系统的噪声量级增大。
|
图 2 分流调节方式 Fig. 2 Shunting adjustment mode |
节流调节没有增加系统附件的数量,但往往会引起二次噪声,而分流调节增加了系统管路和附件的数量,也就增加了系统噪声传递的通道及系统整体的规模,带来了系统整体噪声控制的难度。
3.1.2 改变泵的特性曲线在船舶总体设计阶段,专注的是对已有泵运行参数的调节,如转速、进出口管径等,而对泵设计参数的改变,如叶型角等参数,是设备级别的噪声控制措施,本文不予讨论。
当转速变化时,图1中的系统工作点从A点转移至A2点,由于系统的H,Q均减小,从式(6)可知,机械设备自身的噪声量级降低,同时,系统管路中由于流量、压力等参数也相应下降,使得管路中的噪声两级也相应下降。另外,从相同Q1点对应的节流曲线和变速曲线也能看出,改变泵转速能够有效提高系统的声学性能。
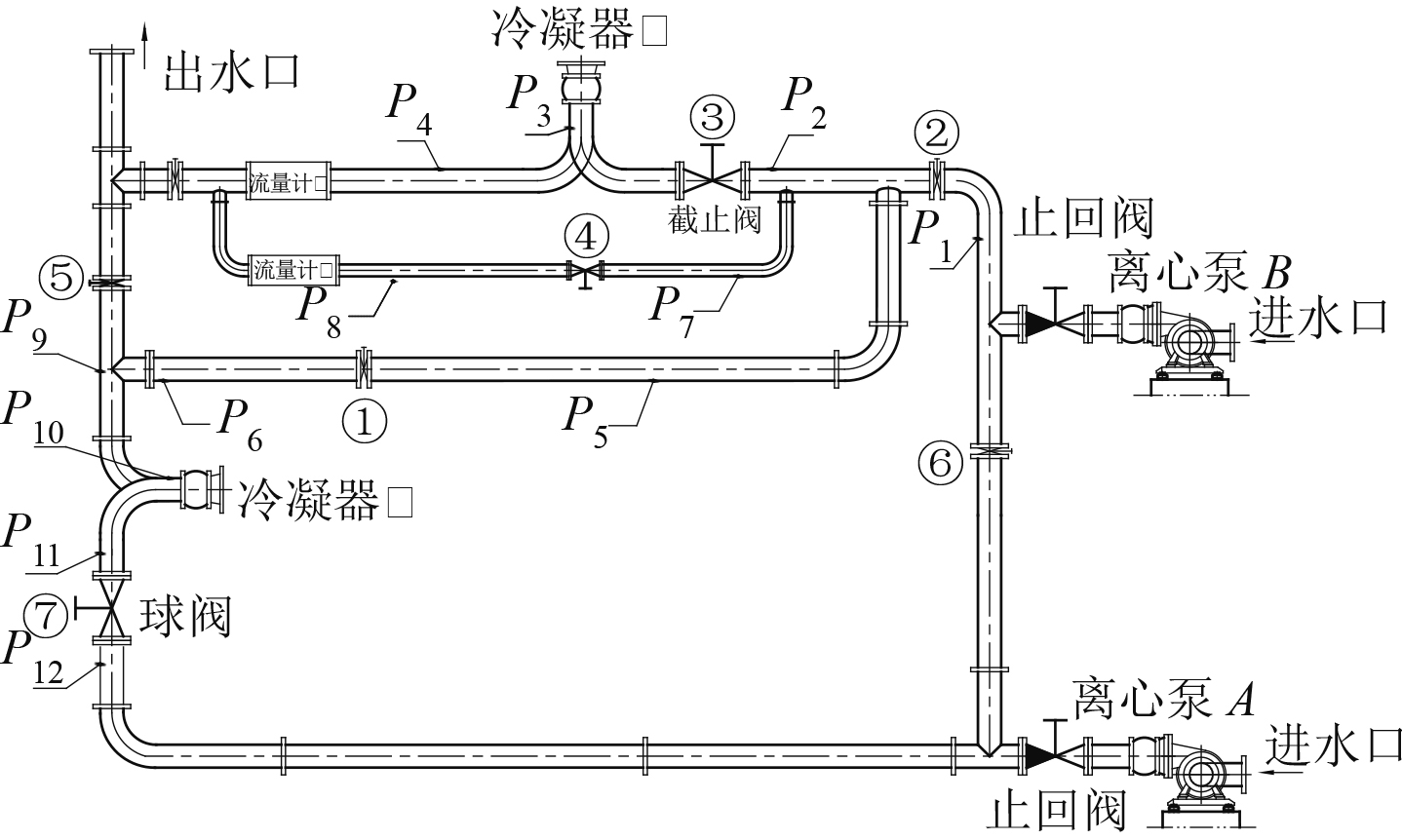
3.2 系统构造型式对系统声学性能的影响系统构造型式表征的是为实现系统功能,基于系统声学目标而开展的系统中多台设备、多用户总体分布形式的规划。船舶系统按照功能的实现情况,其构造型式大体可以分为总管式、总管-支管式以及分区布置等3类。对于图3所示的试验系统,通过阀门的开关组合,可以实现不同的构造型式。
|
图 3 系统不同构造型式试验台架 Fig. 3 Test bench for system modeling |
在船舶系统的设计中,为了适应系统多工况变化的需要,往往会采用多台泵组合工作的方式来实现系统功能。依据船舶设计的实际情况,为了简化对构造型式带来系统声学效果的分析,对于系统中的多台泵,假定全部采用相同的泵。
对于船舶系统不同的构造型式,其运行时的功能曲线由多台泵共同确定。因此,系统中泵的选择要依据系统输入、输出的需求来确定。系统中所用泵的振动噪声可由本文给出的公式计算得到,对于系统中各关键点位的振动噪声,可以用管路振动传递的方法计算得到[9]。
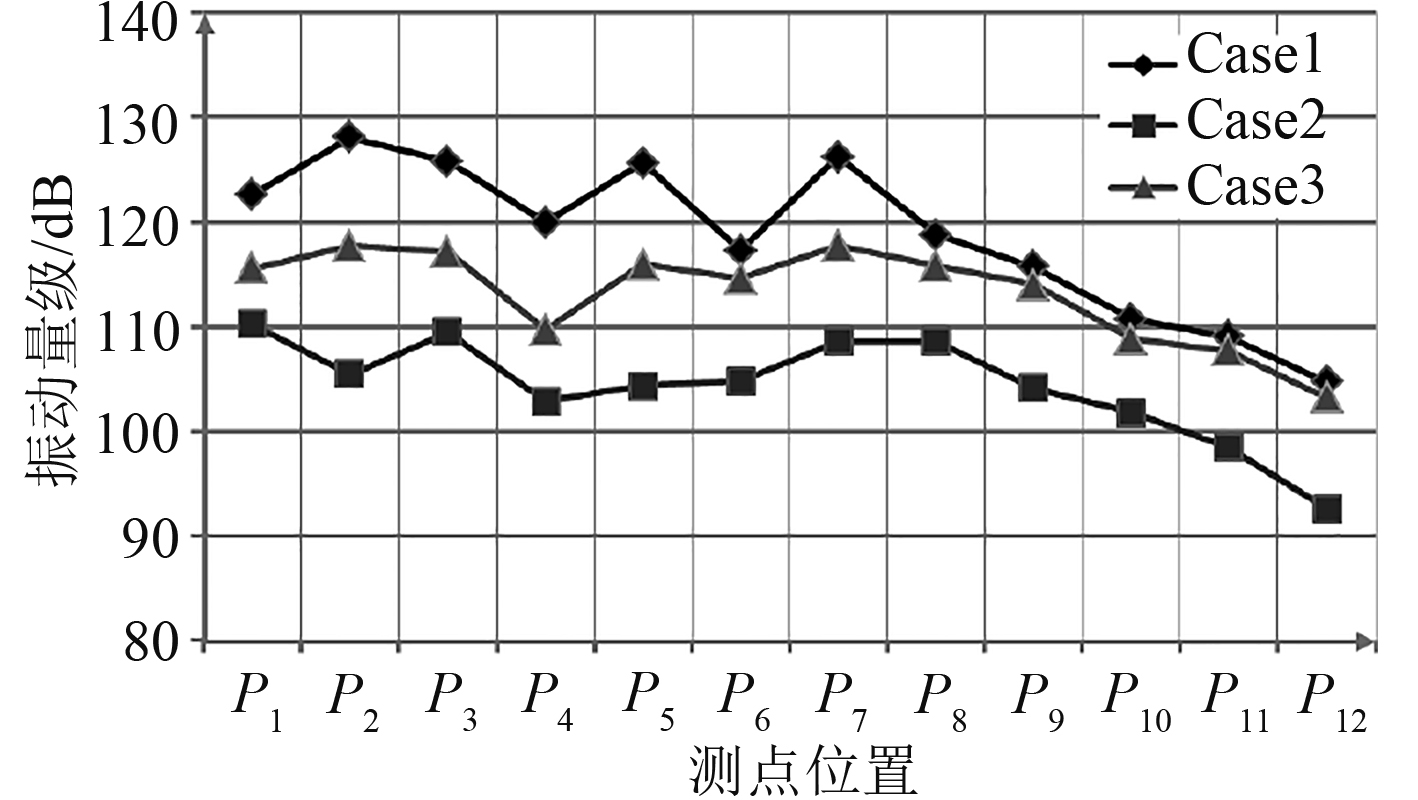
对于图3所示的试验台架,为了对系统中的2台冷凝器提供满足一定要求的冷却水,通过关闭编号为②④和⑤的阀门,可以得到总管构造型式(其他阀门打开,case 1),通过关闭阀门①④和⑥,可以得到分区的构造型式(case 2),通过关闭②和⑤,可以得到总管-支管的构造型式(case 3)。以上3种构造型式分别运行时,由试验台架可以测试得到泵和管路的振动数据,图4是不同测量点位的管路上的振动情况。
|
图 4 系统不同构造型式管路上振动测点情况 Fig. 4 Vibration measurement points on pipes with different configuration models |
从图4可以看出,系统不同方案,在系统上各点的振动特性存在较大的差异。根据台架测试得到的试验数据,应用系统噪声估算程序进行系统声学特性总体计算[6],可以得知case 2是最优的声学设计方案。
根据泵振级与流量的关系曲线可知,距离工况点越远,单台泵的振级越大,因此,为了确保系统中每台泵工作时都具有较好的运行状态,系统中多泵构造型式的确定,应使得系统在全工况下具有较优的声学性能。
3.2.2 系统构造型式的声学评判方法在系统总体方案基本确定的前提下,系统构造型式对系统的声学性能起决定性的作用,它直接影响着系统的运行方式和调节方法。依据设备和系统附件声学状态的影响因素,系统构造型式带来的声学性能可以从系统构造型式对系统中主要设备低噪声运行工况点的贴合程度、系统工况调节对系统介质运行状态及二次噪声的影响、系统参数调节的难易程度、以及系统运行牵连管路、附件的规模等4个方面进行评判。
3.3 系统整体布置对系统声学性能的影响系统不同的总体方案形成不同的系统布置,因此,分析系统整体布置对系统声学性能的影响,是考察系统声学设计有效性的主要方面之一。
3.3.1 整体布置的声学效果分析系统低噪声设计不仅要解决系统自身噪声源的问题、系统内噪声源的匹配问题,同时,还要为系统中设备、管路以及附件的噪声控制创造条件。在系统初步方案设定中,应对其总体布置的可实施性进行考量,以期达到最佳的系统声学效果。
从理论计算和船舶设计的经验来看,在噪声源一定的前提下,对机械设备进行整体隔振是解决机械噪声向船体直接传播的有效措施。因此,系统的设计应避免与船舶体或舱壁的直接连接并为整体隔振的设计创造条件。
在系统整体的布置中,除了噪声源设备、附件的布置应使得噪声源引起的各种振动波在管路或管内介质的传播中尽可能得到抑制外,系统管路的布置也应作为一项非常重要的工作内容,使得管路振动传递通过阻抗的变化得到充分的抑制。
3.3.2 系统整体布置的声学原则为了充分利用系统整体布置来优化的系统声学性能,以船舶设备布置的一般原则为基础,系统中主要机械设备、附件和管路的声学布置应遵循以下基本原则:
1)整体集中原则。为了给隔振装置的设计带来便利,在系统设计时,应尽可能使得系统中的设备、附件以及主要管路的布置位置相对集中。
2)噪声源独立原则。在系统管路的布置中,应尽量使得系统中的噪声源(包括工作时产生噪声的系统附件)之间相互“独立”,减少与其相关联的管路和设备,避免系统中二次噪声的产生,同时也为在噪声源前后施加主、被动式的隔振创造条件,并为噪声源自身内部的流场优化及减小其前后的液力损失创造条件。
当系统噪声源特性已经明确,或者能够充分估算得到噪声源的声学特性时,应根据噪声源之间声波干涉理论,合理设置噪声源之间的距离,使得噪声源之间互相抑制。
3)分区集中原则。当总体某些功能或布置需求需要将系统分割布置在几个不同的区域时,那每个局部区域也应按照“整体集中原则”和“噪声源独立原则”进行布置,在各个分区之间,应尽可能减少它们通过管路的连接通道及连接管路与舱壁或耐压体的连接通道。
4)设备就近布置原则。设备就近原则要求系统中的噪声源设备布置时应尽可能与总体主要功能单元模块靠近,以减少系统噪声的传递路径,同时也为整体隔振的实施提供便利。
3.4 系统噪声传递通道量化平衡的需求对于船舶系统而言,系统声学设计的目标,就是要系统在满足各方面需求的前提下,使得其运行时的声学性能最优。系统噪声通过设备机脚、管路支撑,管路内的介质以及系统空气噪声等4个途径向外传递。系统噪声传递通道的量化平衡,也就是使得系统在噪声传递的通道上,达到综合平衡。
假设以上4个传递通道引起船舶体振动的噪声级用P1~P4表示,从实船测试情况来看,空气噪声对船舶的乘坐舒适性带来影响,而对船体辐射噪声影响很小,在考虑船舶对海洋的环境影响时,可以将其忽略。
对于除空气噪声外的其他3个传递路径,假设P1是最大项,P3是最小项,P1与其他2项的差值分别为a1、a2。这样,对船舶总体声学性能而言,当a1=P1–P2>6时,P2对系统的影响可以忽略。也就是说,在进行系统设计时,各传递通道的声学量值应尽量控制在6 dB以内,否则,系统的声学性能由最大传递通道确定,那么系统声学设计的任务之一是要释放这条传递通道产生的声学“亮点”。
从我国船舶的测试和分析结果来看,对系统中有管道通海的系统而言,通海口传递通道往往是最大的噪声传递通道,其辐射的水下噪声主要由通海设备管口声压级决定,在系统声学设计中,应重点控制通海管内流体传递通道的影响。
4 结 语本文从船舶系统运行特点出发,利用船舶机械系统总功率与系统辐射噪声的关系,分析得到了影响船舶系统声学性能的关键因素:流量、压力、设备状态,以及附件所在部位的状态。确定了船舶系统声学性能4个方面的表征参数:系统工况调节方式、构造型式、整体布置以及系统噪声传递通道的量化平衡等。通过分别对这4个方面带来的船舶系统声学性能影响因素的分析,给出了它们在船舶系统设计时的指导原则。
| [1] |
International Maritime Organization. MEPC.1/Circ.833, 2014. Guidelines for the reduction of underwater noise from commercial shipping to address adverse impacts marine life[S]. London: 4 Albert Embankment, 2014
|
| [2] |
王艳林, 王自东, 宋卓斐. 潜艇管路系统振动噪声控制技术的现状与发展[J]. 舰船科学技术, 2008, 30(6): 34-38. WANG Yan-lin, WANG Zi-dong, SONG Zhuo-fei. Review of vibration and noise control technology in piping system for submarines[J]. Ship Science and Technology, 2008, 30(6): 34-38. DOI:10.3404/j.issn.1672-7649.2008.06.004 |
| [3] |
廖庆斌, 王晓东, 马士虎. 舰船管路系统振动和噪声源机理分析[J]. 舰船科学技术, 2010, 32(4): 23-27. LIAO Qing-bin, WANG Xiao-dong, MA Shi-hu. Mechanism analysis of noise and vibration sources on naval piping system[J]. Ship Science and Technology, 2010, 32(4): 23-27. DOI:10.3404/j.issn.1672-7649.2010.04.006 |
| [4] |
彼得森, 斯托姆. 船舶噪声控制[M]. 北京: 国防工业出版社. 1983.
|
| [5] |
DONALD R. Mechanics of under water noise[M]. Elsevier Science Ltd, 1976.
|
| [6] |
梁向东. 管路振动噪声对船舶总体声隐身特性的影响[J]. 噪声与振动控制, 2010, 15(4): 127-128, 135. LIANG Xiang-dong. Influence of pipeline's vibration noise on acoustic steal nature of ships[J]. Noise and Vibration Control, 2010, 15(4): 127-128, 135. |
| [7] |
胡泽超, 何琳, 李彦. 隔振器分布对浮筏隔振系统隔振性能的影响[J]. 舰船科学技术, 2016, 38(21): 48-52. HU Ze-chao, HE Lin, LI Yan. The influence of the isolator's distribution on floating raft isolation system's performance[J]. Ship Science and Technology, 2016, 38(21): 48-52. |
| [8] |
刘竹溪, 刘景植. 水泵及水泵站(第四版)[M]. 北京: 中国水利水电出版社, 2009.
|
| [9] |
何元安, 杨德森. 水下结构辐射噪声估算方法实验研究[J]. 船舶力学, 1999, 3(2): 58-62. HE Yuan-an, YANG De-sen. Experiment study of predicting method for radiating noise by submerged vibrating structure[J]. Journal of Ship Mechanics, 1999, 3(2): 58-62. |
 2018, Vol. 40
2018, Vol. 40
