2. 船舶振动噪声重点实验室,湖北 武汉 430033;
3. 海军工程大学 动力工程学院,湖北 武汉 430033
2. National Key Laboratory on Ship Vibration and Noise, Wuhan 430033, China;
3. School of Power Engineering, Naval University of Engineering, Wuhan 430033, China
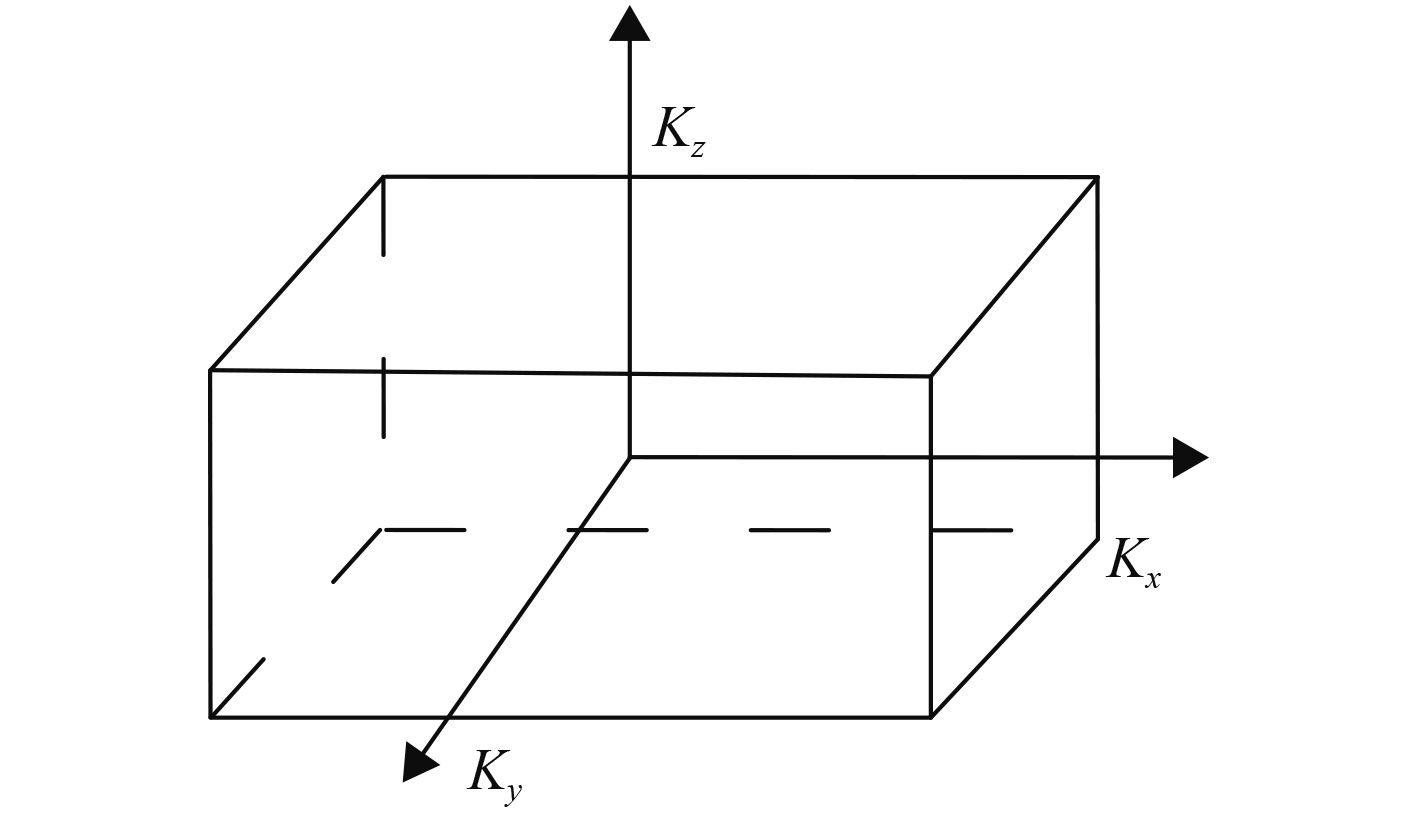
当前,隔振装置技术是控制舰船机械噪声最直接有效的手段,已广泛应用[1]。隔振器选用是隔振装置设计最重要的一个环节[2],目前,隔振器评估主要基于垂向、横向、纵向刚度参数,如图1所示,隔振装置根据实船安装状态,应用所选用隔振器的三向刚度参数开展效果评估。舰船在实际作战航行时,由于外部环境作用或本舰战术机动,不可避免会发生倾斜、摇摆,其弹性安装设备状态会发生变化,使隔振器产生一定角度的偏斜,这将与隔振装置初始设计状态发生偏离,这种偏离有可能恶化舰船辐射噪声。传统理论认为,隔振器不同安装角度下的刚度可通过三向刚度线性叠加获得[3],而实际船用隔振器结构复杂,在不同受力状态下呈现非线性变化。本文选用气囊、钢丝绳和橡胶等三型常用的舰用隔振器,如图2所示,通过设计不同角度安装夹具,对这三型隔振器不同倾斜角度下的刚度变化规律进行试验研究,这对于评估和控制作战航行状态舰船的实际辐射噪声具有重要的指导意义。
|
图 1 隔振器三向刚度 Fig. 1 Stiffness of vibration isolator in X, Y, Z direction |

|
图 2 三型常用的舰用隔振器 Fig. 2 Three common vibration isolators on ship |
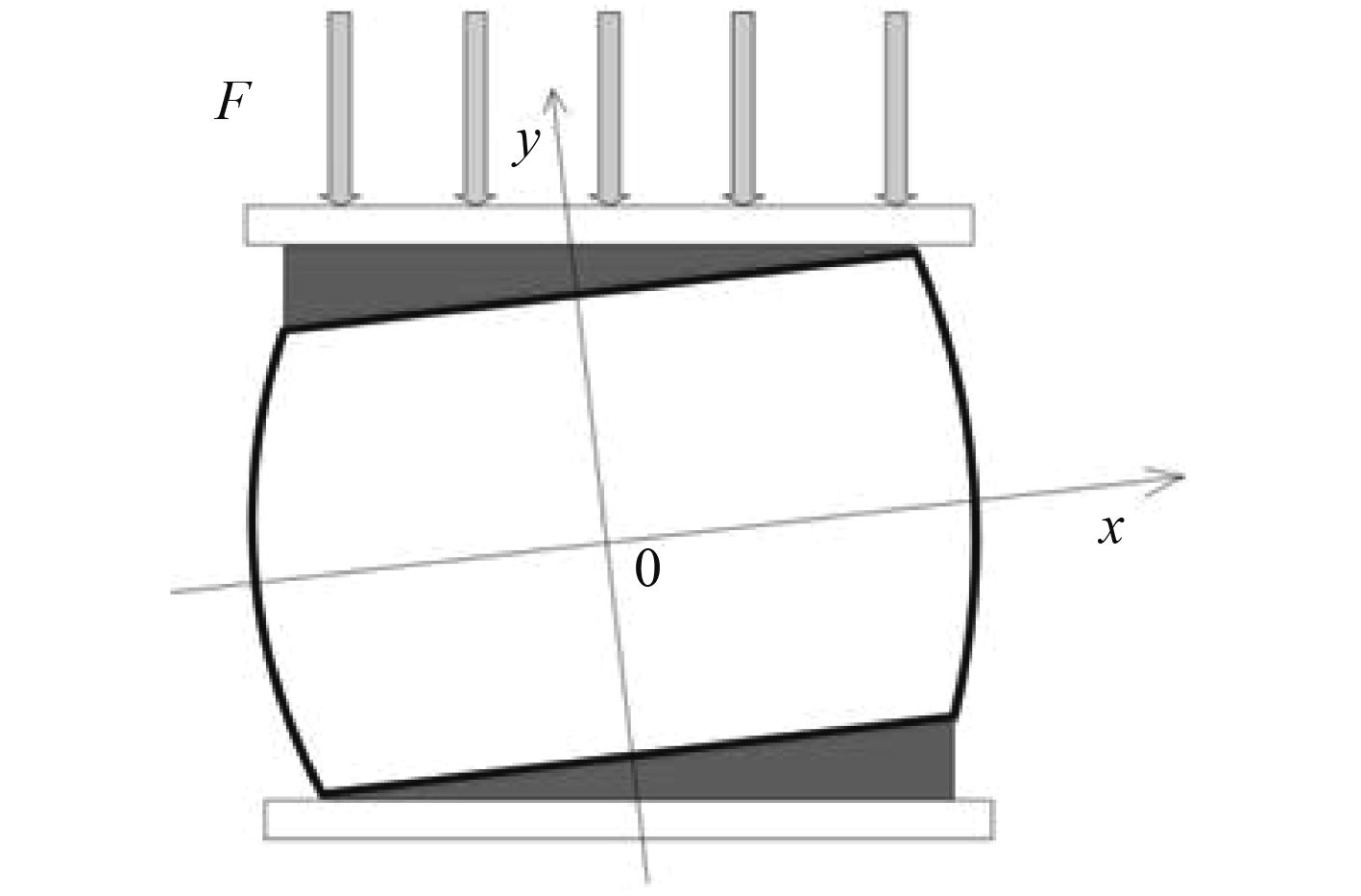
以JYQN-2500型圆形舰用气囊隔振器为例[4],模拟发生倾斜后的情况,如图3所示,图中以气囊中心为坐标原点,平行和垂直与隔振器底板方向为x、y轴建立平面直角坐标系,阴影部分斜角为倾斜角α,激振力F方向与重力方向保持一致。
|
图 3 气囊隔振器发生倾斜后的受力示意图 Fig. 3 Force diagram of acclivitous air spring |
理想情况下,JYQN-2500型隔振气囊水平安装时的垂向、横向静刚度特性可按下式进行分析计算[5]。
垂向刚度特性
| ${K_z} = n\left( {{P_u} + {P_a}} \right)\frac{{S_e^2}}{V} + 2{\text{π}} {P_u}{R_e}A_z^R\text{,}$ | (1) |
式中:在确定静刚度时n=1.0,动刚度时n=1.4;其中,
横向刚度特性
| ${K_{X,{\text{静}}}} = \chi {\left( {\frac{{{R_{k0}}}}{{{\rho _0}}}} \right)^2}{K_{z,{\text{静}}}}\left( {1 - \gamma \Delta _x^m} \right)\text{,}$ | (2) |
横向动刚度
| ${K_{X,{\text{动}}}} = \lambda {K_{X,{\text{静}}}}\text{,}$ | (3) |
式中:
计算时要换算成上述指定的单位。
基础倾斜情况下,倾斜角度α分别取3°,6°,9°,12°,设机械设备质量对气囊作用力为F,沿力F方向位移为L,满足
| $\left\{ {\begin{aligned}& {F = \sqrt {F_x^2 + F_y^2} }\text{,}\\& {L = x\sin \alpha + y\cos \alpha }\text{。}\end{aligned}} \right.$ | (4) |
显然隔振器受力点位移方向和F方向并不一致,F方向上的位移与受力F满足
| $\begin{array}{l}K = F/L\text{,}\\{\text{即}}\;\;\;\;K = 1/\left( {\displaystyle\frac{{{\rm{si}}{{\rm{n}}^2}\alpha }}{{{K_x}}} + \displaystyle\frac{{{\rm{co}}{{\rm{s}}^2}\alpha }}{{{K_y}}}} \right)\text{,}\end{array}$ | (5) |
式中,K为垂向刚度。
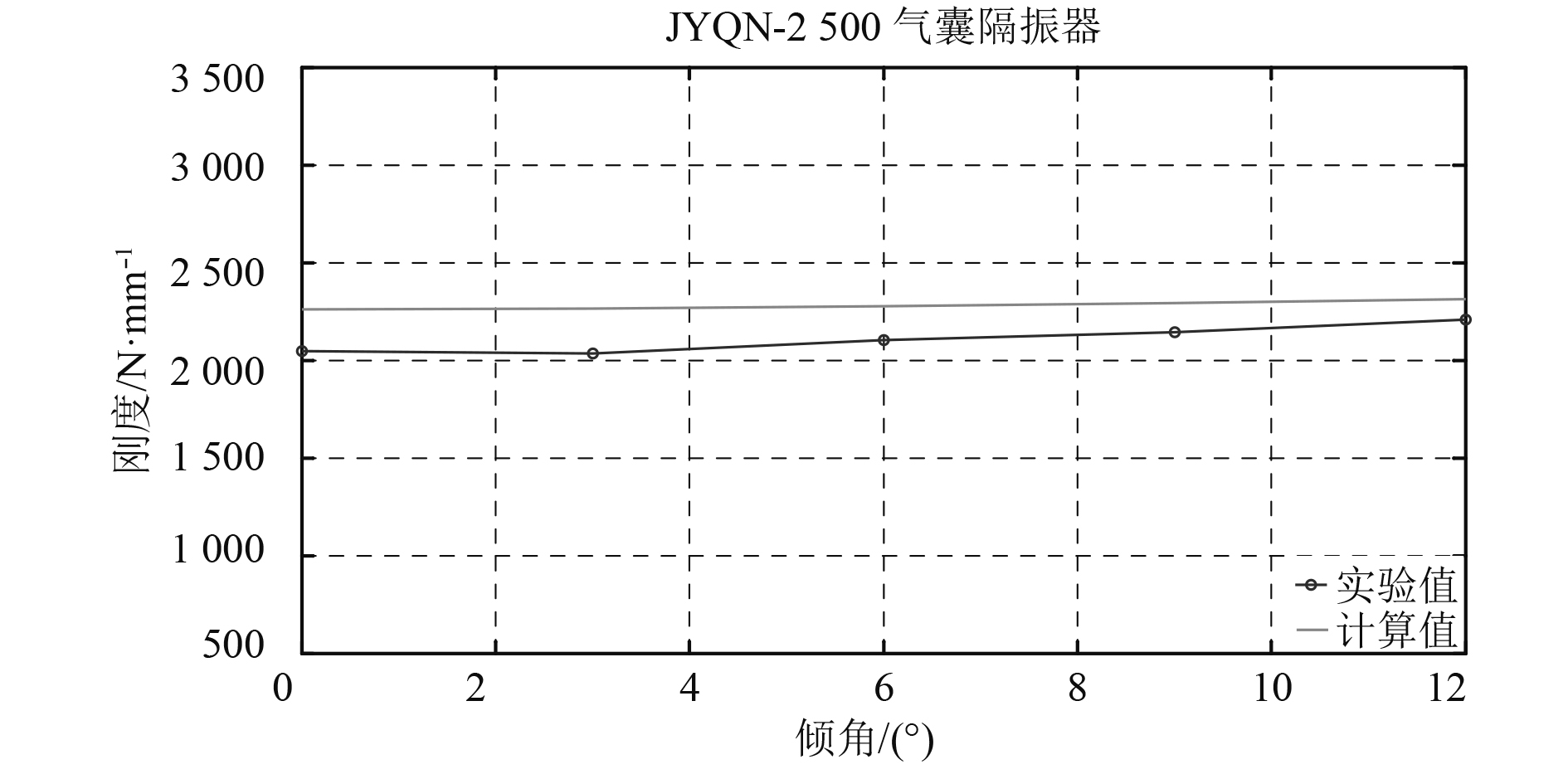
为了方便计算,在计算过程中给定垂直于气囊的y方向位移和斜面倾斜角度,通过垂向和横向负载与位移的对应关系分别计算出横向及垂向位移x,y,再将x,y方向位移在力F方向上投影得到位移L,即隔振器在作用力F下的位移。因垂向和横向动刚度计算时取值不尽相同,因此在理论和试验中均选取平均值进行比较分析(见图8),通过计算得到竖直方向隔振器刚度及其倾斜角度之间的关系如图4所示。
|
图 8 气囊隔振器倾角-平均动刚度曲线 Fig. 8 The curve of angle verse average dynamic stiffness of air spring |
|
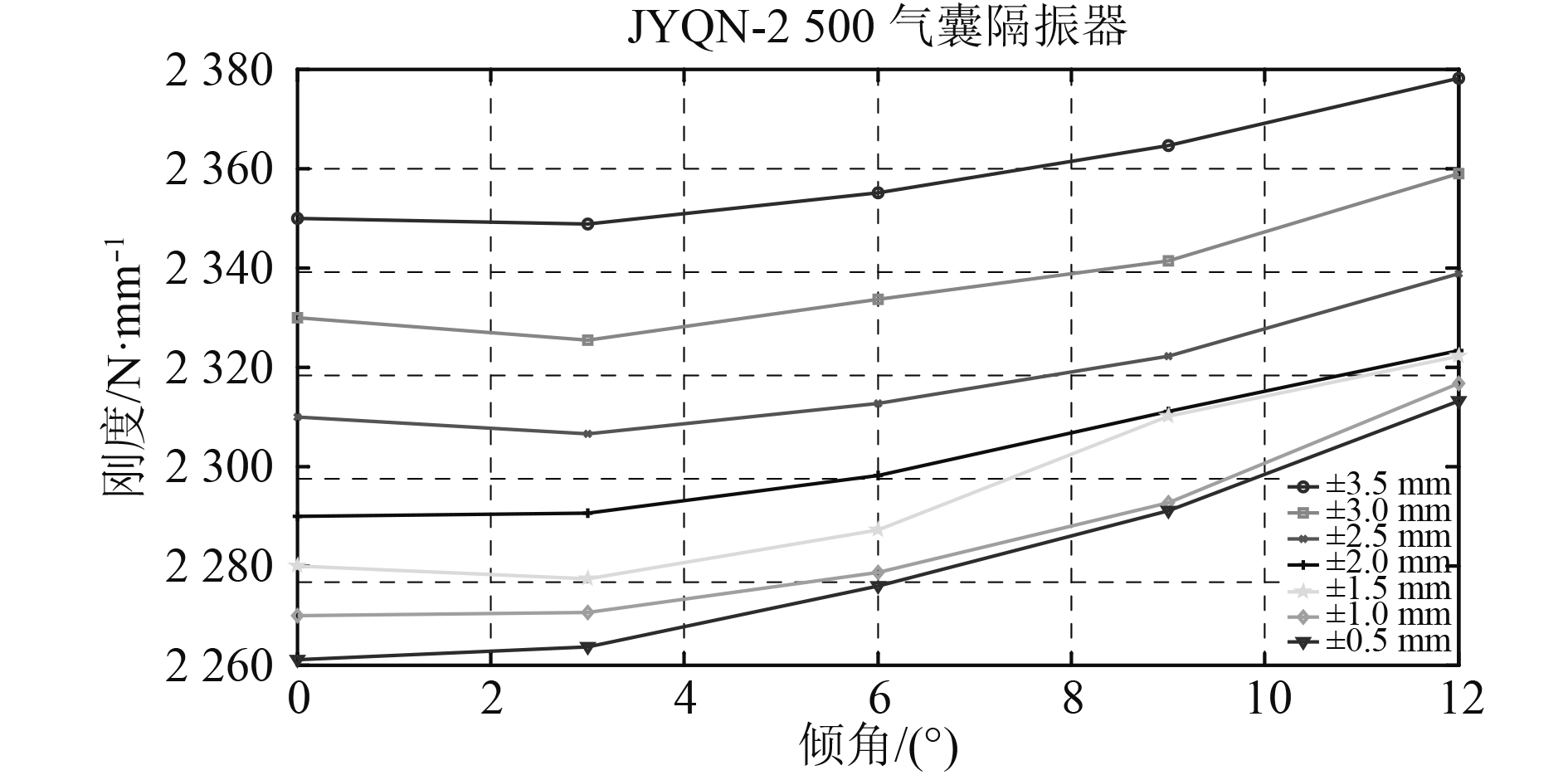
图 4 气囊隔振器不同载荷下倾角-静刚度曲线 Fig. 4 The stiffness of air spring at different angles of inclination |
图中隔振器的不同位移用不同标注的曲线表示,隔振器不同的位移也反映其不同的负载,从图中可以发现:随着倾斜角度的不断增加,隔振器的垂向静刚度会发生一定变化,但变化量不大,刚度最大变化量和0°时相比不超过3%。
2 隔振器刚度性能试验 2.1 试验设计隔振器刚度特性试验按照相关技术标准在10吨级MTS万能试验机上进行,利用加载法测试三型隔振器负载-位移曲线,每次测试分别进行3次,记录选用第3次时的测试数据。根据测试要求,气囊隔振器预定位移分段进行加载(额定载荷下囊内实际压力1.6 Mp),另外两型隔振器直接缓慢加载到额定载荷1.25倍。隔振器所处基础斜面(测试夹具)倾角分别为0°,3°,6°,9°,12°,不同角度的测试夹具依靠螺栓和试验台工装刚性联接。试验根据倾斜角度的不同分为5组,每组试验依次进行完三型不同隔振器的试验后,更换斜面进行下一组试验。所选的三型隔振器分别为:JYQN-2500气囊隔振器、PBE-400橡胶隔振器和HGGS-600钢丝绳隔振器,试验设计如图5所示。

|
图 5 隔振器性能试验台架 Fig. 5 Vibration isolators stiffness test bench |
根据试验数据,整理得到的隔振器倾角-刚度曲线如图6所示。
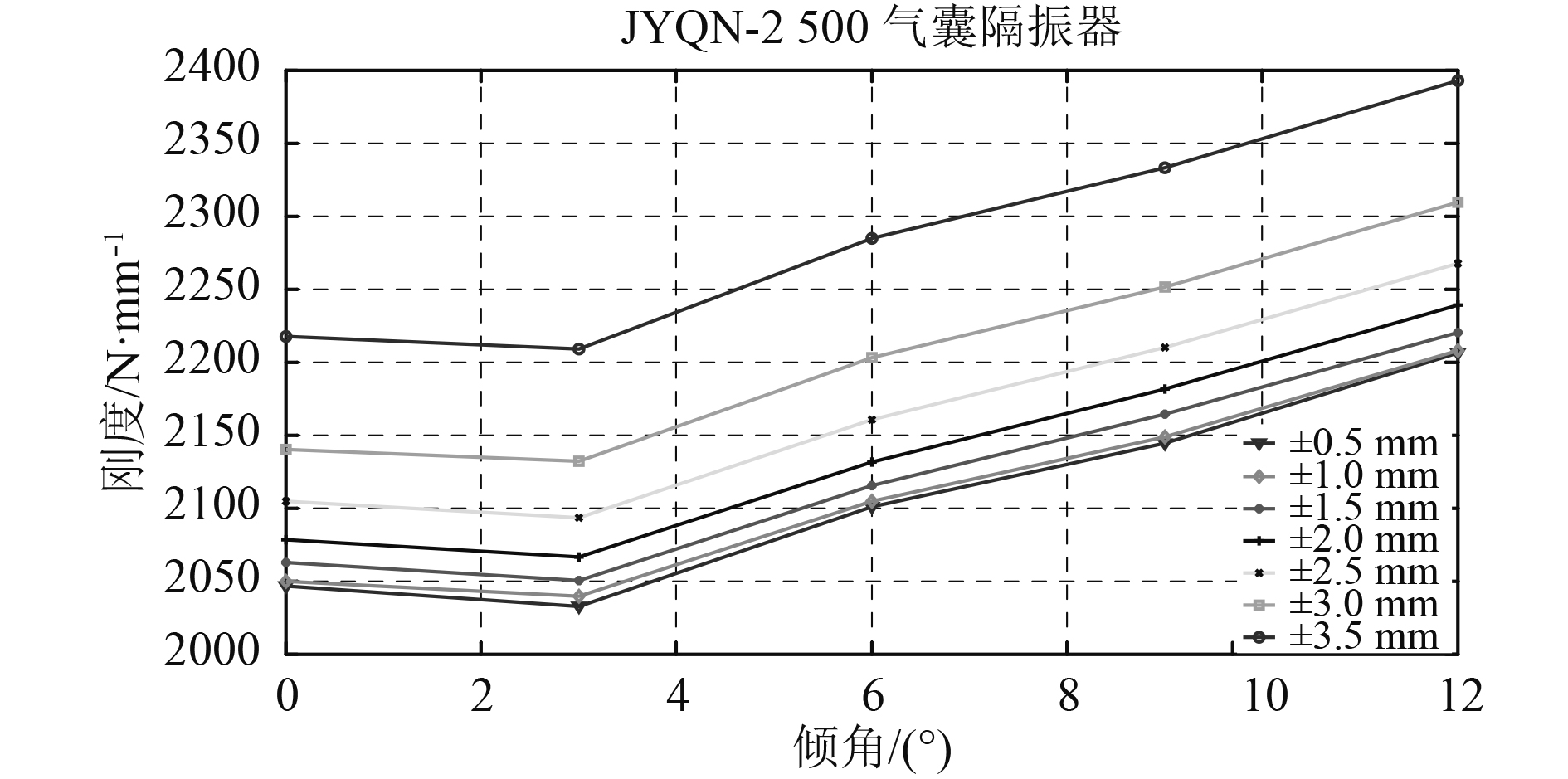
|
图 6 气囊隔振器不同载荷下倾角-静刚度曲线 Fig. 6 The curve of angle verse static stiffness of air spring with different loads |
试验与理论计算得出的曲线图(见图4)变化趋势较为相似,但和理论计算相比,试验中隔振器刚度随倾角增大而增大的量更大。静刚度的理论和试验曲线对比在隔振器的额定载荷下进行(见图7),动刚度的对比则是同一倾角下取平均值(见图8)。从图中可以看出隔振器动、静刚度随隔振器倾斜角度变化的情况类似,都随隔振器倾斜角度的增加先减小后增加,理论值变化幅度小于试验值,动刚度变化幅度大于静刚度。
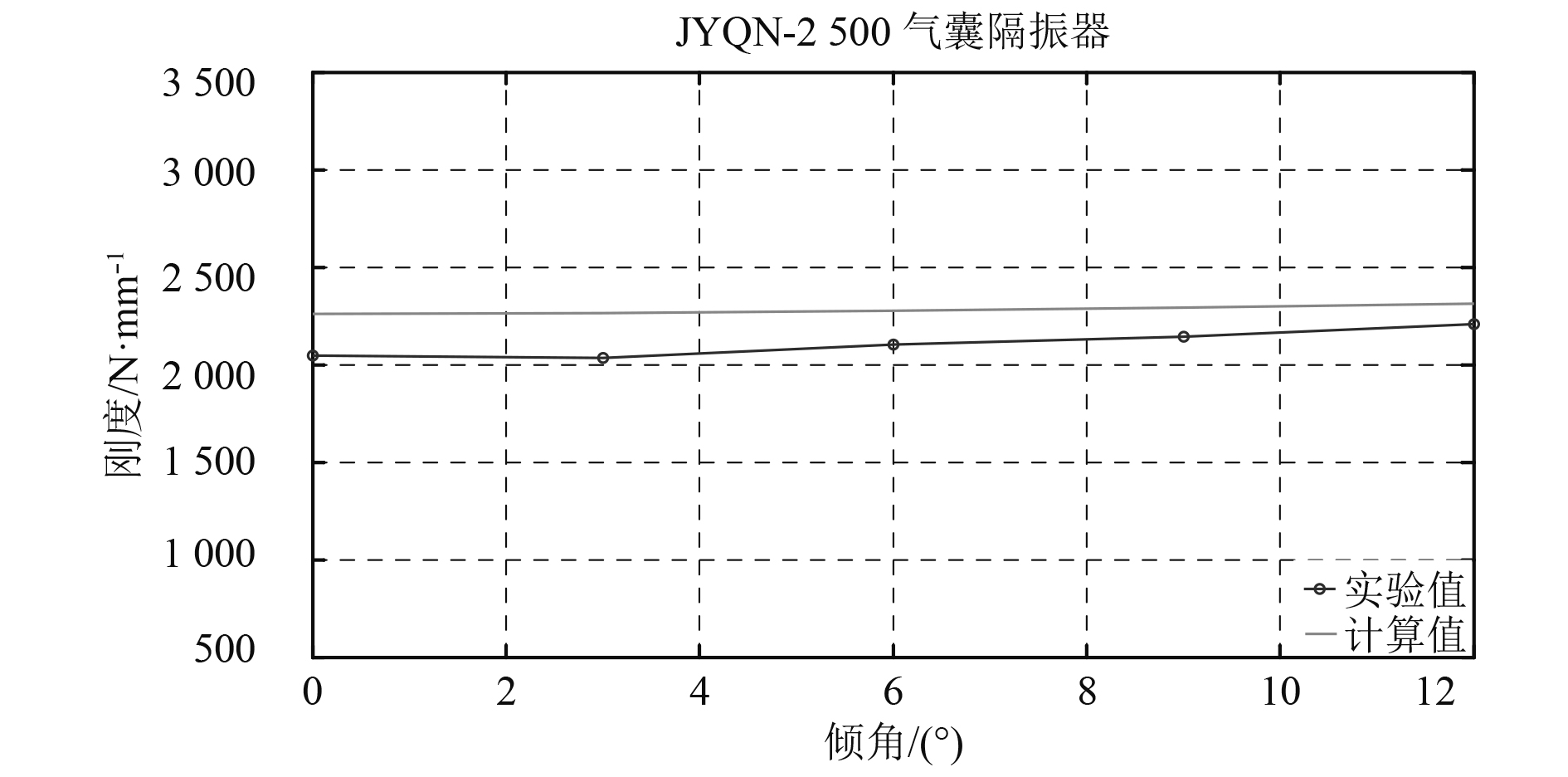
|
图 7 气囊隔振器额定载荷下倾角-静刚度曲线 Fig. 7 The curve of angle verse static stiffness of air spring atstandard load |
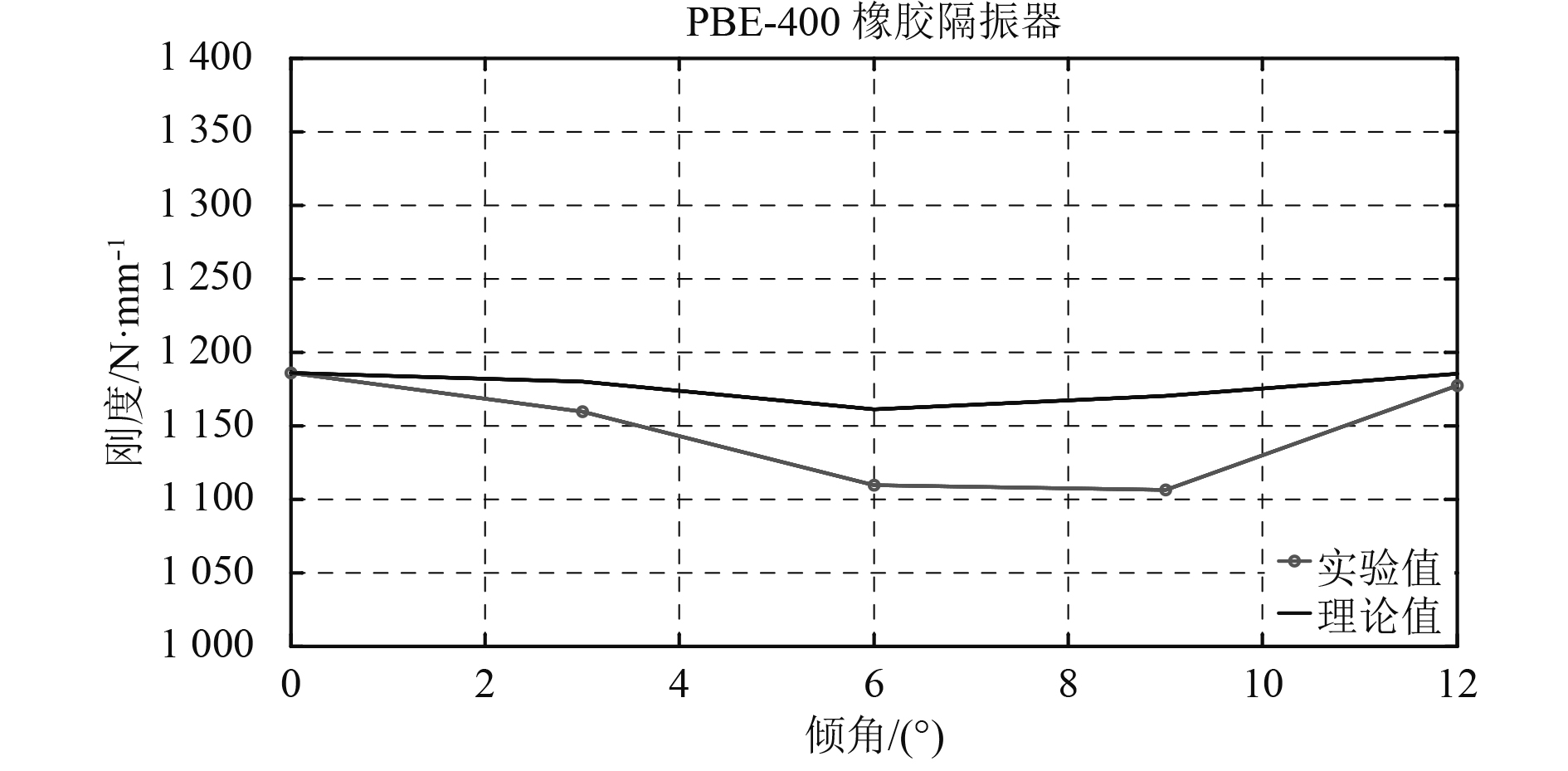
图9~图11 3组曲线图依次为橡胶隔振器倾角-刚度曲线,静、动刚度试验值和理论值对比曲线。从图中试验曲线可以看出,该型橡胶隔振器的静刚度随倾角变化而变化,先随倾角增大而减小,后随倾角增大而增大,倾角为6°~9°时静刚度最小;隔振器静刚度随负载增加(形变增大)而减小,刚度的变化量最大可达水平状态时的17%左右;动刚度在倾斜角度小于9°时变化较小,超过9°后迅速随倾角增加而增加。
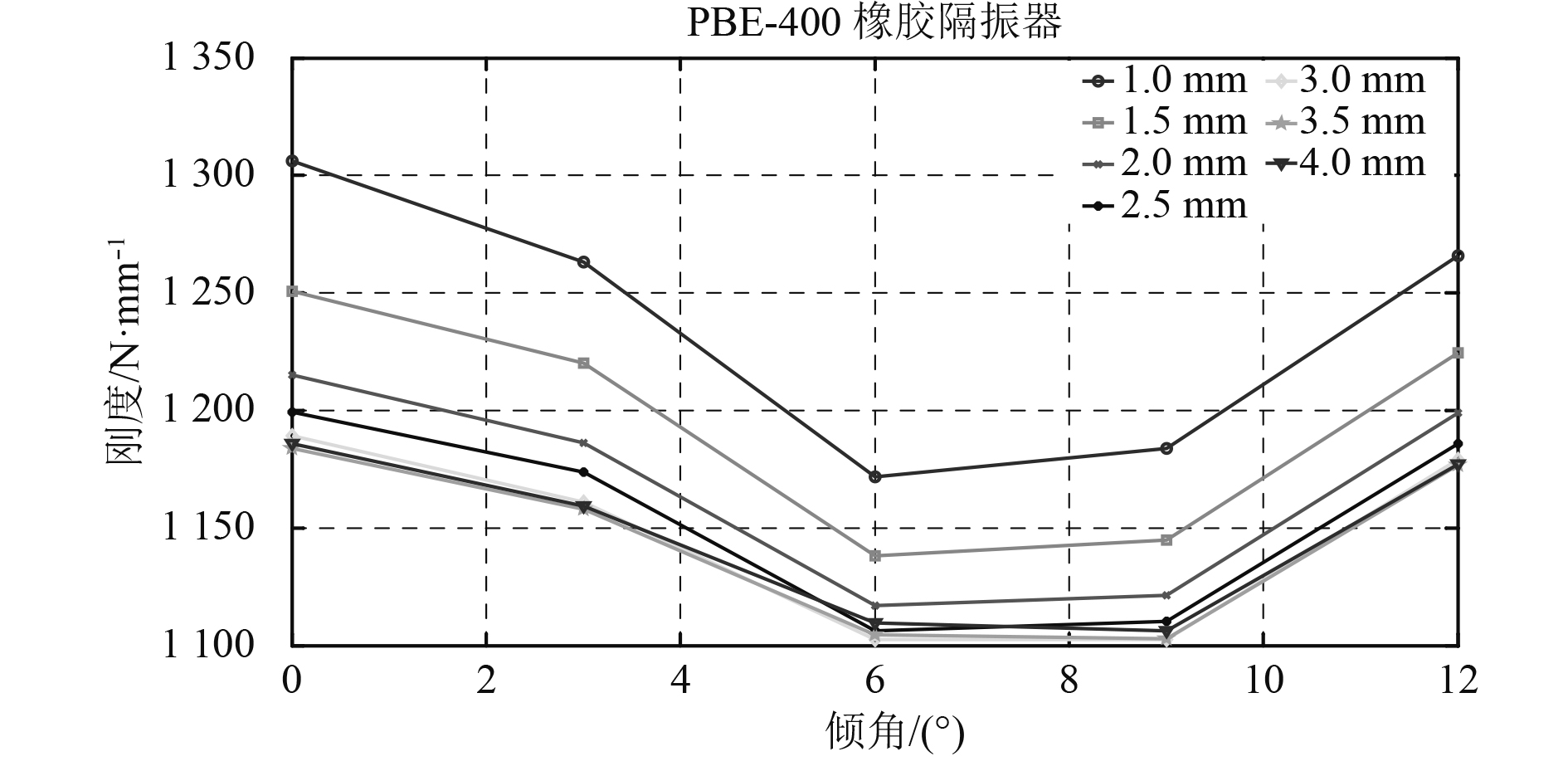
|
图 9 橡胶隔振器不同载荷下倾角-静刚度曲线 Fig. 9 The curve of angle verse static stiffness of rubber absorber with different loads |
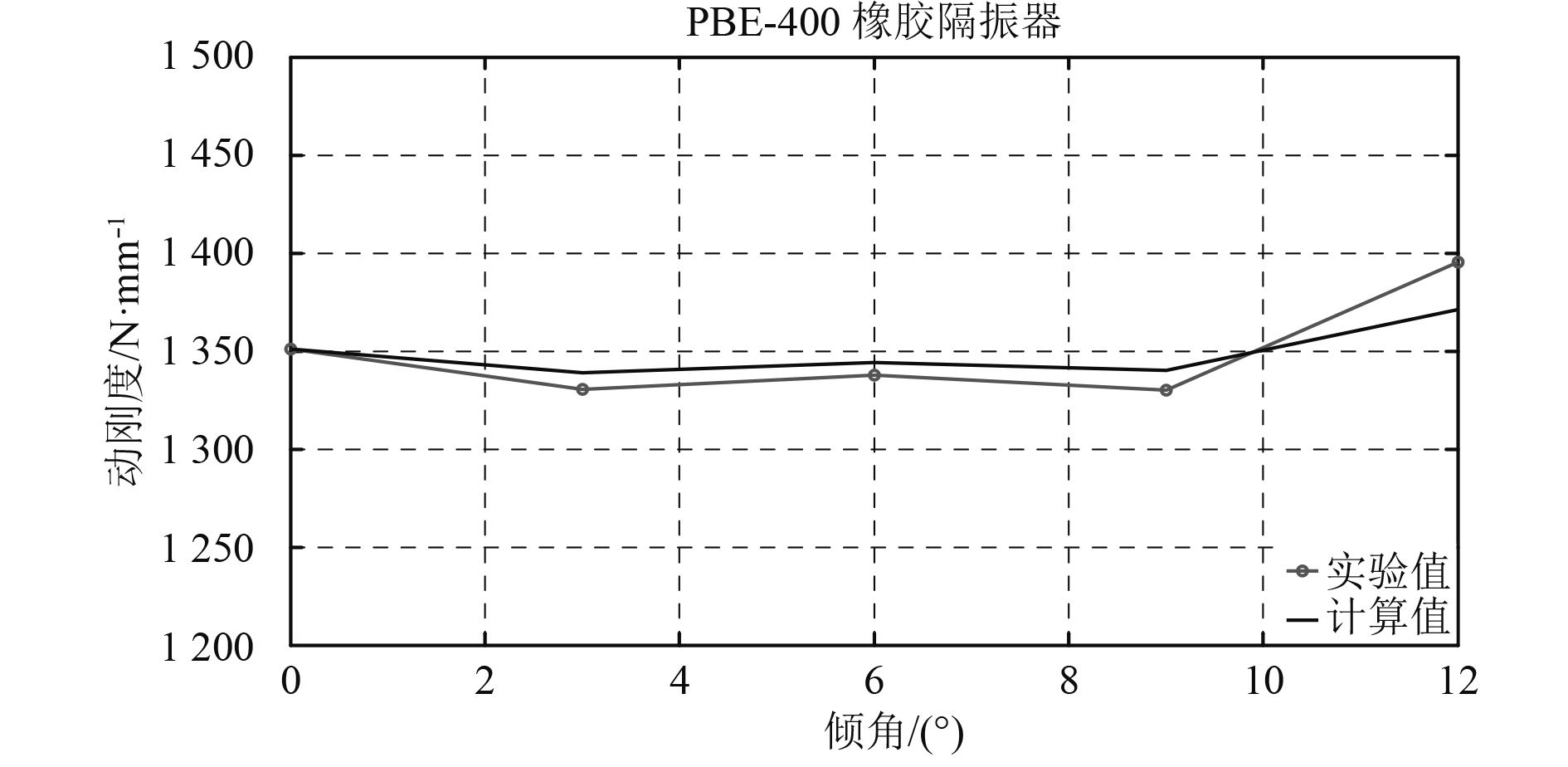
|
图 11 气囊隔振器倾角-平均动刚度曲线 Fig. 11 The curve of angle verse average dynamic stiffness of rubber absorber |
|
图 10 橡胶隔振器额定载荷下倾角-静刚度曲线 Fig. 10 The curve of angle verse static stiffness of rubber absorber at standard load |
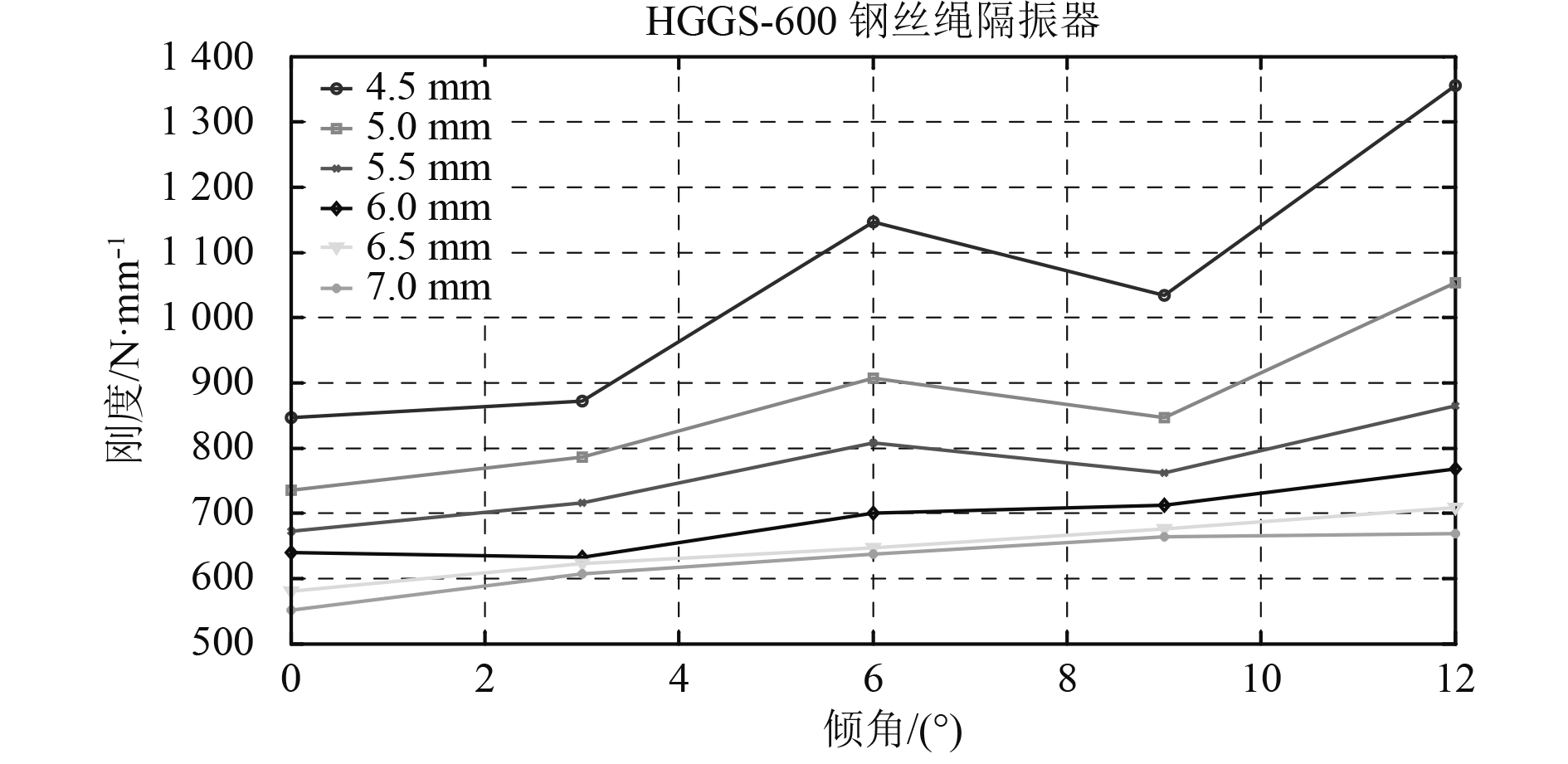
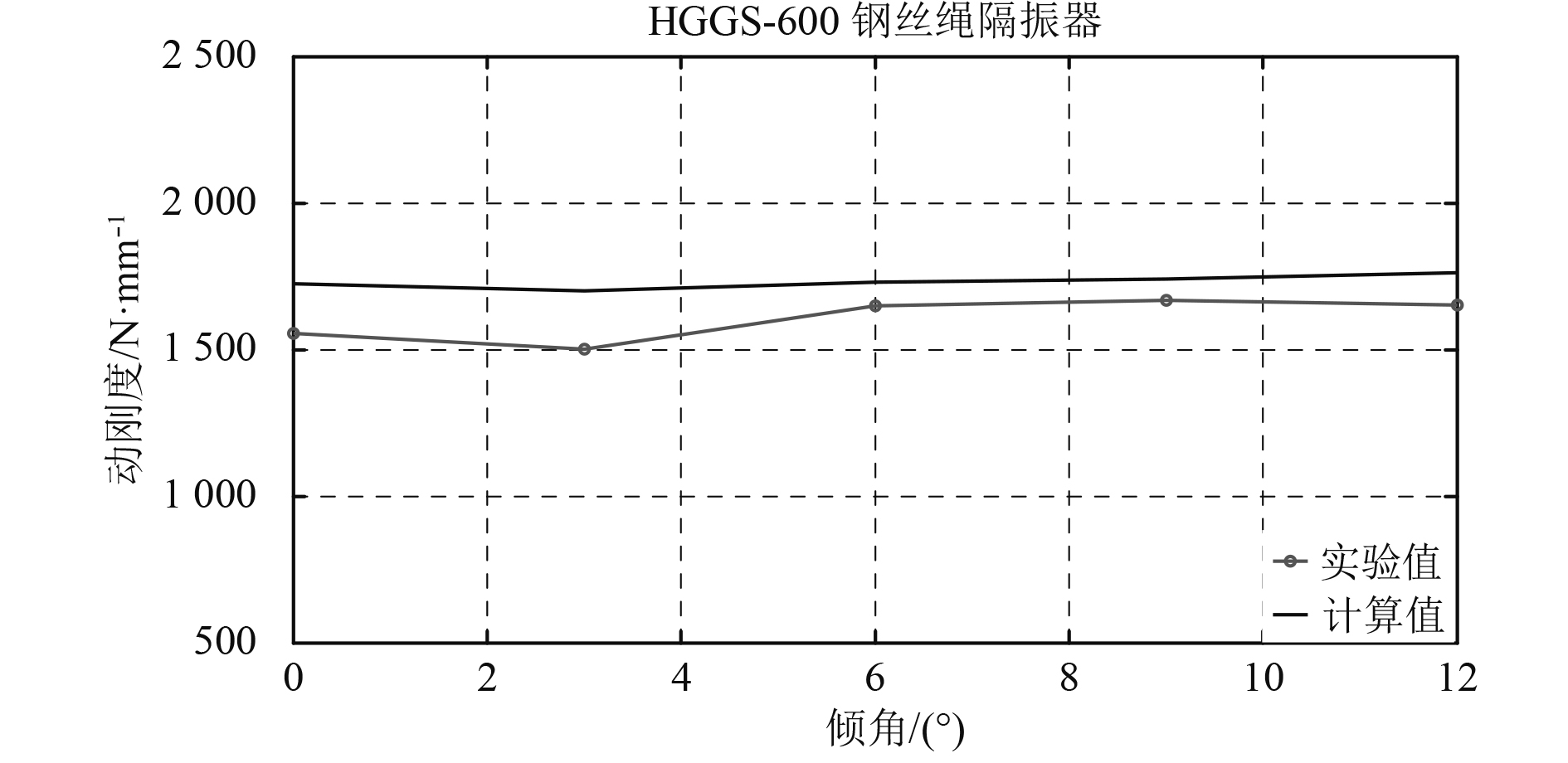
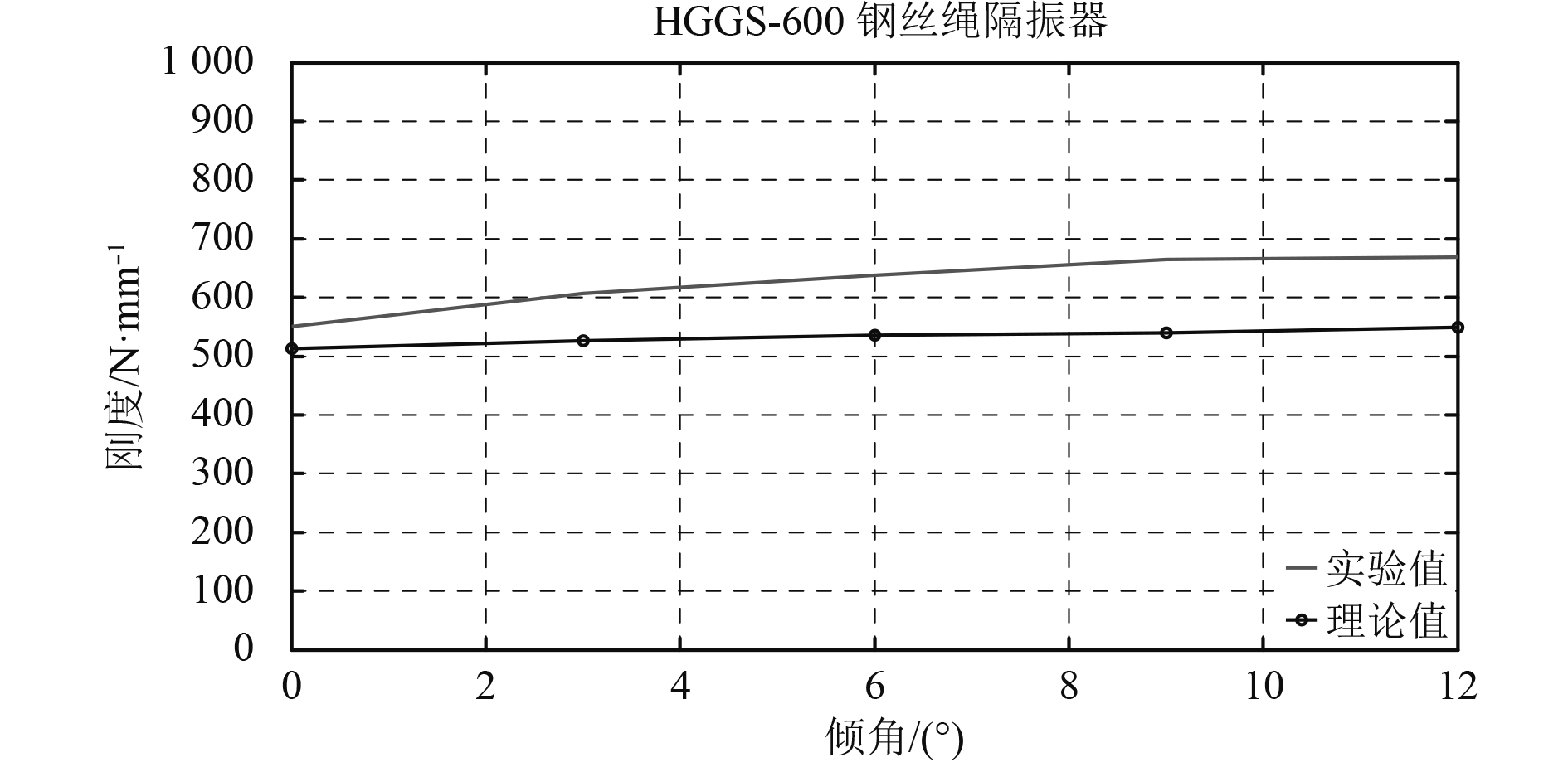
图12~图14 3组曲线图依次为钢丝绳隔振器倾角-刚度曲线,静、动刚度试验值和理论值对比曲线。从试验结果来看:钢丝绳隔振器残余变形较大,偏离额定载荷越多其刚度越不稳定;刚度会随倾角增大而缓慢增大,特别是位移较小时;隔振器在额定负载附近工作时,其刚度特性比较稳定,受倾角影响较小。
|
图 12 钢丝绳振器不同载荷下倾角-静刚度曲线 Fig. 12 The curve of angle verse static stiffness of wire rope isolator with different loads |
|
图 14 钢丝绳隔振器倾角-平均动刚度曲线 Fig. 14 The curve of angle verse average dynamic stiffness ofwire rope isolator |
|
图 13 钢丝绳振器额定载荷下倾角-静刚度曲线 Fig. 13 The curve of angle verse static stiffness of wire rope isolator at standard load |
正常航行时,在垂向以及横向载荷允许范围内,舰船发生一定倾斜时,不同隔振器的刚度特性变化各不相同。总的来看:1)隔振器工作在额定载荷附近时倾斜对刚度影响比较小,偏离额定载荷越多,隔振器刚度受倾斜的影响越大;2)隔振器负载(形变)对其刚度有较大影响,有时甚至会超过隔振器倾斜所造成的影响;3)同一隔振器动、静刚度随隔振器倾斜角度变化而变化的趋势较为一致;4)隔振器传统的三向刚度评估法理论值和试验值在变化趋势上较为一致,但在变化幅度上差异比较明显,因此传统的叠加计算法只能简单评估隔振器发生倾斜时刚度的变化趋势。影响隔振器隔振性能的不单是其刚度[6],下一步可继续深入研究倾斜时隔振器阻尼特性及最终振动传递率(减振效果)和舰船倾斜之间的关系。
| [1] |
张宝成, 徐雪仙. 舰艇水下噪声源贡献的分析[J]. 舰船力学情报, 1994(10): 40-46. |
| [2] |
何琳, 帅长庚. 振动理论与工程应用[M]. 北京: 科学出版社. 2015.
|
| [3] |
王全娟 , 宋孔杰. 斜置式隔振系统的最优设计[J]. 噪声与振动控制, 1992(2):8-12.
|
| [4] |
赵应龙, 吕志强, 何琳. JYQN舰用气囊隔振器研究[J]. 舰船科学技术, 2006, 28(52): 89-92. ZHAO Ying-long, LV Zhi-qiang,HE Lin. Study of pneumatic vibration isolator of type JYQN[J]. Ship Science and Technology, 2006, 28(52): 89-92. |
| [5] |
赵应龙, 何琳, 吕志强, 等. 回转型气囊隔振器的冲击刚到研究[J]. 舰船科学技术, 2006, 28(52): 112-116. |
| [6] |
张猛, 胡毅钧, 钱江等. 刚度对隔振效果的影响[J]. 武汉船舶职业技术学院学报, 2004, 6(2): 25-27. DOI:10.3969/j.issn.1671-8100.2004.02.008 |
 2018, Vol. 40
2018, Vol. 40
