三体船由于具有较大的甲板空间和较佳的稳定性、耐波性、快速性和适航性,在军用和民用船上得到越来越广泛的应用。有关三体船在航行过程中的船型与耐波性关系问题也越来越受到人们的关注。在三体船航行状态下的砰击问题研究目前以模型耐波性试验[1 – 4]和波浪载荷预报结合有限元分析[5 – 8]的手段为主;以数值计算方法分析三体船的砰击问题目前也多限于二维问题[9]。陈康等[10]曾在三体船数值模拟中运用三维模型进行阻力性能计算,但其研究的对象只限于三体船的快速性问题分析,并没有对三体船船体砰击问题予以详细的分析。
船体的砰击过程往往表现出一种很强的非线性水动力作用问题,对于航行中的三体船而言,由于其特殊的结构形式,设计者尤其是船首、连接桥等部分的砰击载荷往往会予以特别的关注。因此无论是从三体船船体结构强度分析的角度,还是航行过程中操作安全的角度来看,更深入地了解与分析三体船船体结构在航行过程中由于砰击所引起的结构动力载荷的力学机理,观察砰击所引起的兴波现象,对于设计、研发一种性能优良的三体船具有重要的科学意义与工程分析价值。
本文采用计算流体力学方法,应用商业软件Fluent对一艘三体船在一定航速下船体结构的砰击问题进行三维数值模拟。计算中,采用动网格技术来对三体船航行过程中的垂荡运动时所引起的砰击及兴波问题进行数值模拟,在此基础上,对航行过程中的垂荡三体船导致的船体结构砰击压力、兴波与流场变化进行观察与分析。
1 计算模型与数值方法 1.1 计算模型由于本文涉及的雷诺数较大,因此数值模拟里采用湍流模型中最典型也是目前使用最广泛的标准k-ε模型。标准k-ε模型是在连续性方程
| $\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}} = 0\text{,} $ | (1) |
以及动量方程
| $\frac{{\partial u}}{{\partial t}} \!+ \! u\frac{{\partial u}}{{\partial x}} \!+\! v\frac{{\partial u}}{{\partial y}}\! +\! w\frac{{\partial u}}{{\partial z}}\! = \! - \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} \!+\! \mu \left( {\frac{{{\partial ^2}u}}{{\partial {x^2}}}\! +\! \frac{{{\partial ^2}u}}{{\partial {y^2}}}\! +\! \frac{{{\partial ^2}u}}{{\partial {z^2}}}} \right)\text{,} $ | (2) |
| $\frac{{\partial v}}{{\partial t}} \!+\! u\frac{{\partial v}}{{\partial x}}\! +\! v\frac{{\partial v}}{{\partial y}} \!+ \! w\frac{{\partial v}}{{\partial z}} \!= \! - \frac{1}{\rho }\frac{{\partial p}}{{\partial y}}\! +\! \mu \left( {\frac{{{\partial ^2}v}}{{\partial {x^2}}} \!+\! \frac{{{\partial ^2}v}}{{\partial {y^2}}}\! +\! \frac{{{\partial ^2}v}}{{\partial {z^2}}}} \right)\text{,} $ | (3) |
| $\begin{split}\frac{{\partial w}}{{\partial t}} \!+\! u\frac{{\partial w}}{{\partial x}} \!+ \! v\frac{{\partial w}}{{\partial y}} \!+ \! w\frac{{\partial w}}{{\partial z}} \!=& \! - \frac{1}{\rho }\frac{{\partial p}}{{\partial z}} \!+\\&\! \mu \left( {\frac{{{\partial ^2}w}}{{\partial {x^2}}}\! + \! \frac{{{\partial ^2}w}}{{\partial {y^2}}}\! +\! \frac{{{\partial ^2}w}}{{\partial {z^2}}}} \right)\text{,} \end{split}$ | (4) |
的基础上再加入关于湍动能k和湍流耗散率ε的方程所组成的。在应对本课题中的不可压流动等条件下,关于k和ε的方程简化如下:
| $\frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho k{u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} - \rho \varepsilon \text{,} $ | (5) |
| $\begin{split}\frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} \! \!+\! \frac{{\partial \left( {\rho \varepsilon {u_i}} \right)}}{{\partial {x_i}}} \!\!= & \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu +\! \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] +\\ & \! \frac{{{C_{1\varepsilon }}\varepsilon }}{k}{G_k}\! -\! {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k}\text{,} \end{split}$ | (6) |
其中,ρ是流体密度,Gk是由于平均速度梯度引起的湍动能k的产生项,C1ε和C2ε是经验常数,μt是湍流粘性系数,σk和σε分别是湍动能k和耗散率ε对应的普朗特数。根据实验验证,模型常数C1ε,C2ε,σk和σε的取值分别为1.44,1.92,1.0和1.3。
1.2 算法本文采用的是PISO算法。PISO算法全称压力的隐式算子分割算法,起初是针对非稳态可压流动的无迭代计算所建立的一种压力速度计算程序。它的精度依赖于所选取的时间步长,在预测修正过程中,压力修正与动量方程计算所达到的精度分别是3(Δt3)和4(Δt4)的量级。使用越小的时间步长,可取得越高的计算精度。PISO算法是基于瞬态问题所建立的,它在收敛性方面表现的更好,效率也较高。
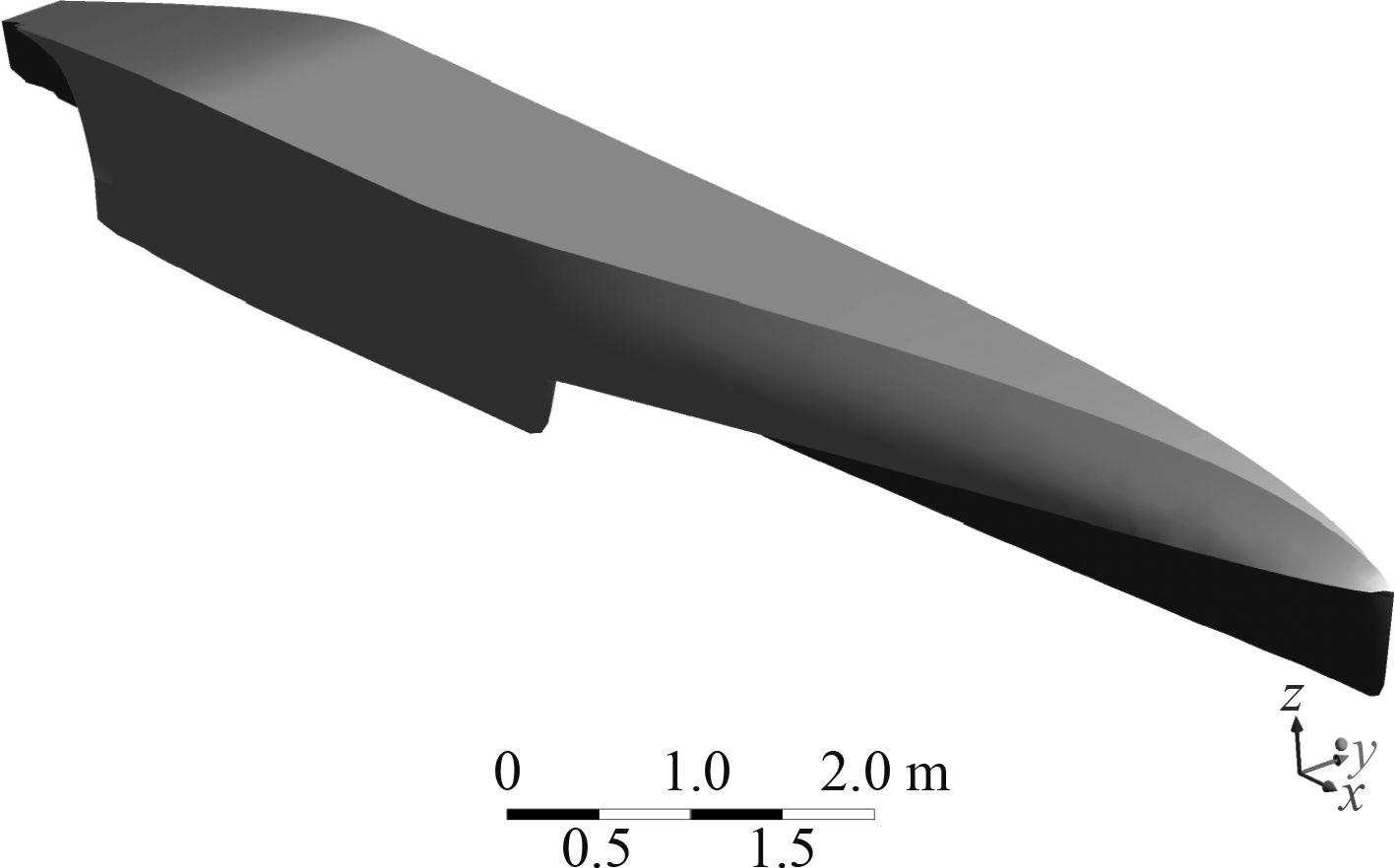
1.3 模型计算域计算中,船体几何模型采用实际船型尺寸1/10的比例来构建,表1给出的是船体计算几何模型的主尺度。由于三体船的上层建筑不在本文的研究范围之内,因此为了提高建模以及计算效率,对三体船的上层建筑部分进行适当的简化。同时因为所计算的三体船具有结构对称的特点,在计算中将三体船计算几何模型沿船长纵剖面方向截取其右舷的一半船体作为计算对象,以达到节省网格数、减少数值运算时间的目的。图1所显示的是本文所采用的三体船右舷部分的计算几何模型。本文所采用的计算域如图2所示,计算域为长×宽×高=84 m×6.5 m×5.8 m的长方体,其中长方体前面是流场的入口,后面是流场的出口,左侧面和上下两面是固壁面,右侧面是对称面,船体几何模型沿船长纵剖面处于该计算与右侧对称面上。
|
图 1 三体船船体模型 Fig. 1 Geometrical trimaran model |

|
图 2 计算域示意图 Fig. 2 Sketch of computational domain |
|
|
表 1 船体几何模型主尺度 Tab.1 Main dimensions of geometrical trimaran model |
本文模型网格的划分使用ICEM CFD软件。由于模型的流场较大,为了适当的加快运算速度的同时也能应对船体附近变化较为复杂的流场,本文将对流场壁面附近的网格进行适当的放大,对船体表面及附近的网格进行加密布置。
1.5 边界条件本文针对砰击模型计算域中不同类型的边界分别进行定义,其具体边界条件的设置如表1所示。由于本文主要研究的三体船砰击模型具有一定航速,因此这里通过设置入口的边界条件使流场经过三体船模型来模拟航行中的三体船;而其他大部分边界没有特殊要求的情况下均可设置为无滑移壁面,便于加快数值计算的速度。
而对于空气与水交界面的自由表面将采用VOF法处理。Volume of Fluid是流体体积函数,该函数定义为流场中的每个网格里目标流体的体积与网格体积的比值。只要知道了每个网格单元的流体体积,就能够对运动界面进行追踪,进而很好地捕捉好自由表面的存在。采用VOF法将可以帮助我们更好更直观地理解三体船砰击模性流场兴波的特点。表2给出了本文所使用的计算域边界条件的坐标与边界条件设置。
|
|
表 2 计算域边界条件 Tab.2 Boundary conditions of computational domain |
为了能较好地体现船体在垂直方向上的反复振荡,本文采用了动网格的方法进行模拟。三体船船体表面的边界将定义为不发生形变的刚体结构,并将所编写的运动方程导入到其中以实现对船体垂荡的模拟;对于对称面,由于与船体表面边界相连的缘故,网格将随之发生变化,因此将会被定义为变形面;而其他远场边界则定义为固壁面。由于船体砰击运动较为剧烈,因此动网格将使用Remeshing(网格重构)法来进行。
2 数值模拟与结果分析本文采用以上所述的计算模型和数值方法,运用流体力学软件Fluent对特定航速下的三体船砰击问题进行数值模拟,并对其在考虑了船体表面动边界和水面自由表面边界条件下引起的主体船体、侧体船体和连接桥部分的砰击压力分布以及船体周边的流场变化进行观察与分析。由于本文主要是研究船体的砰击带来的动力响应,因此在这里只会着重关注砰击入水这一段时间的过程,而在本文中这段时间大概是在1.5~2.4 s之间。
2.1 主体船首砰击压力特征主体船体在入水砰击过程中船首部分分别在1.6 s,1.8 s,2 s,2.2 s和2.4 s所受的压力分布云图如图3所示。

|
图 3 主体船首砰击压力云图 Fig. 3 Slamming pressure nephograms of main bow |
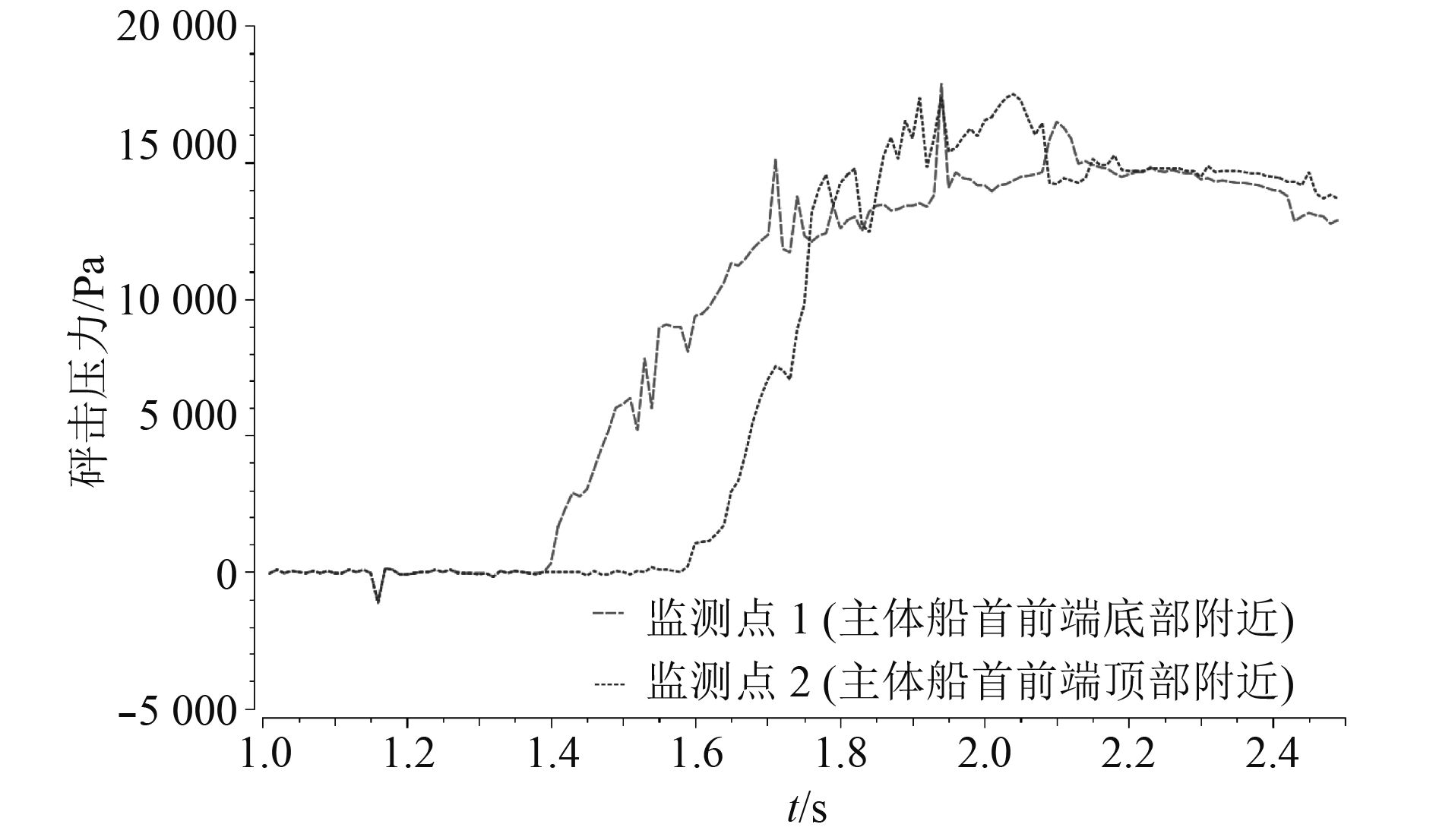
由图可知,主体船首前部承受主要的砰击压力,其次是船首底部,船首侧体部分受到的影响较小。而在主体船首的前端部分,由于前端向上倾斜,其法向方向与船体结合砰击运动后和速度的方向相近,因此整个前端的受力分布较为均匀,没有出现较大的应力集中现象。为了可以更好地了解船首前端部分砰击压力随砰击时间变化的特征,本文在前端长度三等分处取了2个监测点(分别靠近主体船首前端底部附近和顶部附近)来观察其砰击压力变化,得到的曲线如图4所示。
|
图 4 船首前端监测点砰击压力曲线图 Fig. 4 Slamming pressure graph of front main bow |
由图可知,更靠近船首底部的监测点(曲线1)率先在1.4 s左右有砰击压力产生,而曲线2的砰击压力发生在1.6 s左右;虽然压力没有同步产生,但是2个监测点从砰击压力出现到1.75 s前都表现出压力急剧增大的变化特征,随后压力增长速度趋于平缓,在1.9 s左右达到压力峰值之后趋于稳定,并且在2.2~2.5 s之间砰击压力开始缓慢减小;同时由于受到砰击所造成的流场兴波的变化影响,靠近前端顶部的监测点(曲线2)在压力峰值过后所表现的砰击压力变化波动要更强烈一些。因此可以看作这2个监测点所受砰击压力的大小基本一致,与之前的描述相符合。但值得注意的是相对于船首前端底部,其顶部砰击压力达到峰值的时间较短,压力变化率大,对船首材料承载能力要求相对要高一些。
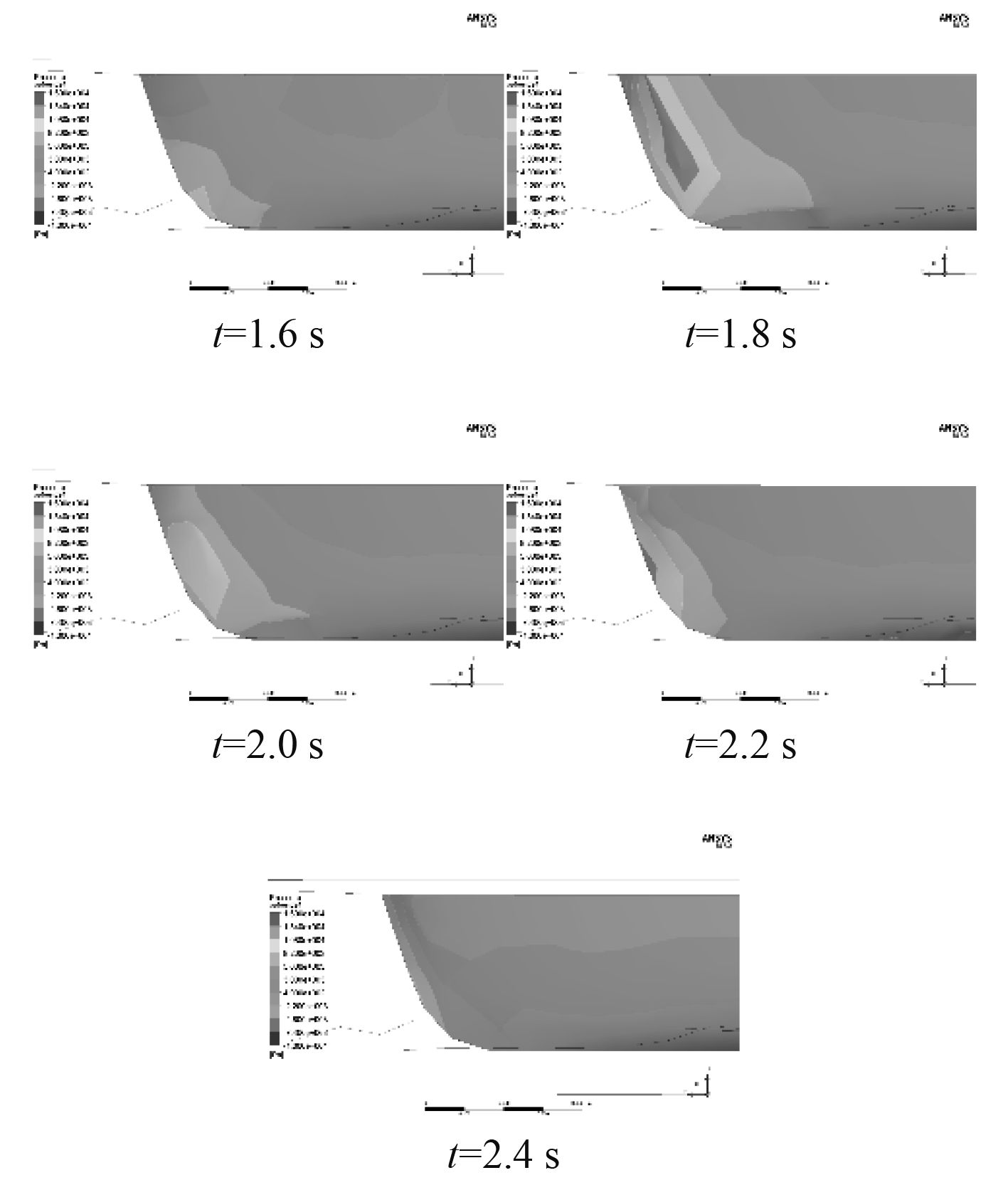
2.2 侧体船首砰击压力特征在砰击过程的1.6 s,1.8 s,2 s,2.2 s和2.4 s,侧体船首外侧和内侧的砰击压力分布云图如图5和图6所示。

|
图 5 侧体船首外侧砰击压力云图 Fig. 5 Slamming pressure nephograms of side bow outboard |
|
图 6 侧体船首内侧砰击压力云图 Fig. 6 Slamming pressure nephograms of side bow inboard |
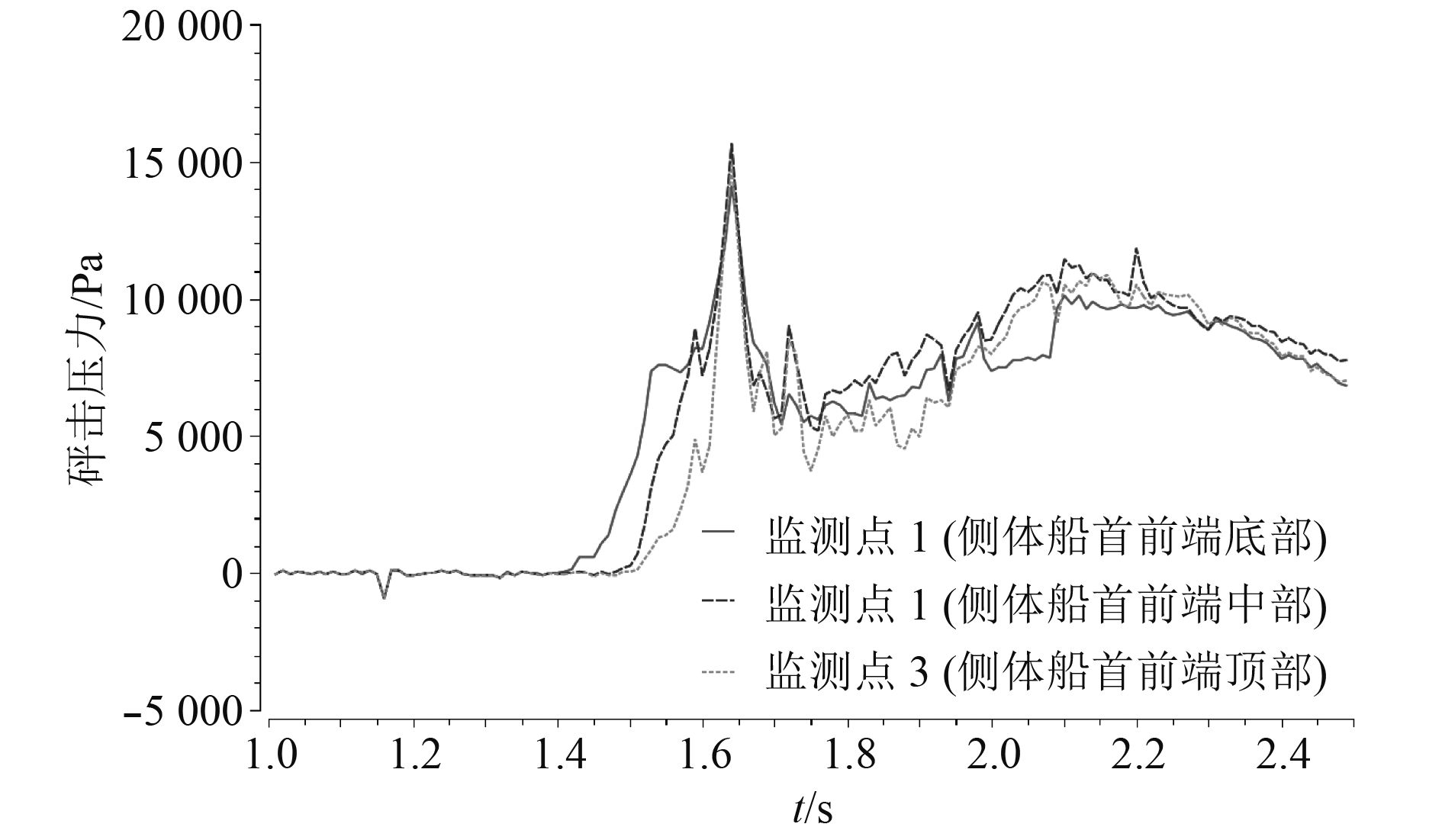
与主体船首相似,在图5和图6中可以观察到侧体船首主要承受砰击压力的部位同样也是前端,其次是底部。但是对比图7和图8可以清晰地观察到侧体船首内侧与外侧受砰击压力影响的情况是有差别的,对于船首的外侧,砰击开始时所受压力较低,随着砰击运动的进行,压力逐渐增大,前端部分出现一个逐渐后移的较大压力集中区域;对于船首的内侧,在砰击开始时就受到了较大的砰击压力,随着砰击运动的进行会逐渐减小,而在砰击初期阶段前端部分就出现一个较大压力的集中区域并且逐渐向船首移动直至消失。结合流场分析,在侧体船首内外两侧相反的压力变化表现中可以判断,受到主体船首砰击入水过程中排挤开的来流的影响,侧体船首内侧首先受到来流的砰击,产生了一个较大压力的集中区域,随后侧体船首开始排开这些来流,压力集中区域开始向船首以及外侧转移。为了进一步验证这个结论,类似地,本文在侧体船首前端四等分点处取了3个监测点(分别位于侧体船首前端的底部、中部和顶部)并绘制其砰击压力随砰击时间变化的曲线如图7所示。
|
图 7 侧体船首前端监测点砰击压力曲线图 Fig. 7 Slamming pressure graph of front side bow |
在曲线图中可以观察到3个监测点的曲线走向基本一致,都呈现出2个主要的起伏趋势。在1.4 s过后侧体船首开始砰击入水,船首压力急剧增大,在1.65 s左右达到压力峰值;但随后就受到了排挤开来的来流的影响,船首内侧的前端部分成了迎接来流的主要区域,船首前端压力随之急剧下降;而在1.8~2.2 s之间侧体船首开始排挤开来流,船首压力开始缓慢增大,压力集中区域向船首前端移动;在2.2~2.4 s之间船首压力又开始缓慢减小,压力集中区域向船首外侧移动。因此侧体船首在船体砰击过程中会受到2次来自来流的砰击,出现2个压力峰值,而第2次可以体现出侧体船首的压力集中区域迁移现象。
综上所述,该船型的侧体船体在一定航速下的砰击入水,船首会产生2次砰击现象并且伴随着船体内侧前端部分出现较大压力的集中区域,其压力峰值大小与船首砰击压力峰值相当。这些出现压力集中区域的船体部分值得引起重视。
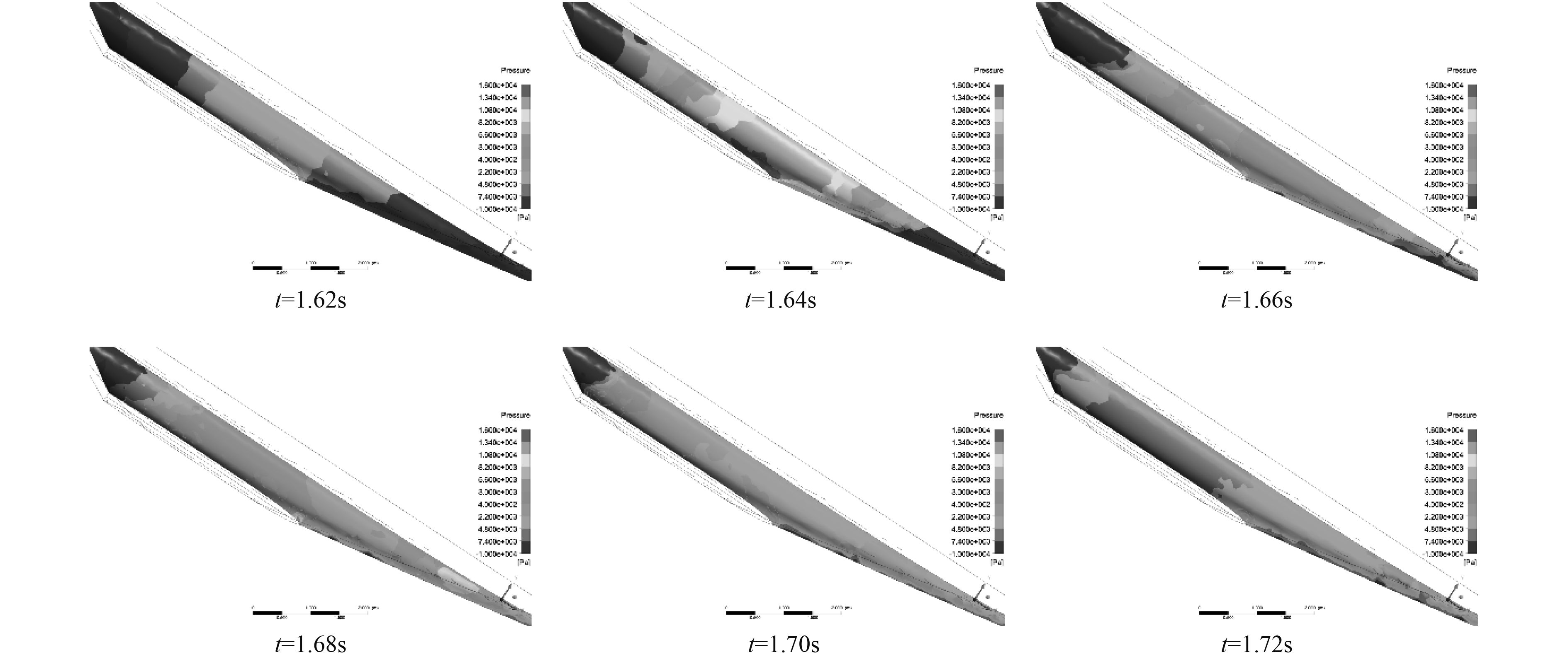
2.3 连接桥砰击压力特征在三体船船体中,虽然连接桥的位置偏高,但是在本算例这样的砰击状况下连接桥底部仍然会受到水流的冲击和挤压。这段砰击的时间大概发生在1.62~1.72 s之间,在这段时间内连接桥底部所受砰击压力分布云图(俯视图)如图8所示,其中右下角方向是船首方向。
|
图 8 连接桥底部砰击压力云图 Fig. 8 Slamming pressure nephograms of bottom cross-structure |
观察图中连接桥底部压力云图的变化可以发现随着砰击运动的进行,连接桥中部会首先受到砰击的影响从而产生砰击压力,同时连接桥靠近侧体船体的部分由于更接近水面的缘故,要更早发生砰击并产生较大的砰击压力,在1.64 s的时候达到了压力峰值。随后压力分布区域开始向船首和船尾方向扩散,压力也逐渐变小。最后除了受兴波影响形成的部分压力集中区域,连接桥整体的压力较小且分布均匀。
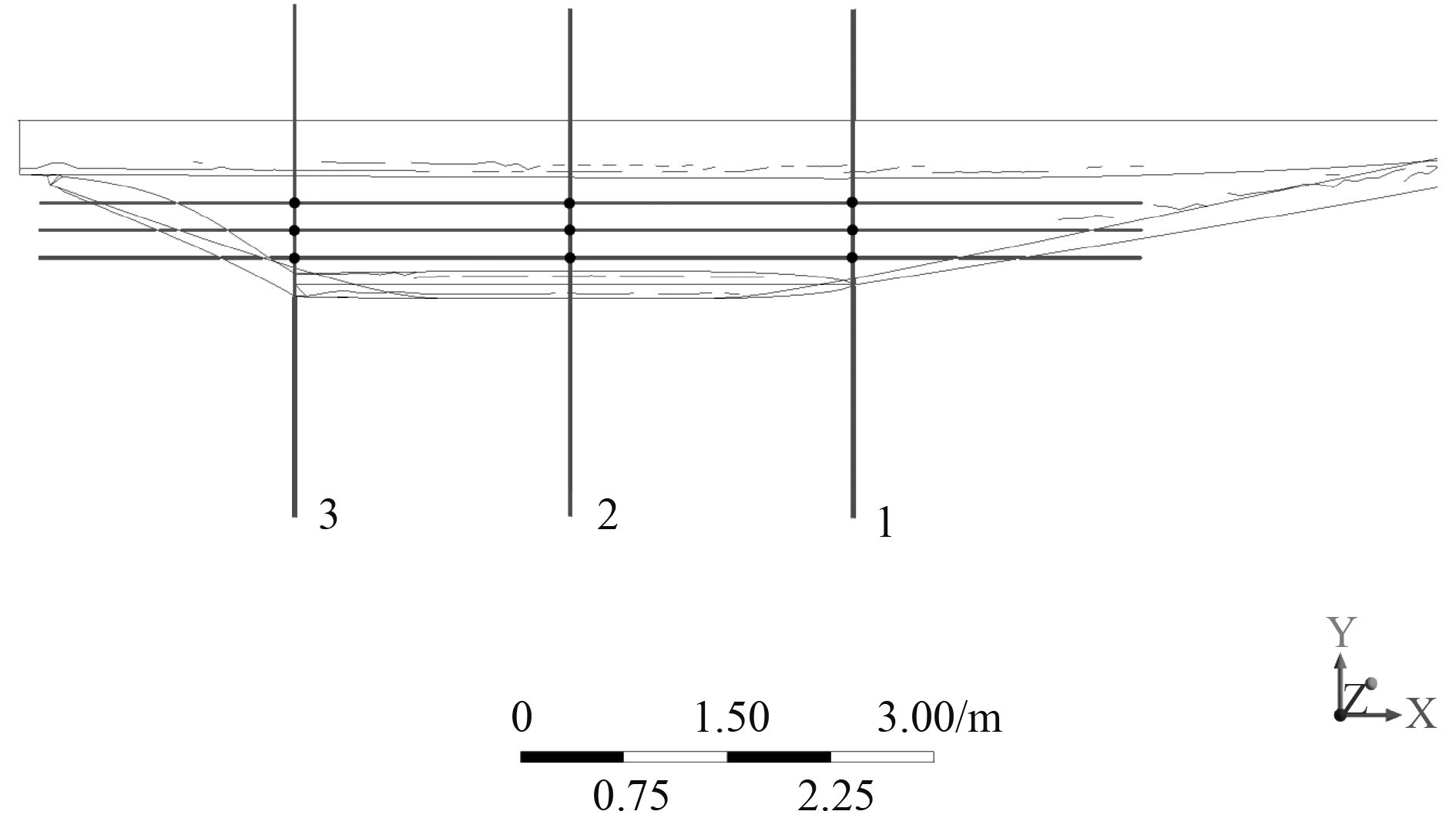
为了更好地观察连接桥底部砰击压力随砰击时间的变化,本文如图9所示截取了连接桥底部3个横截面(纵向方向)并在每个横截面上取3个监测点来描绘曲线图。其中图中右方是船首方向。
|
图 9 监测点分布示意图 Fig. 9 Distribution sketch of monitoring points |
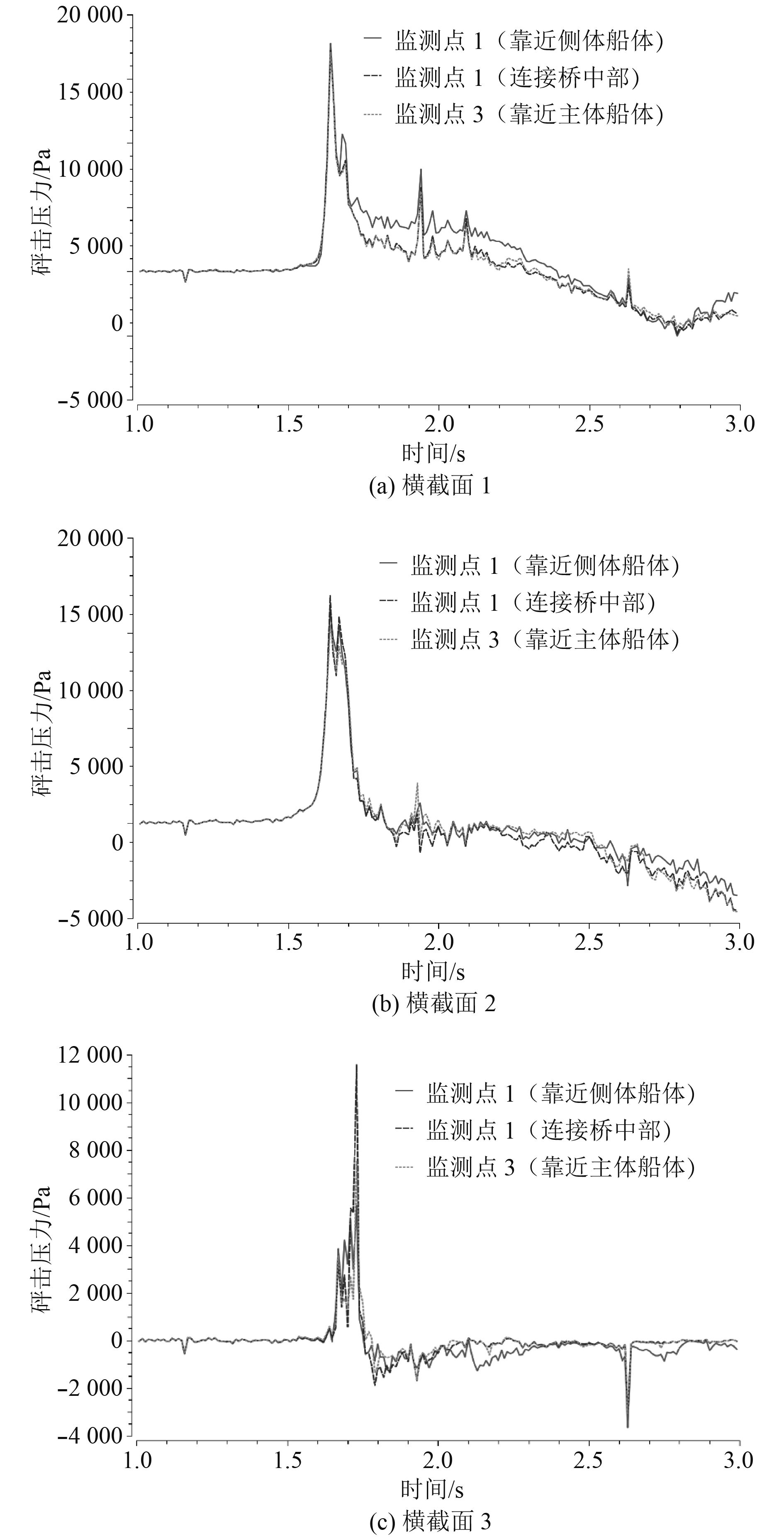
图9中横截面1、横截面2和横截面3中监测点砰击压力随时间变化的曲线图如图10所示。在横截面1中,3个监测点的砰击压力都在1.6 s连接桥砰击水面之后开始产生并且急剧增大,在1.64 s左右达到压力峰值,随后开始急剧减小;在1.7 s又突然增大产生另一个较小的压力峰值之后再次开始减小,受流场产生的兴波影响,压力曲线出现波动;第3个压力峰值产生在1.93 s左右,在该时刻受到主体船首排开的来流砰击在侧体船首的影响,监测点上的砰击压力迅速增大随后迅速减小到原来的数值;最后随着砰击入水过程的完成,压力逐渐下降,在船体向上运动的时候还会出现一定的负压。另一方面,在图中可以观察到曲线2和曲线3的压力变化趋势基本一致,而监测点位置更靠近侧体船体的曲线1在第一次压力峰值过后其压力数值均比曲线2和曲线3高,说明该横截面上靠近侧体船体的区域所承受的砰击压力要更大一些。
|
图 10 监测点砰击压力曲线图 Fig. 10 Slamming pressure graphs of monitoring points |
在横截面2中,由于连接桥的中部先与水面发生砰击,因此监测点在1.5 s后就开始有砰击压力的产生,在1.65 s左右压力急剧增大形成第1个压力峰值;随后在1.7 s再次形成第2个较小的压力峰值,并随后压力迅速下降,在1.8 s左右压力值降低到零值附近;在1.93 s附近产生第3个不太明显的压力峰值;同时3个位置的监测点的曲线基本一致,说明连接桥中段受到主体船首排开来流的影响较小,这部分的砰击压力分布较为均匀。
在横截面3中,由于处在连接桥尾部,监测点在大概1.65 s左右才开始监测到砰击压力的产生,而且在1.65~1.73 s之间,由于受到连接桥中段压力区域的扩散,该部分的压力曲线波动较大;在1.73 s左右达到压力峰值,随后迅速减小到0值;最后砰击压力不再增加,甚至出现负压的情况。而在砰击压力产生的1.65~1.73 s之间3个监测点的压力曲线走向有差别,体现出同一横截面内砰击压力分布不均匀的现象,说明在靠近船尾部分的连接桥底部压力变化波动较大且分布不均。
对比3个横截面砰击压力变化的特征可以判断:连接桥的砰击压力产生区域始于中段且随后扩散到前后两端;对于主体船首排开的来流,受到影响最大的是连接桥的前段,其次是中段,两者都在迎接来流第2次砰击中呈现出一定的压力变化波动而且出现额外且较小的压力峰值,而连接桥的后段则几乎不受影响;连接桥底部所有监测点的砰击压力变化率都比较高,对船体材料的承载能力要求要更高。
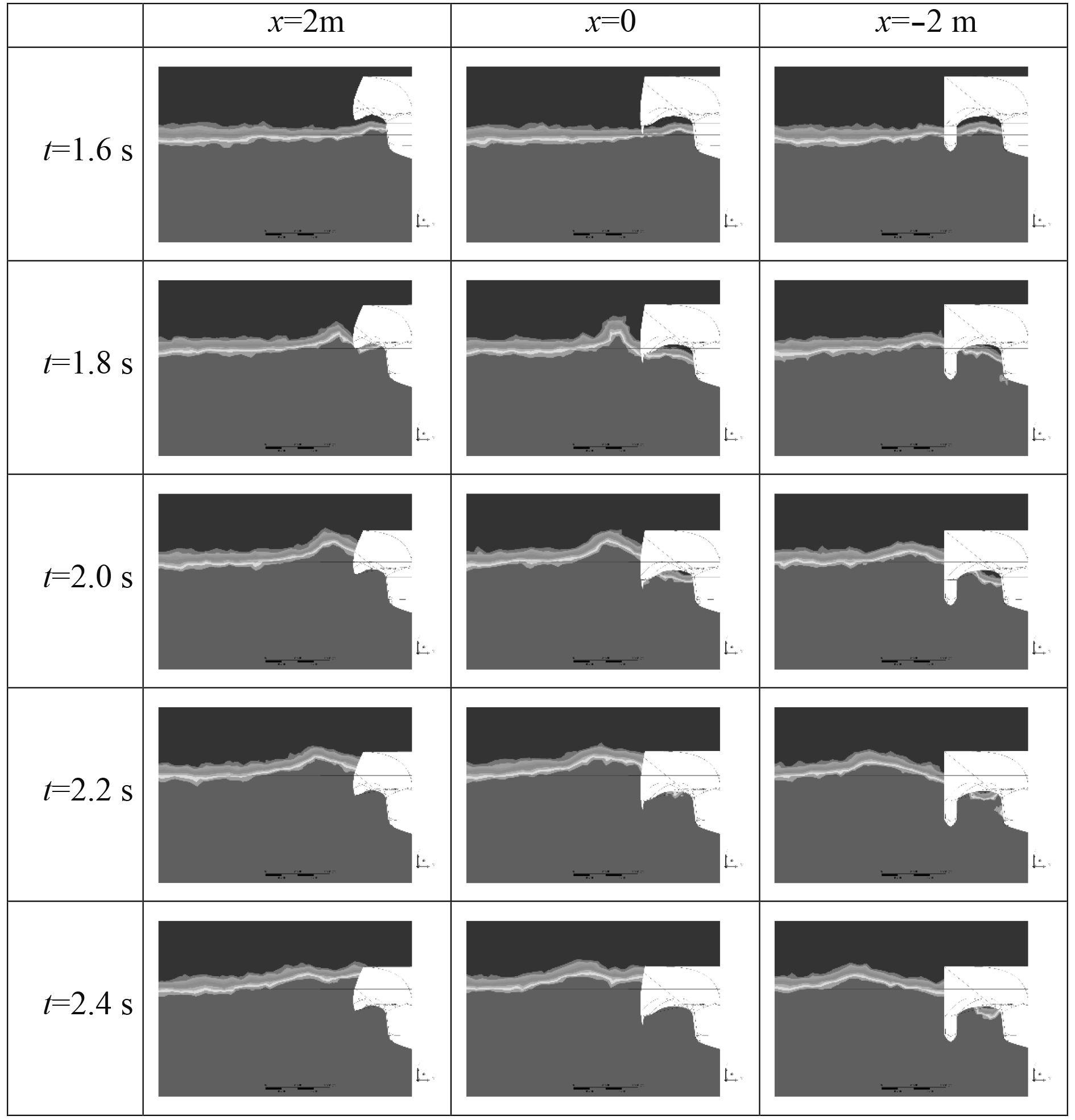
2.4 流场兴波变化特征在三体船砰击入水的过程中,船体周围的流场兴波主要发生在主体船首附近和连接桥底。本节将截取砰击模型的横剖面来观察船体砰击入水引起的流场兴波变化,其中3个横剖面分别为主体船首附近(x=2 m)、侧体船首及连接桥前端(x=0)和连接桥中段(x=–2 m),随时间变化的两相流云图如图11所示。
|
图 11 横剖面两相流云图变化 Fig. 11 Two-phase nephograms variation of cross sections |
由图可知,在船体砰击入水的过程中,靠近主体船首的流场产生了一个明显向外扩散的兴波,且在砰击运动完成后不久也消失在较远的流场中;在靠近侧体船首及连接桥前端的流场,砰击运动在侧体船体外侧形成一个兴波,且砰击运动完成后也没有消散,同时在连接桥底部也形成了一个由来不及逃逸出去的气体与紊乱的兴波组成的气囊区域,但是由于受到前方来流的影响,气囊在砰击尚未完成时(2.2 s)就开始逐渐消失;而在连接桥中段的流场,侧体船体外侧产生的兴波不消散和连接桥底部的气囊现象都体现的更明显,在图中可以观察到在整个砰击阶段连接桥底部的气囊一直存在,有逐渐变小的趋势且位置逐渐向主体船体方向靠拢。
3 结 语本文通过对该船型的三体船船体砰击入水的三维数值模拟得到了主体船体、侧体船体和连接桥一系列的砰击压力数据和流场变化图,通过观察和分析得到以下结论:
1)在三体船以该航速砰击入水的过程中,船体有3个部分产生的砰击压力峰值最大,一个位于主体船首前端,在与来流的砰击中能受到接近18 000 Pa的砰击压力,其中越靠近船首上方压力的变化率越高;第2个位于侧体船首前端,该区域在与水面砰击的过程中压力峰值能达到15 000 Pa,且相似地,越靠近船首上方压力变化率越高;第3个位于连接桥前端靠近侧体船体的区域,该区域与水面正面砰击所产生的压力峰值接近18 000 Pa。
2)在该航速下的砰击入水过程中,侧体船首内侧以及连接桥靠近侧体船首的区域都会受到由于主体船体排开的来流造成的二次砰击的影响。在侧体船首内侧与来流发生二次砰击时,其压力峰值能达到10 000 Pa,同时会扰乱连接桥底部的压力分布,引起底部尤其是前中部分的压力波动;来流也会对连接桥底部在第一次砰击过程中形成的气囊结构造成冲击,使得气囊结构向后向主体船体方向移动,令连接桥底部的压力分布情况更加复杂。
3)连接桥底部在砰击入水过程中,砰击压力分布较广且普遍压力数值较高,部分监测点的压力峰值甚至达到了18 000 Pa,短时间内大规模的砰击压力急剧变化说明该区域的压力变化率要远高于主体和侧体船首,对于连接桥底部船体材料承载能力的要求要更高。
综上所述,该船型的三体船中,这些受到砰击压力影响较大的部位,尤其是连接桥这种连接主体船体和侧体船体的重要结构,其材料的承载能力必须要引起重视,这些部位的牢固程度将很大程度上决定三体船在航行过程中的安全程度。要得到更多关于这些部位的砰击参数用于船体材料的检验,需要做更多不同条件下砰击入水的数值模拟,而本文仅是完成了一个算例用以抛砖引玉,希望可以为以后三体船的砰击研究带来参考。
| [1] |
何术龙, 李百齐, 程明道, 等. 三体船船型分析及兴波干扰的模型试验研究[J]. 水动力学研究与进展, 2006, 21(1): 122-129. HE Shu-long, LI Bai-qi, CHENG Ming-dao, et al. Hull form study and wave-making model test for a trimaran ship[J]. Journal of Hydrodynamics, 2006, 21(1): 122-129. DOI:10.3969/j.issn.1000-4874.2006.01.019 |
| [2] |
张文鹏, 宗智, 倪少玲, 等. 三体船耐波性的模型试验研究[J]. 水动力学研究与进展, 2007, 22(5): 619-624. DOI:10.3969/j.issn.1000-4874.2007.05.012 |
| [3] |
李培勇, 裘泳铭, 顾敏童, 等. 三体船阻力模型试验[J]. 中国造船, 2002, 43(4): 6-12. LI Pei-yong, QIU Yong-ming, GU Min-tong, et al. Experimental investigation on resistance of trimaran[J]. Shipbuilding of China, 2002, 43(4): 6-12. DOI:10.3969/j.issn.1000-4882.2002.04.002 |
| [4] |
YU Hao,LI Zheng-jie,HU Jia-jun,et al. Slamming load forecasts and analyses of a trimaran model test[J]. Journal of Ship Mechanics, 2014, 18(6): 623-634. |
| [5] |
任慧龙, 陈亮亮, 李辉, 等. 三体船波浪设计载荷的三维时域水弹性理论研究[J]. 哈尔滨工程大学学报, 2016, 37(1): 19-23. REN Hui-long, CHEN Liang-liang, LI Hui, et al. Study of the design wave loads of a trimaran based on 3D time-domain hydroelastic theory[J]. Journal of Harbin Engineering University, 2016, 37(1): 19-23. |
| [6] |
黄晓琼, 陈立, 杨雄辉, 等. 三体船波浪诱导载荷计算研究[J]. 中国舰船研究, 2008, 3(5): 16-20. HUANG Xiao-qiong, CHEN Li, YANG Xiong-hui, et al. Calculation of wave induced loads on trimaran[J]. Chinese Journal of Ship Research, 2008, 3(5): 16-20. DOI:10.3969/j.issn.1673-3185.2008.05.004 |
| [7] |
吴帆行, 刘见华, 黄守成. 三体船垂向波浪载荷预报[J]. 船舶, 2008, 12(6): 13-18. |
| [8] |
黄晓琼, 陈立, 杨雄辉, 等. 三体船连接桥结构波浪载荷研究[J]. 中国舰船研究, 2009, 4(4): 42-46. HUANG Xiao-qiong, CHEN Li, YANG Xiong-hui, et al. Long term prediction and analysis of wave loads on trimaran cross structure[J]. Chinese Journal of Ship Research, 2009, 4(4): 42-46. DOI:10.3969/j.issn.1673-3185.2009.04.009 |
| [9] |
贾敬蓓, 宗智, 曾艳彬, 等. 三体船砰击压力数值计算方法研究[J]. 中国造船, 2012, 53(3): 111-120. JIA Jing-bei, ZONG Zhi, ZENG Yan-bin, et al. Study on numerical computation method for trimaran slamming pressure[J]. Shipbuilding of China, 2012, 53(3): 111-120. |
| [10] |
陈康, 黄德波. CFD技术在三体船阻力性能研究中的应用[J]. 哈尔滨工程大学学报, 2006, 27(3): 362-366. CHEN Kang, HUANG De-bo. Application of CFD technology to the research of resistance performance of trimaran[J]. Journal of Harbin Engineering University, 2006, 27(3): 362-366. DOI:10.3969/j.issn.1006-7043.2006.03.010 |
 2018, Vol. 40
2018, Vol. 40
