2. 北京宇航系统工程研究所,北京 100076;
3. 中国工程物理研究院 流体物理研究所冲击波物理与爆轰物理国防科技重点实验室,四川 绵阳 621900
2. Beijing Institute of Astronautical Systems Engineering, Beijing 100076, China;
3. National Key Laboratory of Shock Wave and Detonation Physics, Institute of Fluid Physics, China Academy of Engineering Physics, Mianyang 621900, China
加筋圆柱壳在船舶与海洋工程、航空航天等领域得到了广泛应用,其在瞬态外压载荷下的动力屈曲特性是固体力学及流固耦合等领域的重要研究课题,动载荷时间参数引起的惯性效应、应力波效应以及材料应变率效应使动力屈曲明显不同于静力屈曲[1]。网格加筋结构形式的复杂性和动力屈曲的强非线性,导致理论方法局限于未加筋或单向加筋结构,且忽略了结构几何缺陷及应变率效应的影响[2],尚未形成较为成熟的可用于网格加筋圆柱壳动力屈曲求解的理论方法;同时由于加工成本高,生产难度大,相关实验研究也相当有限。
针对未加筋圆柱壳结构,Anderson等[3]采用理论方法探讨了加载时间对冲量型载荷下厚壳模型、准静态载荷下薄壳模型动力屈曲的影响;Pegg[4]采用三维数值软件ADINA分析了径向冲击载荷作用时间对圆柱壳动力屈曲的影响;Bisagni[5]讨论了矩形脉冲轴压下碳纤维增强复合材料壳体的动力屈曲,结果表明脉宽增加时动力屈曲临界载荷降低,当脉宽增大到一定程度时动力屈曲临界载荷低于静力屈曲临界载荷。针对环向加筋圆柱壳,Pedron[6]分别采用Geers双渐进近似法处理流固耦合问题、摄动理论处理结构稳定性问题,研究了水下爆炸冲击波脉宽对环向加筋圆柱壳动力屈曲的影响。江松青等[7]借助增量数值法研究了冲击载荷下环向加筋圆柱壳的弹塑性动力屈曲,探讨了几何及材料参数的影响。袁建红等[8]采用三维数值软件MSC.Dytran分析了水下爆炸载荷下环向加筋圆柱壳的弹塑性动力屈曲特性,探讨了几何参数对动力屈曲特性的影响。
尽管很多学者对未加筋或单向加筋圆柱壳屈曲开展了较为广泛的研究,但关于网格加筋圆柱壳的动力屈曲问题很少有公开发表的文献。本文基于Abaqus/Explicit并结合Budiansky-Roth(B-R)动力屈曲准则[9],分析了轴向压力和径向瞬态外压耦合作用下网格加筋圆柱壳动力屈曲特性,针对瞬态外压载荷峰值和脉宽特点,分别基于横向和纵向搜索方法得到临界脉宽或临界峰值,探讨了瞬态外压时间特性对动力屈曲临界失稳线的影响。
1 三维数值计算模型本文所研究的网格加筋圆柱壳几何模型如图1所示,在蒙皮两端设置过渡区,过渡区采用较大尺寸环向加强筋进行加强;网格加筋圆柱壳材料为铝合金,具体参数如表1所示,应力-应变曲线如图2所示[10]。蒙皮和加强筋均采用S4单元进行模拟[11],为保证计算精度,单元尺寸应不大于

|
图 2 应力-应变近似拟合曲线 Fig. 2 Stress-strain approximate fitting curve |

|
图 1 网格加筋圆柱壳几何模型 Fig. 1 Geometric model of grid stiffened cylindrical shell |
网格加筋圆柱壳底端所有节点刚性固定,在圆柱壳顶端中心处设置参考点,参考点与顶端节点设置运动耦合,约束参考点除轴向其他方向自由度。参考点处施加轴向压力,圆柱壳外表面作用径向均布瞬态外压载荷。当只作用轴向压力时,图1所示网格加筋圆柱壳一阶固有周期T为3 ms。
2 非线性屈曲三维数值方法实验验证本文通过对比网格加筋圆柱壳动力与静力屈曲模态及临界载荷,探讨瞬态外压载荷脉宽、幅值、作用形式等对动力屈曲特性的影响。其中,静力屈曲计算分别采用Abaqus/Standard弧长法和阻尼因子法[13];动力屈曲计算时采用Abaqus/Explicit进行非线性分析,得到结构P-Y特征曲线,其中P为载荷峰值或脉宽参数,Y为结构动力响应参数,在此基础上结合B-R动力屈曲准则[9]判断临界载荷或临界脉宽,当载荷的微小增量引起结构响应的巨大变化,即P-Y特征曲线斜率发生较大变化时判定结构发生动力屈曲[8, 12]。由于公开发表的网格加筋圆柱壳屈曲实验极少,本文采用光筒金属圆柱壳屈曲实验对上述数值方法的有效性进行验证。
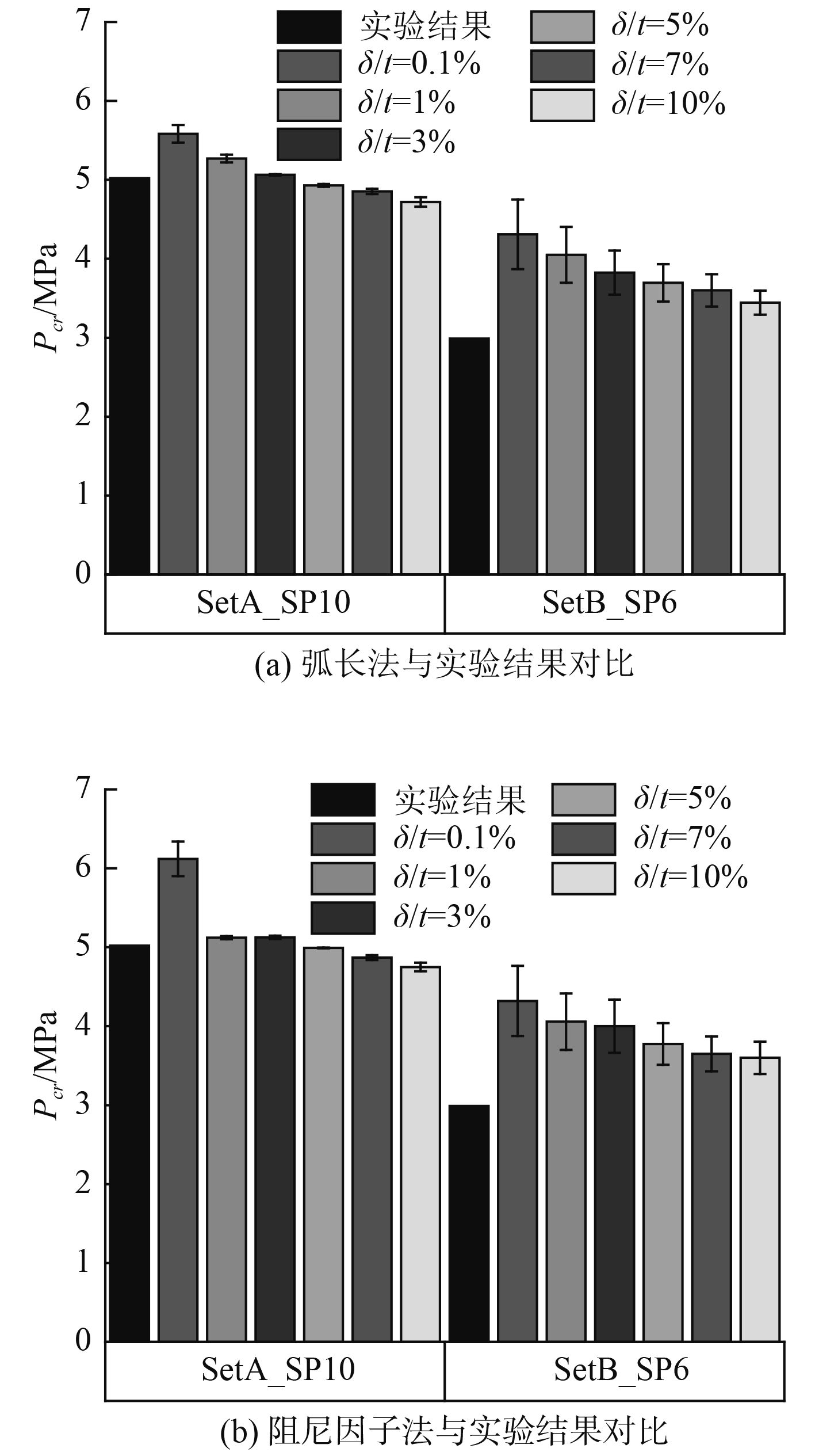
2.1 静力屈曲数值方法验证采用Giezen[14]给出的光筒铝壳静力屈曲实验验证静力屈曲三维数值方法的有效性。数值计算时轴向预紧力大小与实验保持一致,分别取为9 408.0 N和11 777.4 N,记为SetA_SP10和SetB_SP6模型,保持轴力不变,逐步增加径向压力直至结构发生静力屈曲。数值计算时采用实验测量到的轴向半波数为1、环向全波数为4的初始几何缺陷,缺陷幅值δ取为圆柱壳厚度t的10%[14]。图3结果表明当初始几何缺陷幅值接近实验模型几何缺陷时,数值与实验得到的径向压力屈曲临界载荷Pcr偏差越小,当均采用10%的初始缺陷时,数值和实验误差在15%以内,验证了弧长法和阻尼因子法的有效性。
|
图 3 光筒圆柱壳静力屈曲数值与实验结果[13]对比 Fig. 3 Static buckling comparison between numerical and experimental results[13] of the cylindrical shell |
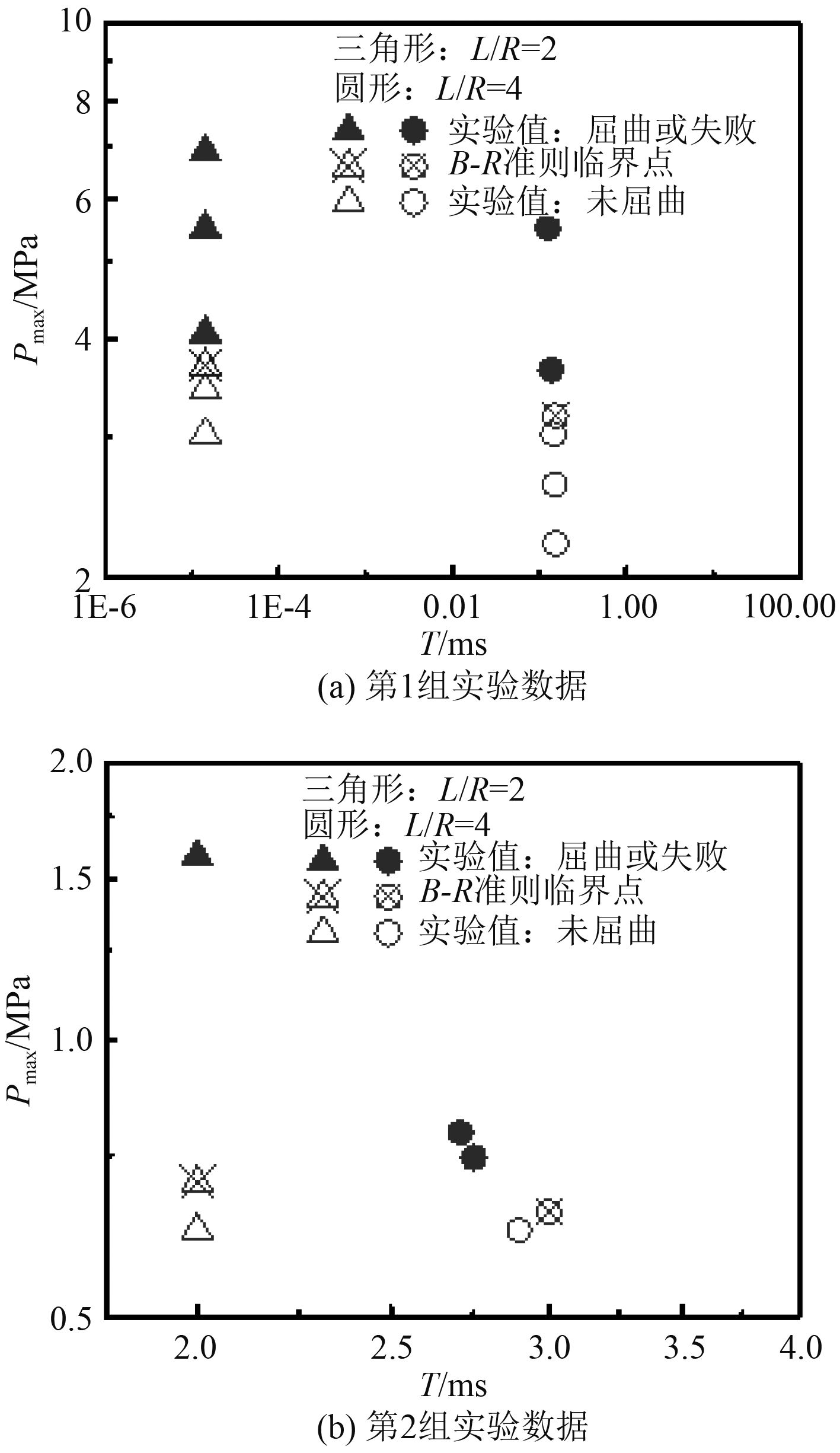
采用Lindberg和Florence[15]给出的6061-T6铝合金薄壁圆柱壳冲击屈曲实验进行动力屈曲数值方法验证。圆柱壳两端刚性固定,通过爆炸装置获得沿圆柱壳外表面均匀分布的指数衰减冲击波载荷。动力屈曲实验及三维数值结果如图4所示,图中采用双对数坐标,Pmax为冲击波压力峰值,T为冲击波衰减时间常数,三角形表示长径比L/R=2的圆柱壳,圆形表示L/R=4的圆柱壳;实心代表实验时发生动力屈曲,空心代表实验时未发生动力屈曲,带叉符号表示基于B-R准则得到的动力屈曲临界载荷数值结果。由图可知数值方法预测到的临界屈曲载荷位于实验屈曲和未屈曲载荷之间,与实验结果吻合较好,验证了本文动力屈曲数值方法的有效性。
|
图 4 薄壁光筒圆柱壳动力冲击屈曲数值及实验[14]结果对比 Fig. 4 Dynamic buckling comparison between numerical and experimental results[14] of thin-walled cylindrical shell |
采用上述弧长法和阻尼因子法得到400 t轴向预紧力下网格加筋圆柱壳径向屈曲载荷
|
|
表 2 轴向预紧力下网格加筋圆柱壳结构径向屈曲载荷 Tab.2 Radial buckling load of grid stiffened cylindrical shell under a pre-loaded axial compression |
采用Abaqus/Explicit研究轴压和如图5所示的径向均布对称三角波脉冲瞬态外压耦合作用下网格加筋圆柱壳动力屈曲特性。首先定义无量纲参数

|
图 5 Pmax=1.5 MPa时网格加筋圆柱壳结构P-Y特征曲线及其所对应的Southwell曲线 Fig. 5 P-Y curve ofgrid stiffened cylinders under the condition of Pmax=1.5 MPa and the corresponding Southwell plot |
图5给出了Pmax=1.5 MPa下的P-Y特征曲线及对应的Southwell曲线,此时P对应载荷脉宽T。由动力屈曲准则定义可知,P-Y曲线的突变处,即T=54.7 ms处为临界屈曲脉宽,Southwell曲线[8, 16]斜率的倒数为临界屈曲脉宽Tcr=55.55 ms,2种方法得到的误差约为1.5%,说明了本文数值方法在网格加筋圆柱壳动力屈曲分析的可行性。
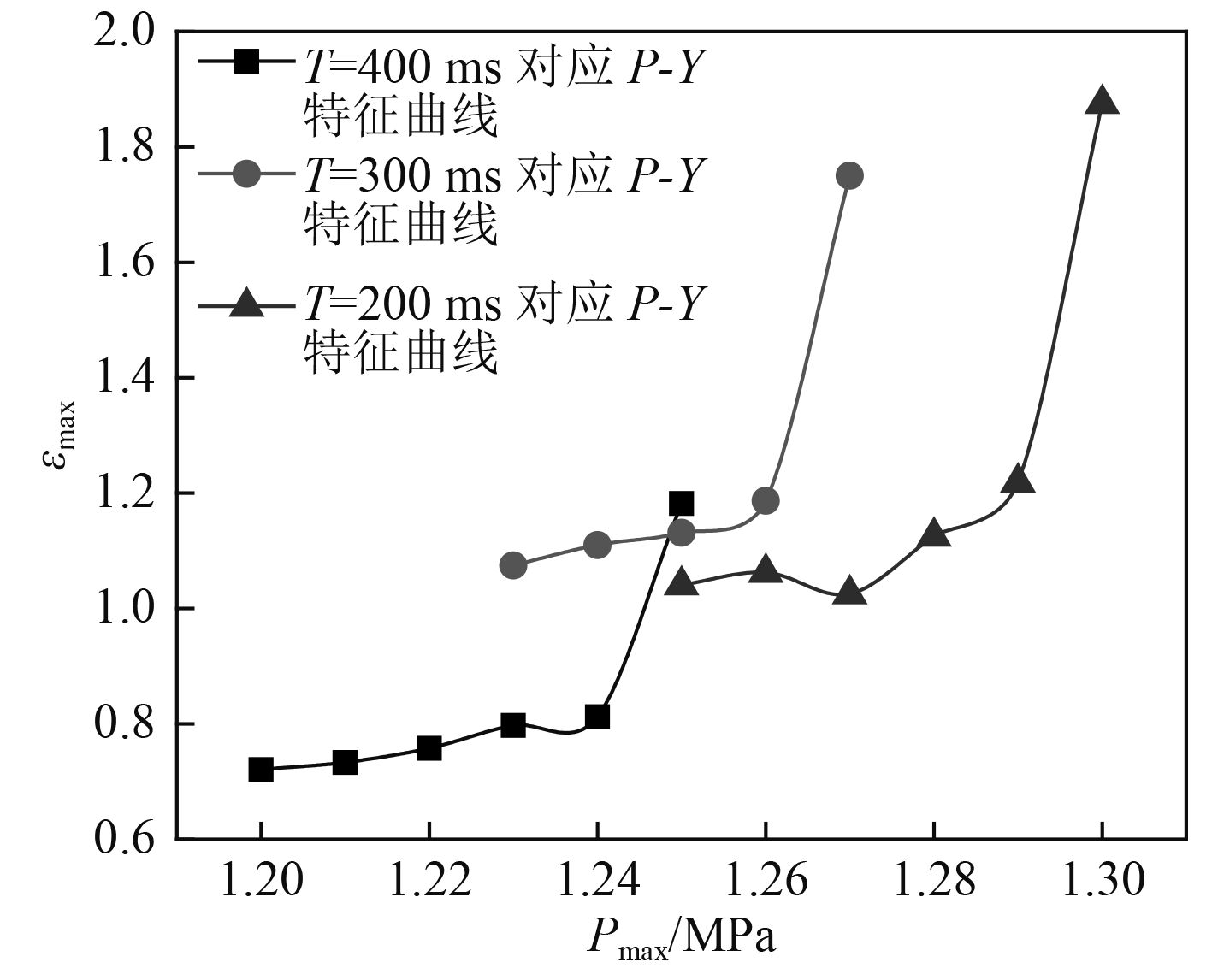
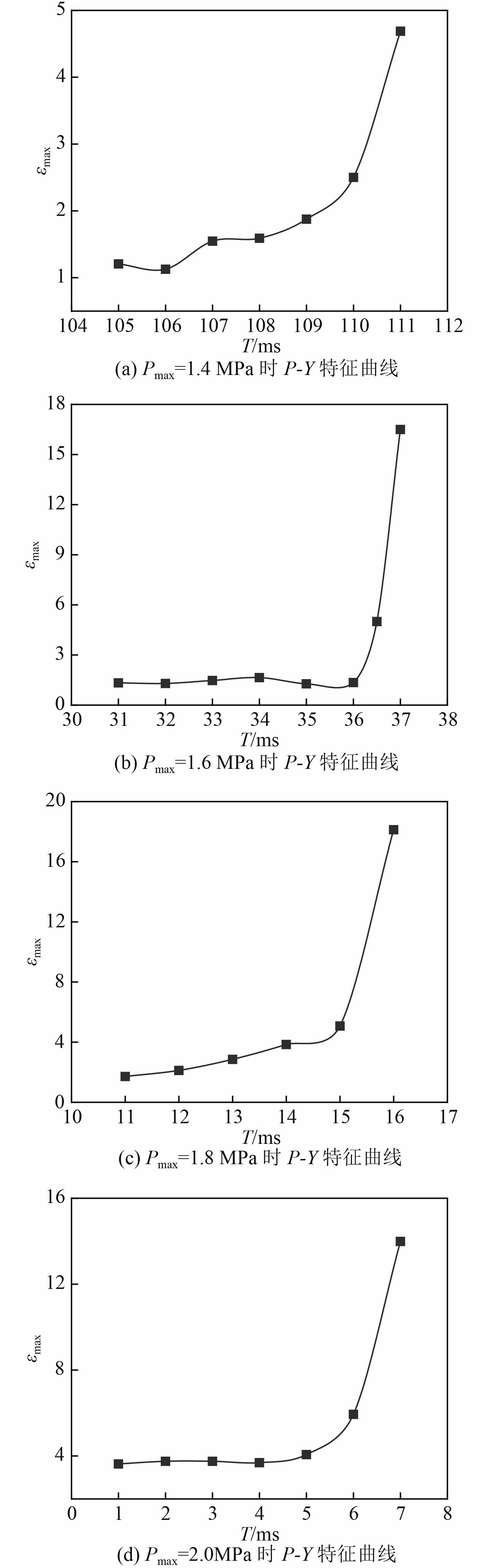
为快速得到临界失稳线,针对不同载荷幅值和脉宽下结构动力屈曲响应特征,采用不同的搜索方法。低峰值、长脉宽载荷下,网格加筋圆柱壳屈曲前后处于小变形、线弹性应力状态,载荷近似为准静态型,此时采用纵向搜索,即保持载荷脉宽不变,搜索使结构发生弹性动力屈曲所对应的临界载荷峰值。高峰值、短脉宽载荷下,结构发生动力屈曲时处于塑性应力状态,载荷为动力型和冲量型,此时采用横向搜索,即保持载荷峰值不变,搜索使结构发生塑性动力屈曲所对应的临界脉宽[10]。图6和图7分别给出了本文所研究的网格加筋圆柱壳在典型低峰值长脉宽、高峰值短脉宽载荷下结构的P-Y特征曲线。
|
图 6 不同脉宽下P-Y特征曲线 Fig. 6 Influences of load durationon P-Y curve |
|
图 7 不同载荷峰值时网格加筋圆柱壳P-Y特征曲线 Fig. 7 Influences of load amplitudeon P-Y curve of the grid stiffened cylindrical shell |
根据B-R动力屈曲准则,根据上述搜索方法得到图6、图7载荷下临界失效参数分别如表3和表4所示。
根据表3及表4等结果绘制瞬态对称三角波脉冲载荷下网格加筋圆柱壳动力屈曲Pmax-T临界失稳线、不同脉宽幅值下圆柱壳动力屈曲模态以及动力屈曲放大因子λ(动屈曲载荷与静屈曲载荷之比)随脉宽变化曲线如图8所示,其中,
|
|
表 4 横向搜索路径下得出的临界载荷参数值 Tab.4 Critical load obtained by horizontal search path |
|
|
表 3 纵向搜索路径下得出的临界载荷参数值 Tab.3 Critical load obtained by vertical search path |
由图8中Pmax-T临界失稳线可知:1)当载荷脉宽在结构固有周期范围内时,动力屈曲模态及临界失效载荷明显高于静力屈曲载荷,且随着脉宽增加动力屈曲载荷迅速下降,此时结构动力屈曲特性表现为冲量型屈曲。2)当脉宽增加到7 ~ 55 ms范围时,动力屈曲模态及临界载荷同样高于静力屈曲载荷,但动力屈曲临界载荷下降速度减小,且以塑性动力屈曲特性为主,此时结构动力屈曲特性表现为动力型屈曲。3)当脉宽增加到100 ~ 500 ms时,动力屈曲模态及临界载荷均逐渐趋于静力屈曲载荷,这主要是因为长脉宽载荷激起了与结构自由振动固有模态相类似的失稳模态,此时结构发生弹性动力屈曲,表现为准静态型屈曲。
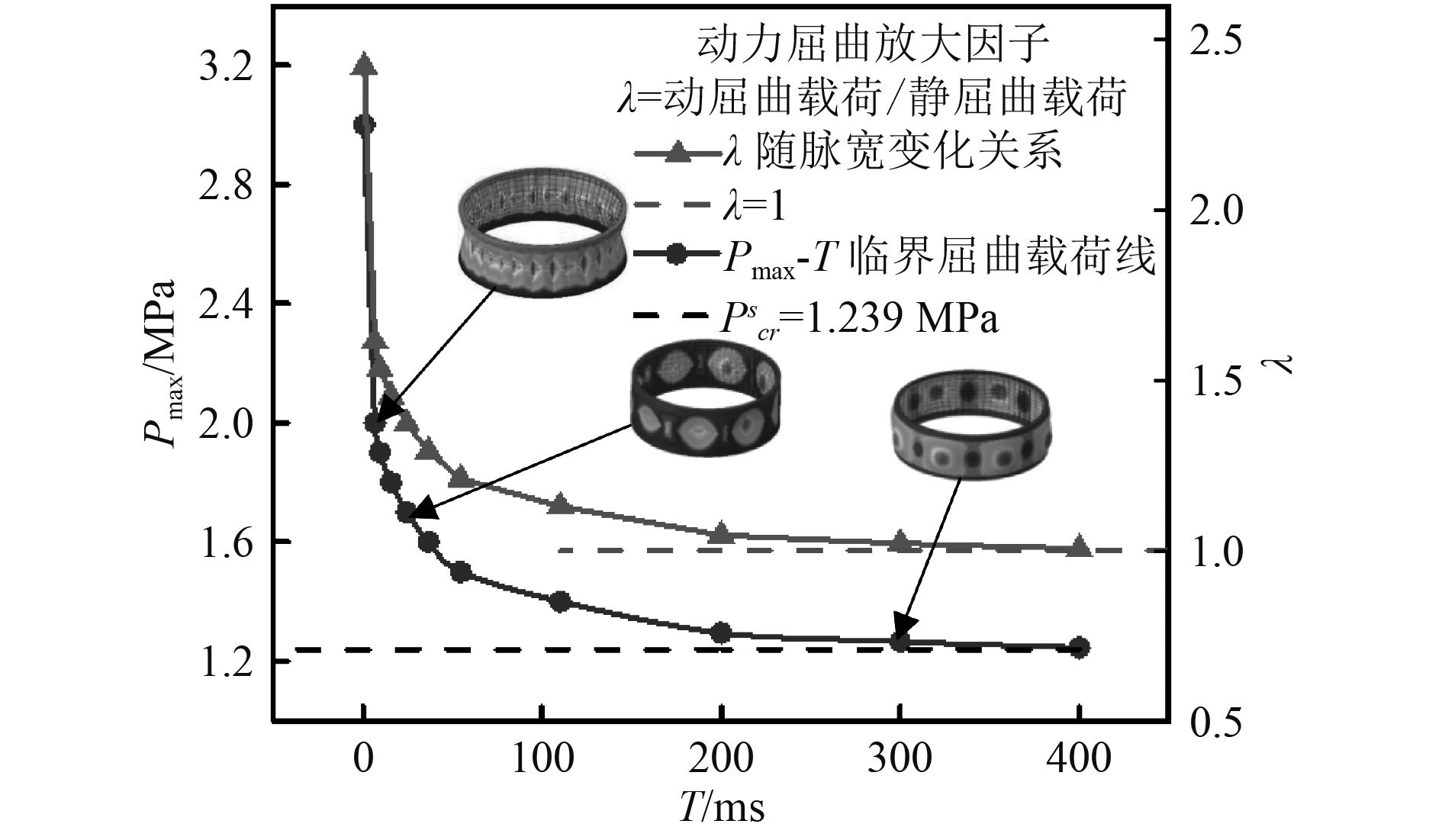
|
图 8 网格加筋圆柱壳临界动力屈曲载荷线 Fig. 8 Critical dynamic buckling load curve of the grid stiffened cylindrical shell |
保持对称三角波脉冲加载形式不变,不同轴向预紧力下网格加筋圆柱壳临界失稳线如图9所示,由图可知轴向预紧力越大,动力屈曲临界失稳线就越低,结构越易发生动力屈曲。保持轴向预紧力不变,对称三角波和半正弦函数脉冲载荷下网格加筋圆柱壳动力屈曲临界载荷线如图10所示,由图可知半正弦函数波载荷比对称三角波脉冲瞬态外压更容易使结构发生稳定性失效,这种现象对于高幅值、低脉宽的冲量型载荷表现不明显,而对于脉宽范围为30 ~ 60 ms内的动力型载荷表现尤为显著。
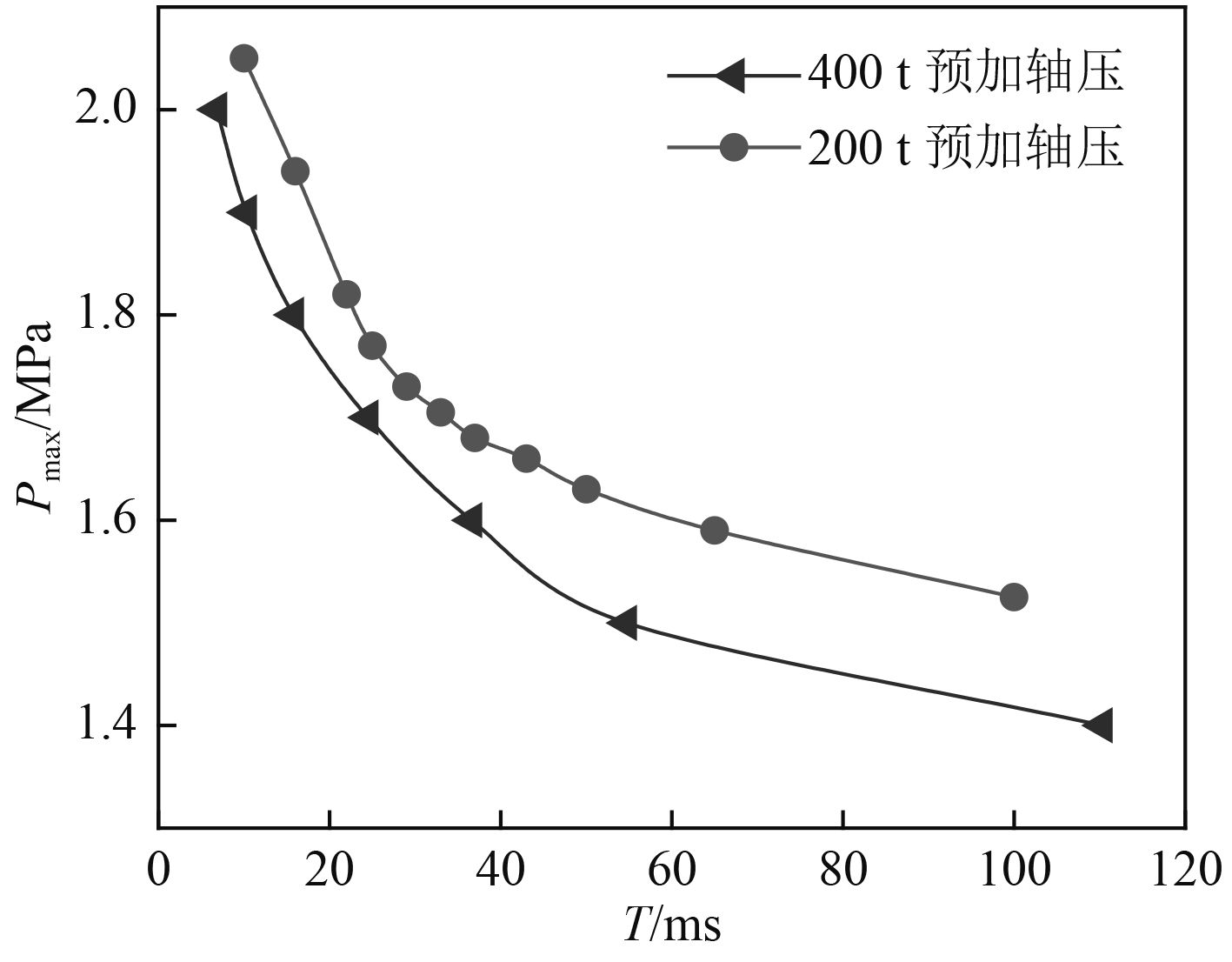
|
图 9 预加轴压对临界失稳线影响 Fig. 9 Influence of pre-loaded axial compression on the critical dynamic buckling load curve |

|
图 10 外压脉冲波形状对临界失稳线影响 Fig. 10 Influence of the pulse shapes on the critical dynamic buckling load curve |
本文探讨了瞬态外压载荷时间特性对网格加筋圆柱壳结构动力屈曲影响规律,依据三维数值计算方法和B-R动力屈曲准则,开展了网格加筋圆柱壳非线性静力及动力屈曲特性研究。针对瞬态外压载荷峰值和脉宽特点,分别通过横向和纵向搜索方法得到了网格加筋圆柱壳动力屈曲临界失稳线,并分析了瞬态外压载荷时间特性对网格加筋圆柱壳的影响规律,得到以下结论:
1)瞬态外压载荷时间特性对网格加筋圆柱壳动力屈曲特性影响较大。当载荷脉宽在结构固有周期范围内时,脉宽为动力屈曲主要影响因素;当载荷脉宽增加到大于结构固有周期时,脉宽、峰值同时影响动力屈曲特性;当载荷脉宽增加到远大于结构固有周期时,峰值则为主要影响因素。
2)低幅值、长脉宽载荷作用下网格加筋圆柱壳发生弹性动力屈曲,而高幅值、低脉宽载荷作用下结构主要发生塑性动力屈曲;且随着脉宽的增加,临界屈曲载荷减小,屈曲波纹数减小;当脉宽增加到一定范围时,动力屈曲放大因子趋近1,该阶段所对应的临界失稳线趋于一条渐进线。
3)使网格加筋圆柱壳结构发生动力稳定性失效的径向瞬态外压载荷危险区域随预加轴压的增大而增加;脉冲波载荷形式会影响动力稳定性失效。在特定脉宽范围内,半正弦函数脉冲波载荷比对称三角脉冲波载荷更容易使圆柱壳结构发生动力稳定性失效。
| [1] |
严东晋, 宋启根. 结构冲击屈曲准则讨论[J]. 工程力学, 1997, 14(4): 18-28. |
| [2] |
彭英. 冲击载荷下加筋板结构的非线性动力响应及屈曲研究[D]. 武汉: 武汉理工大学, 2007.
|
| [3] |
ANDERSON D L, LINDBERG H E. Dynamic pulse buckling of cylindrical shells under transient lateral pressures[J]. AIAA Journal, 1968, 6(4): 589-598. DOI:10.2514/3.4549 |
| [4] |
PEGG N G. Effects of impulse duration and combined impulse-hydrostatic pressure on buckling stability of cylindrical structures[J]. Journal of Ship Research, 1994, 38(2): 164-171. |
| [5] |
BISAGNI C. Dynamic buckling of fiber composite shells under impulse axial compression[J]. Thin-Walled Structures, 2005, 43(3): 499-514. DOI:10.1016/j.tws.2004.07.012 |
| [6] |
PEDRON C. Dynamic buckling of stiffened cylindrical shells of revolution under a transient lateral pressure shock wave[J]. Thin-Walled Structures, 1995, 23(1-4): 85-105. DOI:10.1016/0263-8231(95)00006-Y |
| [7] |
江松青, 李永池, 王红五, 等. 环向加筋圆柱壳轴向弹塑性动力屈曲[J]. 振动与冲击, 2001, 20(4): 81-86. DOI:10.3969/j.issn.1000-3835.2001.04.025 |
| [8] |
袁建红, 朱锡, 张振华. 水下爆炸载荷作用下环肋加筋圆柱壳结构的弹塑性动力屈曲[J]. 爆炸与冲击, 2012, 32(6): 585-591. DOI:10.3969/j.issn.1001-1455.2012.06.005 |
| [9] |
BUDIANSKY B, ROTH R S. Axisymmetric dynamic buckling of clamped shallow spherical shells[C]//Collected Papers on Instability of Shell Structures. Hampton: NASA Langley Research Center, 1962: 597–606.
|
| [10] |
李朋波. 薄壁加筋圆柱壳静动力屈曲特性数值模拟与实验研究[D]. 哈尔滨: 哈尔滨工程大学, 2017.
|
| [11] |
Dasssault Systèmes Simulia Corp. ABAQUS User’s Manual[M]. (Version 6.11). Pawtucket USA: ABAQUS, Inc., 2011.
|
| [12] |
MEYER-PIENING H R, FARSHAD M, GEIER B, et al. Buckling loads of CFRP composite cylinders under combined axial and torsion loading experiments and computations[J]. Composite Structures, 2001, 53(4): 427-435. DOI:10.1016/S0263-8223(01)00053-8 |
| [13] |
彭大炜, 张世联. 结构极限强度分析的三种有限元解法研究[J]. 中国海洋平台, 2010, 25(2): 1-5. DOI:10.3969/j.issn.1001-4500.2010.02.001 |
| [14] |
GIEZEN J J, BABCOCK C D, SINGER J. Plastic buckling of cylindrical shells under biaxial loading[J]. Experimental Mechanics, 1991, 31(4): 337-343. DOI:10.1007/BF02325990 |
| [15] |
LINDBERG H E, FLORENCE A L. Dynamic pulse buckling-theory and experiment[M]. Dordrecht: Martinus Nijhoff Publishers, 1987.
|
| [16] |
SOUTHWELL R V. On the analysis of experimental observations in problems of elastic stability[C]//Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character. London: Royal Society Publishing, 1932: 601–616.
|
 2018, Vol. 40
2018, Vol. 40
