重量曲线是描述船舶重量沿船长分布状况的曲线[1],其纵坐标表示作用于单位长度上的重量分布载荷强度,是船舶防纵倾设计的重要设计指标[2]。通常将各项重量按静力等效原则分布在相应的理论站距范围内,再逐项迭加得到各站距内的重量分布载荷强度,以便绘制船舶重量曲线分布图。
在计算单个设备或物品的重量分布载荷强度时,一般将重量沿设备或物品所处标准理论站距进行等效分布载荷计算[3 – 4]。当设备或物品在船首/船尾有一定的延伸部分时,若突出部分未超过理论站距一半,且突出部分重量占空船重量的比例小于1%时,一般认为可将突出部分忽略不计处理;若突出部分超过理论站距一半之多时,则将重量按长度进行重量分段处理,再进行船首、船尾的重量等效转移到相邻的2个理论站距内。
随着船舶设计质量的不断提高,对重量分布载荷强度的计算精度提出了更高的要求。针对设备或物品突出部分重量的传统处理方法,在一定程度导致部分重量缺失或等效分段重量失真等情况[5 – 6],无法满足高精度的设计需求。本文将船首、船尾分别视为一个完整的理论站距,将20个理论站距扩充到22个,计算设备在各理论站距内的重量分布载荷强度,再将船首、船尾2个理论站距载荷强度折算到相邻的2个理论站距,得到20个理论站距的船舶重量分布载荷强度,避免船首、船尾的部分重量缺失或失真,使重量分布载荷强的更加准确。
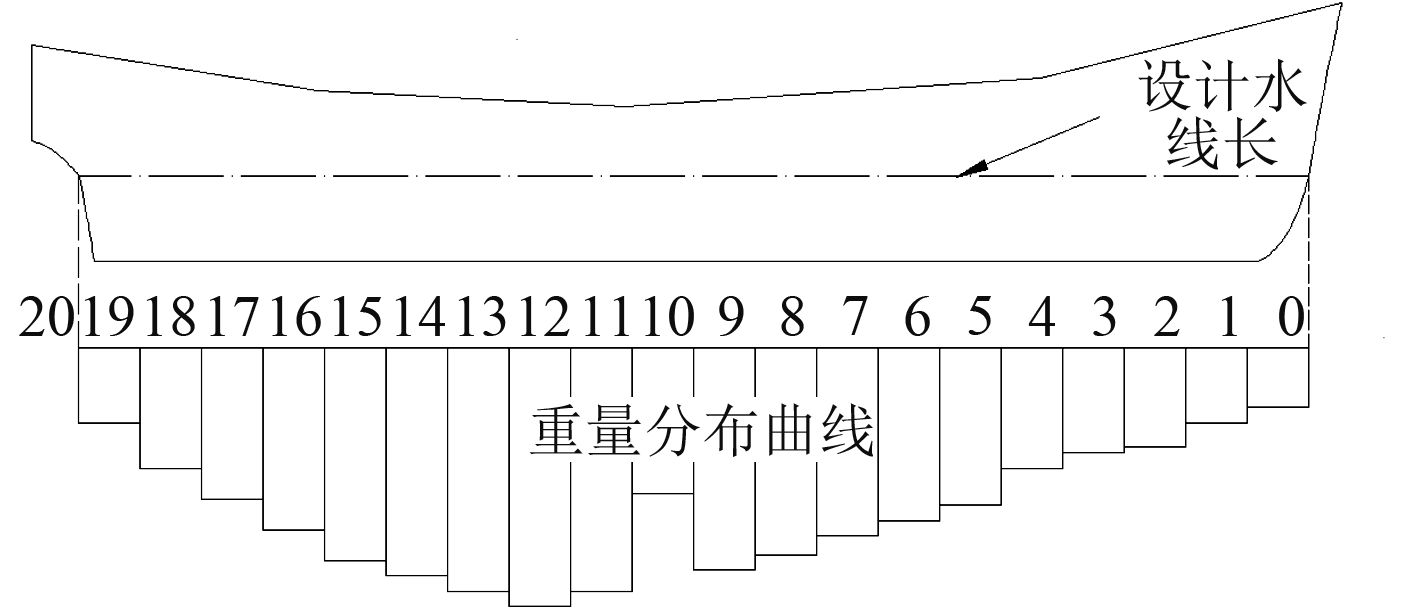
1 重量分布载荷强度分布原则考虑到设计水线是船舶运行过程中稳性安全的重要保证,沿设计水线方向划分理论站距更真实地反映出船舶的重量分布,确保重量分布合理,保障运行安全。图1为船舶重量分布曲线图,将全船沿设计水线方向划分为20个理论站,对各项重量进行近似和理想化分布处理时,必须遵循以下静力等效原则[7]:
|
图 1 船舶重量分布曲线 Fig. 1 Distributed curve of ship weight |
1)保持重量的大小不变,即等效后各理论站距的重量之和应近似等于该设备的实际重量;
2)保持重量重心的纵坐标不变,即等效后形心纵坐标与该设备的重心纵坐标相等;
3)近似分布曲线的范围与该项重量实际分布范围相同或大体相同。
最终,应使重量分布曲线所围面积等于全船的重量,该面积的形心纵坐标与重心的纵坐标相同。
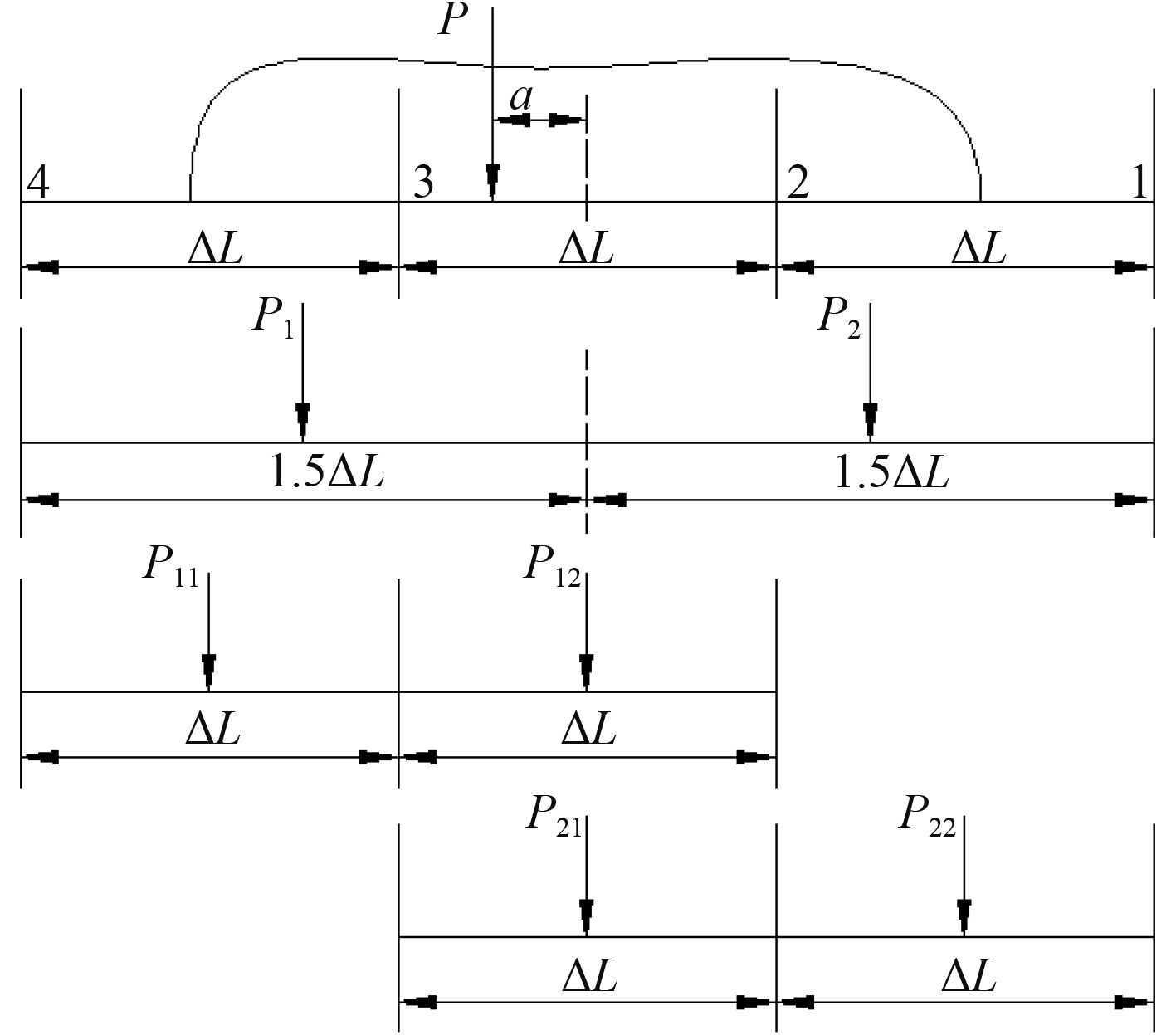
2 重量分布载荷强度计算模型 2.1 两个理论站距内的重量分布载荷强度如图2所示,某项以任意规律分布在2个标准理论站距内的重量为P,重心距2站的距离为α,按照分布原则3,用1-2及2-3两个理论站距内的分布载荷代替真实的重量分布。设2个理论站距内的重量分别是P1和P2,根据分布原则1和分布原则2可得:

|
图 2 在2个理论站距内的重量分布载荷图 Fig. 2 Weight distributed loading between two theoretical stations |
| $\left\{ \begin{array}{l} {P_1} + {P_2} = P \text{,} \\ \displaystyle\frac{1}{2}{P_1}\Delta L - \displaystyle\displaystyle\frac{1}{2}{P_2}\Delta L = P\alpha \text{。} \\ \end{array} \right.$ | (1) |
将P1和P2除以理论站距长度ΔL,即可得到该项重量在2个理论站距内的分布载荷强度。
2.2 三个理论站距内的重量分布载荷强度如图3所示,当重量分布在3个理论站距时,根据静力等效原则只能列出2个方程式,无法求解3个未知数,因此,一般用1.5ΔL代替ΔL,利用公式(1)求得P1和P2,再利用公式(1),将P1和P2分别向其相邻的2个理论站距内分布,最后将中间理论站距迭加来自P1和P2的相应分配值,即为中间理论站距内的重量分布。
|
图 3 在3个理论站距内的重量分布载荷图 Fig. 3 Weight distributed loading between three theoretical stations |
| $\left\{ \begin{array}{l} {P_{11}} + {P_{12}} = {P_1}\text{,} \\ \displaystyle\frac{1}{2}{P_{11}}\Delta L - \displaystyle\frac{1}{2}{P_{12}}\Delta L = \frac{1}{4}{P_{11}}\Delta L \text{,} \\ {P_{21}} + {P_{22}} = {P_2}\text{,} \\ \displaystyle\frac{1}{2}{P_{21}}\Delta L - \displaystyle\frac{1}{2}{P_{22}}\Delta L = - \displaystyle\frac{1}{4}{P_{11}}\Delta L \text{。} \\ \end{array} \right.$ | (2) |
将各理论站距内分配得到的重量分别除以理论站距长度ΔL,即可得到该项重量在3个理论站距内的分布载荷强度。
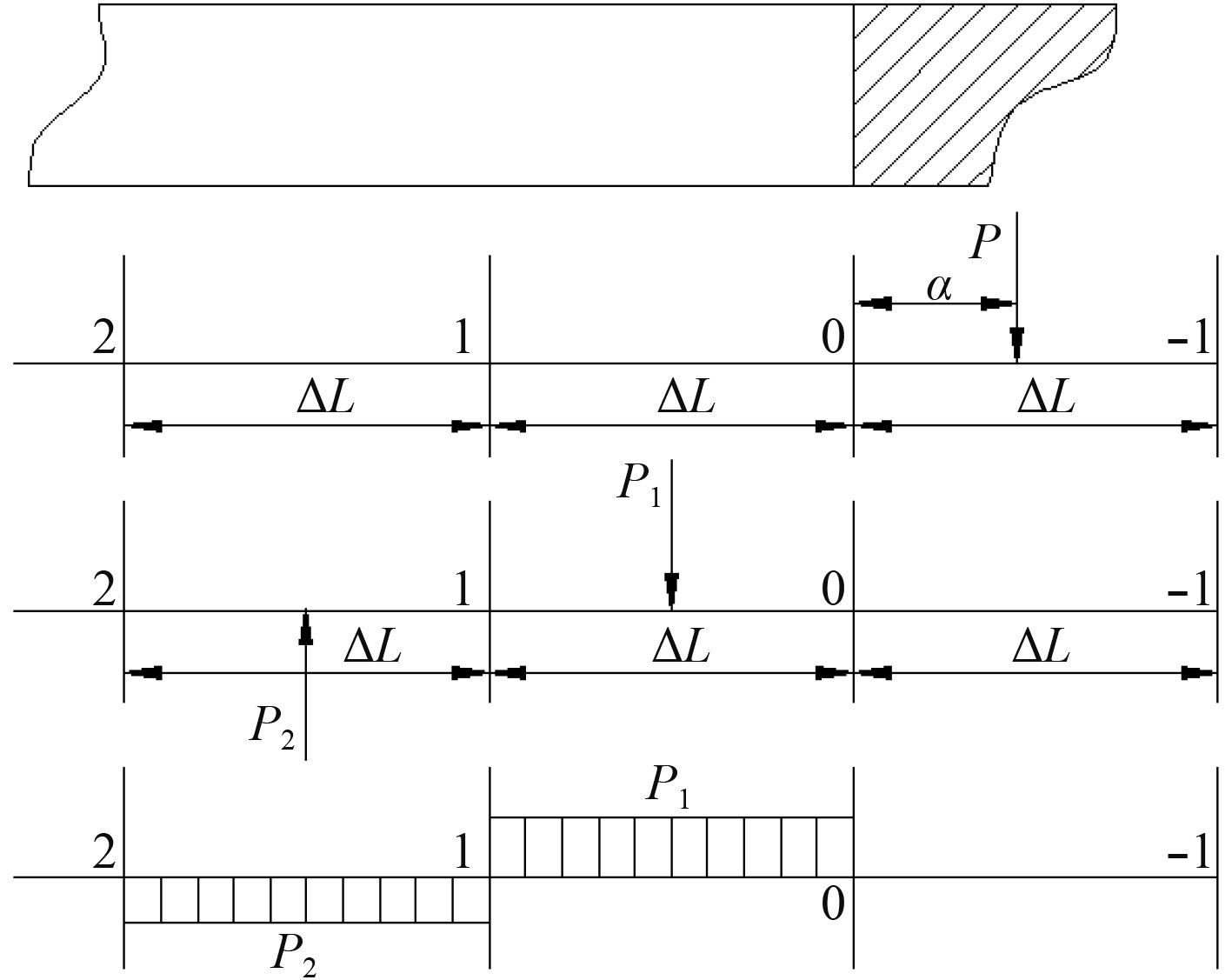
2.3 船首/船尾理论站距的重量分布载荷强度如图4所示,当重量分布在船首、船尾时,将船首、船尾当成一个标准理论站距来处理,将该理论站距内的重量转移到相邻的2个理论站距内,根据静力等效原则不改变其重量大小及其对船中的力矩大小,可得到式(3)。
|
图 4 船首、船尾理论站距的重量分布载荷强度图 Fig. 4 Weight distributed loading between bow and stern |
| $\left\{ \begin{array}{l} {P_1} - {P_2} = P \text{,} \\ \displaystyle\frac{3}{2}{P_2}\Delta L - \displaystyle\frac{1}{2}{P_1}\Delta L = Pa \text{。} \\ \end{array} \right.$ | (3) |
将P1和P2除以理论站距长度ΔL,即可得到船首、船尾的重量折算至相邻2个理论站距内的分布载荷强度。
对于在更长范围内分布的重量,计算时只要将理论站距ΔL用分布范围内的等分段长度代替即可。
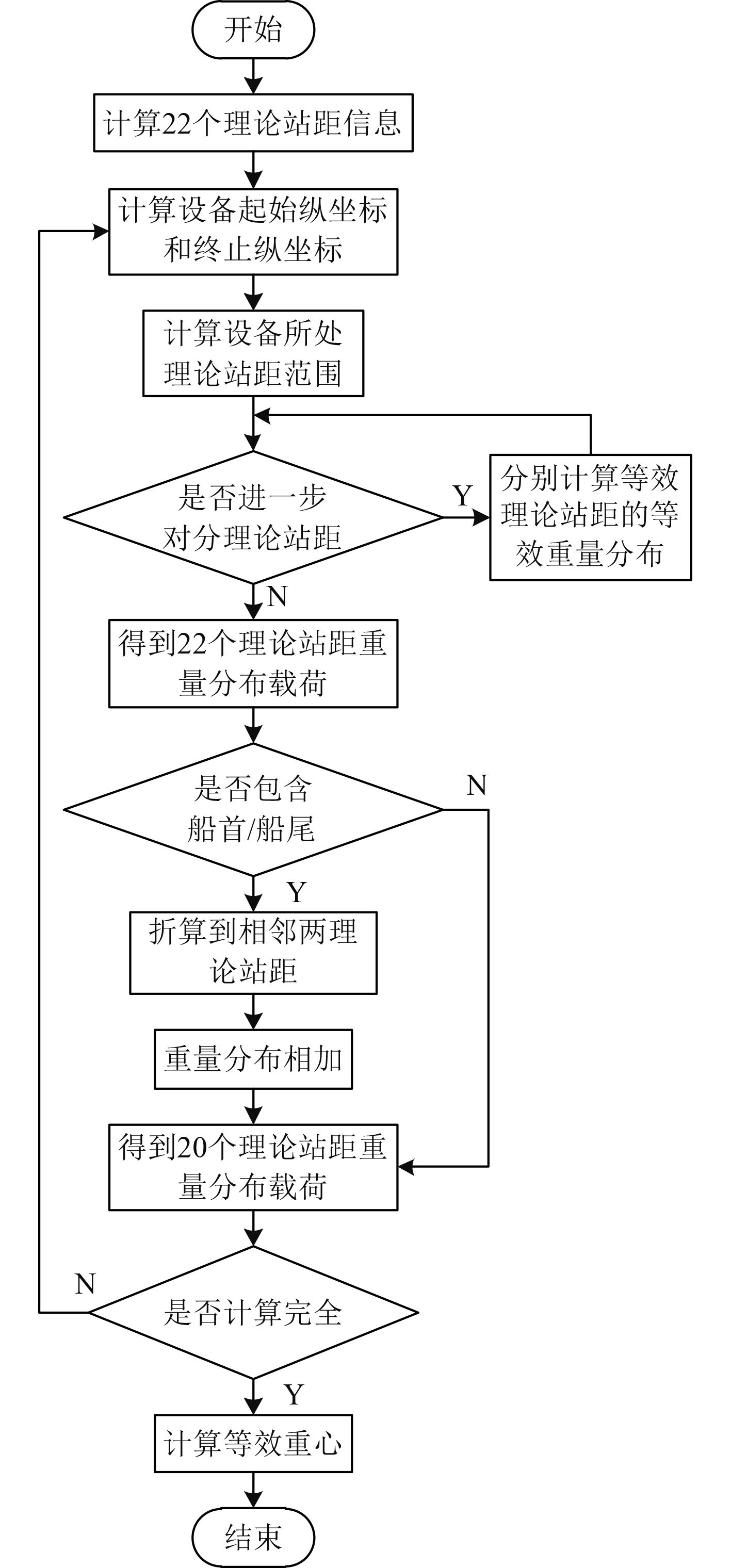
3 重量分布载荷强度计算方法本文将船首和船尾分别作为一个完整的理论站距,将20个标准理论站距扩充到22个标准理论站距,根据静力等效原则将船上各设备或物品的重量等效分布在该设备或物品所在的理论站距范围内的各标准理论站距上,然后将分布在船首标准理论站距和船尾标准理论站距内的重量折算至与其相邻的2个标准理论站距内,最后得到20个标准理论站距的重量分布,具体计算流程如图5所示。
|
图 5 船舶重量分布载荷强度计算流程图 Fig. 5 Calculation flow of ship weight distributed loading |
1) 理论站距信息计算
以船肿肋位号FR的一半为坐标原点,根据设计水线长L、肋骨间距S计算22个标准理论站距信息(包括几何中心纵坐标、起始纵坐标和终止纵坐标):
| $\left\{ {\begin{array}{*{20}{l}}{cP{t_i} = FR \times S - \left( {i - 0.5} \right) \times L/20}\text{,}&{}\\{sP{t_i} = cP{t_i} - 0.5 \times L/20}\text{,}&{i \in \left[ {0,21} \right]}\text{。} \\{eP{t_i} = cP{t_i} + 0.5 \times L/20}\text{,}&{}\end{array}} \right.$ |
其中:i表示第i个理论站距的编号,cPti为第i个理论站距的几何中心纵坐标,sPti为第i个理论站距的起始纵坐标,ePti为第i个理论站距的终止纵坐标;L为设计水线长、S为肋骨间距、FR为船中肋位号。所有理论站距信息都可以表示为向量的形式,形成理论站距中心坐标矩阵cPt和坐标信息矩阵
| ${{cPt}} = \left( {cP{t_0}, \cdot \cdot \cdot ,cP{t_i} \cdot \cdot \cdot ,cP{t_{21}}} \right)\text{,} $ |
| ${{Area}} = \left( \begin{gathered} sP{t_0},eP{t_0} \\ \cdot \cdot \cdot \\ sP{t_i},eP{t_i} \\ \cdot \cdot \cdot \\ sP{t_{21}},eP{t_{21}} \\ \end{gathered} \right)\text{。}$ |
2) 设备信息计算
根据设备的起始肋位号sFR和终止肋位号eFR计算设备的起始纵坐标sX和终止纵坐标eX:
| $\left\{ \begin{gathered} sX = \left( {FR - sFR} \right) \times S\text{,} \\ eX = \left( {FR - eFR} \right) \times S \text{。}\\ \end{gathered} \right.$ |
3) 计算设备所处理论站距范围
根据设备的起始纵坐标sX、终止纵坐标eX和理论站距矩阵
特殊地,当设备或物品的重心纵坐标cX处于船首、船尾标准理论站距时(即船首或船尾),则认为该设备重量集中于该标准理论站距,其所处理论站距为船首/船尾标准理论站距,所处标准理论站距个数为1;当设备起始肋位号和终止肋位号相同时,则认为该设备重量集中于重心纵坐标cX处,其所处理论站距为重心纵坐标cX所在标准理论站距,所处标准理论站距个数为1。
4) 计算设备所处的各理论站距内的重量分布
当设备所处的理论站距范围内标准理论站距的个数大于或等于2时,将该设备的重量按照静力等效原则等效至该设备所处的各标准理论站距上,计算设备所处的各标准理论站距内的重量分布,具体计算步骤如下:
将该设备所处的理论站距个数n对分(n
| $\left\{ \begin{array}{l}{P_1} = P \times \left( {0.5 + \displaystyle\frac{\alpha }{{\Delta L}}} \right)\text{,}\\{P_2} = P \times \left( {0.5 - \displaystyle\frac{\alpha }{{\Delta L}}} \right)\text{。}\end{array} \right.$ |
其中:P为设备重量,α为该设备重量作用点与所处的理论站距范围的几何中心之间的距离;∆L为对分后的等效理论站距的长度。
5) 若该设备跨船首、船尾标准理论站距,则将船首、船尾标准理论站距的重量分布折算至相邻的2个标准理论站距内(见图4),可用公式(3)计算得:
| $\left\{ \begin{array}{l}{P_1} = P \times \left(\frac{3}{2} + \displaystyle\frac{{\alpha '}}{{\Delta L'}}\right)\text{,}\\{P_2} = - P \times \left(\frac{1}{2} + \displaystyle\frac{{\alpha '}}{{\Delta L'}}\right)\text{。}\end{array} \right.$ |
其中:
6)将该设备各理论站距内重量分布相加,除以标准理论站距长度,即可得到各理论站距的重量载荷分布强度:
| $subP = \left( {{P_1}, \cdot \cdot \cdot ,{P_i}, \cdot \cdot \cdot ,{P_{20}}} \right)\text{,}$ |
其中,Pi表示第i个理论站距的重量载荷分布强度。
7)依次对全船所有设备计算各理论站距的重量载荷分布强度:
| $subP = \left( \begin{gathered} sub{P_1} \\ \cdot \cdot \cdot \\ sub{P_i} \\ \cdot \cdot \cdot \\ sub{P_n} \\ \end{gathered} \right) = \left( {\begin{array}{*{20}{c}} {{P_{1,1}}}&{ \cdot \cdot \cdot }&{{P_{1,j}}}&{ \cdot \cdot \cdot }&{{P_{1,20}}} \\ {}&{}&{ \cdot \cdot \cdot }&{}&{} \\ {{P_{i,1}}}&{}&{{P_{i,j}}}&{}&{{P_{i,20}}} \\ {}&{}&{ \cdot \cdot \cdot }&{}&{} \\ {{P_{n,1}}}&{ \cdot \cdot \cdot }&{{P_{n,j}}}&{ \cdot \cdot \cdot }&{{P_{n,20}}} \end{array}} \right)\text{。}$ |
其中:subPi为第i个设备的重量载荷分布,Pij为第i个设备在第j个理论站距的重量载荷分布强度,n为设备个数。将各理论站内所有设备的重量分布载荷强度相加,即可得到第j个理论站距内的重量分布载荷强度:
| $Dis{P_j} = \sum\limits_{i = 1}^n {{P_{ij}}} \text{。}$ |
将每一个理论站距的重量载荷分布强度表示为向量形式,形成重量纵向分布载荷强度矩阵:
| $DisP = \left( {Dis{P_1}, \cdot \cdot \cdot ,Dis{P_j}, \cdot \cdot \cdot ,Dis{P_{20}}} \right)\text{。}$ |
8)根据各理论站距的中心坐标cPt和等效重量分布载荷DisP计算重量分布之后的等效重心坐标:
| $IPT = \frac{{\displaystyle\sum\limits_{i = 1}^{20} {cP{t_i} \times Dis{P_i}} }}{{\displaystyle\sum\limits_{i = 1}^{20} {Dis{P_i}} }}\text{。}$ |
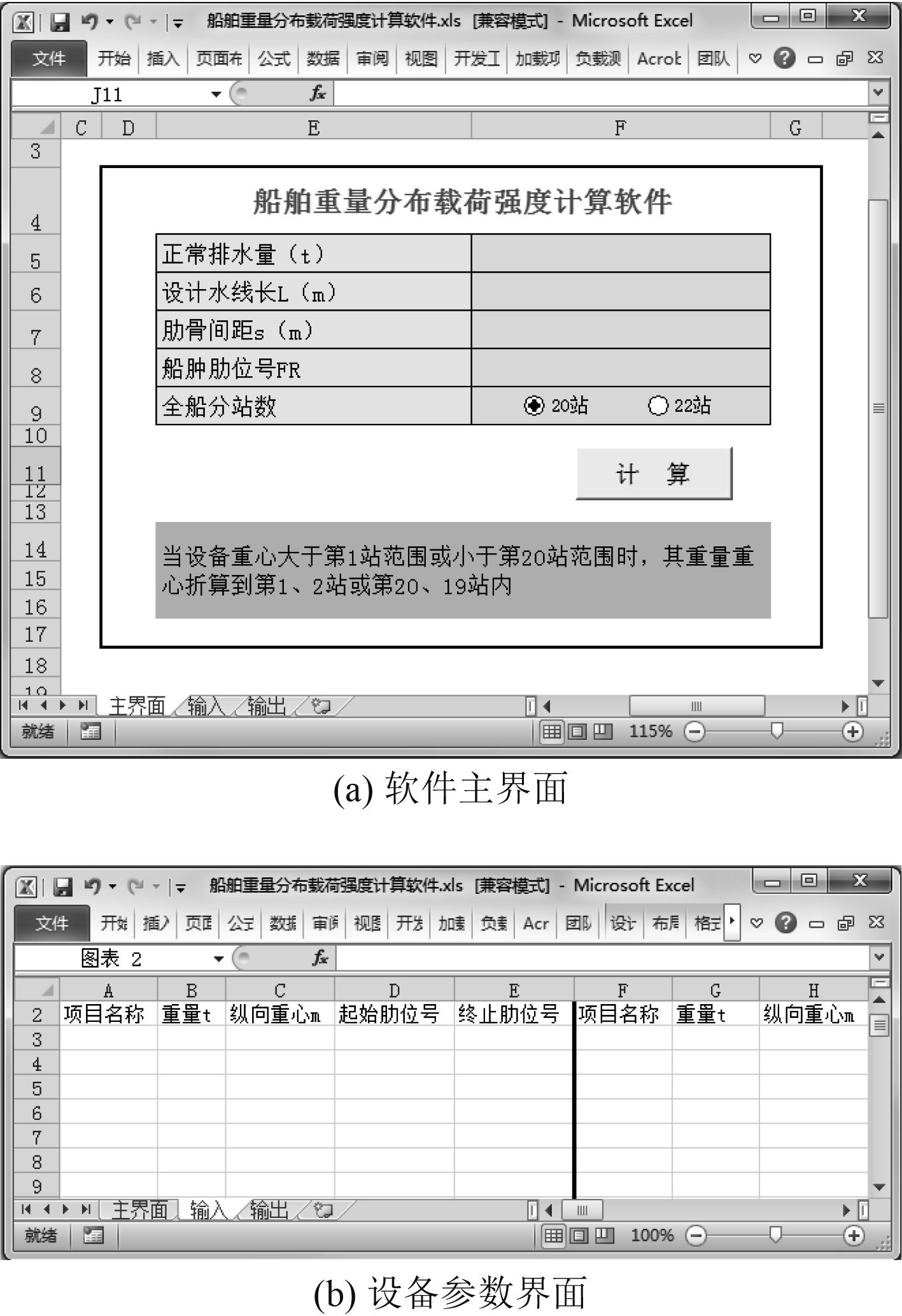
船舶重量分布载荷强度计算软件以Excel为计算工具,利用Office软件内嵌的面向对象编程语言VBA(Visual Basic for Application)语言对其进行了二次开发[8 – 9],通过XML DOM Document对象实现Excel与PDM之间的数据交互[10],读取PDM系统中各设备的坐标信息,如图6和图7所示。

|
图 7 PDM中设备重量中心信息 Fig. 7 Information of device weight center in PDM |
|
图 6 船舶重量分布载荷强度计算软件界面 Fig. 6 Software interface of ship weight distributed loading |
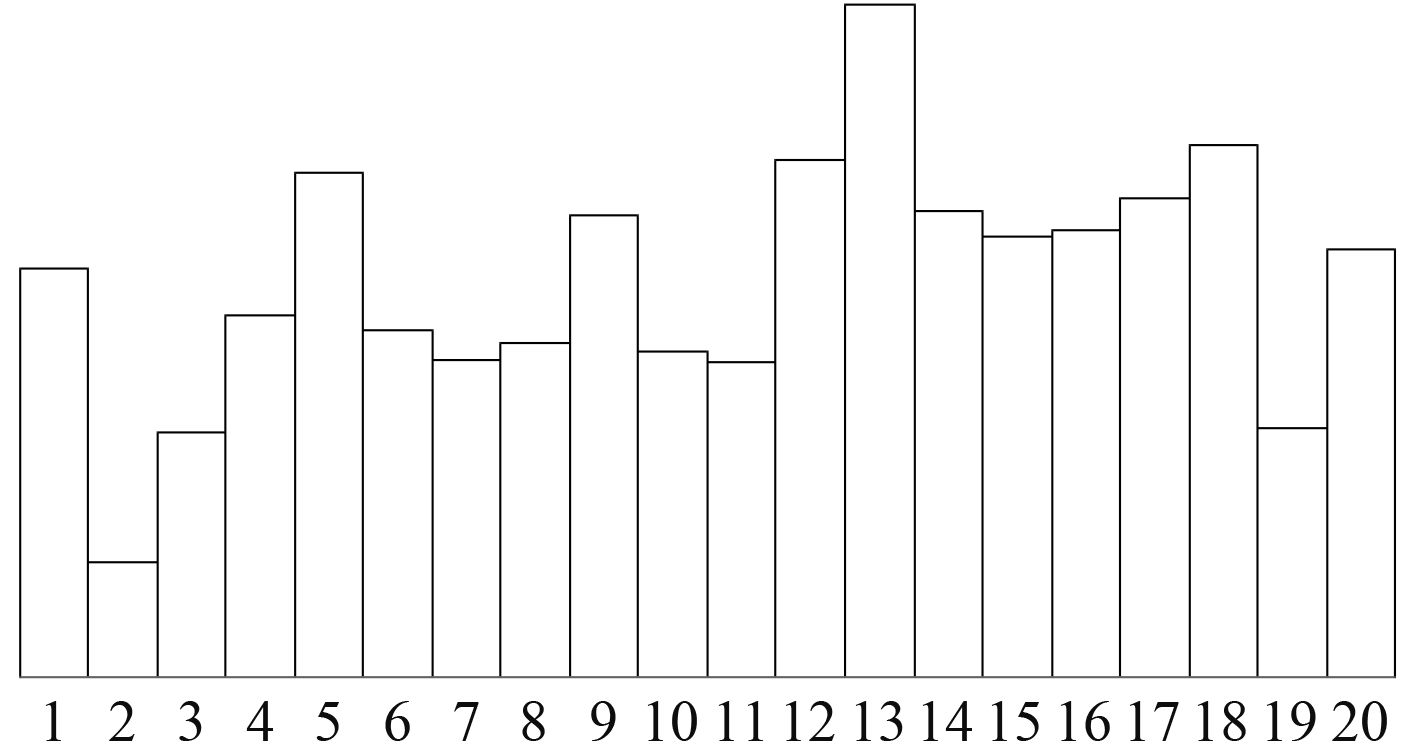
以某型船舶为例,其总体参数如表1所示,经船舶某设计专业计算后,该设备重量分布载荷强度如图8所示。
|
图 8 重量载荷强度分布图 Fig. 8 Distributed curve of ship weight |
|
|
表 1 船舶总体参数表 Tab.1 Overall parameters of ship |
可知,此重量载荷强度分布方法较为真实地反映了实际的重量分布规律,在此基础上可进一步实现货物、燃油、淡水、旅客等重量分布设计,以及静水剪力、弯矩、扰度等计算。
5 结 语本文在分析了船舶重量分布载荷强度分布原则的基础上,研究了重量分布载荷强度的基本计算模型,设计了将船首、船尾分别视为一个完整的理论站距的重量分布载荷强度计算方法,以Excel为计算工具,通过VAB开发与PDM实现数据交互,读取PDM系统中各设备的坐标信息,并结合实例进行了应用。该计算方法能够避免设备在船首、船尾的部分重量缺失或失真,能更真实地反映出船舶的重量分布,也为船舶行业重量分布载荷强度计算提供了一种快速、规范的计算方法。
| [1] |
邵开文, 马运义. 舰船技术与设计概论[M]. 北京: 国防工业出版社, 2009.
|
| [2] |
李培勇, 裘泳铭, 顾敏童, 等. 多体船型完整稳性计算[J]. 上海交通大学学报, 2002, 2: 1560-1564. LI Pei-yong, QIU Yong-ming, GU Min-tong, et al. Intact stability research for multi-hulls[J]. Journal of Shanghai Jiaotong University, 2002, 2: 1560-1564. DOI:10.3321/j.issn:1006-2467.2002.11.006 |
| [3] |
江雪云, 冯国庆, 张清越, 等. 纵向重量分布对SWATH波浪载荷的影响[C]// 中国钢结构协会海洋钢结构分会学术论文集, 2015: 57–61. ZHAO Li-shuang. XIA Guo-fa. JIA Xiao-yu. The impact on ship structural vibration caused by wave disturbance[J]. Ship Science and Technology, 2016, 38(8A): 4-6. |
| [4] |
刘向东. 船体结构与强度设计[M]. 北京: 人民交通出版社, 2007.
|
| [5] |
徐志海. 海洋平台建造中重量、重心控制的意义和基本方法[J]. 船舶设计通讯, 2011, 1: 12-15. XU Zhi-hai. The significance and basic means of weight and center of gravity control during construction of offshore platforms[J]. Journal of Ship Design, 2011, 1: 12-15. |
| [6] |
李菊红, 黄晓琼. 三体船重量分布对波浪载荷的影响[J]. 舰船科学技术, 2011, 33(9): 30-35. LI Ju-hong, Huang Xiao-qiong. The influence of the weight distribution on trimaran's wave loads[J]. Ship Science and Technology, 2011, 33(9): 30-35. DOI:10.3404/j.issn.1672-7649.2011.09.006 |
| [7] |
王杰德, 杨永谦. 船体强度与结构设计[M]. 北京: 国防工业出版社, 1995.
|
| [8] |
李晓玫, 杨小平. Excel中的VBA程序设计[J]. 四川师范大学学报(自然科学版), 2004, 27(4): 423-426. LI Xiao-mei, YANG Xiao-ping. VBA program design in Excel[J]. Journal of Sichuan Normal University (Natural Science), 2004, 27(4): 423-426. DOI:10.3969/j.issn.1001-8395.2004.04.023 |
| [9] |
常守明, 汪学锋. 船舶PDM管理Windchill系统中大批量数据导入技术究[J] 中国造船, 2012, 53(1): 199-206. CHANG Shou-ming, WANG Xue-feng. Research on technology of uploading large quantities of data in Windchill system for ship PDM management[J]. Ship Building of China, 2012, 53(1): 199-206. |
| [10] |
武彤, 陆昱霖. 基于XML映射模板实现不规则Excel数据的转换[J]. 计算机技术与发展, 2015, 25(7): 209-212. WU Tong, LU Yu-lin. Realization of conversion of irregular Excel data based on XML mapping Template[J]. Computer Technology and Development, 2015, 25(7): 209-212. |
 2018, Vol. 40
2018, Vol. 40
