由于水声环境的复杂性及水声对抗技术的不断发展,传统被动声呐目标识别中,基于经验及数学推理的模糊专家系统的局限性日益明显。而人耳听觉系统在多目标、低信噪比下的优异性能,成为新的研究热点。王磊等[1]提出基于听觉外周模型的水声目标识别方法。李秀坤等[2]利用Gammatone滤波器构建人耳听觉模型,进行水下目标识别。
随着计算机硬件技术、信号处理技术的进一步发展,以机器学习(Machine Learning,ML)、深度学习(Deep Learning,DL)技术为代表的人工智能(Artificial Intelligence,AI)技术,已经在手写字符识别、语音识别、图像理解、机器翻译等各个方面取得了一定成就,也为水声目标识别提供了新的思路。常国勇等[3]提出了从能量角度出发,采用小波变换、经验模态分解处理,以BP神经网络进行水声目标识别的方法。吴姚振等[4]提出了提取目标听觉特征,经BP神经网络和支持向量机进行分类的水声目标识别方法。曾向阳等[5]提出了智能水声目标识别系统的理论和设计实例。
本文根据水声目标信号特点,提取目标经典听觉感知特征——梅尔倒谱(Mel Frequency Cepstrum Coefficient,MFCC)特征,并引入机器学习中的几种典型方法——K近邻算法(K-nearest Neighbor,KNN)、支持向量机(Support Vector Machine,SVM)、卷积神经网络(Convolutional Neural Network,CNN)、深度置信网络(Deep Belief Network,DBN),对两类水声目标进行监督学习识别研究。根据样本特性及算法特点,建立目标样本集及网络模型;调整网络模型参数,分别进行预训练,并进行泛化性能测试,以获得网络参数最优设置方案;建立海试数据测试样本集,对预训练网络模型的识别性能进行统计分析。并给出了相应的样本集建立、网络模型设计和参数设置方案。
1 水声目标MFCC特征目标识别能力是声呐性能的重要部分,目标特征的提取和选择是提高目标识别率的关键。当前被动声呐目标识别主要依靠声呐员听觉感知,结合目标时域、频域、时频域特征来完成。因此,对人类视觉、听觉等生理感知特征的研究具有重要的现实意义。
在被动声呐发现水下快速目标并进行初步判断后,经过大致距离估算,启用主动声呐对目标进行精确定位。本文对被动声呐目标辐射噪声提取MFCC特征进行识别研究。
MFCC特征是一种经典的人耳听觉感知特征。根据听觉机理的相关研究发现,人耳对不同频率声波的灵敏度不同。Mel频率尺度反映了人耳频率感知的非线性特征,更符合人耳听觉特性,而MFCC是在Mel频率域提取的倒谱参数。
Mel频率与实际频率的具体关系可表示为:
| $Mel(f) = 2595\lg (1 + f/700){\text{,}}$ | (1) |
式中,f为实际频率,临界频率带宽随频率的变化而变化,并与Mel频率的增长一致,在1 000 Hz以下大致呈线性分布,带宽为100 Hz左右,在1 000 Hz以上呈对数增长,这就使得人耳对低频信号比高频信号更敏感。Mel频率的提出是为了方便人耳对不同频率声学信号的感知特性的研究。
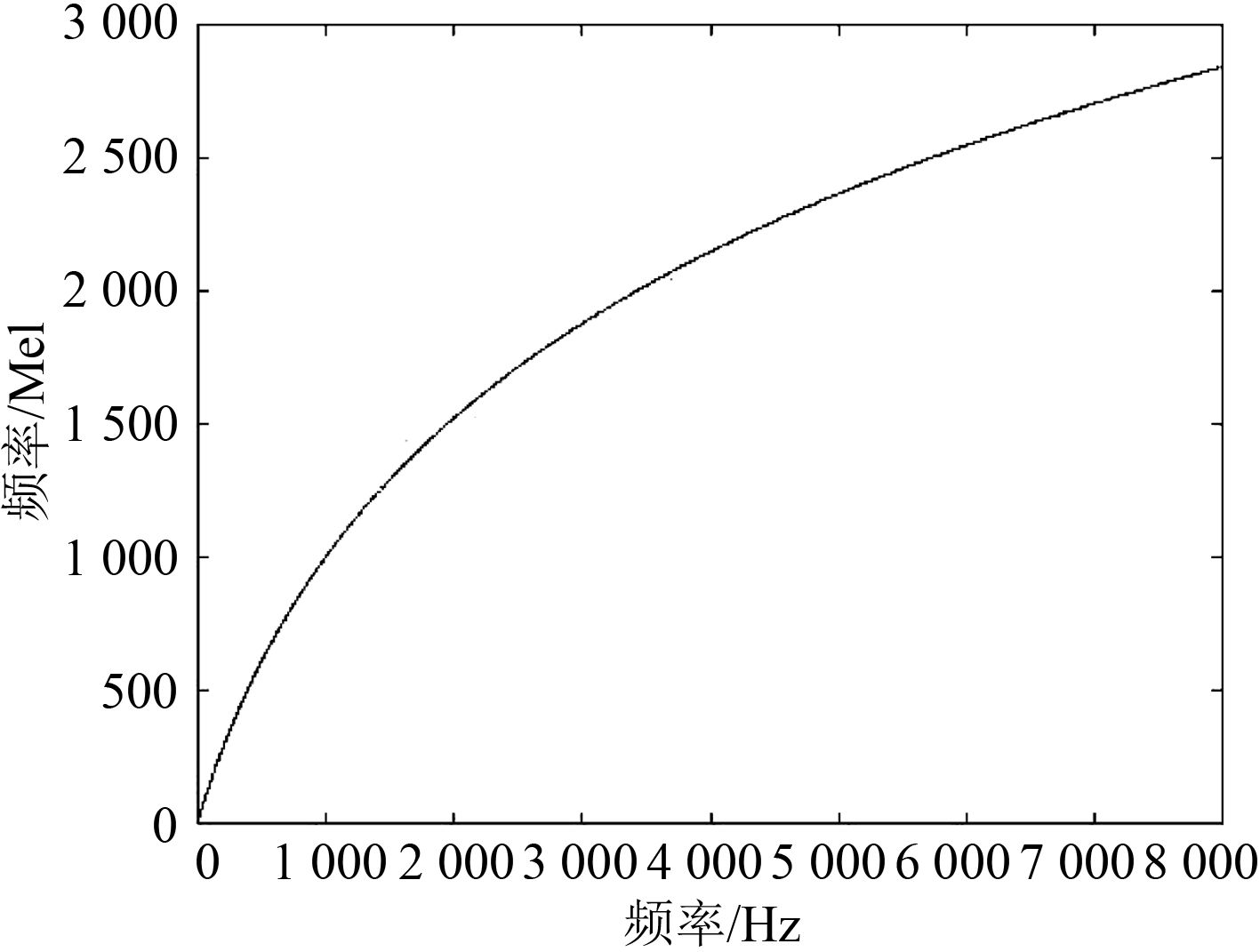
|
图 1 Mel频率与实际频率的对应关系 Fig. 1 Relationship between Mel frequency and actual frequency |
按式(1)变换到Mel域后,Mel带通滤波器组的中心频率按照Mel频率刻度均匀划分。用Mel滤波器组对语音频谱进行滤波和加权使语音信号更加逼近人类的听觉特性。
MFCC的计算过程如下:
将端点检测后的目标噪声信号经过预加重、分帧、加窗处理,再将时域分帧信号
| $X(k) = \sum\limits_{n = 0}^{N - 1} {x(n){e^{ - j2\pi nk/N}}}, 0 \leqslant n, k \leqslant N - 1{\text{。}}$ | (2) |
将上述线性频谱
| $S(m) = \ln [\sum\limits_{k = 1}^N {{{\left| {X(k)} \right|}^2}{H_m}(k)}], m = 1, 2, ...M{\text{。}}$ | (3) |
将上述对数频谱经过离散余弦变换(DCT)得到Mel频率倒谱系数
| $c(n) = \sum\limits_{m = 1}^M {S(m)\cos (n(m - 0.5)\frac{\pi }{M})}, (1 \leqslant n \leqslant m){\text{。}}$ | (4) |
监督学习(Supervised Learning)是指:给定一组输入x和输出y的训练集,学习如何关联输入和输出的过程。即利用一组已知类别的样本,通过调整分类器的参数,使其达到所要求性能的过程。
本文选取机器学习中经典的KNN、SVM、CNN和DBN识别模型,对两类被动声呐目标MFCC特征进行监督学习和识别分析。
2.1 KNN模型KNN学习模型工作机制为:给定测试样本,基于某种距离度量找出训练集中与其最靠近的k个训练样本,然后基于这k个近邻样本的信息来进行预测[6 – 7]。
KNN通过测量不同特征值之间的距离进行分类。其思路为:如果一个样本在特征空间中的k个特征空间中最邻近的样本中的大多数属于某一个类别,则该样本也属于这个类别。
具体流程为:
1)计算已知类别数据集合汇总的点与当前点的距离;
2)按照距离递增次序排序,选取与当前点距离最近的k个点;
3)确定距离最近的前k个点所在类别的出现频率;
4)返回距离最近的前k个点中频率最高的类别作为当前点的预测分类。
KNN算法的结果很大程度上取决于近邻数k的选择,此处距离一般使用欧氏距离或曼哈顿距离:
欧氏距离:
曼哈顿距离:
KNN算法的优势在于:依据k个对象中占优的类别进行决策,而非单一的对象类别决策;且通过计算对象间距离作为各个对象之间的非相似性指标,避免了对象之间的匹配问题。
2.2 SVM模型SVM由Vapnik等于1995年提出,是一种基于统计学习理论的模式识别方法。SVM基于结构风险最小化准则,能够在训练误差和分类器容量之间达到较好的平衡,在解决小样本、非线性及高维模式识别中表现出许多独特优势[8]。
分类问题最基本的思路,就是基于训练集在样本空间找到一个划分超平面,将不同类别的样本分开。样本空间中,划分超平面可通过式(5)描述:
| ${\omega ^{\rm {T}}}x + b = 0{\text{,}}$ | (5) |
其中ω为超平面法向量,b为偏置项,满足关系:
| $\left\{ \begin{array}{l}{\omega ^{\rm {T}}}{x_i} + b > + 1\;\;\;{y_i} = + 1{\text{,}}\\{\omega ^{\rm {T}}}{x_i} + b \leqslant - 1\;\;\;{y_i} = - 1{\text{。}}\end{array} \right.$ | (6) |
距离超平面最近的几个训练样本点使式(6)等号成立,被称为“支持向量”,2个异类支持向量到超平面的距离之和被称为间隔:
| $\gamma = \frac{2}{{\left\| \omega \right\|}}{\text{。}}$ | (7) |
求解分类最优超平面的过程即寻找最大间隔的过程,而最大化间隔,仅需最大化
| $\begin{array}{l}\mathop {\min }\limits_{\omega ,b} \displaystyle\frac{1}{2}{\left\| \omega \right\|^2}\\{\rm{s}}.{\rm{t}}.\;\;\;{y_i}({\omega ^{\rm {T}}}{x_i} + b) \geqslant 1,\;\;i = 1,2, \ldots ,m{\text{。}}\end{array}$ | (8) |
对非线性可分问题,则将样本从原始空间映射到高维特征空间,将非线性可分为题转化为线性可分为题。常用的核函数有:线性核函数、高斯核函数、Sigmoid核函数等[6,9]。
2.3 CNN模型CNN最初是针对二维形状的识别而设计的一种多层传感器,在平移情况下具有高度不变性,在缩放和倾斜的情况下也具有一定的不变性。LeCun等提出了权值共享技术,又将卷积层和降采样层结合构成卷积神经网络的主要结构,形成了现代卷积神经网络的雏形LeNet结构,这是第一个真正的多层结构学习网络,利用空间相对关系减少参数数目以提高训练性能[10, 11]。本文主要选用LeNet结构进行改进和识别研究。
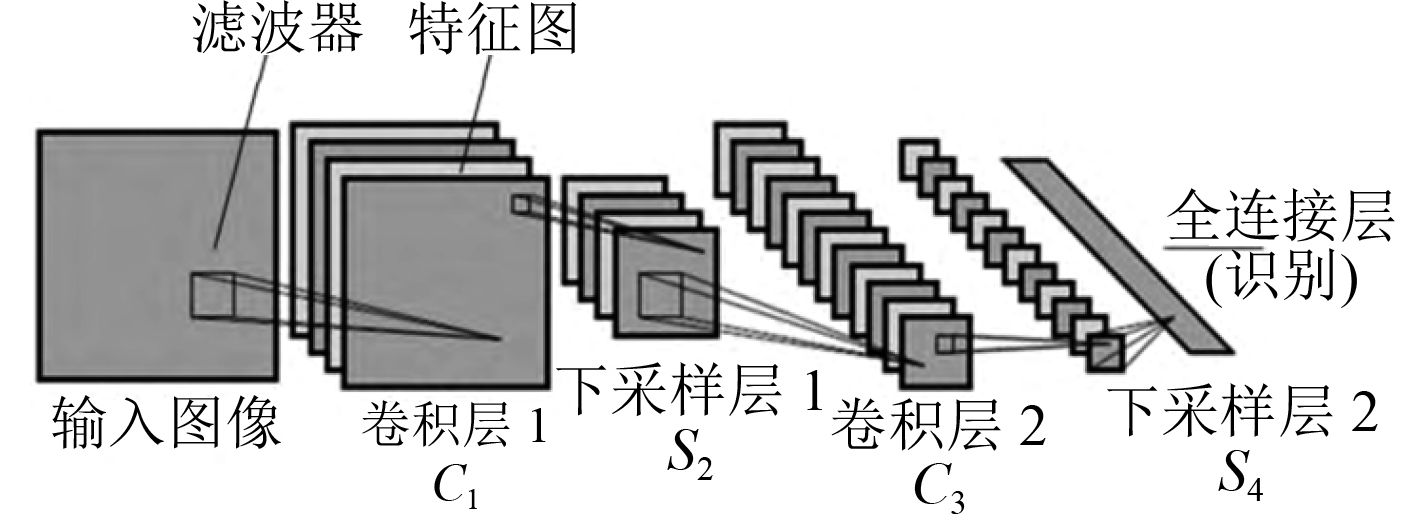
|
图 2 用于手写字符识别的LeNet网络 Fig. 2 LeNet network applied in handwriting recognition |
CNN是一种特殊的前馈神经网络模型,其最显著的特点在于其局部感受野的概念和层层迭代的结构[12]。CNN一般由输入层、卷积层、下采样层、全连接层及输出层组成。
以图2中用于手写字符识别的LeNet网络为例:先将样本图像进行规整后输入网络;经过卷积层C1、C3将样本图像与卷积核进行卷积操作,得到若干特征图;在降采样层C2,C4进行模糊和泛化;最后通过全连接层,生成和输出识别结果。
其中,样本与卷积核进行卷积后,经激活函数映射,可得到输出特征:
| $x_j^{(l)} = f\left(\sum\limits_{i \in {M_j}} {x_j^{(l - 1)} * W_{ij}^{(l)} + b_j^{(l)}} \right){\text{,}}$ | (9) |
其中
由卷积层和下采样层的组合迭代,可不断将目标低维特征提取出来,并组合成为抽象的高维特征,某种程度上实现了网络的“抽象思维”,而且在多维特征的学习中可以有效关注维度之间的关联性。同时,引入BP算法,使CNN网络训练更高效,应用更广泛。
在网络训练过程中,将训练样本集分为相同大小批次(batch)进行训练,对误差函数采用梯度下降算法进行迭代训练直至收敛。学习率
DBN由Hinton等于2006年提出,是一种无监督贪婪逐层训练算法,为解决深层结构相关的优化难题提供了新的途径。DBN以受限波兹曼机(RBM:Restricted Boltzmann Machine)为基础网络结构,可以进行逐层堆叠。这种结构对于形成逐层抽象网络结构比其他网络模型更容易实现[14]。
RBM是一种特殊的马尔可夫随机场(MRF:Markov Random Field,MRF),一个RBM包含一个由随机单元构成的隐层(一般为伯努利分布)和一个由随机的可见预测单元构成的可见层(一般为伯努利或者高斯分布)[15]。RBM网络的特点是:在给定可视层单元状态时,各隐层单元的激活条件独立;给定隐层单元状态时,可见层单元的激活条件也独立。且只要隐层单元的数目足够,RBM可以拟合任意离散分布[16 – 18]。
假设目标由一组
| $P(\vec v = v, \vec h = h) = \frac{1}{Z}\exp ( - E(v, h)){\text{,}}$ | (10) |
其中E为RBM能量函数:
| $E(v, h) = - {b^{\rm {T}}}v - {c^{\rm {T}}}h - {v^{\rm {T}}}Wh{\text{,}}$ | (11) |
其中Z为归一化函数:
| $Z = \sum\limits_v {\sum\limits_h {\exp \left\{ { - E(v, h)} \right\}} } {\text{。}}$ | (12) |
DBN由多个RBM堆叠,进行无监督预训练获得权值,再对生成模型进行调优。DBN训练过程中,首先充分训练第1个RBM;固定第1个RBM的权重和偏移量,然后使用其隐性神经元的状态,作为第2个RBM的输入向量;充分训练第2个RBM后,将第2个RBM堆叠在第1个RBM的上方;重复上述步骤多次直至所有RBM训练结束。DBN调优过程中,除了顶层RBM,其他层RBM的权重被分成向上的认知权重和向下的生成权重;之后经Contrastive Wake-Sleep算法调整和更新网络参数。
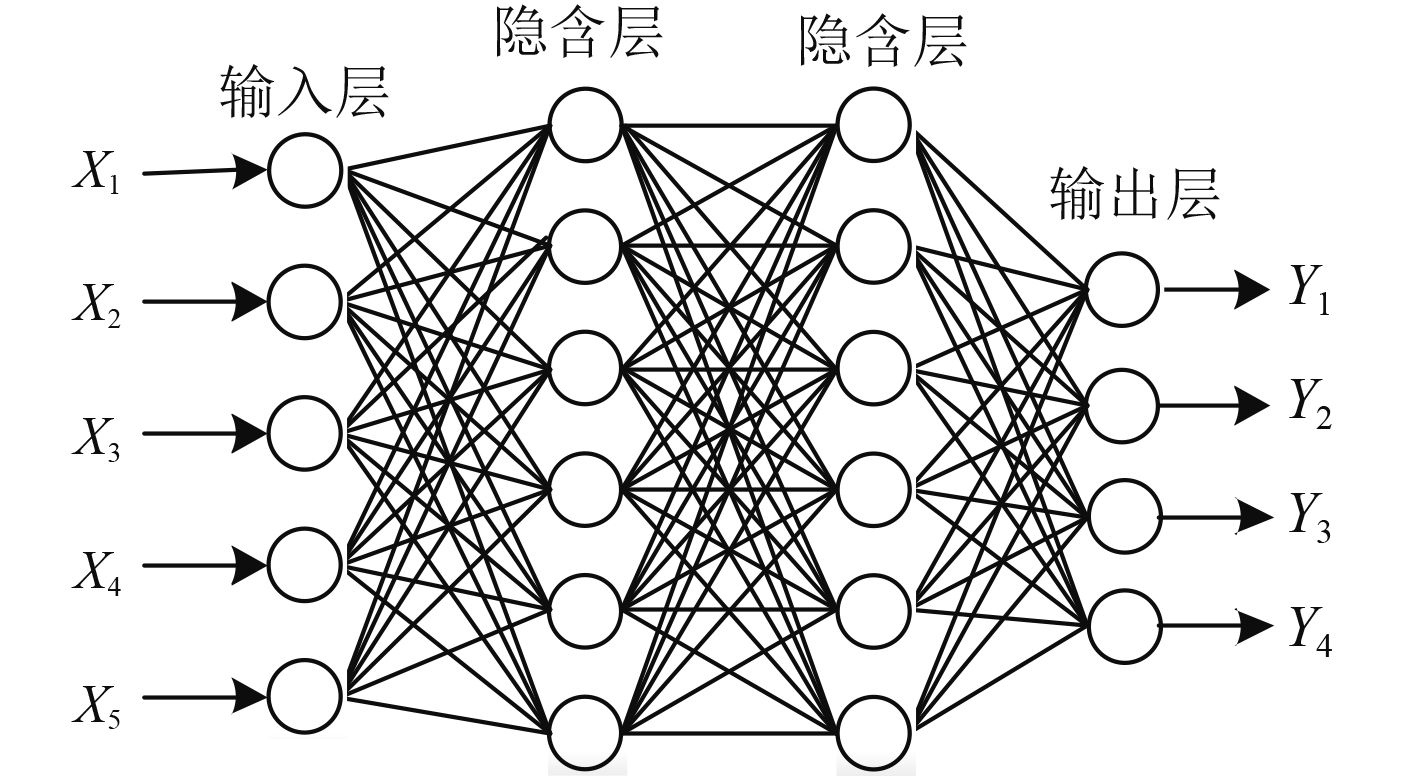
|
图 3 深度置信网络结构 Fig. 3 Structure of deep belief network |
DBN网络可以用来对数据的概率分布建模,也可以用来对数据进行分类。试验中,为每种目标样本分别建立了DBN模型进行识别研究,DBN模型经RBM逐层预训练之后,再进行参数调优。
3 海试数据处理及监督学习网络设计试验中对A、B两类水声目标海试数据进行分析和识别研究。先选取海试数据建立样本集,对网络进行预训练及泛化性测试,以获得最优网络参数设置方案及预训练网络;再另选海试数据建立样本集,以预训练网络对新样本集进行识别研究。
监督学习模型的识别泛化性能可通过试验测试进行评估,常采用一个“测试集”来测试模型的识别性能,并以测试集“测试误差”作为模型泛化误差的近似[6]。测试集样本也从样本真实分布中独立同分布采样而得,且与训练集互斥,即测试样本尽量不在训练集中出现、未在模型训练过程中使用过。
试验中,采用“留出法”,将样本集划分为2个互斥的集合,其中A、B类目标各随机抽取80%作为训练集,其余20%作为测试集。
其中,识别率采用预训练网络对样本集的识别正确数,除以样本总数得到,所有试验方案重复3次,结果取均值。
3.1 样本集建立试验中根据样本集参数设置,分别对信号分帧后各自提取特征建立样本集。试验中信号分帧长度80 ms,帧移50%。
首先,对历次海试数据按信噪比进行排序,其中A类目标6次海试数据按信噪比由高到低编为A1–A6,B类目标4次海试数据按信噪比由高到低编为B1–B4,每段数据长约200 s。
选取A类目标数据A1、A3、A5,B类目标数据B1、B3,分别提取MFCC样本构建网络预训练及泛化性测试样本集;另取A类目标数据A2、A4、A6,B类目标数据B2、B4,分别提取MFCC样本建立目标识别样本集,通过预训练网络进行识别分析。
其次,针对不同监督学习模型对样本的要求,对网络预训练及泛化性测试样本集、目标识别样本集分别进行处理。
对KNN、SVM模型,以每帧数据提取的MFCC参数作为一个样本,对样本每一参数进行标记,生成table格式样本;对CNN模型,将10帧数据提取的一维MFCC特征组合生成二维矩阵作为一个样本,样本重叠率80%;对DBN模型,每帧数据提取的MFCC特征作为一个样本,所有样本分别归一化至[0,1]。
|
|
表 1 为各监督学习模型建立的样本集大小 Tab.1 Databases for various unsupervised learning models |
试验中,结合Matlab平台Classification Learner APP、DeepLearnToolbox,对各样本集分别建立识别网络进行相关研究。
首先对KNN、SVM、CNN、DBN模型,分别设定不同网络参数,以预训练样本集进行训练,直至网络误差函数收敛;再以泛化性测试集对预训练网络进行泛化性测试,对比各参数设置方案下的网络泛化性能,获得最优参数设置方案,保存预训练网络进行新样本集识别研究。
对KNN模型,根据目标信号特点,分别以近邻数为1、10、100,距离选择欧氏距离、平方反比加权欧氏距离进行预训练。
对SVM模型,根据目标信号特点,调整核函数为线性核函数、二次多项式核函数、三次多项式核函数、高斯核函数进行预训练。
对CNN模型,根据目标信号特点,在LeNet5结构的基础上进行相关改进,调整参数预训练多个CNN网络进行识别。设定学习率
对DBN模型,根据目标信号特点,设定学习率
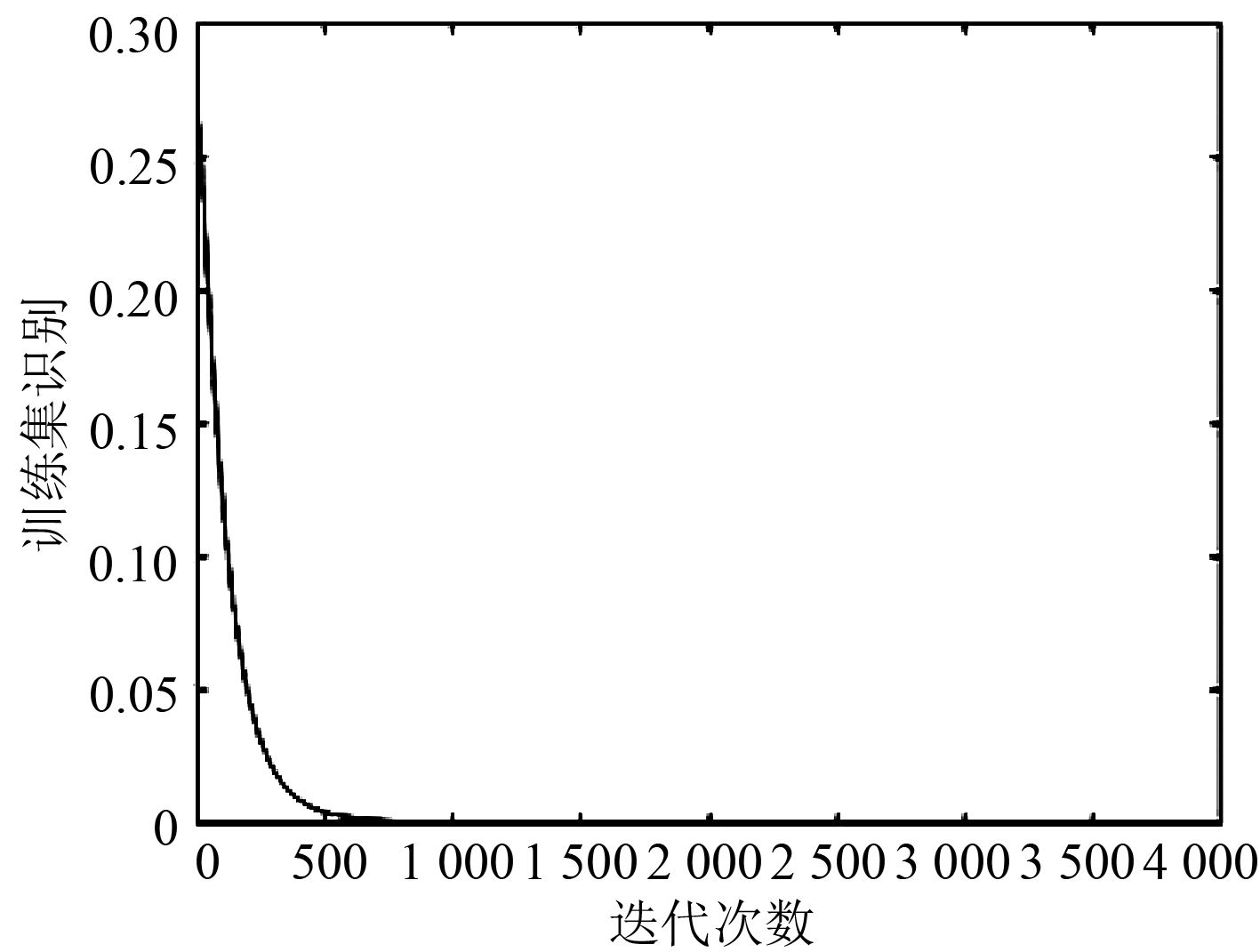
|
图 4 CNN模型参数选择卷积核大小为5×5,分批训练规模为50个样本,网络隐含层数为4层时的网络均方误差 Fig. 4 Mean square error of the pre-trained CNN when kernelsize=5×5, batchsize=50, and constructed from 4 hidden layers |
各参数设置方案对应的网络预训练完毕后,对泛化性测试集进行识别,统计识别误差以表征预训练网络泛化性能。得到预训练网络泛化性能最优的参数设置方案为:KNN模型参数选择欧氏距离,10个近邻样本;SVM模型参数选择高斯核函数;CNN模型参数选择学习率
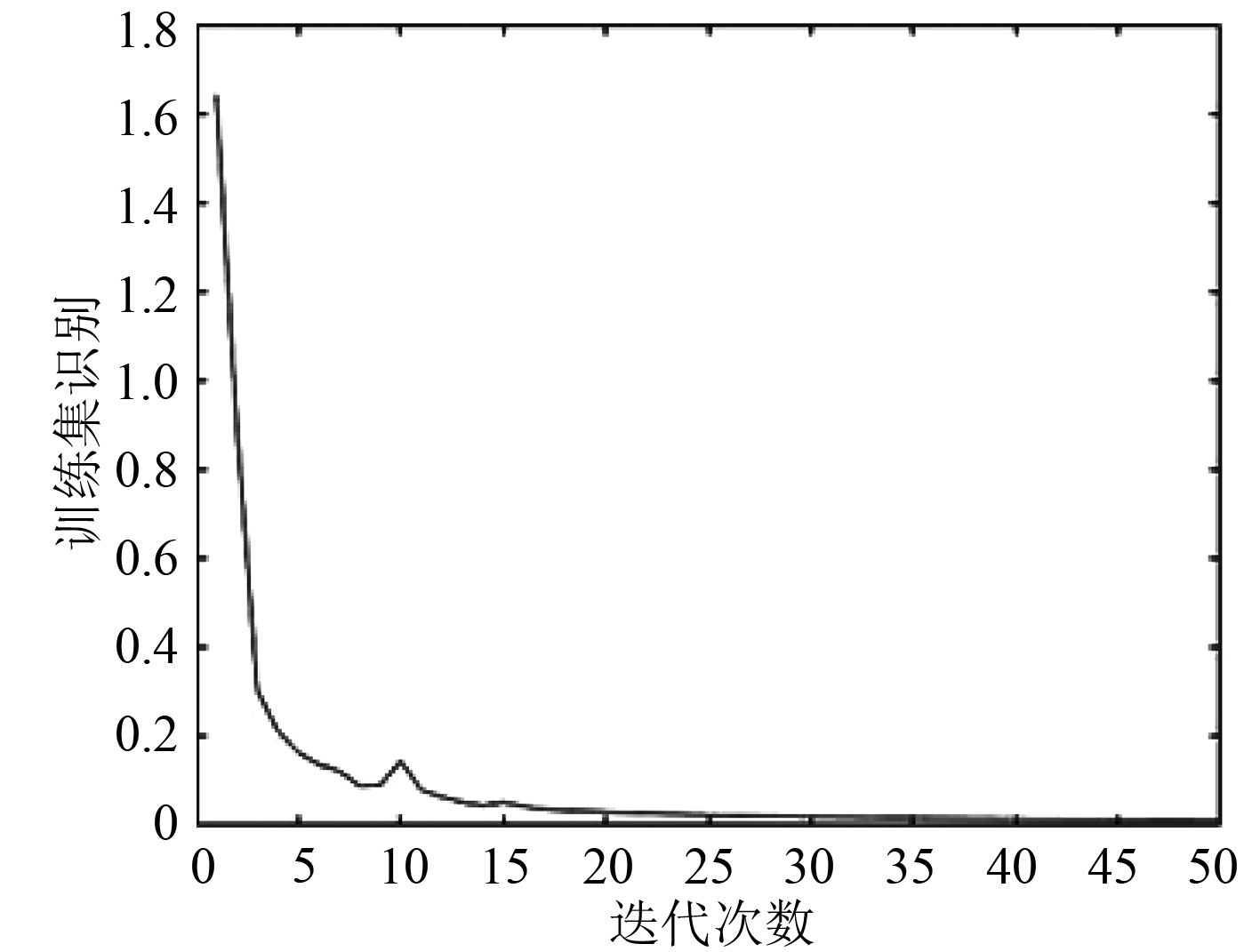
|
图 5 DBN模型参数选择分批训练规模为50个样本,网络由3个200隐层单元RBM组成时,网络均方误差 Fig. 5 Mean square error of the pre-trained DBN when batchsize=50, and constructed from 3 RBM with 200 elements |
以预训练网络对目标识别样本集进行识别分析,所有试验重复3次结果取均值。分别计算预训练网络对两类目标的识别性能,识别结果如表2所示。
|
|
表 2 各预训练网络目标识别性能(%) Tab.2 Recognition accuracy of various pre-trained networks (%) |
试验结果表明,4种模型对A类目标识别率达到100%,KNN模型对B类目标的识别率较低,SVM、CNN、DBN模型对B类目标的识别结果相近,其中DBN模型对B类目标识别性能最佳。
4 结 语本文从被动声呐目标识别出发,用4种监督学习模型对A、B两类水声目标,不同次海试、不同信噪比数据中提取的MFCC特征样本进行了识别研究。分析海试数据处理及多种模型识别结果可得到以下结论:
提取目标MFCC特征并以监督学习模型进行识别的方法,用于被动声呐目标识别具有可行性,其运算速度快、识别率较高的特点对于提高被动声呐目标识别性能有一定优势;水声环境复杂多变,试验中仅对有限数据按照信噪比粗略排序后进行识别分析,信噪比条件对各识别模型性能的影响有待进一步量化和分析研究;由于样本集规模及特征维数较小,CNN、DBN两种深度学习模型在大数据、高阶特征挖掘中的优势未得到充分体现。
| [1] |
王磊, 彭圆. 听觉外周计算模型在水中目标分类识别中的应用[J]. 电子学报, 2012, 40(1): 199-203. WANG Lei, PENG Yuan. The application of computational auditory peripheral model in underwater target classification[J]. Acta Electronical Sinica, 2012, 40(1): 199-203. |
| [2] |
李秀坤, 孟祥夏. 水下目标回波和混响在听觉感知特征空间的分类[J]. 哈尔滨工程大学学报, 2015, 36(9): 1183-1187. LI Xiu-kun, MENG Xiang-xia. Classification of under-water target echoes and reverberation in auditory per-ception feature spaces[J]. Jornal of Harbin Engineeri-ng University, 2015, 36(9): 1183-1187. |
| [3] |
常国勇, 袁富宇, 崔杰. 基于不同能量值特征优选的水声目标识别[J]. 指挥控制与仿真, 2016, 38(2): 60-65. CHANG Guo-yong, YUAN Fu-yu, CUI Jie. Underwat-er acoustic target recognition based on feature select-ion of different energy feature[J]. Command Control and Simulation, 2016, 38(2): 60-65. DOI:10.3969/j.issn.1673-3819.2016.02.013 |
| [4] |
吴姚振. 水下目标辐射噪声生理感知特征的提取方法研究[D]. 西安: 西北工业大学, 2014.
|
| [5] |
曾向阳. 智能水中目标识别[M]. 北京: 国防工业出版社, 2016.
|
| [6] |
周志华, 机器学习[M]. 北京: 清华大学出版社, 2016.
|
| [7] |
HARRINGTON P. Machine learning in action[M]. Manning Publications Co. 2012.
|
| [8] |
戴冬, 卫娟. K-means与SVM结合的水下目标分类方法[J]. 舰船科学技术, 2015, 37(2): 204-207. DAI Dong, WEI Juan. Research on target identificat-ion underwater method by K-means and SVM[J]. Ship Science and Technology, 2015, 37(2): 204-207. DOI:10.3404/j.issn.1672-7649.2015.02.046 |
| [9] |
NEUMANN J, SCHNÖRR C, STEIDL G. Combined SVM based feature selection and classification[J]. Machine Le- arning, 2005, 61: 129-150. DOI:10.1007/s10994-005-1505-9 |
| [10] |
王强, 曾向阳. 深度学习方法及其在水下目标识别中的应用[J]. 声学技术, 2015, 34(2): 138-140. WANG Qiang, ZENG Xiang-yang. Deep learning methods and their applications in underwater targets rec-ognition[J]. Technical Acoustics, 2015, 34(2): 138-140. |
| [11] |
LECUN Y, BENGIO Y, HINTON G. Deep learning[J]. Nature, 2015, 521(7553): 436-444. DOI:10.1038/nature14539 |
| [12] |
张大伟, 章新华. 基于听觉感知与卷积神经网络识别舰船目标[J]. 声学技术, 2015, 34(6): 182-184. ZHANG Da-wei, ZHANG Xin-hua. Recognition of ships based on auditory sense and convolutional neural networks[J]. Technical Acoustics, 2015, 34(6): 182-184. |
| [13] |
史鹤欢, 许悦雷. PCA预训练的卷积神经网络目标识别算法[J]. 西安电子科技大学学报, 2016, 43(3): 161-166. SHI He-huan, XU Yue-lei. Convolutional neural networks recognition algorithm based on PCA[J]. Journal of Xidian University, 2016, 43(3): 161-166. DOI:10.3969/j.issn.1001-2400.2016.03.028 |
| [14] |
鲁铮. 基于T-RBM算法的DBN分类网络的研究[D]. 吉林: 吉林大学, 2014.
|
| [15] |
LI D, DONG Y. Deep learning methods and applicati-ons[M]. Foundations and Trends in Signal Processing, 2015.
|
| [16] |
BENGIO Y. Learning deep architecture for AI[M]. Fo-undations and Trends in Machine Learning: 2009.
|
| [17] |
焦李成, 赵进, 杨淑媛, 等. 深度学习优化与识别[M].北京: 清华大学出版社, 2017. JIAO Licheng, ZHAO Jin, YANG Shuyuan, et al. D-eep learning, optimization and recognition[M]. Beijing: Tsinghua University Press, 2017. |
| [18] |
GOODFELLOW I, BENGIO Y, COURVILLE A. 深度学习[M]. 北京: 人民邮电出版社, 2017.
|
 2018, Vol. 40
2018, Vol. 40
