自适应阵列处理作为阵列信号处理的重要分支,其关键在于依托自适应方向图来实现对特定信号的接收和对干扰的抑制[1]。Applebaum在自适应阵列最优权方面的工作,使得自适应阵列处理能够直接对各阵元加自适应权而得到适合于信号干扰环境的自适应方向图[2]。在Widrow和Capon等基础上,Frost将单一的无失真响应约束推广为线性约束最小方差波束形成器(LCMV)[3],可根据信号干扰环境得到更好的自适应方向图。然而,LCMV在存在多重干扰[4 – 5]、快拍数较少[6 – 7]时,输出信干噪比下降,方向图恶化严重,甚至不能保留主瓣特性和生成准确零陷。
自适应方向图控制作为一个困难的非线性优化问题,已有的许多经典方法可以参考,但常常无法推广[8],而进化算法被证明是得到此类问题最优解的有效方法[2]。因此,诸如遗传算法(Genetic Algorithm)[9]、蚁群优化算法(Ant Colony Optimization)[10]、模拟退火算法(Simulated Annealing)[11]等进化算法均被广泛应用于阵列方向图的最优化问题之中。粒子群优化算法(Particle Swarm Optimization,PSO)相较于传统分析方法、经典优化算法和其他进化算法,易于理解和实现、程序清晰和简单,且因算法兼顾个体特征和全体特征故可更快收敛[12],在求解此类非线性优化问题时表现出优越的性能。
PSO算法最早由J. Kennedy和R. Eberhart提出[13],受到人工生命的研究结果启发,其基本概念源于对蜂群采蜜行为的研究。目前,PSO算法已广泛应用于电力系统领域[14]、系统可靠性设计[15]、图像处理[16]等领域。本文结合LCMV自适应波束形成及PSO算法,基于最大信干噪比(SINR)准则,提出一种多虚拟干扰改进PSO算法,有效改善了LCMV方法的输出信干噪比,且在处理自适应方向图控制问题方面效果显著。
1 LCMV波束形成处理模型 1.1 阵列数据模型考虑
由阵列信号处理理论可知,阵列接收数据可表示为[1]
| ${{x}}\left( t \right) = {{As}}\left( t \right) + {{n}}\left( t \right){\text{,}}$ | (1) |
其中:
| ${\beta _i} = \frac{{2\pi }}{\lambda }d\sin \left( {{\theta _i}} \right){\text{,}}$ | (2) |
阵元接收到的远场信号经其后接收机加权相加后,得到的阵列输出为:
| $y = {{{w}}^H} \cdot {{x}}\left( t \right){\text{,}}$ | (3) |
式中,
线性约束最小方差波束形成器的权矢量可表示为
| ${{{W}}_{LCMV}} = \mathop {\arg }\limits_{{{{w}}^H}{{C}} = {{{f}}^H}} \min {{{W}}^H}{{{R}}_X}{{W}}{\text{,}}$ | (4) |
式中:
| ${{{W}}_{LCMV}} = {{R}}_X^{ - 1}{{C}}{\left( {{{{C}}^H}{{R}}_X^{ - 1}{{C}}} \right)^{ - 1}}{{f}}{\text{。}}$ | (5) |
LCMV作为经典的自适应波束形成算法,广泛应用于抑制干扰和增强期望信号等方面,下文将引入改进的粒子群算法以改善LCMV在多重干扰、低快拍等情况下性能较差的缺陷。

|
图 1 自适应阵列空间位置关系 Fig. 1 Spartial locations of adaptive array |
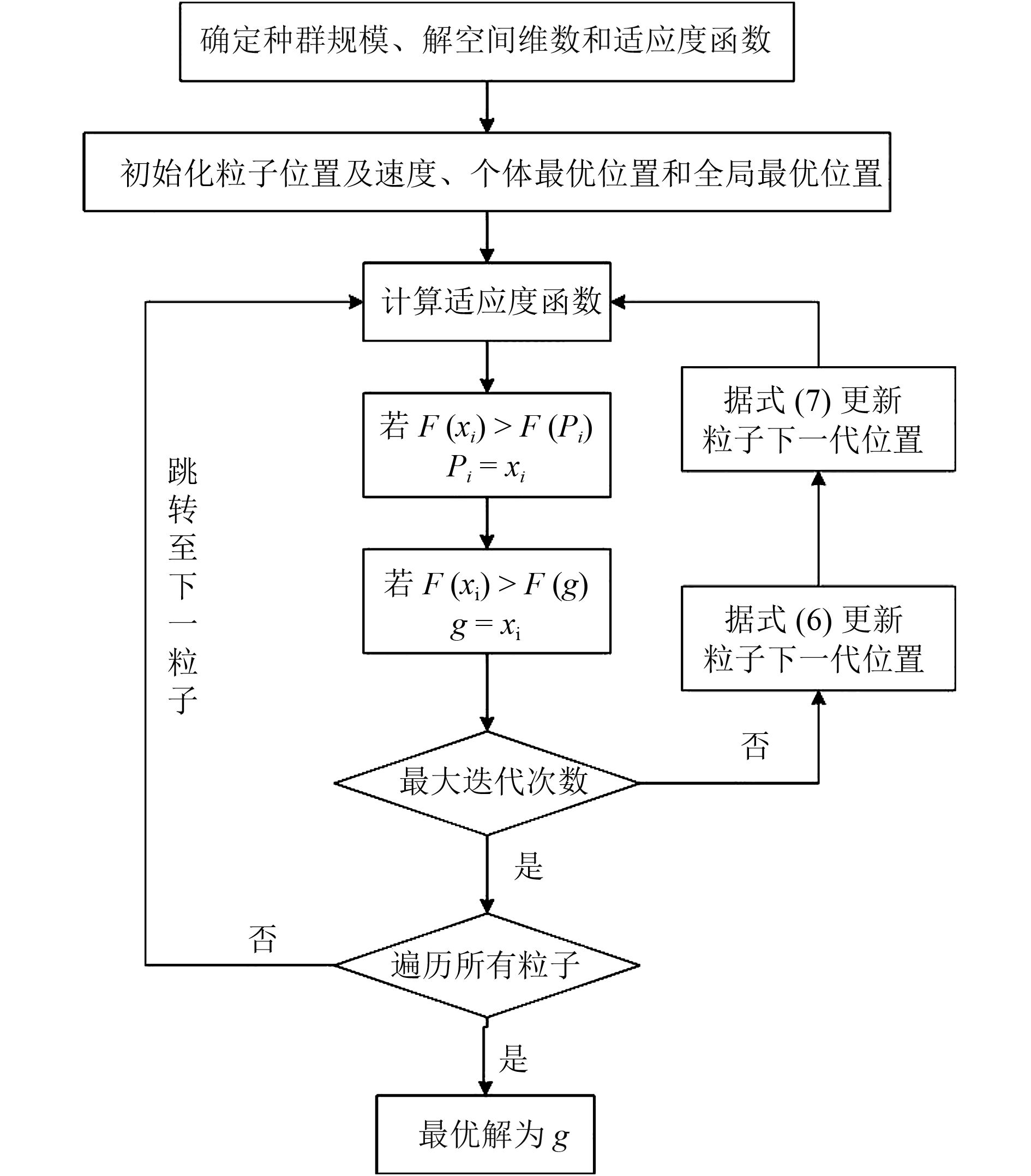
PSO算法作为一种有效的解决非线性优化问题的遗传算法,受启发于鸟类群体运动的规律性,利用群体智能建立一个简化模型,相较于GA、SA等遗传算法,更不易于早熟或停滞于局部极值。算法发展迅速,且研究者的改进很多,但其基本原理相差无几。
PSO算法利用种群群体及其
粒子群中第
| $\begin{split}{v_{ij}}\left( {t + 1} \right) = & w{v_{ij}}\left( t \right) + {c_1}{r_{1j}}\left( {{p_{ij}} - {x_{ij}}\left( t \right)} \right) +\\& {c_2}{r_{2j}}\left( {{g_{ij}} - {x_{ij}}\left( t \right)} \right){\text{,}}\end{split}$ | (6) |
| ${x_{ij}}\left( {t + 1} \right) = {x_{ij}}\left( t \right) + {v_{ij}}\left( {t + 1} \right){\text{。}}$ | (7) |
其中,
PSO算法的核心在于每次迭代中对粒子速度和位置的更新,基于式(6)和式(7),粒子在整个空间内飞行进行搜索,不断学习个体最优和种群最优,调整飞行速度和粒子位置,直到寻找到最优解或达到最大迭代次数。通过设计合适的适应度函数,PSO算法可有效应用于阵列方向图控制领域。
|
图 2 粒子群算法基本流程 Fig. 2 Flowchart showing the main steps of the basic PSO algorithm |
在应用于阵列方向图控制的基本粒子群算法中,粒子位置可被视为阵列权矢量,算法开始于随机初始化
| ${{X}} = \left[ {\begin{array}{*{20}{c}}{{{W}}_{LCMV}^{\rm {T}}}\\{{{{x}}_2}}\\{{{{x}}_3}}\\ \vdots \\{{{{x}}_N}}\end{array}} \right]{\text{。}}$ | (8) |
其中
PSO算法通过计算粒子的适应度函数值来指导粒子的整个搜寻过程,其设计的好坏直接决定了优化效果。在阵列方向图优化问题中,阵列增益、旁瓣级、方向图形状等参量均可作为其适应度函数的设计依据。为提高自适应阵列的干扰抑制能力,在特定方向得到期望的零陷,本文提出了一种基于最大信干噪比准则的改进适应度函数,该适应度函数通过添加虚拟干扰的方法以加深或展宽零陷,从而达到抑制干扰的目的。其设计形式如下:
| $F\left( {{x}} \right) = \frac{{\sum\limits_{s = 1}^S {\sigma _s^2{{\left| {{{{x}}^*}{{a}}\left( {{\theta _s}} \right)} \right|}^2}} }}{{\sum\limits_{i = 1}^I {\sigma _i^2{{\left| {{{{x}}^*}{{a}}\left( {{\theta _i}} \right)} \right|}^2}} + \sigma _n^2}}\text{,}$ | (9) |
其中
通过控制阵列权矢量,自适阵列处理可通过零陷生成技术在特定方向生成零陷以抑制干扰,本节会深入分析文中提出的基于LCMV自适应波束形成的改进PSO算法,该方法所求得的阵列权矢量在增强期望信号和抑制干扰信号方面的性能表现将通过仿真实例验证。下文将主要讨论在增强期望信号前提下的两类自适应方向图控制问题,其一为在干扰方向自适应零陷加深,其二为干扰区域自适应零陷展宽。同时,通过与LCMV方法的横向对比和自身的纵向对比,研究并分析算法的有效性。
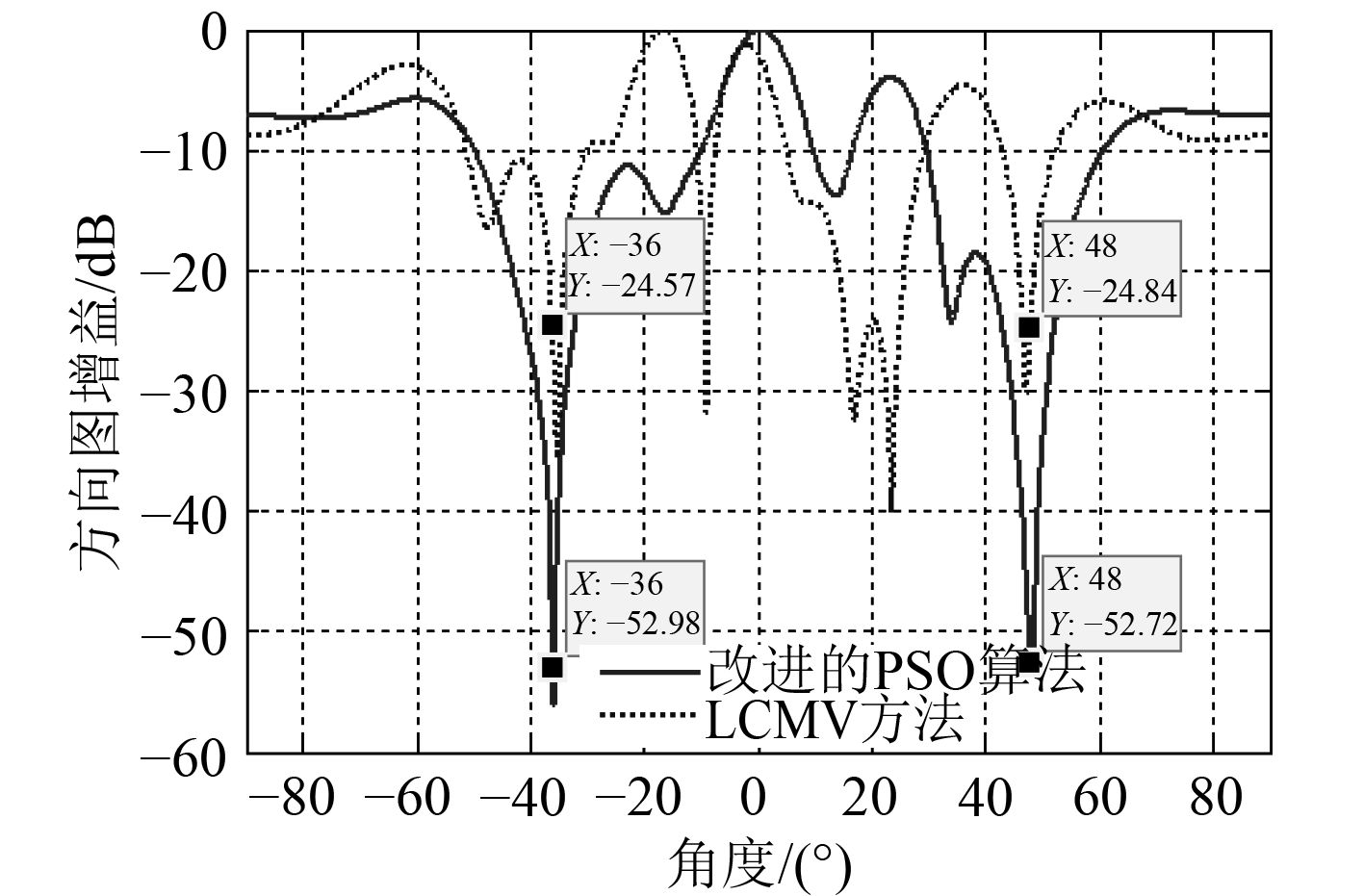
3.1 干扰方向自适应零陷加深本实例将讨论文中提出的改进PSO算法在干扰方向形成自适应深零陷的有效性。考虑一个阵元间距为半波长的均匀线阵,阵元个数
|
图 3 200次迭代结果 Fig. 3 Simulation result when the total number of iterations generations is 200 |
|
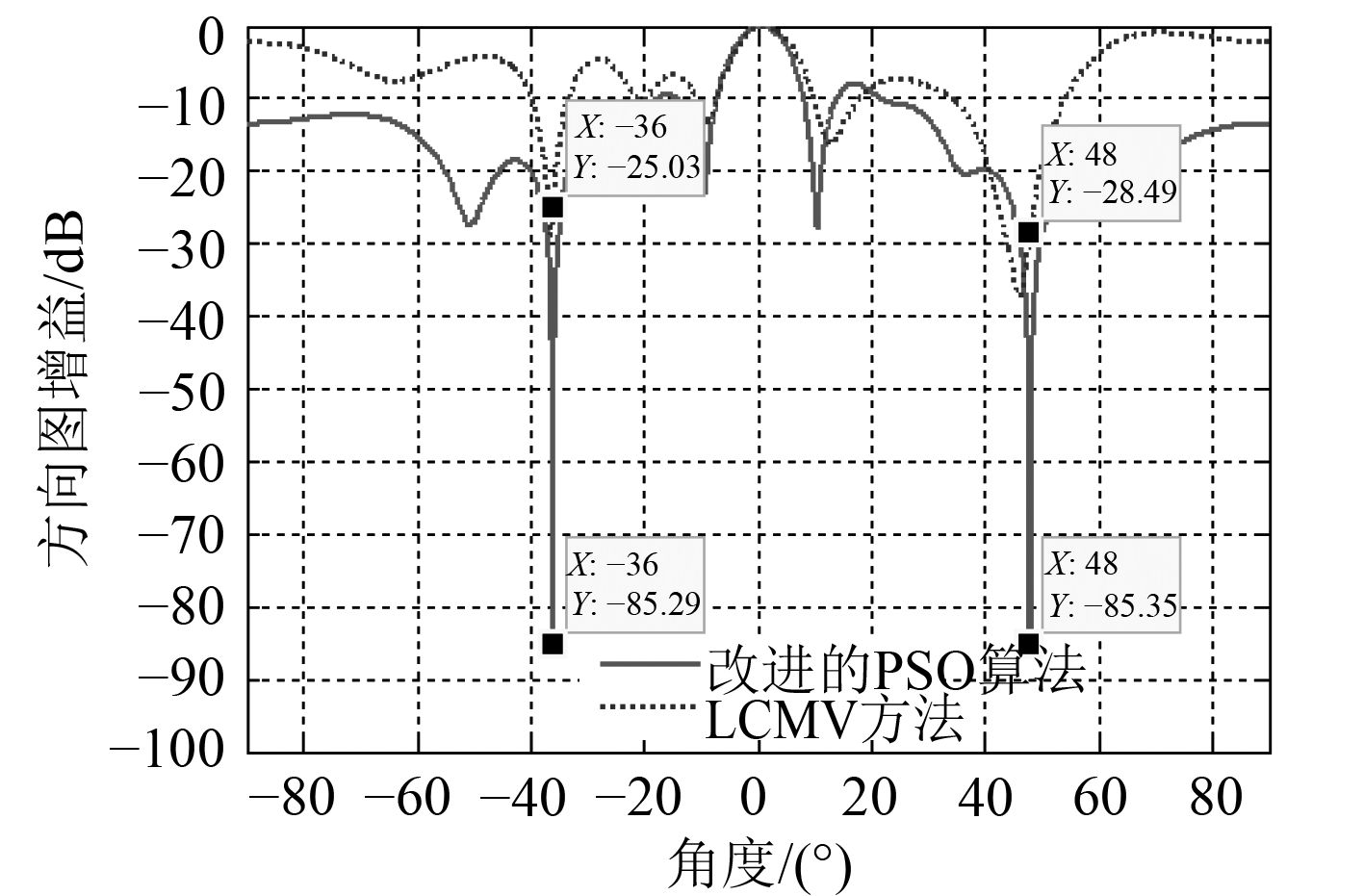
图 4 500次迭代结果 Fig. 4 Simulation result when the total number of iterations generations is 500 |
|
|
表 1 输出信干噪比对比 Tab.1 Comparison of SINE calculation |
通过图3和图4可以看出,在快拍数低的情况下,LCMV自适应波束形成方法已不能很好地增强期望信号,特别地,图3中的主瓣方向已与期望信号方向偏离甚远。可以看到,LCMV方法方向图旁瓣普遍较高,基本失去增强期望信号的能力,其零陷位置生成不准确且偏差较大。图3结果表明,通过设定干扰方向的虚拟干扰源,结合式(9)所示的适应度函数,改进的PSO算法可以准确地在增强期望信号的同时于干扰方向形成零陷,200次迭代后在–36°和48°的零陷电平分别达到–52.98 dB和–52.72 dB,零陷电平远低于LCMV方法的–24.57 dB和–24.84 dB,干扰抑制能力更强。对比图4与图3可以看到,两例均能在期望信号方向形成主瓣,在迭代次数提高至500次之后,干扰方向零陷电平进一步降低至–85.29 dB和–85.35 dB,且旁瓣电平整体降低,普遍压制在–10 dB以下,表明提高PSO算法的迭代次数可以获得方向图控制能力更好的阵列权矢量。表1中数据表示,改变自适应方向图控制的方法对阵列输出信干噪比的提升效果显著,但增大迭代次数对改进PSO算法性能的提升有限。由于在进化后期种群多样性逐渐丧失等多种原因,并不能单纯通过提高迭代次数来无限制获得更好的优化结果[17 – 18]。
本实例表明,文中提出的改进PSO算法在增强期望信号、形成干扰处零陷方面的性能远优于LCMV自适应波束形成方法。
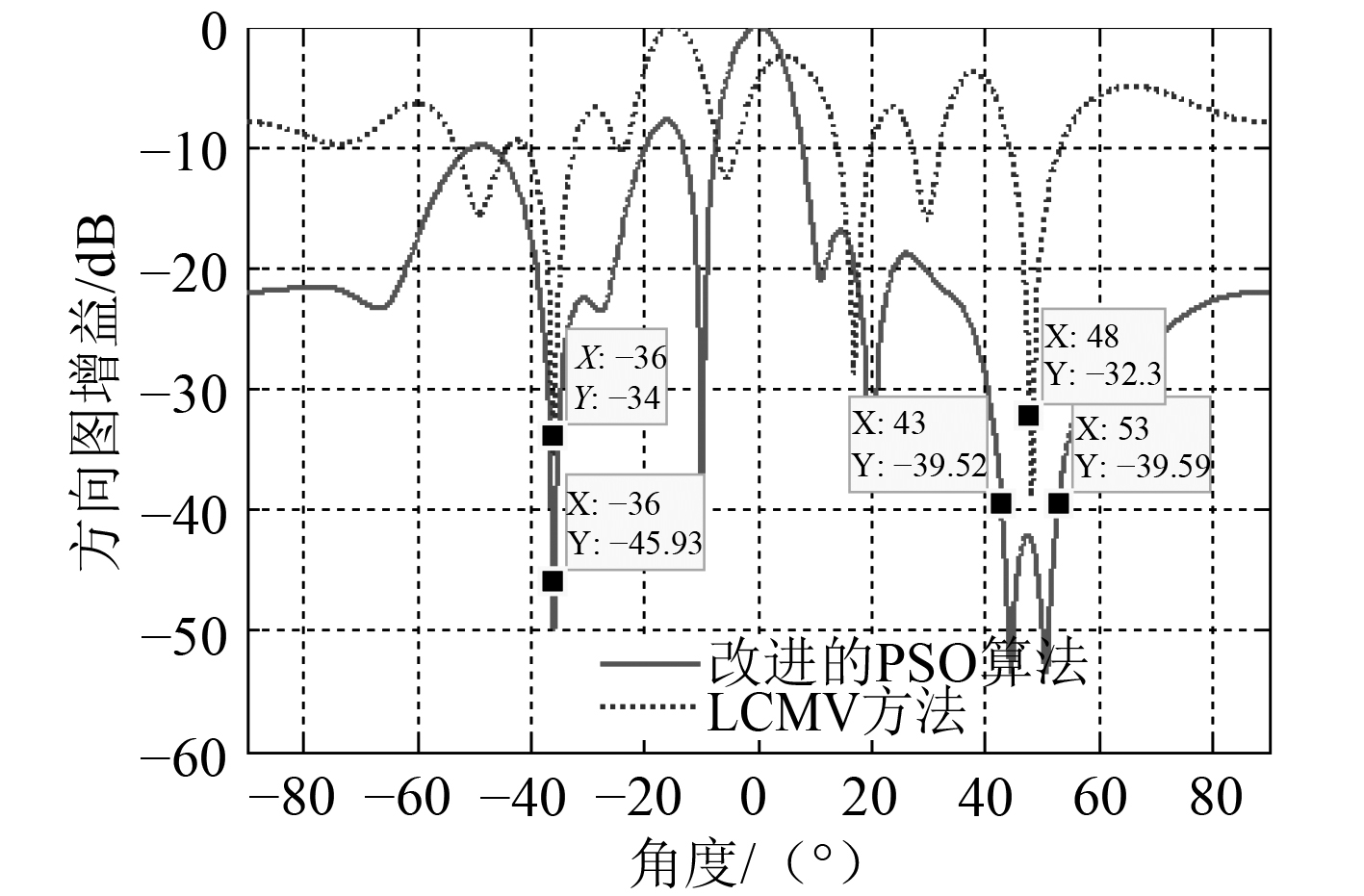
3.2 干扰区域自适应零陷展宽零陷展宽是抑制快速运动强干扰的有效手段,有利于弱目标信号的检测,本实例将讨论改进的PSO算法在零陷展宽方面的性能。本实例要求方向图在干扰方向形成深零陷、增强期望信号的同时在(43°,53°)范围内形成抑制区域,其余仿真条件与上一例相同。经过500次迭代后阵列方向图综合结果见图5。
|
图 5 自适应零陷展宽仿真结果 |
可知,通过在抑制区域内添加虚拟干扰源,可以有效在其间形成零深低于–40 dB的宽零陷。同时,–36°处也可生成约–46 dB深的零陷,主瓣位置也准确。仿真分析表明,文中提出的改进PSO算法可有效实现干扰区域自适应零陷展宽。
4 结 语粒子群优化算法等自然启发类算法是寻找非线性问题最优解的有效工具,相较于传统自适应波束形成算法有很大优势。利用PSO算法,可有效降低阵列方向图旁瓣级,形成深而宽的零陷以抑制干扰,还可综合出特定形状的阵列方向图。本文提出一种基于LCMV自适应波束形成的改进粒子群算法,并将其应用于自适应方向图控制方面。通过仿真分析的结果对比可以看出,该方法有效改善了LCMV自适应波束形成技术在低快拍数下增强主瓣、抑制干扰等方面的性能,可显著加深及展宽零陷,有效提升阵列输出信干噪比,在自适应阵列处理方面有广阔的应用前景。但该算法在迭代次数过少时性能不稳定,且在面对高维复杂问题时有时会陷入早熟收敛问题,因此仍然有待深入研究并改进。
| [1] |
王永良, 丁前军, 李荣锋. 自适应阵列处理[M]. 北京: 清华大学出版社, 2009.
|
| [2] |
APPLEBAUM S P. Adaptive arrays[C]//IEEE Transactions on Antennas and Propagation, 1976, 24(5): 585–598.
|
| [3] |
FROST O L. An algorithm for linear constrained adaptive array processing[J]. Proceedings of the IEEE, 1972, 60(8): 926–935.
|
| [4] |
GUNEY K, DURMUS A. Pattern nulling of linear antenna arrays using backtracking search optimization algorithm[J]. International Journal of Antennas and Propagation, 2015.
|
| [5] |
DARZI S, SIEH T KIONG, TARIQUL ISLAM M, et al. Null steering of adaptive beamforming using linear constraint minimum variance assisted by particle swarm optimization, dynamic mutated artificial immune system, and gravitational search algorithm[J]. The Scientific World Journal, 2014.
|
| [6] |
GHADIAN M, JABBARIAN-JAHROMI M, KAHAEI M Recursive sparsitybased mVDR algorithm for interference cancellation in sensor arrays[J]. IETE Journal of Research, 2015, 1–9.
|
| [7] |
CHEN Y L, LEE J H. Finite data performance analysis of LCMV antenna array beamformers with and without signal blocking[J]. Progress In Electromagnetics Research, 2012, 130: 281–317.
|
| [8] |
焦永昌, 杨科, 陈胜兵. 粒子群优化算法用于阵列天线方向图综合设计[J]. 电波科学学报, 2006, 21(1): 16-20. JIAO Yong-chang, YANG Ke, CHEN Sheng-bing. Application of particle swarm optimization in antenna array pattern synthesis[J]. Chinese Journal of Radio Science, 2006, 21(1): 16-20. DOI:10.3969/j.issn.1005-0388.2006.01.003 |
| [9] |
LU, Y YEO B K. Adaptive wide null steering for digital beamforming array with the complex coded genetic algorithm[C]//IEEE Int. Conf. Phased Array Systems and Technology, 557–560, Dana Point CA, USA, 2000.
|
| [10] |
KARABOGA, D, GUNEY K, AKDAGLI A. Antenna array pattern nulling by controlling both the amplitude and the phase using modifled touring ant colony optimisation algorithm[J]. Int. Journal of Electronics, 2004, 91, 241–251.
|
| [11] |
MURINO V, TRUCCO A, REGAZZONI C S. Synthesis of equally spacedarrays by simulated annealing[J]. IEEE Trans. Signal Process., 1996, 44(1): 119–122.
|
| [12] |
PAPPULA L, GHOSH D. Linear antenna array synthesis for wirelesscommunications using particle swarm optimization[C]//15th International Conference on Advanced Computing Technologies, Rajampet, India, 2013, 780–783.
|
| [13] |
KENNEDY J, EBERHART R, Particle swarm optimization[C]//IEEE International Conference on Neural Networks, 1995, 4.
|
| [14] |
M. ABIDO Optimal design of power-system stabilizers using particle swarm optimization[C]// IEEE Transactions on Energy Conversion, 2002.
|
| [15] |
ZAVALA A, DIHARCE E Particle evolutionary swarm for design reliability optimization[C]// Lecture Notes in Computer Science, 2005.
|
| [16] |
OMRAN M, SALMAN A, ENGELBRECHT A. Dynamic clustering using particle swarm optimization with application in image segmentation[C]// Pattern Analysis & Applications, 2006.
|
| [17] |
王维博. 粒子群优化算法研究及其应用[D]. 成都: 西南交通大学, 2012.
|
| [18] |
KHODIER M M, C G CHRISTODOULOU. Linear array geometry synthesis with minimum sidelobe level and null control using particle swarm optimization[C]//IEEE Transactions on Antennas and Propagation, 2005, 53, 2674–2679.
|
 2018, Vol. 40
2018, Vol. 40
