2. 大连测控技术研究所,辽宁 大连 116013
2. Dalian Scientific Test and Control Technology Institute, Dalian 116013, China
在水下舰艇实际噪声测量中,以高分辨的声源定位算法辅助大孔径多元线阵为平台可以有效的识别和定位舰船噪声源。然而,对于部署在实验海域中的水下大型多元线性阵列噪声测试系统,受到浪涌、海流等海洋环境因素影响,不可避免的会产生形变,此外,阵元水听器之间还存在一定的幅相误差,若将阵列的阵列流形按照理想阵列的阵列流形进行处理,声源定位算法的性能势必会受到较大的影响[1]。在当前水声测量领域中,水下噪声源定位识别中得到广泛应用的高声源定位算法大多是子空间声源定位算法,典型的如最大似然方法(ML),ESPIRT算法和MUSIC算法等[2],大多基于特征分解理论。在实际水声噪声测试中,上述算法对于阵列的误差有较为苛刻的要求,算法的性能可能会因为较小的阵列误差而急剧下降甚至失效[3],所以采用一种有效的方法对阵列误差进行校正是水声测试领域一个亟待解决的热点问题。
在水声相关领域,国内外学者提出了多种阵列误差校正算法,然而针对水下多元直线阵列幅相误差和位置误差同时进行校正的方法鲜有提及。可以实时校正阵列的阵形误差对传感器直接测量的方法增加了整个测试系统的复杂性,从而导致系统的可靠性降低,且传感器精度和数量限制了阵列估计的精度,故此方法只适合作为水下大尺度多元直线阵列校正的辅助手段。充分利用水下均匀线阵的协方差矩阵信息的结构特征法,可以用于校正阵列位置误差[4],但不能同时对阵元的幅度误差和相位误差进行校正。自校正方法的优点是无需知道声源的确切方位信息,摆脱了算法对辅助声源精确方位信息的依赖,可以完成噪声源实际方位的在线估计,但由于辅助源源方位参数与阵列误差参数(阵元幅度、相位及位置等)之间存在的耦合问题以及部分阵列本身的病态结构影响,算法难以保证参数估计的唯一辨识。更为重要的是想要支撑参数联合估计对应的高维、多模非线性搜索及优化问题,算法所需的运算量非常庞大,在这种情况下参数估计的全局收敛性难以保证,且搜索时间较长。利用精确已知的辅助校正源先验信息(位置、数量、功率等)来完成阵列误差的校正的方法被称作有源校正方法[5]。有源校正方法可以根据实际需求对辅助源参数进行选择,例如选择大功率校正源来提高信噪比,从而削弱噪声的影响;调整校正源的方位和深度信息以解决多维搜索中常见的多解问题;调整辅助源个数使校正结果更加精确。由于有源校正方法无需对校正源自身的信息进行计算,所以其具有运算量较小、校正精度较高的优点[6]。
针对水下噪声测量中多元阵列幅相误差和位置误差校正的迫切需求,本文提出一种引入模拟退火法的远场阵列误差有源校正方法[7],该方法利用单一辅助源分时工作的方式,利用改变辅助源方位3次以解决搜索中的多解问题,通过子空间基本原理构建目标函数,并引入模拟退火算法,同时完成对阵元位置误差和幅相误差的寻优。利用Matlab软件对算法进行仿真,结果表明,该算法具有较好的鲁棒性、精度以及稳健性。
1 信号模型
|
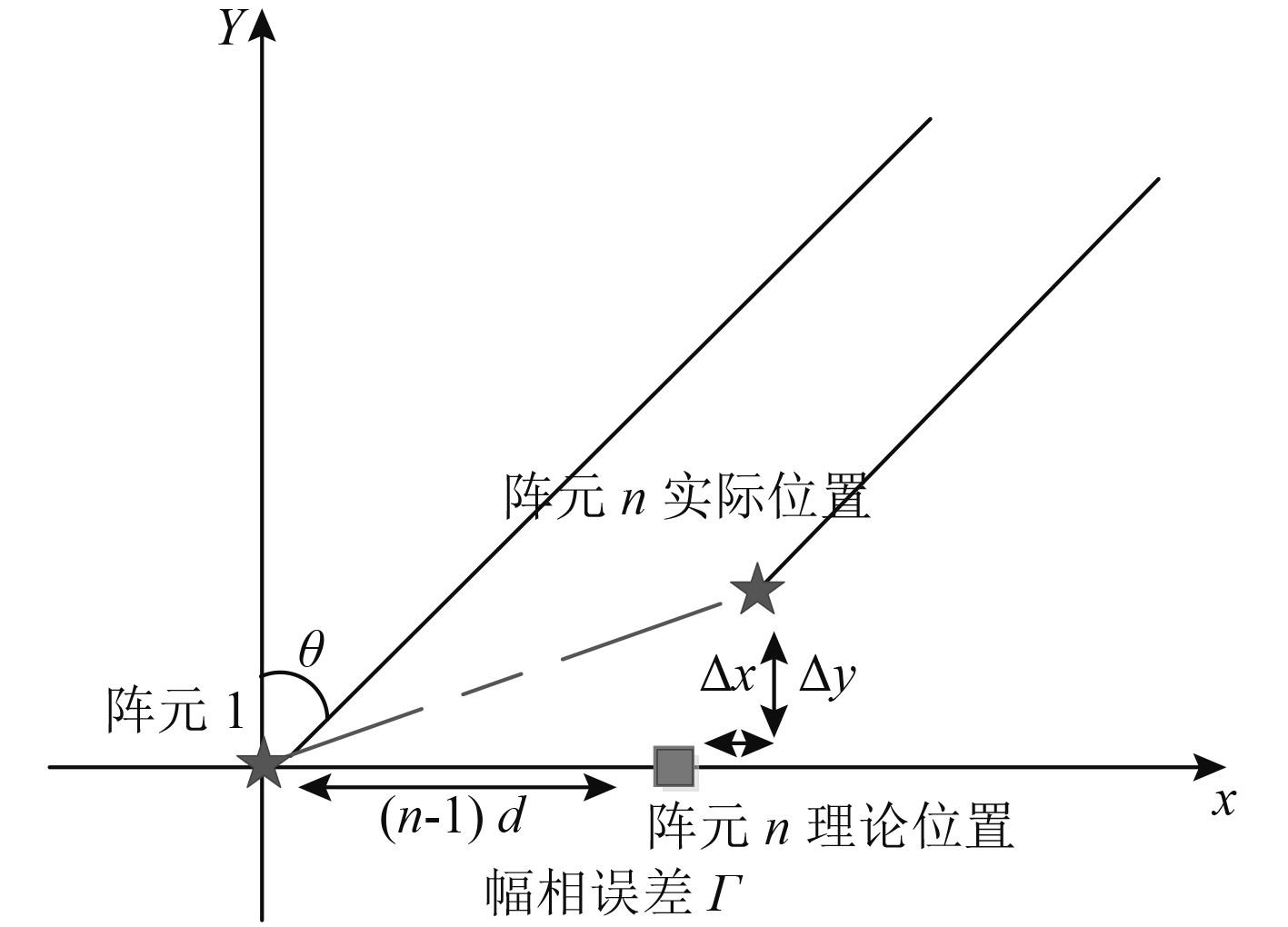
图 1 远场阵列示意图 Fig. 1 The array-source geometry of the far-filed case |
选取均匀直线阵如图 1所示,阵列由N个阵元组成,阵元间距为d,位于远场的辅助源发射窄带不相干信号M次,分别从方向θm入射到该阵列上,m=1,2…M,信号波长为λ。不失一般性,本文以二维平面内阵列误差校正为例,即假设声源与阵元均在同一深度平面内。建立坐标系,选取首阵元位置为原点,阵列平面为XY平面,理想阵元坐标为[xn,yn],各阵元的位置误差δn=[Δxn,Δyn],故第n个阵元的实际位置为[xn+Δxn,yn+Δyn],阵元n的幅相误差为τn=ρneiφn(Г=diag(τn)),一般情况下,可认定阵元误差在校正过程中恒定不变。
在上文基础上,由阵列处理相关知识推导出,远场阵列的阵列流形A中的第nm个元素为:
| $\begin{split}&{A}\left( {{\theta _m},{\delta _n}} \right) = \\&{\rho _n}{{\rm{e}}^{i{\varphi _n}}}{\rm{exp}}\left\{j\displaystyle\frac{{2\pi }}{\lambda }[\left( {{x_n} + \Delta {x_n}} \right){\rm{sin}}{\theta _m} + ({y_n}+\Delta {y_n}){\rm{cos}}{\theta _m}]\right\} ,\end{split}$ | (1) |
则第k次快拍的输出矢量为
| ${X}\left( k \right) = {AS}\left( k \right) + {N}\left( k \right),$ | (2) |
式中S(k)和N(k)分别为N×1的接收数据矢量和噪声矢量,噪声为零均值,方差为σ2的高斯加性白噪声。阵列的协方差矩阵为:
| ${{R}_{{xx}}} = E\left[ {{X}\left( k \right){{X}^H}\left( k \right)} \right] = {AS}{{A}^H} + {\sigma ^2}{I}],$ | (3) |
其中,S为信号协方差矩阵,对Rxx进行特征分解,得到信号特征向量ES和噪声特征向量EN两部分。两者张开的空间就是信号子空间和噪声子空间,且两者满足:
| ${{E}_S}{E}_S^H + {{E}_N}{E}_N^H = {I},$ | (4) |
构造UML算法目标函数[8]为:
| $\widehat {\;\alpha } = {\rm{arg}}\underbrace {{\rm{max}}}_\alpha \left\{ { - {\rm{lndet}}\left[ {{{P}_{{A}}}{\hat R}{{P}_{{A}}} + \frac{{{\rm{tr}}\left[ {{P}_{{A}}^ \bot {\hat R}} \right]{P}_{{A}}^ \bot }}{{N - M}}} \right]} \right\},$ | (5) |
其中,
| ${\hat R} = \frac{1}{K}\mathop \sum \limits_1^k {X}\left( K \right){{X}^H}\left( K \right){\text{。}}$ | (6) |
信号入射方向由目标函数所得到的谱函数的峰值对应的方向求得。在进行空间谱搜索时,必须先对阵列流形A进行修正以减少阵元位置误差和幅相误差的影响。
2 基于模拟退火法的阵形校正方法 2.1 模拟退火法算法模拟退火法(simulated annealing,SA)作为一种由Metropolis等提出的较为成熟的概率演算算法[8],可用于解决复杂搜索空间中的命题最优解搜索问题。模拟退火法的思想源自金属退火原理,是一种将经典热力学理论运用于统计学范畴的方法。其主要思路是将某种金属充分加热至定温后慢慢进行降温冷却。在加热过程中,粒子随温度的升高逐渐变为无序状,其内能增加;进行降温处理时,金属粒子趋于一种有序状态,在每个温度其状态都可以达到平衡,最后在常温时达到内能最小的基态。这种算法求得的解与初始值无关且具有渐近收敛性,原则上对目标函数的维数也没有限制,是一种较为成熟可靠,应用广泛的全局优化算法[9]。
根据Metropolis准则,在温度为T时,金属粒子有
由信号模型可知,对于远场模型,选择一个分时工作的辅助声源,放置3次,与阵列的夹角分别为
| ${{F}_{{n}}} = - {\rm{det}}\left[ {{{P}_{{An}}}\widehat {{{R}_1}}{{P}_{{An}}} + \frac{{{\rm{tr}}\left[ {{P}_{{An}}^ \bot \widehat {{{R}_2}}} \right]{P}_{{An}}^ \bot }}{{N - M}}} \right],\,n = 1,2,3,$ | (7) |
| ${F} = {\rm{arg}}\;{\rm{min}}\left( {{{F}_1} + {{F}_2} + {{F}_3}} \right){\text{。}}\quad\quad\quad\quad\quad\,\!$ | (8) |
式(8)即为所需的目标函数。
确定初始温度T0,初始解x,迭代次数K,使得初始幅相误差Г=I,位置误差为0。
进行迭代,计算
继续迭代,当迭代次数达到链长或满足中止条件时,结束计算,得到寻优解。
综上所述,校正过程如下:
1)基于UML算法式(7)和式(8)构建目标函数F;
2)根据信号模型,确定初始值和实验参数;
3)利用模拟退火法进行迭代,直至达到终止条件;
4)利用搜索结果构建阵列流形,再利用校正过的阵列进行DOA估计,以验证校正算法的性能。
3 性能仿真结果分析选取水下多元均匀阵列做为实例进行仿真,取阵列阵元数为8,采样数为1 000,阵元间距为0.5λ,调整信噪比snr=10 dB,建立坐标系,将辅助源分别放置在–10°,20°和50°,以阵元所在平面为XY平面,以首阵元位置为原点,设置阵元随机位置误差δn=[Δxn,Δyn](n=2,3…8)在±0.2λ之间,阵列的相位误差在[–pi,pi]之间,幅度误差在[0,1]之间。
设置模拟退火法参数,进行寻优,设置模拟退火参数如表 1所示。
|
|
表 1 模拟退火法参数设置 |
利用模拟退火法进行寻优及蒙特卡罗实验,重复100次,取平均值,其估计结果如表2和表 3所示。
|
|
表 2 位置误差估计结果 |
|
|
表 3 幅相误差估计结果 |
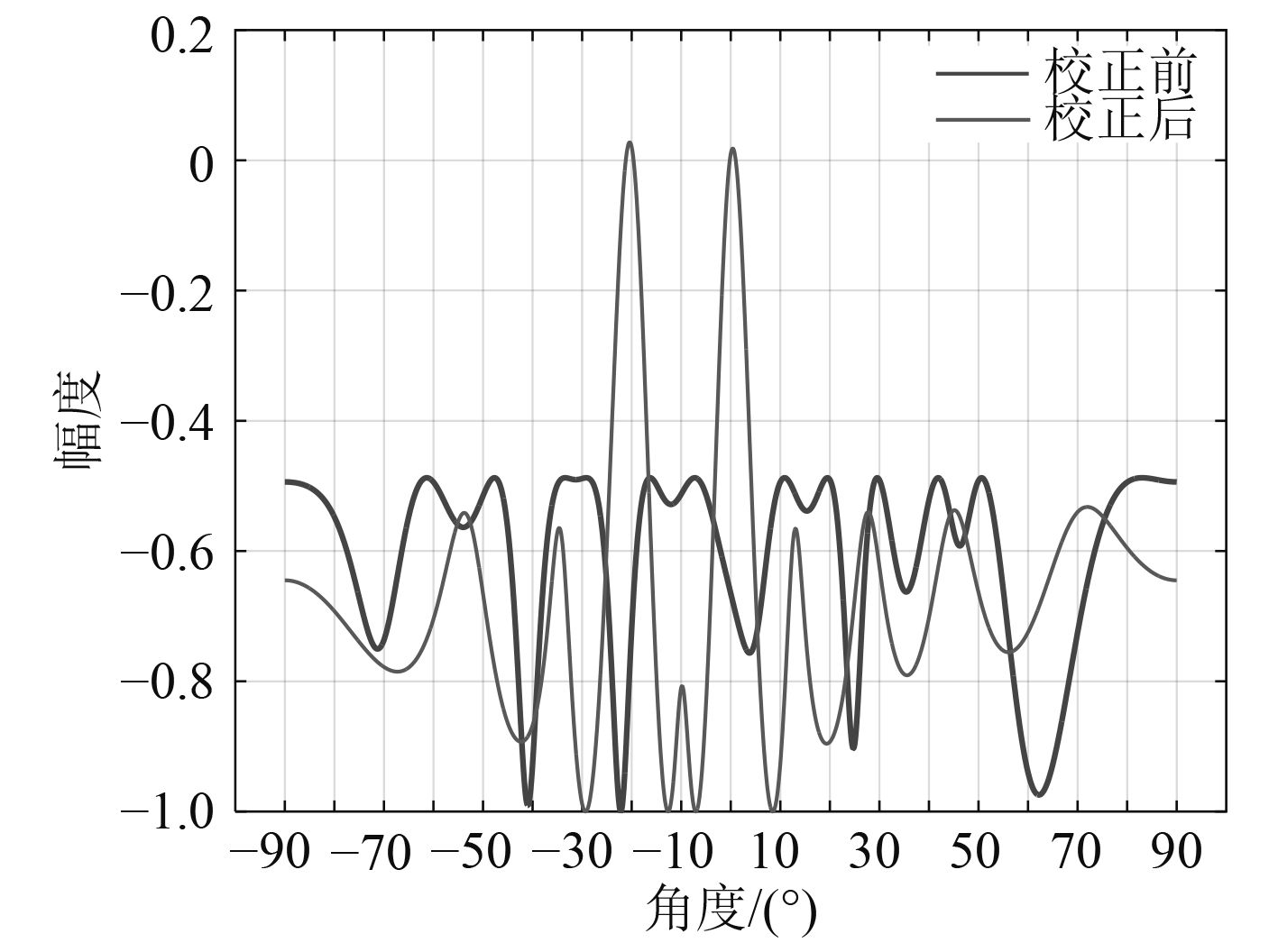
对校正好的阵列进行DOA估计测试,在两声源入射角分别为–20°和0°时,得到校正前后的DOA示意图。
|
图 2 校正前后UML谱 Fig. 2 The DOA spectrum before and after calibration with UML |
由表 2和表 3可知,基于模拟退火法的阵列误差校正方法得到的估计误差与真实误差较为接近,算法具有较好的阵列误差校正能力。由图 2可以看出,利用模拟退火法进行校正后,阵列DOA估计精确度显著提高,这表明此校正方法有效。
4 结 语为解决阵列误差校正这一水下舰船噪声测试领域中的热点问题,本文提出一种基于模拟退火法的水下多元直线阵列远场阵列误差校正方法。采用单一辅助源分时工作的方式,将声源分别放置于3个不同位置发射信号,进行数据采集,根据子空间基本原理构造目标函数,最后引入模拟退火法对阵元位置误差和阵列幅相误差同时进行估算,并运用蒙特卡罗试验检测算法的性能。实验结果表明,该算法具有较好的鲁棒性、精度及适应性。通过适当增加辅助源的数量,调节辅助源频率,优化辅助源位置等方法,可进一步提高阵形校正精度。
本算法可以通过改变阵列模型的设置及改变算法参数设定的方法应用于其他阵型的近、远场有源校正,故其在水下舰船噪声测量领域具有较为广阔的前景。
| [1] |
SCHMIDT R O. Multiple emitter location and signal parameter estimation[J]. IEEE Trans.Antennas and Propagation, 1986, 34: 276-280. DOI:10.1109/TAP.1986.1143830 |
| [2] |
SWINDLEHURST A L, KAILAITH T. A Performance Analysis of Subspace Based Methods in the Presence of Model Errors, Part Ⅰ: The MUSIC Algorithm[J]. IEEE Trans. On TASSP, 1992, 40(2): 1578-1774. |
| [3] |
STOICA P, NEHORAI A. MUSIC, Maximum likelihood, and Cramer-Rao bound[C]//In Proc. ICASSP, 1998: 2296–2299.
|
| [4] |
PAULRAJ A, KAILATH T. Direction of arrival estimation by eigenstructure methods with unknown sensor gain and phase[C]//Acoustics, Speech, and Signal Processing, 1985. ICASSP-85, 1985 IEEE International Conference on, Tampa, FL, 1985, 640–643.
|
| [5] |
HUNG E.. Matrix-construction calibration method for antenna arrays[J]. IEEE Trans. on Aerospace and Electronic Systems, 2000, 36(3): 819-828. DOI:10.1109/7.869501 |
| [6] |
CHUNG P J, WAN S.. Array self-calibration using sage algorithm[J]. IEEE Trans. Sensor Array and Multichannel Signal Processing Workshop, 2008, 7: 165-169. |
| [7] |
HARRY L, VAN Trees . Optimum array processing part Ⅳ of detection, estimation, and modulation theory[M]. Beijing: Tsinghua University Press, 2008.1
|
| [8] |
FENG J, YUE Q. Solving TSP problem using SA method[J]. Forest engineering, 2008, 24(01): 94-96. |
| [9] |
XIE Yun. The research on parallel algorithm of simulation annealing[J]. Journal of wuhan university, Journal of parallel computing, 1991, 84-91. |
 2018, Vol. 40
2018, Vol. 40
