为了保证海上风机的结构完整性,国际电工委员会在设计标准IEC 61400-3[1]中,对支撑结构和叶轮-机舱组合件的设计提出了极限强度分析的要求,其中设计载荷
为了减少仿真数量,反向一阶可靠度法IFORM(Inverse First-Order Reliability Method)逐渐被运用到考虑多维变量时极限载荷的求解上。P.J. Moriarty等[3]曾采用直接积分法求解WP_Baselline1.5MW风机叶片根部面外弯矩在1年重现周期下的极端载荷,而Korn Saranyasoontorn等[4]采用2维IFORM法(环境等值线法)以更少的仿真数据便得到了同样良好的结果。K. Saranyasoontorn等[5]曾根据IFORM的3种形式建立了求解风机名义载荷的基本模型,求解了某600 kW陆上风机叶片的极端载荷;D. Karmakar等ADDIN EN.CITE.DATA [6 – 8]利用IFORM法求解了3种不同浮式基础NREL5MW海上风机的极限载荷,并对计算结果与浮式基础的关系进行比较;Puneet Agarwal等[9]在样本经验分布函数的基础上采用环境等值线法求取了工作在20 m浅水区域NREL5MW海上风机的长期载荷。
但是在上述研究中,一般都是等间距地在搜索区域上选取搜寻点,外推结果的精度由间隔搜寻角的大小直接决定,间隔角越小外推结果就越精准,但同时仿真数量也会增加。而采用IFORM求解极端载荷实际上也是一个最优化过程,因此本文将环境等值线法与1维最优化方法二分法结合起来,形成一种具有搜寻策略的算法来求解极端载荷,通过多级搜寻逐步缩小搜寻区间,减少不必要的搜寻工作,提高外推精度。同时与传统的直接积分法进行对比验证。
1 计算原理 1.1 IFORM原理简介直接积分法的计算公式如下
| $\begin{aligned}{P_T} = {Pr} \left\{ {L > {l_T}} \right\} = \int\nolimits_{{X_1}} {\int\nolimits_{{X_2}} { \cdots \int\nolimits_{{X_n}} {Pr \{ {L > {l_T}\left| {{X_1}} \right. ={x_1} ,{X_2} =}}}}\\{{{{ {x_2}, \ldots ,{X_n} \!=\! {x_n}} \}{f_{{X_1}{X_2}, \ldots ,{X_n}}}\left( {{x_1},{x_2}, \ldots ,{x_n}} \right){\rm d}{x_1}{\rm d}{x_2}, \ldots ,{\rm d}{x_n}} } } \text{。} \end{aligned}$ | (1) |
其中:
从反向可靠性的角度分析积分法求解极限载荷
| ${P_f} = {Pr} \left\{ {L > {l_{dec}}} \right\}\text{。}$ | (2) |
为了简化问题,忽略给定环境下短期载荷极值
| $L = l\left( U \right) \text{。} $ | (3) |
在“正向”的一阶可靠度问题中,设计抗力
| $\begin{array}{l}{\text{优化变量}}:{\text{标准正态变量}}U\text{,}\\{\text{约束条件}}:g\left( U \right) = {l_{dec}} - l\left( U \right) = 0\text{,}\\{\text{目标函数}}:\beta = \min \left\{ {\left| U \right|} \right\}\text{。}\end{array}$ |
而在“反向”的一阶可靠度问题中,事先已知的是可靠性指标
| $\begin{array}{l}{\text{优化变量}}:{\text{标准正态变量}}U\text{,}\\{\text{约束条件}}:\left| U \right| = \beta\text{,} \\{\text{目标函数}}:{l_{dec}} = \max \left\{ {l\left( U \right)} \right\}\text{。}\end{array}$ |
对比可知,在对结构进行可靠性分析中,搜寻的目标,即可靠性指标
对于海上风机,通常主要考虑环境变量为风速
| $\begin{aligned}{P_f}\!\!= \! \!\! &\Pr \left\{ {L \!>\! {l_{dec}}} \right\} \!\!=\!\! \int\nolimits_{{V_{in}}}^{{V_{out}}} {\int\nolimits_0^\infty \!\!{{Pr} \left\{ {L\! >\! {l_{dec}}\left| {V \!\!=\!\! v\text{,}\!\!\!Hs \!\!= \!\!hs} \right.} \right\}}} \text{,} \\ &{{{f_{Hs\left| V \right.}}\left( {hs\left| v \right.} \right){f_V}\left( v \right){\rm d}v{\rm d}hs} } \text{。} \end{aligned}$ | (4) |
其中
| $\varPhi \left( {{u_1}} \right) = {F_V}\left( v \right) \text{,} $ | (5) |
| $\varPhi \left( {{u_2}} \right) = {F_{Hs\left| V \right.}}\left( {hs\left| v \right.} \right) \text{,} $ | (6) |
| $\varPhi \left( {{u_3}} \right) = {F_{L\left| {V,Hs} \right.}}\left( {l\left| {v,hs} \right.} \right) \text{,} $ | (7) |
| $u_1^2 + u_2^2 + u_3^2 = {\beta ^2} \text{。} $ | (8) |
由此便可在标准正态空间内搜寻引起短期载荷极值

|
图 1 IFORM的3种基本形式 Fig. 1 3 Basic forms of IFORM |
图 1(c)为IFORM法最基本的形式,即三维IFORM法。图 1(b)为IFORM法的二维简化形式。设
| $\Pr \left\{ {L \geqslant {F_{L\left| {V,Hs} \right.}}\left( {{l_{0.5}}\left| {v,hs} \right.} \right)} \right\} = 0.5\text{。}$ | (9) |
则当式(7)等号右边
需要注意的是,在EC法的搜寻过程中,只比较中位数
将
| $L = {L^*} \cdot \varepsilon \text{,} $ | (10) |
其中:
| ${\sigma _{\ln {L^*}}} = \frac{{\ln \left( {L_{T_1}^*/L_{T_2}^*} \right)}}{{{\beta _{T_1}} - {\beta _{T_2}}}} \text{,} $ | (11) |
| ${\sigma _{\ln \varepsilon }} = \frac{{{\varepsilon _{p2}} - {\varepsilon _{p1}}}}{{{\varPhi ^{ - 1}}\left( {p_2} \right) - {\varPhi ^{ - 1}}\left( {p_1} \right)}} \text{。} $ | (12) |
其中:
| ${R_T} = \frac{{{L_{T_1}}}}{{L_{T_1}^*}} = \exp \left[ {\left( {{\sigma _{\ln L}} - {\sigma _{\ln {L^*}}}} \right){\beta _{T_1}}} \right] \text{,} $ | (13) |
其中
如果在式(10)中取
NREL海上5MW风机是美国国家可再生能源实验室(National Renewable Energy Laboratory)开发的一款风机[12],根据子结构和基础形式的不同分为多种类型。其中,OC3Hywind是一种Spar型浮式基础的海上风机,如图 2所示。基本参数见表 1。
|
图 2 Spar风机示意图 Fig. 2 Schematic diagram of Spar wind turbine |
|
|
表 1 基本参数 Tab.1 Basic parameters |
计算工况以IEC 61400-3中正常发电工况的DLC 1.1为例,风机等级IECⅠ-A。参考Korn Saranyasoontorn等[13]中丹麦Horns Rev处的海洋气象条件,调整相应的参数使风机运行在一个较合理的环境下。假定平均风速服从韦伯分布
| ${F_V}\left( v \right) = 1 - \exp \left[ { - {{\left( {\frac{v}{a}} \right)}^k}} \right],\;\;\;a = 12.258\;3,k = 1.8 \text{,} $ | (14) |
并且只考虑在工作风速区间内失效的情况,因此对切入风速以下和切出风速以上进行截断,将平均风速的实际分布函数改写为
| ${F_V}\left( v \right) = \frac{{G\left( {{v_{in}}} \right) - G\left( v \right)}}{{G\left( {{v_{in}}} \right) - G\left( {{v_{out}}} \right)}} \text{,} $ | (15) |
| $G\left( v \right) = \exp \left[ { - {{\left( {\frac{v}{a}} \right)}^k}} \right] \text{。} $ | (16) |
假定有义波高服从正态分布。
| $\begin{aligned}& {F_{Hs\left| V \right.}}\left( {hs\left| v \right.} \right) \!=\! \Phi \left[ {\frac{{hs - {\mu _{Hs}}\left( v \right)}}{{{\sigma _{Hs}}}}} \right],\\\;\;\;& {\mu _{Hs}}\left( v \right) \!=\! 0.13v,{\sigma _{Hs}} \!=\! 0.24\text{。}\end{aligned}$ | (17) |
为了简化问题,将谱峰周期
| $11.1\sqrt {{H_{S,NSS}}\left( V \right)/g} \leqslant T \leqslant 14.3\sqrt {{H_{S,NSS}}\left( V \right)/g} \text{,} $ | (18) |
对谱峰周期取值如下:
| ${T_p} = \frac{{\left( {11.1 + 14.3} \right)}}{2}\sqrt {\frac{{Hs\left( V \right)}}{g}}\text{。} $ | (19) |
式中
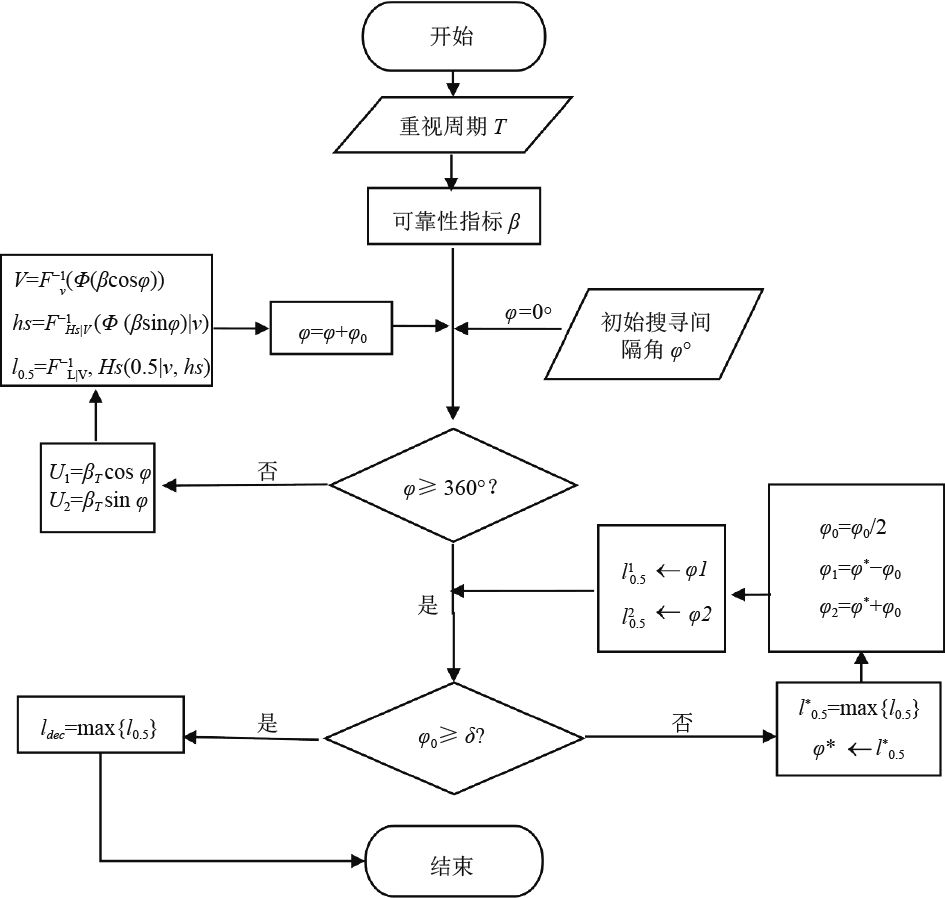
采用环境等值线法求解该风机1年重现周期和20年重现周期下的长期载荷,求解对象为叶片根部面外弯矩OOPB(Out-of Plane Blade Root Moment)以及塔筒基底首尾弯矩TBM(Fore-aft Tower Base Moment)。基本流程如图 3所示。
|
图 3 搜索算法流程图 Fig. 3 Flow chart of search method |
设定收敛条件
|
|
表 2 1年重现周期OOPB搜寻结果 Tab.2 Search results of OOPB in 1 year return period |
|
|
表 3 1年重现周期OOPB设计点修正 Tab.3 Correction of the OOPB design point in 1 year return period |
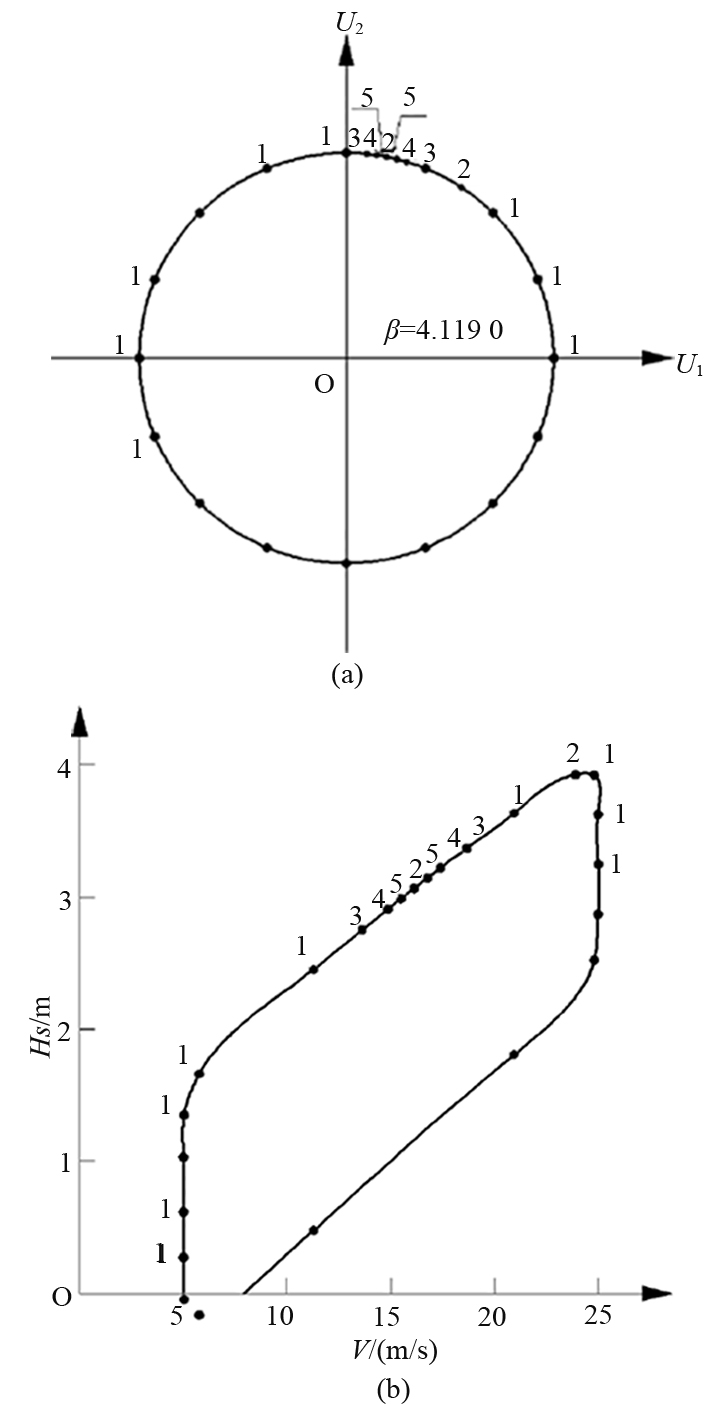
最终获得1年重现周期下OOPB极限载荷
|
图 4 1年OOPB搜寻过程及等值线对比 Fig. 4 Search process of OOPB in 1 year return period and isolines contrast |
由于计算中发现TBM短期极值的不确定性比OOPB更大,因此设定收敛条件为
|
|
表 4 1年重现周期TBM搜寻结果 Tab.4 Search results of TBM in 1 year return period |
|
|
表 5 1年重现周期TBM设计点修正 Tab.5 Correction of the TBM design point in 1 year return period |
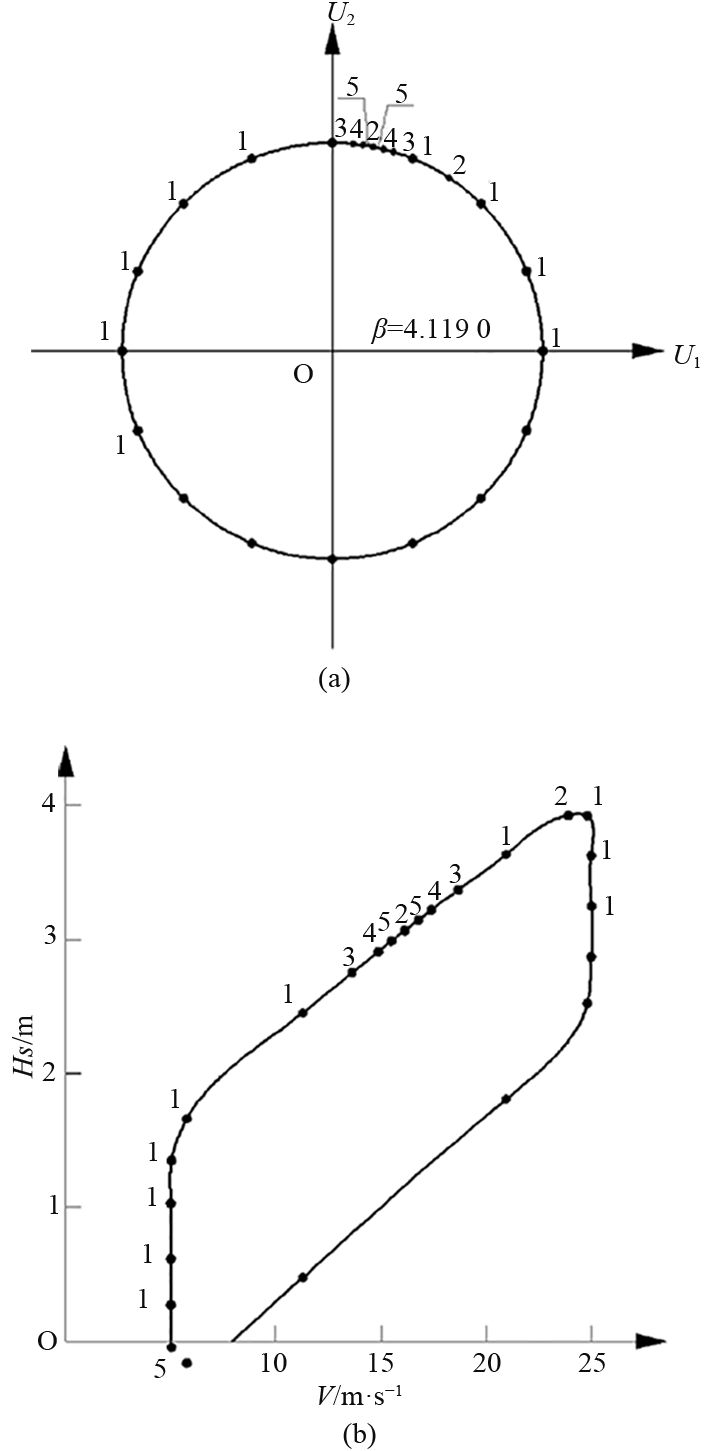
最终获得1年重现周期下的TBM极端载荷
|
图 5 1年TBM搜寻过程及等值线对比 Fig. 5 Search process of TBM in 1 year return period and isolines contrast |
为了之后与直接积分法进行更多的对比验证,同时还计算了20年重现周期时的极限载荷。搜寻过程与1年重现周期类似,在此不予赘述。最终获得20年重现周期下OOPB极限载荷为
为了对比验证搜索算法的外推结果,根据式1采用直接积分法求解OOPB和TBM的长期分布。首先确定整个2重积分的积分域。根据前文定义的计算工况和平均风速的分布函数,取平均风速的积分区间为5 m/s~25 m/s;根据有义波高的分布函数取积分区间0 m~5 m。然后将各自的积分区间划分成多个子区间。为此将平均风速按照2 m/s的分辨率划分成11个子区间,各子区间平均风速为5 m/s,7 m/s,···,25 m/s。将有义波高按照1 m的分辨率划分成5个子区间,各子区间平均有义波高分别为0.5 m,1.5 m,···,4.5 m。综上所述,总积分域被划分成55个子区间。
确定好各子区间后根据其风浪参数,对风机在该环境条件下的运行进行数值仿真,以获取短期极值点
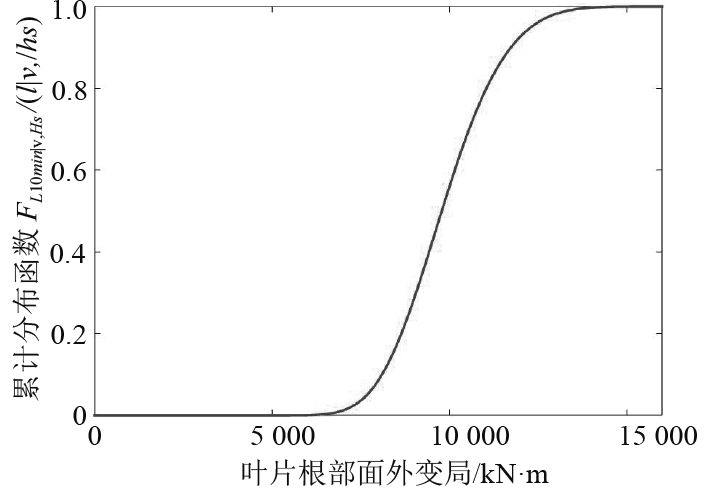
|
图 8 短期极值分布累积分布函数 Fig. 8 CDF of fitted distribution |
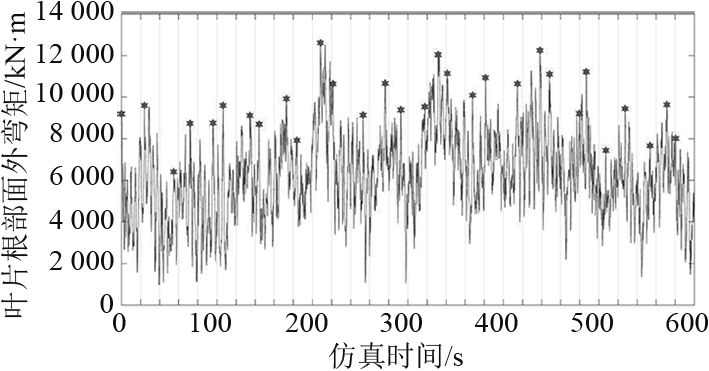
|
图 6 10 min短期载荷极值点,v=15 m/s,Hs=4.5 m Fig. 6 10 minutes short-term load extremes, v=15 m/s, Hs=4.5 m |
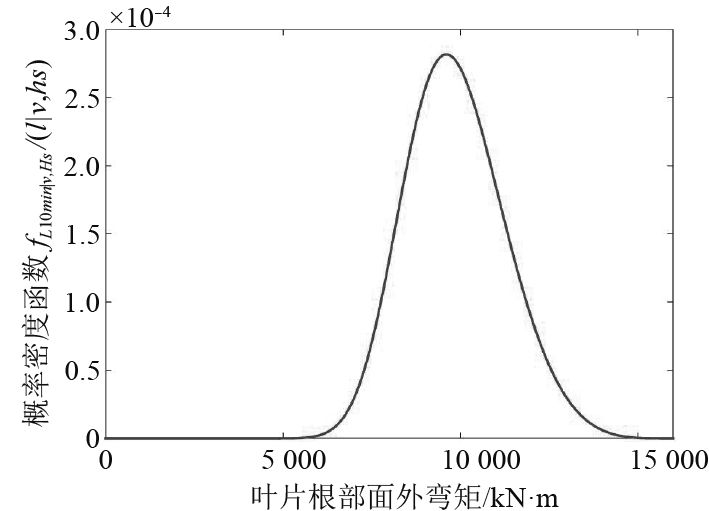
|
图 7 短期极值分布概率密度函数 Fig. 7 PDF of fitted distribution |
在获得短期极值点后,需要对其分布进行拟合,计算
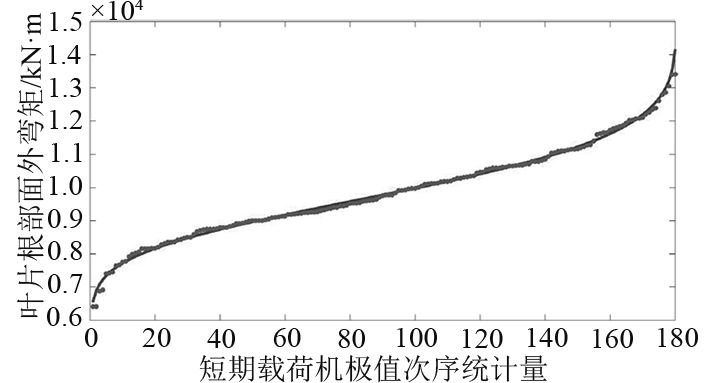
|
图 9 短期载荷极值Q-Q图 Fig. 9 Quantile-Quantile plot of short-term extreme load |
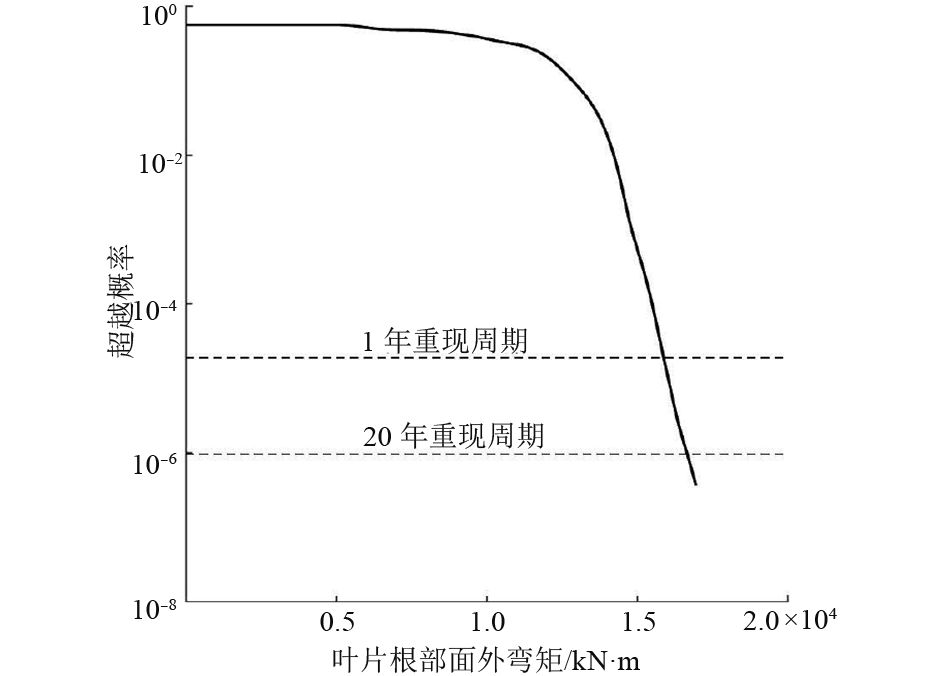
|
图 10 叶片根部面外弯矩超越概率分布 Fig. 10 Exceedance probability distribution of OOPB |
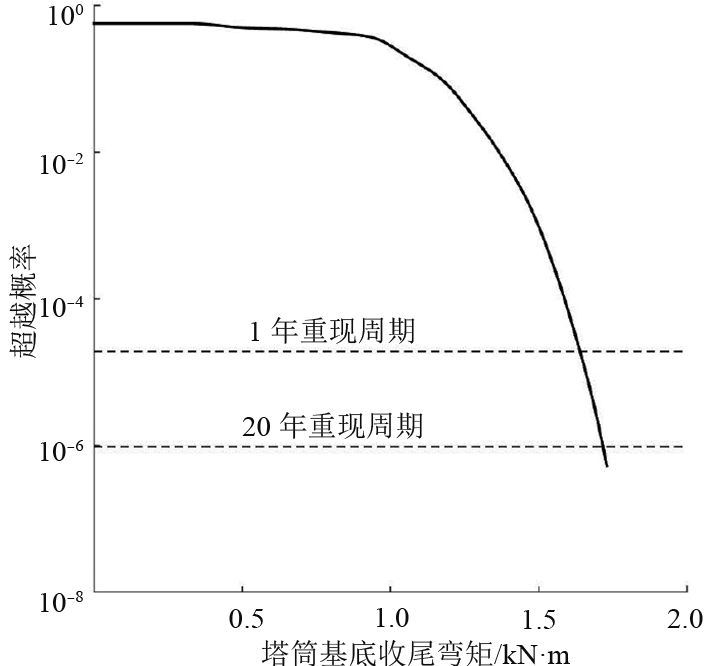
|
图 11 塔筒基底首尾弯矩超越概率分布 Fig. 11 Exceedance probability distribution of TBM |
注意以上求解
1年和20年重现周期下搜索算法与积分法的对比如表 6所示。其中OOPB1和TBM1为搜索算法直接搜寻的结果,OOPB2和TBM2为经修正点修正之后的结果。
|
|
表 6 搜索算法与积分法外推结果对比 Tab.6 Comparison of extrapolation results of search method and integration method |
由表中数据可见,在4项对比中,搜索算法预估的失效点与积分法预估的设计点均较一致,平均风速的误差不超过1 m/s,这表明搜索算法具有良好的识别能力,能够有效地分析出风机正常发电时最有可能出现失效的情况。
对于不确定性较小的叶片根部首尾弯矩OOPB,搜索算法外推结果与积分法更接近,修正因子
将EC法与二分法结合起来形成一种新的搜索算法,应用于求解Spar型浮式风机叶片根部面外弯矩和塔筒基底首尾弯矩在1年和20年重现周期下的极端载荷,主要可得以下结论:
1)相较于积分法55组的仿真数量,搜索算法仅利用17~19组仿真便获得了相应的极限载荷与设计点,因此在计算成本上具有较大的优势。
2)经过与传统直接积分法的外推结果对比验证,发现在极限载荷数值和引发失效的设计点上均较一致,说明了搜索算法同时也具有较高的可靠性。
3)作为参考,EC法还可结合其他最优化方法以进一步减少仿真需要的数量,提高求解精度。
| [1] |
IEC 61400-3: 2009, Wind turbines-Part 3: Design requirements for offshore wind turbines, Edition 1. 0, 2009[S].
|
| [2] |
IEC 61400-1: 2005, Wind turbines-Part 1: Design requirements, Edition 3. 0, 2005 [S].
|
| [3] |
MORIARTY PJ, HOLLEY W, BUTTERFIELD CP. Extrapolation of extreme and fatigue loads using probabilistic methods[EB/OL]. (2004-11) [2017-02]. http://www.nrel.gov/docs/fy05osti/34421.pdf.
|
| [4] |
SARANYASOONTORN K, MANUEL L. Design loads for wind turbines using the environmental contour method[J]. Journal of Solar Energy Engineering, 2006, 128(4): 554-61. DOI:10.1115/1.2346700 |
| [5] |
SARANYASOONTORN K, MANUEL L. Efficient models for wind turbine extreme loads using inverse reliability[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2004, 92(10): 789-804. DOI:10.1016/j.jweia.2004.04.002 |
| [6] |
KARMAKAR D, GUEDES SOARES C. Reliability based design loads of an offshore semi-submersible floating wind turbine[J]. Developments in Maritime Transportation and Exploitation of Sea Resources, Guedes Soares, C and FL Pena, eds, Taylor & Francis Group, London. 2014: 919–26.
|
| [7] |
KARMAKAR D, SOARES C G. Extreme response prediction of offshore wind turbine using inverse reliability technique[C]//ASME 2015 34th International Conference on Ocean, Offshore and Arctic Engineering. American Society of Mechanical Engineers, 2015: V003T02A065-V003T02A065.
|
| [8] |
KARMAKAR D, BAGBANCI H, SOARES CG. Long-term extreme load prediction of spar and semisubmersible floating wind turbines using the environmental contour method[J]. Journal of Offshore Mechanics and Arctic Engineering, 2016, 138(2): 021601. DOI:10.1115/1.4032099 |
| [9] |
AGARWAL P, MANUEL L. Simulation of offshore wind turbine response for long-term extreme load prediction[J]. Engineering structures, 2009, 31(10): 2236-46. DOI:10.1016/j.engstruct.2009.04.002 |
| [10] |
WINTERSTEIN SR, UDE TC, CORNELL CA, et al. Environmental parameters for extreme response: Inverse FORM with omission factors[J]. Proceedings of the ICOSSAR-93, Innsbruck, Austria, 1993, 551-7. |
| [11] |
ROSENBLATT M. Remarks on a multivariate transformation[J]. The Annals of Mathematical Statistics, 1952, 23(3): 470-2. DOI:10.1214/aoms/1177729394 |
| [12] |
JONKMAN J, BUTTERFIELD S, MUSIAL W, et al. Definition of a 5-MW reference wind turbine for offshore system development[EB/OL]. (2009–02) [2017–04]. http://www.nrel.gov/docs/fy09osti/38060.pdf
|
| [13] |
SARANYASOONTORN K, MANUEL L. On assessing the accuracy of offshore wind turbine reliability-based design loads from the environmental contour method[J]. International Journal of Offshore and Polar Engineering, 2005, 15(02). |
| [14] |
JONKMAN BJ. TurbSim User's Guide: Version 1. 06. 00[EB/OL]. (2012–09)[2017–04]. https://nwtc.nrel.gov/system/files/TurbSim.pdf
|
| [15] |
JONKMAN JM, BUHL Jr ML. FAST user's guide[EB/OL]. (2005–08)[2017–04]. http://wind.nrel.gov/public/bjonkman/TestPage/FAST.pdf
|
| [16] |
夏一青, 王迎光. 应用统计外推求解近海风机面外叶根部弯矩最大值[J]. 上海交通大学学报, 2013, 47(12): 1968-1973. XIA Yi-qing, WANG Ying-guang. Calculation of out-of-plane bending moment at the blade root of offshore wind turbines by statistic extrapolation[J]. Journal of Shanghai Jiaotong University, 2013, 47(12): 1968-1973. |
 2018, Vol. 40
2018, Vol. 40

