浅海区域服役的FPSO采用的系泊形式多为软刚臂式单点系泊系统,单点系泊系统对实现FPSO浅海作业的功能至关重要。系泊性能是软刚臂式单点设计的关键指标,国内外学者为此开展了一系列的研究,研究方法主要包括准静力分析法和动力分析法。
范模[1]根据单点系泊系统的力系和力矩平衡方程得到系泊系统刚度特性,基于准静态法计算程序分析压载水重、系泊腿长度及软刚臂长度对系泊性能的影响。温宝贵[2]通过与模型试验对比,研究了SZ36-1油田单点系泊性能及低频慢漂运动阻尼和单点系统刚度。准静力法采用定常模型进行分析,未能考虑不定常环境载荷的作用,与实际不符,现已逐渐被取代。其肖龙飞等[3]建立了FPSO-软刚臂单点系泊系统的耦合模型,计算单点系泊系统的动力响应,并通过与试验结果对比验证单点模型。唐永刚等[4]通过对比模型试验实测得到的软刚臂运动、主轴承载荷及铰接装置内3个自由度方向上的载荷分量,从而选定合理的单点设计方案。Liao等[5]针对“渤海蓬勃”号,分析不同压载水重量条件下单点系泊性能,得到系泊力及软刚臂的运动响应。秦尧[6]开展单点系泊系统对参数的敏感性分析,研究包括装载状态、环境变量及单点设计参数对单点系泊系统受力和FPSO性能的影响,得到谱峰周期、软刚臂长度对系泊力影响最大。刘成义[7]以系泊点高度、系泊支架高度及软刚臂等参数为变化因素,基于多体动力学时域计算方法得到其对单点系泊性能的影响。
目前软刚臂单点系泊系统的研究中,多采用控制变量法来研究系泊性能,从而得到软刚臂参数对系泊性能的敏感性影响。然而,若研究多因素多水平试验参数对系泊性能影响,控制变量法将极大程度地增加试验的规模,不能高效进行全面试验。本文基于正交试验的原理设计试验,利用时域耦合动力分析方法研究软刚臂多个设计参数对单点系泊性能的影响,为单点系泊系统初步设计工作中的主尺度优化提供一定的参考。
1 计算理论 1.1 时域分析理论 1.1.1 运动方程时域运动方程
| $\sum\limits_{i = 1}^6 {\left[ {{{M}_s} \!\!+\! \!{{{ M}}_a}\left( \infty \right)} \right]\ddot x(t)} +\! \int_0^t {{h}\left( {t - \tau } \right)\dot x(\tau ){\rm{d}}\tau } \!+\! {K}x(t) \!\!=\!\! F(t){\text{,}}$ | (1) |
式中:Ms为船舶质量矩阵,由质量及回转半径参数计算得到;Ma(∞)为最大计算频率对应的附加质量矩阵;
计算风载荷时把风当做定常风处理,根据经验公式及经验系数,船体所受的风载荷计算公式为:
| ${F_X}_w = \frac{1}{2}{C_{Xw}}{\theta _w}{\rho _w}{A_X}{V_w}^2{\text{,}}$ | (2) |
| ${F_{Yw}} = \frac{1}{2}{C_{Yw}}{\theta _w}{\rho _w}{A_Y}{V_w}^2{\text{,}}$ | (3) |
| ${M_{XYw}} = \frac{1}{2}{C_{XYw}}{\theta _w}{\rho _w}{L_{pp}}{A_Y}{V_w}^2{\text{,}}$ | (4) |
式中:FXw,FYw和MXYw分别为水平面纵,横风载荷及艏摇力矩;CXwθw,CYwθw和CXYwθw分别为船舶纵荡,横荡风载荷系数和首摇力矩系数;θw为风速入射角度;ρw为空气密度,取1.28 kg/m3;AX,AY分别为纵向,横向受风面积,m2;Lpp为船舶垂线间长,m;Vw为相对风速,m/s。
1.1.3 流载荷船体所受的流载荷计算公式如下:
| ${F_X}_c = \frac{1}{2}{C_{Xc}}{\theta _c}{\rho _c}T{L_{pp}}{V_c}^2{\text{,}}$ | (5) |
| ${F_Y}_c = \frac{1}{2}{C_{Yc}}{\theta _c}{\rho _c}T{L_{pp}}{V_c}^2{\text{,}}$ | (6) |
| ${M_{XY}}_c = \frac{1}{2}{C_{XYc}}{\theta _c}{\rho _c}T{L_{pp}}^2{V_c}^2{\text{。}}$ | (7) |
式中:FXc,FYc和MXYc分别为水平面纵,横流载荷及艏摇力矩;CXcθc,CYcθc和CXYcθc分别为船舶纵荡,横荡流载荷系数和首摇力矩系数;θc为海流入射角度;ρc为海流密度,取1 025 kg/m3;T为船舶吃水,m;Lpp为船舶垂线间长,m;Vc为相对风速,m/s。
1.1.4 波浪载荷在不规则波浪作用下,浮体不仅受到与波高成线性关系的一阶波浪力,还受到与波高成平方的二阶低频波浪力。本文基于三维势流理论,选用JONSWAP谱模拟不规则海浪,利用脉冲响应法,通过傅里叶变换可以得到波浪载荷的时域历程,如下所示。
1阶波浪力的表达式为
| ${F^{(1)}}(t) = \int_0^t {h(t - \tau )} \eta (\tau ){\rm d}\tau {\text{,}}$ | (8) |
式中:h(t)为脉冲响应;η(τ)为波谱生成的随机波面升高的时域历程。
根据波浪在不同频率下的传递函数,依据傅里叶变换得到二次脉冲响应函数g(τ1,τ2):
| $\begin{split}&g({\tau _1}\!,\!{\tau _2}) \!=\\& \quad \! {\left( {\frac{1}{{2\pi }}} \right)^2}\int_{\!-\! \infty }^{ \!+\! \infty } {\int_{ \!-\! \infty }^{ \!+\! \infty } {{G_i}^{(2)}({\omega _1}\!,\!{\omega _2})} } e(i{\omega _1}{\tau _1} \!-\! i{\omega _2}{\tau _2}){\rm d}{\omega _1}{\omega _2}{\text{,}}\end{split}$ | (9) |
| ${G_i}^{(2)}({\omega _1},{\omega _2}) = P({\omega _1},{\omega _2}) + iQ({\omega _1},{\omega _2}){\text{,}}$ | (10) |
式中:ωi,ωj为不同的波浪频率;τ1,τ2为时间间隔。
给定波浪历程ζ(t),即可得到2阶波浪力
| ${F_i}^{(2)} = \int_0^{ + \infty } {\int_0^{ + \infty } {{g_i}} } ({\tau _1},{\tau _2})\varsigma (t - {\tau _1})\varsigma (t - {\tau _2}){\rm d}{\tau _1}{\rm d}{\tau _2}{\text{。}}$ | (11) |
正交试验法是利用正交表来安排与分析多因素试验的一种设计方法。该方法是从试验因素的全部水平组合中,挑选部分有代表性的水平组合进行试验,这些有代表性的组合具备“均匀分散,齐整对比”的特点。均衡分散是指用正交表挑选出来的各因素水平组合在全部水平组合中的分布是均匀的,整齐可比是指每个因素的各水平间具有可比性。因正交表中每一个因素的任一水平下都均衡地包含着另外因素的各个水平,当比较某因素不同水平时,其他因素的效应都彼此抵消。等水平正交表为La(bc),其中a表示无重的试验总次数,b表示因素水平数,c表示因素个数。用部分试验替代全面试验,通过对部分试验结果的分析,了解全面试验的情况,从而找出最优的水平组合。
K为各因素同一水平的结果之和,k为各因素同一水平的平均值,计算方法如下:
| $K = \sum\limits_{i = 1}^N {{T_i}} {\text{,}}$ | (12) |
| $k = \frac{K}{N}{\text{。}}$ | (13) |
式中:N为各因素的水平个数;T为试验结果。
各因素的极差R表示该因素在其取值范围内试验指标变化的幅度,根据极差大小可以判断该因素对目标的主次影响顺序。R越大,表示该因素的水平变化对试验指标的影响越大,因素越重要。
| ${R_i} = \max ({k_i}) - \min({k_i}){\text{。}}$ | (14) |
本文针对作业于渤海海域的海洋核动力平台开展研究,平台采用软刚臂式单点系泊系统进行系泊作业。平台相关参数如表 1所示。
|
|
表 1 平台参数 Tab.1 Parameters of the platform |
利用AQWA软件,建立包括系泊支架、系泊腿、系泊刚臂与平台在内的多体动力学分析模型,坐标系的原点取在船尾水面处,X轴正向由船尾指向船首,Y轴正向指向左舷,Z轴正向竖直向上,模型如图 1所示。船体的网格密度为2 m,系泊腿和软刚臂的网格密度为1.5 m,模型网格总数为9 775。平台与系泊腿以万向节连接,具有横摇和纵摇2个自由度;系泊刚臂与系泊腿、系泊刚臂与固定塔架之间以球铰约束,释放3个转动自由度。
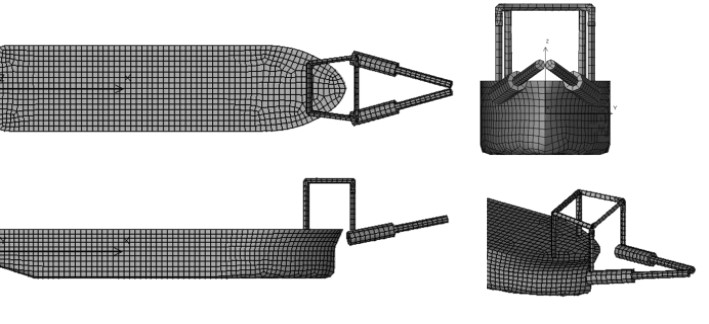
|
图 1 水动力计算模型 Fig. 1 The model for hydrodynamic calculation |
本文计算采用风浪流同向作用于平台的工况,风浪流方向为180°,由船首指向船尾。时域计算持续时间为3 h,时间步长为0.2 s。作业海域重现期为500年的海洋环境条件如表 2所示。
|
|
表 2 海洋环境条件 Tab.2 Environmental conditions |
本次正交试验目的是确定软刚臂的最优主尺度,以系泊力为试验指标,研究系泊腿长度、压载水重量及软刚臂长度3个影响因素对系泊力的影响程度。每个因素包含5个水平,参考“明珠”号母型及本项目工程造价的论证,选择系泊腿长度为11 m,11.5 m,12 m,12.5 m及13 m,压载水重为340 t,350 t,360 t,370 t及380 t,软刚臂长度为28 m,29 m,30 m,31 m及32 m。选择三因素五水平的正交试验,试验工况数为L(35)=25,因素水平表设计如表 3所示。
|
|
表 3 试验因素及水平 Tab.3 Experimental factors and levels |
通过水动力计算,各工况下的系泊力及正交试验结果如表 4所示。
|
|
表 4 试验结果及极差分析 Tab.4 Experimental results and range analysis |
通过比较系泊腿长度、压载水重量和软刚臂长度3个因素极差大小,可以得出R(C)>R(B)>R(A),说明因素对试验指标影响的主次顺序为C、B、A,即软刚臂长度影响最大,其次为压载水重量,影响较小的为系泊腿长度。由于试验目标系泊力越小系泊性能越优良,在三因素的5个水平中,系泊腿11 m时系泊力最小,压载水重380 t时系泊力最小,软刚臂长度32 m时系泊力最小,因此从系泊力的角度考虑,选定最优组合为A1B5C5。
3.3 因素指标趋势图为便于更直观地看出试验目标随因素水平变化的规律,根据试验结果绘制出试验目标随各因素变化的趋势,如图 2所示。可以看出,纵向系泊力随系泊腿长度的增加有增大的趋势,随压载水重的增加先增大后减小,随软刚臂长度的增加而减小。
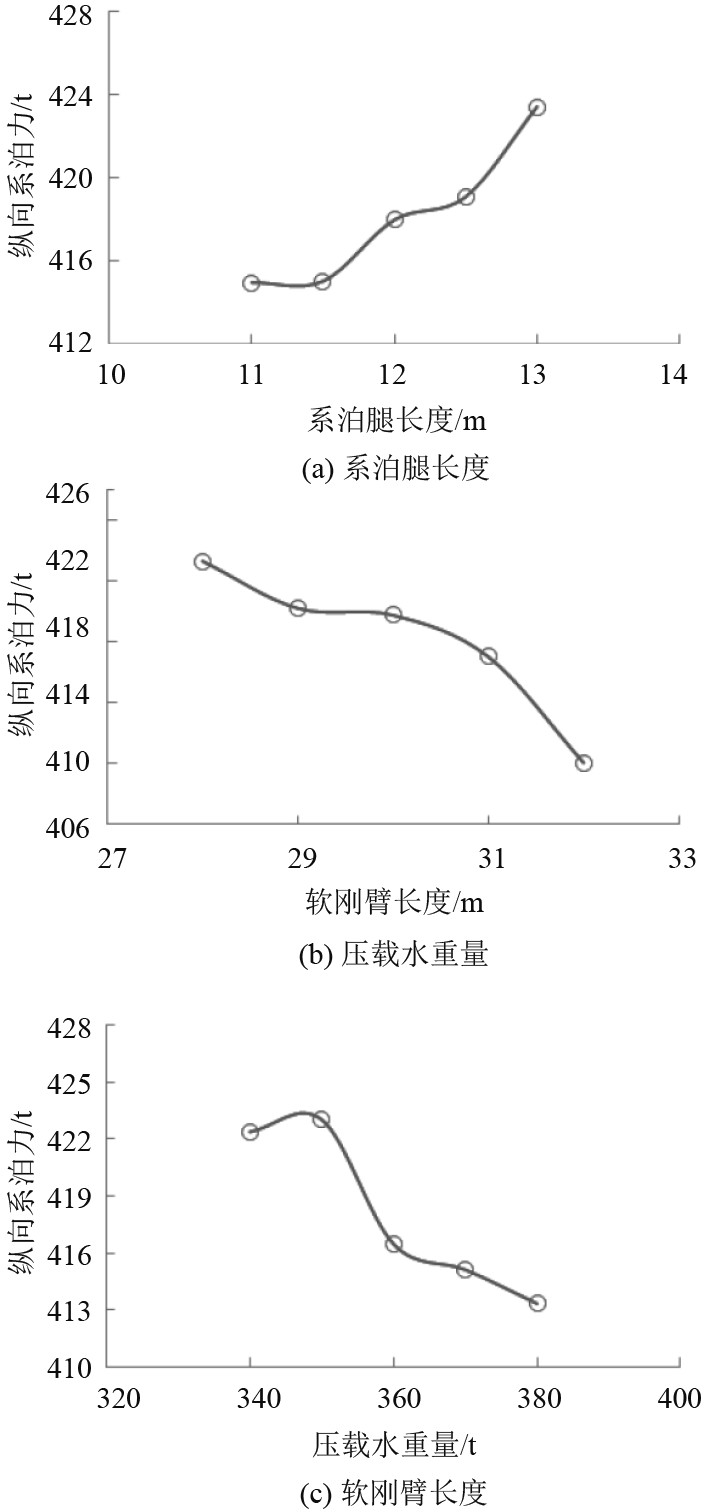
|
图 2 系泊力随因素变化曲线 Fig. 2 The change curve of mooring force with factors change |
本文针对系泊海洋核动力平台的软刚臂式单点系泊系统的设计及系泊性能研究,利用正交试验法设计试验工况进行水动力计算。正交试验以系泊力为试验目标,设计系泊腿长度、压载水重量及软刚臂长度3个试验因素,每个因素设置5个水平变量,共设计25种试验工况。采用时域分析方法计算每种试验下的系泊性能,根据计算结果选出软刚臂最优尺度组合,即系泊力最小值,另外确定影响系泊性能的主次因素,对软刚臂单点系泊系统方案设计中主尺度的优化具有一定的借鉴意义。本文主要结论如下:
1)3个试验因素中,对系泊力影响最大的为软刚臂长度,其次为压载水重,对系泊力影响最小的为系泊腿长度。
2)系泊力随系泊腿长度增加而增加,随压载水重的增加呈现先增大后减小的趋势,随软刚臂长度的增加而减小。
| [1] |
范模. 软刚臂单点系泊系统分析[J]. 中国海上油气(工程), 1992, 4(1): 29-33. |
| [2] |
温宝贵. SZ36-1油田单点系泊力的确定[J]. 中国海上油气(工程), 1992, 4(2): 29-33. |
| [3] |
肖龙飞, 杨建民, 姚美旺. 浮式生产储油轮诱导软刚臂系泊系统的动力响应[J]. 上海交通大学学报, 2007, 41(2): 162-167. DOI:10.3321/j.issn:1006-2467.2007.02.002 |
| [4] |
唐永刚, 毛晖. 超大型FPSO软轭架转塔式单点系泊系统设计研究[J]. 船舶工程, 2010, 32(6): 60-63. DOI:10.3969/j.issn.1000-6982.2010.06.016 |
| [5] |
LIAO S W, CHEN D H. Assessment of SYMS survival limit for "Peng Bo" FPSO during instarlation[C]//Proceeding of ASME,2010 29th International Conference on Offshore Mechanics and Arctic Engineering. Shanghai: ASME, 2010.
|
| [6] |
秦尧. 软刚臂单点系泊FPSO动力响应特性研究[D]. 天津: 天津大学, 2013.
|
| [7] |
刘成义, 唐友刚, 李焱, 等. 浅水单点系泊FPSO软刚臂参数敏感性分析[J]. 中国舰船研究, 2014, 9(5): 69-76. DOI:10.3969/j.issn.1673-3185.2014.05.012 |
 2018, Vol. 40
2018, Vol. 40
