0 引　言

钢/聚氨酯夹层板最早由英国IE公司提出并研发^[1]，其采用聚氨酯弹性体作为芯材，此类材料的强度和弹性模量具有较大调节范围，并具有良好的粘弹性^[2]。钢/聚氨酯夹层板通常采用三明治结构，具有形式简单、比强度高、比刚度大、减震效果好、抗疲劳等优点^{[3 – 6]}，已被欧美国家应用于船舶与海洋工程领域的结构制造、维修等各个方面。动态性能是固体材料在高加载速率、高压和高温等因素下物理和力学性质^[7]，通常与静态性能有着较大差异。由于船舶与海洋工程结构遭受碰撞和冲击等动态载荷作用的几率很高，故此类结构在强度设计和校核时必需考虑其动态力学响应是否超限，而此类计算和分析首先必须获得材料的动态本构关系。对于船舶与海洋工程结构而言，动态压缩是一种比较常见的载荷形式，所以研究夹层板材料的动态压缩本构关系有着重要的研究意义和工程应用价值。

为此，利用LS-DYNA有限元软件构建了霍普金森压杆（SHPB）实验的数值模型，并对不同厚度比的钢/聚氨酯夹层板进行了SHPB实验的数值模拟和分析，研究了钢/聚氨酯夹层板的动态压缩力学特性，构建并对比分析了钢/聚氨酯夹层板动态压缩本构关系，以期能为工程应用提供有益参考。

1 SHPB实验的数值模拟 1.1 SHPB实验

分离式霍普金森压杆（Split Hopkinson Pressure Bar，SHPB），是目前获取材料在中高应变率下的动态本构关系的重要实验手段，其实验数据通常采用二波法或三波法^[8]进行处理分析，本文全部采用经典二波法进行数据处理，见式（1）～式（3）。

$\dot \varepsilon \left( t \right) = - \frac{{2{C_0}}}{{{L_s}}}({\varepsilon _i} - {\varepsilon _t}) = - \frac{{2{C_0}}}{{{L_s}}}{\varepsilon _r}\text{，}$

(1)

$\varepsilon \left( t \right) = - \frac{{2{C_0}}}{{{L_s}}}\int_0^t {({\varepsilon _i} - } {\varepsilon _t}){\rm d}t = - \frac{{2{C_0}}}{{{L_s}}}\int_0^t {{\varepsilon _r}} {\rm d}t\text{，}$

(2)

$\sigma \left( t \right) = \frac{{EA}}{{{A_s}}}({\varepsilon _i} + {\varepsilon _r}) = \frac{{EA}}{{{A_s}}}{\varepsilon _t}\text{。}$

(3)

式中： ${C_0}$ ， $A$ ， $E$ 分别为SHPB装置中波导杆的弹性纵波波速，横截面积和弹性模量； ${A_s}$ ， ${L_s}$ 分别为试样横截面积及厚度； ${\varepsilon _i}$ ， ${\varepsilon _r}$ 和 ${\varepsilon _t}$ 分别为作用在试样端面上的入射波，反射波和透射波应变信号。 $\varepsilon (t)$ ， $\sigma (t)$ 和 $\dot \varepsilon (t)$ 分别是试样的应变，应力和应变率。

1.2 SHPB实验的有限元模型

考虑到夹层板试样制备时在钢和聚氨酯粘接面上可能存在粘结强度差异或者其他缺陷，以及SHPB实验本身的误差影响会影响后续分析，故本文利用LS-DYNA有限元软件对SHPB实验进行数值模拟，通过数值实验实现对钢/聚氨酯夹层板动态压缩本构关系的分析研究。

1.2.1 试样设计

本文仿真分析选择5种不同厚度比的试样，详细尺寸见表1，A面板为受冲击面

1.2.2 子弹与波导杆设计

在对SHPB实验进行数值仿真时首先需要保证实验装置的准确模拟，其中最重要的是必须保证SHPB装置的波导杆能满足一维应力波理论，即波导杆杆径必须远小于应力波波长^[8]，数值分析中实验装置的具体几何尺寸见表2。

1.2.3 有限元模型构建与材料参数

本文采用8节点Solid164动态显式实体单元建立SHPB系统中的子弹、输入杆、输出杆和试样的几何模型，各接触面采用自动面面接触，静摩擦系数为0.05，动摩擦系数为0.01，接触刚度因子为0.1。子弹与波导杆选用同种铝材，模型中采用各向同性线弹性材料，并设置较高的屈服强度以保持其弹性；铝材的密度取为2 816 kg/m³，弹性模量为73.02 GPa，泊松比为0.33，则杆内弹性波波速为5 093 m/s。

夹层板试样的面板材料选用45钢，夹层板芯材选用聚氨酯弹性体，首先利用万能试验机测定了两者在准静态下强度及弹性常数，再利用SHPB实验装置获得了2种材料在不同应变率下的应力应变关系，实验表明两者均符合Cowper-Symonds模型，并通过数据拟合得到对应的材料模型中的应变率料参数，具体见表3。

1.3 数值仿真的可靠性分析

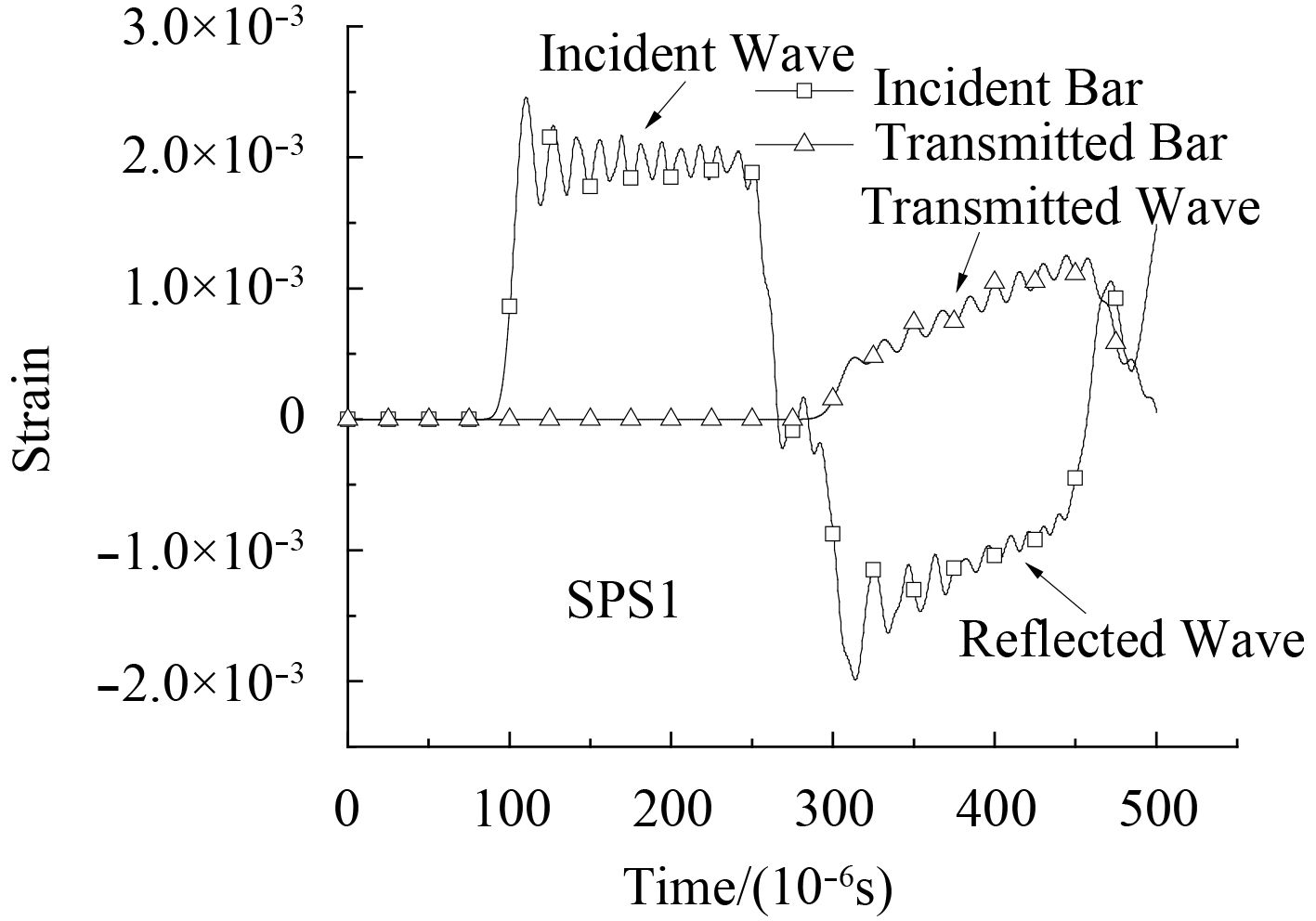
按前文的方法模拟厚度比为0.182的钢/聚氨酯夹层板在SHPB实验中的典型应变时程曲线如图1所示，从图中可以看到入射波具有典型的上升沿、振荡平台和下降沿，平台头部的振荡是由径向效应引起的，在上升沿波形中点处没有不规则波形，这说明入射杆在仿真分析中整体性能良好。

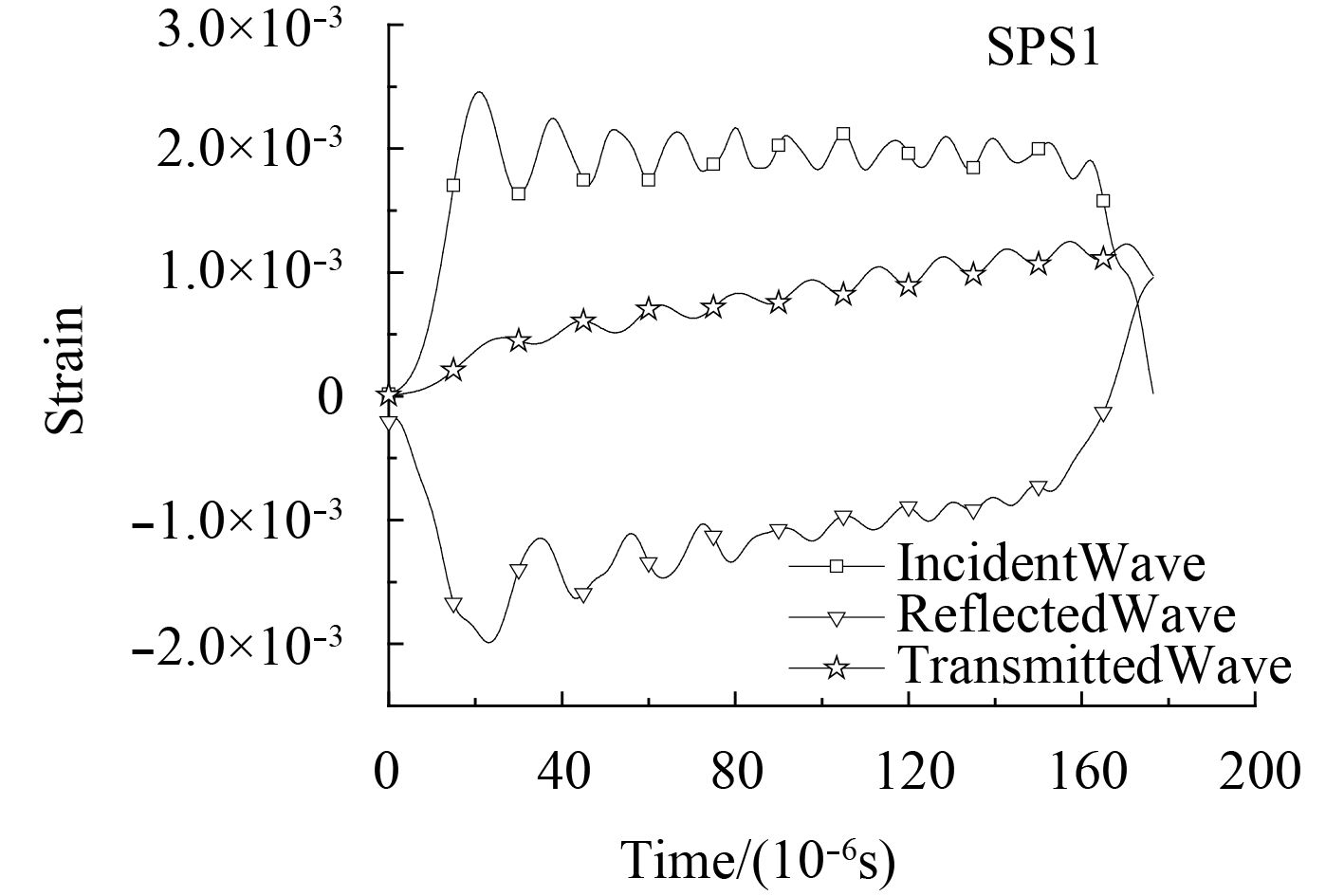
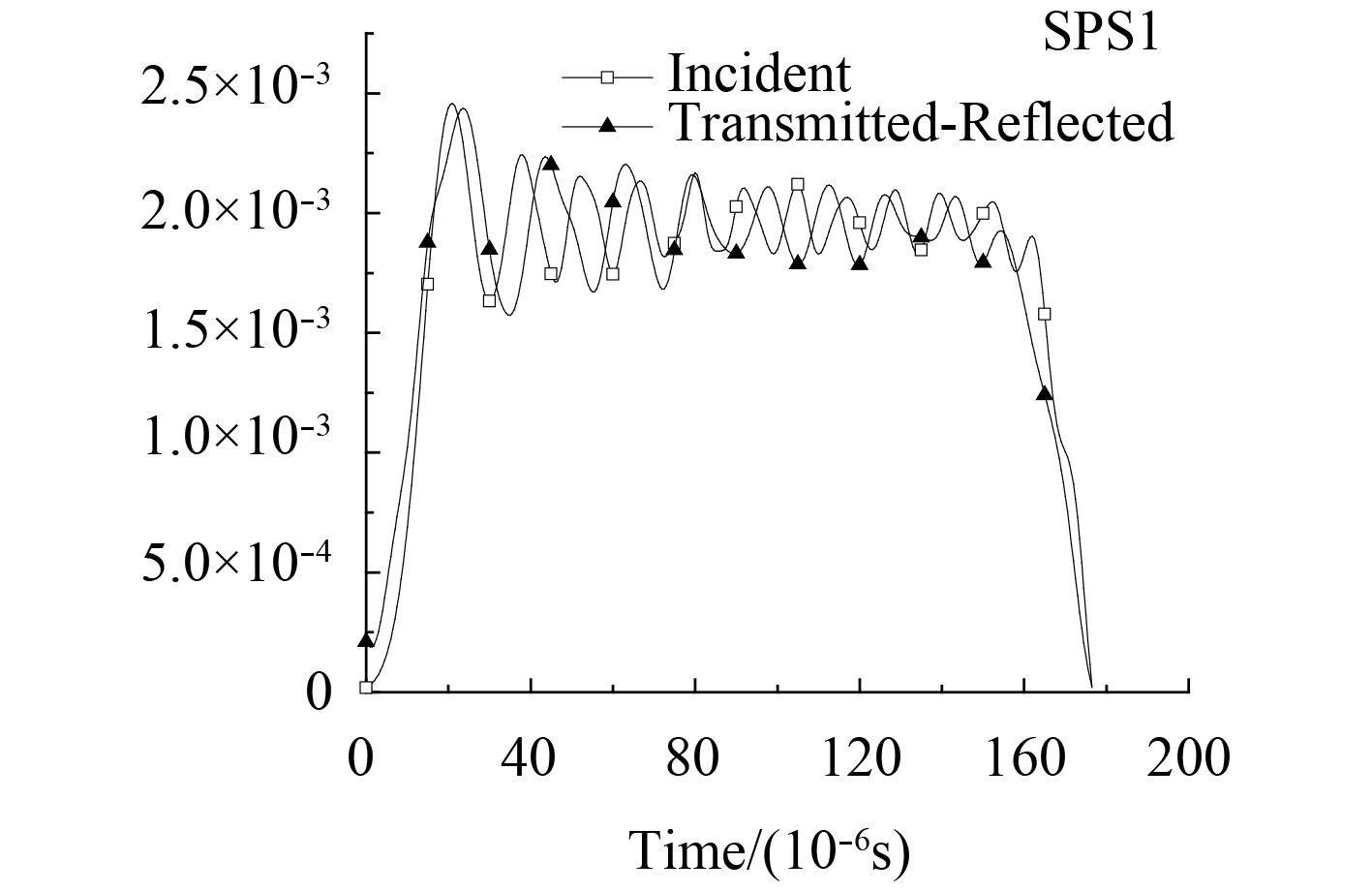
将入射、反射和透射的3个应力波的头部对齐后的波形图如图2所示，在此基础上，将入射波与反射波叠加得到的波形和入射波波形对比图如图3所示。

按一维应力波理论，应力波的波宽为子弹长度的2倍。因此，入射波、反射波和透射波的波宽应当相同，且三波的历时均为

$\Delta t = {{2L}/{{C_0}}}$

(4)

式中： $L$ 为子弹长度，为400 mm； ${C_0}$ 波导杆中的弹性纵波波速，采用铝杆时取为5 093 m/s。

由此可得， $\Delta t = 157.1$ μs，即三波的单周期历时应在 $157.1$ μs左右。由图2可知，仿真分析的结果与经典理论完全符合。由图3可知，透射波应变与反射波应变之差等于入射波应变，仿真结果也符合均匀性假设。

2 数值计算结果与分析 2.1 不同厚度比的夹层板在相同子弹速度下的应变率分析

本文中子弹分别以20 m/s，30 m/s，40 m/s的速度冲击不同厚度比的试样得到的应变率如表4。

由表4分析可知，相同子弹速度下不同厚度比试样的应变率基本一致，且在一定厚度比范围内，应变率随着厚度比的提高而减少。进一步分析可知，应变率的减小量与试样厚度比的增量呈正相关，且在一定厚度比范围内变化比较明显，这表明随着钢板厚度的增加，钢板起到的吸收能量作用越来越明显。

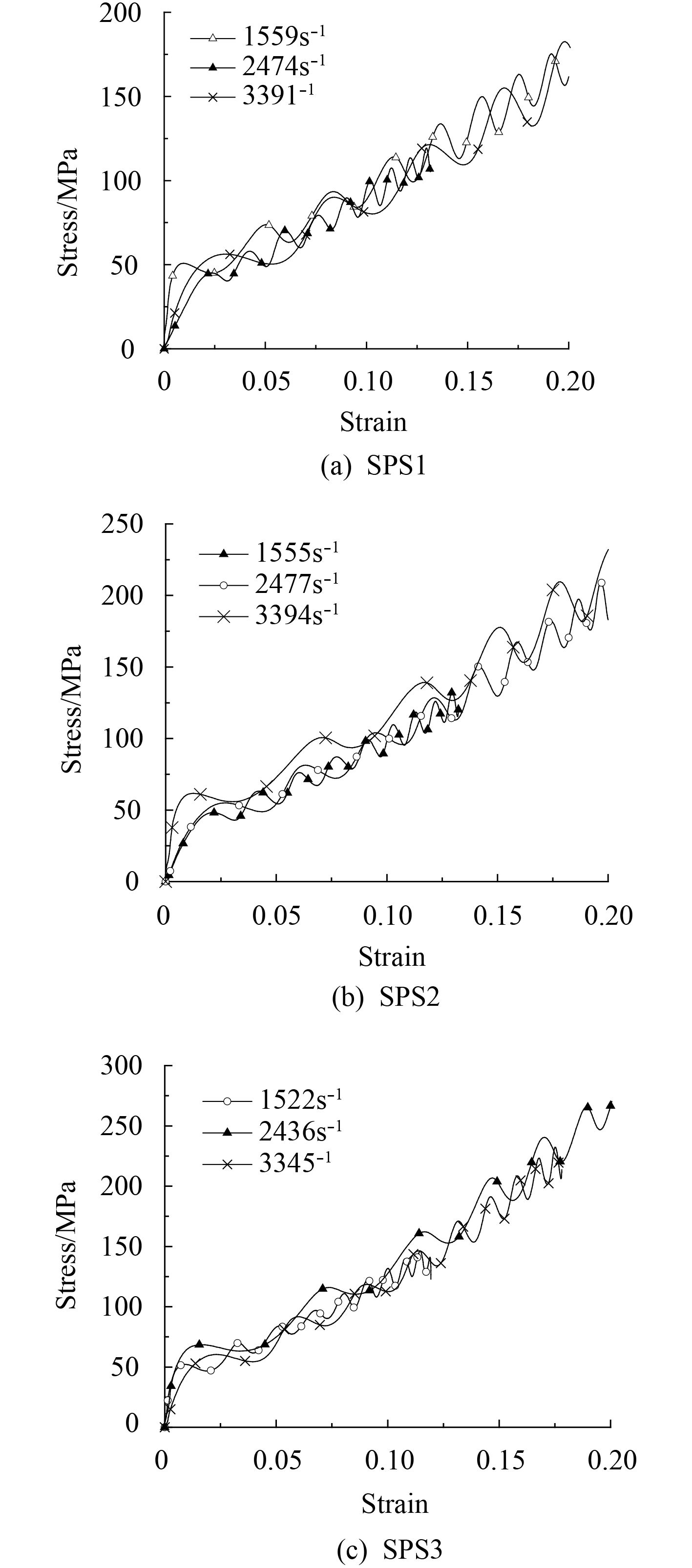
2.2 相同厚度比的夹层板的应变率效应分析

通过经典二波法公式处理得到试样SPS1，SPS2和SPS3在不同应变率下的应力应变曲线如图4所示。本文将应力第一次下降前的峰值定义为屈服强度。依据图4得到的钢/聚氨酯夹层板在不同应变率下的屈服强度见表5。

由表5可知，不同厚度比的钢/聚氨酯夹层板试样的屈服强度均随着应变率的增大而增大。因此，钢/聚氨酯夹层板材料是对应变率较为敏感的材料。当夹层板厚度比为0.18时，屈服强度的增幅随着应变率的增加而明显增加；而当材料厚度比为0.3和0.44时，屈服强度的增幅随应变率的增加而有稍微下降，即夹层板的应变率敏感度随厚度比的增加会逐渐下降。

3 钢/聚氨酯夹层板动态压缩本构关系 3.1 钢/聚氨酯夹层板动态本构关系建立

基于实际工程应用的需要，夹层板的厚度通常较小，本文中试样的厚度比为0.18～0.625，即钢面板较薄而聚氨酯芯材占据大部分厚度。当钢/聚氨酯夹层板收到法向的冲击载荷时，前侧钢面板会首先作出响应，而后将应力波向聚氨酯芯材及后侧面板传递。一方面，钢面板虽然较薄，但其动态响应对应力脉冲的形成至关重要，而聚氨酯芯材则由于厚度占比大而使得其力学性能也将对夹层板的整体性能产生显著影响。因此，本文分别采用适用于粘弹性材料的ZWT模型^[9]和适用于金属材料的Johnson-Cook模型构建钢/聚氨酯夹层板的动态压缩本构方程^[10]，并对方程的适用性及精度进行对比分析。

3.1.1 ZWT本构关系模型的建立

ZWT本构方程的力学模型由一个非线性弹簧和两个Maxwell单元组成，本构方程中后2个积分式分别代表的是2个不同松弛时间的Maxwell体，松弛时间为θ₁的Maxwell体用来表示低应变率时材料的粘弹性响应，松弛时间为θ₂的Maxwell体则用来表示高应变率下材料的粘弹性响应。其本构关系为：

$\sigma = \left( {{E_0} + {E_1}} \right)\varepsilon + \alpha {\varepsilon ^2} + \beta {\varepsilon ^3} + {E_2}\dot \varepsilon {\theta _2}\left( {1 - {e^{ - \frac{\varepsilon }{{\dot \varepsilon {\theta _2}}}}}} \right)\text{。}$

(5)

通过拟合得到各参数分别为 ${E_0} + {E_1} = 1\;801{\rm{MPa}}$ ， $\alpha = - 12\;652{\rm{MPa}}$ ， $\beta = 38\;113{\rm{MPa}}$ ， ${E_2} = 123.14{\rm{GPa}}$ 和 ${\theta _2} = 5.21{\rm{E - 11}}$ 。

3.1.2 Johnson-Cook本构关系模型的建立

描述粘弹塑性材料力学性能的本构关系的Johnson-Cook方程与应变率和温度相关，其数学模型为：

$\sigma = \left[ {A + B{\varepsilon ^n}} \right]\left[ {1 + C\ln {{\dot \varepsilon }^*}} \right]\left[ {1 - {{\left( {{T^*}} \right)}^m}} \right]\text{，}$

(6)

式中： $\sigma $ 为应变； $\varepsilon $ 为塑性应变； ${\dot \varepsilon ^*} = {{\dot \varepsilon }/{{{\dot \varepsilon }_0}}}$ 是无量纲塑性应变率， $\dot \varepsilon $ 表示应变率， ${\dot \varepsilon _0}$ 表示初始应变率，在大量文献中一般令其为1； ${T^*} = (T - {T_r})/({T_m} - {T_r})$ ， $T$ 为环境温度， ${T_r}$ 为室温， ${T_m}$ 为材料的熔点；A为静态屈服应力，B为硬化参数，n为硬化指数，C为应变率参数，m为温度指数； $\left[ {A + B{\varepsilon ^n}} \right]$ ， $\left[ {1 + C\ln {{\dot \varepsilon }^*}} \right]$ 和 $\left[ {1 - {{\left( {{T^*}} \right)}^m}} \right]$ 分别描述了材料的硬化效应，应变率效应和温度软化效应。

通过拟合调整，取 $A = 0.2{\rm{MPa}}$ ， $B = 4.0{\rm{MPa}}$ ， $n = 0.5$ 。由对上文仿真分析结果的分析可知，不同厚度比的夹层板结构具有不同的应力应变曲线和屈服强度。所以本文在Johnson-Cook本构方程中引入厚度比 $\eta $ 。对Johnson-Cook本构方程中的C进行变换，取 $C = f\left( {\dot \varepsilon ,\eta } \right)$ 根据试样的动态压缩应力应变曲线，得到

$\begin{split} C = &1.856 + 12.267\eta - 2.265{\eta ^2} + \\ & {(457.9 - 12.6\eta - 199.3{\eta ^2})^{ - 1}}\dot \varepsilon \text{。}\end{split}$

(7)

本实验不考虑温度软化效应，故忽略温度变化对材料力学性能的影响，由此可得钢/聚氨酯夹层板的本构关系模型为：

$\sigma = \left[ {0.2 + 4{\varepsilon ^{0.5}}} \right]\left[ {1 + C\ln \frac{{\dot \varepsilon }}{{{{\dot \varepsilon }_0}}}} \right]\text{。}$

(8)

3.2 本构关系模型一般性验证 3.2.1 ZWT本构方程一般性验证

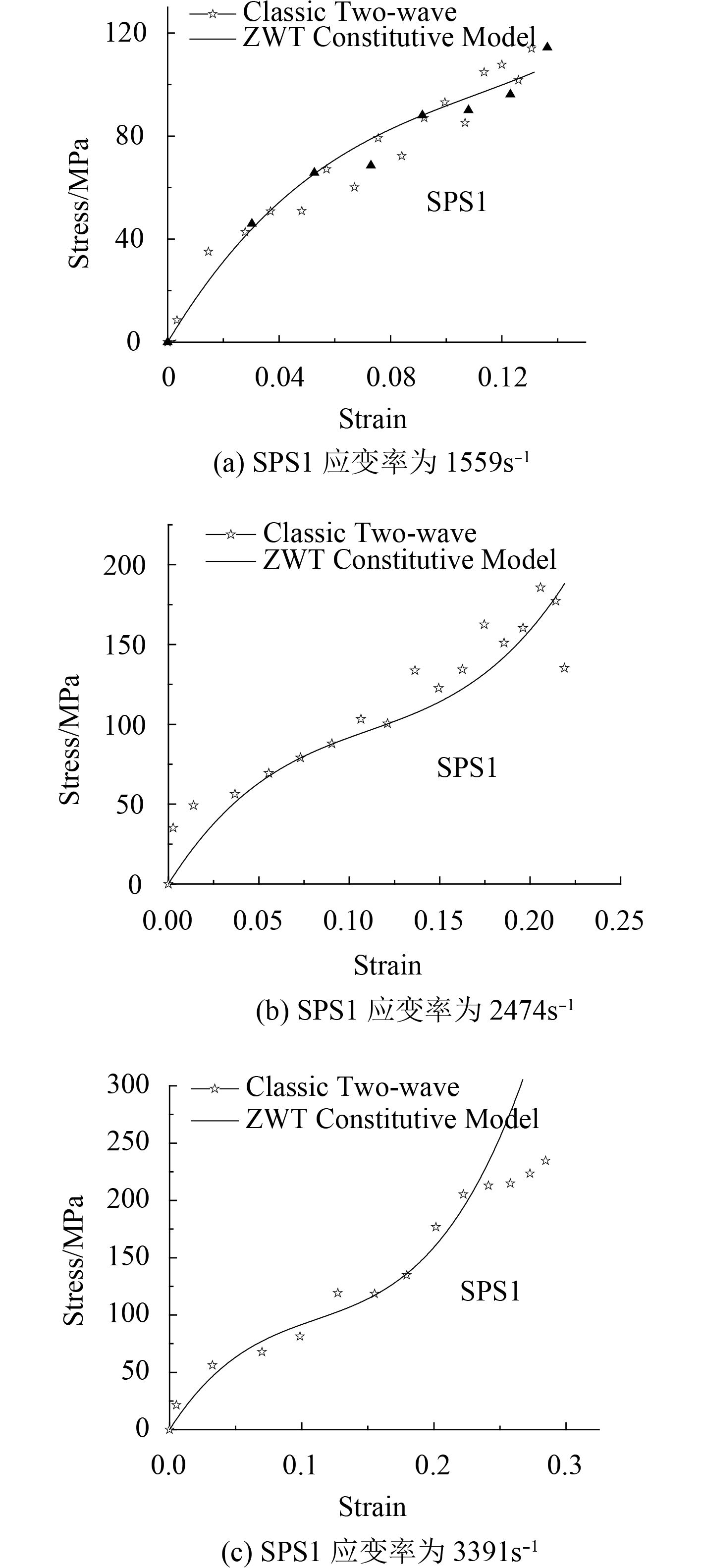
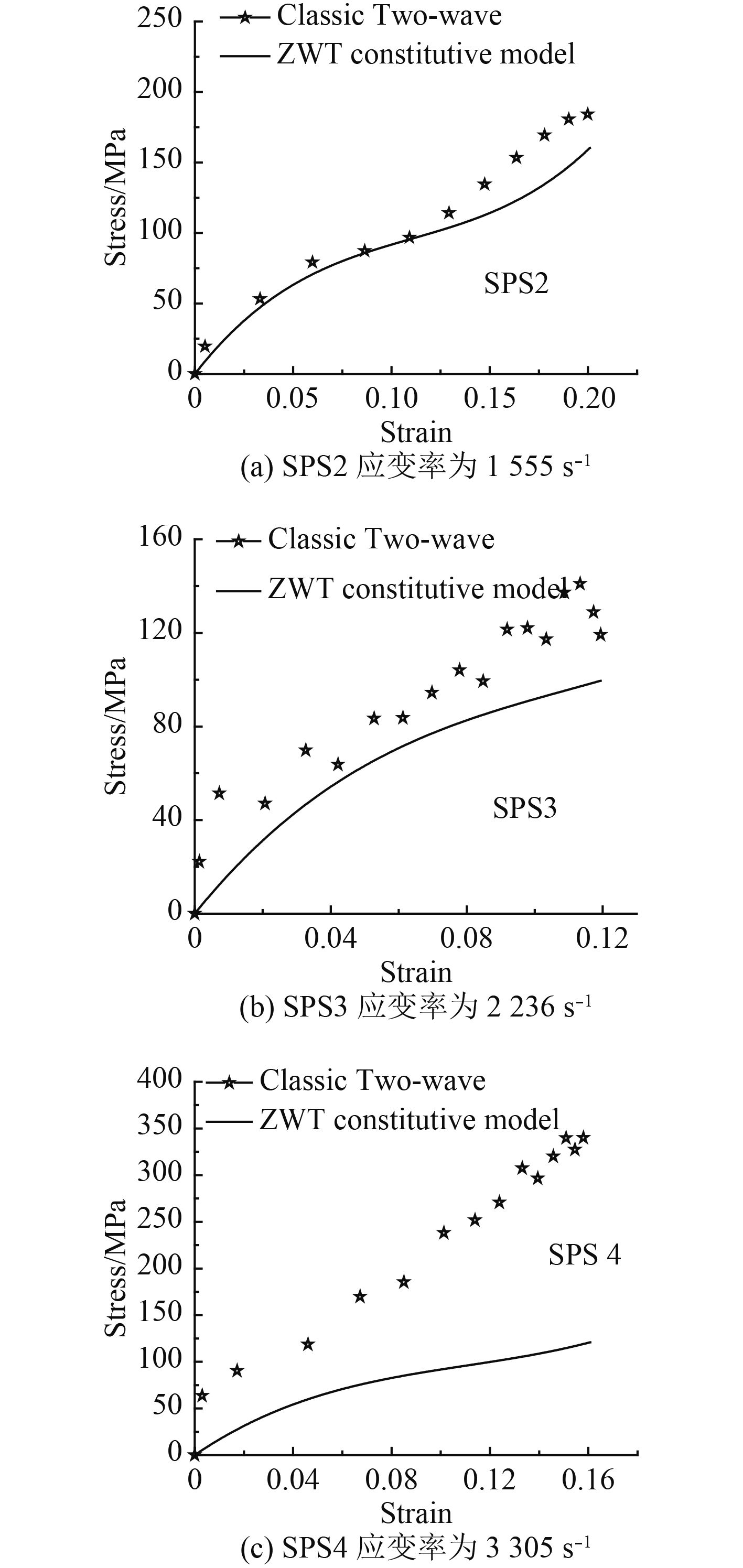
以SPS1为例，如图5，可知夹层板的厚度比比较小时，ZWT方程能够精确的适用于本文，与仿真结果吻合度很高，而SPS2，SPS3，SPS4在几种阶段的应变率下ZWT本构方程拟合曲线与仿真分析曲线如图6所示。

通过图6分别与图4进行对比。可知随着厚度比的增大，由ZWT本构方程拟合的应力应变曲线逐渐与仿真分析曲线分离直至完全不吻合。因此，本文中的ZWT本构方程不适用于描述厚度比较大的钢/聚氨酯夹层板结构，即ZWT本构方程不具一般性。当厚度比增大时，夹层板中钢面板具有的弹塑性对夹层板的动态压缩力学性能的影响逐渐明显，夹层板的动态性能将更趋向于粘弹塑性材料。

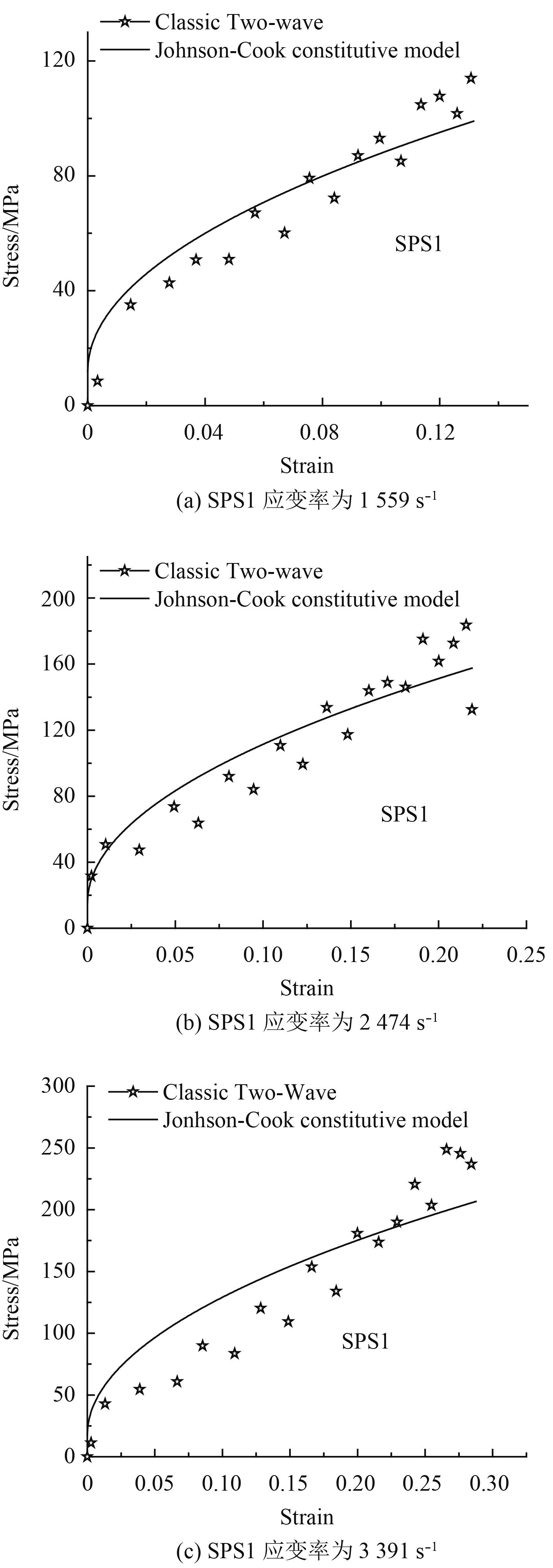
3.2.2 Johnson-Cook本构方程一般性验证

对于厚度比较小的SPS1钢/聚氨酯夹层板，采用Johnson-Cook本构方程拟合的曲线与仿真实验曲线如图7所示。

从图5分别与图7对比可知，Johnson-Cook本构方程拟合曲线与仿真曲线基本吻合，但是精确度低于ZWT本构方程。

对于厚度比比较大的SPS2、SPS3和SPS4试样在几种应变率下的实验曲线与方程给出的计算曲线，具体如图8所示。

从图8分别与图6对比可知Johnson-Cook本构方程在厚度比比较大时候也同样适用于本文，所以Johnson-Cook本构方程对不同厚度比钢/聚氨酯夹层板不失一般性。最初适用于描述金属材料动态本构关系的Johnson-Cook本构关系模型经修正后可用于本文描述钢/聚氨酯夹层板的动态力学本构关系。

4 结　语

本文基于有限元数值仿真对SHPB实验技术进行模拟，分析了钢/聚氨酯夹层板的动态压缩力学性能，在此基础上分别基于ZWT模型和Johnson-Cook模型建立了动态本构关系模型，并对2种模型进行了对比分析，得到结论如下：

1）钢/聚氨酯夹层板对应变率非常敏感，其屈服强度随应变率的提高将显著提升，但其应变率敏感度随厚度比的增加将逐渐下降。

2）在相同应变率下，钢/聚氨酯夹层板的屈服强度与其厚度比呈正相关关系，试样屈服强度的增幅与厚度比的增幅呈正相关关系。

3）ZWT模型在厚度比较小时精度高于Johnson-Cook模型，但当厚度比较大时不具一般性，Johnson-Cook模型能比较精确的描述不同厚度比的钢/聚氨酯夹层板在高应变率下的应力应变关系，本文基于Johnson-Cook模型拟合得到的钢/聚氨酯夹层板动态压缩本构方程具有较高精度，对工程实践具有较好的参考价值。