2. 武汉第二船舶设计研究所,湖北 武汉 430205;
3. 武昌船舶重工集团有限公司,湖北 武汉 430060
2. Wuhan Second Ship Design and Research Institute, Wuhan 430205, China;
3. Wuchang Shipbuilding Industry Group Co. Ltd, Wuhan 430060, China
通过水下航行器的动力学模型可以发现,影响水下航行器动力学建模精度的关键因素有3个:水动力阻尼模型、推进器推力模型和舵翼作用力模型,而建模的难点不仅在于选择合理的表达式以描述这3个模型,准确获取表达式中的水动力参数亦非常困难。通过试验或数值计算等方法虽然可以确定水下航行器的动力学模型,但往往需要花费大量的人力和物力,或需要有很好的计算机软硬件条件,而且所建立的模型通常也只适用于一些特定的操纵运动[1]。近年来得到较大发展的自航模或实尺度试验加系统辨识的方法虽然能够较有效地用于建立操纵运动数学模型,但系统辨识本身仍存在一些固有缺陷,如动力相消效应、参数漂移和多重共线等,会影响其建模精度。另外,目前尚没有较好的方法可对六自由度非线性模型进行水动力导数的辨识。
人工智能方法的出现,为克服上述困难提供了一种有效途径。为精确描述水下航行器的非线性动力学特性,通过智能算法建立一个同动力学模型等价的非线性映射函数,该非线性函数内的参数不具有物理意义,只是数学意义上的等价关系,这种建模方法即为非线性动力学辨识建模,也即黑箱建模方法。该方法的显著优点在于所建立的数学模型仅与系统输入和输出有关,不用考虑模型的真实动力学特性,这就避免了机理建模中的水动力参数的获取,而且可以顾及在机理建模中被忽略的高阶小量,因此,黑箱建模的精度通常较机理建模要高。人工神经网络经过多年的发展和应用,被认为是一种更有效的人工智能算法,在非线性动力学辨识建模方面得到了广泛的应用。
1 水下航行器操纵运动数学模型根据文献[2],水下航行器的六自由度数学模型如下:
| $ { M} \dot \nu + { C}\left( \nu \right)\nu + { D}\left( \nu \right)\nu + { g}\left( \eta \right) = \tau {\text{,}}$ | (1) |
其中:M为包含附加质量在内的惯性矩阵;
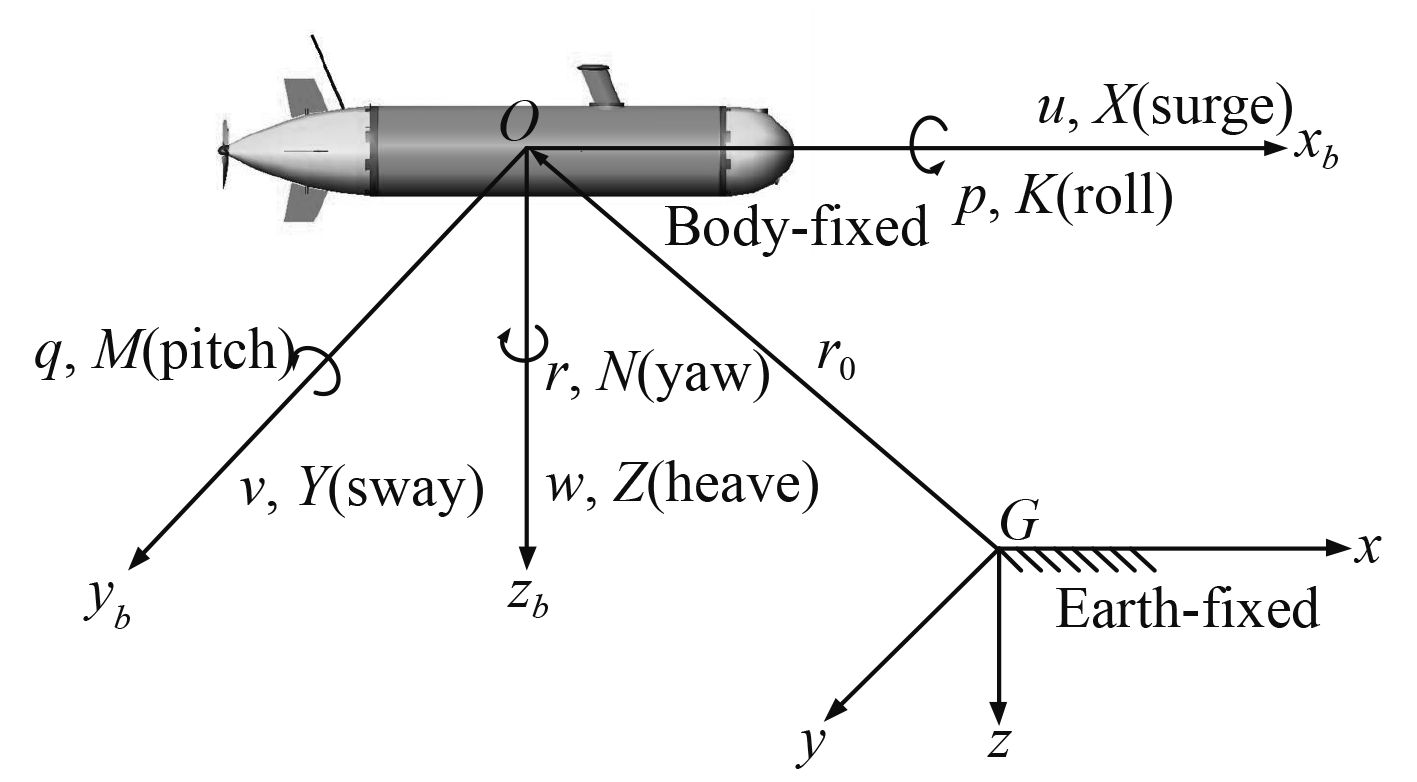
各参数定义如图1所示。
|
图 1 水下航行器运动变量描述 Fig. 1 Description of motion variables for underwater vehicles |
在式(1)所示的动力学模型中,影响水下航行器动力学建模精度的关键项即为水动力阻尼
为实现对水下航行器的操纵运动黑箱建模,对式(1)进行变换得到:
| ${ C}\left( \nu \right)\nu + { D}\left( \nu \right)\nu {\rm{ = }}\tau {\rm{ - }}{ g}\left( \eta \right){\rm{ - }}{ M}\dot \nu {\text{,}}$ | (2) |
式中,
在实际应用中,通过自航模或实船试验获取式水下航行器的速度和加速度信息,再通过试验或数值计算获取式(2)右端项中的不确定项,即可以
人工神经网络是一种类似于人类大脑处理信息的人工智能算法,在近20年间得到广泛的研究和应用,被认为是一种非常有效的算法,被广泛应用于几乎所有领域。它的一般结构包括输入层、隐含层和输出层3部分,隐含层可包含一个或多个,其中隐含层的不同结构以及所选择的不同激活函数便形成了不同的人工神经网络算法,常用的包括BP神经网络、径向基函数(Radial Basis Function,RBF)神经网络、Hopfield神经网络等。

|
图 2 神经网络结构图 Fig. 2 Structure of artificial neural network |
人工神经网络对非线性函数具有良好的拟合能力,为水下航行器的非线性动力学辨识提供了一种有效手段。其中的RBF神经网络在理论上已被证明,若隐含层节点数目足够多,则可一致逼近任意非线性函数[3]。RBF神经网络中常用的径向基函数为高斯函数,RBF神经网络的激活函数可表示如下:
| $R\left( {{x_p} - {c_i}} \right) = \exp \left( { - \frac{1}{{2{\sigma ^2}}}{{\left\| {{x_p} - {c_i}} \right\|}^2}} \right){\text{,}}$ | (3) |
其中:
根据图2所示的RBF神经网络的结构,可得到网络输出为:
| ${y_i} = \sum\limits_{i = 1}^h {{\omega _{ij}}\exp \left( { - \frac{1}{{2{\sigma ^2}}}{{\left\| {{x_p} - {c_i}} \right\|}^2}} \right)} \;\;\;\;\;{\text{,}}j = 1,2, \cdots ,n{\text{。}}$ | (4) |
其中,
本文采用文献[4]中给出的某小型水下机器人的模型试验,通过约束模试验获取的水动力导数值详见该文献,该水下航行器模型如图3所示。

|
图 3 小型水下航行器 Fig. 3 Small underwater vehicle |
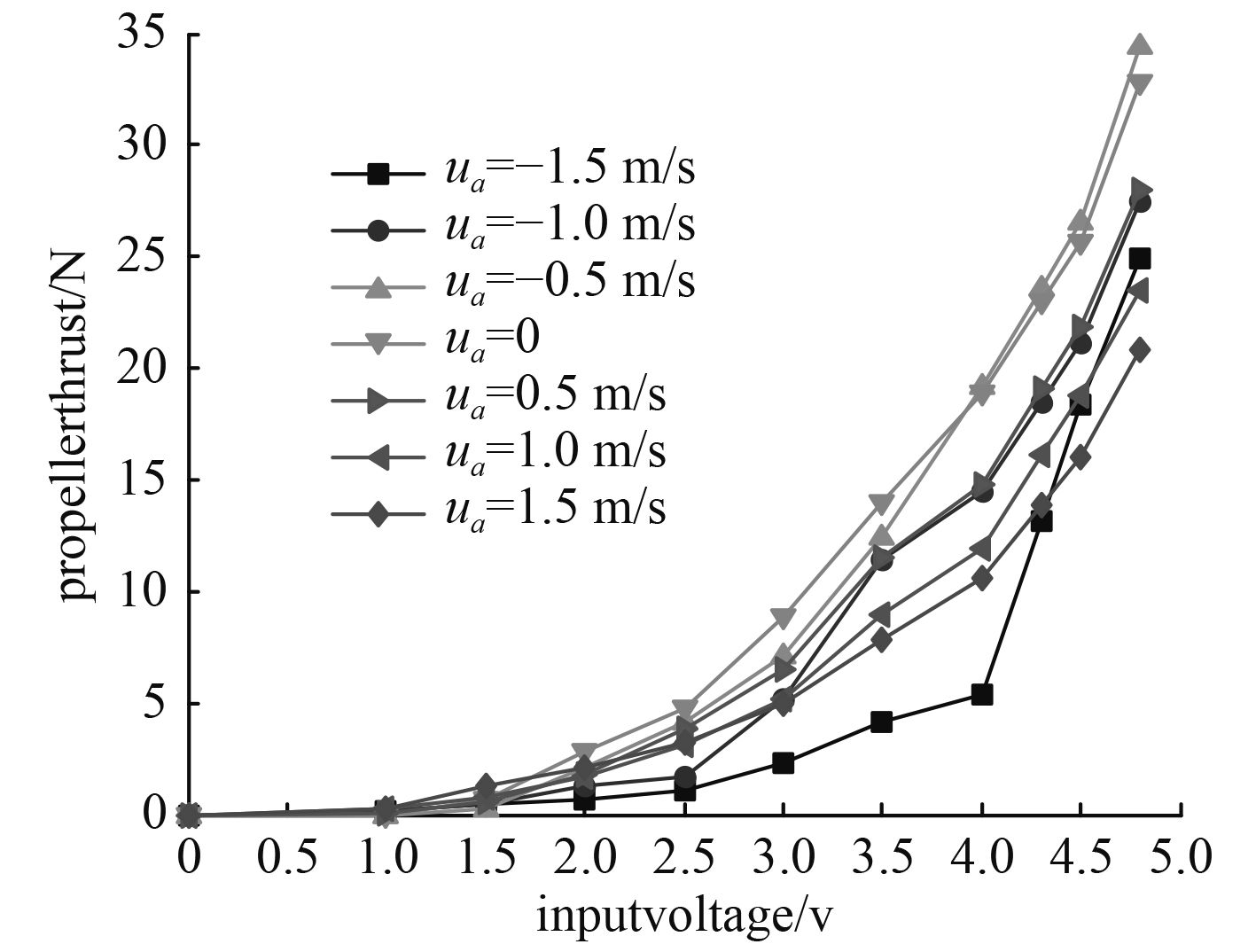
其螺旋桨推力模型如下:
| ${\tau _T} = f\left( {{u_a},vol} \right){\text{,}}$ | (5) |
式中:
|
图 4 推力随电压、迎流速度变化曲线 Fig. 4 Propeller thrust v.s. input voltage and surge velocity |
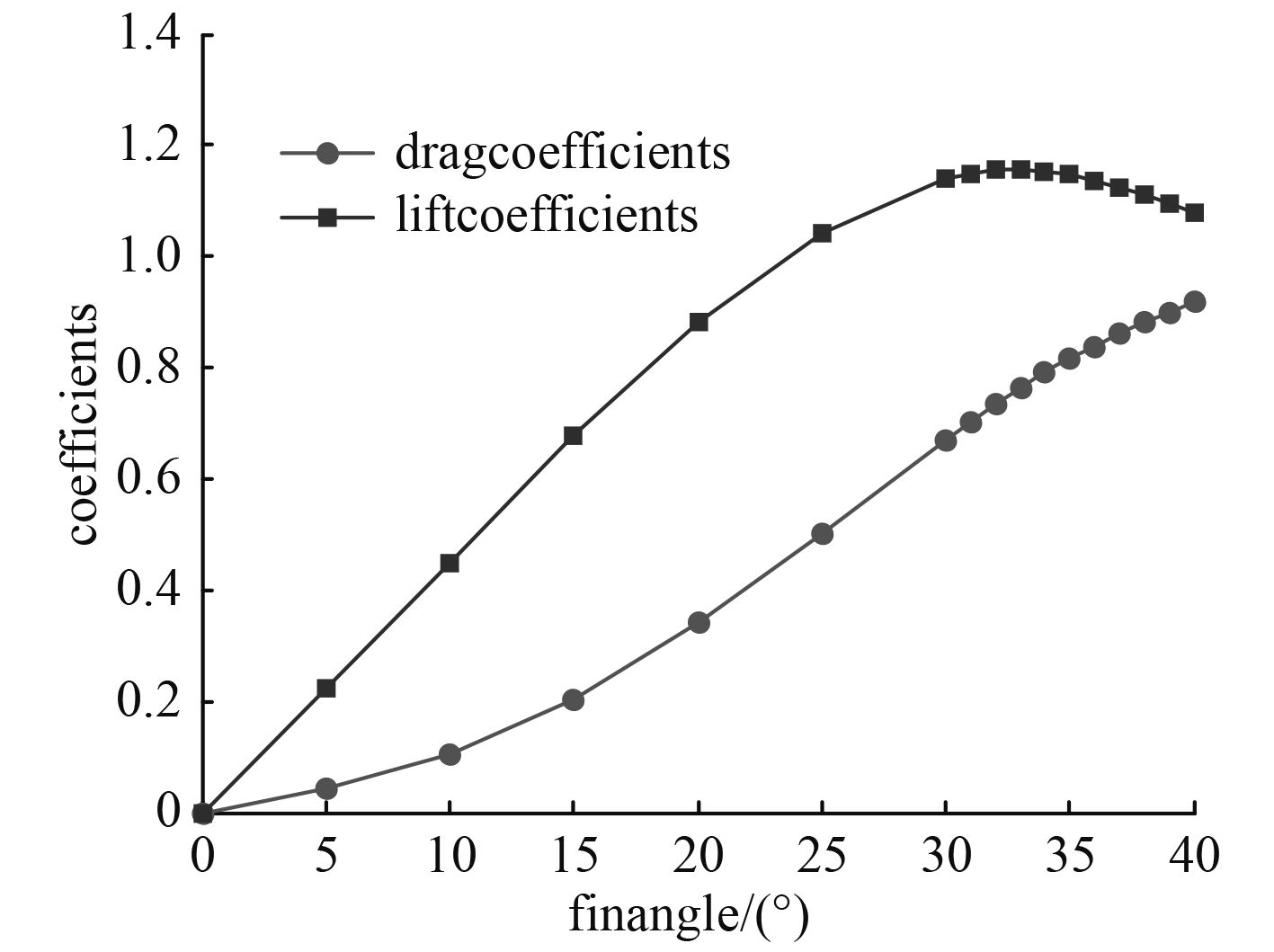
其舵翼作用力模型可通过舵翼的升阻力进行换算得到,升阻力计算公式如下:
| $\left\{ \begin{gathered} L = \frac{1}{2}{C_L}\rho {A_R}{V^2} \hfill {\text{,}}\\ D = \frac{1}{2}{C_D}\rho {A_R}{V^2} \hfill {\text{。}}\\ \end{gathered} \right.$ | (6) |
式中:L为升力;D为阻力;CL,CD分别为升力和阻力系数;ρ为水密度;
|
图 5 舵翼升阻力系数随攻角变化曲线 Fig. 5 Lift and drag coefficients v.s. fin angles |
数值求解式(1)即可进行操纵运动仿真。在仿真中,时间步长取为0.1 s,仿真时间为120 s,设置控制电压为4 V并保持恒定,航行器的运动状态通过舵翼进行控制。值得注意的是,舵翼角的变化形式决定了建模所需的输入输出样本,从而对所建立的支持向量机回归模型具有较大的影响。为获取能够充分反映模型特征的输入输出样本对,参考文献[5],舵翼角的时历曲线如图6所示。

|
图 6 舵翼角的时历变化曲线 Fig. 6 Time histories of fin angles |
在使用支持向量机进行建模时,采样间隔取为0.5 s,共得到240个样本对。根据式(2),建模所需的输入输出样本对为:
| $ \left\{ \begin{array}{l}{\rm{input}}:\left\{ {u\left( k \right),w\left( k \right),p\left( k \right),q\left( k \right),r\left( k \right)} \right\}{\text{,}}\\{\rm{output}}:\left\{ {{C_{k,i}}\left( \nu \right)\nu + {D_{k,i}}\left( \nu \right)\nu } \right\}{\text{。}}\end{array} \right. $ |
其中,k为时间步,i=1,…,6分别代表航行器的六自由度运动。
使用RBF神经网络进行学习,即可得到科氏力、向心力与阻尼项的黑箱模型。在建立RBF神经网络黑箱模型过程中,对水下航行器的6个自由度的向心力、科氏力和阻尼项分别进行建模,鉴于6个自由度具有不同的非线性耦合特性,对其分别采用不同的训练参数。
在使用黑箱模型进行操纵运动预报时,把该黑箱模型取代式(2)中的对应项即可。
| $ { M}\dot \nu +\tilde { C}\left( \nu \right)\nu +\tilde { D}\left( \nu \right)\nu + { g}\left( \eta \right) = {\tau _{trust}} + {\tau _{fin}} {\text{。}}$ |
式中,
为对RBF神经网络黑箱建模的有效性进行验证,使用模型试验得到的水动力模型与黑箱模型进行相同的水平面和垂直面操纵运动预报。
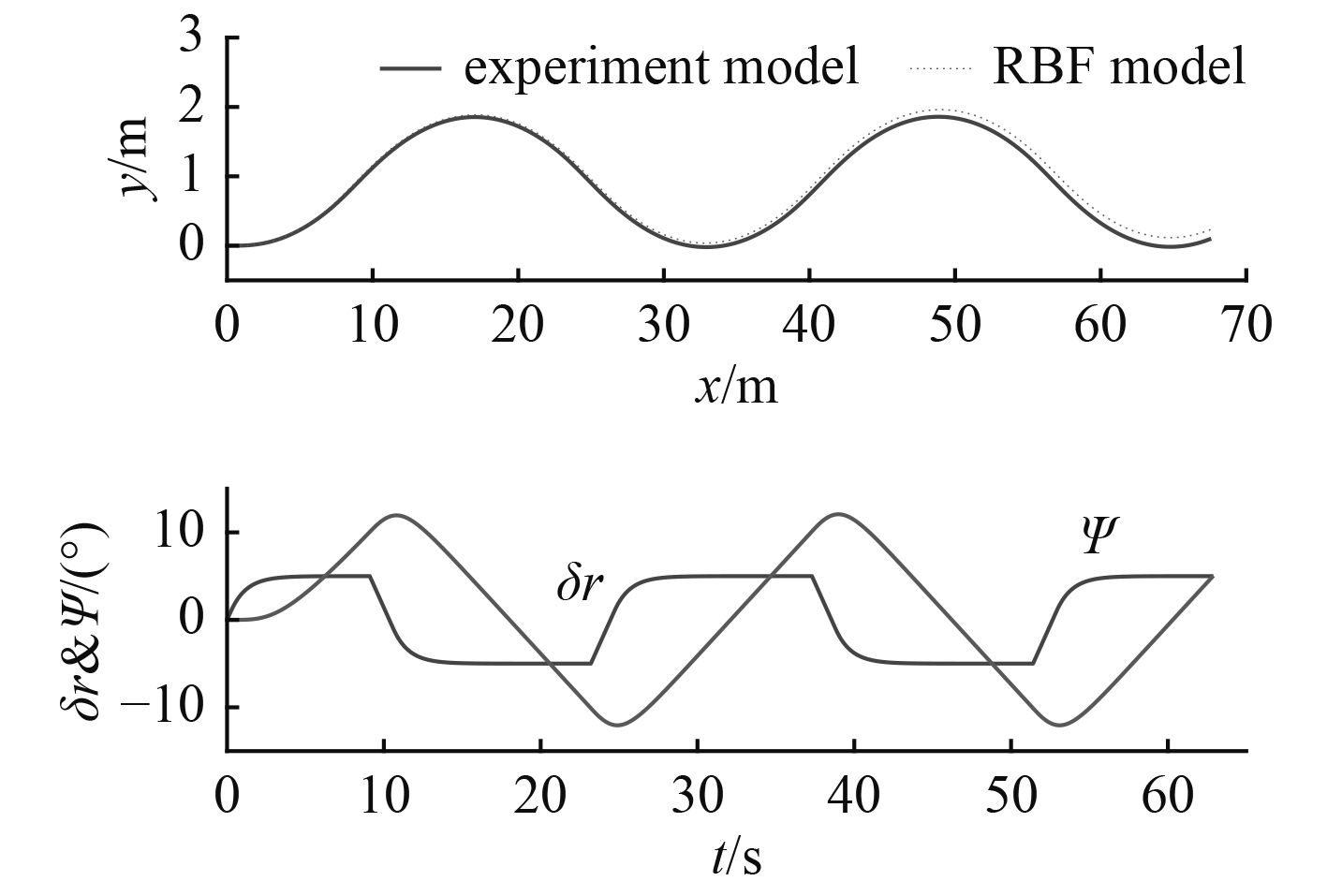
水平面内的操纵运动仿真为3.5 V控制电压下的5°/10°Z形试验仿真。在零初始运动状态条件下,仿真时间步长为0.1 s,仿真时间为60 s。分别使用试验模型和支持向量机模型进行运动仿真,其比较结果如图7所示。
|
图 7 输入电压3.5 V 的5°/10° Z形试验 Fig. 7 5°/10° zigzag test with 3.5 V input voltage |
垂直面内的操纵运动仿真为4.5 V控制电压下的10°/15°类Z形试验仿真。在零初始运动状态条件下,设航行器的初始潜深为5 m,仿真时间步长为0.1 s。基于2种模型的操纵运动仿真对比结果如图8所示。
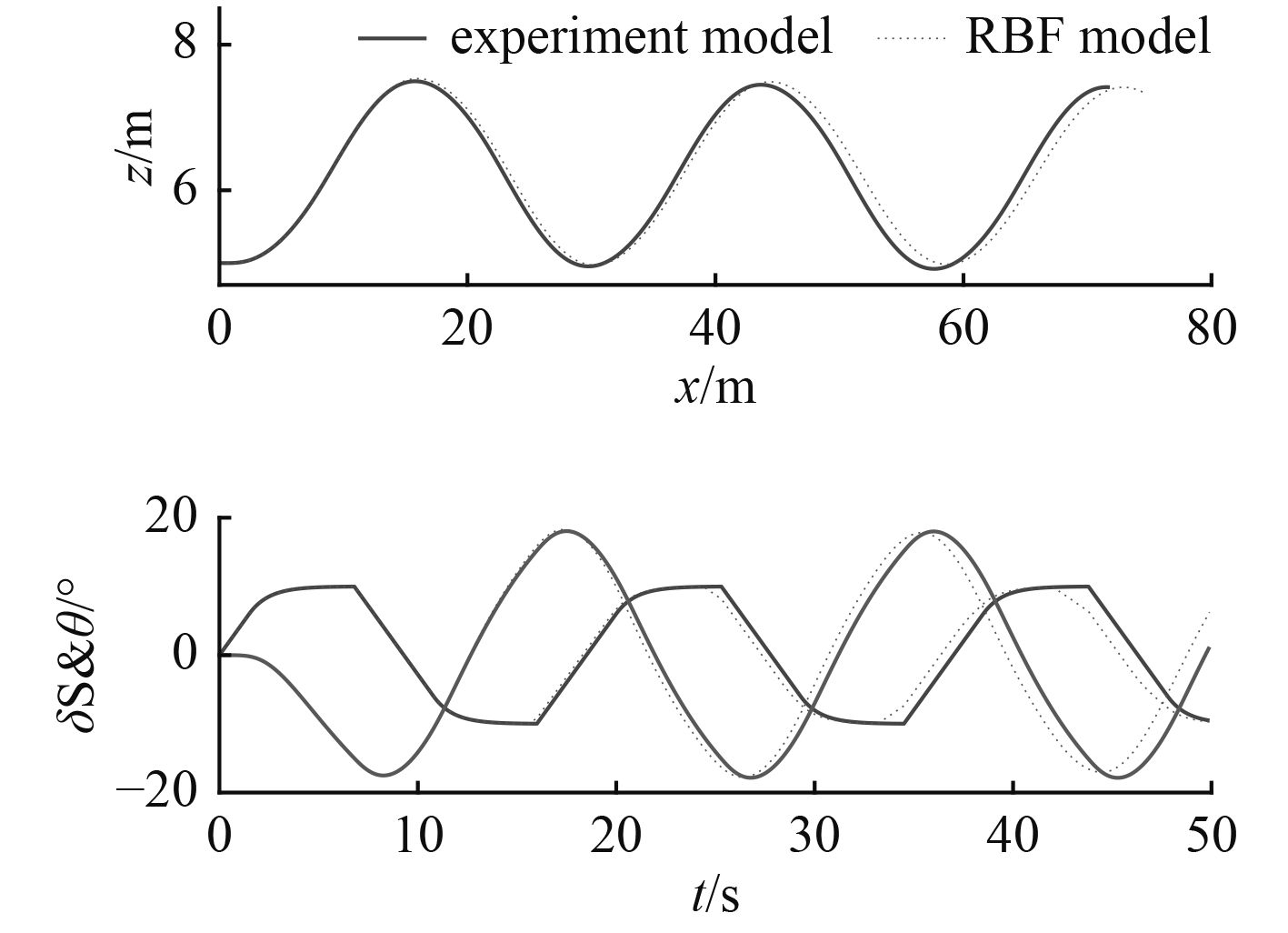
|
图 8 输入电压4.5 V 的10°/15° Z形试验 Fig. 8 10°/15° zigzag test with 4.5 V input voltage |
本文基于试验模型进行操纵运动仿真,获取辨识建模所需要的数据样本,进而分别建立了关于科氏力、向心力和阻尼力在6个自由度的回归模型。然后,通过操纵运动仿真对RBF神经网络回归模型进行了验证,从图7和图8中可以发现,RBF神经网络黑箱模型能够很好的与原始水动力模型吻合,证明了所建立的模型对动力学模型中的科氏力、向心力和阻尼力进行辨识可行。
| [1] |
FOSSEN T I. Marine control systems: Guidance, navigation and control of ships, rigs and underwater vehicles[M]. Marine Cybernetics Trondheim, Norway, 2002.
|
| [2] |
FOSSEN T I. Guidance and control of ocean vehicles[M]. John Wiley & Sons, New York, 1994.
|
| [3] |
SANDBERG I W. Structure theorems for nonlinear systems[J]. Multidimensional Systems and Signal Processing, 1991, 2(3): 267-286. DOI:10.1007/BF01952236 |
| [4] |
王波, 苏玉民, 秦再白. 微小型水下机器人操纵性能与运动仿真研究[J]. 系统仿真学报, 2009, 2(13): 4149-4152. |
| [5] |
YEO D J, RHEE K P. Sensitivity analysis of submersibles’ manoeuvrability and its application to the design of actuator inputs[J]. Ocean Engineering, 2006, 33(17): 2270-2286. |
 2018, Vol. 40
2018, Vol. 40

