目标强度是水声探测的重要参数,潜艇的目标强度对水声探测设备的探测效果、潜艇自身的隐身性能等具有重要意义,因此备受关注。潜艇具有复杂的外形和内部结构,潜艇的子结构会对目标强度产生影响[1]。此外,不同型号的潜艇具有不同的形状和结构,因此具有不同的目标强度。为了使对潜艇目标强度的研究具有统一的标准,国际上提出了BeTSSi-I标准潜艇模型[2]。目前,许多研究正是基于BeTSSi-I标准潜艇模型[3 – 5]。然而BeTSSi-I标准潜艇模型只提供了由若干个规则几何体组成的外壳,其线型与真实潜艇有较大差距,并且缺少内部结构。因此国际上提出了BeTSSi-II标准潜艇模型[6, 7],这种潜艇模型具有复杂且更接近真实潜艇的线型,并且具有较为完整的内部结构。
有多种方法可以计算水下目标的目标强度,包括解析法[8]、边界元方法[9 – 10]、板块元方法[11]、有限元方法等[5]。解析法物理概念清晰,但是很难用于计算结构复杂的BeTSSi-II标准潜艇模型。边界元方法计算准确且计算开销相对不大,但是处理较为复杂的内部结构有一定难度。板块方元法具有较快的计算速度,但是这一方法是基于高频近似,不适用于低频情况。而有限元方法可以处理较为复杂的内部结构,且理论上在所有频率范围内都具有较高的计算准确性,因此本文采用有限元方法计算BeTSSi-II标准潜艇模型的目标强度。但是有限元法的开销较大,这在一定程度上限制了计算频率范围,因此本文计算低频目标强度。
1 声-壳耦合有限元法目标强度的计算本质上是对模型散射特性的计算,因此考虑无限大自由空间中的BeTSSi-II标准潜艇模型。根据物理模型的不同,潜艇模型主要采用线弹性压力声学模型和线弹性壳模型耦合的有限元模型进行分析。考虑到有限元模型较为成熟,并且其离散展开形式较为复杂[12],因此本文仅简要介绍采用的物理模型及边界条件。
1.1 线弹性压力声学模型BeTSSi-II标准潜艇模型的外部和内部空间为声传播的流体介质,采用线弹性压力声学模型和四面体网格,其基本方程为各项同性Helmholtz方程:
| ${\nabla ^2}{p_t}\left( {{r}} \right) + {k^2}{p_t}\left( {{r}} \right) = 0{\text{,}}$ | (1) |
其中:
| ${p_i}\left( {{r}} \right) = {p_0}{\rm{exp}}\left( { - {j}k{{r}} \cdot {{{e}}_k}} \right){\text{,}}$ | (2) |
其中:
| ${p_t}\left( {{r}} \right) = \left\{ {\begin{array}{*{20}{c}} {{p_i}\left( {{r}} \right) + {p_s}\left( {{r}} \right),{\rm{ }}{{r}} \notin G} {\text{;}}\\ \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{{p_s}\left( {{r}} \right),{\rm{ }}{{r}} \in G} {\text{。}}\end{array}} \right.$ | (3) |
其中:G为散射体,即为潜艇模型空间。这样,对BeTSSi-II标准潜艇模型目标强度的求解即为对散射声压
BeTSSi-II标准潜艇模型的外壳、内壳以及内部结构采用线弹性壳模型和三角形网格,这主要是考虑到这些结构的厚度远小于另外2个方向的尺度,采用壳模型和面网格可以有效减少计算量,避免病态网格,同时又能保证计算的准确性。线弹性壳模型的基本方程为
| $\rho \frac{{{\partial ^2}{{u}}\left( {{r}} \right)}}{{\partial {t^2}}} = \nabla \cdot {{\sigma }} + {{{F}}_V}\left( {{r}} \right){\text{,}}$ | (4) |
其中:
对于压力声学模型,在模型耦合处满足动力学条件。在边界的法向一侧,即
| ${{n}} \cdot \frac{{\nabla {p_t}\left( {{{{r}}_ + }} \right)}}{\rho } = {{n}} \cdot \frac{{{\partial ^2}{{u}}\left( {{r}} \right)}}{{\partial {t^2}}}{\text{,}}$ | (5) |
其中,
| ${{n}} \cdot \frac{{\nabla {p_t}\left( {{{{r}}_ - }} \right)}}{\rho } = - {{n}} \cdot \frac{{{\partial ^2}{{u}}\left( {{r}} \right)}}{{\partial {t^2}}}{\text{,}}$ | (6) |
其中
对于壳模型,在模型耦合处声压差即为载荷,因此边界条件为
| ${{{F}}_A}\left( {{r}} \right) = {p_t}\left( {{{{r}}_ - }} \right){{n}} - {p_t}\left( {{{{r}}_ + }} \right){{n}}{\text{,}}$ | (7) |
其中
| ${{{F}}_V}\left( {{r}} \right) = \frac{{{{{F}}_A}\left( {{r}} \right)}}{{d\left( {{r}} \right)}}{\text{,}}$ | (8) |
其中
联立式(1)~式(8)并且将其离散化,即可求得散射声压
| ${TS} = 20{\log _{10}}\left| {\frac{{{p_s}\left( {{r}} \right){{r}}}}{{{p_0}{r_0}}}} \right|\text{,}$ | (9) |
其中r0=1 m。
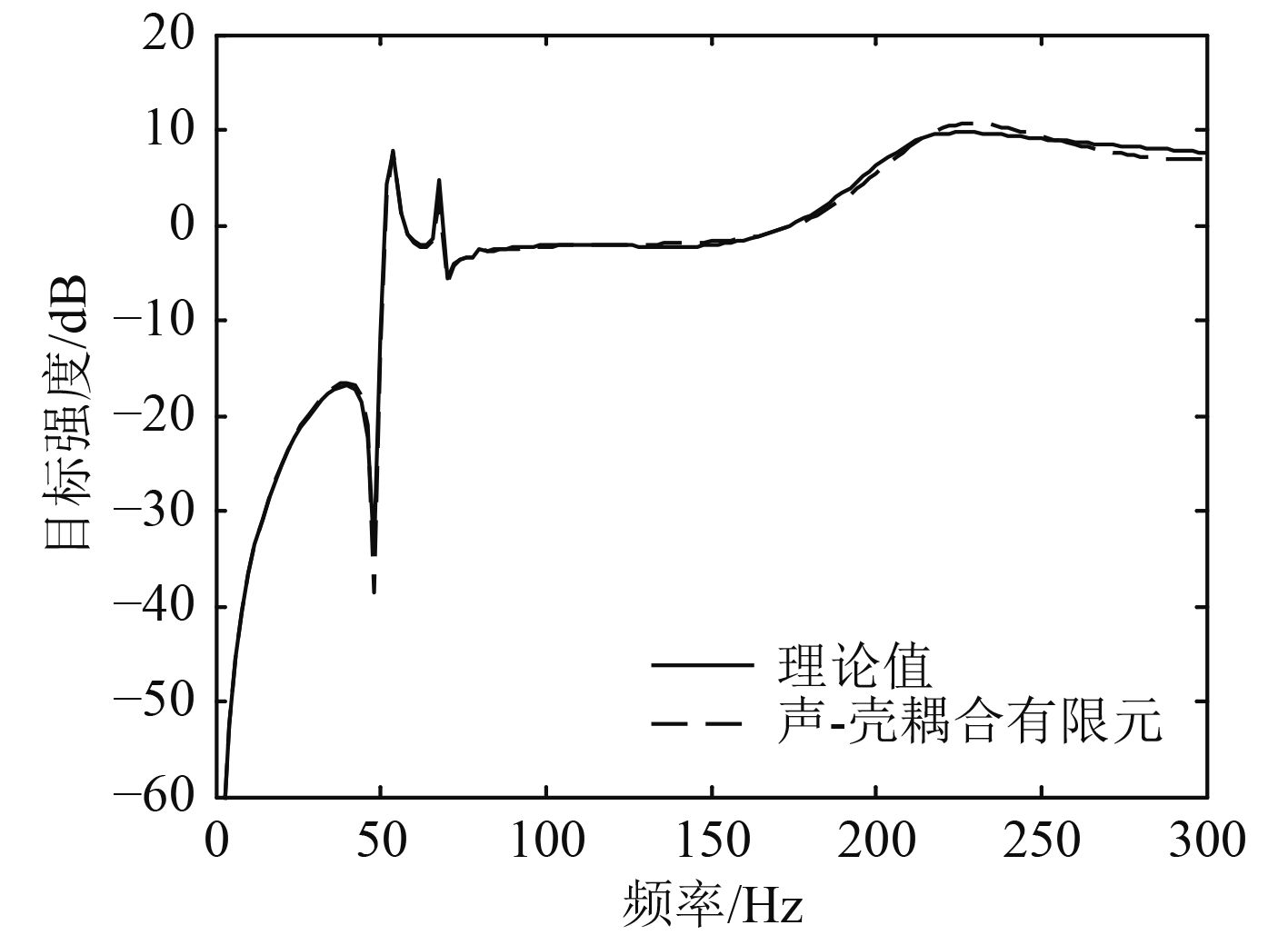
1.4 模型验证为了验证声-壳耦合有限元模型的准确性,计算水中的钢质球壳的目标强度。钢质球壳内部充水,壁厚为30 mm,半径取为BeTSSI-II潜艇模型的内壳半径,即3.5 m。采用声-壳耦合有限元模型计算球壳收发合置目标强度,并与理论值比较[3],如图1所示。由图可见,声-壳耦合有限元模型的计算结果与理论值较为吻合,两者相差小于1 dB,由此验证了声-壳耦合有限元模型的准确性。
|
图 1 声-壳耦合有限元方法验证 Fig. 1 Validation of finite element method for acoustic-shell interaction |
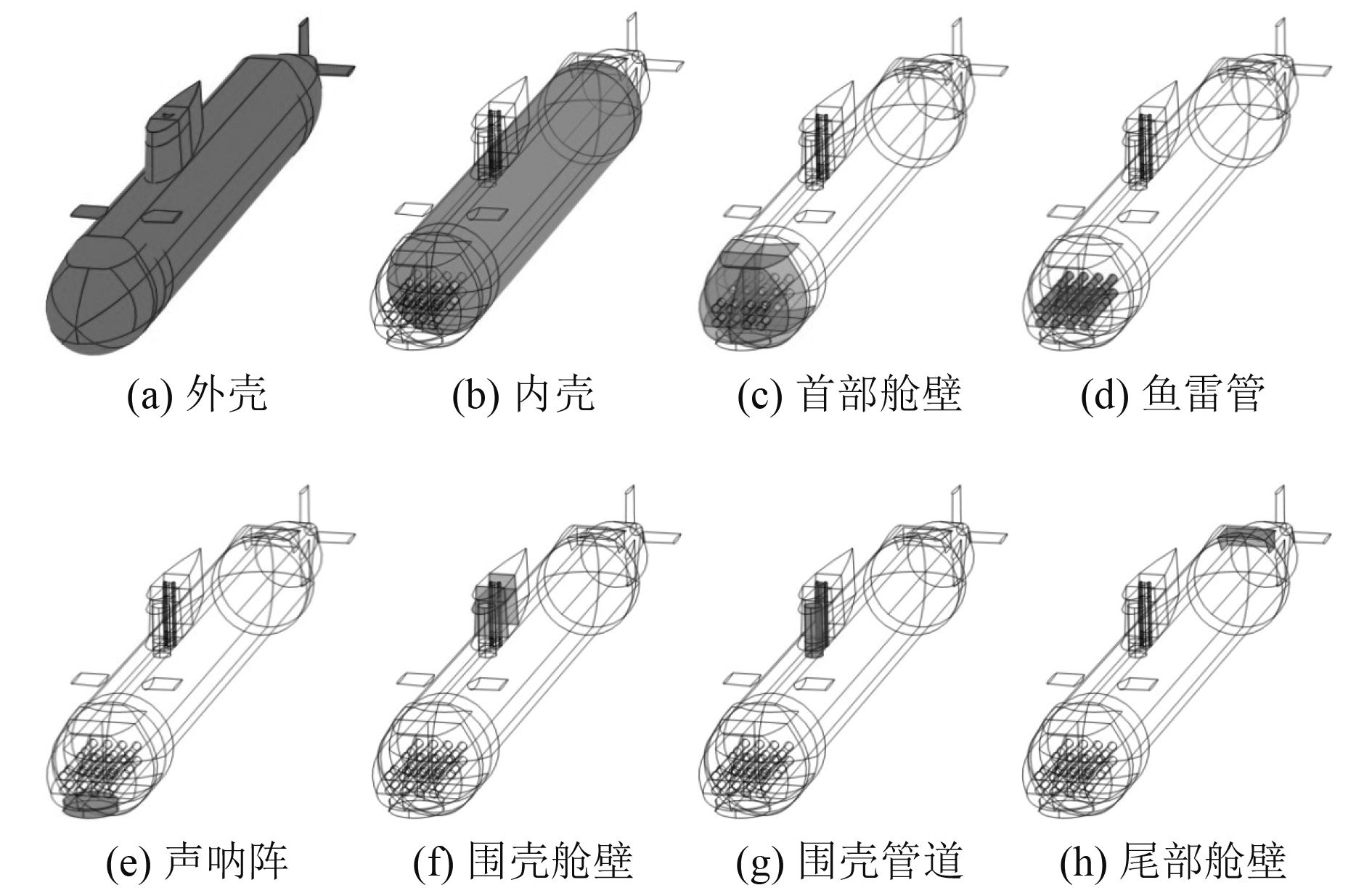
BeTSSi-II标准潜艇模型由外壳、内壳、首部舱壁、鱼雷管、声呐阵、围壳舱壁、围壳管道和尾部舱壁组成[6],如图2所示。潜艇模型全长为62 m,主体结构直径为7 m。外壳为10 mm厚的非耐压钢板,内壳为40 mm厚的耐压钢板,首部舱壁、鱼雷管、围壳舱壁、围壳管道和尾部舱壁均为30 mm厚的钢板,首部声呐阵为1 mm厚的钢板。内壳内部以及围壳管中的通气管中介质为空气,其余空间中的介质为水。钢板的材料参数为:密度
|
图 2 BeTSSi-II标准潜艇模型 Fig. 2 Geometry and substructures of BeTSSi-II benchmark submarine |
以内壳中心为原点O建立直角坐标系,以首部方向为x轴正方向,以左舷方向为y轴正方向,则潜艇模型所在水平面为xy平面,本文考虑声呐的发射基地和接收基地均位于xy平面内。另外,以首部方向(x轴正方向)为0°方向,以左舷方向(y轴正方向)为90°方向,以尾部方向为180°方向。
本文取计算频率的上限为300 Hz,为了保证有限元模型的计算精度,网格的最大尺寸取为
|
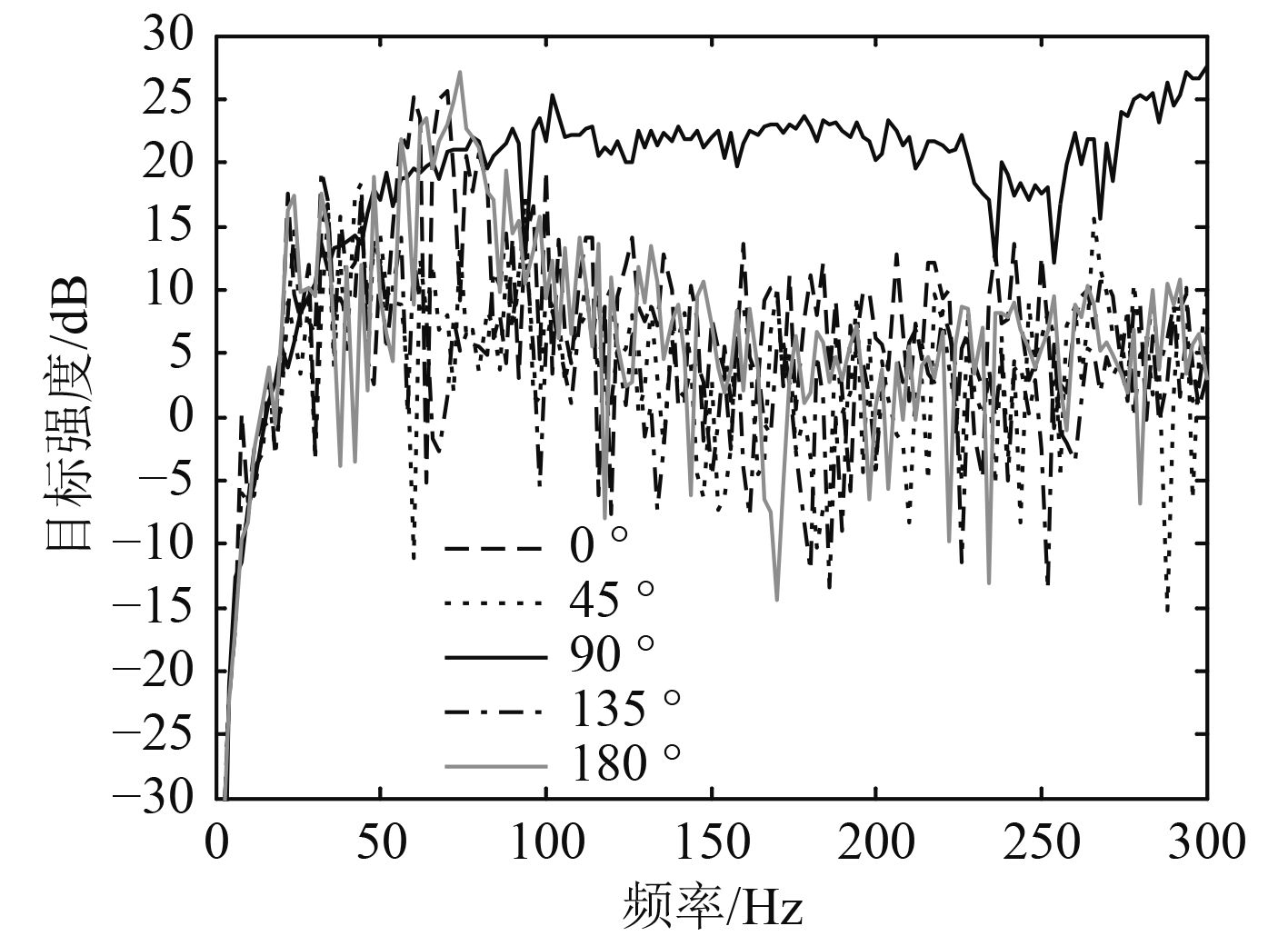
图 3 不同入射角收发合置BeTSSi-II标准潜艇模型目标强度频率响应 Fig. 3 Frequency response of target strength of BeTSSi-II benchmark submarine at various incident angles |
|
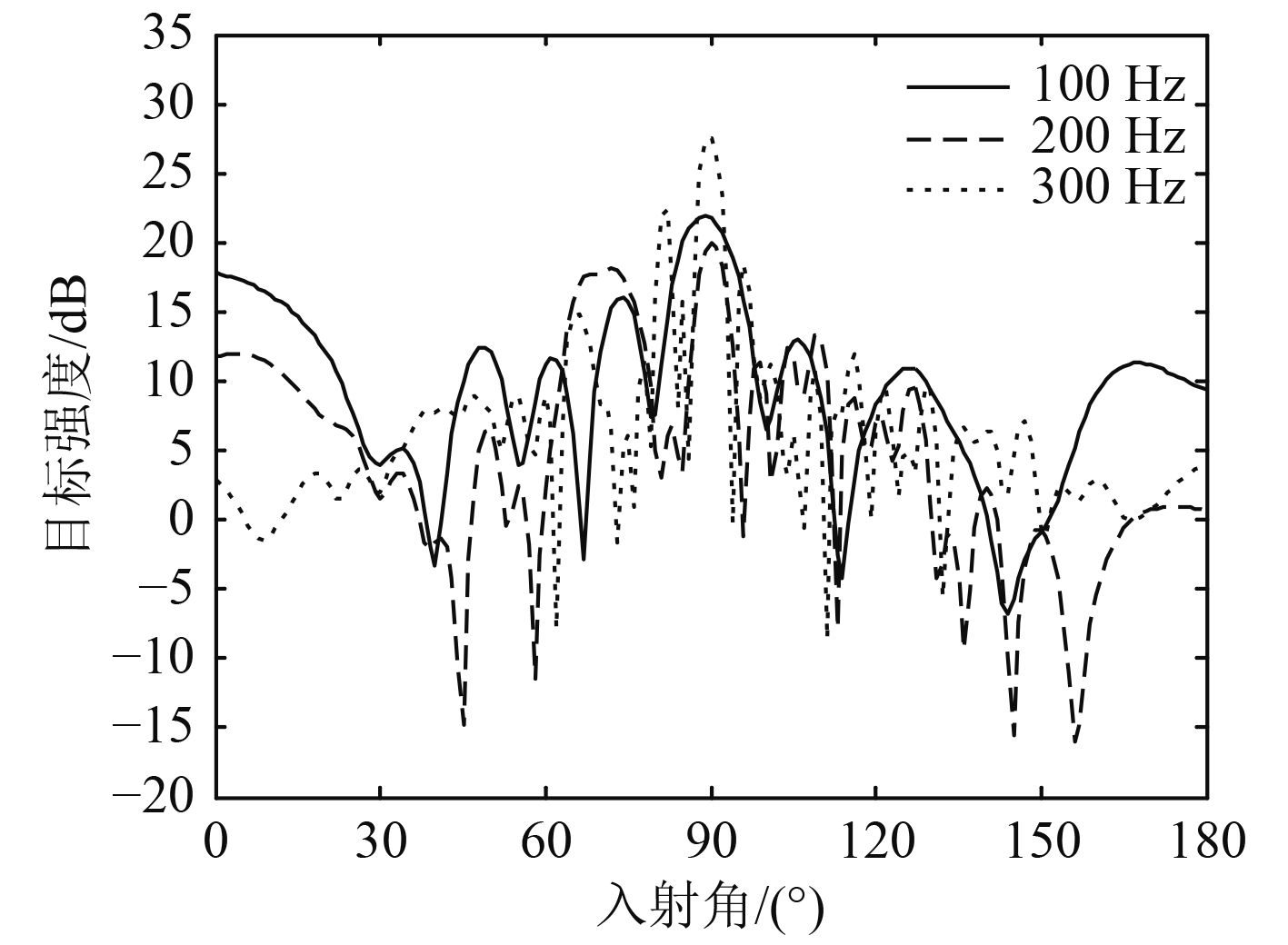
图 4 不同频率收发合置BeTSSi-II标准潜艇模型目标强度随入射角的变化 Fig. 4 Target strength vs. incident angle for BeTSSi-II benchmark submarine at various frequencies |
如图3所示为收发合置BeTSSi-II标准潜艇模型目标强度的频率响应,考虑到模型的对称性,本文只计算了入射角0°~180°的情形。由图3可知,当频率小于约30 Hz时,各个入射方向的目标强度较小,且频率越低目标强度越小,主要是由于在这一频率范围内,波长相对于模型尺寸较大,潜艇模型对声波的散射较小。当频率大于约30 Hz,除90°外各个入射方向的目标强度出现较大起伏,起伏的峰-峰值约为20 dB,这主要是由于潜艇模型的结构较为复杂,内部各个子结构的共振模态较多。而入射角为90°(即正横)方向时,起伏相对较小,这可能是由于潜艇模型整体与有限长圆柱相似,在正横方向对声波的散射较大[16],因此潜艇模型的整体散射是目标强度的主要贡献,而掩盖了子结构的共振散射。此外,当频率大于约100 Hz时,正横入射方向的目标强度大于其他方向的目标强度,因此对潜艇探测时希望入射角接近于正横方向。
如图4所示为收发合置BeTSSi-II标准潜艇模型目标强度随入射角的变化,考虑到模型的对称性,本文只计算了入射角0°~180°的情形。由图4可知,所有计算频率情况下,当入射角为90°(即正横)方向时目标强度最大,这与图3得到的结论向对应。此外频率越高,曲线越复杂,峰谷越多,正横方向对应的束瓣越窄,这与图3中非正横方向入射的目标强度频率响应曲线起伏较大对应。仔细观察不难发现,0°~90°范围内的目标强度略大于90°~180°范围内的目标强度,约2.3 dB,这提示当入射角位于首向半圆内时略有利于探测。
|
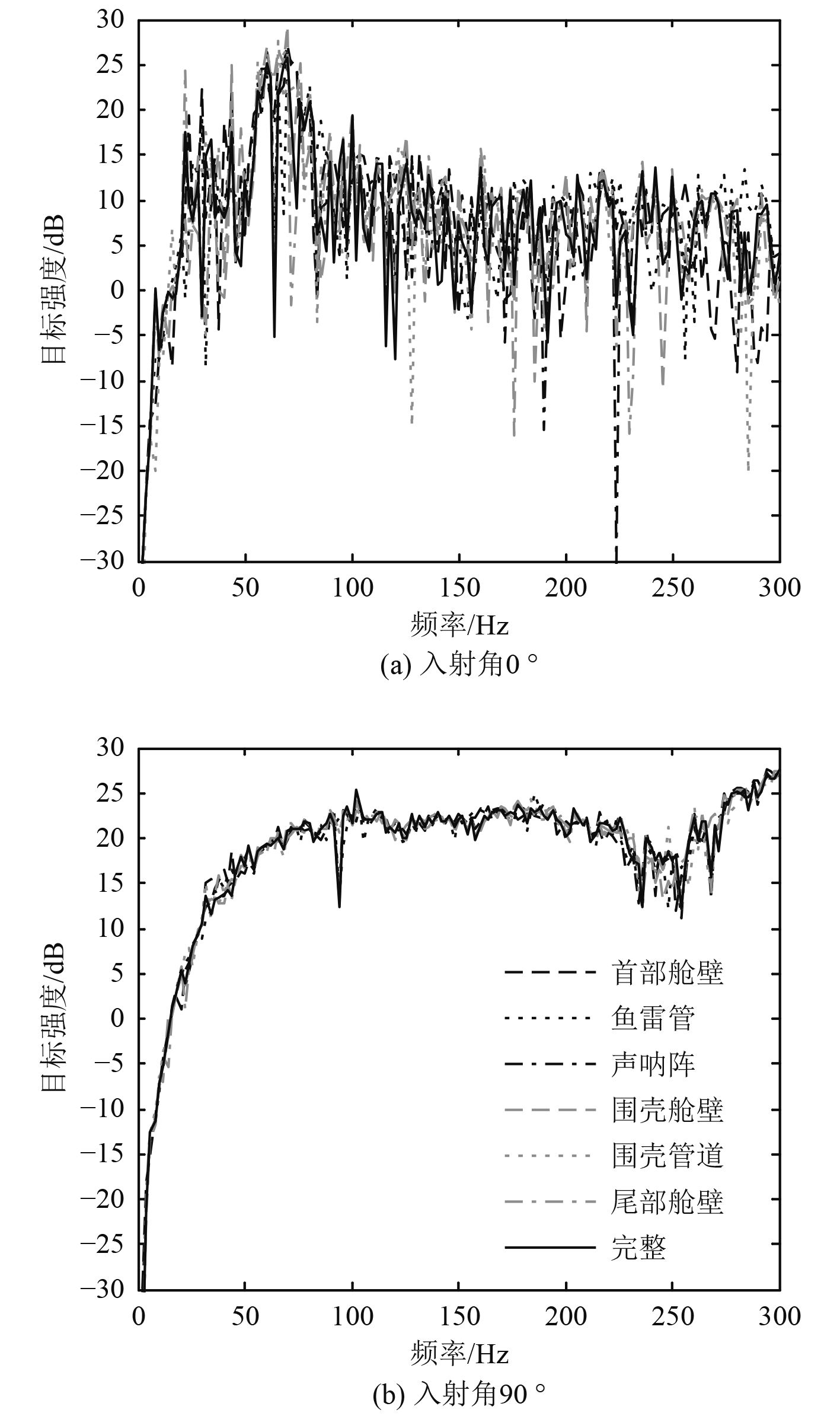
图 5 收发合置BeTSSi-II标准潜艇模型内部结构对目标强度频率的影响 Fig. 5 Influence of substructures on frequency response of target strength of BeTSSi-II benchmark submarine |
|
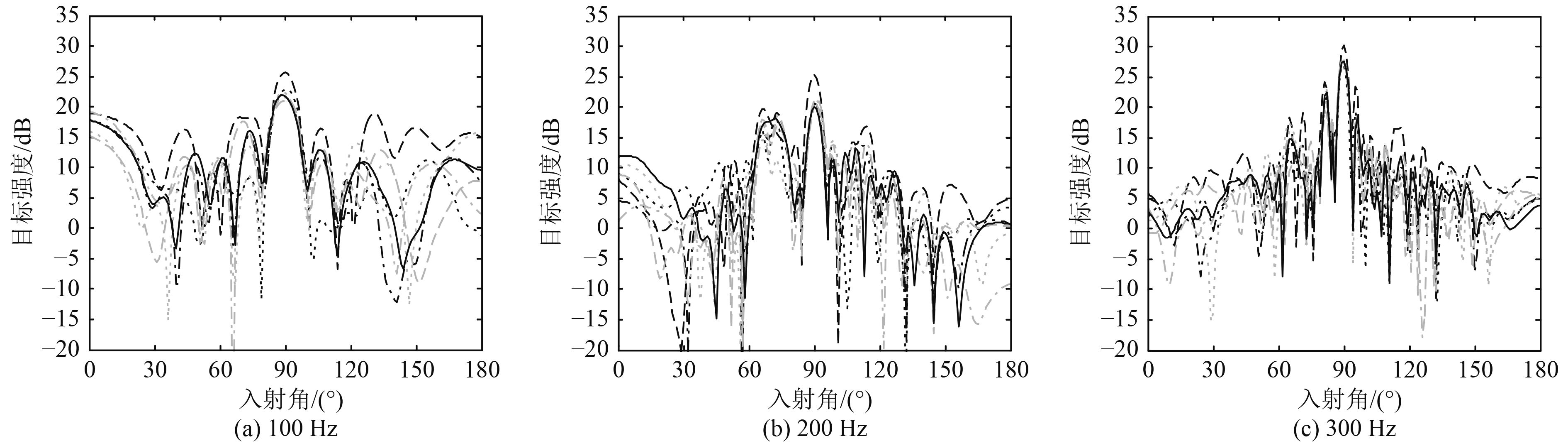
图 6 收发合置BeTSSi-II标准潜艇模型内部结构对目标强度随入射角变化的影响 Fig. 6 Influence of substructures on target strength vs. incident angle for BeTSSi-II benchmark submarine |
研究表明,潜艇模型的子结构对目标强度有影响,已有工作已经对潜艇模型外部结构的影响进行了详细研究[1, 3]。考虑到模型的相似性,本文讨论内部结构的影响,而不再讨论外部结构的影响。
如图5所示为BeTSSi-II标准潜艇模型内部结构对收发合置目标强度频率响应的影响。由图5可知,内部结构对目标强度频率响应的整体趋势影响不大。由图5(a)可知,内部结构主要影响0°入射角目标强度频率响应峰谷出现的位置;由图5(b)可知,大部分频率下内部结构对90°入射角目标强度频率响应的影响小于±3 dB。
如图6所示为BeTSSi-II标准潜艇模型内部结构对收发合置目标强度随入射角变化的影响。由图6可知,各个计算频率下各条曲线的整体趋势和峰谷位置变化不大。进一步观察发现,各个子结构对正横方向(90°)附近入射的目标强度影响较小,而对首尾方向附近入射的目标强度影响较大,这也与图5的结论相对应。
4 讨 论 4.1 BeTSSi-II简化潜艇模型的影响完整的BeTSSi-II标准潜艇模型拥有复杂的内部结构,这使得建模较为复杂,并且增加网格数量和计算规模,因此希望在一定近似条件下简化BeTSSi-II标准潜艇模型。通常的简化策略是将完整的模型简化为单壳体模型,或者更进一步将外壳简化为刚硬边界。本文分别计算单壳体和刚硬边界BeTSSi-II简化潜艇模型的目标强度,其中单壳体模型保留BeTSSi-II标准潜艇模型的外壳,但是外壳修改为40 mm厚的耐压钢板,材料参数不变,内部为空气并近似为真空。
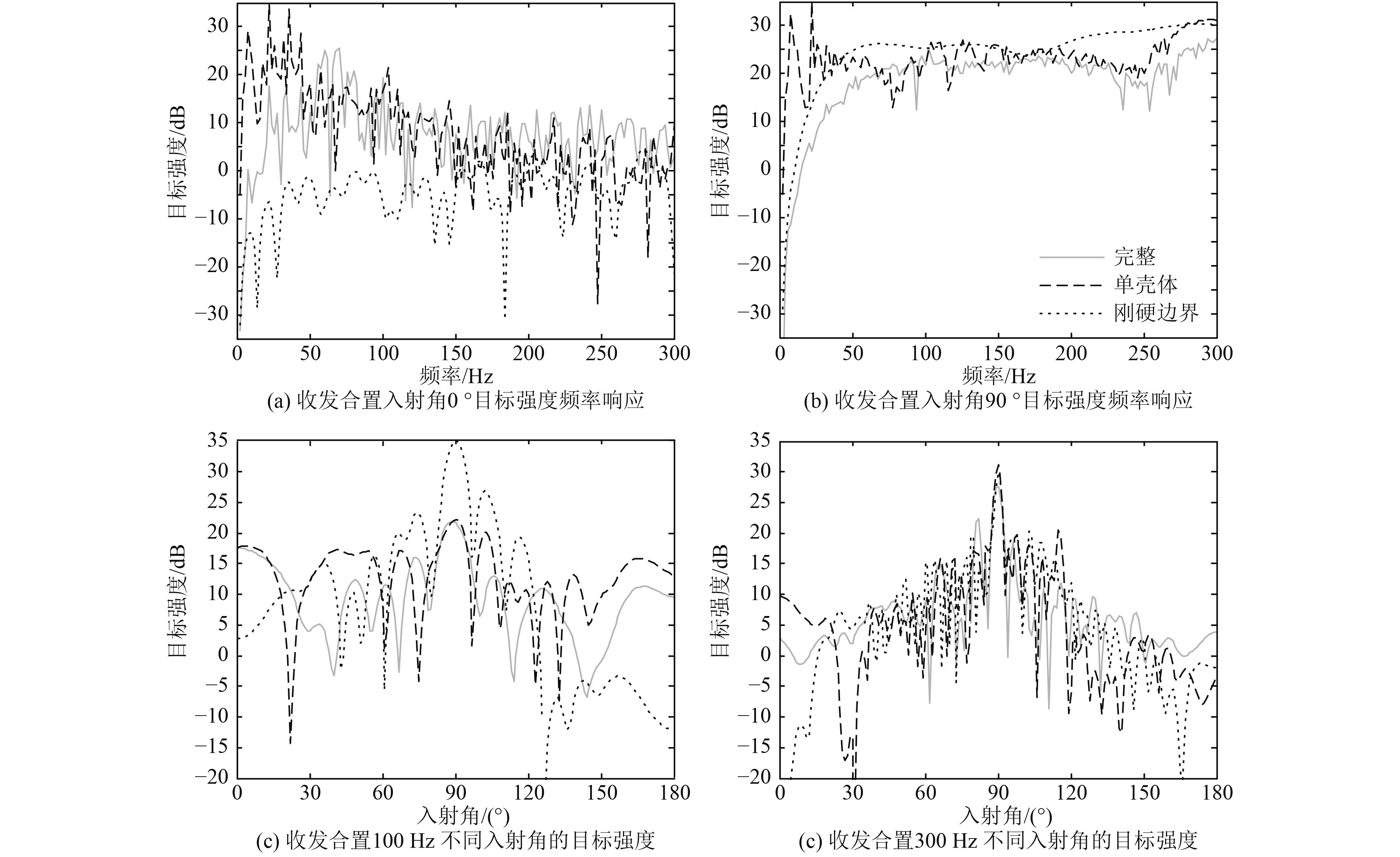
如图7所示为BeTSSi-II简化潜艇模型的目标强度频率响应和目标强度随入射角变化。由图7(a)和图7(b)可知,当频率小于100 Hz时,模型简化的影响较大,此时简化模型不适用。而当频率大于100 Hz时,模型简化的影响较小,曲线的趋势和起伏变化较为一致,此时在允许一定误差的情况下可以采用简化模型。虽然BeTSSi-II标准潜艇模型各个内部结构对目标强度的影响较小,但是对比完整模型和单壳体模型不难发现,内壳和所有内部结构的整体影响不可忽略。值得注意的是,刚硬边界模型的目标强度略大于单壳体模型的目标强度,单壳体模型的目标强度略大于完整双壳体模型的目标强度。由图7(c)和图7(d)可知,简化模型在正横(90°)方向附近的近似程度较好,而在首尾方向附近的误差较大。此外不难发现,单壳体模型较刚硬边界模型的近似程度更好。
|
图 7 收发合置BeTSSi-II标准潜艇模型简化对目标强度的影响 Fig. 7 Influence of simplified model on target strength of BeTSSi-II benchmark submarine |
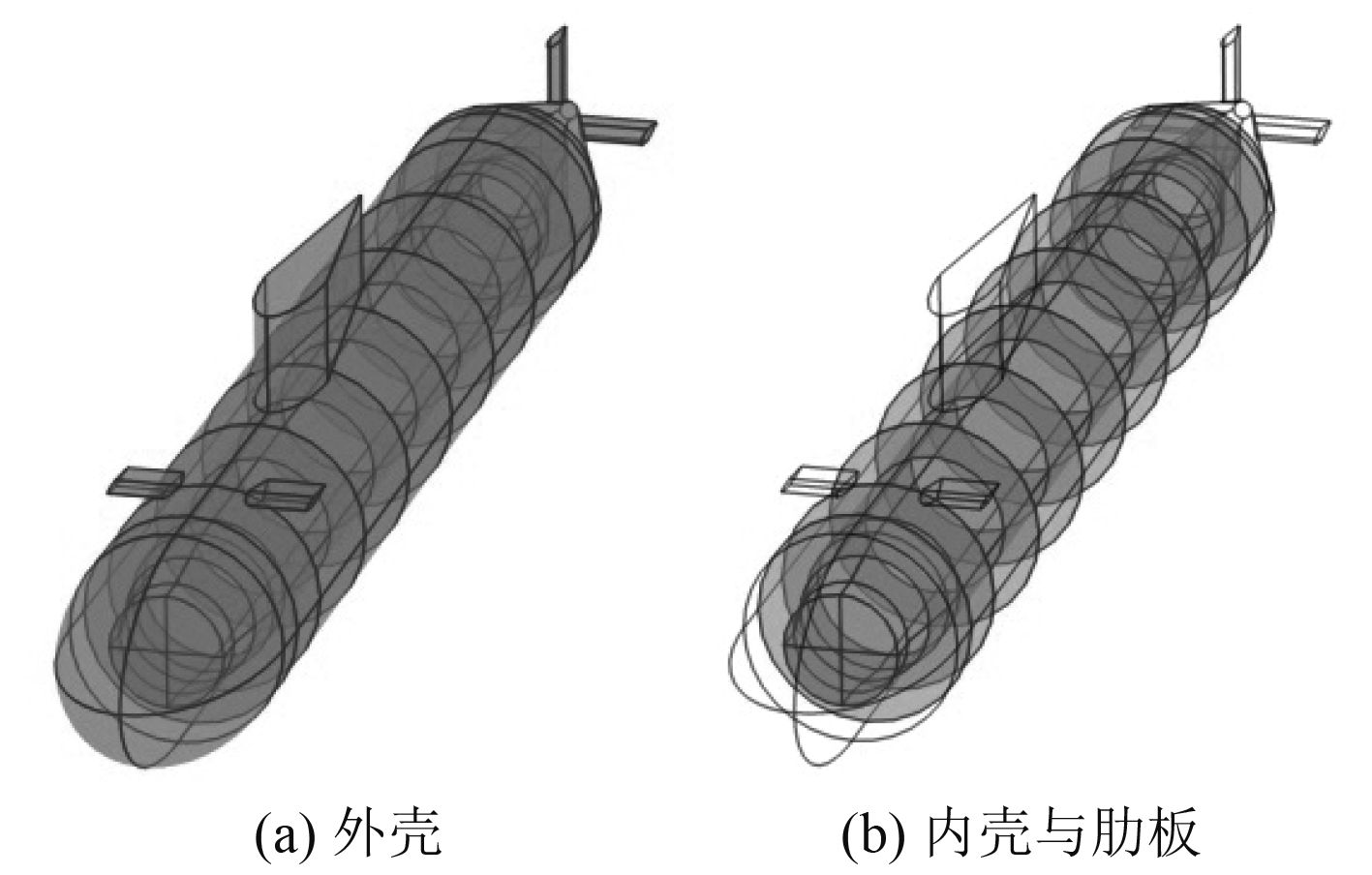
由于结构相对简单,国内外很多研究采用BeTSSi-I标准潜艇模型,因此有必要比较这2种潜艇模型的差别。如图8所示为BeTSSi-I标准潜艇模型,其中外壳采用国际通用模型[2],内壳和肋板采用已有研究常用的模型[17]。为了便于比较,BeTSSi-I标准潜艇模型的外壳取为10 mm厚非耐压钢板,内壳为40 mm厚的耐压钢板,肋板为30 mm厚的耐压钢板,外壳和内壳之间充水,内壳内部为空气并近似为真空。
|
图 8 BeTSSi-I标准潜艇模型 Fig. 8 Geometry and substructures of BeTSSi-I benchmark submarine |
|
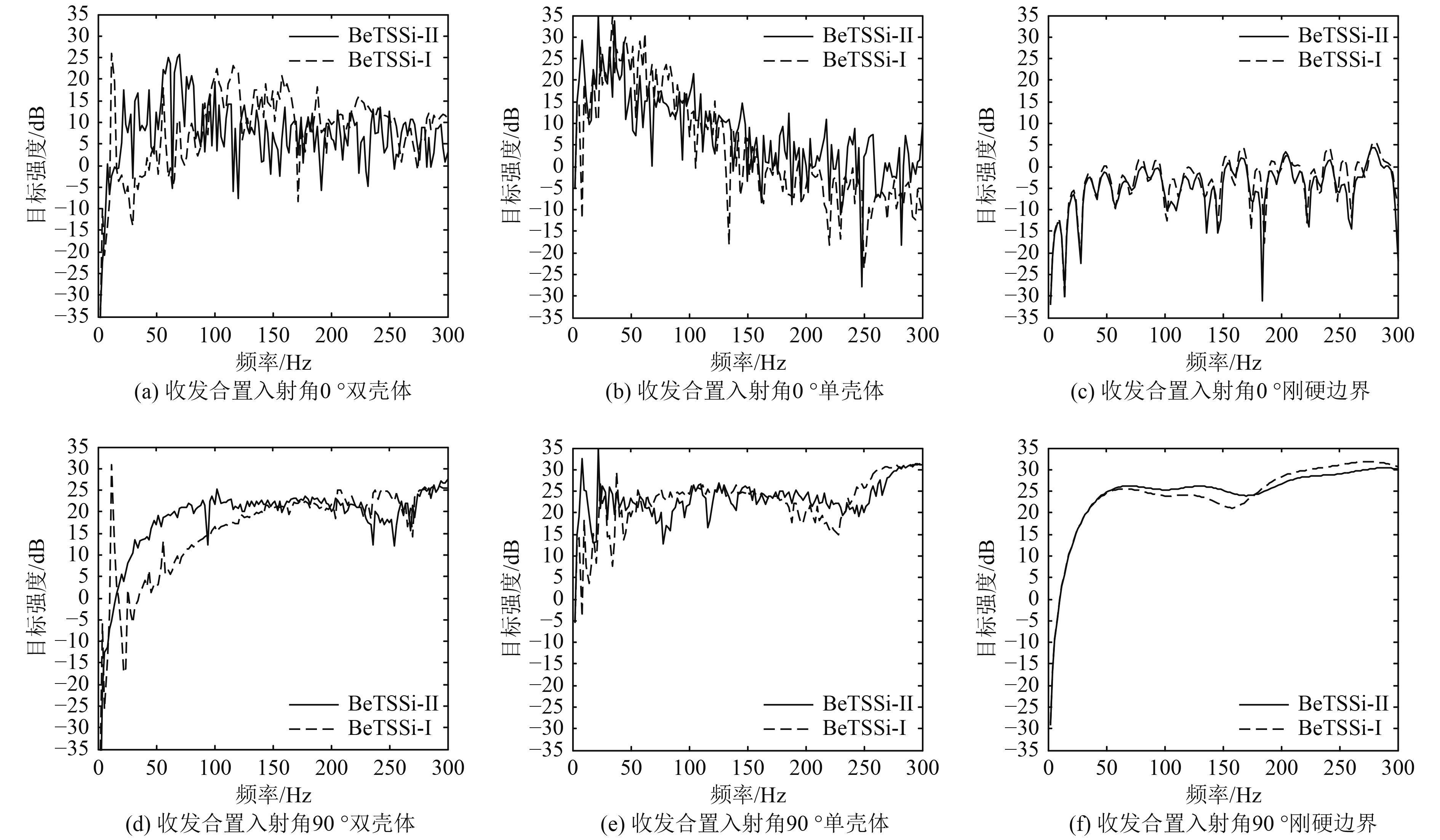
图 9 BeTSSi-II标准潜艇模型与BeTSSi-I标准潜艇模型目标强度频率响应比较 Fig. 9 Differences between frequency responses of target strengths of BeTSSi-II and BeTSSi-I benchmark submarine |
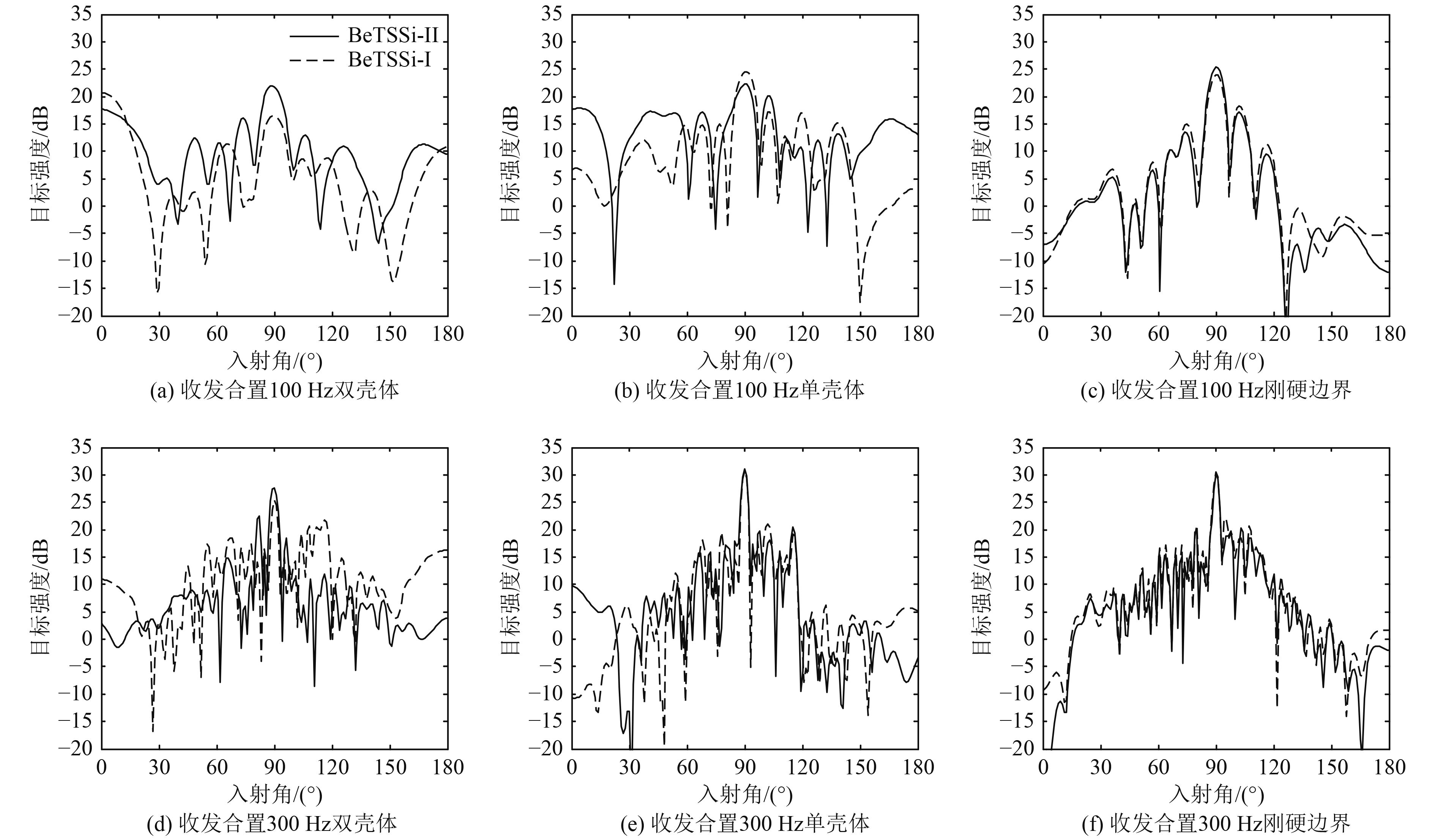
分别计算完整双壳体、单壳体和刚硬边界BeTSSi-II和BeTSSi-I两种潜艇模型的目标强度,如图9和图10所示分别为目标强度频率响应和目标强度随入射角的变化。可知,对于完整双壳体模型,BeTSSi-II和BeTSSi-I两种潜艇模型的目标强度差别较大;对于单壳体模型,BeTSSi-II和BeTSSi-I两种潜艇模型的目标强度在首尾方向附近差别较大,而在正横方向附近差别不大;对于刚硬边界模型,BeTSSi-II和BeTSSi-I两种潜艇模型的目标强度几乎一致。由此提示BeTSSi-II和BeTSSi-I两种潜艇模型的主要区别在于内壳和内部结构,如果忽略内壳和内部结构,BeTSSi-II和BeTSSi-I两种模型区别不大,此时BeTSSi-I潜艇模型由于几何结构更为简单而更具计算上的优势。
|
图 10 BeTSSi-II标准潜艇模型与BeTSSi-I标准潜艇模型目标强度指向特性比较 Fig. 10 Differences between target strengths vs. incident angle of BeTSSi-II and BeTSSi-I benchmark submarine |
首先,本文验证了声-壳耦合有限元方法的有效性。其次,本文采用声-壳耦合有限元方法分析了收发合置BeTSSi-II标准潜艇模型的目标强度,结果表明当频率小于100 Hz时,各个方向入射的目标强度差别不大,而当频率大于100 Hz时,正横方向附近入射的目标强度明显大于其他方向的目标强度。此外,本文还进一步分析了BeTSSi-II标准潜艇模型各个内部结构的影响,结果表明各个内部结构对正横方向附近入射的目标强度影响较小,而对首尾方向附近入射的目标强度影响较大。最后,本文比较了BeTSSi-II简化潜艇模型、BeTSSi-I标准潜艇模型和BeTSSi-II标准潜艇模型的差异,结果表明BeTSSi-II简化潜艇模型对正横方向附近入射的目标强度影响较小,而对首尾方向附近入射的目标强度影响较大;BeTSSi-I标准潜艇模型和BeTSSi-II标准潜艇模型的差异主要为内部结构的差异,如果忽略内部结构,两者的差别不大。
| [1] |
胡泊, 曾革委. Benchmark潜艇子结构回波干涉特性分析[C]//第十五届船舶水下噪声学术讨论会. 郑州, 2015, 449-505.
|
| [2] |
NELL C W, GILROY L E. An improved BASIS model for the BeTSSi submarine [R]. 2003, Canada: Defence Research and Development Canada–Atlantic, TR 2003–199.
|
| [3] |
魏克难, 李威, 雷明, 等. 基于耦合边界元法的水下目标低频声散射特性[J]. 舰船科学技术, 2014, 36(10): 32-36. WEI Ke-nan, LI Wei, LEI Ming, et al. The low-frequency acoustic scattering characteristics study on underwater targets by the coupled boundary element method[J]. Ship Science and Technology, 2014, 36(10): 32-36. DOI:10.3404/j.issn.1672-7649.2014.10.008 |
| [4] |
徐忠昌, 张明敏, 王旅. BeTSSi模型低频散射声场仿真研究[J]. 计算机与数字工程, 2015, 43(4): 551-553, 575. DOI:10.3969/j.issn1672-9722.2015.04.003 |
| [5] |
张建民, 安俊英, 慈国庆, 等. 并行计算水下大尺度弹性壳体的低频声散射[J]. 计算机科学, 2017, 44(3): 48-50, 54. |
| [6] |
GILROY L, DE JONG C, NOLTE B, et al. BeTSSi II benchmark target strength simulation [C]//Forum Acusticum. Krakow, Poland, 2014.
|
| [7] |
SCHNEIDER H G, FIEDLER C. Benckmark target strength simulation workshop [C]// UDT Europe. Malmo, Sweden, 2003.
|
| [8] |
范军, 刘涛, 汤渭霖. 水中双层无限长圆柱壳体声散射[J]. 声学学报, 2003, 28(4): 345-360. DOI:10.3321/j.issn:0371-0025.2003.04.010 |
| [9] |
GONG J, AN J, CI G, et al. Computation of acoustic scattering from objects in shallow waters by conventional and fast multipole BEM [C]//IEEE/OES China Ocean Acoustics Symposium COA 2016, 2016.
|
| [10] |
龚家元, 安俊英, 马力, 等. 边界元奇异与近奇异数值积分方法及其应用于大规模声学问题[J]. 声学学报, 2016, 41(5): 768-775. GONG Jia-yuan, AN Jun-ying, MA Li, et al. Numerical quadrature for singular and near-singular integrals of boundary element method and its applications in large-scale acoustic problems[J]. Acta Acustica, 2016, 41(5): 768-775. |
| [11] |
范军, 汤渭霖, 卓琳凯. 声呐目标回声特性预报的板块元方法[J]. 船舶力学, 2012, 16(1-2): 171-180. FAN Jun, TANG Wei-lin, ZHUO Lin-kai. Planar elements method for forecasting the echo characteristics from sonar targets[J]. Journal of Ship Mechanics, 2012, 16(1-2): 171-180. |
| [12] |
JIN J. The finite element method in electromagnetics [M]. New York: John Wiley & Sons, 2002.
|
| [13] |
KALVIN V. Analysis of perfectly matched layer operators for acoustic scattering on manifolds with quasicylindrical ends[J]. J. Math. Pures Appl., 2013, 100(2): 204-219. |
| [14] |
CHAPELLE D, BATHE K J. The finite element analysis of shells - fundamentals [M]. Berlin: Springer-Verlag, 2003.
|
| [15] |
安俊英, 刘彩芬, 徐海亭. 准确测量水下目标的目标强度[J]. 声学技术, 2000, 19(4): 228-232. DOI:10.3969/j.issn.1000-3630.2000.04.025 |
| [16] |
苗涛, 葛青, 王志伟, 等. 有限长双层弹性圆柱壳体声散射研究[J]. 舰船科学技术, 2010, 32(1): 71-75. MIAO Tao, GE Qing, WANG Zhi-wei, et al. The character of scattering sound from finite length double-layer cylindrical shells[J]. Ship Science and Technology, 2010, 32(1): 71-75. DOI:10.3404/j.issn.1672-7649.2010.01.012 |
| [17] |
胡泊, 张均平. 潜艇艏端耐压舱壁构型对声目标强度的影响[J]. 中国舰船研究, 2016, 11(6): 22-27. HU Bo, ZHANG Jun-ping. Effect analysis for the shape of submarine bow pressure bulkhead upon the acoustic target strength[J]. Chinese Journal of Ship Research, 2016, 11(6): 22-27. DOI:10.3969/j.issn.1673-3185.2016.06.004 |
 2018, Vol. 40
2018, Vol. 40
