2. 威海海洋职业学院,山东 威海 264300
2. Weihai Ocean Vocational College, Weihai 264300, China
现代潜艇的主要发展方向是大潜深、大尺寸,随着潜艇结构尺寸的变大,端部球面舱壁的尺寸亦随之增大。随着端部球面舱壁的变大,会随之出现很多问题,如在加工过程中出现的不可避免的加工误差、局部缺陷等造成的对舱壁结构的强度及稳定性。增加舱壁结构强度和稳定性的方法通常有增加球面壳的厚度、在球面壳上增添加强结构。当结构局部出现缺陷时,可以考虑在缺陷部分采用加厚或者采用加强筋的方式来增加结构的强度和稳定性。加厚,工艺简单,但是增加的厚度值不容易确定;采用加强筋形式,可以同时顾及缺陷周围部分,但加工工艺复杂,容易引入其他影响因素。同时如果因为采用加强形式而引起结构重量突变,将不利于潜艇人员及武备的配置。球面壳加强筋通常有经向加筋和纬向加筋,经向和纬向组合加筋。不同的加筋形式、不同的加强筋截面形状等对舱壁结构的强度及稳定性有较大的影响。
1 纬线加筋球壳稳定性 1.1 纬线加筋球壳局部稳定性当球壳肋骨间丧失局部稳定性时,壳的两端可以认为是自由支持在刚性支座上。壳体失稳后的变形是连续的,位移的3个分量应该是坐标θ的周期函数,取坐标原点在左端肋骨处,于是球壳失稳位移可以选为:
| $\normalsize\left\{ \begin{array}{l}w = A\sin \displaystyle\frac{{\pi \left( {\varphi - \alpha } \right)}}{\beta }\cos n\theta \text{,}\\v = B\sin \displaystyle\frac{{\pi \left( {\varphi - \alpha } \right)}}{\beta }\sin n\theta \text{,}\\u = C\cos \displaystyle\frac{{\pi \left( {\varphi - \alpha } \right)}}{\beta }\cos n\theta \text{。}\end{array} \right.$ | (1) |
式中:n为壳失稳时沿壳的圆周方向形成的整波数;β为两肋骨之间的中心角;A,B,C均为未知常数。
球壳的应变位移关系可由文献[1]得到:
| $\normalsize\left\{ \begin{array}{l} {{\varepsilon }_{x}}=\displaystyle\frac{\partial u}{\partial x}\text{,}{{\varepsilon }_{y}}=\frac{\partial v}{\partial y}\text{,}{{\varepsilon }_{z}}=\frac{\partial w}{\partial z} \text{,}\\ {{\gamma }_{xy}}=\displaystyle\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y},{{\gamma }_{yz}}=\displaystyle\frac{\partial w}{\partial y}+\frac{\partial v}{\partial z},{{\gamma }_{zx}}=\displaystyle\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}\text{。}\end{array} \right.$ | (2) |
下面确定球形环壳的总势能,将其写成如下形式
| $\normalsize{V_{sph}} = {U_m} + {U_b} + {C_1},$ | (3) |
式中:Um为球形环壳的薄膜应变能;Ub为球形环壳的弯曲应变能;C1为球形环壳的外力功。
球壳的薄膜应变能为
| $\normalsize{U_m} = \frac{1}{2}\int\nolimits_\alpha ^{\alpha + \beta } {\int\nolimits_0^{2{\text{π}}} {\left( {{{n'}\!\!\!_x}{{\varepsilon '}\!\!\!_x} + {{n'}\!\!\!_\theta }{{\varepsilon '}\!\!\!_\theta } + 2{{n'}\!\!\!_{x\theta }}{{\varepsilon '}\!\!\!_{x\theta }}} \right)} } {R^2}\sin \varphi {\rm{d}}\theta {\rm{d}}\varphi ,$ | (4) |
式中:
| $n_x' = K\left( {\varepsilon _x' + \mu \varepsilon _\theta '} \right),\;\;\;n_\theta ' = K\left( {\varepsilon _\theta ' + \mu \varepsilon _x'} \right), \;\;\; n_{x\theta }' = K\left( {1 - \mu } \right)\varepsilon _{x\theta }',$ | (5) |
式中:
将式(4)积分得环形球面壳板的薄膜应变能为:
| $\normalsize\begin{aligned}{U_m} =& K\left[ {CA(\mu {\rm{ + 1}})\left( {{P_7} + \frac{{2\pi {P_5}}}{\beta }} \right) + {B^2}\biggr( {{P_1}{n^2} - 2{P_3}(\mu - 1) + } } \right.\\& \frac{{2{P_6}{\pi ^2}}}{{{\beta ^2}}} - {P_7}\pi \frac{{1 + \mu }}{{0.5\beta }}\biggr) + {\rm{2}}(\mu {\rm{ + 1}}){A^{\rm{2}}}{P_{\rm{5}}} - \left( {\mu {\rm{ + 1}}} \right)B\beta nA + \end{aligned}$ |
| $\small\begin{aligned} BC\left( { - 4\mu n{P_8} + 6n{P_8} - 2\pi n + \mu n\pi } \right) +\quad\quad\quad\quad\\{C^2}\left. {\left( {2{P_4}{n^2} + {P_2} + \frac{{{P_5}{\pi ^2}}}{{{\beta ^2}}} - 2\mu {P_4}{n^2}} \right)} \right],\quad\quad\quad\;\;\;\end{aligned}$ |
式中:
| $\normalsize\begin{array}{l}\displaystyle{P_1} = \int\nolimits_\alpha ^{\alpha + \beta } {{{\sin }^2}} \left( {{\text{π}} \left( {\varphi - \alpha } \right)/\beta } \right)/\sin \varphi {\rm{d}}\varphi, \\\displaystyle{P_2} = \int\nolimits_\alpha ^{\alpha + \beta } {\sin \varphi {{\cos }^2}} \left( {{\text{π}} \left( {\varphi - \alpha } \right)/\beta } \right){\cot ^2}\varphi {\rm{d}}\varphi,\end{array}$ |
| $\normalsize\begin{array}{l}\displaystyle{P_3} = \int\nolimits_\alpha ^{\alpha + \beta } {\sin \varphi {{\sin }^2}} \left( {\pi \left( {\varphi - \alpha } \right)/\beta } \right){\cot ^2}\varphi {\rm{d}}\varphi, \\\displaystyle{P_4} = \int\nolimits_\alpha ^{\alpha + \beta } {{{\cos }^2}} \left( {\pi \left( {\varphi - \alpha } \right)/\beta } \right)/\sin \varphi {\rm{d}}\varphi, \\\displaystyle{P_5} = \int\nolimits_\alpha ^{\alpha + \beta } {{{\sin }^2}} \left( {\pi \left( {\varphi - \alpha } \right)/\beta } \right)\sin \varphi {\rm{d}}\varphi,\end{array}$ |
| $\normalsize\begin{array}{l}\displaystyle{P_6} = \int\nolimits_\alpha ^{\alpha + \beta } {{{\cos }^2}} \left( {\pi \left( {\varphi - \alpha } \right)/\beta } \right)\sin \varphi {\rm{d}}\varphi, \\\displaystyle{P_7} = \int\nolimits_\alpha ^{\alpha + \beta } {\cos \varphi \sin \left( {2\pi \left( {\varphi - \alpha } \right)/\beta } \right){\rm{d}}\varphi }, \\\displaystyle{P_8} = \int\nolimits_\alpha ^{\alpha + \beta } {\cot \varphi \sin \left( {\pi \left( {\varphi - \alpha } \right)/\beta } \right)\cos \left( {\pi \left( {\varphi - \alpha } \right)/\beta } \right){\rm{d}}\varphi }{\text{。}} \end{array}$ |
球壳的弯曲应变能为
| $\normalsize{U_b} = \frac{1}{2}\int\nolimits_\alpha ^{\alpha + \beta } {\int\nolimits_0^{2\pi } {\left( {m_x'\gamma _x' + m_\theta '\gamma _\theta ' + m_{x\theta }'\gamma _{x\theta }'} \right)} } {R^2}\sin \varphi {\rm{d}}\theta {\rm{d}}\varphi ,$ | (7) |
式中:
| $m_x' = D\left( {\gamma _x' + \mu \gamma _\theta '} \right) ,\;\;\; m_\theta ' = D\left( {\gamma _\theta ' + \mu \gamma _x'} \right) ,\;\;\; m_{x\theta }' = D\left( {1 - \mu } \right) \gamma _{x\theta }' ,$ | (8) |
式中:
将式(7)积分得环形球面壳板的弯曲应变能为:
| $\normalsize\begin{split}{U_b} =& \displaystyle\frac{{D{P_5}{\pi ^2}}}{{{R^2}{\beta ^2}}}{\left( {\frac{{\pi A}}{\beta } + C} \right)^2} + \frac{{D{n^2}A}}{{{R^2}}}\left( {{P_9}{n^2}A - {P_{10}}C} \right)- \\ & \displaystyle\frac{{D\mu AC{P_7}{\pi ^2}}}{{{R^2}{\beta ^2}}} + \frac{{2D{P_4}{n^2}}}{{{R^2}}}\left( {1 - \mu } \right){\left( {\frac{{\pi A}}{\beta } + C} \right)^2}+ \\ & \displaystyle\frac{{2D{P_1}{n^2}}}{{{R^2}}}\left( {\frac{{{\pi ^2}\mu {A^2}}}{{{\beta ^2}}} + \frac{{\pi \mu AC}}{\beta }} \right),\end{split}$ | (9) |
式中:
| $\normalsize\begin{array}{l}\displaystyle{P_9} = \displaystyle\int\nolimits_\alpha ^{\alpha + \beta } {{{\sin }^2}} \left( {\pi \left( {\varphi - \alpha } \right)/\beta } \right)/{\sin ^3}\varphi {\rm{d}}\varphi, \\\displaystyle{P_{10}} = \int\nolimits_\alpha ^{\alpha + \beta } {\frac{{\cot \varphi \sin \left( {\frac{{\pi \left( {\varphi - \alpha } \right)}}{\beta }} \right)\cos \left( {\frac{{\pi \left( {\varphi - \alpha } \right)}}{\beta }} \right)}}{{\sin \varphi }}{\rm{d}}\varphi } {\text{。}}\end{array}$ |
在均匀外压下,球壳的外力功为:
| $\small\displaystyle{C_1} \!\!=\!\! \frac{1}{2}\int\nolimits_\alpha ^{\alpha + \beta } {\int\nolimits_0^{2\pi } {\left( {N_x^F{{\varepsilon ''}\!\!\!\!\!_x} \!\!+\!\! {{n''}\!\!\!\!\!_x}E_x^F \!\!+\!\! N_\theta ^F{{\varepsilon ''}\!\!\!\!\!_\theta } \!\!+\!\! {{n''}\!\!\!\!\!_\theta }E_\theta ^F} \right)} } {R^2}\sin \varphi {\rm{d}}\theta {\rm{d}}\varphi, $ | (10) |
式中:
| $n_x^{''} = K\left( {\varepsilon _x^{''} + \mu \varepsilon _\theta ^{''}} \right), \;\;\; n_\theta ^{''} = K\left( {\varepsilon _\theta ^{''} + \mu \varepsilon _x^{''}} \right),$ | (11) |
忽略肋骨影响,假设环形球面壳内应力均匀分布,则
| $N_x^F = - \frac{{pR}}{{2t}}, \;\;\; N_\theta ^F = - \frac{{pR}}{{2t}},$ | (12) |
将式(11)和式(12)代入式(10)并积分得
| ${C_1} = - \frac{{pR{A^2}}}{2}\left( {{P_1}{n^2} + \frac{{{\pi ^2}{P_6}}}{{{\beta ^2}}}} \right) ,$ | (13) |
将式(6)、式(9)、式(13)代入式(4)即为环形球面壳的总势能。由壳体稳定条件
| $\frac{{\partial {V_{sph}}}}{{\partial A}} = 0,\;\;\;\;\frac{{\partial {V_{sph}}}}{{\partial B}} = 0,\;\;\;\;\frac{{\partial {V_{sph}}}}{{\partial C}} = 0,$ | (14) |
将式(4)代入式(14),得
| $\left[ {\begin{array}{*{20}{c}}{{A_{11}}} & {{A_{12}}} & {{A_{13}}}\\{{A_{21}}} & {{A_{22}}} & {{A_{23}}}\\{{A_{31}}} & {{A_{32}}} & {{A_{33}}}\end{array}} \right]\left\{ {\begin{array}{*{20}{c}}A\\B\\C\end{array}} \right\} = 0,$ | (15) |
其中:
| $\begin{aligned}{A_{11}} =& 4K{P_5}\left( {1 + \mu } \right) + \frac{{4D{P_4}{\pi ^2}{n^2}}}{{{R^2}{\beta ^2}}}\left( {1 - \mu } \right) + \frac{{2D}}{{{R^2}}}\left( {\frac{{{P_5}{\pi ^4}}}{{{\beta ^4}}}} \right.+ \\& \frac{{2{P_1}\mu {\pi ^2}{n^2}}}{{{\beta ^2}}} + {P_9}{n^4}\biggr) - pR\left( {{P_1}{n^2} + \frac{{{P_6}{\pi ^2}}}{{{\beta ^2}}}} \right),\\{A_{12}} = & - K\beta n\left( {1 + \mu } \right),\\{A_{13}} = & - K{P_7}\left( {1 + \mu } \right) + \frac{{2K{P_5}\pi }}{\beta }\left( {1 + \mu } \right) + \\&\frac{{2D\pi }}{{{R^2}\beta }}\left( {\frac{{{P_5}{\pi ^2}}}{{{\beta ^2}}} \!+\! {P_1}\mu {n^2} \!+\! 2{P_4}{n^2}\left( {1 - \mu } \right) \!- \!\frac{{\mu {P_7}\pi }}{\beta } - \frac{{{P_{11}}{n^2}}}{\pi }} \right),\\{A_{22}} = & 2K{P_1}{n^2} + 4K{P_3}\left( {1 - \mu } \right) + \frac{{4K{P_6}{\pi ^2}}}{{{\beta ^2}}}\left( {1 - \mu } \right) + \\&\frac{{4K{P_7}\pi }}{\beta } + \frac{{2D{P_1}{n^2}}}{{{R^2}}},\\{A_{23}} =& Kn{P_8}\left( {6 - 4\mu } \right) + K\pi n\left( {\mu - 2} \right),\end{aligned}$ |
| $\begin{aligned}\!\!\!{A_{33}} =& 4K{P_4}{n^2}\left( {1 - \mu } \right) + 2K{P_2} - \frac{{2K{P_7}\mu \pi }}{\beta } + \frac{{2K{P_5}{\pi ^2}}}{{{\beta ^2}}}+\;\,\,\, \\&\frac{{2D}}{{{R^2}}}\left( {\frac{{{P_5}{\pi ^2}}}{{{\beta ^2}}} + 2{P_4}{n^2}\left( {1 - \mu } \right) - \frac{{\mu {P_7}\pi }}{\beta } + {P_2}} \right){\text{。}}\end{aligned}$ | (16) |
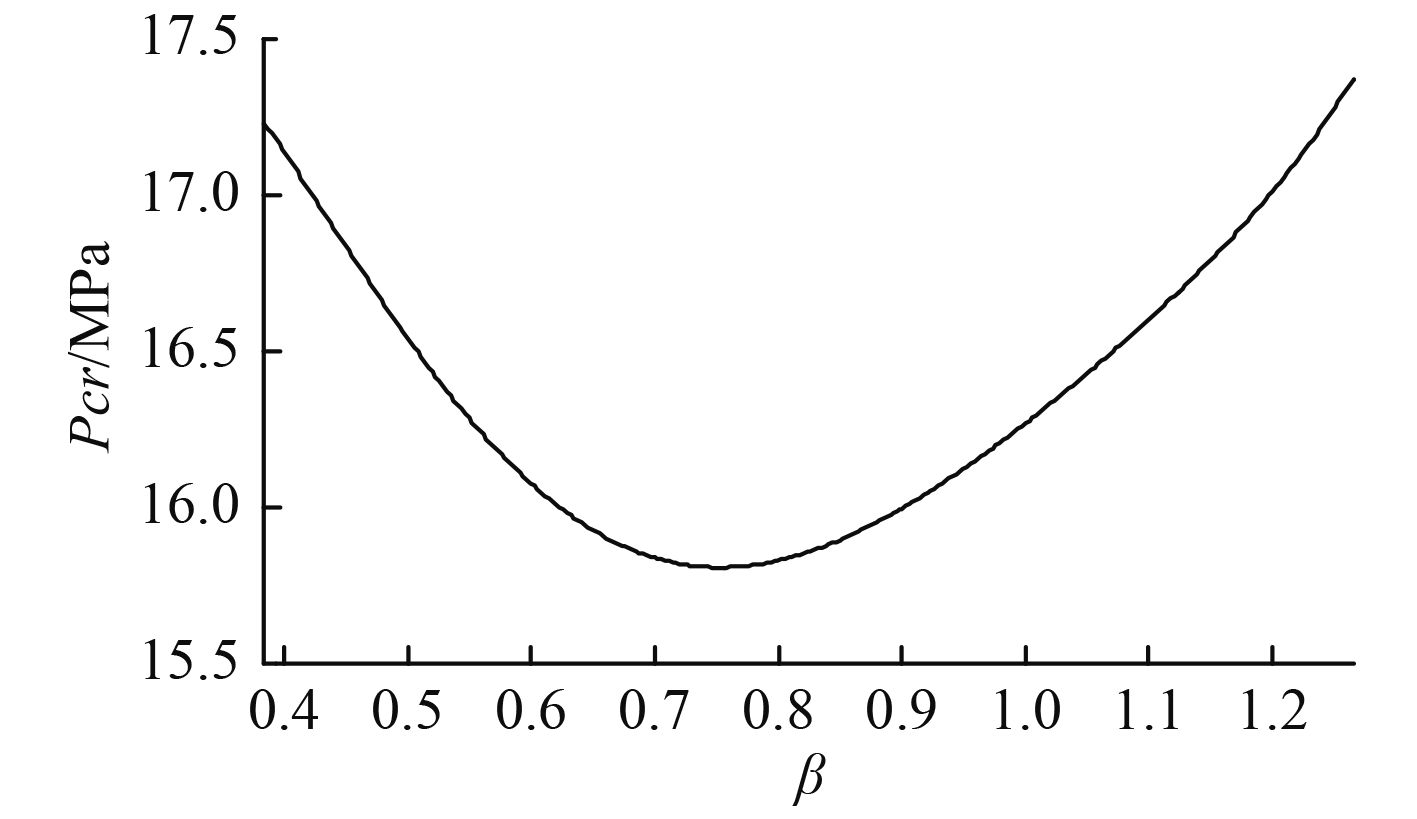
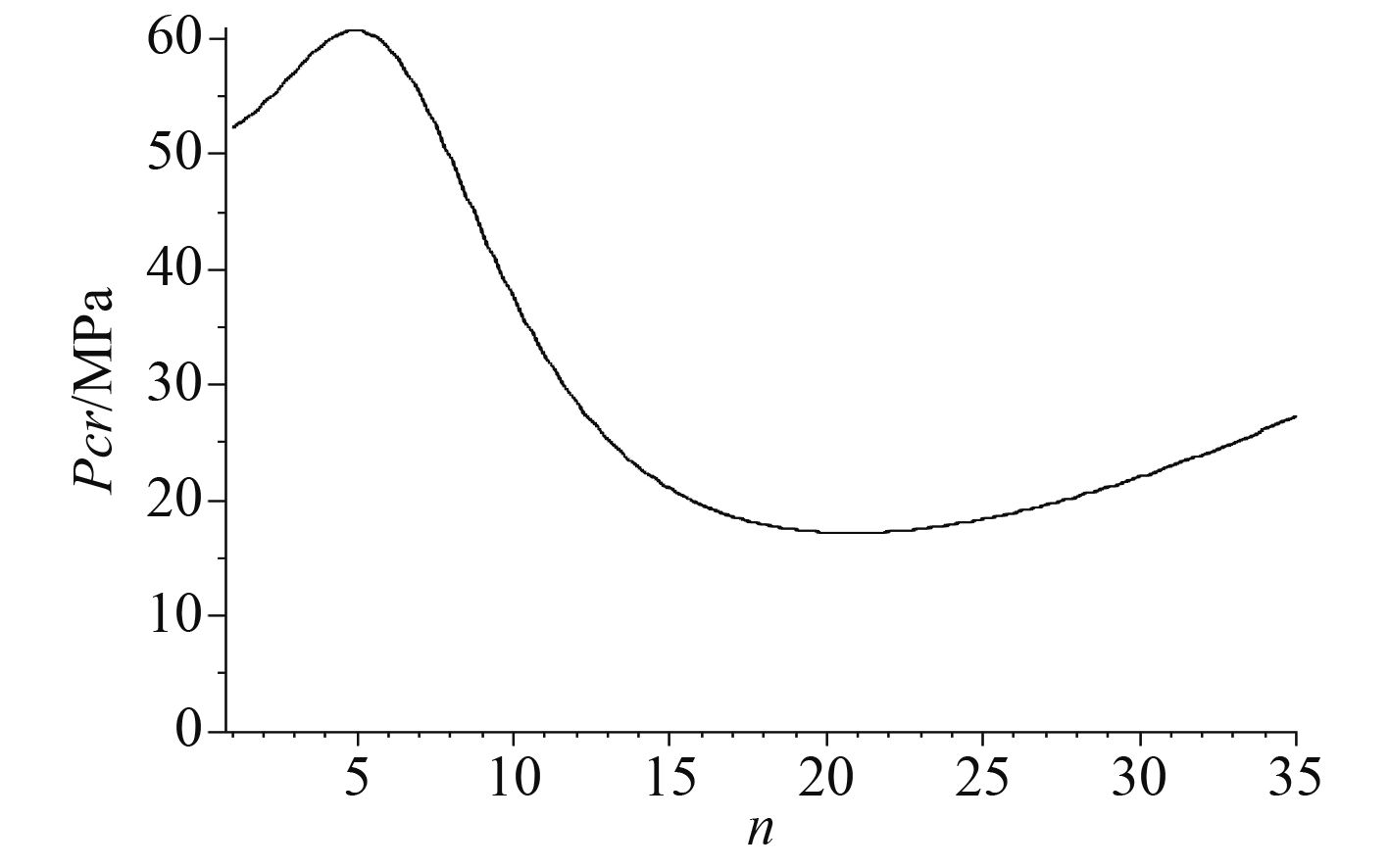
令式(15)中系数矩阵的行列式为0,即可求得环形球面壳失稳临界载荷。下面应用如下参数研究加筋球面壳稳定性能:R=5 000 mm,t=40 mm。首先给出环形球面壳失稳载荷随着经线中心角β的变化规律,如表1和图1所示。从表1可以看出,随着β角的增加,环形球面壳的周向失稳波数逐渐减少,失稳载荷先减少后增加,从图1中可以看出,当β=0.75时,临界载荷达到最小值。图2给出的是β=π/8,α=3π/8时加筋球面壳局部失稳载荷随着周向失稳波数的变化规律。
|
图 1 临界载荷随着β角的变化规律 Fig. 1 The variation of the critical load with angle β |
|
|
表 1 不同中心角β下的临界载荷 Tab.1 The critical load under different central angle β |
|
图 2 临界载荷随着周向波数的变化规律 Fig. 2 The variation of the critical load with circumferential wave number |
|
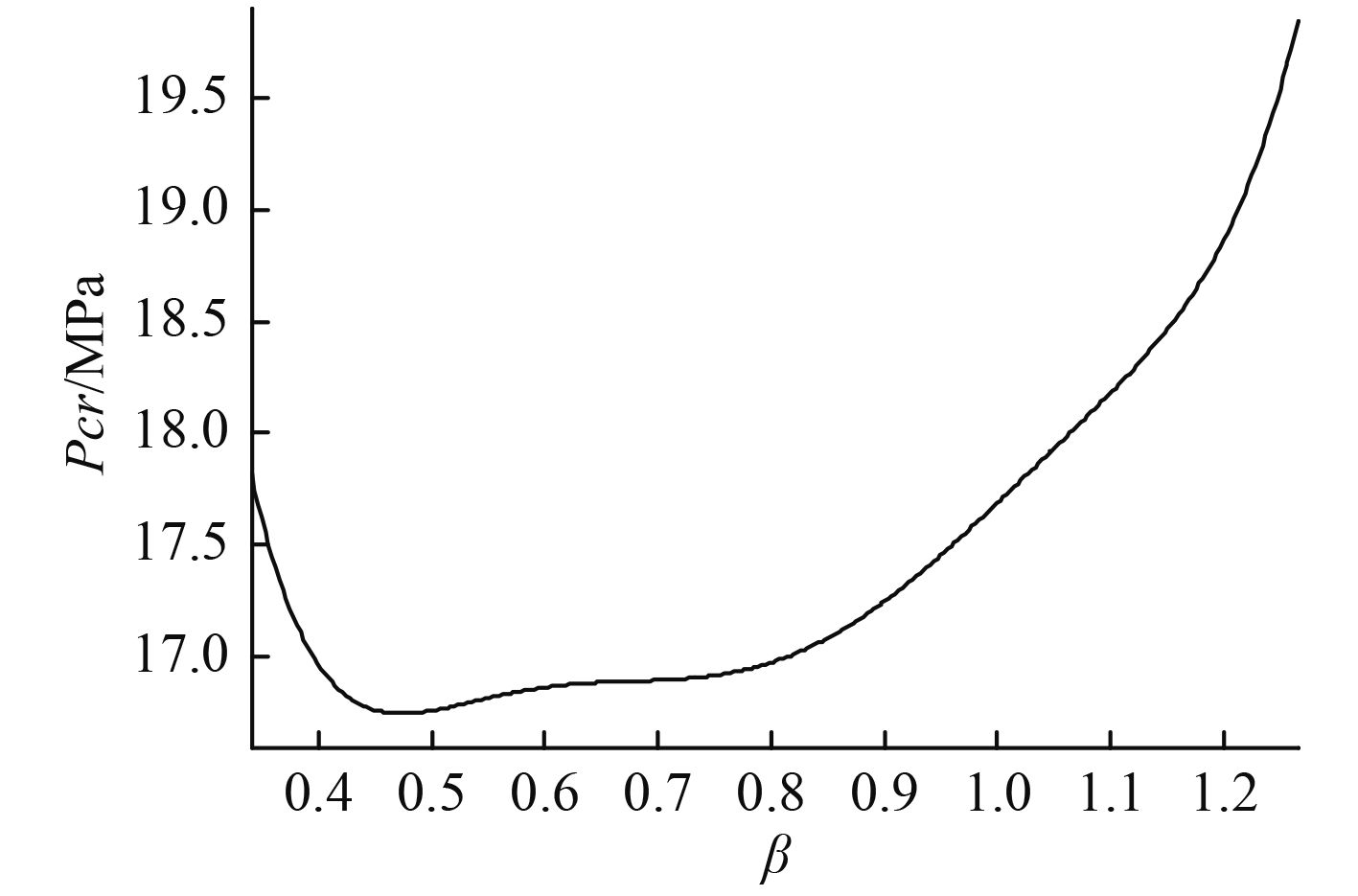
图 3 临界载荷随着β角的变化规律 Fig. 3 The variation of the critical load with β angle |
图3给出了环形球面壳位于α=π/4位置时,球面壳失稳载荷随着β角的变化规律。与图1相比,位于中间的环形球面壳的失稳载荷随着环形球面的增加也是先减少后增加,不同的是在β=0.5~0.8之间失稳载荷增加很小,随后迅速的增加。通过分析还发现,位于球壳中间部分的环形球面壳的周向失稳波数随着β角的变化不大,只减少了2个波形。
|
图 4 不同位置环形球面壳的失稳载荷 Fig. 4 Buckling load on different location of annular spherical shell |
表2给出了同样β角下不同位置的环形球面壳的失稳载荷,从表中可以看出随着α的增加环形球面壳的失稳波数增加而临界载荷逐渐降低,在半球壳边缘位置有缓慢的上升,图4给出了不同位置的环形球面壳失稳载荷的变化趋势。
|
|
表 2 不同位置的环形球面壳的临界载荷 Tab.2 Different position of the critical spherical shell in a circleload of |
|
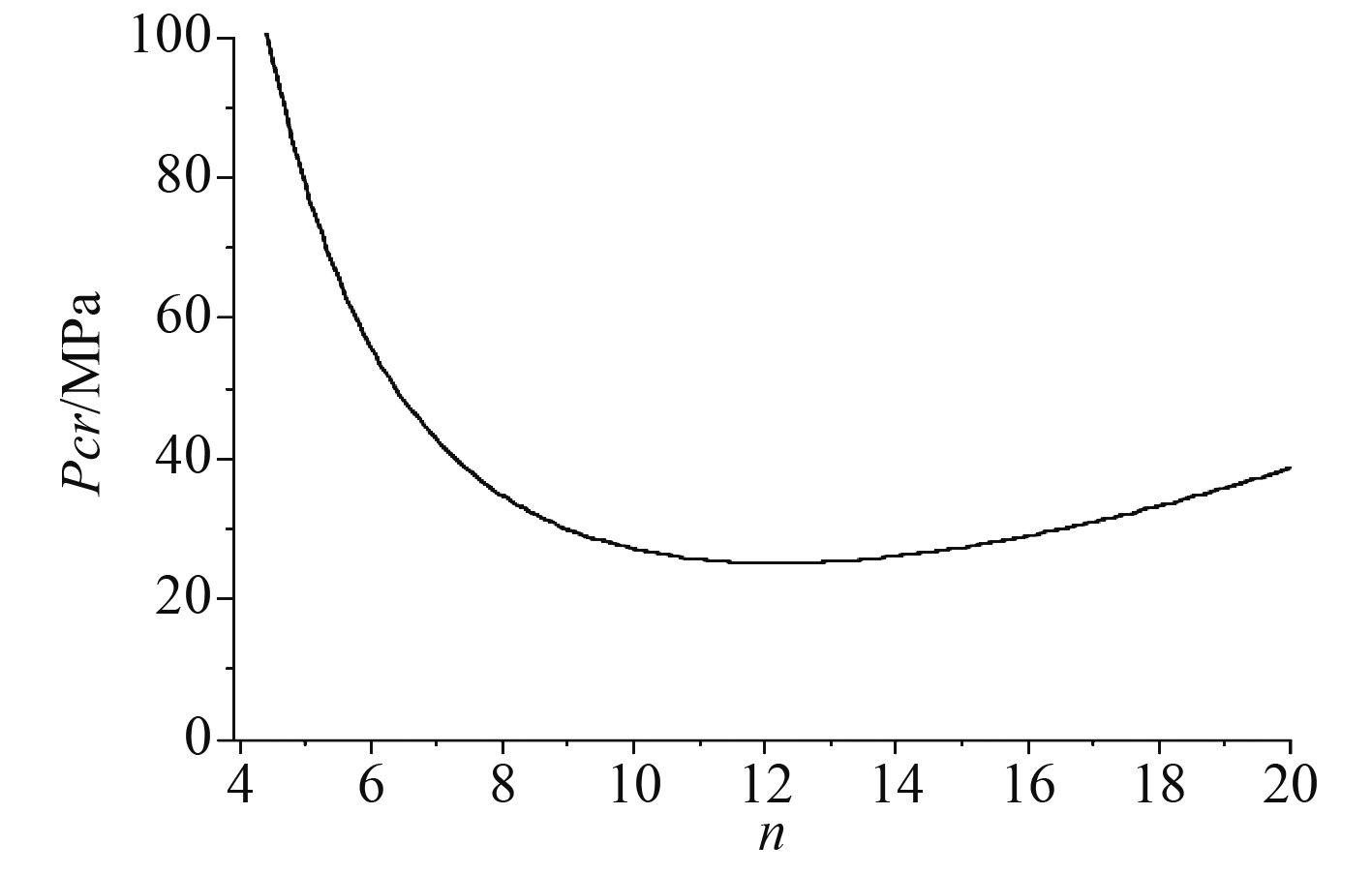
图 5 加筋球面壳失稳载荷 Fig. 5 Buckling load on reinforcement of spherical shell |
通过以上的分析可知,在设计纬线加筋球面壳时,为使材料充分的利用,加1条肋骨时应靠近球壳顶点,加2条肋骨时应分别加在顶点和边缘附近,加3条肋骨时可均匀布置于半球壳。加更多的肋骨对球壳局部失稳意义不大。
1.2 纬线加筋球壳总体稳定性研究纬线加筋球壳总体稳定性时,需要考虑纬线肋骨的影响,忽略肋骨的压缩应变能,则第i根肋骨的应变能为
| $\small{V_i} = \frac{{EI}}{2}\int\nolimits_0^{2\pi } {\gamma _\theta ^{'2}R\sin {\varphi _i}{\rm{d}}\theta },$ | (17) |
将上式积分得
| $\small\begin{split}{l}{V_i} =& \frac{{EI}}{{{R^3}}}\sin {\varphi _i}\left( {\frac{{A{n^2}\sin \left( {\pi {\varphi _i}/\beta } \right)}}{{{{\sin }^2}{\varphi _i}}} + C\cos \left( {\pi {\varphi _i}/\beta } \right)\cot {\varphi _i}} \right.+\\ & {\frac{{Bn\sin \left( {\pi {\varphi _i}/\beta } \right)}}{{\sin {\varphi _i}}}\biggr)^2}\text{。}\end{split}$ | (18) |
将所有肋骨应变能叠加,即可求得整个加筋球面壳全部肋骨的应变能。
此时方程(15)的系数行列式为
| $\begin{split}{A_{11}} = & {4K{P_5}\left( {1 + \mu } \right) + \frac{{4D{P_4}{\pi ^2}{n^2}}}{{{R^2}{\beta ^2}}}\left( {1 - \mu } \right) }+ \\& {\frac{{2D}}{{{R^2}}}\left( {{\frac{{{P_5}{\pi ^4}}}{{{\beta ^4}}} + \frac{{2{P_1}\mu {\pi ^2}{n^2}}}{{{\beta ^2}}} + {P_9}{n^4}}} \right)}-\\& { pR\left( {{P_1}{n^2} + \frac{{{P_6}{\pi ^2}}}{{{\beta ^2}}}} \right) + \frac{{2EI{n^4}}}{{{R^3}}}\sum\limits_{i = 1}^n {\frac{{{{\sin }^2}\left( {\pi {\varphi _i}/\beta } \right)}}{{{{\sin }^3}{\varphi _i}}}} },\\{A_{12}} =& { - K\beta n\left( {1 + \mu } \right) - \frac{{2EI{n^3}}}{{{R^3}}}\sum\limits_{i = 1}^n {\frac{{{{\sin }^2}\left( {\pi {\varphi _i}/\beta } \right)}}{{{{\sin }^2}{\varphi _i}}}} },\\{A_{13}} = & - K{P_7}\left( {1 + \mu } \right) + \frac{{2D\pi }}{{{R^2}\beta }}\left( {{\frac{{{P_5}{\pi ^2}}}{{{\beta ^2}}} + {P_1}\mu {n^2} + }} \right.\\& 2{P_4}{n^2}\left( {1 - \mu } \right) - \frac{{\mu {P_7}\pi }}{\beta } - \frac{{{P_{11}}{n^2}}}{\pi }\biggr)+\\& { \frac{{2K{P_5}\pi }}{\beta }\left( {1 + \mu } \right) + \frac{{EI{n^2}}}{{{R^3}}}\sum\limits_{i = 1}^n {\frac{{\sin \left( {2\pi {\varphi _i}/\beta } \right)\cot {\varphi _i}}}{{\sin {\varphi _i}}}} },\end{split}$ |
| $\begin{split}{A_{22}} =& 2K{P_1}{n^2} + 4K{P_3}\left( {1 - \mu } \right) + \displaystyle\frac{{4K{P_6}{\pi ^2}}}{{{\beta ^2}}}\left( {1 - \mu } \right) +\\&+ \frac{{4K{P_7}\pi }}{\beta } \displaystyle\frac{{2D{P_1}{n^2}}}{{{R^2}}} + \frac{{2EI{n^2}}}{{{R^3}}}\sum\limits_{i = 1}^n {\frac{{{{\sin }^2}\left( {\pi {\varphi _i}/\beta } \right)}}{{\sin {\varphi _i}}}} ,\end{split}$ |
| $\begin{split}\displaystyle{A_{23}} =& Kn{P_8}\left( {6 - 4\mu } \right) + K\pi n\left( {\mu - 2} \right) +\\ &\displaystyle\frac{{EIn}}{{{R^3}}}\sum\limits_{i = 1}^n {\sin \left( {2\pi {\varphi _i}/\beta } \right)\cot {\varphi _i}}, \\ {A_{33}} =& 4K{P_4}{n^2}\left( {1 - \mu } \right) - \displaystyle\frac{{2K{P_7}\mu \pi }}{\beta } +\\& \frac{{2D}}{{{R^2}}}\left( \begin{array}{l}\displaystyle\frac{{{P_5}{\pi ^2}}}{{{\beta ^2}}} + 2{P_4}{n^2}\left( {1 - \mu } \right)\\ - \displaystyle\frac{{\mu {P_7}\pi }}{\beta } + {P_2}\end{array} \right)+ \displaystyle\frac{{2K{P_5}{\pi ^2}}}{{{\beta ^2}}} +\\& 2K{P_2} + \displaystyle\frac{{EI}}{{{R^3}}}\sum\limits_{i = 1}^n {\cos \left( {\pi {\varphi _i}/\beta } \right){{\cot }^2}{\varphi _i}} \sin {\varphi _i}{\text{。}}\end{split}$ | (20) |
应用式(18)中的系数即可求得加筋球面壳在均匀外压下的总体失稳载荷。应用1.1节中的球壳尺寸,肋骨采用12号球缘钢。图5给出了只有1根肋骨并且位于半球壳中点时球壳失稳载荷随着周向失稳波数变化规律。

|
图 6 肋骨位置对球壳失稳载荷的影响 Fig. 6 Effect of spherical shell buckling load by Frame position |
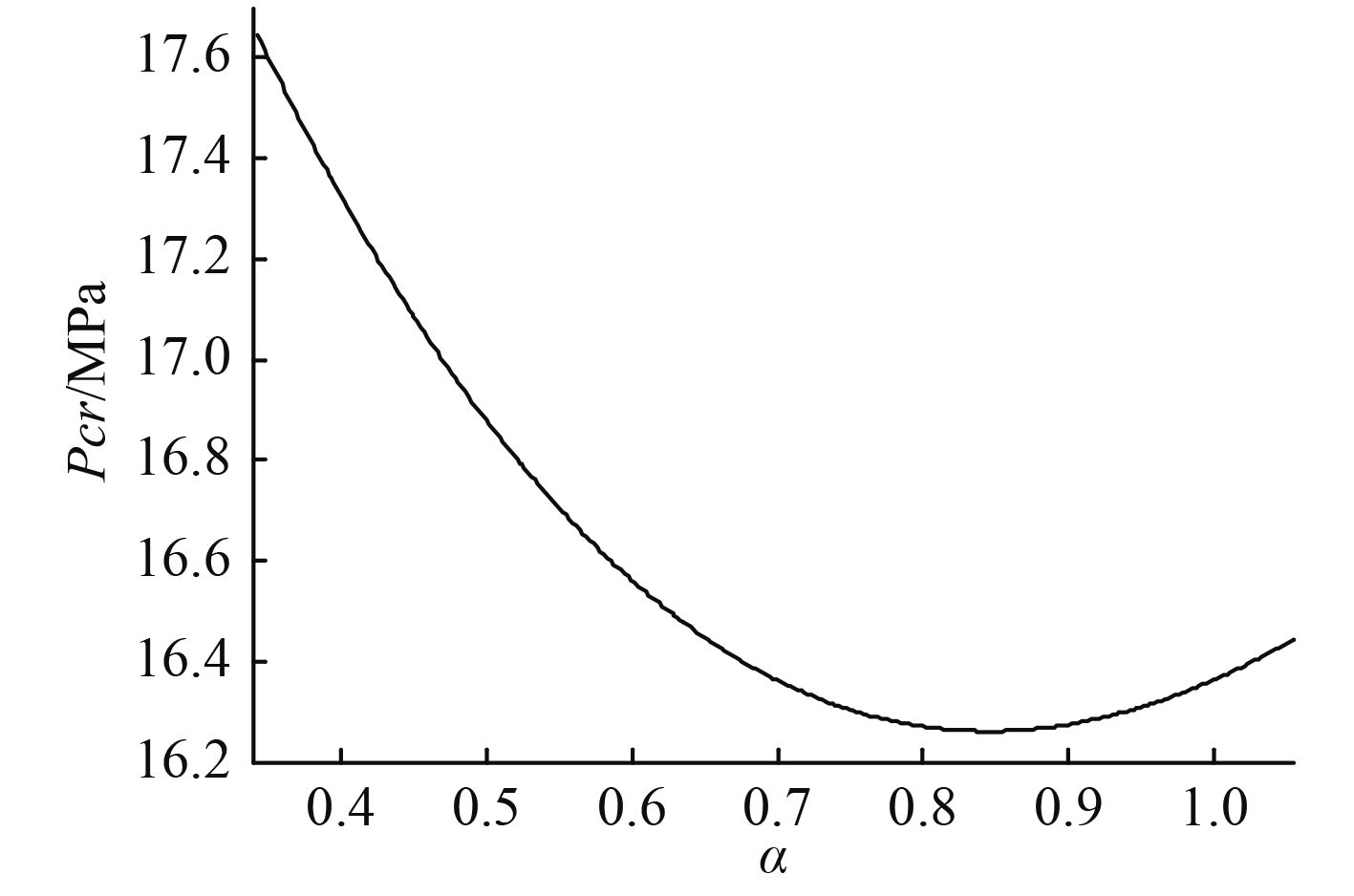
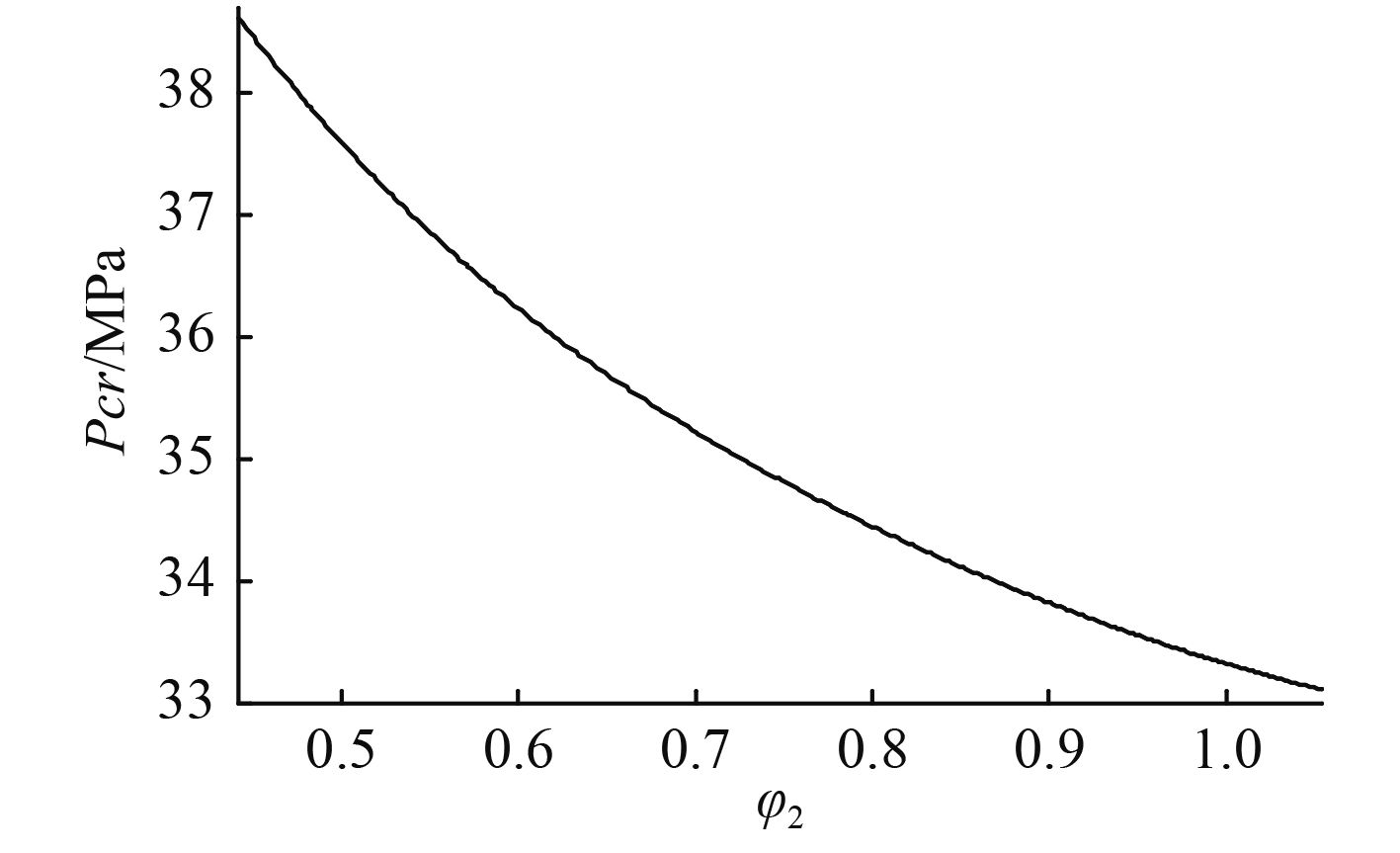
图6给出了单根肋骨位置对加筋球面壳失稳载荷的影响,从中可以看出,肋骨在距离球壳顶点近的位置越有利,综合上面的分析,单根肋骨应布置在球壳顶点附近。图7给出了2条肋骨对球壳总体稳定性的影响,横坐标为两肋骨之间的夹角。
|
图 7 两条肋骨对屈曲载荷的影响 Fig. 7 The Effect of two ribs on the buckling load |

|
图 8 经线加筋球面壳示意图 Fig. 8 Meridian reinforced spherical shell |
综上所述,加筋可以增加球面壳的稳定性,但是布置肋骨时应首先考虑壳板失稳载荷满足稳定性要求。
2 经线加筋球壳稳定性对于经线加筋圆柱壳,其位移函数可以选为:
| $\normalsize\left\{ \begin{array}{l}w = A\sin \displaystyle\frac{{\pi \varphi }}{\beta }\sin n\lambda \theta \text{,}\\v = B\sin \displaystyle\frac{{\pi \varphi }}{\beta }\cos n\lambda \theta \text{,}\\u = C\cos \displaystyle\frac{{\pi \varphi }}{\beta }\sin n\lambda \theta \text{。}\end{array} \right.$ | (21) |
其中:
将式(19)和式(2)代入式(4)积分,得
将式(19)和式(2)代入式(10)积分,得
| $\normalsize{C_1} = - \displaystyle\frac{{pR{A^2}\gamma }}{4}\left( {{P_1}{\delta ^2} + \displaystyle\frac{{{\pi ^2}{P_6}}}{{{\beta ^2}}}} \right),$ | (24) |
此时方程(15)的系数行列式为
| $\small\left\{\begin{aligned}{A_{11}} = &{4K{P_5}\left( {1 + \mu } \right) + \frac{{4D{P_4}{\pi ^2}{\delta ^2}}}{{{R^2}{\beta ^2}}}\left( {1 - \mu } \right) + \frac{{2D}}{{{R^2}}}\left( {\frac{{{P_5}{\pi ^4}}}{{{\beta ^4}}}} \right.}+ \\&{ \frac{{2{P_1}\mu {\pi ^2}{\delta ^2}}}{{{\beta ^2}}} + {P_9}{\delta ^4}\biggr) - pR\left( {{P_1}{\delta ^2} + \frac{{{P_6}{\pi ^2}}}{{{\beta ^2}}}} \right)},\\{A_{12}} = &{ - K\beta \delta \left( {1 + \mu } \right)},\\{A_{13}} = &{ - K{P_7}\left( {1 + \mu } \right) + \frac{{2K{P_5}\pi }}{\beta }\left( {1 + \mu } \right) + }\\& {\frac{{2D\pi }}{{{R^2}\beta }}\left( {\frac{{{P_5}{\pi ^2}}}{{{\beta ^2}}} + {P_1}\mu {\delta ^2} + 2{P_4}{\delta ^2}\left( {1 - \mu } \right) - \frac{{\mu {P_7}\pi }}{\beta } - \frac{{{P_{11}}{\delta ^2}}}{\pi }} \right)},\\{A_{22}} =& 2K{P_1}{\delta ^2} + 4K{P_3}\left( {1 - \mu } \right) + \frac{{4K{P_6}{\pi ^2}}}{{{\beta ^2}}}\left( {1 - \mu } \right) + \frac{{4K{P_7}\pi }}{\beta }+ \\& \frac{{2D{P_1}{\delta ^2}}}{{{R^2}}}{A_{23}} = K\delta {P_8}\left( {6 - 4\mu } \right) + K\pi \delta \left( {\mu - 2} \right), \\& {A_{33}} ={ 4K{P_4}{\delta ^2}\left( {1 - \mu } \right) + 2K{P_2} - \frac{{2K{P_7}\mu \pi }}{\beta } + \frac{{2K{P_5}{\pi ^2}}}{{{\beta ^2}}}}+\;\;\,\,\,\, \\& { \frac{{2D}}{{{R^2}}}\left( {\frac{{{P_5}{\pi ^2}}}{{{\beta ^2}}} + 2{P_4}{\delta ^2}\left( {1 - \mu } \right) - \frac{{\mu {P_7}\pi }}{\beta } + {P_2}} \right)},\end{aligned}\right.$ | (25) |
应用式(21)中的系数,令式(15)中的系数行列式为0,即可求得纵横加筋球壳在静水压力下的失稳载荷。对于图8中经线加筋球面壳,采用第1节中的球壳参数,图9给出了γ=π/2时球壳失稳载荷随着两肋骨之间周向波数的变化规律,从图中可以看出,两肋骨之间失稳周向波数要远小于无肋骨时球壳周向失稳波数。

|
图 9 γ=π/2时经线加筋球面壳失稳载荷 Fig. 9 Meridian reinforced spherical shell buckling load on γ=π/2 |
|
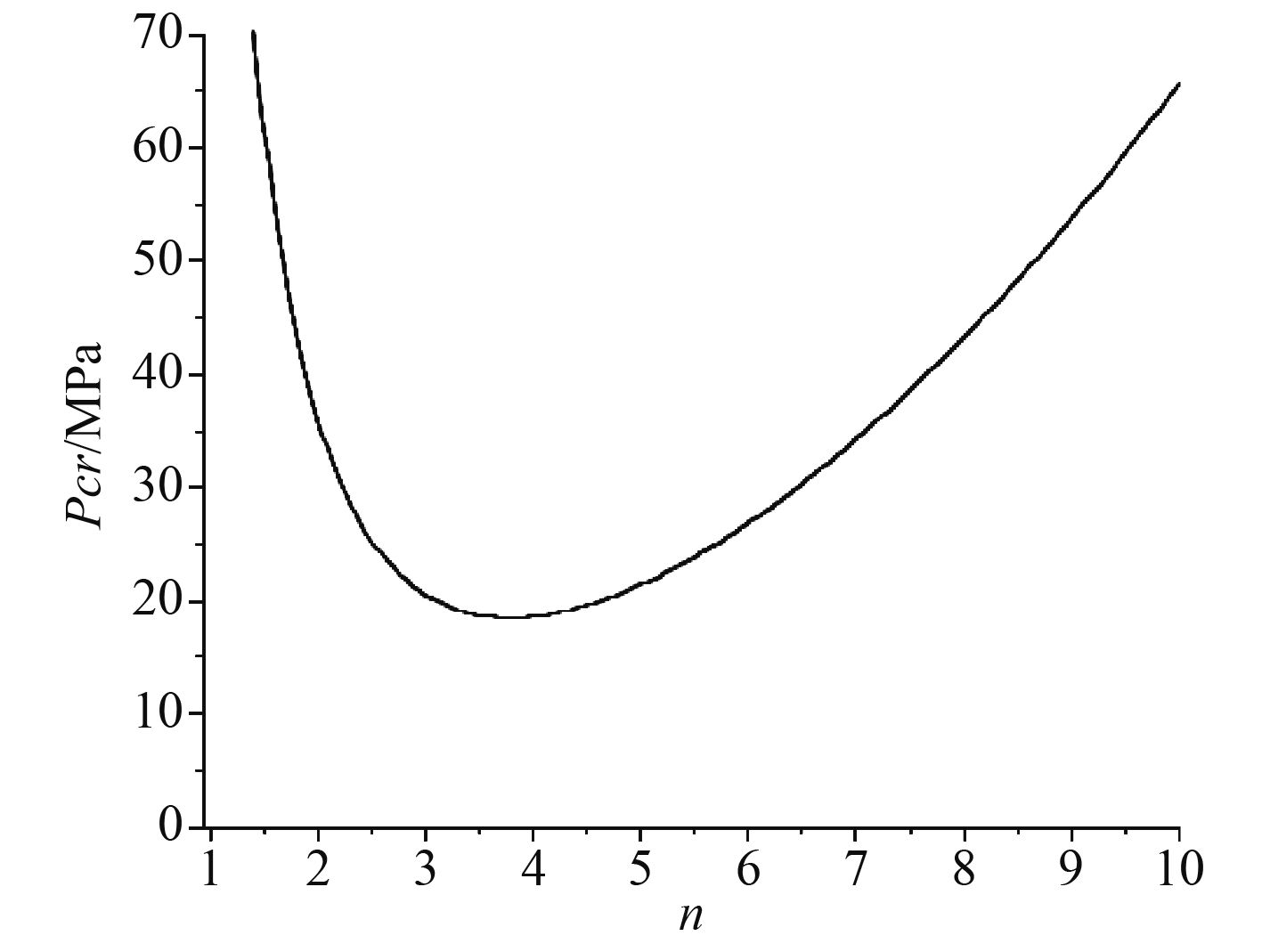
图 10 经线方向肋骨数对失稳载荷的影响 Fig. 10 The effect of buckling load by warp direction frame number |
图10给出了球面壳失稳载荷随着经线方向肋骨数目的变化规律,从图中可以看出,经线方向肋骨数很少时,对球壳失稳载荷几乎没有影响,当经线肋骨根数很多时,可以使球壳稳定性有所提高,但是效果并不明显,没有纬线方向加肋骨效果好。
3 结 语球壳加筋可以提高球面壳的稳定承载能力,对于纬向加筋球壳,应主要考虑肋骨间壳板失稳问题,纬线加筋的数目不应过多,过多对肋骨间壳板稳定性的增加意义不大;对于经线加筋球壳,只要当肋骨数目很大时增加球壳的失稳载荷,因此设计加筋球壳时应首先考虑纬线加筋的形式。
| [1] |
刘鸿文. 板壳理论[M]. 杭州: 浙江大学出版社, 1987
|
| [2] |
石德新, 王晓天. 潜艇强度[M]. 哈尔滨: 哈尔滨工程大学出版社, 1997.
|
| [3] |
庞福振, 姚熊亮, 缪旭弘, 等. 加筋球壳结构稳定性及其优化研究[J]. 机械强度, 2012, 34(3): 342-350. PANG Fu-Zhen, YAO Xiong-liang, MIAO Xu-hong, et al. Stability of reinforced spherical shell structure and its optimization study[J]. Journal of Mechanical Strength, 2012, 34(3): 342-350. |
| [4] |
伍莉, 徐治平, 张涛, 等. 球形大深度潜水器耐压壳体优化设计[J]. 船舶力学, 2010, 14(5): 509-515. WU Li, XU Zhi-ping, ZHANG Tao, et al. The spherical deep submersible pressure shell design[J]. Journal of Ship Mechanics, 2010, 14(5): 509-515. DOI:10.3969/j.issn.1007-7294.2010.05.009 |
| [5] |
范名琦, 王永军, 刘鑫. 潜艇端部舱壁结构分析[J]. 船舶力学, 2007, 11(4): 594-599. FAN Ming-qi, WANG Yong-jun, LIU Xin. Submarine end bulkhead structure analysis[J]. Journal of Ship Mechanics, 2007, 11(4): 594-599. DOI:10.3969/j.issn.1007-7294.2007.04.014 |
| [6] |
张锦岚, 刘勇, 李铭. 加筋圆柱壳开孔结构强度分析[J]. 舰船科学技术, 2017, 39(1): 12-16. ZHANG Jin-lan, LIU Yong, LI Ming. Strength analysis of open-hole structure of reinforced cylindrical shell[J]. Ship Science and Technology, 2017, 39(1): 12-16. DOI:10.3404/j.issn.1672-7619.2017.01.003 |
| [7] |
李学斌, 潘治, 甘霖. 基于改进非支配排序遗传算法的纵横加筋圆柱壳多目标优化[J]. 舰船科学技术, 2008, 30(4): 37-39. LI Xue-bin, PAN Zhi, GAN Lin. Multi-objective optimization of vertically and horizontally stiffened cylindrical shells based on improved non-dominated sorting genetic algorithm[J]. Ship Science and Technology, 2008, 30(4): 37-39. DOI:10.3404/j.issn.1672-7649.2008.04.005 |
| [8] |
唐文勇, 陈铁云. 加筋板结构的塑形动力响应分析[J]. 上海交通大学学报, 1996(8): 73-80. TANG Wen-yong, CHEN Tie-yun. SPlastic dynamic response analysis of stiffened plate structure[J]. Shanghai Jiaotong University Journal, 1996(8): 73-80. |
 2018, Vol. 40
2018, Vol. 40
