2. 武汉第二船舶设计研究所, 湖北 武汉 430064;
3. 中国人民解放军61139部队, 福建 漳州 363000
2. The Second Ship Design Institute, Wuhan 430064, China;
3. No.61139 Unit of PLA, Zhangzhou 363000, China
现代潜艇是集各种高技术于一体的海上作战平台,是世界各国海军的主要作战力量之一。潜艇的操纵性是指借助其操纵装置来改变或保持艇的运动速度、姿态、航向和深度等的性能[1]。它是潜艇的重要航海性能,对于保证潜艇航行安全、充分发挥潜艇的战术技术性能、提高经济性都有着非常重要的意义[2]。
潜艇的水下运动是六自由度的空间运动。潜艇只有在推进系统作用下获得航速,才能通过操舵改变潜艇的运动状态,反过来操舵也会增大潜艇的航行阻力,使推进系统的负载增大,可见潜艇的操舵系统和推进系统相互耦合、相互影响。但是,长期以来潜艇操舵系统和推进系统的设计与控制相对独立,为了充分发挥操舵系统与推进系统的潜能,有必要综合考虑潜艇机动与推进系统之间的相互耦合作用,使潜艇达到整体性能最优。潜艇水下机动与飞机飞行机动具有相似性,都是通过操纵和控制舵(翼)的偏转来控制潜艇(飞机)的运动,其运动特性均可看作物体在三维空间的六自由度运动,故本文借鉴飞机的飞/推综合系统模型将飞机模型和推进系统模型有机结合的建模思想[3],把潜艇机动和推进系统作为一个整体研究对象,全面考虑潜艇机动和推进系统之间的耦合关系,建立机动与推进一体化的潜艇操纵运动新型动力学模型。
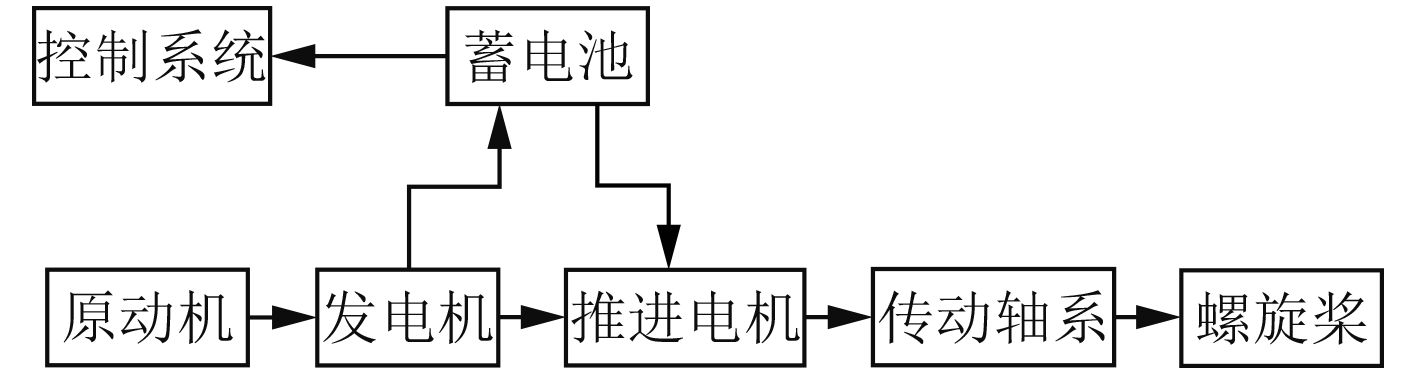
1 潜艇操纵运动的新型动力学模型 1.1 潜艇电力推进系统模块化建模潜艇电力推进系统一般由推进电机、传动轴系、螺旋桨装置、变速控制装置及蓄电池等组成,如图1所示。常规潜艇动力系统的原动机一般为柴油机。
|
图 1 常规潜艇电力推进系统 Fig. 1 The electric propulsion system of conventional submarine |
根据潜艇推进系统的特点,将系统划分成多个模块,保证分解模块之间的物理独立性和数学独立性[4],本文按功能将潜艇推进系统划分为蓄电池模块、直流推进电机模块和螺旋桨模块。本文考虑潜艇处于水下航行工况的情况。此时,主要由蓄电池向推进电机提供电力;推进电机产生扭矩,通过推进轴系带动螺旋桨旋转;同时螺旋桨旋转产生推力,通过推力轴承推动潜艇运动,使潜艇航行。
1)蓄电池放电模块
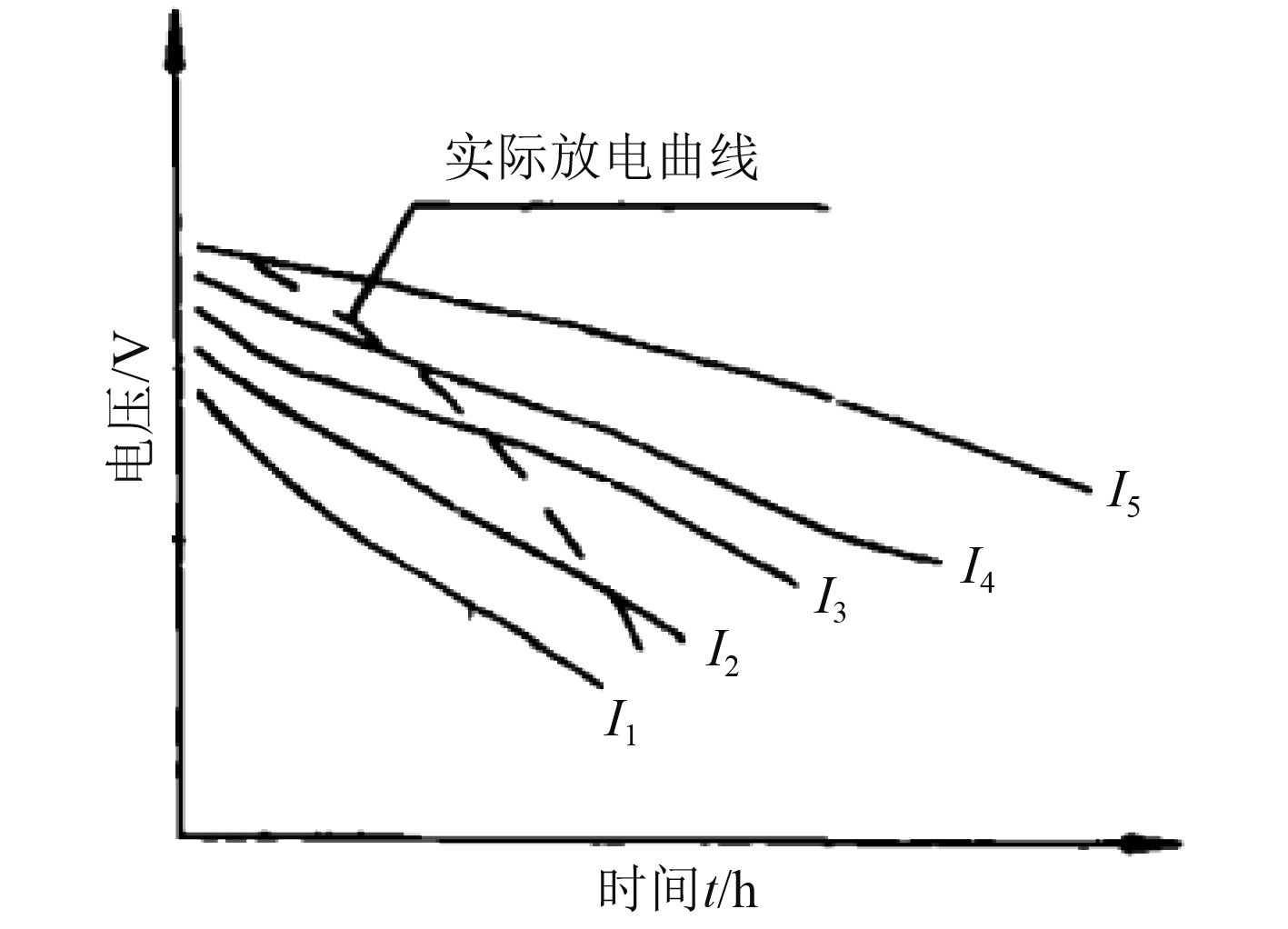
潜艇水下航行时,要求推进电机能发出稳定功率,但是,由于蓄电池在放电过程中电压、电流及电解质密度不断变化,几乎没有规律可循,因此直接模拟其电压及电流随时间变化的规律难度很大,建模有一定的困难。蓄电池作为产品交付使用时都提供放电特性曲线(见图2),这些曲线反映了蓄电池放电过程中电流、电压的变化规律。根据这些规律,结合电化学经验公式Peukert方程进行适当变化,可以用于模拟潜艇蓄电池的放电过程[5],如式(1)和式(2)所示。
| $I_{\rm{i}}^a{t_{iz}} = I_m^a{t_{mz}}{\text{,}}$ | (1) |
| $I_i^{{\rm{a}} - 1}{Q_{iz}} = I_m^{a - 1}{Q_{mz}}{\text{,}}$ | (2) |
|
图 2 蓄电池放电特性曲线 Fig. 2 The curve of battery discharge characteristics |
式中:tiz为电流Ii的放电率;Qiz为对应电流Ii下的总容量;Im,tmz,Qmz分别表示蓄电池的标称电流、标称放电率和标称容量;上标a一般为常数。
2)直流推进电机模块
本文研究的潜艇动力系统中所有推进电机均为直流电机,其基本工作原理一致,只是电机的特征参数不同。忽略电枢回路的自感电势、电枢反应、互感等因素,恒定电流直接传动的单电枢直流推进电机运行时应满足方程(3)~方程(7)。
| $K\frac{{{\rm d}\omega }}{{{\rm d}t}} = {M_{\rm{e}}} - {M_p} - {M_f}{\text{,}}$ | (3) |
| ${T_e} = {C_{{m}}}\varPhi {I_{{a}}}{\text{,}}$ | (4) |
| $U = E + {I_{{a}}}{R_a} + {L_{{a}}}\frac{{{\rm d}{I_a}}}{{{\rm d}t}}{\text{,}}$ | (5) |
| $E = {C_{{e}}}\varPhi \omega {\text{,}}$ | (6) |
| $\varPhi {\rm{ = }}\varPhi \left( {{I_f}} \right){\text{,}}$ | (7) |
式中:K为电机轴系转动惯量;ω为轴系角速度;Me为电枢电磁扭矩;Mp为螺旋桨的阻力矩;Mf为推进系统总的扭矩损失;Cm为电机的扭矩常数;Ф为电机励磁磁通,由励磁电流If及电机的磁化特性曲线决定;U为电机电枢端电压;E为电机的感应电动势;Ce为电机电动势常数;Ia为电枢电流;La为电枢绕组的电感;Ra为电枢总内阻。
3)螺旋桨、艇体模块
潜艇推进系统模型中的艇体、推进电机和螺旋桨3个部分共同组成的船机桨系统,仅考虑推进装置的回转运动部分和潜艇直线运动2种运动,它们的数学模型除了式(3)以外,还包括方程(8)。
| ${k_w}m\frac{{{\rm d}{V_s}}}{{{\rm d}t}} = Z{P_e} - {R_T}{\text{,}}$ | (8) |
式中:m为潜艇的总质量;kw为附水系数,是为了考虑海水附着在潜艇表面,随着艇体一起运动,根据不同的航行工况,一般取kw=1.05~1.16;Vs为潜艇航速;Z为同时工作的螺旋桨数目;Pe为螺旋桨的有效推力;RT为艇体阻力。螺旋桨阻力矩Mp及螺旋桨的有效推力Pe的计算公式如式(9)和式(10)。
| ${M_p} = {K_M}\rho {{\rm{n}}^2}{D^5}{\text{,}}$ | (9) |
| ${P_e} = {K_p}\rho {{\rm{n}}^2}{D^4}(1 - t){\text{,}}$ | (10) |
| ${R_T} = r{V_s}^2{\text{,}}$ | (11) |
式中:KM,Kp分别为螺旋桨的扭矩系数和推力系数;ρ为海水密度;D为螺旋桨直径;t为螺旋桨的推力减额系数;n为螺旋桨转速;w是螺旋桨伴流系数,r为阻力系数,本文中取作常数。
| $J = \frac{{{V_s}(1 - w)}}{{nD}}{\text{,}}$ | (12) |

|
图 3 螺旋桨敞水特性曲线 Fig. 3 The open-water characteristic curve of screw propeller |
由式(11),KM和Kp是进速比J的函数,常可以用螺旋桨敞水特性曲线拟合,如图3所示。该曲线是螺旋桨特性和航行特性分析的重要参考[6]。
1.2 潜艇空间运动模型为了研究潜艇的操纵运动规律,确定潜艇的姿态和位置,并考虑到计算潜艇所受外力的方便性,本文采用文献[7]的坐标系和符号规则。潜艇空间运动模型使用的潜艇运动方程与DTNSRDC于1979年发表的“修正的潜艇标准运动方程”基本一致,具体如下[7–8]:
轴向方程
| $\begin{aligned}&{{m}}\left[\dot u - vr + wq - {x_G}\left({q^2} + {r^2}\right) + {y_G}(pq - \dot r) + {z_G}(pr + \dot q)\right] =\\ &\displaystyle\frac{1}{2}\rho {L^4}\left[{X_{pp}}{p^2} + {X_{qq}}{q^2} + {X_{rr}}{r^2} + {X_{pr}}pr\right] + \displaystyle\frac{1}{2}\rho {L^3}\left[{X_{\dot u}}\dot u \right. +\\ & {X_{wq}}wq+ {X_{vp}}vp + {X_{vr}}vr + uq({X_{q{\delta _s}}}{\delta _s} +\\ &\left. {X_{q{\delta _{b/2}}}}{\delta _{bp}} + {X_{q{\delta _{b/2}}}}{\delta _{bs}}) + {X_{r{\delta _r}}}ur{\delta _{br}}\right] + \displaystyle\frac{1}{2}\rho {L^2}\left[{X_{vv}}{v^2} \!+\! {X_{ww}}{w^2} \right.+\\ & {X_{{\rm{v}}{\delta _r}}}uv{\delta _r} + uw\left({X_{w{\delta _s}}}{\delta _{bs}} + {X_{w{\delta _{b/2}}}}ur{\delta _{bs}} + {X_{w{\delta _{b/2}}}}{\delta _{bp}}\right)+ \\ &\left. {u^2}\left({X_{{\delta _s}{\delta _s}}}{\delta _s}^2 + {X_{{\delta _b}{\delta _{b/2}}}}{\delta _{bp}}^2 + {{X'}_{{\delta _b}{\delta _{b/2}}}}{\delta _{bs}}^2 + {{X'}_{{\delta _r}{\delta _r}}}{\delta _r}^2\right)\right]-\\ & (W - B)\sin \theta + \displaystyle\frac{1}{2}\rho {L^3}{X_{q{\delta _{sn}}}}uq{\delta _s}\varepsilon (n) +\displaystyle\frac{1}{2}\rho {L^2}\left[{X_{w{\delta _{sn}}}}uw{\delta _{sn}}+ \right.\\ &\left. {X_{{\delta _s}{\delta _{sn}}}}{u^2}\delta _s^2\right]\varepsilon (n) + \displaystyle\frac{1}{2}\rho {L^2}{u^2}{X_{prop}}{\text{,}}\end{aligned}$ | (13) |
横向方程
| $\begin{aligned}&{{m}}\left[{{\dot v}} + ur - wp + {x_G}(pq + \dot r) - {y_G}\left({r^2} + {p^2}\right) + {z_G}\left(qr - \dot p\right)\right]=\\ & \displaystyle\frac{1}{2}\rho {L^4}\left[{Y_{\dot p}}\dot p + {Y_{\dot r}}\dot r + {Y_{p{\rm{q}}}}pq + {Y_{qr}}qr\right]+\\ & \displaystyle\frac{1}{2}\rho {L^3}\left[{Y_{\dot v}}\dot v + {Y_p}up + {Y_r}ur + {Y_{vq}}vq + {Y_{wp}}wp + {Y_{wr}}wr\right]+\\ & \displaystyle\frac{1}{2}\rho {L^2}\left[{Y_v}uv + {Y_{vw}}vw + {Y_{{\delta _r}}}{u^2}{\delta _r}\right]-\\ & \displaystyle\frac{1}{2}\rho \int_{{x_{tail}}}^{{x_{nose}}} {\left[{C_{dy}}h(x){{(v + xr)}^2} \!\!+\! {C_{dz}}b(x){{(w - xq)}^2}\right]} \frac{{(v + xr)}}{{U{}_{cf}(x)}}{\rm d}x+\\ & (W - B)\cos \theta \sin \phi {\text{,}}\end{aligned}$ | (14) |
垂向方程
| $\begin{aligned}&{{m}}\left[{{\dot w}} - uq + vp + {x_G}(rp - \dot q) + {y_G}(rq + \dot p) - {z_G}\left({p^2} + {q^2}\right)\right] = \\&\displaystyle\frac{1}{2}\rho {L^4}\left[{Z_{\dot q}}\dot q + {Z_{{\rm{pp}}}}{p^2} + {Z_{rp}}rp + {Z_{rr}}{r^2}\right] + \frac{1}{2}\rho {L^3}\left[{Z_{\dot w}}\dot w\right.+\\ & {Z_q}uq + {Z_{vp}}vp + {Z_{vr}}v{\rm{r]}} + \displaystyle\frac{1}{2}\rho {L^2}\left[{Z_w}uw + {Z_{vv}}{v^2}+\right. \\ &\left. {u^2}({Z_{{\delta _s}}}{\delta _s} + {Z_{{\delta _{b/2}}}}{\delta _s} + {Z_{{\delta _{b/2}}}}{\delta _{bp}})\right]- \\ & \displaystyle\frac{1}{2}\rho \int_{{x_{tail}}}^{{x_{nose}}} {\left[{C_{dy}}h(x){{(v \!+\! xr)}^2} \!+\! {C_{dz}}b(x){{(w - xq)}^2}\right]} \displaystyle\frac{{(w \!-\! xq)}}{{U{}_{cf}(x)}}{\rm d}x+\\ & (W - B)\cos \theta \cos \phi + \displaystyle\frac{1}{2}\rho {L^3}{{Z'}_{qn}}uq\varepsilon (n) +\\ & \displaystyle\frac{1}{2}\rho {L^2}\left[{Z_{wn}}uw + {Z_{{\delta _{sn}}}}{u^2}{\delta _s}\right]\varepsilon (n){\text{,}}\end{aligned}$ | (15) |
横倾方程
| $\begin{aligned}&{I_x}\dot p + ({I_z} - {I_y})qr + {I_{xy}}(pr - \dot q) - {I_{yz}}\left({q^2} - {r^2}\right) - {I_{xz}}(pq + \dot r)+\\ & m\left[{y_G}(\dot w - uq + vp) - {z_G}(\dot v + ur - wp)\right] = \\&\displaystyle\frac{1}{2}\rho {L^5}\left[{K_{\dot p}}\dot p + {K_{\dot r}}\dot r + {K_{pq}}pq + {K_{qr}}qr\right]+\\ & \displaystyle\frac{1}{2}\rho {L^4}\left[{K_{\dot v}}\dot v + {K_p}up + {K_r}ur + {K_{vq}}vq + {K_{wp}}wp + {K_{wr}}wr\right]+\\ & \displaystyle\frac{1}{2}\rho {L^3}\left[{K_v}uv + {K_{vw}}vw + {u^2}\left({K_{{\delta _{b/2}}}}{\delta _{bp}} + {K_{{\delta _{b/2}}}}{\delta _{bs}}\right)\right]+\\ & \left({y_G}W - {y_C}B\right)\cos \theta \cos \phi - ({z_G}W - z{}_CB)\cos \theta \sin \phi+ \\ & \displaystyle\frac{1}{2}\rho {L^4}{K_{pn}}up\varepsilon (n) + \displaystyle\frac{1}{2}\rho {L^3}{K_{prop}}{u^2}{\text{,}}\end{aligned}$ | (16) |
纵倾方程
| $\begin{aligned}&{I_{\rm{y}}}\dot q + \left({I_x} - {I_z}\right)rp - {I_{{\rm{xy}}}}\left(qr + \dot p\right) + {I_{yz}}(pq - \dot r) + {I_{{\rm{xz}}}}\left({p^2} - {r^2}\right)-\\ & m\left[{x_G}(\dot w - uq + vp) - {z_G}\left(\dot u - vr + wq\right)\right]=\\ & \displaystyle\frac{1}{2}\rho {L^5}\left[{M_{\dot q}}\dot q + {M_{pp}}{p^2} + {M_{pr}}pr + {M_{rr}}{r^2}\right]+\\ & \displaystyle\frac{1}{2}\rho {L^4}\left[{M_{\dot w}}\dot w + {M_{uq}}uq + {M_{vp}}vp + {M_{vr}}vr\right]+\\ & \displaystyle\frac{1}{2}\rho {L^3}\left[{M_{uw}}uw \!+\! {M_{vv}}{v^2} \!+\! {u^2}\left({M_{\delta s}}{\delta _s} \!+\! {M_{\delta b/2}}{\delta _{bp}} \!+\! {M_{\delta b/2}}{\delta _{bs}}\right)\right]-\\ & \displaystyle\frac{1}{2}\rho \int_{{x_{tail}}}^{{x_{nose}}} {\left[{C_{dy}}h(x){{(v \!+\! xr)}^2} \!+\! {C_{dz}}b(x){{(w - xq)}^2}\right]} \displaystyle\frac{{(w \!+\! xq)}}{{U{}_{cf}(x)}}{\rm d}x-\\ & ({x_G}W - {x_B}B)\cos \theta \cos \phi - ({z_G}W - z{}_BB)\sin \theta +\\ & \displaystyle\frac{1}{2}\rho {L^4}{M_{qn}}uq\varepsilon (n) + \displaystyle\frac{1}{2}\rho {L^3}\left[{M_{wn}}uw + {M_{\delta {\rm{sn}}}}{u^2}{\delta _s}\right]\varepsilon (n){\text{,}}\end{aligned}$ | (17) |
偏航方程
| $\begin{split}&{I_{\rm{z}}}\dot r + ({I_y} - {I_x})pq - {I_{x{\rm{y}}}}\left({p^2} - {q^2}\right) - {I_{yz}}(pr + \dot q) + {I_{xz}}(qr - \dot p)+\\ & m\left[{x_G}(\dot v + ur - wp) - {y_G}\left(\dot u - vr + wq\right)\right] = \\&\displaystyle\frac{1}{2}\rho {L^5}\left[{N_{\dot p}}\dot p + {N_{\dot r}}\dot r + {N_{pq}}pq + {N_{qr}}qr\right]+\\ & \displaystyle\frac{1}{2}\rho {L^4}\left[{N_{\dot v}}\dot v + {N_p}up + {N_r}ur + {N_{vq}}vq + {N_{wp}}wp + {N_{wr}}wr\right]+\\ & \displaystyle\frac{1}{2}\rho {L^3}\left[{N_v}uv + {N_{vw}}vw + {N_{{\delta _r}}}{u^2}{\delta _r}\right]-\\ & \displaystyle\frac{1}{2}\rho \int_{{x_{tail}}}^{{x_{nose}}} {\left[{C_{dy}}h(x){{(v + xr)}^2} + {C_{dz}}b(x){{(w \!-\! xq)}^2}\right]} \frac{{(v \!+\! xr)}}{{U{}_{cf}(x)}}{\rm d}x+\\ & ({x_G}W - {x_B}B)\cos \theta \sin \phi + ({y_G}W - y{}_BB)\sin \theta+\\ & \displaystyle\frac{1}{2}\rho {L^3}{u^2}{N_{prop}}{\text{,}}$ | (18) |
辅助方程
| $\begin{aligned}&\dot \phi = p + q\tan \theta \sin \phi + r\tan \theta \cos \phi{\text{,}} \\&\dot \theta = q\cos \phi - r\sin \phi {\text{,}}\\&\dot \psi = {{q\left[\sin \phi + r\cos \phi \right]} / {\cos \theta }}{\text{,}}\\&\dot X = {{{u}}_{c0}} + u\cos \psi \cos \theta + v\left[\cos \psi \sin \theta \sin \phi - \sin \psi \cos \phi \right]\\ &+ w\left[\cos \psi \sin \theta \cos \phi + \sin \psi \sin \phi \right]{\text{,}}\\&\dot Y = {v_{c0}} + u\sin \psi \cos \theta + v\left[\sin \psi \sin \theta \sin \phi + \cos \psi \cos \phi \right]\\ &+ w\left[\sin \psi \sin \theta \cos \phi - \cos \psi \sin \phi \right]{\text{,}}\\&\dot Z = {w_{c0}} - u\sin \theta + v\cos \theta \sin \phi + w\cos \theta \sin \phi{\text{,}} \\&{U_{cf}}(x) = {\left[{(v + xr)^2} + {(w - xq)^2}\right]^{1/2}}{\text{,}}\\&{X_{prop}} = {C_{d0}}(\eta \left| \eta \right| - 1);\eta = 0.012{{n}}/u{\text{,}}\\&{C_{d0}} = 0.0385 + \left(1.296{e^{ - 17}}\right){\left[(uL/v - 1.2{e^7})\right]^2}{\text{,}}\\&\varepsilon (n) = - 1 \!+\! sign(N)/sign(u)*\left(\sqrt {{C_t} \!+\! 1} - 1\right)/\left(\sqrt {{C_{t11}} \!+\! 1} - 1\right){\text{,}}\\&{C_t} = 0.008{L^2}\eta \left| \eta \right|/2.0{\text{,}}\\&{C_{t1}} = 0.008{L^2}/2.0{\text{。}}\end{aligned}$ | (19) |
由于缺少具体潜艇的螺旋桨特性曲线,本文对螺旋桨的推力采用文献[8]的经验公式来替代,该公式本质上和螺旋桨的有效推力公式(10)相同。
除此之外,潜艇的运动模型还要考虑控制执行机构的响应问题,建立潜浮系统、均衡系统、方向舵、升降舵等的响应模型。对潜艇而言,舵机电液伺服系统是一个具有延迟、死区、滞环等非线性特性的液压系统,通常采用以下模型:
| $ {T_E}\dot \delta = {K_E}({\delta _E} - \delta ){\text{,}}$ | (20) |
其中,δE为期望舵角;TE为舵机时间常数,一般TE=2.5 s;KE为舵机的控制增益,KE=1。
1.3 潜艇机动-推进系统综合模型分别建立了潜艇推进系统模型和空间运动模型之后,本文把潜艇和推进系统看成整体研究对象,将潜艇空间运动模型和推进系统模型作为综合模型的模块有机结合起来形成综合模型。潜艇机动和推进系统之间相互耦合,推进系统螺旋桨的旋转产生推力推动潜艇运动,推力的改变会引起潜艇运动状态的变化;同时,潜艇运动状态的变化也会改变螺旋桨的负载。潜艇运动状态对推进系统的影响主要体现在艇体阻力和航速的改变会引起螺旋桨负载的变化上。潜艇进行转向和潜浮时,舵装置偏转一定角度,使潜艇在斜水流中前进,形成一定的攻角或漂角,潜艇航行的阻力增大,推进系统的负载变大,从而影响推进系统的运行状态,如果不增加推力,潜艇的航速会降低。
|
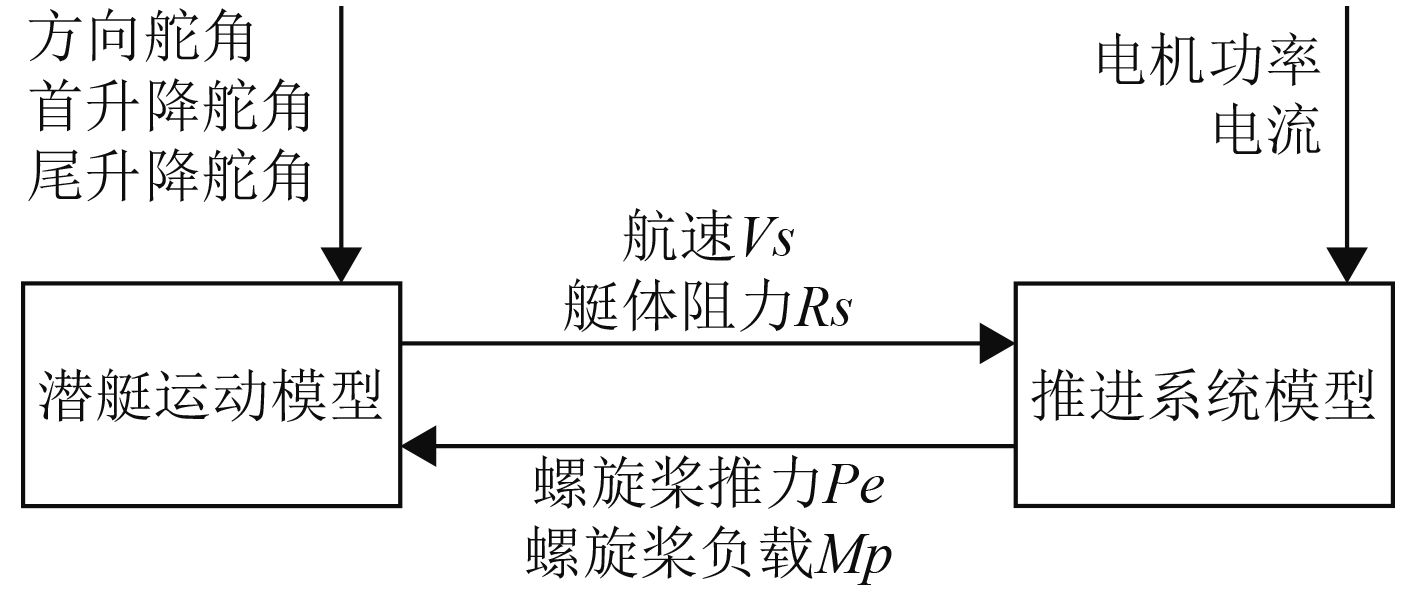
图 4 潜艇机动-推进系统综合模型 Fig. 4 The integrated motion/propulsion system model of submarine |
图4给出了推进系统和潜艇机动之间的相互关系。由图可知,这里的结合并非把空间运动模型和推进系统模型简单的相连,而是要考虑两者的匹配问题,需要根据潜艇的航行条件和运动状态进行推力解算,得到推进电机相应的状态参数,以使综合模型可在航行轨迹的任意一点开始仿真。这里的潜艇机动-推进综合模型是一个开环模型,潜艇的舵角和推进电机的控制量作为输入。
2 仿真试验与分析对1艘在广阔无限大静水水域,处于水下航行工况的潜艇进行仿真,并作如下假设:1)潜艇在稳定航行过程中蓄电池在短时间内保持电枢电流不变;2)忽略电机功率在传输过程中的损耗;3)不考虑电机电枢反应的去磁作用,磁通Φ和电枢电流Ia没有关系;4)螺旋桨转速和电机的输出转速相同。
仿真计算时,将潜艇的航行过程分为有序的时间间隔,并逐步递推得出其在各时间间隔点上的状态参数。具体的仿真计算流程如图5所示。

|
图 5 潜艇机动与推进综合仿真流程图 Fig. 5 The flow chart of integrated motion/propulsion system modeling and simulation for submarine |
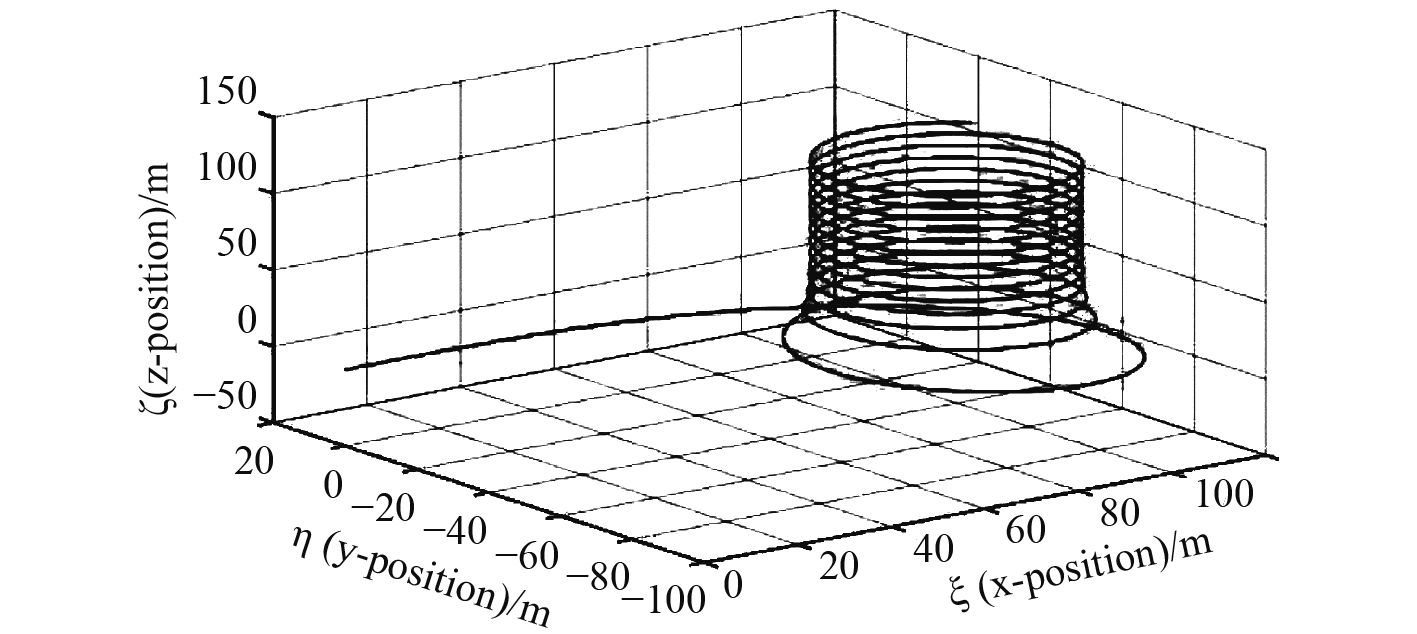
本文利用Matlab软件对某潜艇进行水下回转运动仿真。初始条件:期望方向舵舵角12°,初始航速12 m/s,推进电机转速1 042.70 rpm。本文研究的是潜艇进行回转运动时,潜艇的航行轨迹、推进系统的输出转速n,水下回转的航行速度Vs、方向舵舵角δr和螺旋桨负载Mp的变化规律。仿真得出的结果分别如图6~图9所示。
|
图 6 潜艇运动轨迹 Fig. 6 The motion track of submarine |
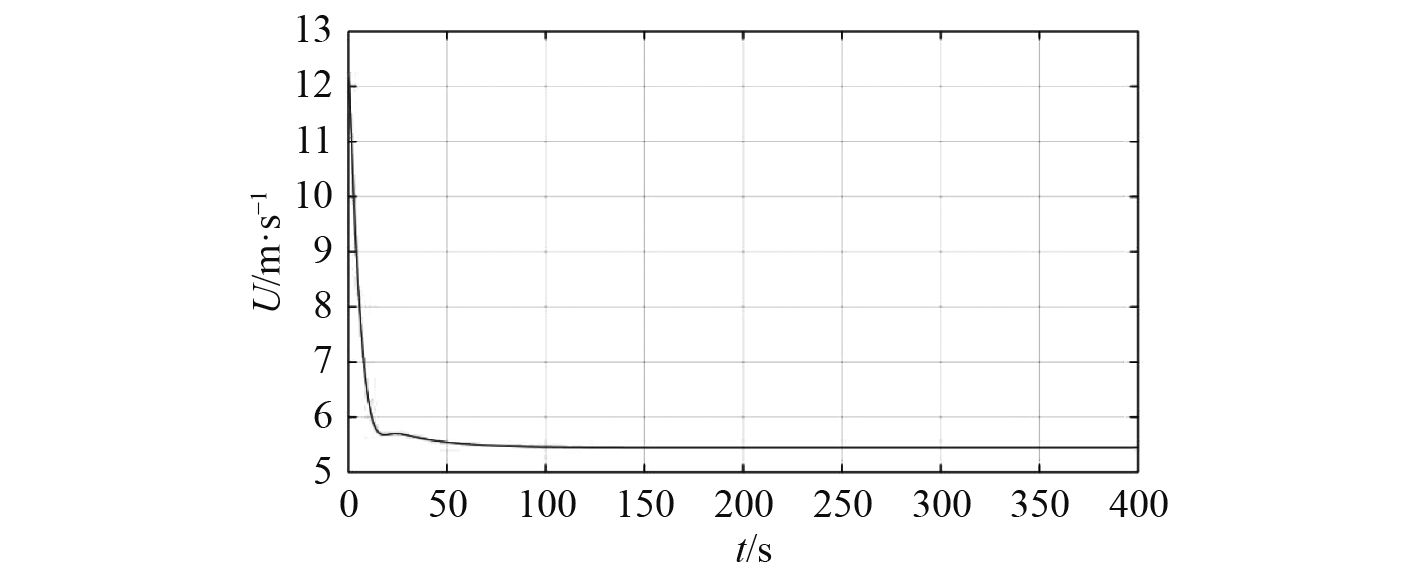
|
图 7 潜艇水下回转运动航速 Fig. 7 The underwater rotary speed of submarine |

|
图 8 螺旋桨转速 Fig. 8 Rotational velocity of propeller |

|
图 9 方向舵角度 Fig. 9 The angle of rudder |
分析图像结果可知:
1)只对方向舵进行操纵后,潜艇由水下直线运动逐渐进入空间定常螺旋运动,潜艇的航速随着仿真次数的增加而逐渐降低,最后达到一个新的较低的定常航速。
2)推进系统和螺旋桨直接相连,则螺旋桨转速和推进系统转速相同,由于潜艇水下回转航速降低,导致螺旋桨负载增大,转速逐渐降低后趋于一个稳定值。
3)由于舵机电液伺服系统是一个具有延迟、死区、滞环等非线性特性,下达操舵命令后,达到期望舵角需要一段时间。
仿真结果经与分析实艇运动的结论比较,能较好地吻合,从而说明本文所用潜艇数学模型和建模仿真方法正确有效。潜艇直线航行时操方向舵,随着舵的偏转,根据潜艇的空间六自由度运动方程式(13)~式(19)可知舵力及力矩不断增大,潜艇在推力及舵力(矩)的作用下边前进边旋转并有着反向横移;在回转过程中,由于偏舵的效果使航速Vs下降,由式(12)以及螺旋桨的敞水曲线图像可知,螺旋桨的进速比J降低,使得螺旋桨扭矩系数KM变大,螺旋桨负载增加,又由式(9)可知,在恒电枢电流的情况下,推进电机的电磁转矩Me不变,因此,由式(3)可知螺旋桨的转速n降低。
根据不同航行工况,可以为实现潜艇最优化航行工作制提供科学、合理的理论依据。由于选取的工况较少,且缺少实艇测试,所以有必要对不同工况下模型的准确性进行进一步的验证。
3 结 语本文参考飞机飞/推综合系统的建模方法,建立了一个潜艇推进系统与空间运动相互耦合的一体化数学模型,并对潜艇在水下回转运动工况进行了仿真试验。仿真结果与实艇操纵规律基本一致,说明本文所建立的潜艇机动与推进综合数学模型及其建模与仿真方法正确有效。此外本文研究表明,潜艇在水下空间运动时推进系统和空间运动通过转速相互影响、相互耦合,但模型的准确性还需进一步验证。
| [1] |
冯俊梅, 连琏, 葛彤. 潜艇操纵控制方法的现状与发展[J]. 海洋工程, 2005, 23(1): 114-122. DOI:10.3969/j.issn.1005-9865.2005.01.019 |
| [2] |
林雄伟, 胡大斌, 戴余良, 等. 潜艇操纵控制方法[J]. 舰船科学技术, 2013, 35(5): 7-10. DOI:10.3404/j.issn.1672-7649.2013.05.002 |
| [3] |
王日先. 飞/推综合系统建模与控制研究[D]. 南京: 南京航空航天大学, 2011.
|
| [4] |
胡锦晖, 胡大斌, 徐国印. 常规潜艇电力推进系统仿真研究[J]. 计算机仿真, 2008, 25(8): 6-8. DOI:10.3969/j.issn.1006-9348.2008.08.002 |
| [5] |
许建. 潜艇蓄电池放电过程的仿真研究[J]. 电源技术, 1998(2): 75-78. |
| [6] |
李俊科. 电力推进船舶螺旋桨模拟负载的研制[D]. 厦门: 集美大学, 2013.
|
| [7] |
HEALEY A J, LIENARD D. Multivariable sliding mode control for autonomous diving and steering of unmanned underwater vehicles[J]. Oceanic Engineering IEEE Journal of, 1993, 18(3): 327-339. DOI:10.1109/JOE.1993.236372 |
| [8] |
戴余良. 潜艇应急上浮操纵运动分析与控制技术研究[D]. 武汉: 武汉理工大学, 2007.
|
 2018, Vol. 40
2018, Vol. 40
