快速开启机构是一种利用较小力快速开启高压容器的装置,通常安装在高压容器的进出口上,例如高压气瓶、高压机构阀门等设备上[1],是舰船消防系统中的重要部件[2 – 3]。它根据远程遥控信号,采用气动、液压或爆炸冲击等方式,通过较小的力在极短的时间内开启气瓶或者机构门。开启力放大因子是衡量快速开启机构性能的一个重要指标,与结构尺寸、摩擦等因素有关。开启力放大因子越大,则说明开启机构所需要开启设备的力越小,性能越好。
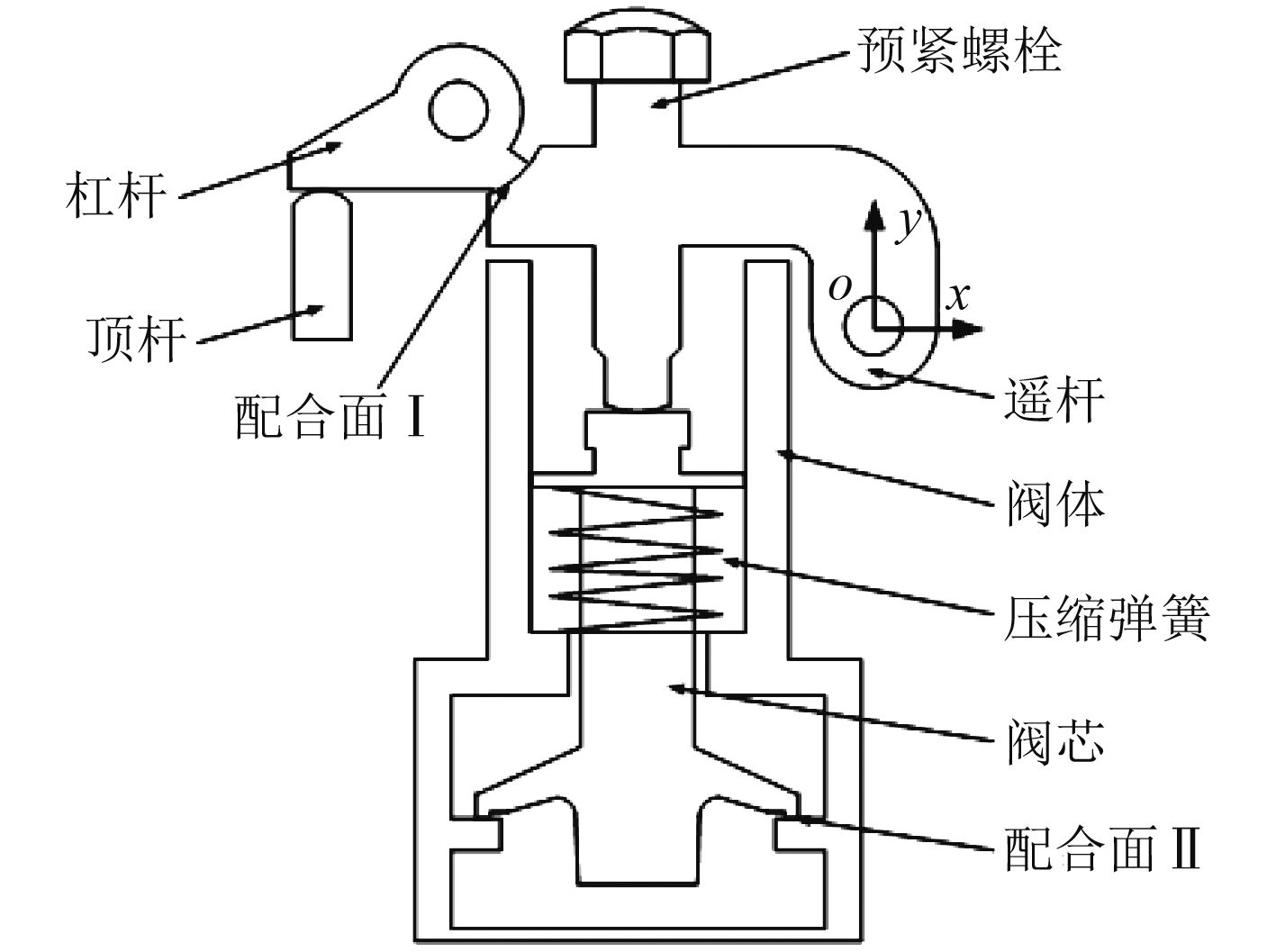
1 开启机构的组成结构快速开启机构主要由顶杆、杠杆、预紧螺栓及摇杆、压缩弹簧、阀芯等零部件组成,其结构如图1所示。预紧螺栓自身与摇杆的螺纹配合,通过摇杆对阀芯施加预紧力,使阀芯闭合;顶杆在外力(例如气动力、液压或者爆炸力等)作用下,推动杠杆旋转,当杠杆旋转一定角度时,杠杆与摇杆脱离接触,摇杆被弹簧等的作用力迅速推动,机构阀芯迅速被释放,打开阀门,使得流体能够通过阀门[1]。
|
图 1 快速开启机构结构图 Fig. 1 The structural drawing of quick opening institution |
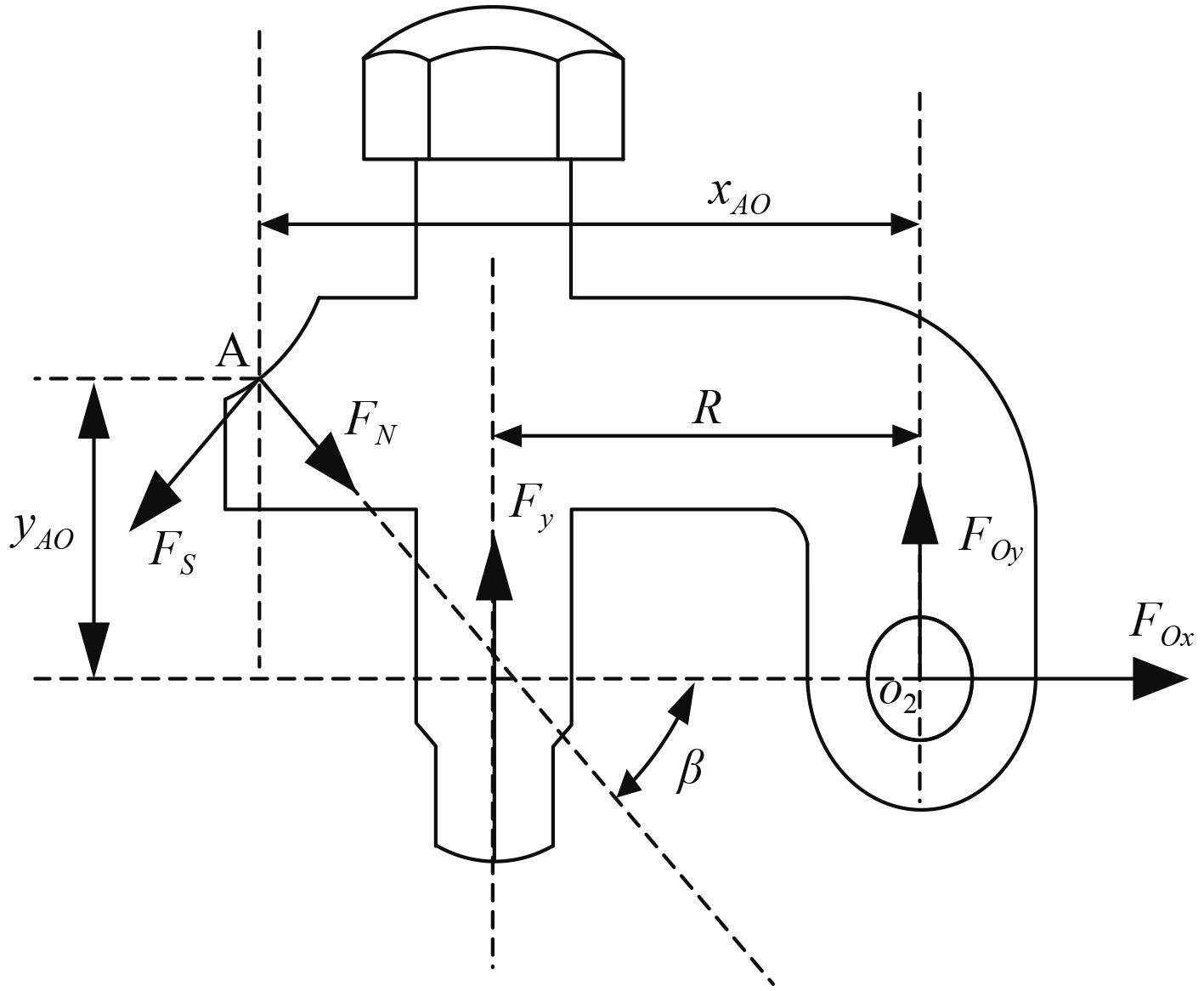
由于开启机构中的顶杆、杠杆和摇杆的结构及质量很小,因此忽略其重力和惯性力的影响;假设快速开启机构各部件为刚体,接触面上的摩擦为库伦摩擦。图2为摇杆的受力分析图[4],根据平衡原理可以得到摇杆在配合面I上所受到的正压力
| $\left\{ \begin{split}{l}{F_N} = \displaystyle\frac{{{F_Y}R}}{{\left( {\sin \beta + {\mu _0}\cos \beta } \right){x_{AO}} - \left( {\cos \beta - {\mu _0}\sin \beta } \right){y_{AO}}}} \text{,} \\{F_S} = \displaystyle\frac{{{F_Y}R{\mu _0}}}{{\left( {\sin \beta + {\mu _0}\cos \beta } \right){x_{AO}} - \left( {\cos \beta - {\mu _0}\sin \beta } \right){y_{AO}}}} \text{。} \end{split} \right.$ | (1) |
式中:
|
图 2 摇杆受力图 Fig. 2 The force diagram of rocker |
|
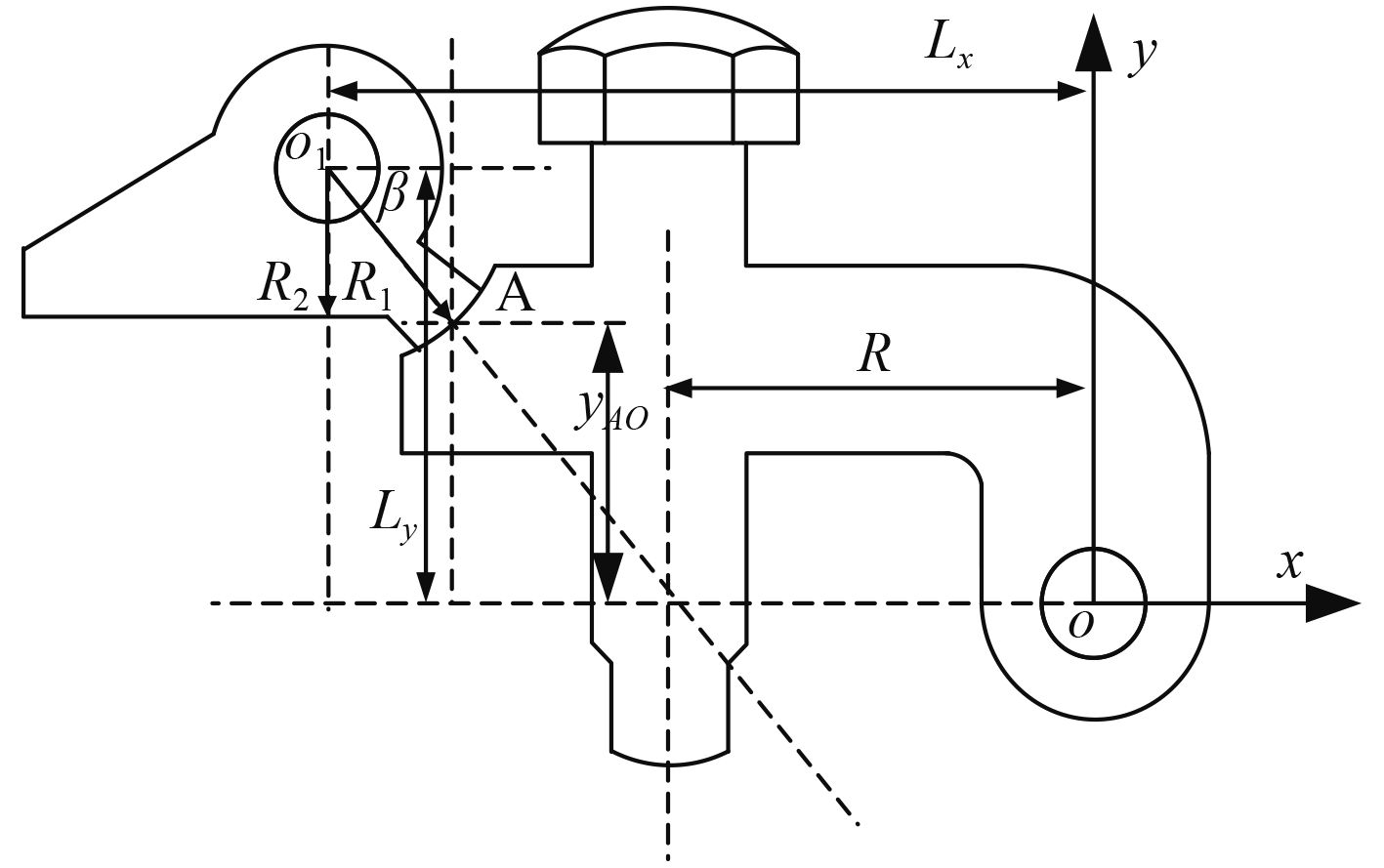
图 3 摇杆与杠杆的位置尺图 Fig. 3 The location diagram between rocker and lever |
|
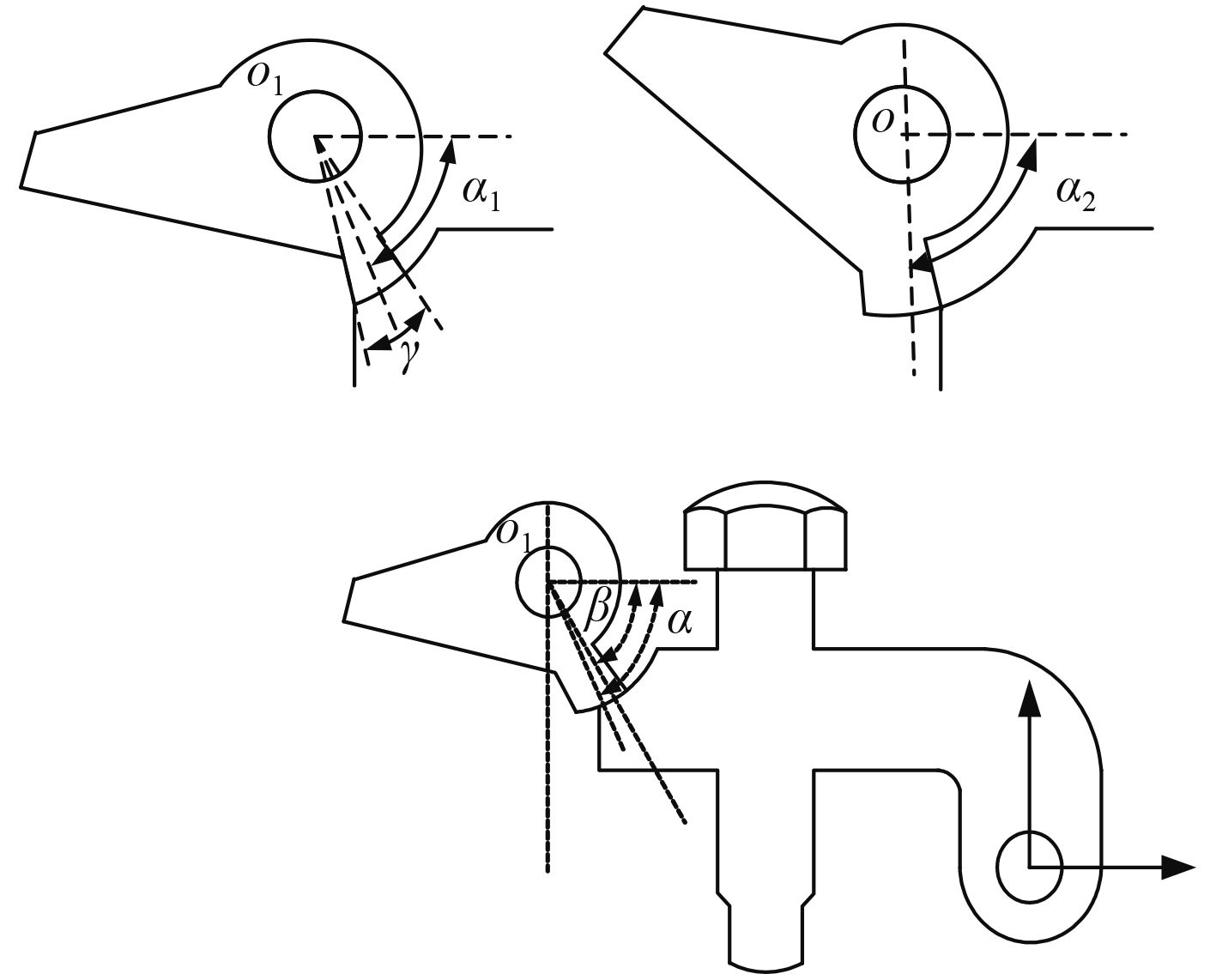
图 4 开启过程中杠杆的三种状态 Fig. 4 Three status of lever when opened |
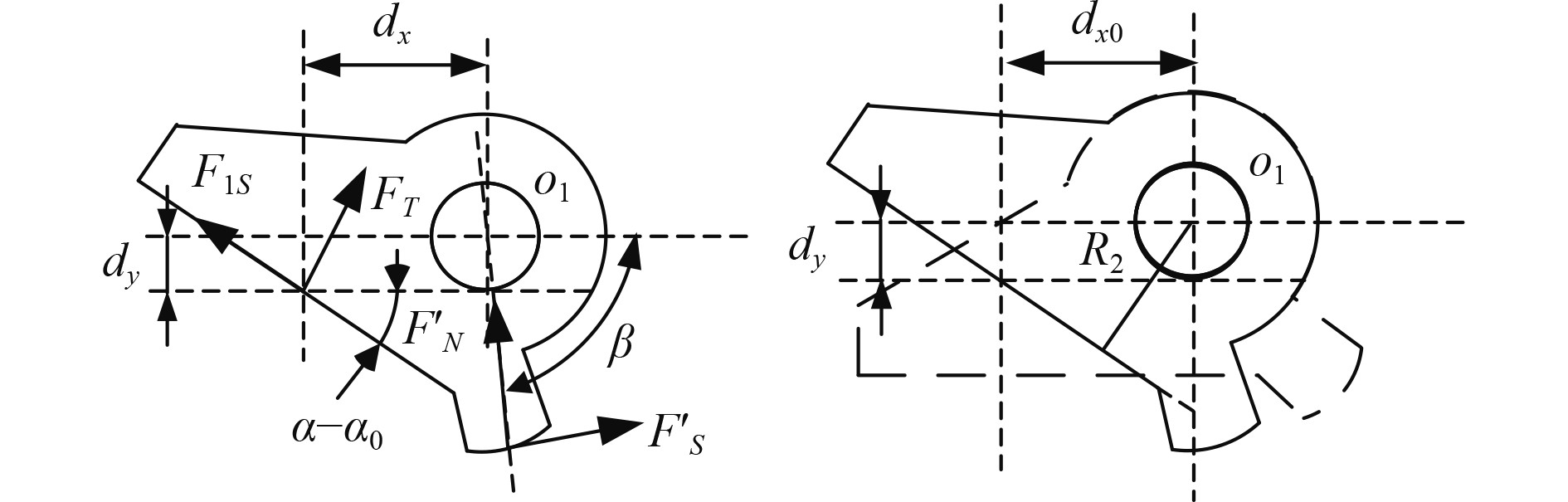
对杠杆进行受力分析,如图5所示,根据平衡方程可以得到顶杆对杠杆的作用力
| $\begin{split}&{F_T} = {{{F'_s}{R_1}} / {\left[ {\cos \left( {\alpha - {\alpha _0}} \right){ d_x} - \sin \left( {\alpha - {\alpha _0}} \right){ d_y}} \right.}} + \\&\left. {{\mu _1}\sin \left( {\alpha - {\alpha _0}} \right){ d_x} + {\mu _1}\cos \left( {\alpha - {\alpha _0}} \right){ d_y}} \right] \text{,}\end{split}$ | (2) |
| ${d_y} = \frac{{{R_2} - {d_{x0}}\sin \left( {\alpha - {\alpha _0}} \right)}}{{\cos \left( {\alpha - {\alpha _0}} \right)}} \text{。} $ | (3) |
式中:
|
图 5 杠杆受力图 Fig. 5 The force diagram of lever |
对顶杆进行受力分析,如图6所示[5 – 6],列出顶杆的平衡方程,可以得到顶杆所受力
| $\begin{split}&{F_P} = {{F'}_T}\left[ {\cos \left( {\alpha - {\alpha _0}} \right) + {\mu _2}\sin \left( {\alpha - {\alpha _0}} \right)} \right] + \\&{{F'}_{1S}}\left[ {\sin \left( {\alpha - {\alpha _0}} \right) - {\mu _2}\cos \left( {\alpha - {\alpha _0}} \right)} \right]\text{,} \end{split} $ | (4) |
式中:

|
图 6 顶杆受力图 Fig. 6 The force diagram of kicker pin |
定义放大因子为
| $\kappa = \frac{{ A}}{{ B}}\text{,} $ | (5) |
式中:
| $\begin{split}&{A \!=\! [\cos \left( {\alpha \!-\! {\alpha _0}} \right){d_x} \!-\! \sin \left( {\alpha \!-\! {\alpha _0}} \right){d_y} \!+\! {\mu _1}\sin \left( {\alpha \!-\! {\alpha _0}} \right){d_x} \!+\! }\\&{\mu _1}\cos \left( {\alpha - {\alpha _0}} \right){d_y}] \times \left[ {\left( {\sin \beta + {\mu _0}\cos \beta } \right){x_{AO}} - } \right.\\&\left. {\left( {\cos \beta - {\mu _0}\sin \beta } \right){y_{AO}}} \right]{\text{,} }\end{split}$ |
| $B = R{R_1}{\mu _0}\left[ \begin{array}{l}\cos \left( {\alpha - {\alpha _0}} \right) + {\mu _2}\sin \left( {\alpha - {\alpha _0}} \right) + \\{\mu _1}\sin \left( {\alpha - {\alpha _0}} \right) - {\mu _1}{\mu _2}\cos \left( {\alpha - {\alpha _0}} \right)\end{array} \right]{\text{。}}$ |
某快速开启机构尺寸参数为R=66 mm,R1=26 mm,R2=22 mm,Lx=116 mm,Ly=60 mm,dxo=38 mm,γ=25°,αo=52.5°,α1=59.5°,α2=84.5°。
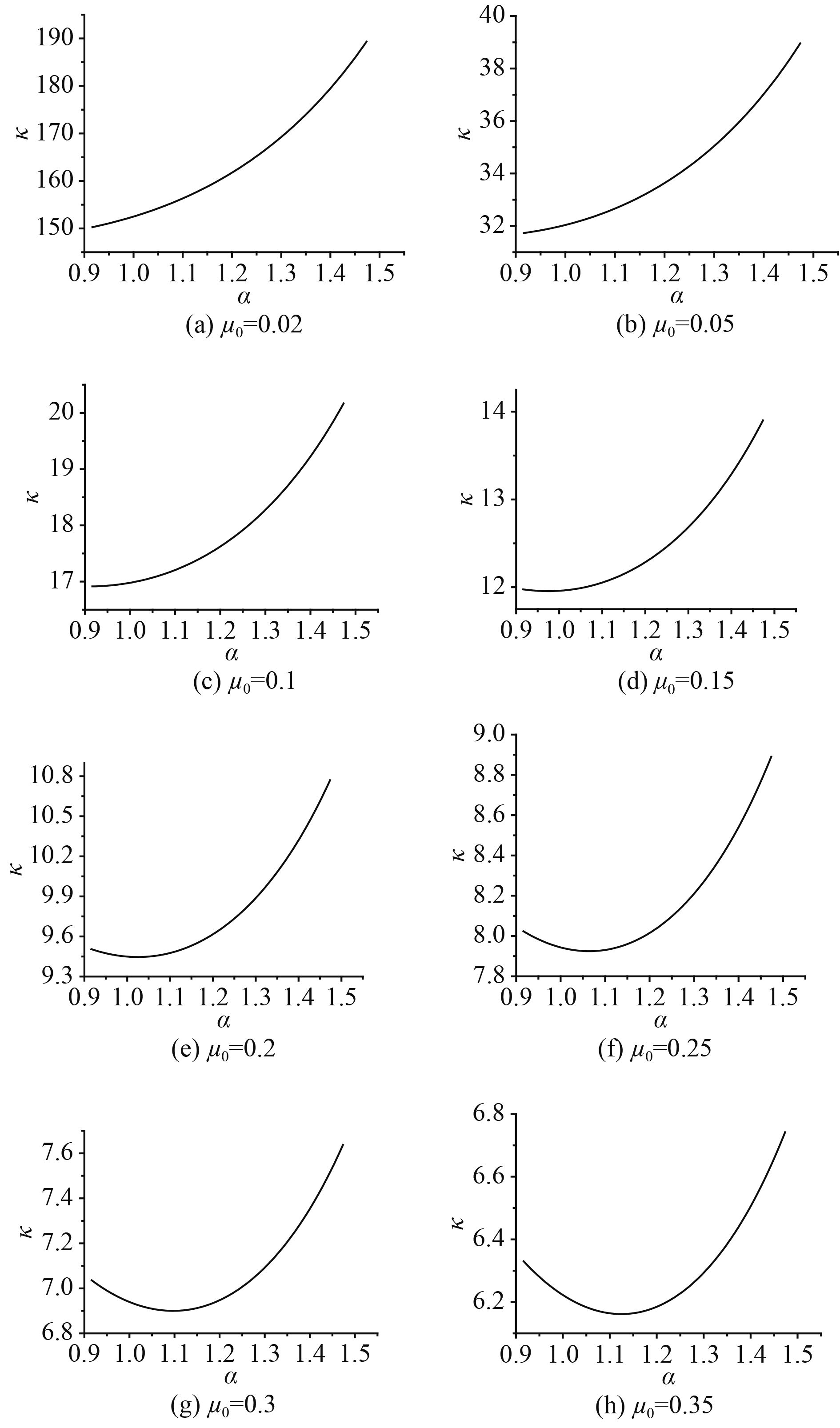
图7分别为取μ1=0.1,μ0=0.02,0.05,0.1,0.15,0.2,0.25,0.3,0.35时,放大因子
|
图 7
μ0取不同值时放大因子
|
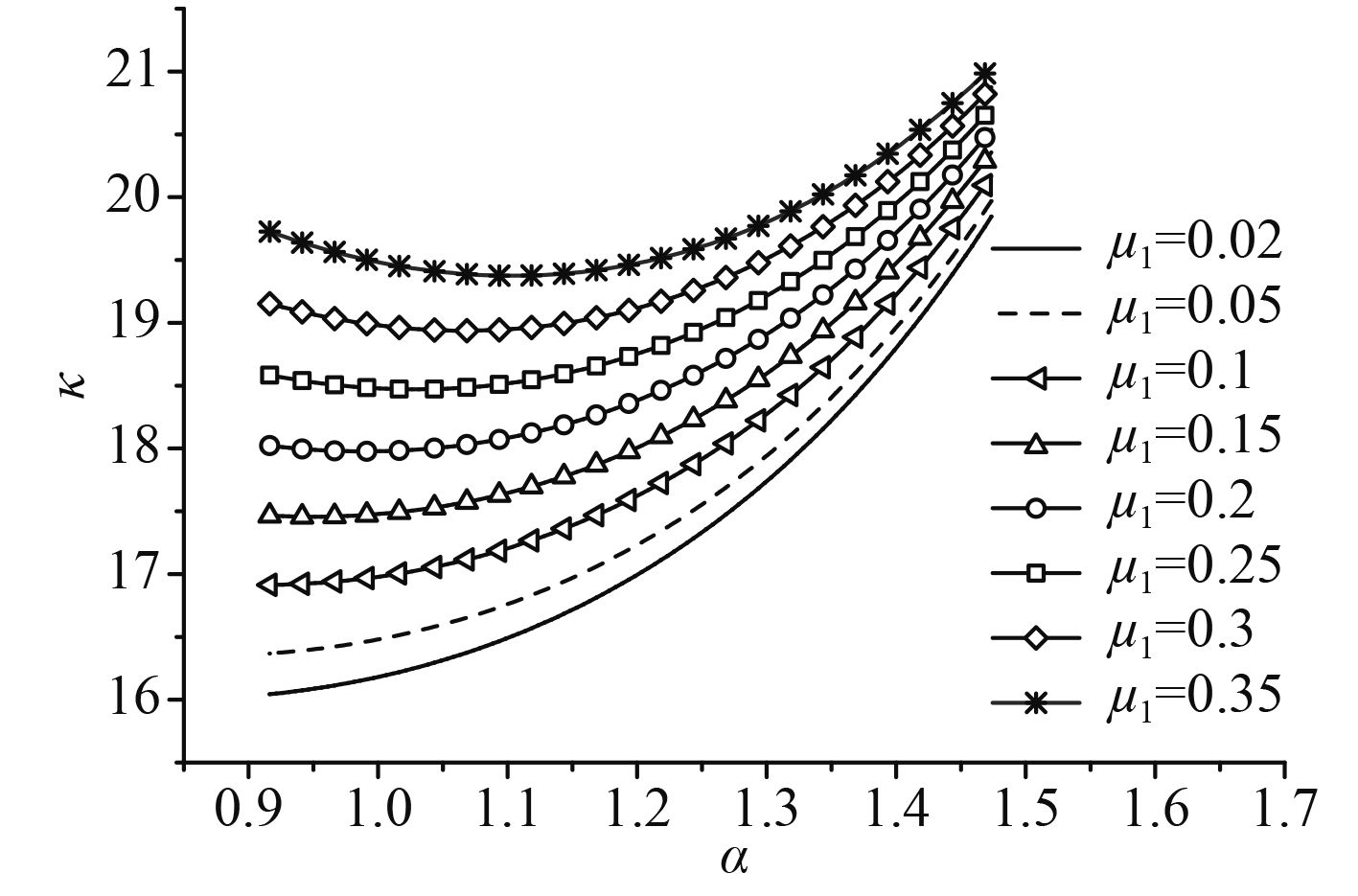
图8为取μ0=0.1,μ1=0.02,0.05,0.1,0.15,0.2,0.25,0.3,0.35时,放大因子
|
图 8
|
|
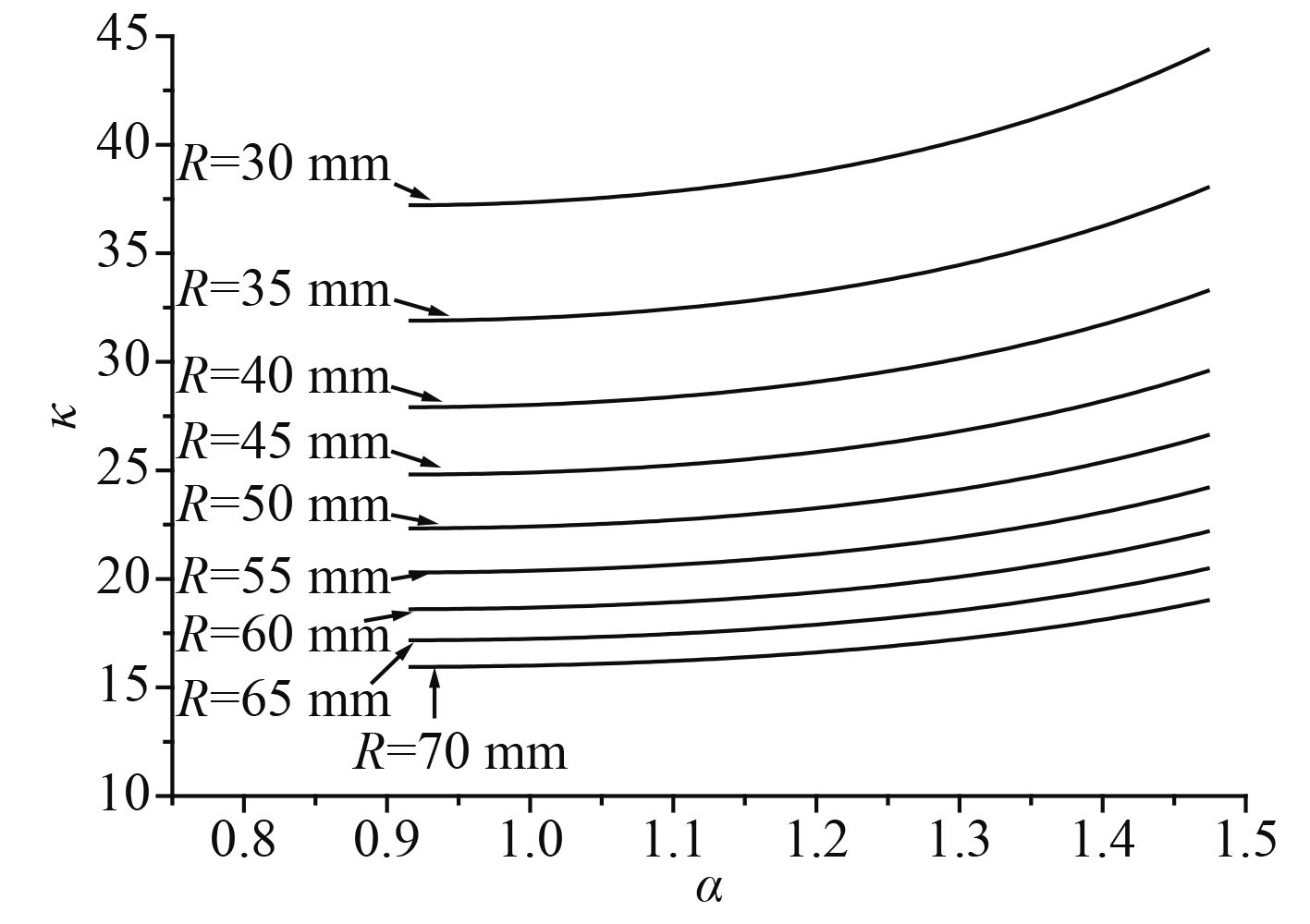
图 9
R对放大因子
|
图9为μ0=0.1,μ1=0.1,R=30,35,40,45,50,55,60,65,70 mm时,放大因子
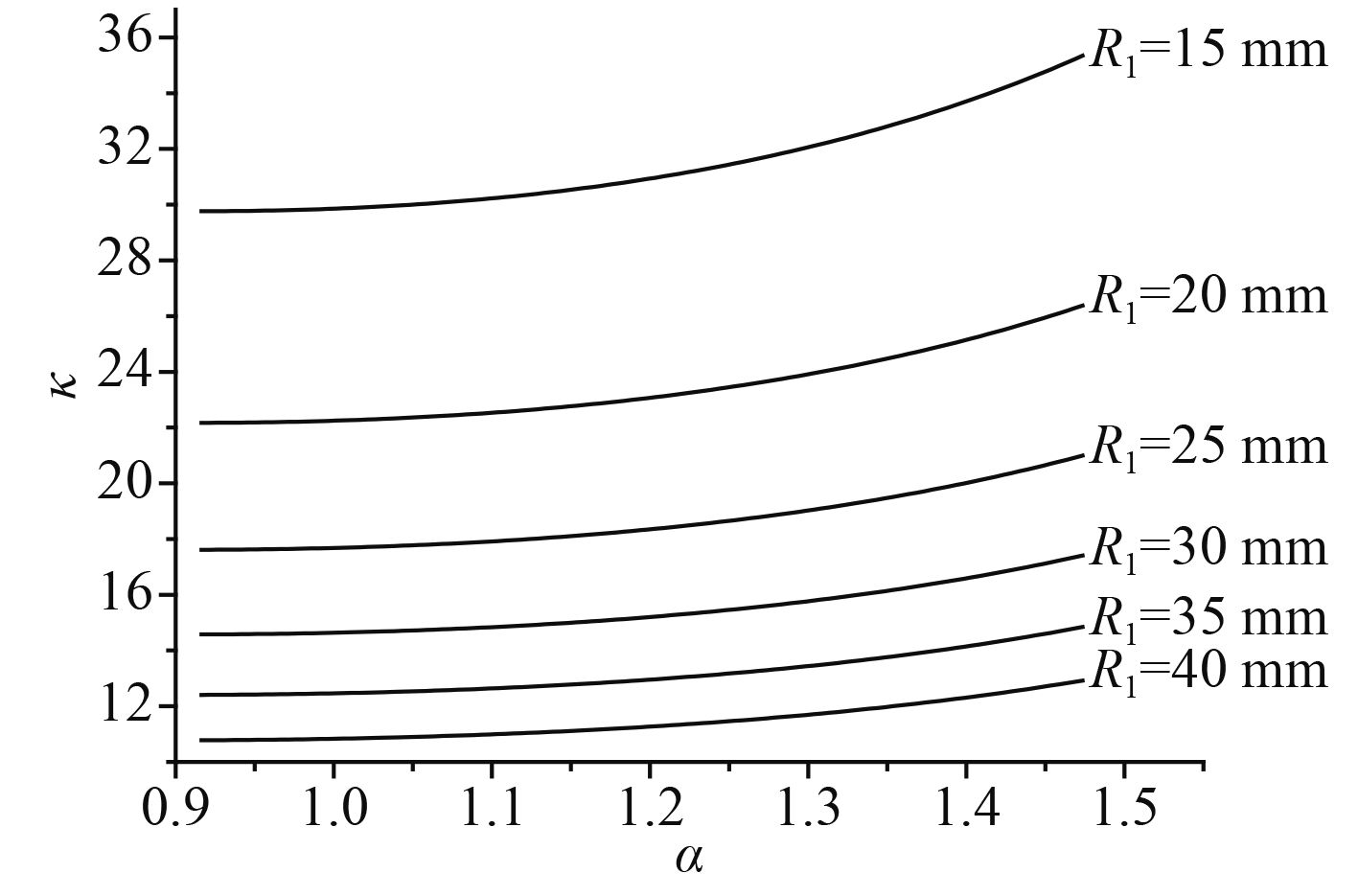
图10为μ0=0.1,μ1=0.1,R1=15,20,25,30,35,40 mm时,放大因子
图11为μ0=0.1,μ1=0.1,dx0=20,25,30,35,40,45,50,55 mm时,放大因子
|
图 10
|

|
图 11
|
本文针对某快速开启机构进行力学分析,得到了放大因子
| [1] |
杨源泉. 阀门设计手册[M]. 北京: 机械工业出版社, 1992.
|
| [2] |
杨永强, 田华安, 孙建华. 船用电动调节阀运行中的常见故障分析[J]. 舰载科学技术, 2011, 33(1): 82-84. YANG Yong-qiang, TIAN Hua-an, SUN Jian-hua. Analysis of common failure in the operation of marine electric regulating valve[J]. Ship Science and Technology, 2011, 33(1): 82-84. |
| [3] |
陆永红, 钟生新. 设计舰载导弹弹库时应考虑的安全问题[J]. 舰船科学技术, 2004, 26(2): 34-36. LU Yong-hong, ZHONG Sheng-xing. Safety questions to be considered while designing ship borne missiles depot[J]. Ship Science and Technology, 2004, 26(2): 34-36. |
| [4] |
沈光平. 理论力学[M]. 昆明: 云南大学出版社, 1991.
|
| [5] |
刘金春. 结构力学[M]. 武汉: 华中科技大学出版社, 2008.
|
| [6] |
张征明, 吴莘馨, 何树延. 核安全级阀门的结构力学分析[J]. 阀门, 2004(4): 1-4. ZHANG Zheng-ming, WU Xin-xin, HE Shu-yan. Structural mechanical analysis of the nuclear safety-related valve[J]. Valve, 2004(4): 1-4. |
| [7] |
李天伟, 樊明波, 王沛, 等. 液压系统电磁换向阀动力学特性仿真[J]. 舰船科学技术, 2012, 34(6): 50-52. LI Tian-wei, FAN Ming-bo, WANG Pei, et al. Simulation research of dynamics for solenoid value in hydraulic system[J]. Ship Science and Technology, 2012, 34(6): 50-52. DOI:10.3404/j.issn.1672-7649.2012.06.011 |
 2018, Vol. 40
2018, Vol. 40
