悬臂结构形式广泛应用于舰船附体结构设计之中,如舵、潜艇稳定翼等。目前此类结构主要以钢质内部横纵骨架外敷钢质薄壳板为典型结构形式[1–2],以确保满足翼体结构的刚度和强度要求,但此类常规交叉骨架结构并非舵翼承载状态下的最佳方案,因此,质量过大,冗余较多。为了进一步减轻结构质量,工程师们也会进行一些常规的结构优化,如:调整肋骨板材厚度、加减轻孔、调整骨架位置或数量等,这些优化方式往往要基于大量的静力学计算和分析以及一定的工程经验,优化周期长,效率低。随着增材制造技术的逐渐成熟,目前大尺度复杂构型的铸造技术已能够为更高效的结构拓扑优化技术提供工程实现基础,因此,通过结构优化寻找一种更合理的骨架结构是可以实现的。
结构拓扑优化一直被认为是具有潜在经济效益的研究领域之一。自1904年由Michell提出桁架理论以来,人们不断的在拓扑优化领域进行研究进步,针对连续体的拓扑优化研究,最具代表性的便是Bendsoe和Kikuchi[3]提出的均匀化方法、Mlejnek[4]的变密度法及Xie[5 – 8]的渐进结构拓扑优化法等,而且这些方法也被大量的应用于各类有限元优化软件中。
增材制造技术(additive manufacturing,AM),是一种以三维数字模型文件为基础直接制造几乎任意形状三维实体的制造技术[9]。FDM技术是增材技术的一个分支,它一般使用于桌面级打印机,以PLA和ABS塑料为主要原材料,它可为拓扑优化结构的实现和验证,提供可行的技术途径。
本文拟应用拓扑优化技术开展悬臂结构骨架优化设计,然后利用FDM技术制作模型,并通过对比模型试验,最终验证了拓扑优化结构与传统典型结构的设计优劣特性。
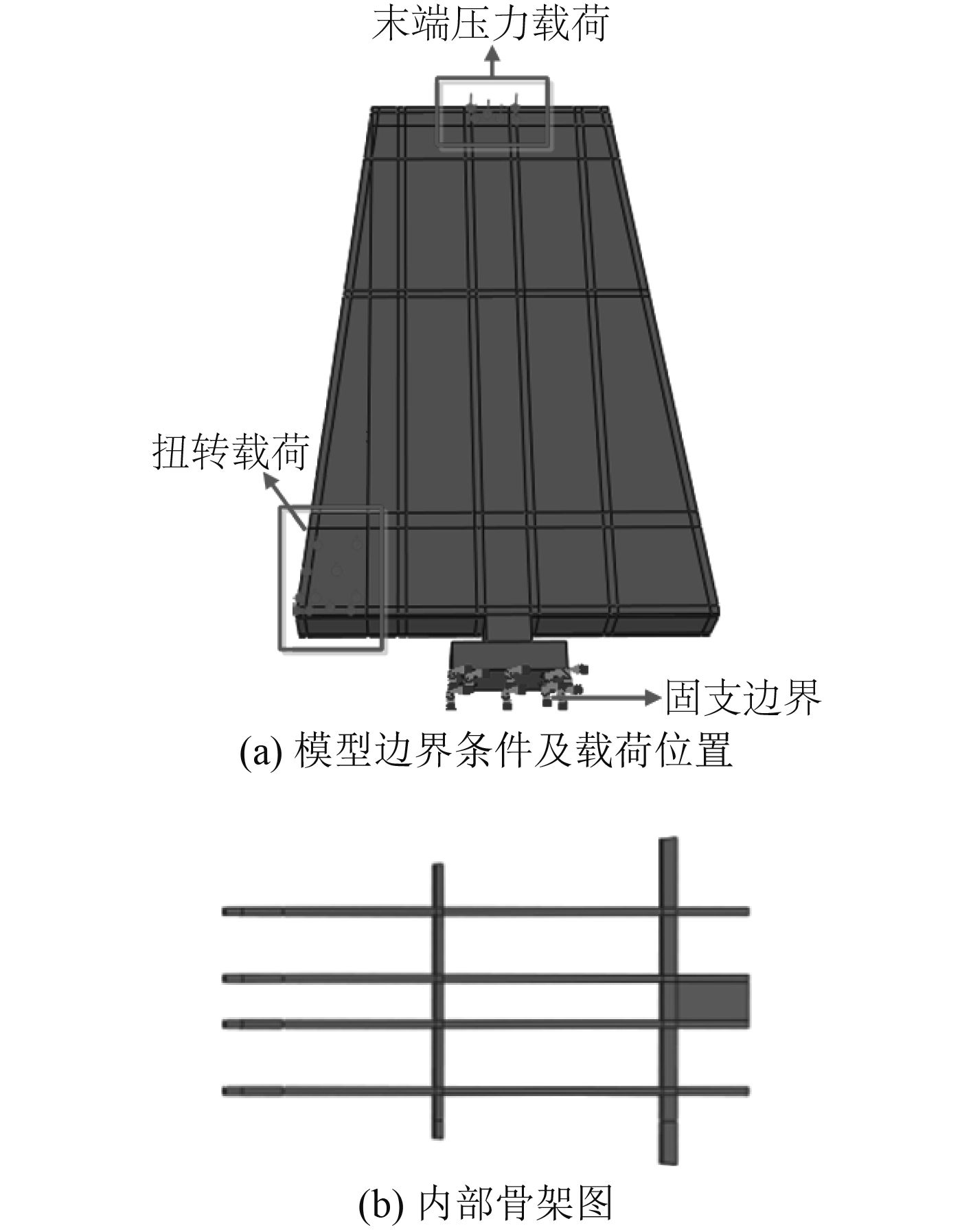
1 典型模型计算分析 1.1 典型变截面悬臂含筋结构模型根据实际模型进行简化缩比,建立典型含横纵筋板模型(统称典型模型),如图1所示。变截面悬臂含筋结构模型外形尺寸长225 mm,厚度25 mm,最大截面宽度150 mm,最小截面宽度100 mm。图1(b)为内部横纵筋板。边界固支,分别施加2种载荷工况:1)末端压力载荷;2)扭转载荷。
|
图 1 典型模型 Fig. 1 Typical model |
材料采用PLA塑料,杨氏模量为1.9 GPa[10],泊松比为0.42,密度为1 250 kg/m3。
利用有限元软件,对典型模型进行静力学计算分析,确定出2种工况可施加55 N,80 N,105 N三种级别的载荷。且具体的施加位置及形式如图1(a)所示。
1.2 位移及应力分布特征仿真分析最大应力总是出现在舵轴区,扭转作用下的变形以结构最大端面的转角为标准。给出仿真计算的相应数据,分别如表1和表2所示,并给出同时施加2种载荷的应力分布图(见图2),以便与优化后的结构进行整体的对比分析。

|
图 2 两种载荷同时作用下的应力分布 Fig. 2 Stress distribution at the same time of two loads |
|
|
表 1 各工况下最大应力值 Tab.1 Maximum stress under each working condition |
|
|
表 2 各工况下最大变形 Tab.2 Maximum deformation under each working condition |
从图2中的应力分布可以看出,高应力区主要集中在舵轴区,只要保证舵轴区安全,整个悬臂结构仍可以进行优化减重,使应力的分布更加合理。
2 基于渐进结构拓扑法进行优化设计及FDM模型制作 2.1 基于渐进结构法的拓扑优化设计本文基于Abaqus中的渐进结构拓扑优化法进行优化。即在满足一定的体积(质量)约束条件的前提下,以应变能最小化(即静柔度最小化,静刚度最大化)为设计目标,则该拓扑优化的数学表达式如下:
| $\begin{array}{l}\mathop {\min }\limits_{\kappa \left( x \right)} \left\{ {C = \int_{{S_\sigma }} {{u^{\rm T}}\overline T } {\rm d}S + \int_V {{u^{\rm T}}\overline f } {\rm d}V} \right\} \text{,}\\{\rm s.t.} \int_V {\kappa \left( x \right)} {\rm d}V \leqslant {V^*}\\\;\quad \kappa \left( x \right) = \left\{ \begin{array}{l}0,x \in {V_{void}}{\text{,}}\\1,x \in {V_{solid}}{\text{。}}\end{array} \right.\end{array}$ | (1) |
其中:
设计变量
为了保证边界的一致性,进行拓扑优化时,采用与静力学分析时相同的边界条件;考虑到外形的完整性和模型的安全性,设置模型除前端面外的包络层2 mm的区域以及舵轴区为冻结区域;设置约束条件为优化后体积为原来的35%(不包括冻结区域);设计目标为结构整体的应变能最小。
利用Abaqus分别在2种载荷和2种载荷共同作用下进行拓扑优化,为偏于安全考虑,所施加载荷均取设计的最大载荷。结果如图3所示(结构为剖面图)。在2种载荷的单独作用下,优化结果分别为模型中间区域出现类似桁架形式的骨架和舵轴区域向两侧延伸的支撑结构;而2种载荷共同作用下的优化结构为含筋箱体梁形式,整体表现为2种单一载荷下优化结构形式的选择性叠加,在模型中间出现类似桁架形式的纵骨,舵轴末端为类似桁架形式的横骨架。

|
图 3 优化后模型的变形特征与应力分布 Fig. 3 Deformation characteristics and stress distribution of the optimized model |
基于渐变结构法和数学表达式(1)分析,单独施加末端压力载荷时,模型内部会有传力的纵筋,外表也可能被优化,所以必须设置冻结区域;单独施加扭转载荷时,由于剪力流的作用,内部应力接近0,所以优化后为空,仅余外层足够的厚度,成箱体状态;但同时施加2种载荷时,则会选择性保留2种载荷作用的传力路径,出现含筋的箱体形式。所以,在应力水平较低的区域中只保留传力路径以维持应有的强度刚度,其余区域材料分布状态则为0。
而且,将优化后的模型与典型模型的应力和位移云图比较后发现,优化模型在变形和应力的峰值上都有一定程度的增加,但是优化后模型应力的分布更均匀,过渡区域大,变化相对更加平缓,说明拓扑优化有效地提高了模型的材料利用率,保留了更加有效且精简的传力路径。
2.2 FDM模型制作应用FDM技术制备有横纵筋板的标准模型和拓扑优化后的模型,完成后的模型如图4和图5所示。各模型的质量对比如表3所示。制备的模型由于工艺及后处理工艺的原因,使模型存在一定的误差。而且由于PLA和钢的材料属性相差甚远,但却都是均质材料,所以利用FDM技术制做的模型仅能验证优化模型结构的合理性及优势。
|
|
表 3 模型质量对比 Tab.3 Model quality comparison |

|
图 4 典型骨架模型 Fig. 4 Typical skeleton model |

|
图 5 拓扑优化后模型 Fig. 5 Topology optimization model |
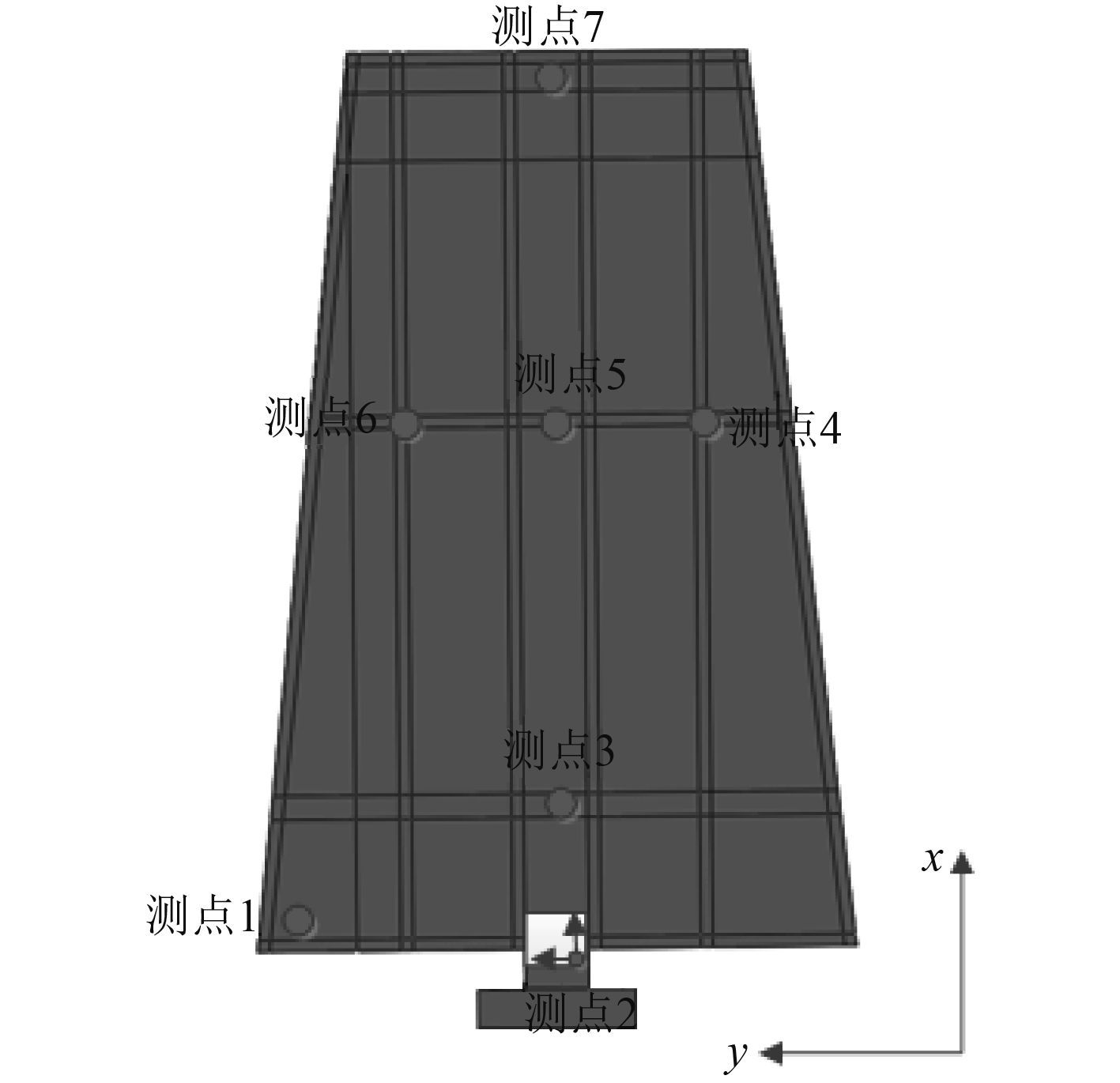
分别对典型模型和优化后模型进行静强度刚度试验,设置如图6所示的直角坐标系(平面的垂向为z向)和测点。其中测点2测量应变值,对应仿真计算的应力云图为应力最大值;其余测点测量位移值。
|
图 6 测点布置图 Fig. 6 Arrangement of measuring points |

|
图 7 试验加载方式 Fig. 7 Test loading mode |
加载方式如图7所示,在载荷区域贴上PLA薄片,以便将载荷均匀分布到与有限元计算中相同的加载区域上,以保证载荷条件的统一性,同时尽量避免应力集中的问题;在薄片上再粘贴一个连接基座,以便于与质量块连接,利用质量块加载相应大小的力。
3.2 试验结果采用位移计测量位移,应变片测量应变,利用数据采集器记录并保存各测点相应的位移和应变,并将所得结果进行处理,输出末端压载x方向的应力,输出扭转载荷y方向的应力,以测点1为观测点,输出扭转变形时模型的扭转角度,如表4~表6所示。
|
|
表 4 仿真计算与典型模型试验应力值对比 Tab.4 Comparison of stress value between simulation and standard model test |
|
|
表 5 典型模型与拓扑模型试验应力值对比 Tab.5 Comparison of test stress values between standard model and topological model |
|
|
表 6 各工况下各测点相应位移 Tab.6 The corresponding displacements at different measuring points |
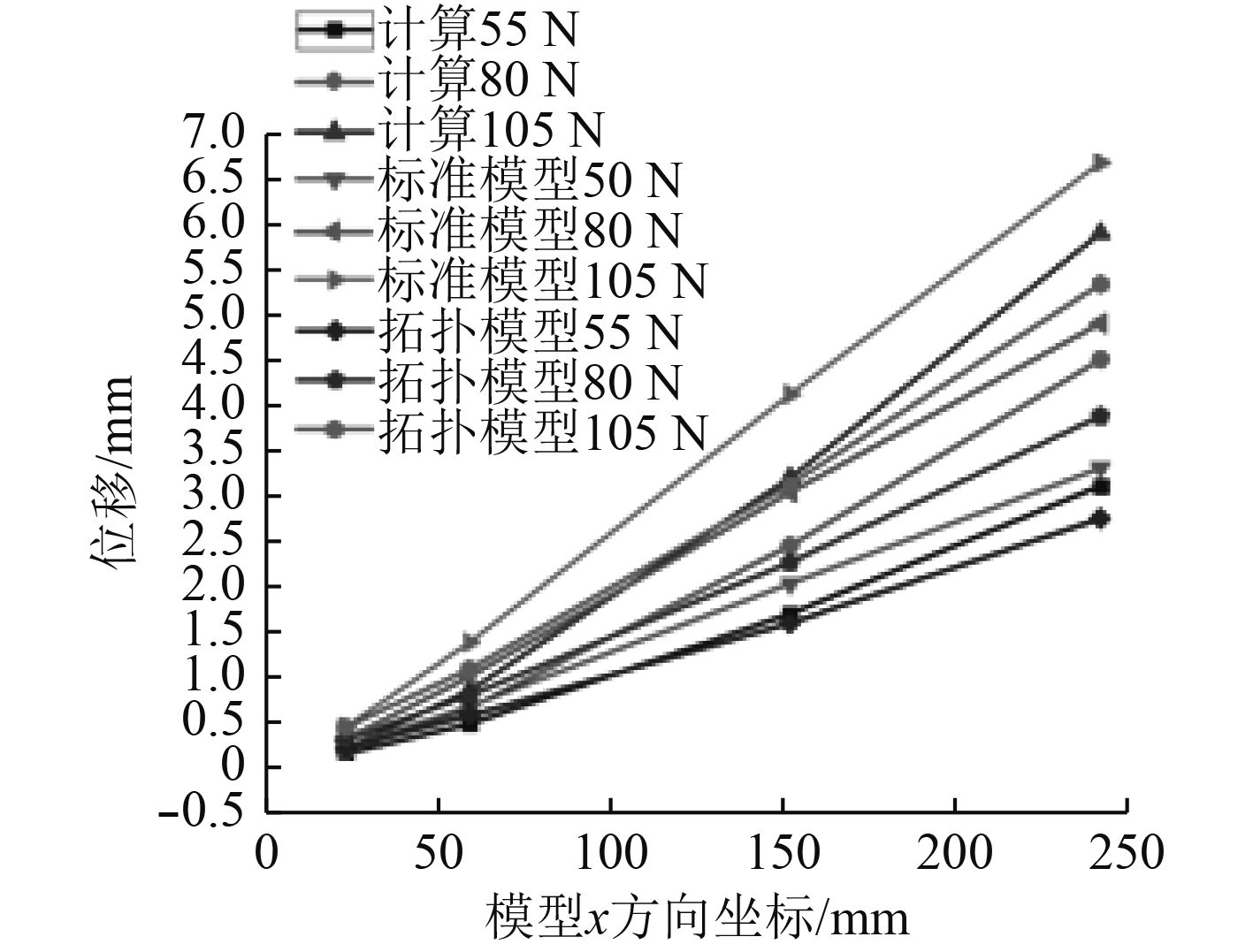
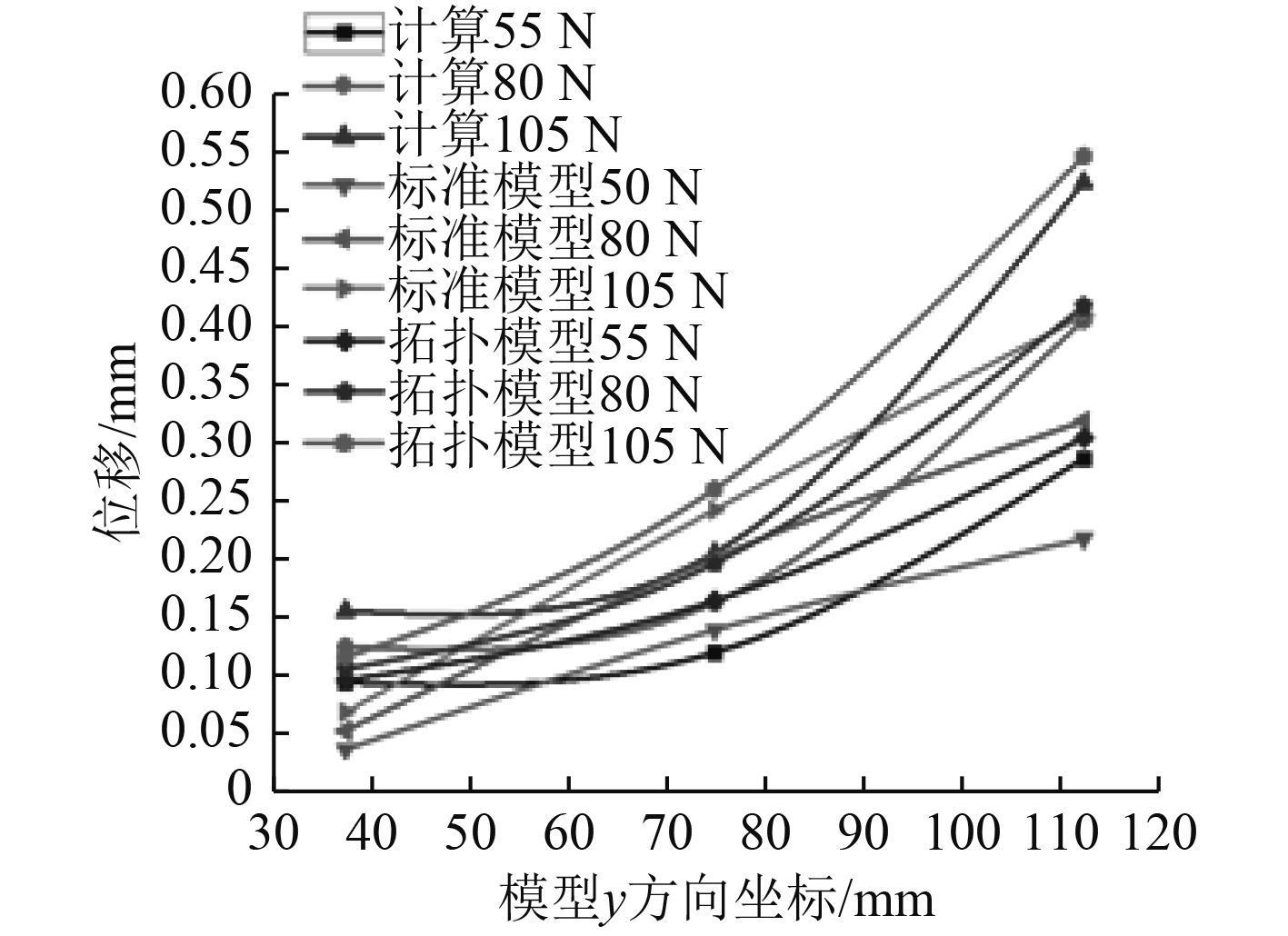
利用表6和计算的数据画出相应的位移对比曲线,如图8和图9所示。
|
图 8 末端压载下模型的位移变化 Fig. 8 Displacement variation of the model under compressive load |
|
图 9 扭转载荷下模型的位移变化 Fig. 9 Displacement variation of the model under torsion deformation |
仿真计算中模型在2种载荷下的最大应力分别为13.97 MPa和5.961 MPa;试验测出的典型模型的最大应力分别为14.273 MPa和4.032 MPa;拓扑模型的最大应力分别为14.824 MPa和4.071 MPa。优化后模型的最大应力有一定的增大。
从图8和图9中可以看出2种模型的试验位移都有很好的线性规律,而仿真计算的位移值线性却不好,在扭转变形中(见图9),仿真计算的位移曲线更接近二次曲线,经分析发现试验的固支边界并非是理想固支,所以在扭转试验中,扭转的中心轴发生了偏移,使整个结构面大部分在扭转轴的一侧,所以线性更好;单独对比2种模型的试验位移值(见表5),拓扑模型的位移都比典型模型的位移小,而且从图8中可以看出,拓扑模型的位移曲线斜率小于典型模型的位移曲线斜率,说明拓扑优化提高了模型的整体抗弯刚度和材料的利用率,使拓扑模型在x方向上的位移变换更平缓;在扭转变形的各工况下,拓扑模型的相应扭转角度和各点位移都有所增大,但与典型模型的试验值相差不大,尽管优化删掉了部分横向骨架,但模型抗扭刚度变化不大,这说明拓扑优化在满足刚度的要求下,有效的提高了材料的整体利用率。
综上所述,拓扑优化出的新型结构在保证满足强度刚度的要求下,有效减轻了结构整体重量,提高了材料的利用率。
4 结 语本文利用FDM技术实现了拓扑优化结构模型的制作,并进行了静刚度强度试验,得出如下结论:
1)优化后的模型较典型模型减重约12.84%,减重明显;
2)拓扑优化出的新型结构模型强度刚度均满足要求,且模型的应力分布更均匀,位移变换更平缓,有效的提高了材料的整体利用率。
| [1] |
张政. 框架结构形状优化理论及基于MSC.Patmi&Nastran软件的二次开发[D]. 北京: 北京工业大学, 2008.
|
| [2] |
翟玉文, 梅志远, 吕岩松, 等. 斜支撑肋板对框架式悬臂结构刚度特性的影响[J]. 海军工程大学学报, 2013, 25(4): 16-21. ZHAI Yu-wen, MEI Zhi-yuan, LV Yan-song, et al. Effect of oblique supporting rib plate on stiffness of framed cantilever structure[J]. Journal of Naval University of Engineering, 2013, 25(4): 16-21. |
| [3] |
BENDSOE M P, KIKUCHI N. Generating optimal topologies in structural design using a homogenization method[J]. Computer Methods in Applied Mechanics and Engineering, 1988, 71: 197-224. DOI:10.1016/0045-7825(88)90086-2 |
| [4] |
MLEJNEK H P , SCHIRRMACHER R. An engineer′s approach to optimal material distribution and shape finding[J]. Comp. Meth. Appl. Mech. Engrg, 1993, 106: l-26. |
| [5] |
XIE YM, STEVEN GP. A simple evolutionary proeedure for struetural optimization[J]. Compoters & Structures, 1993, 49(5): 885-896. |
| [6] |
CHU D N, XIE Y M, HIRA A, et al. Evolutionary structural optimization for problems with stiffness constraints[J]. Finite Elements in Analysis and Design, 1996, 21(4): 239-251. DOI:10.1016/0168-874X(95)00043-S |
| [7] |
QUERIN O M, STEVEN G P, XIE Y M. Evolutionary structural optimization(ESO) using a bidirectioal algorithm[J]. Engineering Computations, 1998, 15(8): 1031-1048. DOI:10.1108/02644409810244129 |
| [8] |
TANSKANEN P. The evolutionary structural optimization method: Theoretical aspects[J]. Computer Methods in Applied Mechanics and Engineering, 2002, 191(47): 5485-5498. |
| [9] |
中国机械工程学会. 3D打印打印未来[M]. 北京: 中国科学技术出版社, 2013.
|
| [10] |
汪绍兴. 基于PLA丝材的FDM试件机械性能分析及优化[D]. 大连: 大连理工大学, 2015.
|
 2018, Vol. 40
2018, Vol. 40
