2. 江苏科技大学船舶与海洋工程学院,江苏 镇江 212003;
3. 武昌船舶重工集团有限公司军贸设计公司,湖北 武汉 430060
2. School of Naval Architecture and Ocean Engineering, Jiangsu University of Science and Technology, Zhenjiang 212003, China;
3. Wuchang Shipbuilding Industry Group Co., Ltd., Wuhan 430060, China
相比于传统加筋板,金属夹层板结构具有轻质、高强度、隔热隔音和可设计性强等优点,能够减轻船体重量,降低制造成本,在船舶与海洋工程领域得到越来越多的关注和应用。如德国的油轮、芬兰的破冰船以及美国海军舰艇已将其应用于天线平台甲板等[1-2]。船体结构中的[1]板,四周由骨架支持,同时受到相邻板格的牵制,工作时最容易发生屈曲和后屈曲破坏。因此,分析多种工况下夹层板屈曲后的极限承载力,确定其与设计载荷水平之间适量的裕度和强度估计,提出更为严谨的结构设计[3],具有重要的经济效益和工程意义,基于极限强度的船舶结构设计方法也将是未来发展的趋势。
为挖掘薄壁结构可观的后屈曲承载能力,有关夹层板屈曲极限强度的研究已成为国内外学者关注的热点[4-5]。Bogdaniuk[6]对计及焊缝的I型金属夹层板屈曲极限强度进行了有限元数值仿真分析,发现初始缺陷对夹层板极限强度影响很大。Augustyniak等[7]对20 mm和60 mm厚度的I型金属夹层板进行了有限元屈曲分析,发现屈曲临界力与夹层板厚度的平方成正比;张伟等[8]对钢-聚氨酯夹层板在不同厚度情况下的屈曲强度进行了研究,发现钢板厚度增加,夹层板临界载荷明显增加。于耀等[9]试验研究了复合材料在轴向载荷和面外载荷作用下的极限强度,发现破坏的发生分为线弹性阶段和非线性破坏阶段。陈庆强等[10]对SPS夹层板的弯曲性能以及受均布载荷作用下的夹层板强度进行强度计算方法研究。Aydogdu等[11]用1阶和3阶剪切变形理论方法,分叉屈曲法,Ritz-Galerkin法及数值方法研究了符合正交异性层合板在面内载荷作用下的屈曲性能,发现边界条件和正交各向异性比率对屈曲性能影响较大。Kozak[12]研究了金属夹层板面内单轴受压条件下的夹层板极限强度,发现夹层板板材厚度及整体厚度对极限强度的影响较大。海洋钢结构的设计(DNV)[13]也已经引入了极限强度设计的方法。
本文基于舰船甲板结构的受力特点,采用非线性有限元Abaqus,建立U型金属折叠式夹层板结构双向面内受压和垂向载荷作用下的数值仿真模型,计算分析结构在不同组合载荷作用下的非线性后屈曲极限承载能力。通过极限强度对比分析,本文所设计的U型金属折叠式夹层板结构的极限承载能力明显优于传统加筋板结构,计算结果为新型金属折叠式夹层板结构的设计与应用提供参考。
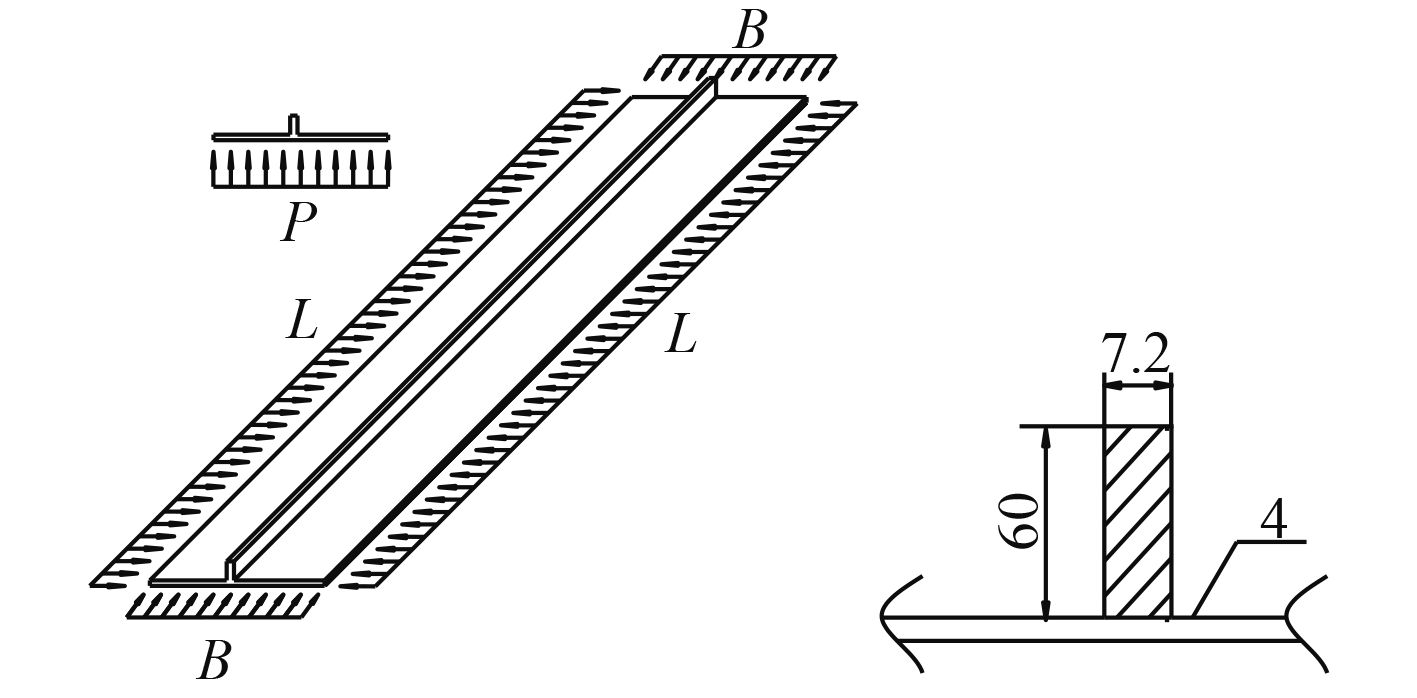
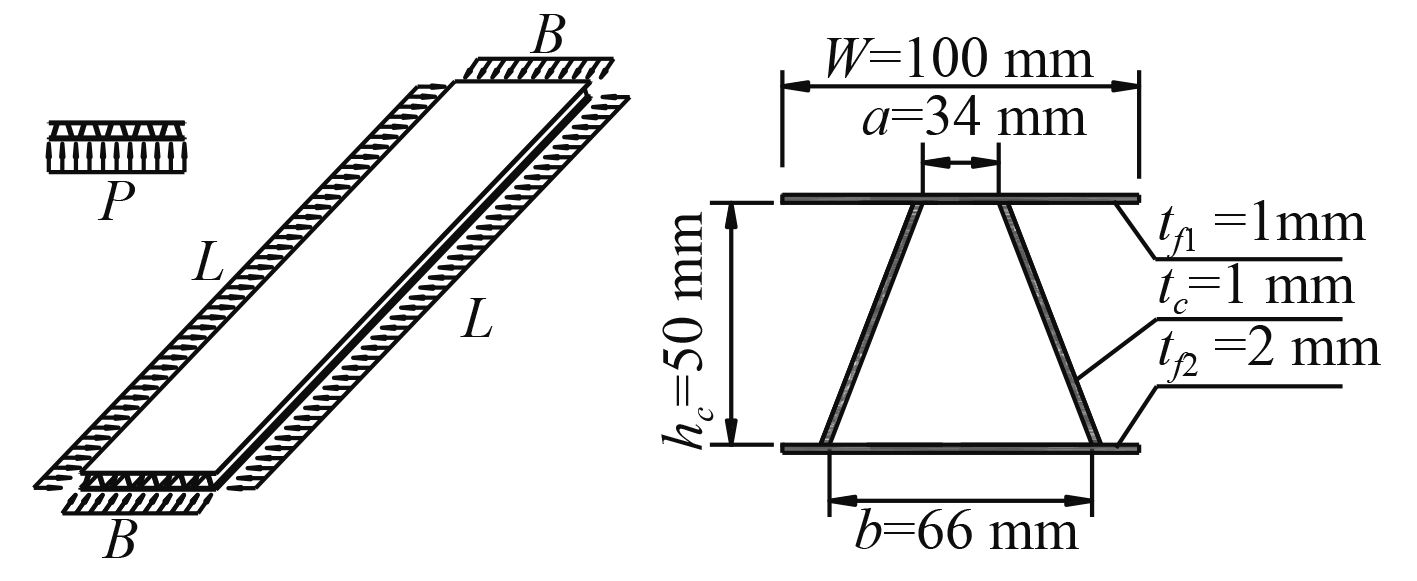
1 有限元仿真模型以某舰船甲板加筋板为比较对象,加筋板长宽为一个肋距,分别为1 950 mm×500 mm,面板厚度为4 mm,加强筋为扁钢,如图1所示,板架结构重量为37.2 kg。根据重量相当原则,设计U型折叠式夹层板结构,概念设计示意图及单元结构尺寸如图2所示,其中W为单元宽度,a为夹层宽边,b为夹层短边,hc为夹层高度,tc为夹层壁宽度,tf1和tf2分别为面板厚度,总重量为36.1 kg,比加筋板重量减少约3%。
U型折叠式夹层板结构与加筋板结构材料均为高强钢,材料密度ρ=7 850 kg/m3,泊松比μ=0.3,弹性模量E=206 GPa,屈服强度为σY=315 MPa。有限元模型中所有构件均采用Shell单元建模,网格尺寸取为5 mm。
|
图 1 加筋板示意图 Fig. 1 Illustration of stiffened plate |
|
图 2 夹层板示意图 Fig. 2 Illustration of U-type corrugated core sandwich panel |
舰船甲板主要受到纵向(B向)、横向(L向)以及垂向载荷的共同作用。考虑船体板受力特性,面内载荷以沿筋方向的面内压力为主,选取σB:σL=1.0:0.0,σB:σL=0.8:0.2,σB:σL=0.7:0.3三种典型工况,并考虑特殊的轴向载荷工况σB:σL=0.0:1.0。垂向载荷考虑有/无均布压力P,即P=0和P=4.91 kPa两种情况,其中P=4.91 kPa是根据该舰船甲板工况确定的。
为了评估板格的极限强度,一般以在极限时刻板格受压截面上的应力σB或σL与材料屈服强度σY比值,即极限比例系数来衡量在轴压载荷作用下的极限强度大小,极限比例系数在0~1之间,越接近于1,说明结构屈曲极限承载能力越高。当极限比例系数达到或者超过1时,即意味着受压船体板已经从失稳破坏转化为强度问题。
在多数研究中,纵骨和横框架之间的板被假定为四周简支,然而船体板是连续的板,每一板格都受到相邻板格的牵制作用,板边不能自由趋近,且当板格受到垂向压力弯曲时,相邻的板格因连续而应具有相同的变形,因此对于轴向压力较大的船体板可以被认为是两长边夹支[14]。
1.2 初始几何缺陷事实上,任何结构都不可避免地存在一定的初始缺陷,即由于技术和工艺等原因引起的变形与理想设计之间的偏差。现有的研究表明,结构的极限承载力不仅取决于结构的设计、尺寸、材料等,而且很大程度上受初始缺陷的影响,因此要充分考虑结构的初始缺陷。然而,初始几何缺陷很难在计算模型中准确地反映[15]。因此,借鉴目前处理该问题的通常做法,分为两步:首先通过模型特征值线性屈曲分析,获得失稳载荷、相应的失稳模态及节点的相对位移;然后,将节点相对位移作为初始的几何缺陷等效引入非线性后屈曲模型,进行后屈曲极限承载力分析。
2 后屈曲极限强度分析 2.1 仿真技术与结果验证结构的非线性有限元分析可以考虑很多影响结构极限强度的主要因素,例如结构的几何非线性行为、材料的弹塑性非线性本构关系以及结构的屈曲和后屈曲强度等,被认为是目前极限强度分析最有效的方法之一,在建模技术使用得当时,能给出任意结构形式的准确的分析结果[16]。弧长法(Riks方法)是目前结构非线性分析中数值计算最稳定、计算效率最高且最可靠的迭代控制方法之一,能够有效的分析结构非线性前、后屈曲及跟踪屈曲路径,成为大多数商业有限元软件的屈曲问题计算模块。
为验证本文所采用的非线性有限元仿真技术及计算结果的有效性和准确性,本文首先对经典薄板结构的后屈曲极限强度进行仿真计算,经典薄板结构四边简支,模型尺寸为4 300 mm×815 mm,板厚t=11.8~32 mm不等(见表1),材料为理想弹塑性材料,屈服极限为315 MPa,E是杨氏模量,板长a=4 300 mm,板宽b=815 mm,采用Shell单元建模。有限元计算结果与Frankland和Faulkner经验公式及其他研究结果进行比较,如表1所示。
Frankland(1940)建立极限比例系数经验式:
Faulkner(1975)建立极限比例系数经验式:
其中
|
|
表 1 薄板极限强度有限元计算结果对比验证 Tab.1 Results comparison of FEM and empirical formula |
从表中对比可以看出,采用非线性有限元仿真计算简支薄板的屈曲极限强度结果与经验公式及文献[17-18]中的结果吻合较好,其中,与Frankland公式最大误差为9.82%;与Faulkner公式最大误差仅为2.2%;与文献[17-18]的最大误差仅为3.4%。误差分析结果表明,本文采用非线性有限元软件进行结构后屈曲极限强度分析的仿真过程与结果有效且准确。
2.2 夹层板后屈曲极限强度分析首先考虑结构只有沿筋方向的面内压力,即σB:σL=1.0:0.0,而垂向载荷考虑有/无压力的载荷工况,分析U型金属折叠式夹层板结构和传统加筋板的后屈曲极限强度(见图3)与极限状态(见图4)。
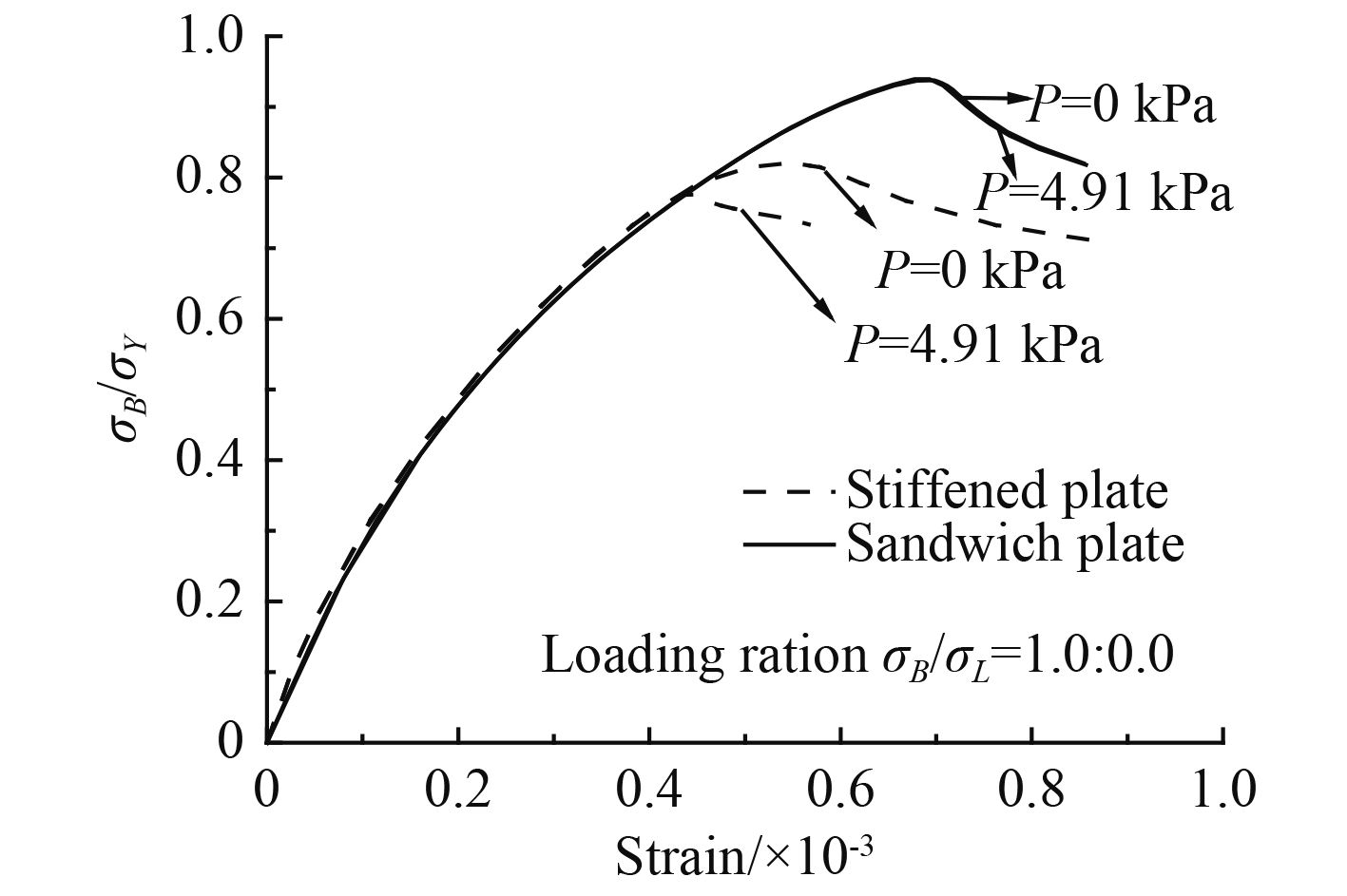
图3中的虚实线分别为2种垂向载荷工况下的加筋板、夹层板极限强度。2种结构材料相同,重量相当(夹层板比加筋板轻3%)。从图中可以看出:
1)2种结构失稳后都存在可观的继续承载能力,主要原因在于板的中面内力。板由于支持骨架的作用以及相邻板格的作用,使板边不能自由弯曲和趋近,当失稳弯曲后,板的中面被拉长,产生中面拉应力,从而使板的变形不能迅速变大。板后屈曲中应力经重新分布,形成约束边的压应力大于板中部应力,如图4所示。这个现象说明板边那部分材料起着更大的作用,承担了外载荷的绝大部分。
|
图 3 夹层板与加筋板纵向应力应变曲线 Fig. 3 Stress versus strain curves along the longitudinal direction of plate |

|
图 4 结构的极限状态(σB:σL=1.0:0.0,变形放大倍数5) Fig. 4 Ultimate limit state with lateral pressure(σB:σL=1.0:0.0, amplification factor of 5) |
2)夹层板结构在有/无垂向载荷的2种工况下的后屈曲极限强度,均优于加筋板结构约20%。
3)垂向载荷的存在,会降低板结构的屈曲极限强度,其中加筋板的后屈曲极限强度对垂向载荷更为敏感,有垂向载荷时,极限比例系数约为0.775,无垂向载荷时,极限比例系数为0.820。而垂向载荷对夹层板结构的影响较小,2种工况下夹层板极限比例系数相当,比加筋板提高14.6%(P=0)和21.0%(P=4.91 kPa)。
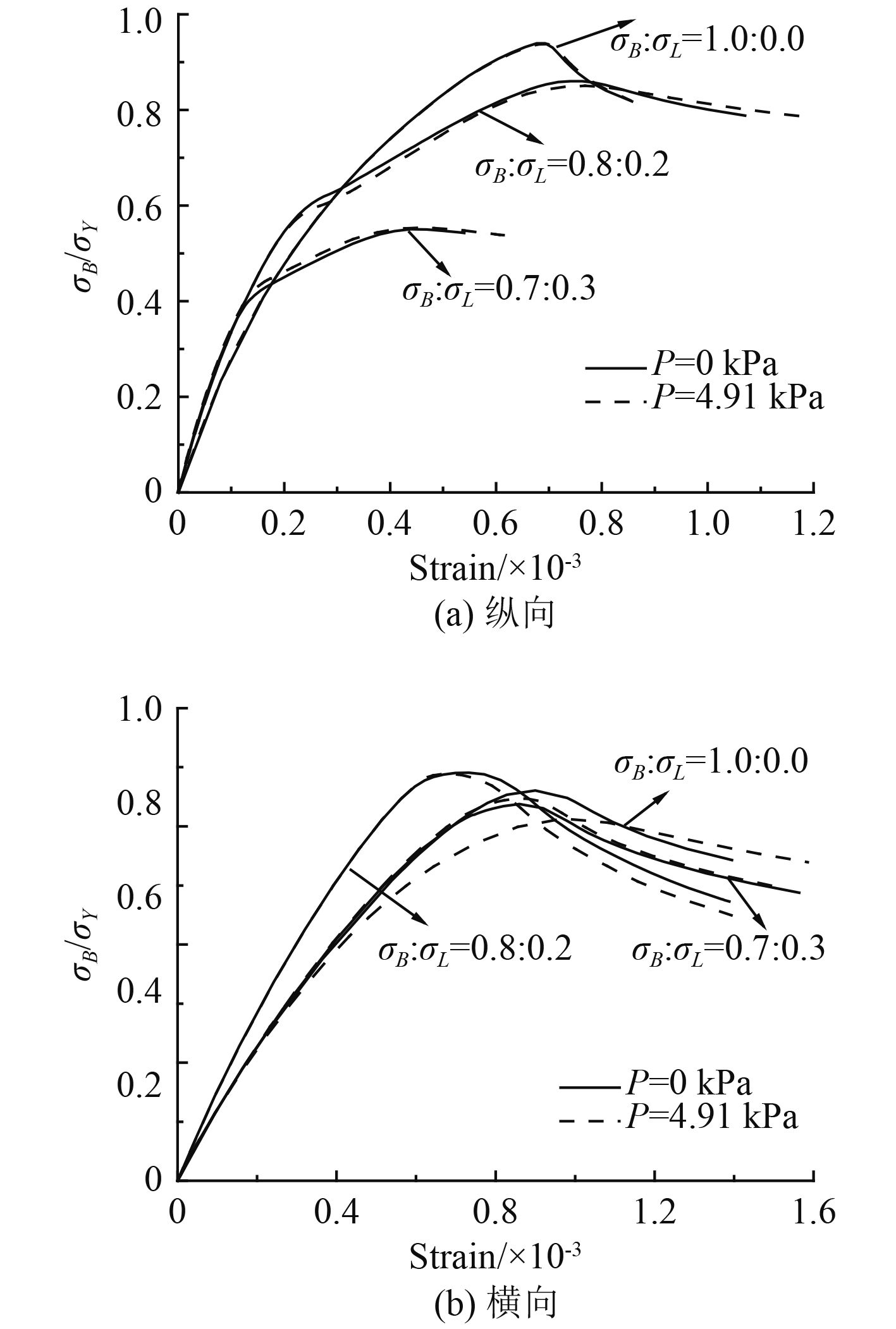
分析金属折叠式夹层板结构在不同组合载荷作用下的后屈曲极限强度。图5为夹层板在σB:σL分别为1.0:0.0,0.8:0.2,0.7:0.3,0.0:1.0工况下纵向和横向后屈曲极限强度。从图中可以看出:1)随着纵向载荷的比例减少,夹层板纵向极限强度降低;2)垂向载荷对纵向极限强度影响较小,对横向极限强度影响较大;3)夹层板横向极限强度明显小于纵向极限强度,主要是因为芯层类似加强筋中的筋,沿纵向排列,所以纵向强度较高;4)横向极限强度随着载荷比例的不同变化较小,有纵向载荷一定程度上提高了夹层板横向强度。图6为夹层板在P=0时σB:σL为1.0:0.0,0.8:0.2,0.7:0.3,0.0:1.0工况下夹层板的极限状态。从图中可以看出夹层板纵向受压变形较小,随着纵向载荷比例升高时,板中间沿短边变形较明显,且面内应力水平较低,即后屈曲极限强度非常小。
|
图 5 夹层板在不同组合载荷作用下的后屈曲极限强度 Fig. 5 Post-buckling ultimate strength of sandwich structure under different combined loads |

|
图 6 无垂向载荷夹层板的极限状态(变形放大倍数5) Fig. 6 Ultimate limit state without lateral pressure(amplification factor of 5) |
本文考虑船体甲板结构的受力特点,设计并计算U型金属折叠式夹层板结构在不同组合载荷作用下的后屈曲承载能力,确定结构屈曲极限强度。通过比较分析,得到如下几点结论:
1)通过与经典理论和经验公式的结果比较,验证了非线性有限元方法计算板结构后屈曲极限强度问题的可行性与准确性,且能够很好地进行初始缺陷模拟、边界条件设置等;
2)船体板结构在屈曲后均具有客观的继续承载能力,且在重量相当的原则下,金属折叠式夹层板结构的后屈曲极限强度明显优于传统加筋板结构;
3)考虑船体板结构的受力特性,对比分析双向面内受压和垂向均布压力的不同组合载荷下夹层板横向、纵向屈曲极限承载能力,金属折叠式夹层板在船体结构中的推广使用提供建议。
| [1] |
PENTTI KUJALA, ALAN KLANAC. Steel sandwich panels in marine applications[J]. Brodogradnja, 2005, 56(4): 305-314. |
| [2] |
KOLSTERS H,WENNHAGE P. Optimization of laser-welded sandwich panels with multiple design constraints[J]. Marine Structures, 2009(22): 154-171. |
| [3] |
PAIK J K, THAYAMBALLI A K. Ultimate limit state design of steel plated structures[M]. John Wiley & Sons, Chichester, U.K., 2003.
|
| [4] |
CHEN Qing-yuan, QIAO Pi-zhong. Post-buckling analysis of composite plates under combined compression and shear loading using finite strip method[J]. Finite Elements in Analysis and Design, 2014, 83: 33-42. DOI:10.1016/j.finel.2014.01.002 |
| [5] |
A. Post-buckling behavior of composite and sandwich skew plates[J]. International Journal of Non-Linear Mechanics, 2013, 55: 120-127. DOI:10.1016/j.ijnonlinmec.2013.05.010 |
| [6] |
MARIAN Bogdaniuk, ZENON Górecki, MARIUSZ Brzóska. FEM analysis of ultimate strength of steel panels[J]. Polish Maritime Research, 2006(S1): 21-23. |
| [7] |
MAREK Augustyniak, GRZEGORZ Porembski. FEM strength analysis of sandwich panels for ship structure applications[J]. Polish Maritime Research, 2006(S1): 24-26. |
| [8] |
张伟, 单成林. 钢-聚氨酯夹层板稳定分析[J]. 低温建筑技术, 2014, 1: 46-49. |
| [9] |
于耀, 王伟. 夹层板复杂弯曲极限强度性能研究[J]. 中国舰船研究, 2014(3): 76-82. DOI:10.3969/j.issn.1673-3185.2014.03.011 |
| [10] |
陈庆强, 张海华, 吴赞. 船体结构钢夹层板强度计算方法研究[J]. 中国造船, 2015(2): 74-80. DOI:10.3969/j.issn.1000-4882.2015.02.009 |
| [11] |
METIN A, TOLGA A. Buckling of cross-ply composite plates with linearly varying In-plane loads[J]. Composite Structures, 2017. DOI:10.1016/j.compstruct.2017.02.085 |
| [12] |
KOZAK J. Problems of strength modeling of steel sandwich panels under in-plane load[J]. Polish Maritime Research, 2006(s1): 9-12. |
| [13] |
DNV. Offshore standard: design of offshore steel structures, general (LRFD method)[S]. 2011.
|
| [14] |
MOHAMMAD Reza Khedmatia, MOHAMMAD Reza Zareei, PHILIPPE Rigo. Sensitivity analysis on the elastic buckling and ultimate strength of continuous stiffened aluminium plates under combined in-plane compression and lateral pressure[J]. Thin-Walled Structures, 2009(47): 1232-1245. |
| [15] |
MARK W H, JAMES H S. Effects of Imperfections of the Buckling Response of Composite Shells[J]. Thin-Walled Structures, 2004(42): 369-397. |
| [16] |
张婧, 施兴华, 顾学康. 具有初始缺陷的船体加筋板结构在复杂受力状态下的极限强度研究[J]. 中国造船, 2013, 54(1): 60-70. DOI:10.3969/j.issn.1000-4882.2013.01.009 |
| [17] |
ZHANG Sheng-ming, IMTAZ KHAN. Buckling and ultimate capability of plates and stiffened panels in axial compression[J]. Marine Structures, 2009(22): 791-808. |
| [18] |
张晓丹. 加筋板极限强度的简化算法[D].武汉: 武汉理工大学, 2010.
|
| [19] |
刘昆, 张延昌, 王璞, 等. 半潜式钻井平台撑杆结构极限承载力数值仿真计算[J]. 江苏科技大学学报:自然科学版, 2012, 26(5): 430-433. |
| [20] |
刘昆, 张延昌, 王自力. 基于Abaqus船体板架极限承载能力仿真分析[C]// 纪念辛一心先生诞辰100周年暨2012年船舶学术会议文集, 2012, 189–198.
|
 2018, Vol. 40
2018, Vol. 40
