2. 中国舰船研究设计中心,湖北 武汉 430064;
3. 华中科技大学 船舶与海洋工程学院,湖北 武汉 430074
2. China Ship Development and Design Center, Wuhan 430064, China;
3. Huazhong University of Science and Technology, School of Naval Architecture and Ocean Engineering, Wuhan 430074, China
船舶结构设计结合了多个学科,是一个复杂的综合分析过程,疲劳强度是其中不可或缺的一个环节。某些船舶在实际应用中,要求能在恶劣的环境条件下长时间进行远洋航行,这就使得船舶在水中承受了更多的交变载荷,也更容易遭到疲劳强度破坏而不是静力破坏。在交变载荷的作用下,疲劳破坏更容易发生,在远远低于强度极限的时候,疲劳失效就有可能产生在局部高应力的区域[1 – 3]。目前对于船舶的疲劳寿命,普遍采用的是基于相关规范运用简化算法来进行校核,这种校核方式计算简单,能快速根据经验公式进行疲劳强度的校核,并估算出疲劳寿命[4]。然而,基于经验公式的简化算法对舰船结构形式,位置带来的应力变化表现并不敏感,故而有时不能有效识别出不同结构形式变化造成的疲劳强度的不同,也不能根据不同海况做出针对性的分析[5 – 7],对后面的舰船结构设计也带来了一些不便。
目前在船舶结构设计中,已经引进了直接计算法对船舶的疲劳强度进行计算,尤其是对于局部疲劳强度的计算。相较于传统的根据相关经验公式进行估算,直接计算法可以更加合理地模拟船舶航行的真实情况,通过有限元法计算船体结构的不同构件在不同海况下的疲劳应力水平和疲劳应力分布,得到更加精确和符合实际航行的计算结果,从而合理地完成船体结构强度的分析和评估[8]。对于疲劳强度计算,直接计算法包括基于谱分析的方法和设计波方法。根据分析范围的不同,分为对整船结构疲劳强度分析和舱段结构疲劳强度分析,全船有限元模拟疲劳强度分析的优点在于可以更好地模拟船只在水中的工作状态,对于船首船尾对船舶结构的影响能更精确地模拟。而舱段有限元直接计算的优点是建模难度小,由于只建立需要校核的舱段,工作量大大减小,缺点是难以准确地模拟船首和船尾对中间舱段的影响,对于边界条件的确定也要根据具体的情况分析[9 – 10]。国内外采用直接计算法进行舱段结构疲劳评估的公开文献比较少,为了丰富船舶疲劳强度分析的技术途径,本文将对舱段结构的疲劳强度直接计算法进行研究,通过谱分析法计算疲劳寿命。
1 船舶舱段结构有限元模型 1.1 船型结构及其有限元模型对于该船舶的舱段模型采用典型的三舱段模型,即取主要分析舱段及其前后各一个舱段来建立舱段的有限元模型。该船舶所要校核的舱段属于双层底结构,该舱段的甲板骨架、船底骨架、内底骨架、舷侧和内壳均采用纵骨架式。模型建立区域共有4个横舱壁,4个强肋位。有限元模型结构主要有:船体内外底板、横舱壁、甲板、底纵桁、舷侧纵桁、甲板纵桁、实肋板,甲板横梁,强框架肋板,纵、横骨架、大肘板等。舱段模型中纵剖面图如图1所示。

|
图 1 舱段模型中纵剖面图 Fig. 1 Longitudinal section in center plane |
采用MSC.PATRAN进行模型的建立,为保证有限元模型结构受力平衡且能真实地反映其工作状态下结构的受力状态,需对舾装、机电设备等上部模块的重量通过一定的质量模型予以计入,本文根据某舰整船的各站质量分布表得出被校核舱段处的排水量,通过对材料密度的调节模拟了模型的重量分布,保证了舱段的总体质量与设计图纸保持一致。有限元模型采用右手坐标系,x轴向船首方向为正;y轴向左舷为正;z轴为向上为正。图2为舱段结构有限元结构的剖视图。

|
图 2 舱段结构有限元模型图 Fig. 2 Model of the cabin |
舱段疲劳强度分析的边界条件如下:舱段有限元模型前后端面各个纵向构件的节点自由度和该剖面中纵剖面中和轴处的独立点采用MPC方式关联,在前端面独立点进行横向线位移、纵向线位移、垂向线位移,绕纵向轴的角位移约束,在后端面独立点释放横向线位移和绕纵向角位移。
2 舱段疲劳强度评估计算工况选取满载巡航这种典型工况来进行舱段疲劳强度的评估,海况分析选择北大西洋海况,浪向角取0~360°每隔30°取1个浪向角,共取13个,波浪圆频率根据浪向角选取不同的圆频率,如表1所示。
|
|
表 1 不同浪向角圆频率选取表(rad/s) Tab.1 The selection of circular frequency in different angles |
准确地模拟船舶在波浪中的航行情况是进行疲劳强度计算的基础。本项工作用三维网格法计算该船舶在北大西洋海况下,船舶在不同浪向下的运动响应和波浪载荷。
3.1 惯性力的计算船舶在规则波中的频域六自由度运动方程可以写为如下复数形式:
| $\sum\limits_{k = 1}^6 {{T_{j,k}} \cdot {{\bar \xi }_k}} = f_j^w\;\;\;j = 1,2, \ldots \ldots ,6{\text{,}}$ | (1) |
| $\begin{aligned}{T_{j,k}} =& - \omega _e^2{{ m}_{ {j,k}}} - \omega _e^2{D_{j,k}} + {{ C}_{ {j,k}}}{\text{,}}\\{D_{j,k}} = &{{ A}_{ {j.k}}} + \frac{i}{{{\omega _e}}}{{ B}_{ {j,k}}}{\text{,}}\\f_j^w = &f_j^i + f_j^d{\text{,}}\\{\xi _k} = &{R_e}\left\{ {{{\bar \xi }_k} \cdot {e^{ - i{\omega _e}t}}} \right\}{\text{,}}\\{\xi _k}(t) =& \left| {{{\bar \xi }_k}} \right|\cos ({\omega _e}t + {\alpha _k}){\text{,}}\\{\alpha _k} = &{\tan ^{ - 1}}\left[ { - \frac{{{\mathop{\rm Im}\nolimits} ({{\bar \xi }_k})}}{{{R_e}({{\bar \xi }_k})}}} \right]{\text{。}}\end{aligned}$ | (2) |
式中:
舰船在工作状态下的波浪载荷是入射波、绕射波、辐射波的作用力、静水压力变化和惯性力共同作用的结果。
假定船舶任一截面Sx处的压力和剪切力为:
| $\vec V = {V_1}i + {V_2}j + {V_3}k{\text{,}}$ | (3) |
式中:
假定船舶任一截面
| $\vec M = {V_4}i + {V_5}j + {V_6}k{\text{,}}$ | (4) |
式中:
作用在截面
| ${V_j} = {I_j} - {R_j} - {E_j} - {D_j} \;\; j = 1,2,3,4,5,6{\text{,}}$ | (5) |
式中:
如果惯性力以截面的质量与截面的加速度的乘积来表达,可以得到:
| $\begin{aligned}{I_2} =& \int {m({{\ddot \eta }_2} + \xi } {{\ddot \eta }_6} - \bar z{{\ddot \eta }_4}){\rm d}\xi {\text{,}}\\{I_3} =& \int {m({{\ddot \eta }_3} - \xi } {{\ddot \eta }_5}){\rm d}\xi {\text{,}}\\{I_4} =& \int {[{i_x}{{\ddot \eta }_4} - m\bar z({{\ddot \eta }_2} + \xi } {{\ddot \eta }_6})]{\rm d}\xi {\text{,}}\\{I_5} = & - \int {m(\xi - x)({{\ddot \eta }_3} - \xi } {{\ddot \eta }_5})]{\rm d}\xi {\text{,}}\\{I_6} =& \int {m(\xi - x)({{\ddot \eta }_2} + \xi } {{\ddot \eta }_6} - \bar z{{\ddot \eta }_4}){\rm d}\xi {\text{。}}\end{aligned}$ | (6) |
式中:
静水回复力和力矩可以写成:
| $\begin{aligned}{R_2} =& 0{\text{,}}\\{R_3} =& - \rho g\int {b({\eta _3} - \xi } {\eta _5}){\rm d}\xi {\text{,}}\\{R_4} =& g{\eta _4}\int {(\rho a\overline {om} - m\bar z)} {\rm d}\xi {\text{,}}\\{R_5} =& \rho g\int {b(\xi - x)({\eta _3} - \xi } {\eta _5})]{\rm d}\xi {\text{,}}\\{R_6} =& 0{\text{。}}\end{aligned}$ | (7) |
式中:
湿表面的压力计算可以由式(8)和式(9)计算:
| $P = {R_e}\left\{ {p \cdot {e^{ - i{\omega _e}t}}} \right\}{\text{,}}$ | (8) |
| $p = {p_w} + {p_d} + {p_m} + {p_s}{\text{,}}$ | (9) |
式中:
| ${p_i} = i\rho \omega {\varphi _I}{\text{,}}$ |
| ${p_d} = i\rho {\omega _e}{\varphi _d} + \rho U\frac{{\partial {\varphi _d}}}{{\partial x}}{\text{,}}$ |
| ${p_k} = \rho {\omega _e}^2{\bar \xi _k}{\varphi _k} - i\rho U{\omega _e}{\bar \xi _k}\frac{{\partial {\varphi _k}}}{{\partial x}}{\text{。}}$ |
波浪载荷幅值
| $\begin{split}&Q(x) = P\left\{ {X \geqslant x} \right\} = \sum\limits_i {\sum\limits_j} {\sum\limits_k}{p_i}({H_{1/3}},\!{T_z}) \times \\& { {{ {p_j}(\beta ) \cdot {p_k}(V) \cdot\exp\left\{ {\frac{{ - {x^2}}}{{E\left[ {({H_{1/3}},{T_z}),{\beta _j},{V_k}} \right]}}} \right\}} } } {\text{,}}\end{split}$ | (10) |
式中:
| $E\left[ {({H_{1/3}},{T_z}),{\beta _j},{V_k}} \right] = 2m({H_{1/3}},{T_z},{\beta _j},{V_k}){\text{,}}$ |
式中
ISSC在1964年建议的双参数谱公式
| $S(\omega ) = \frac{{124H_s^2}}{{T_z^4}}{\omega ^{ - 5}}\exp (\frac{{ - 496}}{{T_z^4}}{\omega ^{ - 4}}){\text{,}}$ | (11) |
Pierson-Moskowits谱(P-M谱)公式
| $S(\omega ) = \frac{{H_s^2}}{{4\pi }}{\left( {\frac{{2\pi }}{{{T_z}}}} \right)^4}{\omega ^{ - 5}}\exp \left( { - \frac{1}{\pi }{{\left( {\frac{{2\pi }}{{{T_z}}}} \right)}^4}{\omega ^{ - 4}}} \right){\text{。}}$ | (12) |
本文应用基于三维势流理论编制的船舶波浪载荷程序,对单位波高规则波下舰船的剖面载荷进行计算分析。规则波取值范围
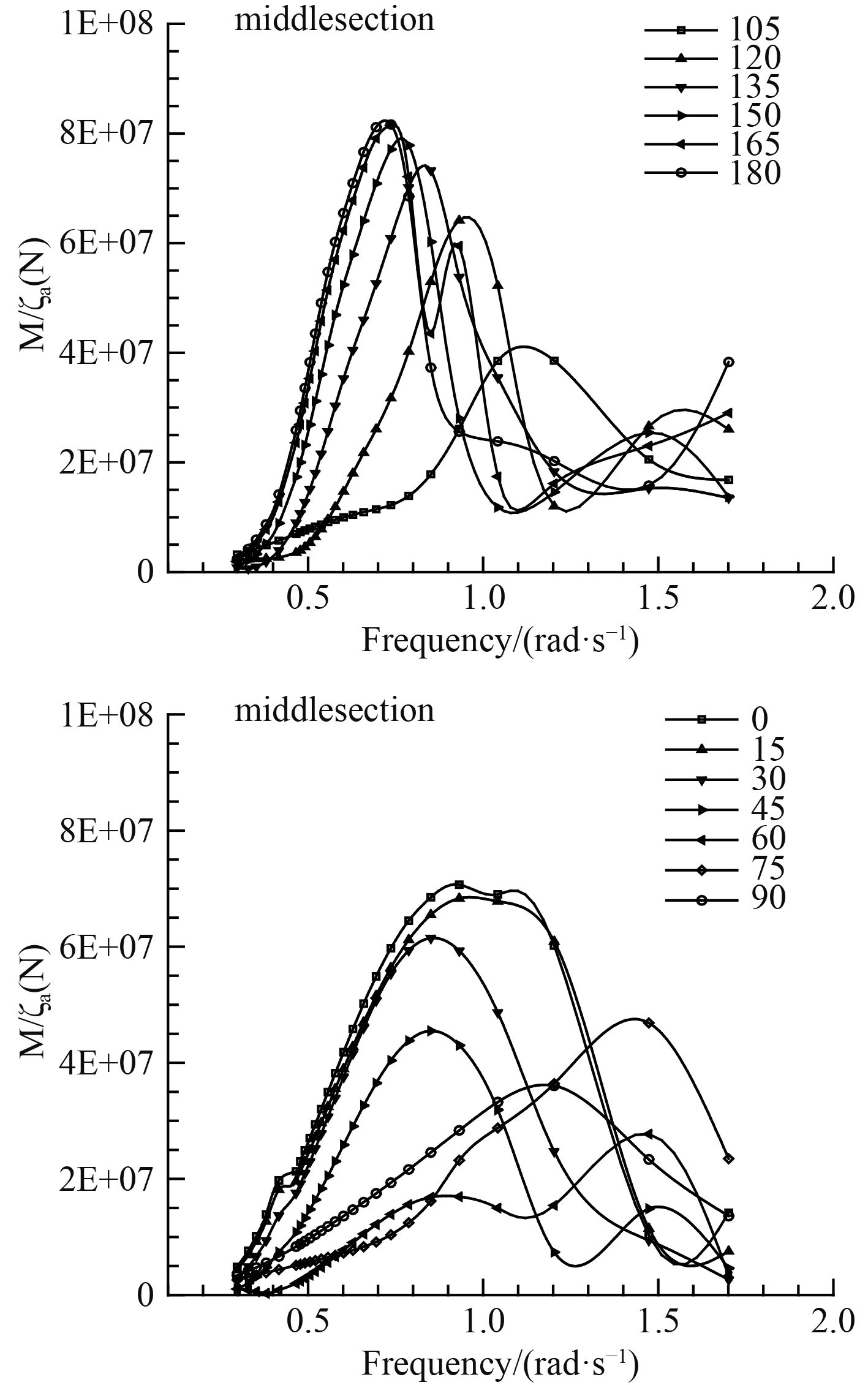
|
图 3 船中剖面垂向波浪弯矩传递函数曲线 Fig. 3 A midship vertical bending moment transfer function curve |
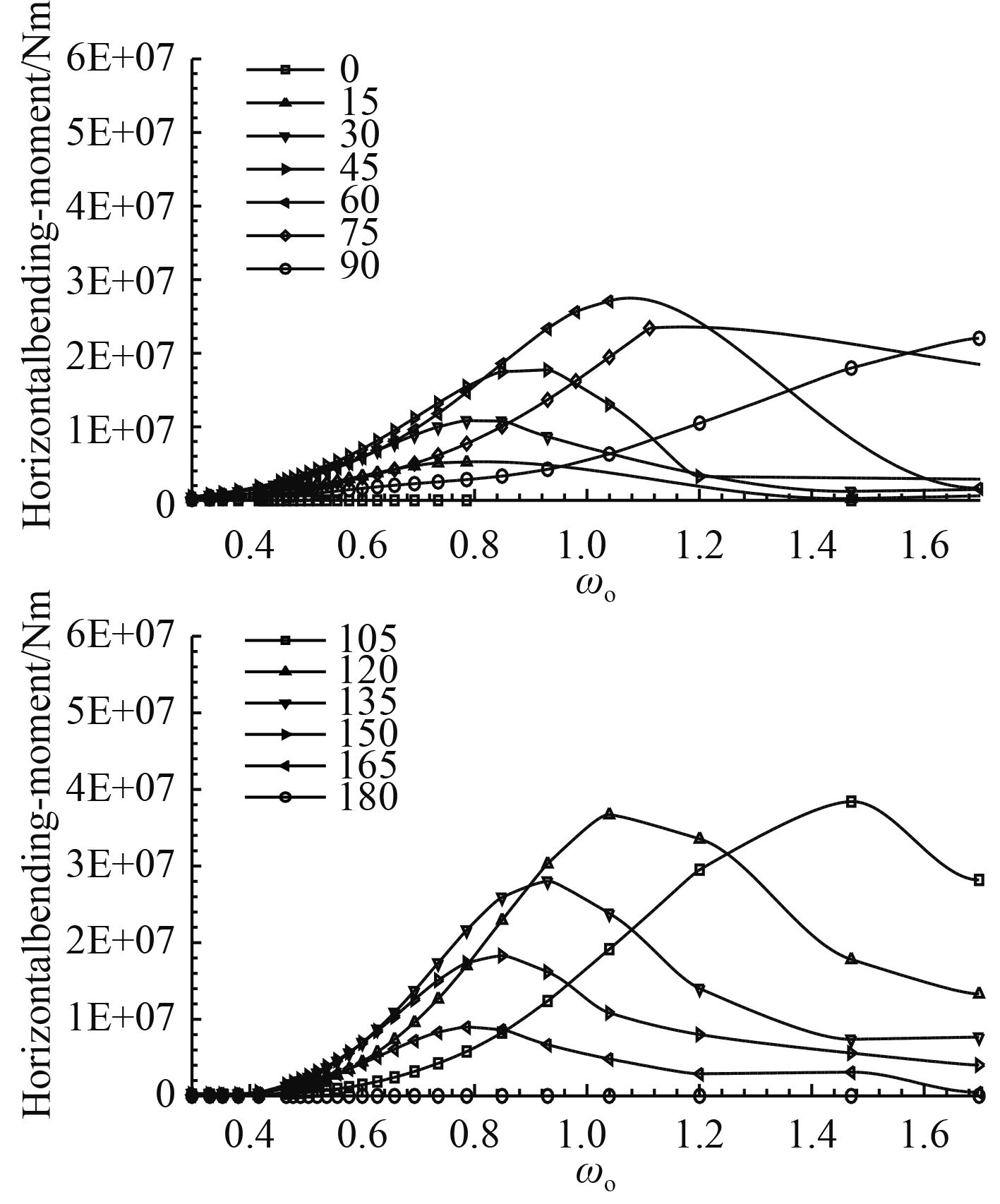
|
图 4 舱段首横截面水平弯矩传递函数曲线 Fig. 4 The horizontal bending moment transfer function curve of bow in the cabin |
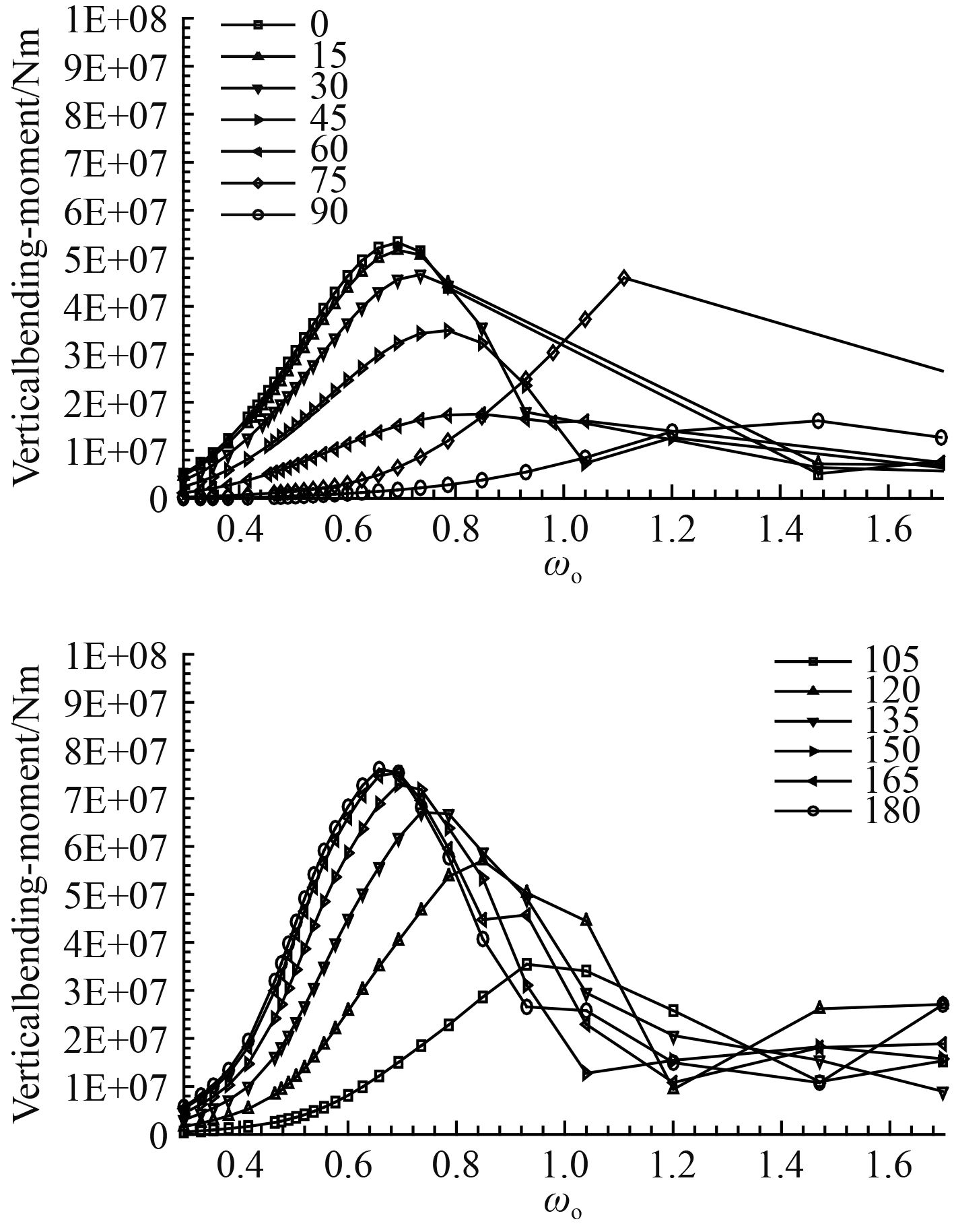
|
图 5 舱段首横截面垂直弯矩传递函数曲线 Fig. 5 The vertical bending moment transfer function curve of bow in the cabin |
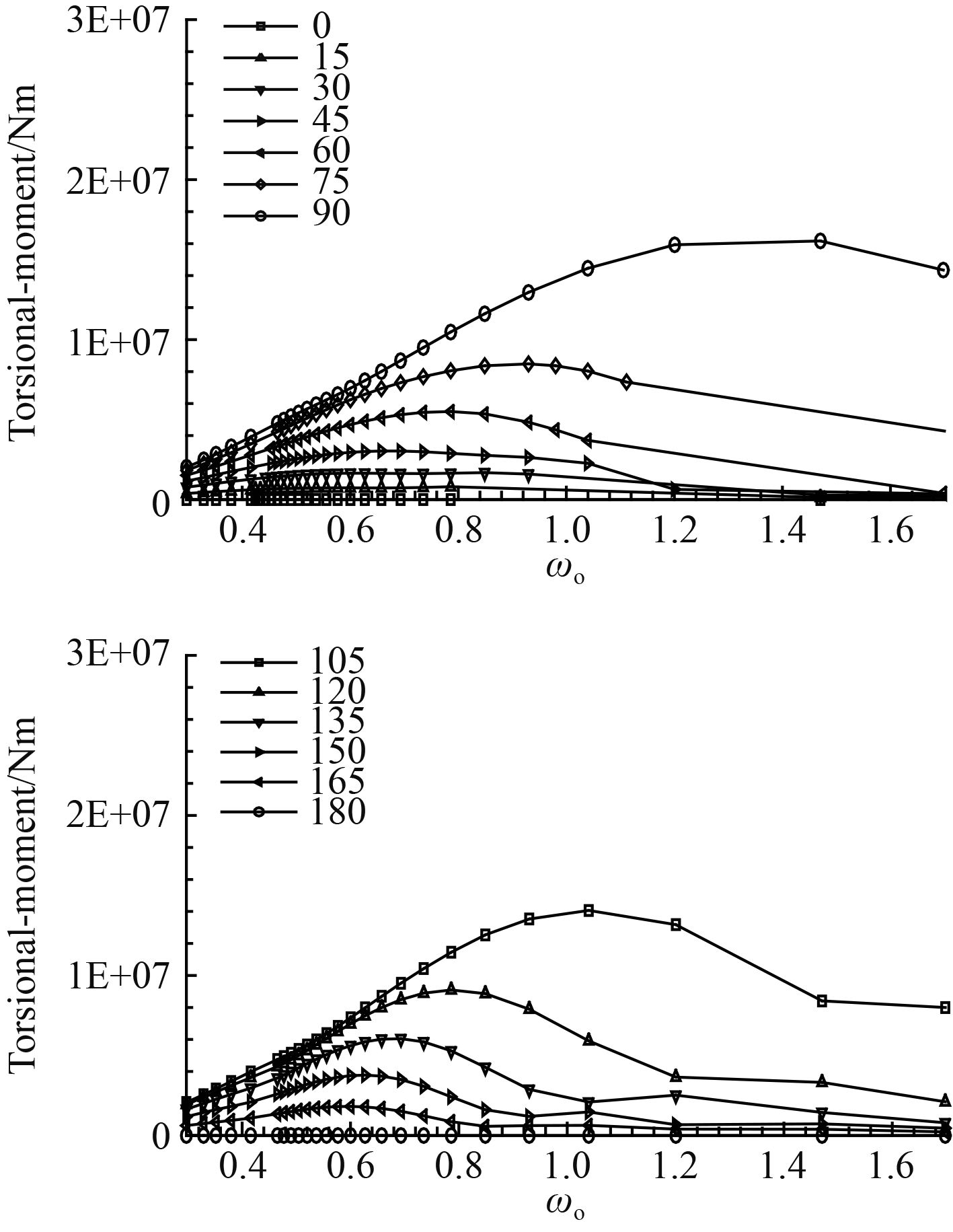
|
图 6 舱段首横截面横向扭矩传递函数曲线 Fig. 6 The torsion moment transfer function curve of bow in the cabin |
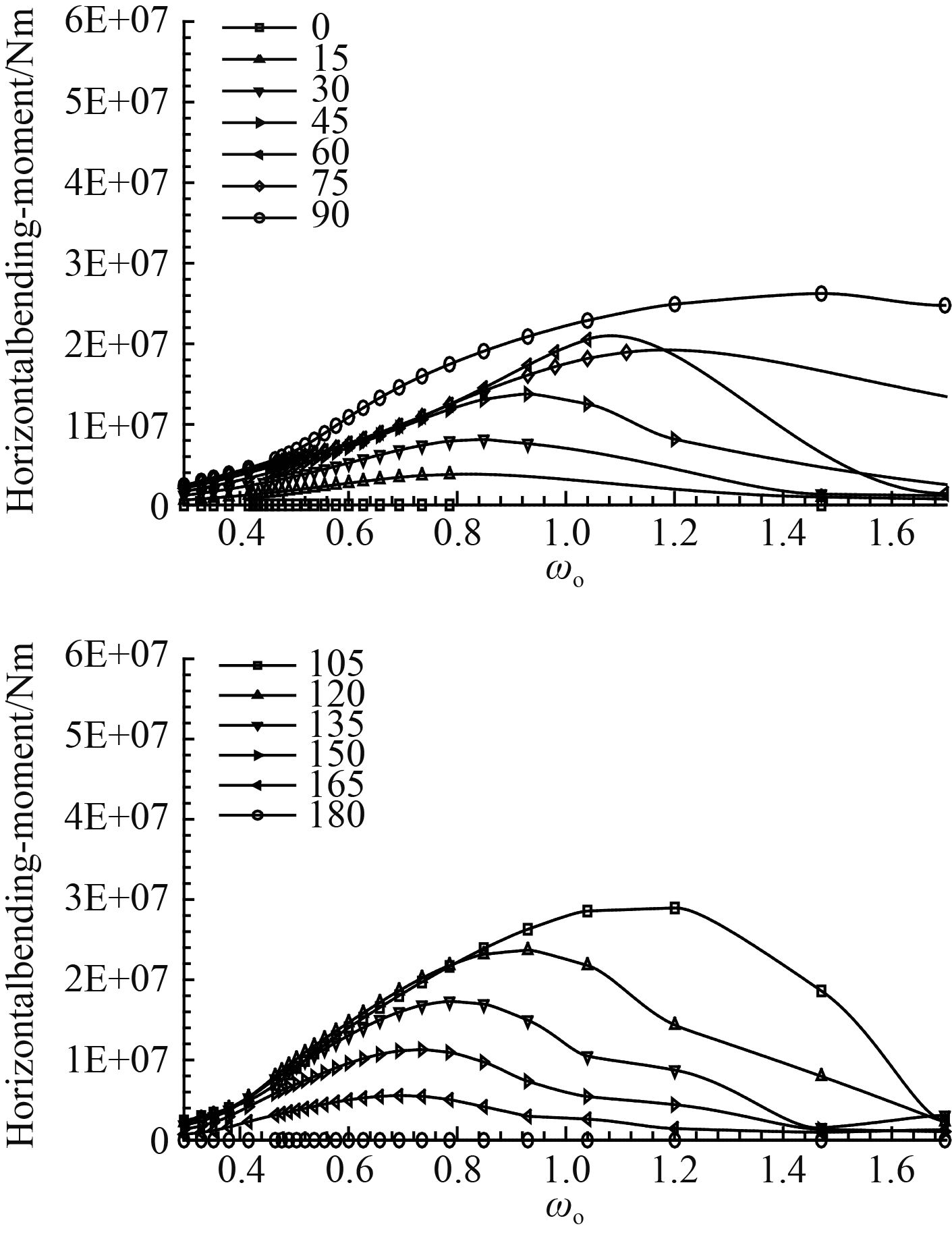
|
图 7 舱段尾横截面水平弯矩传递函数曲线 Fig. 7 The horizontal bending moment transfer function curve of stern in the cabin |
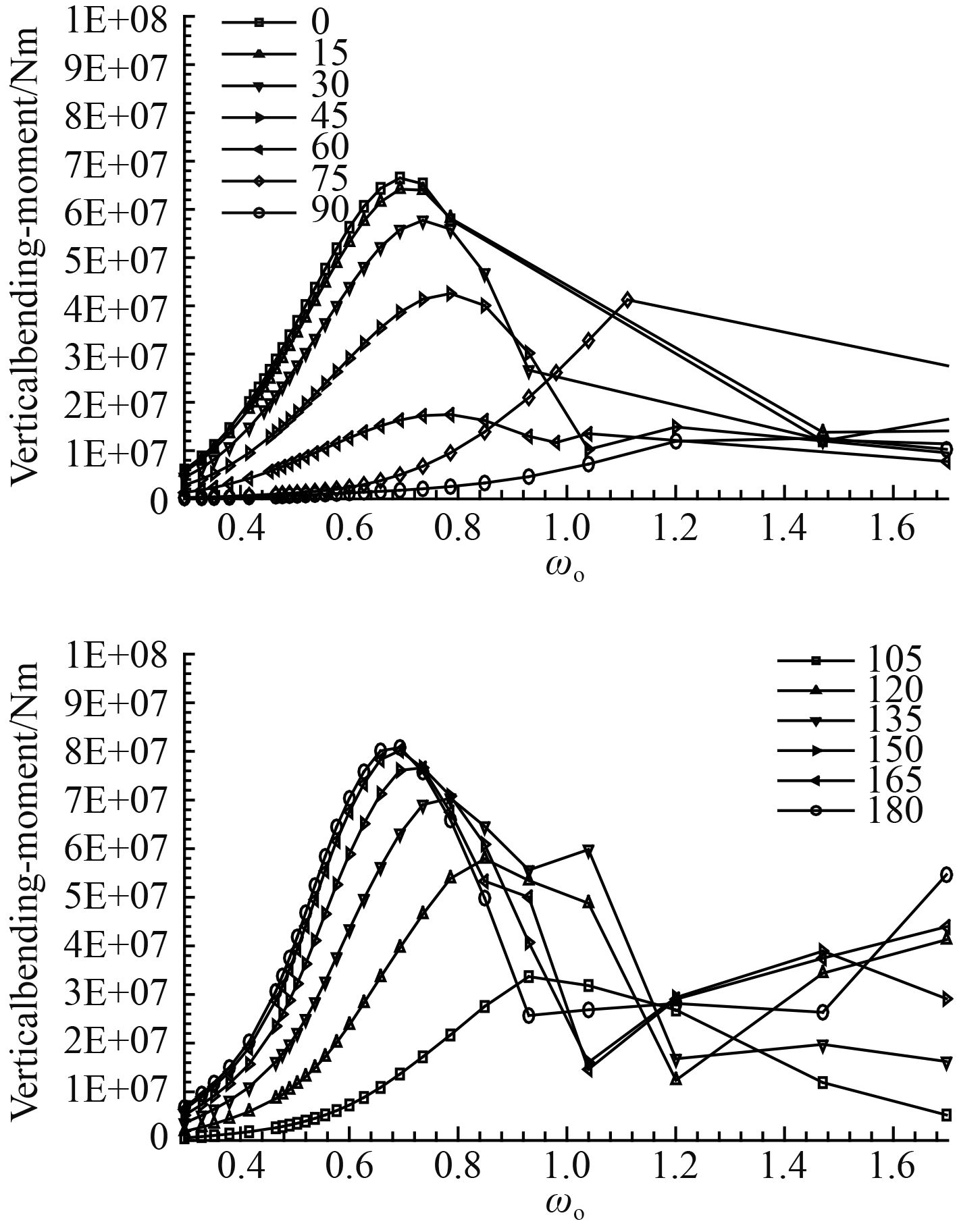
|
图 8 舱段尾横截面垂直弯矩传递函数曲线 Fig. 8 The vertical bending moment transfer function curve of stern in the cabin |
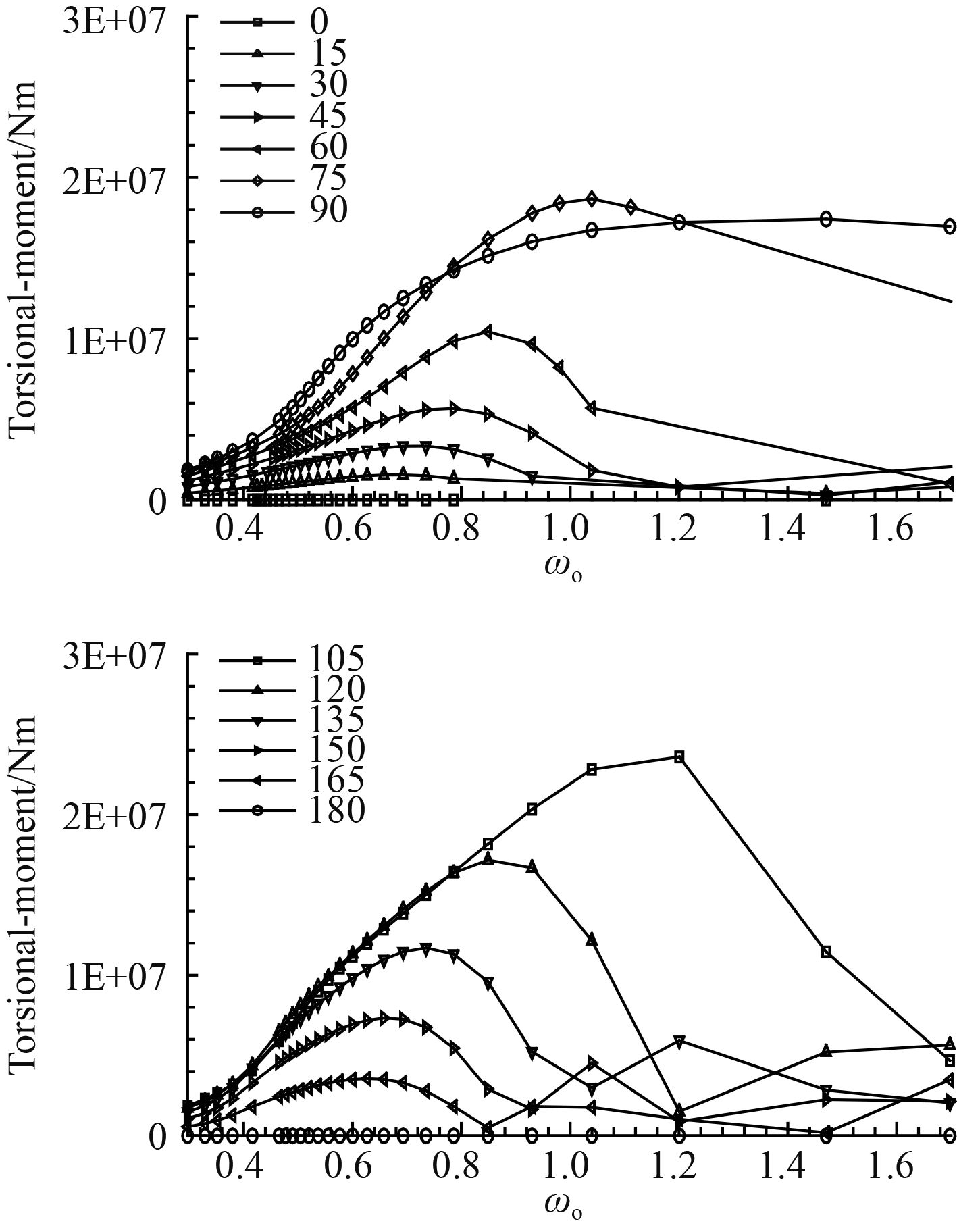
|
图 9 舱段尾横截面横向扭矩传递函数曲线 Fig. 9 The torsion moment transfer function curve of stern in the cabin |
根据船舶基本结构形式和结构疲劳分析要求,并参考《海洋工程结构物疲劳强度评估指南》中关于疲劳强度计算的规定,同时结合强度直接计算的结果,选取承受较大交变载荷的高应力区及构件连接部位的应力集中区域作为疲劳校核的部位。
最后在船中剖面选取了6个热应力点如表2所示,对选定的热应力点按照要求对有限元模型进行细化处理,部分细化效果如图10所示。
|
|
表 2 热应力点选取表 Tab.2 The selection of calculating point |
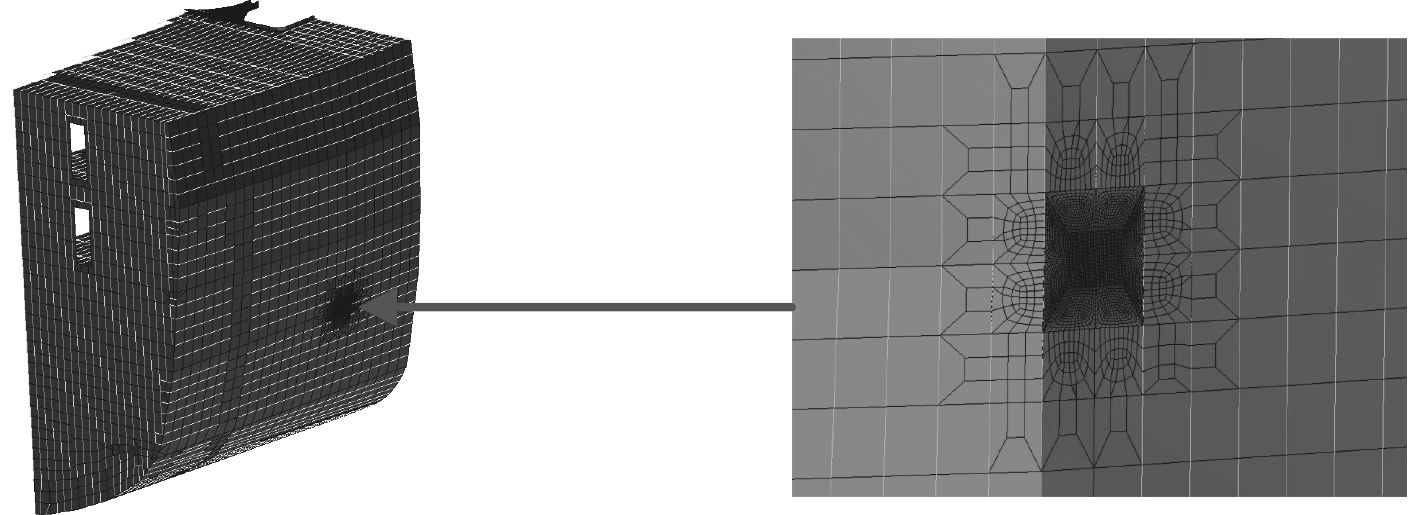
|
图 10 热应力点4的节点细化效果图 Fig. 10 The detail of the calculating point |
疲劳强度的有限元分析需要施加的载荷有波浪压力,惯性力,前后端面的水平弯矩、垂直弯矩、横向扭矩。惯性力的施加通过在整体坐标系中定义线加速度和角加速度来实现,每一个工况施加的具体值由水动力软件计算得出。前后端面的水平弯矩、垂直弯矩、横向扭矩施加在与端面关联的MPC点上,具体数值由水动力软件分析计算得出。波浪压力的添加采用PCL语言编制的加载程序进行模拟,加载效果如图11所示。

|
图 11 150°浪向角某工况湿表面波浪压力分布图 Fig. 11 Wave pressure distribution |
对于船舶与波浪组成的线性系统,应力响应服从线性系统的特征,由方程

|
图 12 热应力点的应力传递函数 Fig. 12 Stress transfer function curve of the calculating point |
本文对于船舶结构疲劳评估采用的波浪功率谱密度为两参数的Pierson-Moskowitz谱(简称P-M谱),P-M谱可以写成不同参数的表示形式,如果用有义波高和平均跨零周期2个参数来表示,波浪谱的表达式为:
| ${G_{\eta \eta }}(\omega ) = {H_s}^2\frac{{{T_z}}}{{8{\pi ^2}}}{\left(\frac{{\omega {T_z}}}{{2\pi }}\right)^{ - 5}}\exp \left[\frac{{ - 1}}{\pi }{\left(\frac{{\omega {T_z}}}{{2\pi }}\right)^{ - 4}}\right]{\text{。}}$ | (13) |
海浪谱
| ${S_\sigma }(\left. \omega \right|{H_s},{T_z},\theta ) = {\left| {{H_\sigma }(\left. \omega \right|\theta )} \right|^2} \cdot {S_\eta }(\left. \omega \right|{H_s},{T_z}){\text{。}}$ | (14) |
第
| ${m_n} = \int_0^\infty {{\omega ^n}} {S_\sigma }(\left. \omega \right|{H_s},{T_z},\theta ){\rm d}\omega {\text{。}}$ | (15) |
一般情况下只考虑主浪向–90°~90°之间的影响。借助波浪扩散函数,谱矩的计算公式可以进一步写为:
| ${m_n} = \int_0^\infty {\sum\limits_{\theta - 90^\circ }^{\theta + 90^\circ } {\left( {\frac{2}{\pi }} \right){{\cos }^2}\theta \cdot } {\omega ^n}} {S_\sigma }(\left. \omega \right|{H_s},{T_z},\theta ){\rm d}\omega{\text{。}} $ | (16) |
如果短期应力范围分布用Rayleigh分布表示,求得谱矩后,应力响应正跨零频率和带宽系数可以表示为:
| $f = \frac{1}{{2\pi }}\sqrt {\frac{{{m_2}}}{{{m_0}}}} {\text{,}}\;\;\; \varepsilon = \sqrt {1 - \frac{{{m_2}^2}}{{{m_0}{m_4}}}} {\text{。}}$ | (17) |
根据Miner的线性累积损伤理论,疲劳损伤是由一系列不同应力幅值的循环载荷引起的,用各短期分布疲劳累积损伤度的组合得到,考虑
| $D \!=\! \frac{{{v_0}{T_d}}}{{\bar a}}\Gamma \left(1 \!+\! \frac{m}{2}\right)\sum\limits_{n = 1}^{{N_{load}}} {{p_n}} \!\cdot\! \sum\limits_{i = 1}^{{n_S}} {\sum\limits_{j = 1}^{{n_H}} {{p_i} \!\cdot\! {p_j}} } \!\cdot\! {r_{ijn}}{(2\sqrt {2{m_{0ij}}} )^m} \leqslant \eta {\text{。}}$ | (18) |
疲劳寿命是设计寿命与疲劳累积损伤度的比值,计算结果如表3所示。由计算结果可知:1)在纵骨穿过强框架中,纵骨结构周围有大开口,并且只有该纵骨支撑,同时穿过其他骨材,细部支撑较弱,故而疲劳寿命最短;2)对于舷侧纵骨,水线以上纵骨比水线下纵骨受到更小的波浪影响,水线上纵骨的疲劳寿命更长;3)外底纵骨由于会承受因波浪载荷引起的交变载荷,故而寿命较短,而内底纵骨由于受到双层底结构内底支撑,故而疲劳寿命有所提高。
|
|
表 3 疲劳寿命计算结果表 Tab.3 The results of fatigue life calculation |
为保证船舶在航行过程中具有足够的疲劳强度安全裕度,在设计中对船舶危险剖面进行疲劳强度直接计算是十分必要的。本文采用基于谱分析法的直接计算法对船中舱段的疲劳强度进行评估,计算结果表明:1)热应力点的疲劳寿命能够满足设计使用年限要求,并且具备一定的安全裕度;2)舷侧热应力点的疲劳损伤度较小,疲劳寿命较大;3)甲板大开口和外底板十字接口处热应力点的疲劳损伤度较大,疲劳寿命较短,因此该处结构将是结构优化的重点区域。
| [1] |
冯国庆. 船舶结构疲劳强度评估方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2006.
|
| [2] |
肖桃云, 徐帅, 梅国辉, 等. 基于谱分析LNG船典型热点疲劳可靠性分析[J]. 海洋工程, 2010, 28(3): 37-43. DOI:10.3969/j.issn.1005-9865.2010.03.006 |
| [3] |
GARBATOV Y, SOARES C G. Assessment of the uncertainties introduced by different fatigue damage models for ship structural details[C]// International Conference on Offshore Mechanics and Arctic Engineering. 2010: 549–559.
|
| [4] |
曾文源. 舰船结构有限元参数化建模与优化研究[D]. 哈尔滨: 哈尔滨工程大学, 2005.
|
| [5] |
IIJIMA K, SHIGEMI T, MIYAKE R, et al. A practical method for torsional strength assessment of container ship structures[J]. Marine Structures, 2004, 17(5): 355-384. DOI:10.1016/j.marstruc.2004.08.011 |
| [6] |
OLAGNON M, GUÉDÉ Z. Rainflow fatigue analysis for loads with multimodal power spectral densities[J]. Marine Structures, 2008, 21(2-3): 160-176. DOI:10.1016/j.marstruc.2007.12.004 |
| [7] |
蒋志岩. 船舶结构疲劳评估及其应力分析方法研究[D]. 大连: 大连理工大学, 2004.
|
| [8] |
李敏. 综合补给船四舱段与三舱段有限元直接计算分析[D]. 上海: 上海交通大学, 2014.
|
| [9] |
朱胜昌, 陈庆强. 基于有限元力矩阵精确确定三舱段有限元模型边界力的计算方法[J]. 船舶力学, 2006, 10(1): 71-79. DOI:10.3969/j.issn.1007-7294.2006.01.010 |
| [10] |
丁宏, 陈美霞, 魏建辉, 等. 舱段截断时边界条件的选取方法[J]. 舰船科学技术, 2014, 36(2): 44-48. DOI:10.3404/j.issn.1672-7649.2014.02.010 |
 2018, Vol. 40
2018, Vol. 40
