船舶在水面航行,当受到较大的风载荷时,船舶的航向轨迹将发生偏移甚至有倾覆的危险,因此船舶的风载荷对船舶的操纵性能以及航行性能有较大的影响。同时当船舶在港口作业、系泊以及动力定位时,船舶受风载荷的影响更大。因此准确地计算评估船舶受到风载荷对预报船舶的运动显得尤为重要,同时对船舶的操纵性能、系泊性能以及航行安全性等方面也有密切的关联。计算风载荷主要有模型的风洞试验、经验公式以及数值计算。模型风洞试验是较为准确的计算风载荷的一种试验方法,通过将一定的小尺度的物理模型置于能够提供风环境的实验室来测量模型的受力继而获得风载荷,但该试验具有成本高、周期长等缺点[1]。
经验公式主要是在风洞试验的基础上对试验数据进行线性回归分析总结归纳得出来的计算方法,国外在这方面研究较早,Isherwood[2]通过对大量船模的风洞试验数据进行回归分析,提出了计算船舶风压力系数和风压力矩系数的回归公式;Blendermann[3 – 5]通过大量的风洞试验得到较为全面的风载荷数据,进而推导出船舶纵向风力、横向风力、首摇力矩和横倾力矩的计算公式;OCIMF通过对风洞试验数据的分析,得出一种计算某超大型油船的载荷计算公式;M.R.Haddara[6]基于神经网格技术,得出计算船舶风载荷的通用计算公式,并通过以某油船对该计算公式进行了验证,发现其精度很高。在国内,汤忠谷[7]通过对13条不同船型的模型在风洞中进行风洞试验,并测定船模的上层建筑的风压系数和风压中心位置,最终归纳出计算风压横倾力矩的计算公式;洪碧光[8]以50条船模风压系数的风洞试验数据作为回归样本,并采用易于得到的基本船型系数,得出了一种根据船型系数来估算风压系数的计算方法。
随着计算技术的快速发展,通过风洞试验的相关原理以及结合计算机流体力学(Computational Fluid Dynamic,CFD)理论的数值建模计算方法运用越来越广泛,以下是国内外研究学者的研究。在国外,James S.Forrest[9]以simple frigate shape(SFS)为研究对象,对其在风场进行数值建模,采用非定常并对时间步长做了相关的敏感性分析,最终计算了该模型的风压系数;Ignation[10]以某帆船为研究对象,通过选择不同湍流模型、不同网格密度对该模型的阻力和升力进行了数值计算,并与风洞试验值进行了对比,验证了该计算方法的可行性。在国内,蔡文山等[11]应用CFD数值计算方法对某大型油船在6级风况下的迎风阻力进行了数值计算,并将计算结果和范·伯利柯姆的计算方法进行了对比,发现吻合度较好;张金鹏等[12]基于ICEM和Fluent软件,对某大型集装箱船的上层建筑部分进行网格划分,分析了该船周围的流场和计算了该船在某工况下的风载荷,并与风洞试验结果进行了对比分析。
1 理论计算 1.1 Isherwood计算方法Isherwood根据各类商船有关压力的大量船模的风洞试验数据,并对不同类型船舶上层建筑的主要尺度参数值作了相关的统计计算和评估,结合相关理论对这些试验数据和统计值进行处理分析,从而获得计算风载荷力系数和力矩系数的计算公式,式(1)是Isherwood计算风载荷的公式。
| $\left\{ \begin{aligned} &{{\rm{C}}_x}\left( \theta \right) \!=\! {a_0} \!+\! {a_1}\frac{{2{A_S}}}{{{{{L}}^{^2}}_{}}} \!+\! {a_2}\frac{{2{A_f}}}{{{B^{^2}}}} \!+\! {a_3}\frac{{{L_{}}}}{B} \!+\! {a_4}\frac{S}{{{L_{}}}} \!+\! {a_5}\frac{d}{{{L_{}}}} \!+\! {a_6}m \text{,}\hfill \\ &{C_y}\left( \theta \right) \!=\! {b_0} \!+\! {b_1}\frac{{2{A_S}}}{{{{{L}}^{^2}}_{}}} \!+\! {b_2}\frac{{2{A_f}}}{{{B^{^2}}}} \!+\! {b_3}\frac{{{L_{}}}}{B} \!+\! {b_{_4}}\frac{S}{{{L_{}}}} \!+\! {b_5}\frac{d}{{{L_{}}}} \!+\!\! {b_6}\frac{{{A_{SS}}}}{{{A_S}}}\text{,} \hfill \\ &{C_N}\left( \theta \right) = {c_0} + {c_1}\frac{{2{A_L}}}{{{{{L}}^{^2}}_{}}} + {c_2}\frac{{2{A_f}}}{{{B^{^2}}}} + {c_3}\frac{{{L_{}}}}{B} + {c_{_4}}\frac{S}{{{L_{}}}} + {c_5}\frac{d}{{{L_{}}}}\text{。} \hfill \\ \end{aligned} \right.$ | (1) |
式中:
Blendermann等基于大量的风洞试验,从试验数据中进行反复回归分析获得了计算侧向、纵向以及首摇的风载荷系数的计算公式。另外,Blendermann在此基础上提出了变化风速下的风载荷计算方法。
| $\left\{ \begin{gathered} {C_x} = - {C_{d1}}\frac{{{A_L}}}{{{A_F}}}\frac{{\cos \theta }}{{1 - \displaystyle\frac{\tau }{2}\left( {1 - \displaystyle\frac{{{{\rm{C}}_{d1}}}}{{{C_{_{dq}}}}}} \right){{\sin }^2}\left( {2\theta } \right)}}\text{,} \hfill \\ {C_y} = - {C_{dq}}\frac{{\sin \theta }}{{1 - \displaystyle\frac{\tau }{2}\left( {1 - \displaystyle\frac{{{{\rm{C}}_{d1}}}}{{{C_{_{dq}}}}}} \right){{\sin }^2}\left( {2\theta } \right)}}\text{,} \hfill \\ {C_m} = \left[ {\frac{{{S_L}}}{L} - 0.18\left( {\theta - \frac{\pi }{2}} \right)} \right] \cdot {C_y}\text{。} \hfill \\ \end{gathered} \right.$ | (2) |
式中:
风载荷的数值计算采用基于RANS方法的质量守恒方程和动量守恒方程,本文以该两大方程作为求解该船舶几种运动的基本方程。
质量守恒方程:
| $\frac{{\partial \rho }}{{\partial {\rm{t}}}} + \frac{{\partial (\rho u)}}{{\partial x}} + \frac{{\partial (\rho v)}}{{\partial y}} + \frac{{\partial (\rho w)}}{{\partial z}} = 0\text{,}$ | (3) |
动量守恒方程:
| $\left\{ \begin{aligned} \frac{{\partial (\rho u)}}{{\partial t}} \!+\! div(\rho u\mathop u\limits^ \to ) \!=\! \frac{{\partial p}}{{\partial x}} \!+\! \frac{{\partial {\tau _{xx}}}}{{\partial x}} \!+\! \frac{{\partial {\tau _{yx}}}}{{\partial y}} \!+\! \frac{{\partial {\tau _{zx}}}}{{\partial z}} \!+\! {F_x}\text{,} \hfill \\ \frac{{\partial (\rho v)}}{{\partial t}} \!+\! div(\rho u\mathop u\limits^ \to ) \!=\! \frac{{\partial p}}{{\partial x}} \!+\! \frac{{\partial {\tau _{xy}}}}{{\partial x}} \!+\! \frac{{\partial {\tau _{yy}}}}{{\partial y}} +\! \frac{{\partial {\tau _{zy}}}}{{\partial z}} \!+\! {F_y}\text{,} \hfill \\ \frac{{\partial (\rho w)}}{{\partial t}} \!+\! div(\rho u\mathop u\limits^ \to ) \!=\! \frac{{\partial \rho }}{{\partial z}} +\! \frac{{\partial {\tau _{xz}}}}{{\partial x}} \!+\! \frac{{\partial {\tau _{yz}}}}{{\partial y}} + \frac{{\partial {\tau _{zz}}}}{{\partial z}} \!+\! {F_z}\text{,} \hfill \\ \end{aligned} \right.$ | (4) |
控制方程的通用形式:
| $\begin{split}&\frac{{\partial (\rho \phi )}}{{\partial t}} + \frac{{\partial (\rho u\phi )}}{{\partial x}} + \frac{{\partial (\rho v\phi )}}{{\partial y}} + \frac{{\partial (\rho w\phi )}}{{\partial z}} = \\&\frac{\partial }{{\partial x}}\left( {\Gamma \frac{{\partial \phi }}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {\Gamma \frac{{\partial \phi }}{{\partial y}}} \right) + \frac{\partial }{{\partial z}}\left( {\Gamma \frac{{\partial \phi }}{{\partial z}}} \right) + S{\text{。}}\end{split}$ | (5) |
式中:
本文选用的湍流模型为
| $ - \rho \overline {{{u'}_i}{{u'}_j}} = \mu \left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) - \frac{2}{3}\rho k{\delta _{ij}}\text{,}$ | (6) |
在
| $\left\{ \begin{gathered} \frac{\partial }{{\partial t}}(\rho k) + \frac{\partial }{{\partial {x_i}}}(\rho k{u_i}) = \frac{\partial }{{\partial {x_j}}}\left( {{\Gamma _k}\frac{{\partial k}}{{\partial {x_j}}}} \right) + {G_k} - {Y_k}\text{,} \hfill \\ \frac{\partial }{{\partial t}}(\rho w) + \frac{\partial }{{\partial {x_i}}}(\rho w{u_i}) = \frac{\partial }{{\partial {x_j}}}\left( {{\Gamma _k}\frac{{\partial w}}{{\partial {x_j}}}} \right) + {G_w} - {Y_w}\text{。} \hfill \\ \end{gathered} \right.$ | (7) |
采用某水面舰船的一定的缩尺比模型(见图1),其模型的无因次主尺度参数如表1所示。
|
|
表 1 无因次主尺度参数 Tab.1 Dimensionless principal scale parameter |

|
图 1 水上部分船体模型 Fig. 1 The main hull above water |
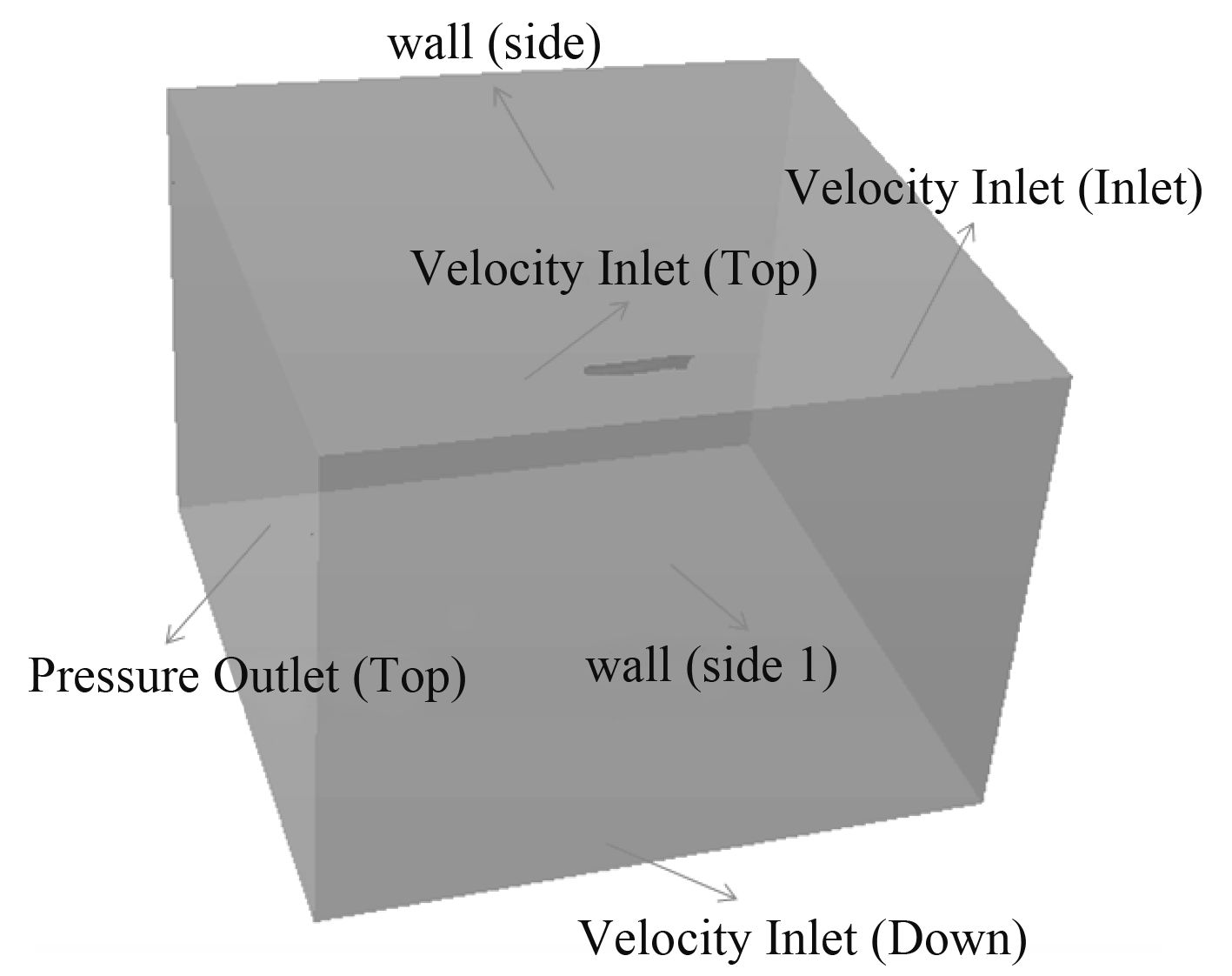
在CFD数值模拟中,根据设定的不同工况和需要模拟的船体运动情况来设定不同的边界条件。边界条件包括速度入口(Velocity Inlet)、压力出口(Pressure Outlet)、对称面(Symmetery)、壁面(Wall)、重叠网格(Overset Mesh)、质量流量进口(Stagnation Inlet)等,船模计算域的边界条件的设置见图2所示。
|
图 2 边界条件 Fig. 2 Boundary condition |
基于STAR-CCM+软件平台,对船体采用剪切非结构化网格,且对船体的首部和尾部的网格进行加密,流域的网格和船体的网格如图3所示。

|
图 3 船体网格及流域网格 Fig. 3 Grid of body and Fluid domain |
在数值模拟中,选取的风速分别为3.086 kn,3.637 kn,4.234 kn,4.86 kn,风向角选取为0°~180°间隔为15°共计13个角度。数值仿真计算每个风速每个风向角下船模受到的力和力矩,然后将其无因次化后取平均值便得到该船型的无因次风载荷系数。
本文对不同风速和不同风向角下该水面船模的水上部分模型的压力场和速度场进行了数值模拟,通过数值模拟发现,其实不同风速下的压力值或速度值只是数值的大小不同而已,数值仿真后现象基本一致,考虑本文工作量,只对风速为3.086 kn和风向角为0°,45°,90°,135°,180°等5个角度所对应的压力云图和速度云图进行分析,具体分析如图4和图5所示。

|
图 4 不同风向角下船体的压力云图 Fig. 4 The hull pressure nephogram under the different wind angle |
从图4中可知:压力最大值随风向角的变化而变化,当风向角为0°和45°时,压力最大值出现在尾部;当风向角为135°和180°时,压力最大值出现在首部,风向角为45°,90°,135°时船体表面的压力及船体周围的压力值小于风向角为0°,180°时的压力值。由于模型的风速较小,数值模拟船体表面压力值随梯度的变化不明显。

|
图 5 不同风向角下船体的速度云图 Fig. 5 The hull velocity nephogram under the different wind angle |
从图5中可知:当风向角为0°和45°时,在船尾部形成了速度漩涡,当风向角为135°和180°时,在船首部形成了速度漩涡;随着风向角由0°到180°逐渐增大,船体纵向切面的速度由大到小再到大的一个过程变化,因为速度是沿纵向切面发生变化的,所以在风向角为90°时,船体表面及其周围速度几乎一样;当风向角从90°开始增大时,船体周围的速度方向发生相反方向的变化。
3 计算结果的对比 3.1 计算结果的无量纲化基于长度的无因次风载荷系数计算公式为:
| $\left\{ \begin{gathered} {C_X} = \frac{{{F_X}}}{{\displaystyle\frac{1}{2}\rho {V_W}^2{L^2}}}{\rm{ }} \text{,}\hfill \\ {C_Y} = \frac{{{F_Y}}}{{\displaystyle\frac{1}{2}\rho {V_W}^2{L^2}}}{\rm{ }} \text{,}\hfill \\ {C_N} = \frac{{{N_{}}}}{{\displaystyle\frac{1}{2}\rho {V_W}^2{L^3}}} \text{。}\hfill \\ \end{gathered} \right.$ | (8) |
式中:
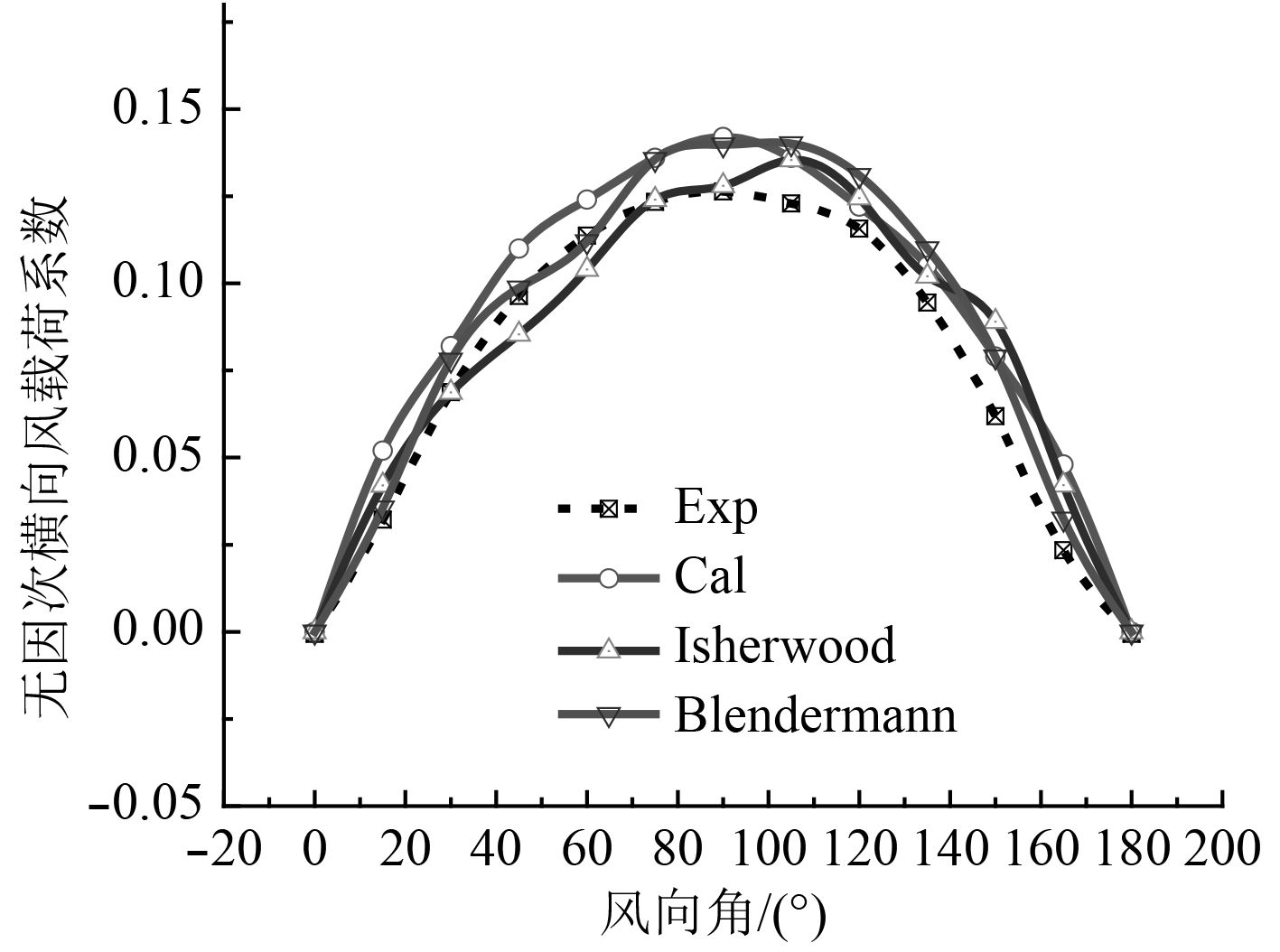
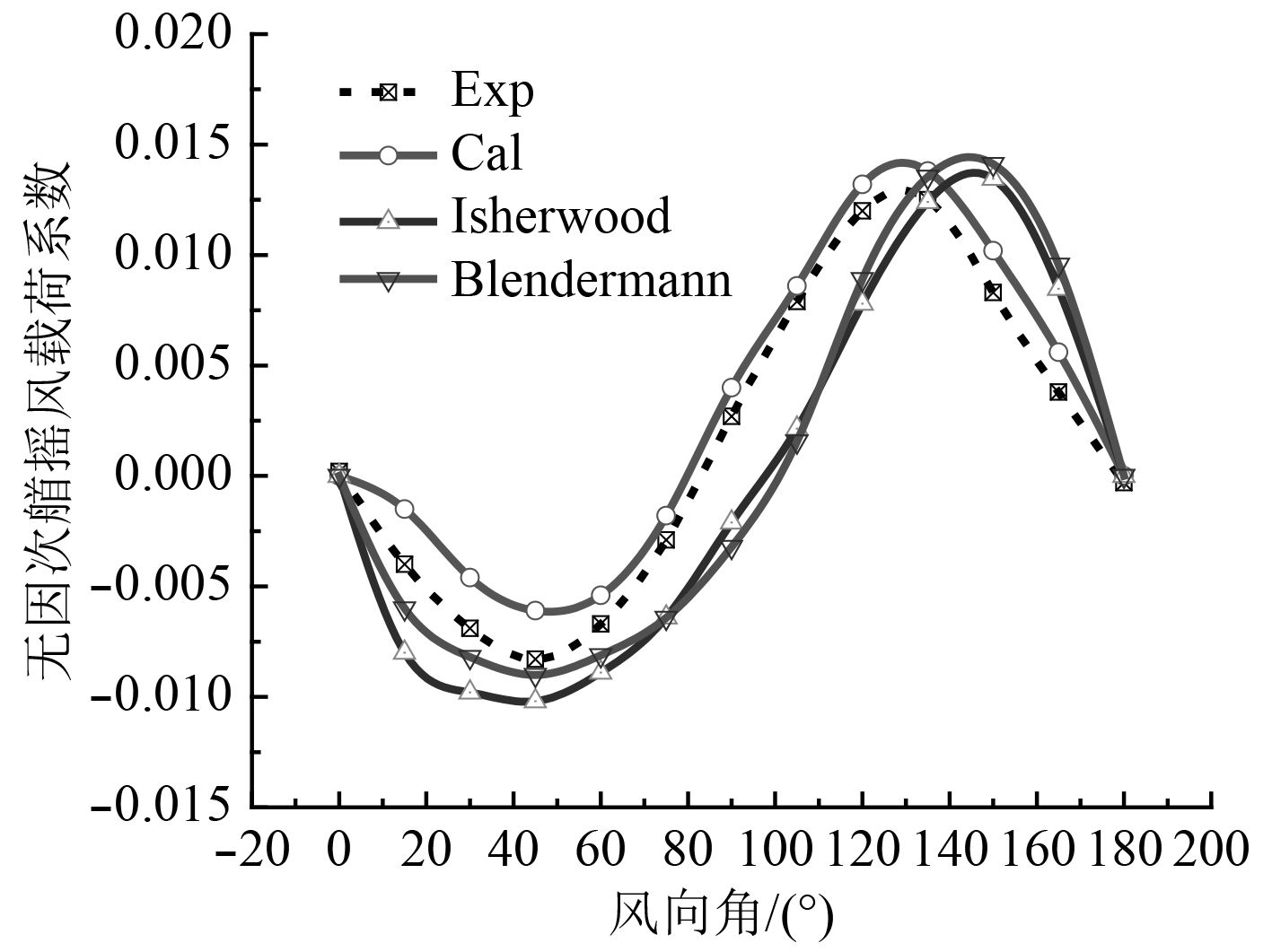
图6~图8分别给出了该水面船模的无因次风载荷系数

|
图 6 无因次纵向风载荷系数CX随风向角的变化曲线 Fig. 6 The changing curve of the coefficient of dimensionless lengthways wind load CX with the wind direction angle |
|
图 7 无因次纵向风载荷系数CY随风向角的变化曲线 Fig. 7 The changing curve of the coefficient of dimensionless crosswise wind load CY with the wind direction angle |
|
图 8 无因次风载荷系数CN随风向角的变化曲线 Fig. 8 The changing curve of the coefficient of dimensionless wind load CN with the wind direction angle |
从图6~图8可知:无因次风载荷系数
对于无因次横向载荷系数
对于无因次首摇风载荷系数
分析误差产生较大的原因,数值计算精度有待进一步提高,Isherwood和Blendermann这种按经验公式的计算方法,公式中对某种船型参数的系数还需不断结合试验数据进行修正。
4 结 语本文以某水面舰船为研究对象,对其风载荷采用风洞试验、数值仿真、经验公式中的Isherwood法和Blendermann法这4种计算方法进行计算,其中将实验值和仿真值进行无因次化,得到了该水面舰船模型的纵向、横向以及首摇的无因次风载荷系数,主要得出以下结论:
1)通过与风洞试验数据的比对,发现无论是纵向、还是横向以及首摇的无因次风载荷系数,另外3种计算方法的变化规律基本一致,从而说明了Isherwood和Blendermann的经验公式法以及数值仿真计算方法的可行性;
2)与试验结果对比进行误差分析,发现数值仿真的误差最小,Isherwood方法其次,Blendermann方法的误差最大。由此可见经验公式法可作为参考,而对于工程应用应采用数值计算或者模型的风洞试验。
| [1] |
陈前昆, 尹奇志, 孙星. 船舶风载荷研究进展及发展趋势[J]. 武汉理工大学学报(交通科学与工程版), 2015(4): 19-25. |
| [2] |
ISHERWOOD RM. Wind resistance of merchant ship[J]. The Royal Institution of Naval Architects, 1972(112): 327-338. |
| [3] |
BLENDERMANN W.Wind loads on moored and manoeuvuring vessels[C]//Proceedings of the 14th International Conference on Offshore Mechanics and Arctic Engineering(OMAE) , New York:ASME,1993, (1): 183.
|
| [4] |
BLENDERMANN W. Parameter identification of wind loads on ships[J]. Journal of Wind Engineering and Industrial Aero-dynamics, 1994(2): 339-351. |
| [5] |
BLENDERMANN W. Estimation of wind loads on ships in with a strong gradient[C]//Proceedings of the 14th International Conference on Offshore Mechanics and Arctic Engineering(OMAE),New York:ASME, 1995, (1A): 271–277.
|
| [6] |
OCIMF.Prediction of wind loads and current loads on VLLCC[M].London: Withertby Co.Ltd,1994.
|
| [7] |
汤忠谷. 水面船舶的空气动力[J]. 武汉水运工程学院学报, 1982, 18(4): 79-89. |
| [8] |
洪碧光. 船舶风压系数的计算方法[J]. 大连海运学院学报, 1991, 17(2): 113-121. |
| [9] |
JAMES S F.. An investigation of ship airwakes using detached eddy simulation[J]. Computers&Fluids, 2010(39): 656-673. |
| [10] |
IGNATION Maria Viola. Downwind sail aerodynamics:A CFD investigation with high grid resolution[J]. Ocean Engineering, 2009(36): 974-984. |
| [11] |
蔡文山, 董国祥, 杨春勤, 等. 船舶风载荷数值计算及风洞试验[C]//第二十五届全国水动力学研讨会暨第十二届全国水动力学学术会议文集, 2013.
|
| [12] |
张金鹏. 大型集装箱船风载荷理论分析及计算[D]. 哈尔滨: 哈尔滨工程大学, 2012.
|
 2018, Vol. 40
2018, Vol. 40
