空泡水筒是开展船舶螺旋桨特性研究的主要实验设备,现在的空泡水筒一般都采用吊舱式动力仪进行螺旋桨水动力试验测量。动力仪的存在和空泡水筒的有限空间使试验研究和无限水域中的螺旋桨存在差异,这也是空泡水筒存在阻塞效应的主要原因。上海交通大学新空泡水筒于2014年投入使用,其试验段长6.1 m,截面是1 m×1 m的正方形。如前所述,新空泡水筒在测量中也会存在阻塞效应,因此有必要对其开展阻塞效应修正的研究。
对于风洞或者水洞的阻塞效应,国内外已经开展了相关研究。Herriot等[1]对回转体和机翼在风洞中的阻塞效应修正方法进行了理论研究,并将总修正系数分为固体和尾流两部分修正系数之和。Hackett等[2]提出了一种估算低速风洞中阻塞效应的方法:首先在流场中布置源汇,并测量风洞侧壁静压,然后利用压力特性来求解源汇强度,最后给出固体和尾流阻塞效应的轴向分布。2011年,Ross等[3]在风洞中对风力涡轮机的尾流和固体阻塞效应展开研究,研究中通过试验段侧壁的静压导出速度增量来研究限制空间内的阻塞效应。Chen等[4]在风洞中对风力涡轮机进行试验并分析了阻塞效应对功率系数的影响,试验中用毕托管测量压力并由伯努利方程计算速度。庞加斌等[5]在风洞中研究了汽车模型阻塞比、体积大小及试验段尺寸对阻塞系数的影响并给出了经验修正方法。王磊等[6]在风洞中对不同尺度的建筑模型进行测压试验,分析了阻塞效应的影响程度并给出了风速修正方法。黄剑等[7]在风洞中对不同尺寸的群体建筑进行了测压试验,分析了阻塞效应影响规律,并利用尾流面积法进行阻塞效应修正。谢克振等[8]在拖曳水池中对10条船模进行阻力试验并研究阻塞效应影响,分析比对了8个阻塞效应修正公式的适用性。赵大刚等[9]采用RANS方法研究在不同阻塞比下阻塞效应对船舶性能的影响规律,并对阻塞效应修正给出了建议。Bahaj等[10]在空泡水筒和拖曳水池中对海流发电机进行了试验,并对尾流阻塞效应进行了修正。黄国燕[11]等采用RANS方法对空泡水筒筒壁效应展开研究,计算对象为P4119桨,通过改变筒径得到不同阻塞比下螺旋桨的性能曲线并与试验值进行比较,最后对筒壁效应修正给出了建议。周景军等[12]对通气超空泡水洞试验进行了CFD数值研究,分析了阻塞效应形成机理并对后续试验提出了建议。
综合来看,国内外对空泡水筒的阻塞效应研究仍然比较少。本文以上海交通大学新空泡水筒为研究对象,采用势流和RANS耦合的方法预报某7叶螺旋桨桨盘面处的实效伴流场,并以此修正螺旋桨进速实现空泡水筒的阻塞效应修正。在本文研究中,首先通过面元法对7叶螺旋桨进行定常计算,将其力场插值到RANS网格中进行体积力模型计算,然后将螺旋桨上游2个盘面的流场线性外插得到桨盘面的实效伴流场,最后根据实效伴流分数对螺旋桨的进速系数进行修正,从而实现空泡水筒到敞水结果的阻塞效应修正。
1 数值方法 1.1 螺旋桨水动力性能预报面元法本文采用低阶速度势面元法计算均流中螺旋桨的力场分布。面元法将空间问题转化到物面上求解,其基本控制方程和求解过程可参考文献[13–15]等。本文面元法计算由作者所在研究组开发的程序进行,计算中螺旋桨尾涡面采用线性尾涡,桨叶在随边处满足压力库塔条件。
本文计算螺旋桨的主要几何参数如表1所示。在面元法计算中,桨叶径向和弦向各布置20个单元,尾涡上布置80个单元,螺旋桨表面面元离散如图1所示。
|
|
表 1 计算螺旋桨的主要几何参数 Tab.1 Main parameters of calculated propellers |
本文计算工况为

|
图 1 螺旋桨离散面元 Fig. 1 Discrete panel of propeller |
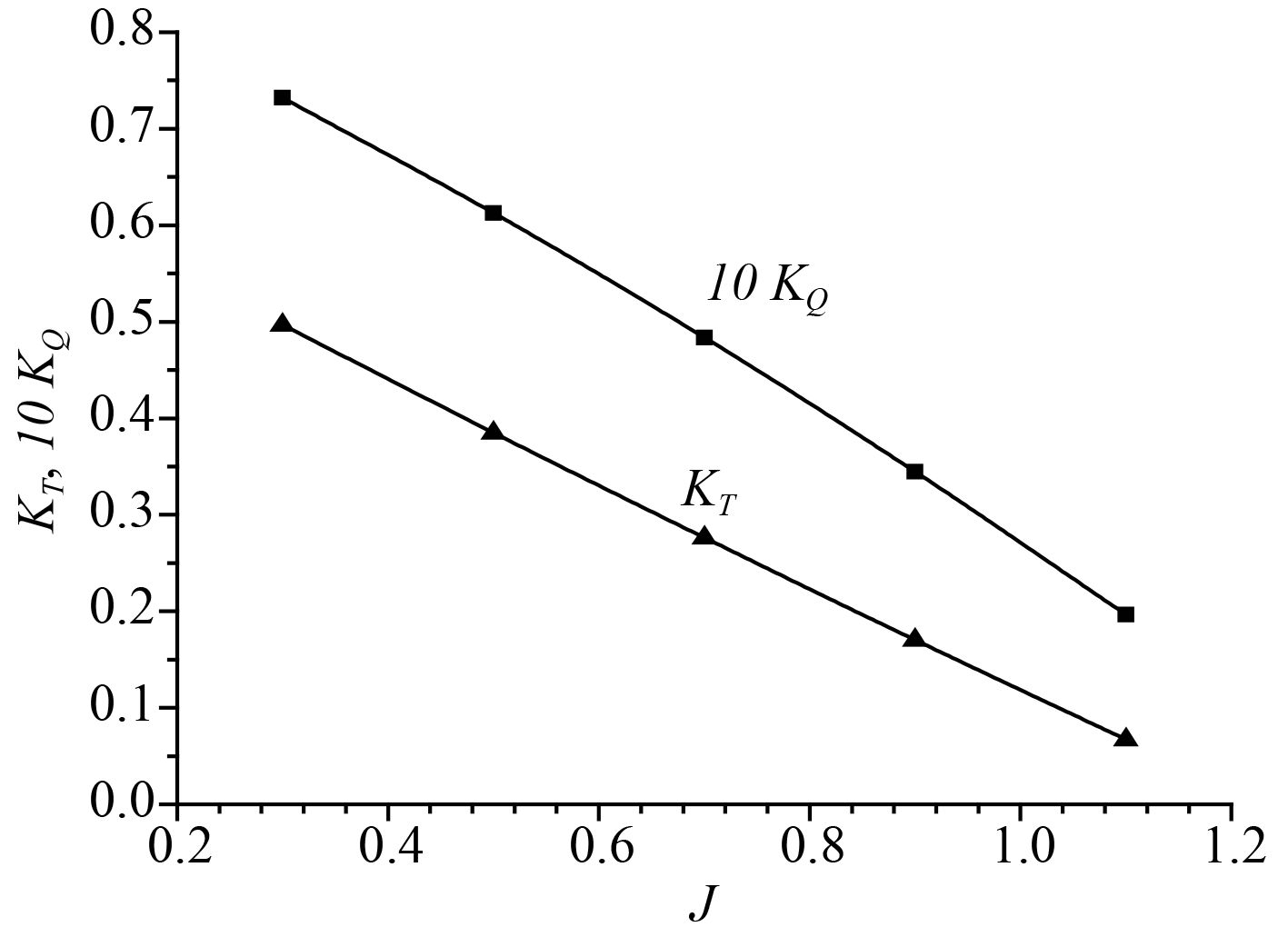
|
图 2 面元法计算螺旋桨敞水性能曲线 Fig. 2 Open water performance curves calculated by panel method |
螺旋桨在空泡水筒和敞水中的性能采用RANS方法计算,湍流采用SST
图3为空泡水筒中的体积力计算模型。螺旋桨在空泡水筒中的作用采用体积力来表达,体积力区域为螺旋桨桨叶轮廓绕桨轴旋转得到的回转体。为了使边界层及尾流场得到充分发展,空泡水筒的计算模型在试验段的上下游各延长了1倍试验段长度。流场的入口处采用流量入口边界条件,出口处采用压力出口边界条件。整个计算域采用六面体单元进行离散,加载体积力区域网格单元数约14.8万,体积力模型和动力仪组成的核心区域网格单元总数约354万,外部网格单元数约265万。在本文的计算工况中,空泡水筒表面的
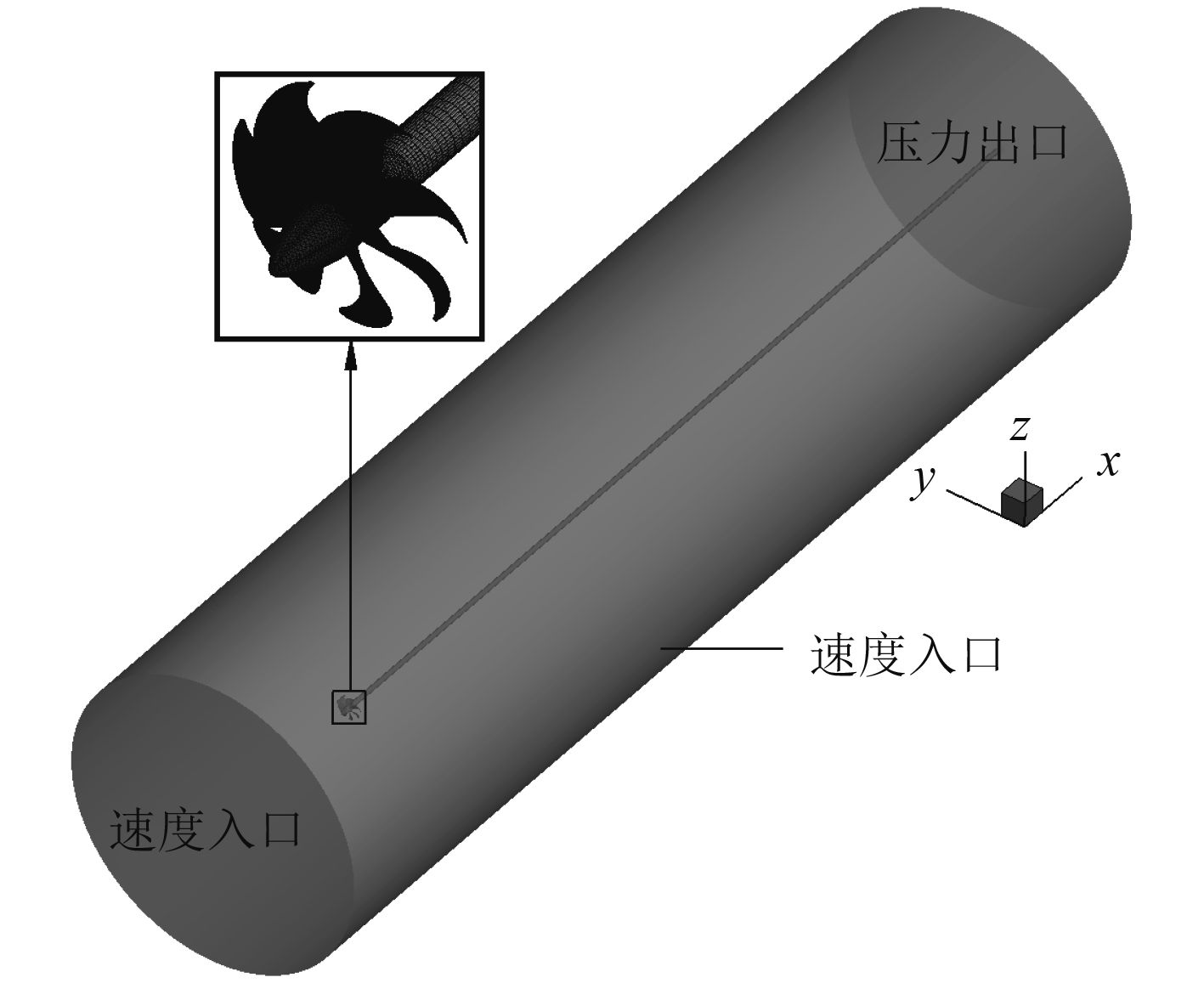
图4为敞水中的体积力计算模型。计算域的速度入口距桨盘面为8D,压力出口距桨盘面为37.4D,远场为速度入口距离桨轴线6D。整个计算域采用六面体单元进行离散,体积力区域及其附近网格与空泡水筒中的体积力计算模型(见图3)保持一致,外部网格单元数约755万。
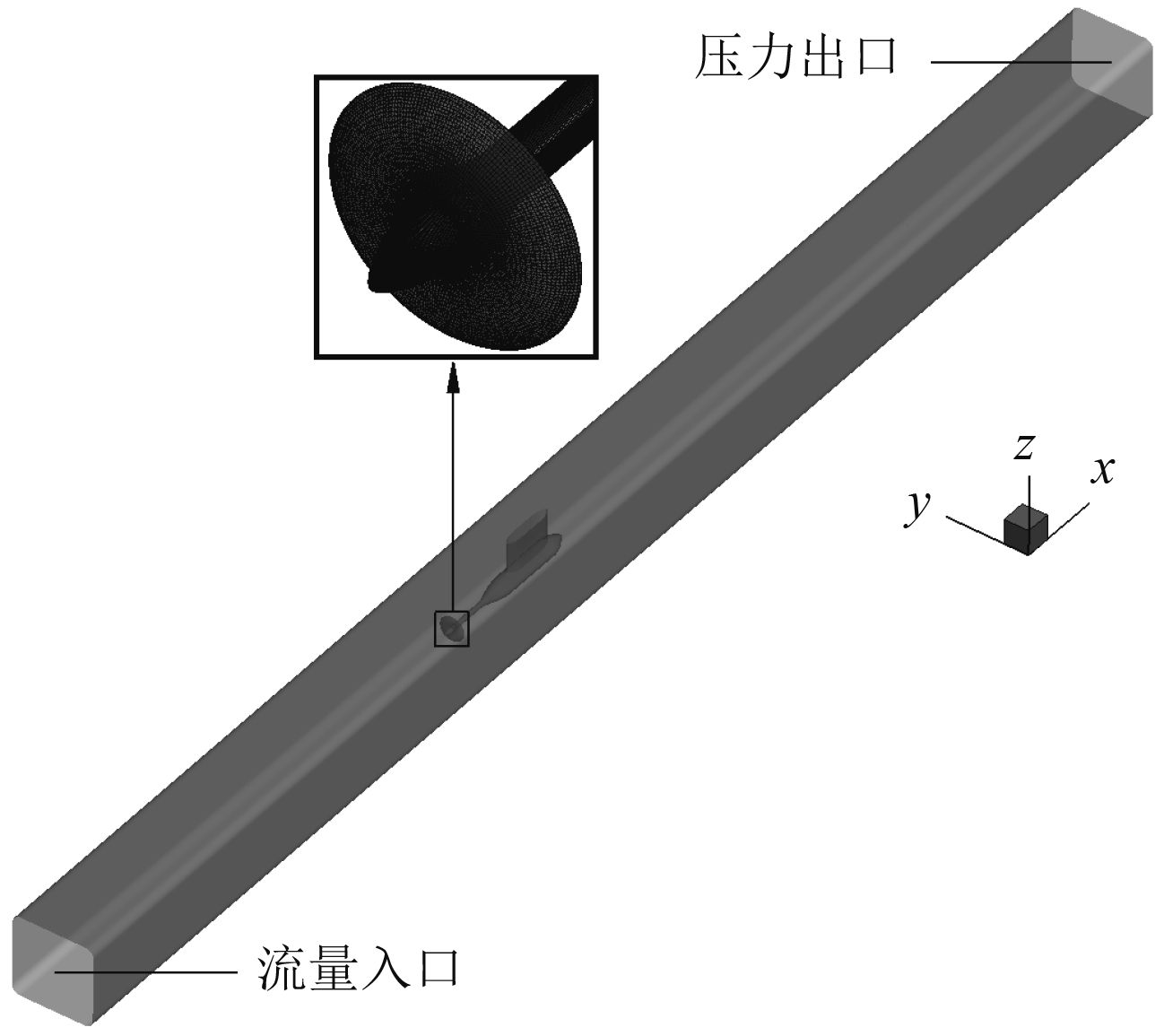
|
图 3 空泡水筒体积力计算模型 Fig. 3 Body force calculation model in cavitation tunnel |
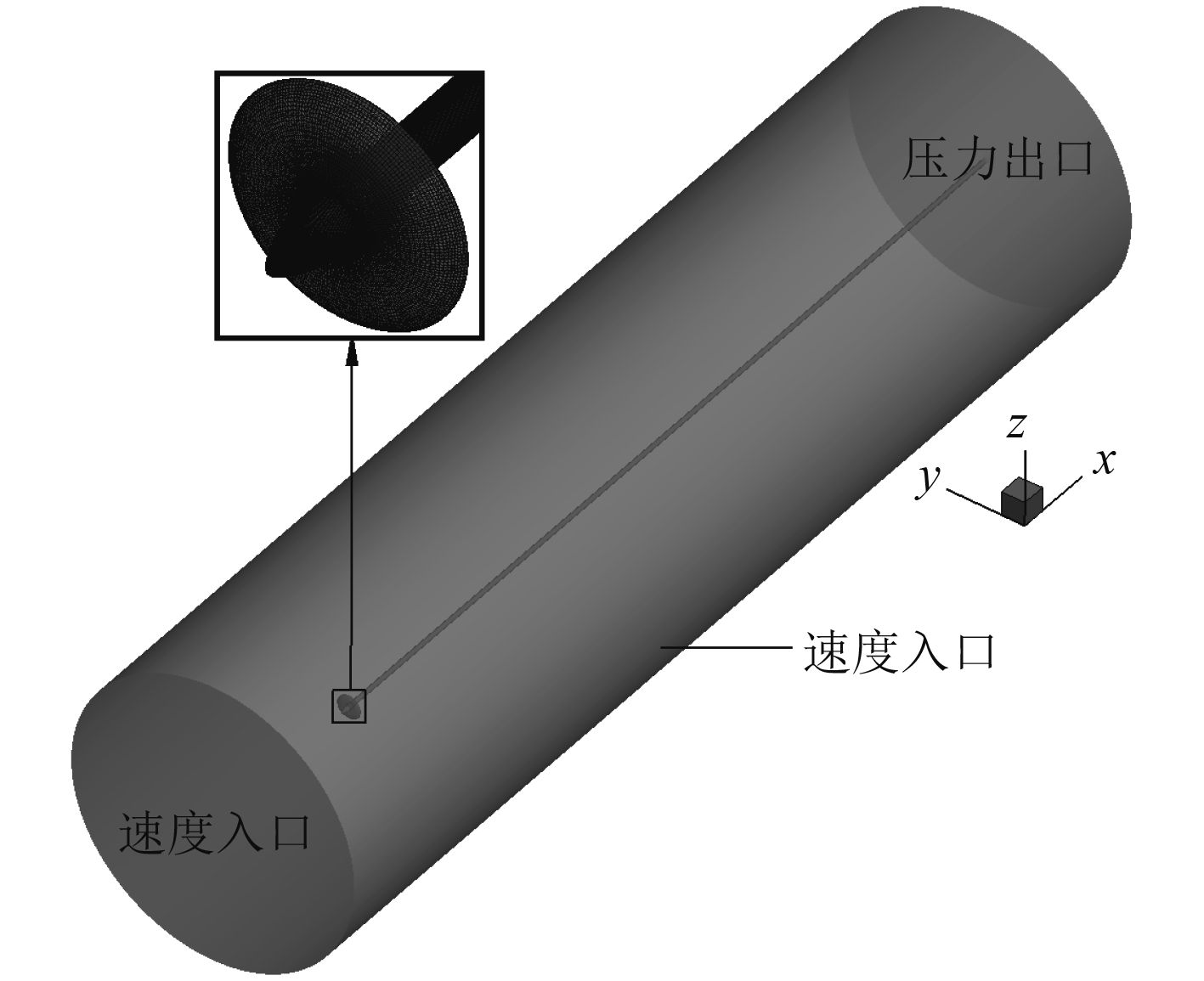
|
图 4 敞水体积力计算模型 Fig. 4 Body force calculation model in open water |
图5为真实螺旋桨在空泡水筒中的数值计算模型。计算域大小及边界条件同图3,仅将加载体积力区域及其附近网格替换为真实螺旋桨,该区域采用四面体单元离散,网格单元总数约2 496万,单片桨叶面网格数约22.5万,桨叶及桨榖表面的
图6为真实螺旋桨在敞水中的数值计算模型。计算域大小及边界条件同图4,螺旋桨所在区域网格与图5保持一致,外部用棱柱网格和六面体网格填充,外部网格单元总数约208万。
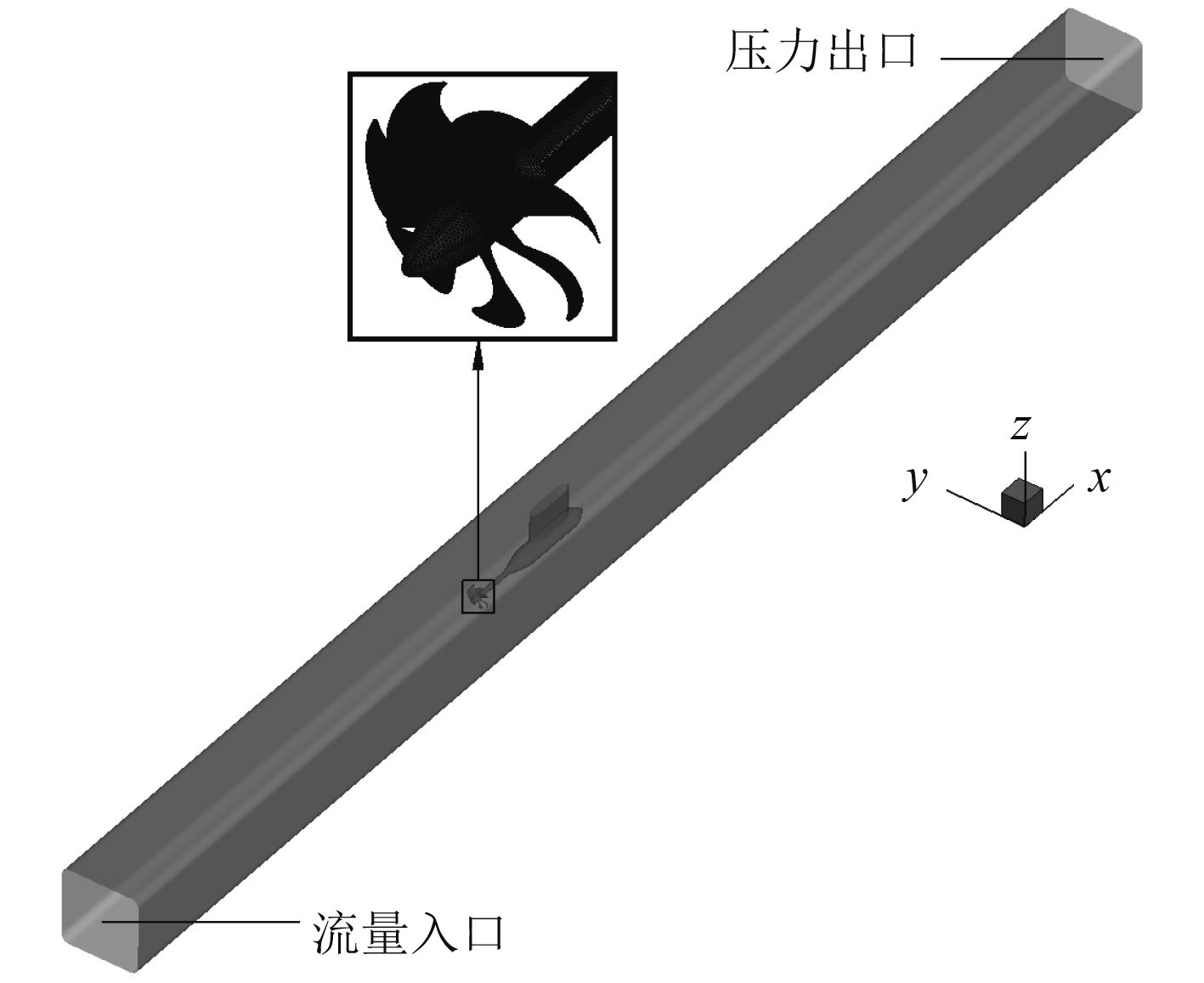
|
图 5 真实螺旋桨空泡水筒计算模型 Fig. 5 Real propeller calculation model in cavitation tunnel |
|
图 6 真实螺旋桨敞水计算模型 Fig. 6 Real propeller calculation model in open water |
由于面元法和RANS计算模型的网格不一致,因此如何将面元法计算的力场准确插值到RANS模型中成为了一个关键问题。Sánchez-Caja等[17]对渔船进行粘势耦合计算时,轴向仅布置一层网格,将升力线法计算所得周向平均后的力场直接进行赋值。Starke等[18]将面元法计算的螺旋桨力场做周向平均后线性插值到RANS网格,文中提到插值可能存在的问题并给出了修正建议。Tian等[19]提出了一种守恒插值方法进行力场插值,但在插值过程中需要将势流单元分割和重组,因而插值过程略显复杂。
本文采用Rao等[20]提出的基于径向基函数的插值方法将面元法力场插值到RANS网格中。RANS网格中加载体积力的区域见图3和图4,在该体积域内体积力的分布只做周向平均化处理,而在轴向和径向的分布则通过插值得到。该插值方法计算过程快速,插值结果精度高,满足本文的计算要求。
2 标称伴流的计算与分析本节计算空泡水筒中标称伴流场分布。在计算中,试验段入口速度与螺旋桨在
| $w = \frac{{\int_0^{2\pi } {\int_{{r_h}}^R {\left( {1 - \frac{{{V_x}\left( {r,\theta } \right)}}{V}} \right)r{\rm{d}}r{\rm{d}}\theta } } }}{{\int_0^{2\pi } {\int_{{r_h}}^R {r{\rm{d}}r{\rm{d}}\theta } } }}{\text{。}}$ | (1) |
式中:
计算中通过多次调整流量使试验段入口速度
|
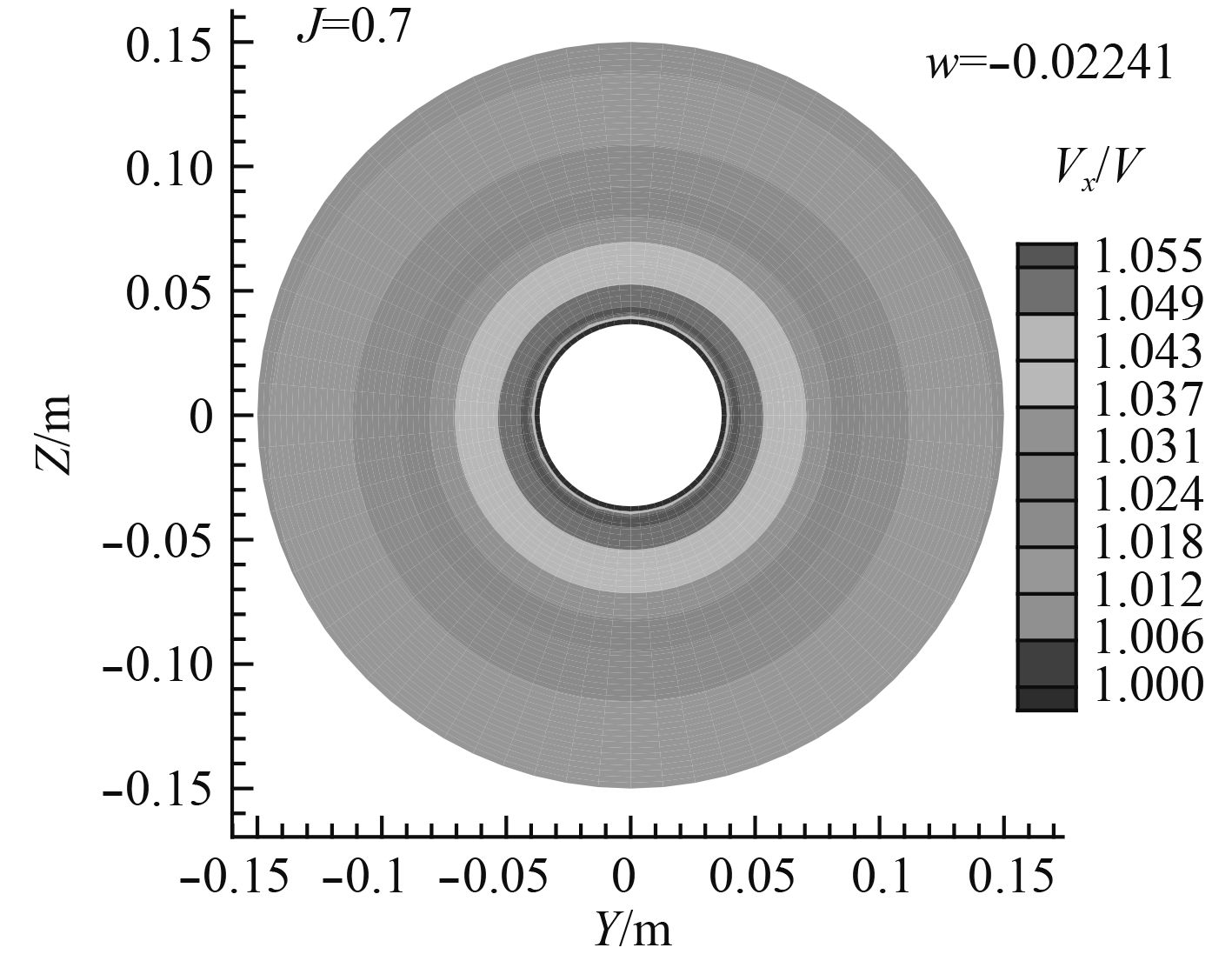
图 7
|
|
图 8
周向平均的
|
标称伴流的计算仅仅考虑动力仪在空泡水筒中的影响。从图7中可以看出,桨盘面中靠近桨毂边界层的轴向速度较低,边界层外的轴向速度均略高于来流速度。
从图8看出,对同一径向位置,
实效伴流是考虑螺旋桨作用的桨盘面处伴流。这里首先采用空泡水筒中的体积力模型(见图3)计算桨盘面处的流场,再从该流场中扣除螺旋桨的诱导速度场即可得到实效伴流场。而螺旋桨的诱导速度则通过敞水中的体积力模型(见图4)计算得到。实效伴流场得到后,可按照式(1)计算整个桨盘面的实效伴流分数,计算工况同标称伴流场计算。
在流场的实际计算中,本文参考文献[18]的做法,在桨盘面上游
|
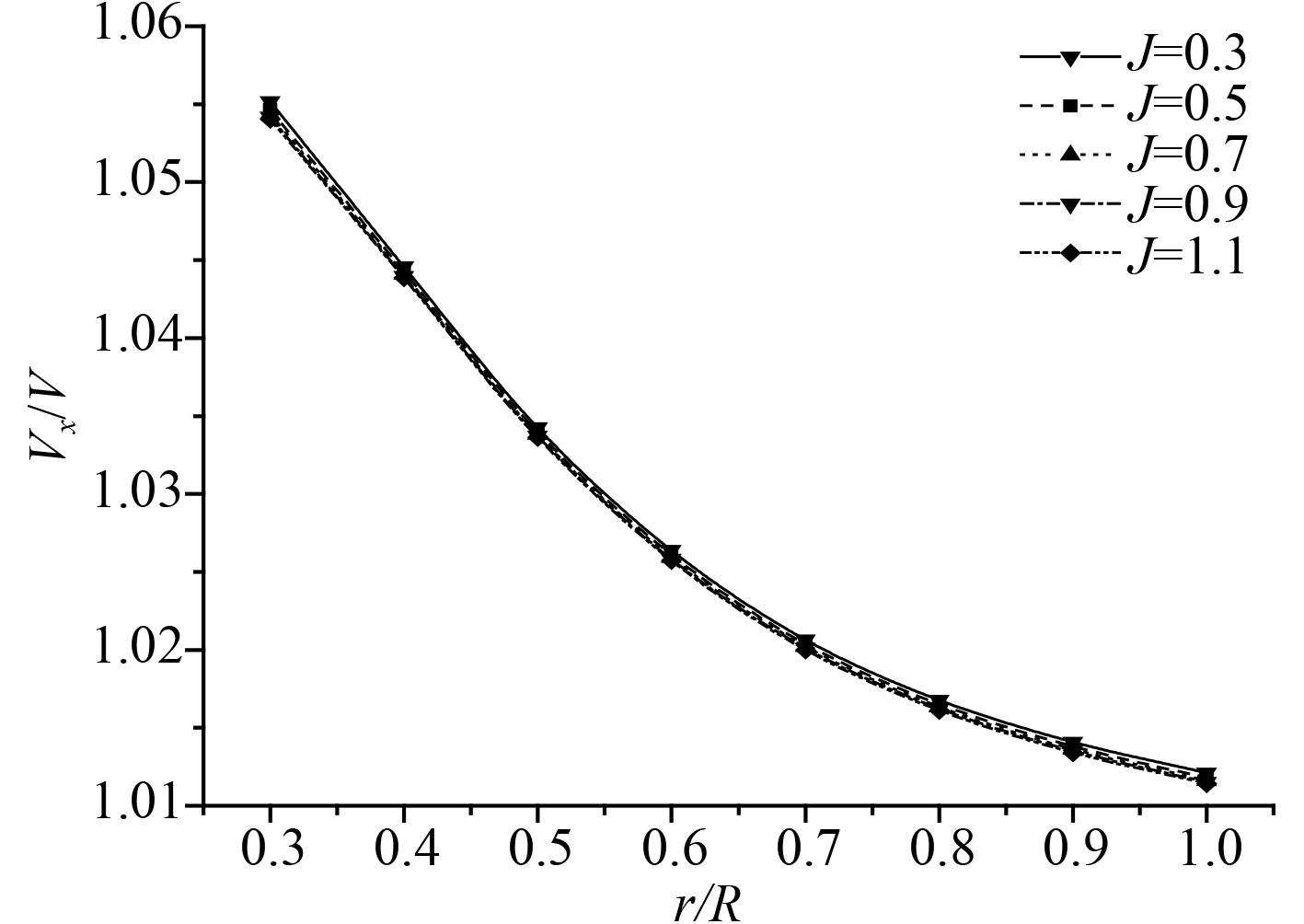
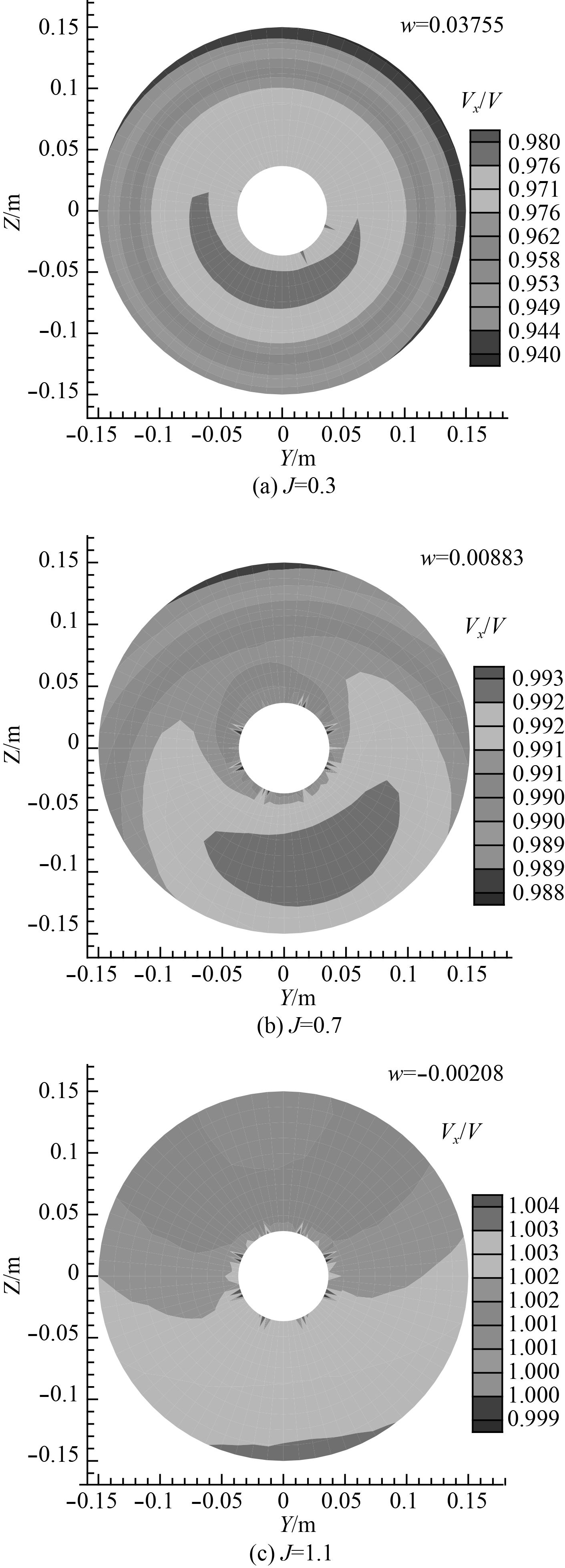
图 9
|
|
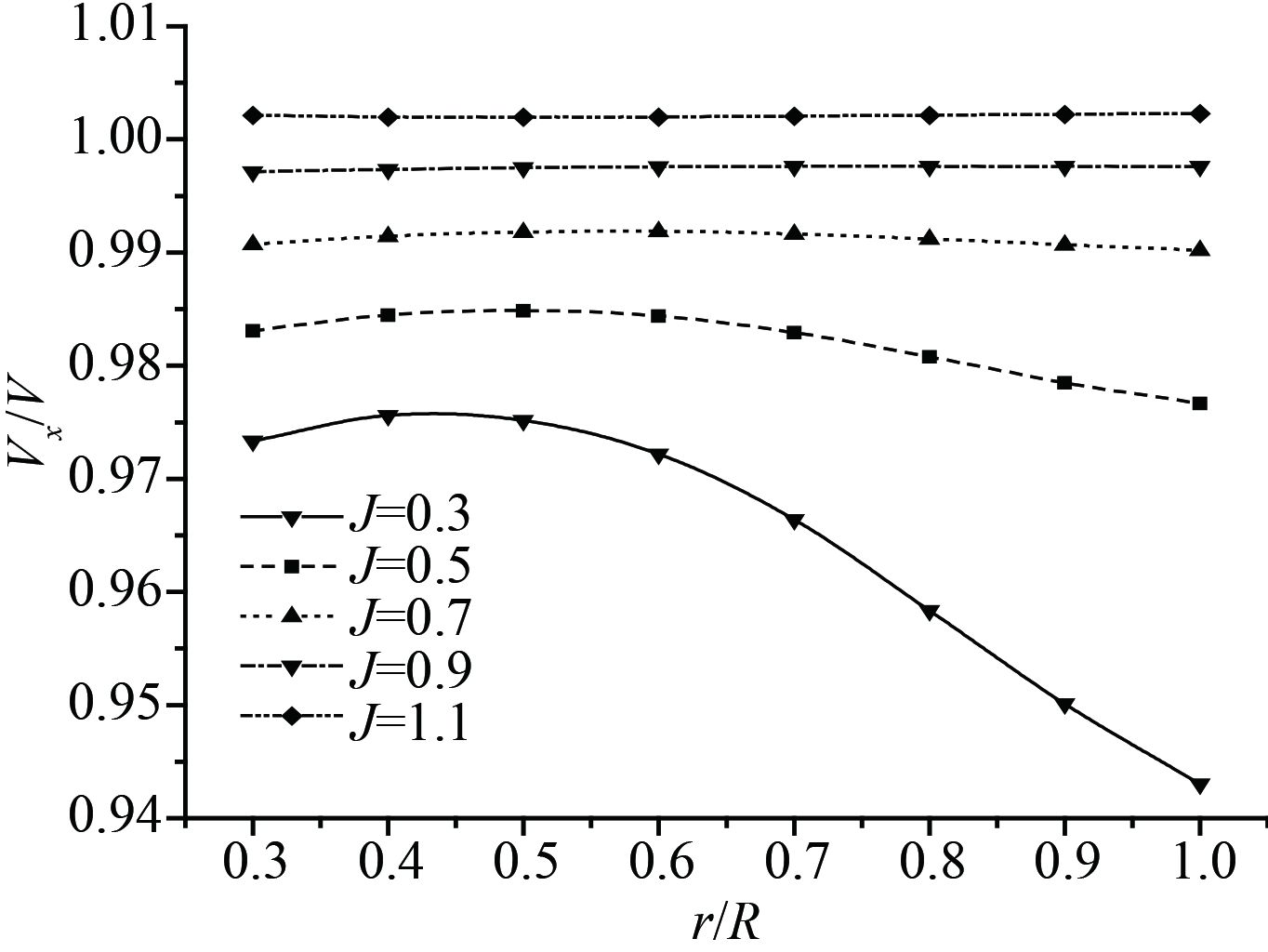
图 10
周向平均的
|
图9选取
图10为所有计算工况下周向平均的
整个桨盘面的实效伴流分数
|
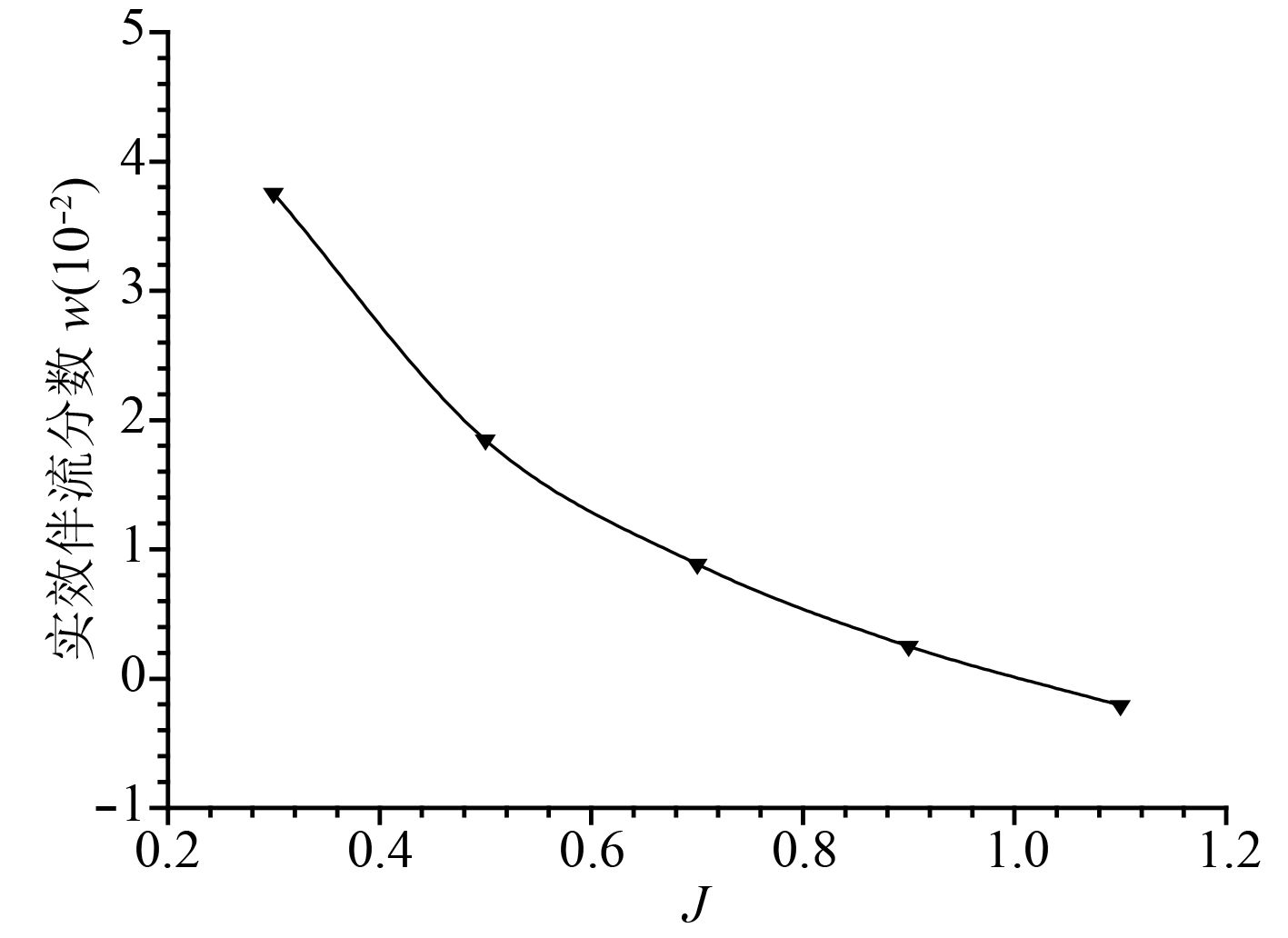
图 11
桨盘面的实效伴流分数
|
根据图11可拟合得到实效伴流分数
| $w \!\!=\!\! 0.109\;4\! \!-\! 0.375\;1J\!\! +\!\! 0.569\;4{J^2} \!\!-\!\! 0.428\;0{J^3}\!\! +\! \!0.124\;2{J^4}{\text{。}}$ | (2) |
为修正空泡水筒阻塞效应并验证修正结果,除了采用体积力模型在空泡水筒及敞水中进行计算外,还对真实螺旋桨在空泡水筒及敞水中的性能进行计算,RANS计算模型如图5和图6所示。对真实螺旋桨在空泡水筒计算结果进行阻塞效应修正,最后与真实螺旋桨的敞水计算结果进行比较和分析。
根据式(2)对真实螺旋桨在空泡水筒中的进流速度进行修正,如下:
| $V' = V\left( {1 - w} \right){\text{,}}$ | (3) |
从而得到修正后的螺旋桨进速系数
| $J' = \frac{{V'}}{{nD}}{\text{。}}$ | (4) |
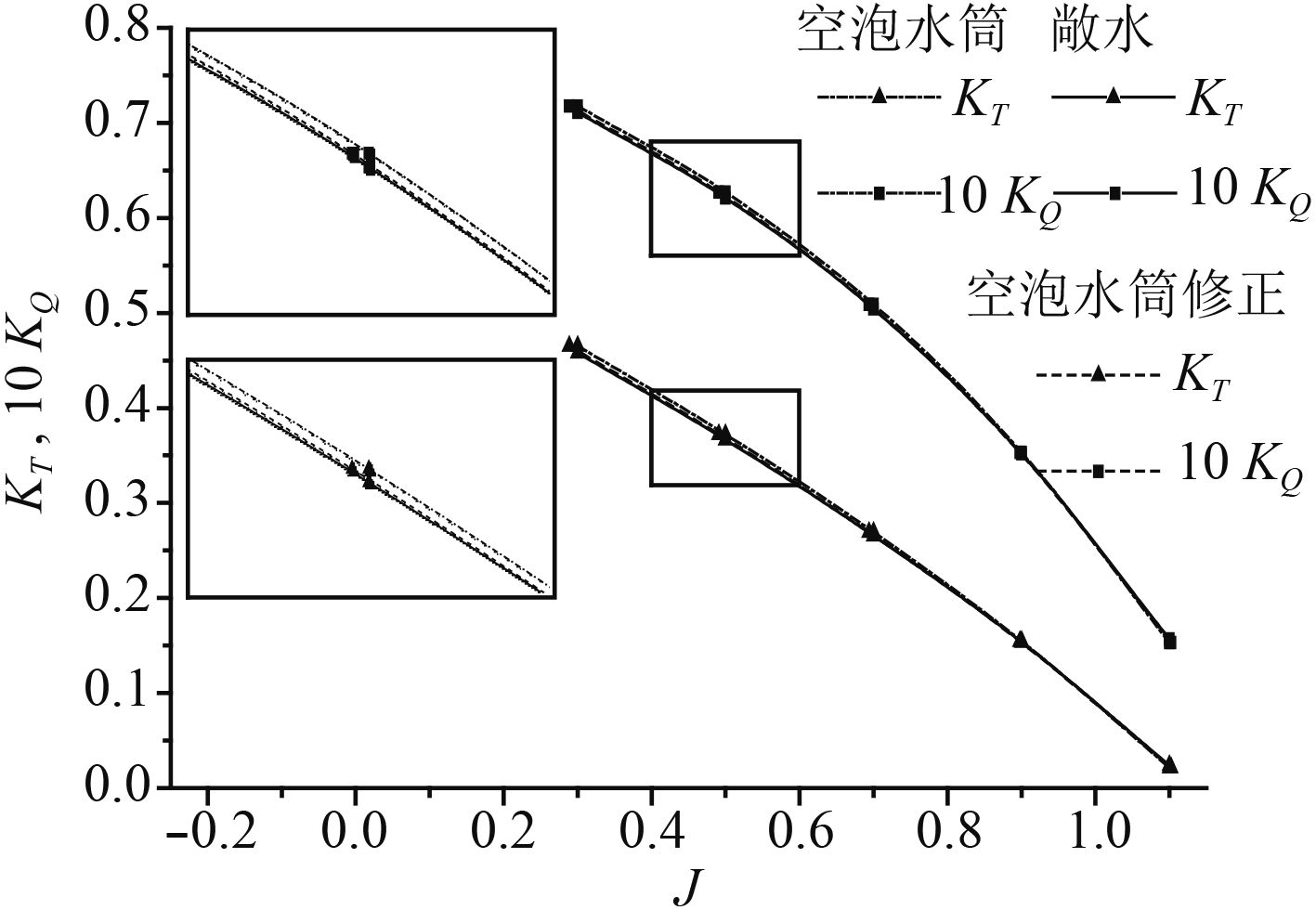
采用上述方法对真实螺旋桨在空泡水筒中的性能计算结果进行修正。图12为空泡水筒中修正前和修正后的螺旋桨性能曲线及其敞水性能曲线的比较。
|
图 12 空泡水筒中修正前和修正后的螺旋桨性能曲线及其敞水性能曲线 Fig. 12 Propeller performance curves before and after correction in cavitation tunnel and open water performance curves |
从图12中可以看出,由于阻塞效应的影响,空泡水筒中计算的水动力系数
本文采用面元法和RANS耦合的方法预报了空泡水筒中螺旋桨盘面的实效伴流场。其中,螺旋桨的水动力性能采用面元法计算,空泡水筒中的流场采用RANS方法模拟,螺旋桨在空泡水筒中的作用采用体积力模型来模拟。预报实效伴流场后,通过实效伴流分数修正进速,继而修正敞水曲线,从而实现空泡水筒中计算结果的阻塞效应修正。
结果表明,螺旋桨在空泡水筒中的推力和扭矩经过修正后和敞水计算得到的曲线吻合良好。本文的研究为空泡水筒试验结果的阻塞效应修正提供了一种新的方法,有望应用于空泡水筒的试验结果修正,提高试验结果的精度,但文中给出的修正公式是否具有一般性仍有待考察。
| [1] |
HERRIOT J G. Blockage corrections for three-dimensional-flow closed-throat wind tunnels, with consideration of the effect of compressibility[R]. Ames Aeronautical Laboratory Moffett Field, Calif, 1947.
|
| [2] |
HACKETT J E, WILSDEN D J, LILLEY D E. Estimation of tunnel blockage from wall pressure signatures: a review and data correlation[R]. NASA CR 15224, 1979.
|
| [3] |
ROSS I, ALTMAN A. Wind tunnel blockage corrections: review and application to savonius vertical-axis wind turbines[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2011, 99(5): 523-538. DOI:10.1016/j.jweia.2011.02.002 |
| [4] |
CHEN T Y, LIOU L R. Blockage corrections in wind tunnel tests of small horizontal-axis wind turbines[J]. Experimental Thermal and Fluid Science, 2011, 35(3): 565-569. DOI:10.1016/j.expthermflusci.2010.12.005 |
| [5] |
庞加斌, 刘晓晖. 汽车风洞试验中的雷诺数、阻塞和边界层效应问题综述[J]. 汽车工程, 2009, 07: 609-615. DOI:10.3321/j.issn:1000-680X.2009.07.007 |
| [6] |
王磊, 梁枢果. 阻塞效应对高层建筑风洞试验的影响分析[J]. 实验力学, 2013, 02: 261-268. DOI:10.7520/1001-4888-12-039 |
| [7] |
黄剑, 顾明. 群体高层建筑模型风洞试验阻塞效应的修正[J]. 同济大学学报: 自然科学版, 2017, 45(1): 31-38. |
| [8] |
谢克振, 周占群. 水池阻塞效应的试验探讨[J]. 上海船舶运输科学研究所学报, 1978(2): 1-27. XIE Ke-zhen, ZHOUZhan-qun. Experimental study on blocking effect of water pool[J]. Journal of Shanghai Ship and Shipping Research Institute, 1978(2): 1-27. |
| [9] |
赵大刚, 郭春雨, 阚梓. 拖曳水池阻塞效应对不同船型影响数值研究[J]. 大连理工大学学报, 2016, 56(6): 575-583. ZHAO Da-gang, GUO Chun-yu, KAN Zi. Numerical study of influence of blockage effect of towing tank on different ship types[J]. Journal of Dalian University of Technology, 2016, 56(6): 575-583. |
| [10] |
BAHAJ A S, MOLLAND A F, CHAPLIN J R, et al. Power and thrust measurements of marine current turbines under various hydrodynamic flow conditions in a cavitation tunnel and a towing tank[J]. Renewable energy, 2007, 32(3): 407-426. DOI:10.1016/j.renene.2006.01.012 |
| [11] |
黄国燕, 李良伟, 赵耀, 等. 基于CFD方法的螺旋桨试验水筒的筒壁影响[J]. 舰船科学技术, 2011, 33(5): 19-23. HUANG Guo-yan, LI Liang-wei, ZHAO Yao, et al. The wall effect of simple propeller water tank by CFD[J]. Ship Science and Technology, 2011, 33(5): 19-23. DOI:10.3404/j.issn.1672-7649.2011.05.005 |
| [12] |
周景军, 李荣融. 通气超空泡水洞试验阻塞效应影响研究[J]. 水动力学研究与进展A辑, 2014, 03: 361-366. ZHOU Jing-jun, LI Rong-rong. Research on the influence of blockage in water tunnel for ventilated supercavitating flow[J]. Chinese Journal of Hydrodynamics, 2014, 03: 361-366. |
| [13] |
谭廷寿. 面元法预报螺旋桨水动力性能[J]. 武汉交通科技大学学报, 1997, 21(5): 534-541. TAN Ting-shou. Prediction ofHydrodynamic performance on propeller by surface panel method[J]. Journal of Wuhan Transportation University, 1997, 21(5): 534-541. |
| [14] |
苏玉民, 黄胜. 用面元法预报船舶螺旋桨的水动力性能[J]. 哈尔滨工程大学学报, 2001, 22(2): 1-5. SU Yun-min, HUANG Sheng. Prediction of hydrodynamic performance of marine propellers by surface panel method[J]. Journal of Harbin Engineering University, 2001, 22(2): 1-5. DOI:10.3969/j.issn.1006-7043.2001.02.001 |
| [15] |
董世汤, 唐登海, 周伟新. CSSRC的螺旋桨定常面元法[J]. 船舶力学, 2005, 9(5): 46-60. DONG Shi-tang, TANG Deng-hai, ZHOU Wen-xin. Panel method of CSSRC for propeller in steady flows[J]. Journal of Ship Mechanics, 2005, 9(5): 46-60. DOI:10.3969/j.issn.1007-7294.2005.05.006 |
| [16] |
MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598-1605. DOI:10.2514/3.12149 |
| [17] |
SÁNCHEZ-CAJA A, PYLKKÄNEN J V. Prediction of effective wake at model and full scale using a RANS code with an actuator disk model[C]//2nd International Conference on Maritime Research and Transportation, Ischia, Italy. 2007: 28–30.
|
| [18] |
STARKE A R, BOSSCHERS J. Analysis of scale effects in ship powering performance using a hybrid RANS-BEM approach[C]//29th Symposium on Naval Hydrodynamics, Gothenburg, Sweden. 2012.
|
| [19] |
TIAN Y, JEON C H, KINNAS S A. On the accurate calculation of effective wake/application to ducted propellers[J]. Journal of Ship Research, 2014, 58(2): 70-82. DOI:10.5957/JOSR.58.2.130048 |
| [20] |
RAO Z, YANG C. Numerical prediction of effective wake field for a submarine based on a hybrid approach and an RBF interpolation[J]. Journal of Hydrodynamics, Ser. B, 2017, 29(4): 691-701. DOI:10.1016/S1001-6058(16)60781-3 |
 2018, Vol. 40
2018, Vol. 40
